Financial Distress Early Warning for Chinese Enterprises from a Systemic Risk Perspective: Based on the Adaptive Weighted XGBoost-Bagging Model

Abstract

This paper aims to tackle the problem of low accuracy in predicting financial distress in Chinese industrial enterprises, attributable to data imbalance and insufficient information. It utilizes annual data on systemic risk indicators and financial metrics of Chinese industrial enterprises listed on the China’s A-share market between 2008 and 2022 to construct the adaptive weighted XGBoost-Bagging model for corporate financial distress prediction. Empirical findings demonstrate that systemic risk indicators possess predictive potential independent of traditional financial information, rendering them valuable non-financial early warning indicators for China’s industrial sector; moreover, they help to enhance the predictive accuracy of various comparative models. The adaptive weighted XGBoost-Bagging model incorporating systemic risk indicators effectively addresses challenges arising from data imbalance and information scarcity, significantly improving the accuracy of financial distress prediction in Chinese industrial enterprises under the 2015 Chinese stock market crash, the Sino-US trade friction, and the COVID-19 epidemic; as such, it can be used as an efficient risk early warning tool for China’s industrial sector.

1. Introduction

The implementation of a financial security strategy was made a high priority in China’s 14th Five-Year Plan, which includes the aim to “improve financial risk prevention, early warning, handling, and accountability systems”. Frequent black swan incidents have accentuated the shocks of systemic risk on global production activities and enterprise financial stability. Thus, using systemic risk indicators to improve predictions of financial distress is of academic and practical value. Against this backdrop, it is of great practical significance to optimize the prediction model of financial distress in Chinese enterprises by combining systemic risk indicators with cutting-edge machine learning algorithms, so as to effectively warn enterprises of financial risks. This will not only help investors adjust investment strategies and assist enterprises in accurately identifying potential risks but also help regulatory agencies improve the risk monitoring and early warning mechanism in key areas, identify weak links vulnerable to systemic risk, and provide a certain reference for China to effectively improve the financial risk disposal mechanism.

China’s A-share market, as one of the largest emerging capital markets in the world, exhibits unique characteristics. Government intervention is significant, with policy changes exerting a significant influence on the market. Retail investors constitute a high proportion, leading to more emotional and volatile behaviors. Additionally, China’s A-share market faces challenges such as weak regulation, information asymmetry, and high market volatility. With China boasting the world’s only complete set of industrial categories, the development of listed industrial sector enterprises in China’s A-share market reflects the country’s industrialization process and the adjustment of its industrial structure. Other emerging economies can learn from China’s experience by focusing on the development trajectory of industrial sector enterprises, the level of support from capital markets, and government policy guidance to promote the healthy development of domestic industrial enterprises and capital markets. This, in turn, objectively promotes the development and integration of global emerging markets and fosters the healthy growth of the global economy. This underscores the unique value and significance of the development of listed industrial sector enterprises in China’s A-share market, serving as a paradigm for other emerging economy markets.

As of 2022, the listed industrial sector enterprises in China account for $70.29\%$ of the A-share market, significantly driving GDP growth and employment stability. However, the industrial sector has faced mounting systemic risk factors due to a confluence of events, including deleveraging policies, slowing economic growth, the 2015 Chinese stock market crash, the Sino-US trade frictions, and the COVID-19 pandemic [1,2,3]. These challenges have also exacerbated financial risks [4,5,6]. Given the interconnectedness within the market, a widespread financial crisis in key industries could propagate risk contagion through various channels, such as technological linkages, commercial credit channels, information interconnections, and emotional spillovers, affecting other industries and potentially spreading to the entire economic and financial system [7,8,9]. Hence, combining systemic risk indicators with cutting-edge machine learning algorithms to optimize financial distress early warning models in China’s industrial sector proves beneficial. This aids financial institutions and investors in early risk detection and loss mitigation. Furthermore, it assists regulatory bodies in establishing a robust multi-channel default resolution mechanism for preventing and resolving financial risks, thereby improving the credit environment in the capital market.

Financial distress prediction for businesses fundamentally falls within the realm of binary classification problems, primarily based on predictive models to classify enterprises into normal and at-risk categories. As statistical methods have evolved, predictive models for financial distress warning have continuously been updated. Beaver (1966) was the first to propose a univariate statistical model, examining the predictive capabilities of 29 financial ratios for forecasting corporate financial distress within 1 to 5 years before it occurs [10]. In 1968, Altman (1968) introduced a multivariate Z-score model, selecting five independent variables to form the Z-score index. A Z-score below $1.81$ and $2.67$ indicates an enterprise’s proximity to bankruptcy and the potential for bankruptcy, respectively [11]. Subsequently, Ohlson (1980) introduced conditional probability regression models to estimate the probability of corporate bankruptcy, addressing the limitation of Z-scores lacking economic significance [12]. With the iterative advancement of modeling techniques, recent researchers have attempted to incorporate methods such as fuzzy set theory, Bayesian networks, survival analysis, decision trees, support vector machines, and artificial neural networks, as well as combinations of the above-mentioned approaches into corporate financial distress prediction models [13]. These methods have further relaxed the requirements on data distribution, enhancing the accuracy and robustness of predictions.

It is worth noting that the corporate financial distress warning dataset usually exhibits a significant class imbalance, with a much larger number of normal enterprises compared to those at risk. Modeling directly with imbalanced samples would result in a bias towards the majority class, leading to a loss of model warning capability. In the context of imbalanced financial distress warning datasets, current research primarily focuses on improvements at both the data and algorithm levels. Data-level processing involves altering the class distribution in the original dataset to reduce or eliminate the imbalance, followed by constructing new models based on balanced datasets. Specific resampling methods include oversampling [14], undersampling [15], and hybrid sampling [16]. Oversampling involves increasing the number of minority class samples, while undersampling reduces the number of majority class samples. Hybrid sampling combines both strategies. Resampling techniques have gained widespread application due to their simplicity and strong operability but still have notable drawbacks. Oversampling may introduce a significant amount of sample noise or lead to model overfitting due to the generation of duplicate samples. In contrast, undersampling may lead to the loss of important samples. Unlike data-level processing, algorithm-level processing aims to enhance traditional classifiers to better adapt to the specific classification requirements of imbalanced datasets. This approach can generally be categorized into cost-sensitive learning and ensemble learning. Cost-sensitive learning introduces the concept of misclassification cost, assigning higher misclassification costs to minority class samples to enhance their importance, thus addressing the problem of learning bias that traditional models may face when dealing with imbalanced datasets [17]. Ensemble learning refers to the combination of decisions from multiple base classifiers to achieve superior performance compared to a single model. Representative techniques in this category include random forests, adaptive boosting, and gradient boosting trees algorithms [18,19,20].

XGBoost, as a gradient boosting tree (GBDT)-based ensemble learning algorithm, has been increasingly applied in the field of financial distress prediction in recent years. Zieba et al. (2016) [21] proposed a novel method utilizing an XGBoost model to predict bankruptcy events in Polish companies. Xia et al. (2017) [22] introduced a sequence ensemble credit scoring model based on the XGBoost model, employing a Bayesian hyperparameter optimization method, the Tree-structured Parzen Estimator (TPE), to fine-tune the model’s hyperparameters. Huang et al.’s (2019) [23] search indicated that among supervised, unsupervised, and mixed supervised-unsupervised algorithms, the XGBoost algorithm provided the most accurate financial distress predictions. Qian et al. (2022) [24] proposed a heuristic algorithm—permutation importance (PIMP)—and found that the PIMP-XGBoost model outperformed other benchmark methods in most evaluation metrics, serving as an effective tool for corporate decision-makers. To address the performance interpretability challenge, Liu et al. (2022, 2023) [25,26] introduced a cost-sensitive XGBoost model for financial distress prediction. Building upon the XGBoost framework, they incorporated a weighted loss function into the cross-entropy loss function, achieving cost-sensitive financial distress prediction.

In addition to the widespread adoption of computer algorithms and models trained on imbalanced data, innovations in early warning research have also been focused on incorporating non-financial early warning indicators into predictive information sets. Early warning research, in its initial stages, primarily emphasized financial metrics of enterprises [27]. In recent years, various non-financial metrics related to corporate operations, repayment, and other aspects have been introduced into financial distress early warning models in both academic and practical literature [28,29,30]. Recent studies indicate that systemic risk, as a non-financial indicator, may have a significant impact on real economic activities, leading to a deterioration of financial indicators such as liquidity and solvency for enterprises. Consequently, this increases the probability of enterprises facing financial distress [31]. The underlying reasons for this phenomenon are as follows: firstly, when financial markets experience risk shocks, banks often limit the scale of lending [32], which may adversely affect the liquidity and debt-servicing capacity of certain enterprises, thus increasing their risk of facing financial distress. Secondly, the shock from systemic risk can also influence consumer behavior [33], thereby negatively impacting the financial condition of enterprises from the demand side. Chinese enterprises often use equity collateral to secure operating capital, but a decline in stock prices triggered by systemic risk may necessitate additional margin calls [34], leading to liquidity risk and further triggering financial distress. Therefore, the introduction of systemic risk indicators may contribute to optimizing the measurement and prediction of corporate financial risk. Jia et al. (2020), by comprehensively considering enterprise financial metrics, market performance, and systemic risk, applied a Logit model to predict future US corporate bankruptcy events [35]. Their research results indicate that systemic risk indicators significantly enhance the predictive performance of corporate bankruptcy models. Yang et al. (2022) found that systemic risk exhibits significant predictive capabilities regarding financial distress in midstream and downstream Chinese enterprises [36]. They demonstrated excellent performance in predicting financial distress caused by long-term losses by combining systemic risk factors with a random forest model framework.

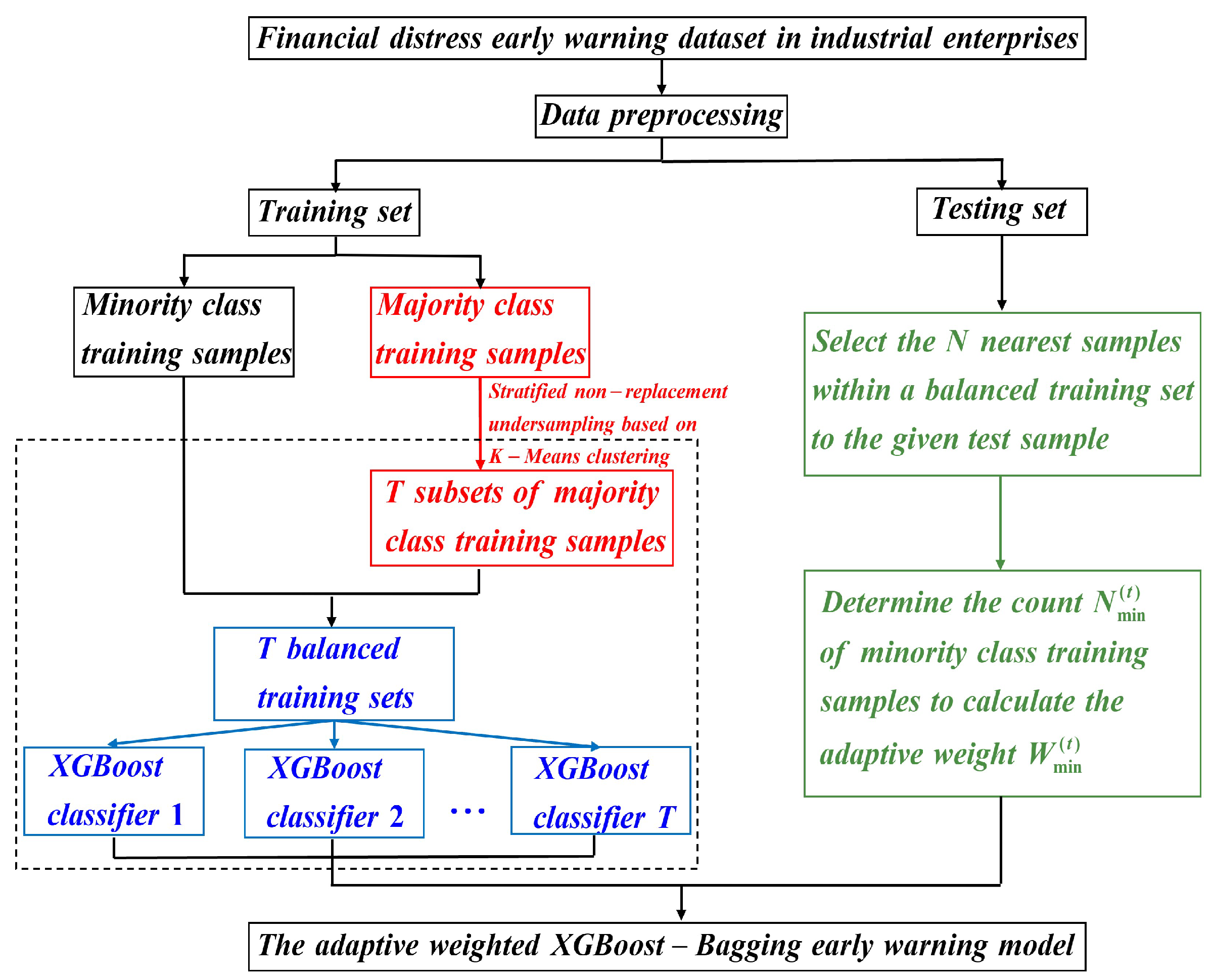
In view of this, this paper attempts to make beneficial supplements based on existing research, combining the reality of the Chinese economy to extend the accounting-systemic risk model proposed by Yang et al. (2022) [36]. Addressing the issue of low recognition rates of financial crises in industrial sector enterprises due to imbalance in early warning data, this paper constructs an early warning model based on the adaptive weighted XGBoost-Bagging algorithm, thoroughly examining the predictive ability of systemic risk indicators for financial distress in Chinese industrial enterprises. Firstly, based on the traditional Logit regression model, this paper analyzes the linear relationship between systemic risk and the probability of financial distress in Chinese industrial enterprises. Subsequently, random forest and gradient boosting algorithms are employed to capture the nonlinear features of the relationship between systemic risk and the probability of financial distress in Chinese industrial enterprises, thereby exploring the potential of systemic risk indicators as non-financial early warning indicators for the industrial sector. Furthermore, drawing on the testing approach of Petropoulos et al. (2020) [37], using the adaptive weighted XGBoost-Bagging model constructed in this paper, out-of-sample testing and out-of-time testing are conducted to compare and optimize the predictive models for financial distress in Chinese industrial enterprises. Through out-of-sample testing and out-of-time testing, compared to the models such as random forest used by Yang et al. (2022) [36], the adaptive weighted XGBoost-Bagging model combined with systemic risk predicts financial distress in Chinese industrial enterprises with higher efficiency. Moreover, when considering the impact of the extreme event of the 2015 Chinese stock market crash on systemic risk in Chinese industrial enterprises, the predictive accuracy of the adaptive weighted XGBoost-Bagging model incorporating systemic risk significantly improves by comparing the predictive accuracy before and after the extreme event. This indicates that the model can better capture the significant impact of systemic risk on financial distress. Additionally, this paper proposes relevant suggestions for improving the regulation of listed companies in China and effectively warning of corporate financial distress.

2. Model Configuration and Methodology Description

2.1. Extreme Gradient Boosting

Extreme Gradient Boosting (XGBoost) is an ensemble learning algorithm based on gradient boosting trees (GBDT), which was proposed by Chen and He (2015) [38]. XGBoost has the characteristics of low computational complexity, high accuracy, and fast execution speed. XGBoost represents a significant improvement over GBDT by incorporating regularization terms in the loss function and by constraining the number of nodes in each tree as well as the scores assigned to leaf nodes. This effectively corresponds to pruning the trees and preventing overfitting.

The objective function of XGBoost is

$${\mathrm{obj}}^{(t)}=\sum _{i=1}^{n}l(y_i,{\widehat{y}}_i^{(t-1)}+f_t({\mathbf{x}}_i))+\mathsf{\Omega }(f_t).$$

(1)

In Equation (1), $x_i$ represents the i-th sample input, ${\widehat{y}}_i^{(t-1)}$ represents the predictions of the preceding $t-1$ decision trees, and $f_t({\mathbf{x}}_i)$ represents the prediction of the current t-th decision tree. $\mathsf{\Omega }(f_t)=\gamma T+\frac{1}{2}\lambda {\parallel \omega \parallel }^2$ serves as a regularization term, utilized to control model complexity and mitigate overfitting. T corresponds to the number of leaf nodes in the t-th tree, and $\omega$ represents the output vector of these leaf nodes.

For optimizing the objective function, GBDT employs gradient descent, whereas XGBoost utilizes a second-order Taylor expansion at $f_t({\mathbf{x}}_i)$:

$${\mathrm{obj}}^{(t)}\simeq \sum _{i=1}^n[l(y_i,{\widehat{y}}^{(t-1)})+g_i{f}_t({\mathbf{x}}_i)+\frac{1}{2}{h}_i{f}_t^2({\mathbf{x}}_i)]+\mathsf{\Omega }(f_t).$$

(2)

In Equation (2), $g_i={\partial }_{{\widehat{y}}^{(t-1)}}l(y_i,{\widehat{y}}^{(t-1)})$, $h_i={\partial }_{{\widehat{y}}^{(t-1)}}^{2}l(y_i,{\widehat{y}}^{(t-1)})$.

When the preceding $t-1$ decision trees have already been determined, the residuals $l(y_i,{\widehat{y}}_i^{(t-1)})$ generated by these $t-1$ decision trees are known and can be considered constant. After eliminating the constant term from Equation (2), it can be represented as follows:

$${\mathrm{obj}}^{(t)}=\sum _{i=1}^n[g_i{f}_t({\mathbf{x}}_i)+\frac{1}{2}{h}_i{f}_t^2({\mathbf{x}}_i)]+\mathsf{\Omega }(f_t).$$

(3)

For a given decision tree structure q, $I_{j=}\left\{i\left|q({\mathbf{x}}_i)=j\right.\right\}$ is defined as the set of samples i all mapped to the j-th leaf node, with the output of this leaf node denoted as ${\omega }_j$. So, Equation (3) can be represented as follows:

$$\begin{array}{cc}\hfill {\mathrm{obj}}^{(t)}& =\sum _{i=1}^n[g_i{f}_t({\mathbf{x}}_i)+\frac{1}{2}{h}_i{f}_t^2({\mathbf{x}}_i)]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{\omega }_j^2\hfill \\ & =\sum _{j=1}^T[\left(\sum _{i\in I_j}{g}_i\right){\omega }_j+\frac{1}{2}(\sum _{i\in I_j}{h}_i+\lambda ){\omega }_j^2]+\gamma T\hfill \end{array}$$

(4)

The minimum value of the objective function ${\mathrm{obj}}^{(t)}$ can be determined using the minimization of a simple univariate quadratic equation, where ${\omega }_i^{*}$ represents the optimal leaf weight at each leaf node, such that ${\omega }_i^{*}=-{\sum }_{i\in I_j}{g}_i/({\sum }_{i\in I_j}{h}_i+\lambda )$. The minimum value of the objective function is as follows:

$${\mathrm{obj}}_{min}^{(t)}=-\frac{1}{2}\sum _{j=1}^T\frac{({\sum }_{i\in I_j}{g}_i{)}^2}{{\sum }_{i\in I_j}{h}_i+\lambda }+\gamma T.$$

(5)

In Equation (5), $g_i$ and $h_i$ vary depending on the specific loss function used. XGBoost supports the customization of loss functions, provided that the chosen loss function is differentiable and its first and second derivatives can be computed.

2.2. Adaptive Weighted XGBoost-Bagging Model

The fundamental principle of Bagging involves the following [39]: It repeatedly selects random samples with replacement from the original dataset to create subsets of samples. Subsequently, individual sub-classifiers are constructed based on these sample subsets. The predictions of these multiple sub-classifiers are then combined using methods such as voting or simple weighted fusion to obtain the final prediction result. Bagging methods exhibit strong generalization capabilities. However, using random sampling with replacement to obtain sample subsets may result in some samples from the original dataset being selected multiple times or not at all. This is especially problematic when dealing with imbalanced financial distress warning data, as it may rarely or never select samples from the minority class, leading to low recognition rates for minority class samples. To address this issue, the study proposes an improved sampling approach for Bagging, which is based on stratified non-replacement undersampling using K-Means clustering. While utilizing all the minority class samples (i.e., risk enterprise samples) from the training dataset, undersampling is employed for the majority class samples (i.e., regural enterprise samples) to achieve a balanced number of samples in both classes. The steps of this approach are as follows:

(a)

Employing the K-Means clustering algorithm to partition the majority class training samples into K clusters and calculating the number of samples $M_m^{(k)}$$(k=1,2,\cdots ,K)$ in each cluster.

(b)

Conducting stratified sampling without replacement for each cluster, with a sample size of $(M_m^{(k)}/\phantom{(M_m^{(k)}{M}_m}{M}_m)\ast M_l$ within each cluster, where $M_m$ represents the total number of training samples in the majority class and $M_l$ represents the total number of training samples in the minority class.

(c)

Combining the sampled samples from each cluster yields a subset of the majority class training samples. These are then merged with the minority class training samples to create a balanced training dataset.

On the basis of this sampling approach for Bagging, as illustrated in Figure 1, the study constructs the adaptive weighted XGBoost-Bagging model. Initially, the stratified non-replacement undersampling method based on K-Means clustering is employed T times on the majority class training samples, yielding T subsets of majority class training samples and consequently resulting in T balanced training datasets. Following that, train T XGBoost classifiers using the balanced training datasets. Within each XGBoost classifier, the count of minority class training samples among the N nearest training samples to a given test sample is denoted as $N_l^{(t)}$$(t=1,2,\cdots ,T)$, the probability of predicting the given test sample as a majority class sample is denoted as $p_m^{(t)}$, and the probability of predicting the given test sample as a minority class sample is denoted as $p_l^{(t)}$. In the study, the adaptive weight for $p_l^{(t)}$ is set to $W_l^{(t)}=(N_l^{(t)}/\phantom{N_l^{(t)}N}N)+1$. Finally, by employing the weighted soft voting method to ensemble the results of all XGBoost classifiers, the final classification result is obtained as follows:

$$\widehat{y}=I\left\{\left(\sum _{t=1}^T\left(p_l^{(t)}\ast W_l^{(t)}-p_m^{(t)}\right)\right)\ge 0\right\}.$$

(6)

In the aforementioned process, the number of clusters K for K-Means clustering, the number of XGBoost classifiers T, and the number of nearest training samples N to a given test sample are all undetermined hyperparameters. These hyperparameters can be optimized using the Non-Dominated Sorting Genetic Algorithm II (NSGA-II). NSGA-II is a multi-objective optimization algorithm designed to achieve Pareto optimality for multi-objective problems while striving to satisfy all constraints to the greatest extent possible [40]. Specifically, with the objective of maximizing the performance evaluation metrics of the model, the NSGA-II algorithm is employed to discover the optimal hyperparameter combination $(K,T,N)$.

2.3. Model Evaluation Metrics

Existing classification methods typically use overall accuracy as a metric to assess model performance. However, in imbalanced datasets, where the number of samples in the minority class is significantly lower than that in the majority class, even achieving high overall accuracy does not accurately reflect the recognition rate of the minority class samples. Therefore, to better evaluate the classification performance of models in imbalanced scenarios, metrics such as AUC, Recall, $F_{\beta }$, and G-means are utilized based on the confusion matrix shown in

Table 1. Confusion matrix.

	Predicted Value = 1	Predicted Value = 0
True Value = 1	$TP$	$FN$
True Value = 0	$FP$	$TN$

.

AUC refers to the area under the ROC curve. If the AUC value of a classification model exceeds $0.80$, it can be considered as having relatively good classification performance [41].

$F_{\beta }$ is determined jointly by Recall and Precision, but a trade-off relationship exists between these two metrics. When modeling for imbalanced data, the study primarily focuses on the recognition rate of the minority class samples, giving more weight to Recall. Therefore, the $\beta$ value is set to 3. The expression for $F_{\beta }$ is as follows:

$$F_{\beta }=\frac{(1+{\beta }^2)\ast Precision\ast Recall}{{\beta }^2\ast Precision+Recall}.$$

(7)

In Equation (7), $Recall=TP/\phantom{=TP(TP+FN)}(TP+FN),$ $Precision=TP/\phantom{=TP(TP+FP)}(TP+FP).$

G-means balances the magnitude of Sensitivity and Specificity, serving as a comprehensive metric that combines both. The expression for G-Means is as follows:

$$G-means=\sqrt{Sensitivity\ast Specificity}.$$

(8)

In Equation (8), $Sensitivity=TP/\phantom{TP(TP+FN)}(TP+FN)$, $Specificity=TN/\phantom{TN(TN+FP)}(TN+FP)$.

3. Empirical Results and Analysis

3.1. Data Source and Sample Description

This study focuses on Chinese industrial enterprises listed on the A-share market in China between 2008 and 2022 and regards special treatment (ST or ∗ST) designation as a signal of corporate financial distress. According to regulations in the Chinese A-share market, ST stocks refer to those of enterprises that have incurred losses for two consecutive years and are subjected to special treatment, while ∗ST stocks refer to enterprises with losses for three consecutive years, warranting a delisting warning. Such enterprises often exhibit abnormal financial conditions or have already entered a distress, facing difficulties in capital turnover and an inability to meet debt obligations. Therefore, in this study, enterprises labeled as ST or ∗ST are considered to be those facing financial distress. In 2007, the Ministry of Finance of China implemented new accounting standards for business enterprises, leading to more standardized and comprehensive financial data disclosure by listed companies. Considering that it takes some time for these regulations to be effectively enforced, the research commences from the year 2008. Furthermore, in accordance with GB/T 4754-2017 Industrial Classification for National Economic Activities and China Industry Statistical Yearbook 2022, China’s industrial sector encompasses mining; manufacturing; and electricity, heat, gas, and water production and supply, identified by industry codes ranging from B06 to D46. Hence, the selection of A-share listed companies is based on these industry codes. The resulting sample comprises 509 ST enterprises and 5090 non-ST enterprises. Notably, this sample set represents an imbalanced dataset, with ST enterprises being the minority class and non-ST enterprises as the majority class.

Drawing from the methodology outlined in Tinoco et al. (2018) [42], the study aims to forecast whether a given enterprise will undergo special treatment (ST or ∗ST) in year t based on annual data for systemic risk indicators and financial metrics from the enterprise’s $t-2$ year. To achieve this, we have selected samples of enterprises spanning 2010 to 2022, and matched their systemic risks and financial data from 2008 to 2020, resulting in the final dataset. It is important to note that all variables in the sample undergo winsorization at the 1st and 99th percentiles to address potential outliers.

In terms of systemic risk indicators, a total of 6 initial indicators have been selected, each denoted as follows: Value at Risk (VaR) as $X_1$, Conditional Value at Risk (CoVaR) as $X_2$, Change in Conditional Value at Risk (ΔCoVaR) as $X_3$, Expected Shortfall (ES) as $X_4$, Marginal Expected Shortfall (MES) as $X_5$, and Beta coefficient as $X_6$. It is important to note that VaR, CoVaR, ΔCoVaR, ES, and MES are all annual computed values at the 5th percentile. Taking inspiration from the practices outlined in Qian et al. (2022) [24] and Liu et al. (2022) [25] in the context of financial metrics and considering data availability, we have selected a total of 31 initial metrics from the domains of solvency, operational efficiency, profitability, growth capacity, and risk level, as detailed in

Table 2. Initial financial metrics.

Primary Indicators	Secondary Indicators
Solvency	Current Ratio ($X_7$)
	Quick Ratio ($X_8$)
	Cash Ratio ($X_9$)
	Operating Working Capital to De bt Ratio ($X_{10}$)
	Cash Flow Interest Coverage Ratio ($X_{11}$)
	Debt Asset Ratio ($X_{12}$)
	Long-Term Debt to Total Assets Ratio ($X_{13}$)
	Equity Multiplier ($X_{14}$)
	Long-Term Debt to Working Capital Ratio ($X_{15}$)
Operational Efficiency	Accounts Receivable Turnover ($X_{16}$)
	Inventory Turnover ($X_{17}$)
	Accounts Payable Turnover ($X_{18}$)
	Current Assets Turnover ($X_{19}$)
	Non-Current Assets Turnover ($X_{20}$)
	Total Assets Turnover ($X_{21}$)
Profitability	Return on Assets ($X_{22}$)
	Net Profit Margin on Current Assets ($X_{23}$)
	Net Profit Margin on Fixed Assets ($X_{24}$)
	Return on Equity ($X_{25}$)
	Return on Invested Capital ($X_{26}$)
	Gross Profit Margin ($X_{27}$)
	Operating Profit Margin ($X_{28}$)
Growth Capability	Fixed Assets Growth Rate ($X_{29}$)
	Revenue Growth Rate ($X_{30}$)
	Sustainable Growth Rate ($X_{31}$)
	Earnings per Share Growth Rate ($X_{32}$)
	Return on Equity Growth Rate ($X_{33}$)
	Net Profit Growth Rate ($X_{34}$)
	Total Assets Growth Rate ($X_{35}$)
Risk Level	Financial Leverage ($X_{36}$)
	Operating Leverage ($X_{37}$)

Note: The data above are sourced from the CSMAR database and the Wind database.

.

3.2. Dual Significance Tests for Initial Indicators

This study categorizes financially distressed ST enterprises as “1” and healthy non-ST enterprises as “0” to obtain two sets of samples. Subsequently, in order to assess the effectiveness of the initial indicators in distinguishing between ST and non-ST enterprises, dual significance tests are conducted on the two sample groups, namely, the two-sample Kolmogorov–Smirnov (K-S) test and Mann–Whitney U (MW-U) test. The two-sample K-S test aims to determine whether there is a significant difference in the distributions between the two groups, while the MW-U test examines whether there is a significant difference in the means of the two groups. The results of the dual significance tests for the initial indicators are presented in

Table 3. The K-S test results.

Indicator	Sig.	Indicator	Sig.	Indicator	Sig.	Indicator	Sig.
$X_1$	0.0000	$X_{11}$	0.0000	$X_{21}$	0.0000	$X_{31}$	0.0000
$X_2$	0.0000	$X_{12}$	0.0000	$X_{22}$	0.0000	$X_{32}$	0.0000
$X_3$	0.0000	$X_{13}$	0.0000	$X_{23}$	0.0000	$X_{33}$	0.0000
$X_4$	0.0000	$X_{14}$	0.0000	$X_{24}$	0.0000	$X_{34}$	0.0000
$X_5$	0.0000	$X_{15}$	0.0000	$X_{25}$	0.0000	$X_{35}$	0.0000
$X_6$	0.0000	$X_{16}$	0.0000	$X_{26}$	0.0000	$X_{36}$	0.0000
$X_7$	0.0000	$X_{17}$	0.0000	$X_{27}$	0.0000	$X_{37}$	0.0000
$X_8$	0.0000	$X_{18}$	0.0000	$X_{28}$	0.0000
$X_9$	0.0000	$X_{19}$	0.0000	$X_{29}$	0.0000
$X_{10}$	0.0000	$X_{20}$	0.0000	$X_{30}$	0.0000

Note: The significance level is set at $5\%$.

and

Table 4. The MW-U test results.

Indicator	Sig.	Indicator	Sig.	Indicator	Sig.	Indicator	Sig.
$X_1$	0.0000	$X_{11}$	0.0051	$X_{21}$	0.0000	$X_{31}$	0.0000
$X_2$	0.0000	$X_{12}$	0.0000	$X_{22}$	0.0000	$X_{32}$	0.0000
$X_3$	0.0000	$X_{13}$	0.0268	$X_{23}$	0.0000	$X_{33}$	0.0000
$X_4$	0.0000	$X_{14}$	0.0000	$X_{24}$	0.0000	$X_{34}$	0.0482
$X_5$	0.0000	$X_{15}$	0.0000	$X_{25}$	0.0000	$X_{35}$	0.0000
$X_6$	0.0000	$X_{16}$	0.0000	$X_{26}$	0.0000	$X_{36}$	0.0000
$X_7$	0.0000	$X_{17}$	0.0289	$X_{27}$	0.0000	$X_{37}$	0.0000
$X_8$	0.0000	$X_{18}$	0.0046	$X_{28}$	0.0000
$X_9$	0.0000	$X_{19}$	0.0000	$X_{29}$	0.0000
$X_{10}$	0.0000	$X_{20}$	0.0000	$X_{30}$	0.0000

Note: The significance level is set at $5\%$.

.

To ensure the rigor of the indicator selection, an indicator is only eliminated when it shows non-significance in both the K-S test and the MW-U test. According to the results of the dual significance tests, all indicators exhibit p-values less than $5\%$; thus, all indicators are retained.

3.3. Principal Components Extraction and Its Importance Analysis

Given to the advantages of composite indicators in terms of predictive power and robustness, the study draws from the methodology outlined in Nucera (2016) [43] by employing principal component analysis (PCA) to extract pertinent information from systemic risk indicators and financial metrics, respectively. Utilizing an $80\%$ cumulative variance contribution rate as the extraction criterion, we conduct PCA for dimensionality reduction on the entire dataset. For systemic risk indicators, the Kaiser–Meyer–Olkin (KMO) statistic yields a value of $0.6822$, and the Bartlett sphericity test indicates a significance level of 0. Consequently, two principal components, denoted as SystemicRisk1 and SystemicRisk2, are selected, collectively contributing to a cumulative variance of $90.84\%$. For financial metrics, the KMO statistic yields a value of $0.7830$, and the Bartlett sphericity test indicates a significance level of 0. A total of ten principal components are chosen: Accounting1, Accounting2, through Accounting10, collectively contributing to a cumulative variance of $80.30\%$.

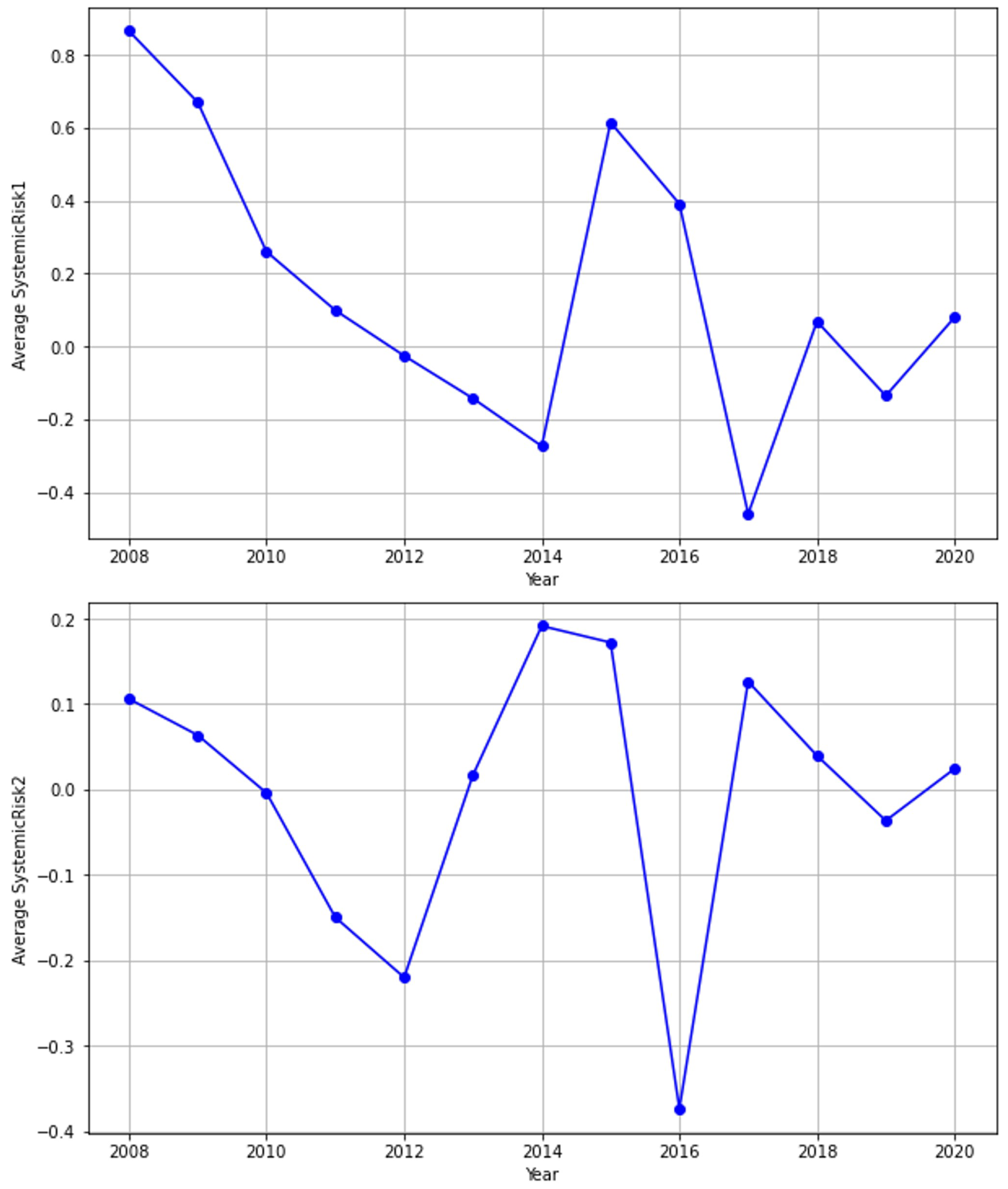
Figure 2 shows the annual averages of SystemicRisk1 and SystemicRisk2 for all industrial enterprises. In the past decade, the annual averages of SystemicRisk1 and SystemicRisk2 in 2015, 2018, and 2020 are all positive, indicating that the systemic risks in the industrial sector are relatively high in these years. This result confirms the conclusion of Yang (2020) [44].

Subsequently, the Logit model is employed to assess the predictive capacity of systemic risk on corporate financial distress. Both columns (1) and (2) in

Table 5. Logit regression analysis of systemic risk on corporate financial distress.

	(1)	(2)	(3)	(4)
SystemicRisk1	1.0389 ***	0.4686 ***	1.1109 ***	0.6638 ***
	(0.094)	(0.116)	(0.110)	(0.142)
SystemicRisk2	2.0867 ***	2.6829 ***	2.4802 ***	3.1322 ***
	(0.182)	(0.215)	(0.221)	(0.260)
Accounting1			−1.8806 ***	−1.9032 ***
			(0.105)	(0.110)
Accounting2			0.7979 ***	0.6858 ***
			(0.110)	(0.115)
Accounting3			−0.3917 ***	−0.4766 ***
			(0.138)	(0.144)
Accounting4			−0.7542 ***	−0.7148 ***
			(0.181)	(0.189)
Accounting5			−0.6884 ***	−0.6471 ***
			(0.174)	(0.183)
Accounting6			0.4484 **	0.4027 **
			(0.189)	(0.198)
Accounting7			1.9306 ***	2.0697 ***
			(0.223)	(0.232)
Accounting8			0.0386	−0.0812
			(0.238)	(0.252)
Accounting9			4.3982 ***	4.4981 ***
			(0.297)	(0.308)
Accounting10			0.5449 **	0.6507 ***
			(0.241)	(0.253)
Year Effect	N	Y	N	Y

Note: ***, ** represent significance at the $1\%$ and $5\%$ levels, respectively, with the coefficient standard errors shown in parentheses.

illustrate that, in the absence of control variables, the coefficients for SystemicRisk1 and SystemicRisk2 are significantly positive at the $1\%$ level. This suggests that systemic risk indicators demonstrate predictive potential independently of financial information, functioning as effective non-financial early warning indicators. Columns (3) and (4) of Table 5 demonstrate that, even after incorporating control variables, the coefficients for SystemicRisk1 and SystemicRisk2 remain significantly positive at the $1\%$ level. Consequently, it can be deduced that systemic risk indicators exhibit substantial predictive capability for corporate financial distress in China’s industrial sector, signifying that the influence of systemic risk enhances the likelihood of a firm encountering financial distress.

The results of the Logit regression analysis can only identify a linear association between systemic risk indicators and the probability of a corporate financial distress. In order to explore the non-linear relationships between systemic risk indicators, financial metrics, and the occurrence of corporate financial distress, the study employs Random Forest and Gradient Boosting models to calculate the relative importance of the principal components of systemic risks and financial data. This assessment aims to evaluate their explanatory capacity in predicting corporate financial distress.

Table 6. Relative importance analysis of predictive variables for corporate financial distress.

Principal Component	Based on the Random Forest Model		Based on the Gradient Boosting Model
	Relative	Relative Importance	Relative	Relative Importance
	Importance	Ranking	Importance	Ranking
SystemicRisk1	$9.49\%$	3	$9.10\%$	3
SystemicRisk2	$6.41\%$	5	$6.42\%$	5
Accounting1	$26.24\%$	1	$39.30\%$	1
Accounting2	$12.85\%$	2	$16.67\%$	2
Accounting3	$6.30\%$	6	$5.92\%$	6
Accounting4	$4.51\%$	12	$1.81\%$	12
Accounting5	$5.90\%$	7	$4.11\%$	7
Accounting6	$5.23\%$	9	$2.24\%$	9
Accounting7	$4.81\%$	10	$2.07\%$	10
Accounting8	$4.75\%$	11	$2.02\%$	11
Accounting9	$7.92\%$	4	$7.69\%$	4
Accounting10	$5.61\%$	8	$2.63\%$	8

reveals that in both the Random Forest and Gradient Boosting models, SystemicRisk1, the primary component of systemic risk indicators, demonstrates relative importance values of $9.49\%$ (ranking third) and $9.10\%$ (ranking third), respectively. Likewise, SystemicRisk2, the secondary component of systemic risk indicators, demonstrates relative importance values of $6.41\%$ (ranking fifth) and $6.42\%$ (ranking fifth), respectively. This suggests that systemic risk indicators possess predictive capabilities independently of financial information, and they can serve as effective non-financial early warning indicators for China’s industrial sector.

3.4. Performance Analysis of Models Incorporating Systemic Risk Indicators

To assess the predictive performance before and after the introduction of systemic risk indicators, a random $20\%$ of the samples are selected as the testing dataset, while the remaining $80\%$ are utilized as the training dataset to construct the adaptive weighted XGBoost-Bagging model, hereafter referred to as XGBoost-Bagging. Within the framework of XGBoost-Bagging, the number of clusters K in K-Means, the quantity of XGBoost classifiers T, and the number of nearest training samples to a given test sample N are all considered as undetermined hyperparameters. Through the employment of the NSGA-II algorithm, the optimal hyperparameter combination is determined as follows: $K=7,T=5,N=2$.

To thoroughly validate the predictive performance, a comparative analysis is conducted among five models: Random Forest, a model employing the Bagging technique; XGBoost, a model employing the Boosting technique; XGBoost-SMOTE, which integrates the SMOTE method for oversampling; XGBoost-KMeans, which integrates K-Means clustering for undersampling; and XGBoost-Bagging. In order to mitigate the potential bias introduced by random partitioning of the training and testing datasets, a five-fold cross-validation approach is employed.

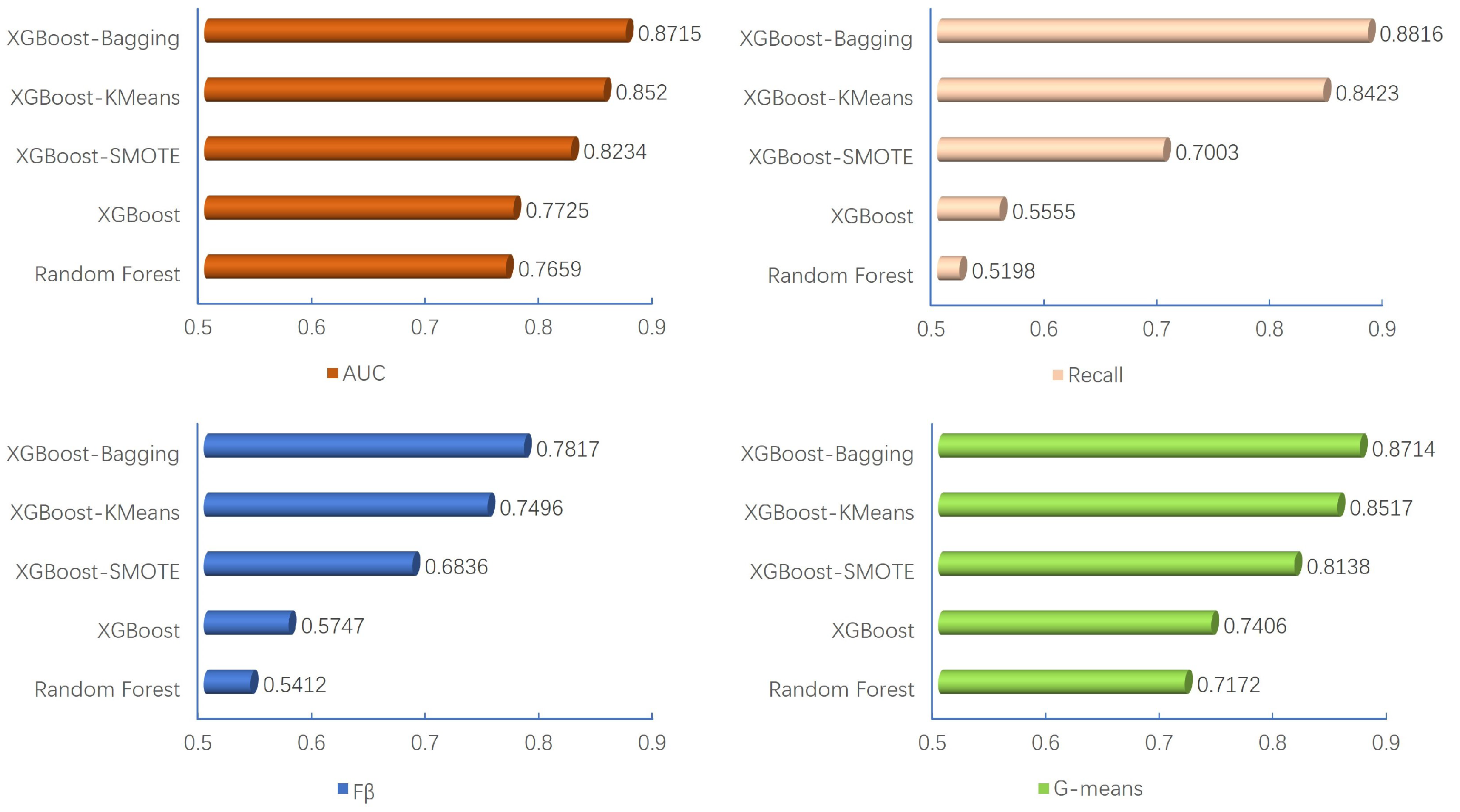
As indicated in

Table 7. Model prediction results with the inclusion of systemic risk indicators.

	Random	XGBoost	XGBoost-	XGBoost-	XGBoost-
	Forest		SMOTE	KMeans	Bagging
AUC	0.7659	0.7725	0.8234	0.8520	0.8715
	(0.0274)	(0.0259)	(0.0203)	(0.0158)	(0.0084)
Recall	0.5198	0.5555	0.7003	0.8423	0.8816
	(0.0534)	(0.0522)	(0.0385)	(0.0349)	(0.0113)
$F_{\beta }$	0.5412	0.5747	0.6836	0.7496	0.7817
	(0.0535)	(0.0507)	(0.0363)	(0.0298)	(0.0201)
G-Means	0.7172	0.7406	0.8138	0.8517	0.8714
	(0.0374)	(0.0347)	(0.0231)	(0.0158)	(0.0084)
ΔAUC	0.0268	0.0290	0.0239	0.0288	0.0346
ΔRecall	0.0325	0.0555	0.0452	0.0400	0.0456
$\mathsf{\Delta }{F}_{\beta }$	0.0327	0.0555	0.0428	0.0446	0.0526
$\mathsf{\Delta }G$-Means	0.0232	0.0384	0.0281	0.0292	0.0346

Note: (1) ΔAUC, ΔRecall, $\mathsf{\Delta }{F}_{\beta }$, and $\mathsf{\Delta }G$-means represent the increments in AUC, Recall, $F_{\beta }$, and G-Means, respectively, when comparing models with and without the inclusion of systemic risk indicators. (2) Values in parentheses indicate the standard deviation of the evaluation metrics.

, upon the inclusion of systemic risk indicators, each model demonstrates notable improvements in evaluation metrics. Specifically, AUC and G-Means exhibit an increment of approximately $2\%$ to $4\%$, while Recall and $F_{\beta }$ score experience enhancements of approximately $3\%$ to $6\%$. These findings underscore the significant enhancement in the predictive accuracy of the early warning models when systemic risk indicators are included.

Furthermore, as illustrated in Figure 3, from any evaluation criterion, with the inclusion of systemic risk indicators, the hierarchy of the model’s predictive performance excellence is consistently as follows: XGBoost-Bagging > XGBoost-KMeans > XGBoost-SMOTE > XGBoost > Random Forest. In the context of Recall, when compared to the Random Forest and XGBoost models without incorporating sampling methods, XGBoost-Bagging demonstrates an increase in predictive accuracy of $36.18\%$ and $32.61\%$ for ST enterprises, respectively. This highlights the necessity of addressing class imbalance when dealing with imbalanced sample classification problems. When compared to the XGBoost-SMOTE model, which integrates oversampling methods, XGBoost-Bagging exhibits a $18.13\%$ enhancement in predictive accuracy for ST enterprises. This improvement can be attributed to the potential introduction of noisy information when synthesizing a large number of ST enterprise samples through oversampling, which can adversely affect the classification performance of XGBoost-SMOTE. Additionally, when compared to the XGBoost-KMeans model, which combines undersampling methods, XGBoost-Bagging yields a $3.93\%$ increase in predictive accuracy for ST enterprises. This indicates that enhancing model diversity while undersampling can indeed improve the predictive performance for minority class samples to some extent.

The events of the 2015 Chinese stock market crash, the 2018 Sino-US trade friction, and the 2020 COVID-19 pandemic led to a substantial increase in systemic risks in China’s industrial sector. Subsequent to these critical time points, financial distress in industrial enterprises became more prevalent. Consequently, drawing inspiration from the testing approach proposed by Petropoulos (2020) [37], we conduct out-of-sample tests based on these time points to analyze the predictive efficacy of XGBoost-Bagging for financial distress events in industrial enterprises two years later (i.e., in 2017, 2020, and 2022), with the financial distress events in 2016 serving as a reference. Specifically, for 2016, we use samples preceding that year as the training set and samples from 2016 as the testing set to construct the XGBoost-Bagging model. Similar procedures were applied for 2017, 2020, and 2022. To ensure robust results, we repeat the process of constructing and predicting with XGBoost-Bagging 100 times and then compute the mean of accurate predictions and the mean of Recall for ST enterprises within these respective years. The results are presented in

Table 8. Performance analysis of out-of-time tests for the adaptive weighted XGBoost-Bagging model.

	XGBoost-Bagging	XGBoost-Bagging	$\mathsf{\Delta }$
	with Systemic Risk	without Systemic Risk
The actual number of ST enterprises in 2016	21	21	0
Mean of accurate predictions for ST enterprises in 2016	18.8	18.5	0.3
Mean of Recall in 2016	0.8976	0.8814	0.0162
The actual number of ST enterprises in 2017	25	25	0
Mean of accurate predictions for ST enterprises in 2017	24.9	23.1	1.8
Mean of Recall in 2017	0.9972	0.9256	0.0716
The actual number of ST enterprises in 2020	75	75	0
Mean of accurate predictions for ST enterprises in 2020	56.2	52.9	3.3
Mean of Recall in 2020	0.7497	0.7057	0.0440
The actual number of ST enterprises in 2022	56	56	0
Mean of accurate predictions for ST enterprises in 2022	52.1	49.7	2.4
Mean of Recall in 2022	0.9306	0.8879	0.0427

.

According to Table 8, in the year 2017, there were a total of 25 ST industrial enterprises. The XGBoost-Bagging, when incorporating systemic risk indicators, can accurately predict an average of 24.9 ST industrial enterprises, resulting in Recall of $99.72\%$. Compared to the XGBoost-Bagging without the inclusion of systemic risk indicators, there is an average reduction of $1.8$ misclassified ST industrial enterprises, leading to a $7.16\%$ increase in Recall. Similarly, with the introduction of systemic risk, the recall rates for XGBoost-Bagging in 2020 and 2022 increased by $4.4\%$ and $4.27\%$, respectively. This outcome clearly established that the inclusion of systemic risk indicators in the framework of the adaptive weighted XGBoost-Bagging model significantly enhances its efficacy in identifying high-risk industrial enterprises.

Furthermore, when comparing the recall rate improvements in 2016 after introducing systemic risk to those in 2017, 2020, and 2022, there is a relatively smaller increase of $1.62\%$. This indicates that as systemic risk intensifies, the efficiency of XGBoost-Bagging, incorporating systemic risk, when predicting financial distress in industrial enterprises two years later, becomes more pronounced.

4. Conclusions and Implications

This paper improved the efficiency of corporate financial distress prediction in China’s industrial sector by using systemic risk indicators and the adaptive weighted XGBoost-Bagging model. The research findings are as follows:

i.

The results from Logit regression models, both with and without time-fixed effects, reveal that systemic risk indicators exhibit significant predictive power for corporate financial distress in China. In the relative importance analysis based on the Random Forest and Gradient Boosting models, the relative importance of SystemicRisk1 is found to be $9.49\%$ and $9.10\%$, respectively, while SystemicRisk2’s relative importance is $6.41\%$ and $6.42\%$, respectively. This underscores the independent predictive capability of systemic risk indicators, separate from financial information, rendering them valuable non-financial warning indicators for China’s industrial sector.

ii.

Upon introducing systemic risk indicators, the predictive accuracies of the adaptive weighted XGBoost-Bagging model and four comparative models all display improvements, with the adaptive weighted XGBoost-Bagging model consistently outperforming its peers across all evaluation metrics. These results demonstrate that the adaptive weighted XGBoost-Bagging model incorporating systemic risk indicators can address issues related to low recognition rates of high-risk Chinese enterprises due to data imbalance and insufficient information.

iii.

This study delves into an analysis of the warning performance of the adaptive weighted XGBoost-Bagging model in the years 2017, 2020, and 2022. In comparison to the model without systemic risk indicators, the model incorporating systemic risk indicators demonstrates a notable increase in Recall of $7.16\%$, $4.40\%$, and $4.27\%$ in 2017, 2020, and 2022, respectively. These findings reiterate the effectiveness of the adaptive weighted XGBoost-Bagging model incorporating systemic risk indicators in predicting corporate financial distress in China’s industrial sector under extreme events such as the 2015 Chinese stock market crash, the Sino-US trade friction, and the COVID-19 epidemic.

The above research conclusions yields some implications as follows:

i.

Considering the significant predictive power of systemic risk indicators for Chinese corporate financial distress, it is recommended that Chinese industrial enterprises bolster their risk management strategies by incorporating these non-financial warning indicators into their existing frameworks. This integration can provide a more comprehensive assessment of potential distress scenarios, enabling proactive measures to mitigate the impact of systemic risk. Chinese enterprises should prioritize the continuous monitoring and evaluation of systemic risk indicators to enhance their resilience in the face of economic uncertainties such as those experienced during the 2015 Chinese stock market crash, the Sino-US trade friction, and the COVID-19 epidemic.

ii.

The superior predictive accuracy of the adaptive weighted XGBoost-Bagging model, particularly when incorporating systemic risk indicators, suggests its potential as an effective tool for addressing issues related to data imbalance and insufficient information. It is recommended that financial institutions and corporate entities consider adopting the adaptive weighted XGBoost-Bagging model as part of their risk assessment toolkit. This model not only improves the recognition rates of high-risk enterprises but also provides a robust framework for incorporating systemic risk indicators into decision-making processes.

iii.

The observed increase in Recall in the adaptive weighted XGBoost-Bagging model with systemic risk indicators highlights their value in predicting Chinese corporate financial distress, especially during periods marked by the frequent occurrence of extreme events. China’s regulatory authorities and industry practitioners are encouraged to integrate systemic risk indicators into their risk assessment protocols. This could involve updating regulatory frameworks to include these indicators and promoting awareness among stakeholders about the importance of considering systemic risk in Chinese corporate financial analysis. Such integrations could contribute to more resilient risk management practices in China’s industrial sector.