Mathematical Modeling Approach to the Optimization of Biomass Storage Park Management

Abstract

This paper addresses the critical issue of managing biomass parks, a key component in the shift towards sustainable energy sources. The research problem centers on optimizing the management of these parks to enhance production and economic viability. Our aim was to bridge the gap in current research by developing and applying mathematical models tailored for biomass park management. The study commenced by constructing a basic model based on assumptions such as uniform biomass and steady input rates. Progressing from this initial model, we explored sophisticated control strategies, including Pontryagin’s maximum principle and dynamic programming, and employed numerical methods to tackle the nonlinearities and complexities inherent in biomass management. Our approach’s scope extended to predicting and managing biomass flow, highlighting each method’s distinct advantages. The simple model laid the groundwork for understanding, while optimal control techniques revealed the system’s intricate dynamics. The numerical methods provided practical solutions to complex equations. We found that while each method is beneficial on its own, their combined use can significantly improve decision-making in biomass park management. This research emphasizes the importance of aligning the chosen method with specific operational challenges and desired outcomes for optimal efficacy, offering both theoretical insights and practical applications in the field of renewable energy management.

1. Introduction

The role of biomass storage parks as complementary sources in the realm of renewable energy production has gained attention in the pursuit of a more sustainable and greener energy mix [1]. Biomass, which is made from organic matter, is one of the more promising options since it offers a practical and environmentally benign alternative to fossil fuels that are quickly running out and harming the environment [2]. Given their potential, it is clear that biomass parks require the best possible management in order to maximize energy production and maintain the long-term financial viability of these endeavors [3].

A deeper understanding of the optimal management of biomass storage parks has been necessitated by the increased reliance on them in the renewable energy sector. The potential for biomass as a sustainable energy source is emphasized in numerous studies. However, comprehensive literature addressing the efficient management of biomass storage parks is found lacking. In this paper, gaps in the current literature will be identified, and methods by which the manuscript intends to address these gaps will be described. Regarding detailed management strategies for biomass parks, general guidelines on biomass management are offered, but a comprehensive strategy accounting for the diverse characteristics and challenges of different biomass types seems absent. A variability in biomass type, composition, and moisture content, each having distinct storage requirements, is observed [4]. A comprehensive set of best practices accounting for this variability, which is essential for maintaining biomass integrity and maximizing energy yield, is not present in the current literature [5,6,7].

Considering economic models for biomass park operations, a gap in models tailored specifically for such operations has been noted [8]. The financial viability of biomass parks has been acknowledged, but the literature is sparse on in-depth models that consider both operational costs and potential energy production revenues [9]. The absence of such detailed financial assessments could potentially deter the long-term sustainability and growth of these parks [10]. While potential energy production from biomass is a primary focus of the current literature, insights into optimal infrastructure and techniques for biomass storage remain limited [11]. The importance of storage conditions, which can influence the quality of biomass and its subsequent energy yield, is evident [12]. However, detailed studies and guidelines on these storage solutions have yet to be extensively explored.

Regarding the impact of external factors on biomass storage, the adverse effects of elements such as climatic conditions, pests, and microbial activities on stored biomass quality are acknowledged [13]. However, systematic studies evaluating the extent of these impacts in diverse geographical and climatic settings are not extensively found in the literature [14]. Although the importance of technology in improving the efficiency of biomass storage parks is recognized, literature critically evaluating the recent technological advancements and their benefits in biomass storage management appears limited [15].

While the significance of biomass as a renewable energy source is understood, its optimal integration with other energy sources, such as solar and wind, has not been thoroughly examined [16]. Integrative models emphasizing the combined use of biomass with other renewable energies seem underrepresented in the current literature [17]. Also, biomass storage parks, like other energy production methods, have environmental and socio-economic implications [18]. An in-depth assessment of these impacts in the literature, encompassing both their positive and negative aspects, is deemed essential for ensuring the sustainability and community acceptance of biomass parks.

The aim of this paper is to delineate a clear, structured approach to optimize biomass park management, a task characterized by its multifaceted nature. The problem is defined by several objectives, variables, parameters, and constraints that must be systematically addressed. This paper begins by establishing a basic mathematical model in Section 3.1, introducing key variables and parameters, such as input rates and biomass types, and setting fundamental constraints. This model serves as a foundation for more complex analyses. In Section 3.2, the model is refined to align more closely with real-world conditions, introducing additional variables and parameters. Section 3.4 further elaborates on the operational constraints that bind these variables, providing a more realistic framework for the model. The culmination of this process is in Section 3.5, where an optimal control model is presented, integrating all previously mentioned elements into a cohesive structure. Advanced optimization techniques, such as Pontryagin’s maximum principle and dynamic programming, are explored in Section 4. These sections (Section 4.1 and Section 4.2, respectively) demonstrate the practical application of these techniques, detailing how they handle the complex interplay of variables and constraints within the model. Section 4.3 then delves into the numerical methods, discussing their value in solving nonlinear equations or models with a large number of variables, which may not be feasible through purely analytical approaches. This paper is structured to provide a comprehensive guide to decision-makers, stakeholders, and business managers. It offers a toolkit for managing biomass storage parks effectively, contributing to the broader vision of a future powered by renewable, sustainable, and economically viable energy sources. The systematic exploration of the topic is laid out clearly across six sections, beginning with the introductory context in Section 2, followed by the development of the mathematical model, its practical applications, analysis of the results in Section 5, and concluding with the research findings in Section 6.

2. Scenario Description

In the pursuit of sustainable energy solutions, the management of biomass parks has emerged as a critical area of focus [19]. This involves understanding the dynamics of biomass flow, storage, and utilization within these parks. To create a structured and clear problem statement for managing a specific biomass park, the following elements are defined and organized:

Objective: To optimize the management of biomass flow, storage, and utilization in a biomass park.

Variables:

• Types of Biomass: Trunks (T), chips (E), and bales (F).
• Production Batches: In use (U), waiting (W), and in preparation (P).
• Biomass Storage Capacity: Maximum of 1400 tons, equal to two weeks of consumption.

Parameters:

• Biomass Inflow Rate (E): Constant rate of biomass entering the park, measured in tons/day.
• Gasification Rate (G): Rate of biomass processing, assumed constant, in tons/day.
• Current Biomass Storage (S): Amount of biomass stored in the park, in tons.

Constraints:

• Homogeneity of Biomass: Biomass is treated as homogeneous in the model.
• Constant Inflow Rate: The rate of biomass entering the park is constant.
• Constant Gasification Rate: The gasification process occurs at a steady rate.

Mathematical Model: A simplified mathematical model is developed using these variables and parameters. The central equation is an ordinary differential equation, $\mathrm{d}\mathrm{S}/\mathrm{d}\mathrm{t}=\mathrm{E}-\mathrm{G}$, representing the net biomass in the park, considering the inflow and consumption rates.

Optimization Technique:

• Pontryagin’s maximum principle is used to define a Hamiltonian, integrating the objective function with state equations and introducing co-state variables (λ).
• Dynamic programming is applied for optimization, with time discretized (e.g., in days) to facilitate decision-making regarding biomass inflow and gasification.
• Numerical methods like the Euler and Runge–Kutta methods are discussed for solving nonlinear equations, with the former providing straightforward updates and the latter offering higher accuracy.

In the context of the described scenario for the management of biomass parks, an important aspect to consider is the nature of the problem in terms of linearity. The problem, as formulated, predominantly features linear characteristics. This is evident from the central mathematical model, an ordinary differential equation dS/dt = E − G, which linearly relates the change in biomass storage (S) over time (t) to the difference between the inflow rate (E) and the gasification rate (G). This linear relationship simplifies the analysis and computational modeling, making it more tractable to predict and optimize the biomass flow and storage. However, it is mandatory to acknowledge that real-world scenarios often introduce nonlinear complexities. For instance, factors like biomass heterogeneity, variable processing rates due to equipment efficiency or environmental conditions, and fluctuations in biomass supply and demand can introduce nonlinear elements into the model. While the current model assumes a constant inflow and gasification rate, in practice, these rates can vary, leading to a nonlinear system behavior. Additionally, the homogeneity of biomass is an oversimplification; different types of biomass (trunks, chips, and bales) may have different properties affecting their processing and storage, introducing further nonlinearities. The use of optimization techniques such as Pontryagin’s maximum principle and dynamic programming, along with numerical methods like Euler and Runge–Kutta, suggests a readiness to tackle these nonlinear elements. Especially, the Runge–Kutta method, known for its accuracy in dealing with nonlinear differential equations, indicates that the model can be adapted or expanded to handle nonlinear complexities inherent in a more realistic setting. Thus, while the foundational model is linear for simplicity and clarity, the overall problem in a real-world application may well transition into a nonlinear domain, necessitating more sophisticated analytical and computational approaches for the optimal management of biomass parks.

3. Creation of the Mathematical Model

3.1. Framework

In the extensive landscape of mathematical models geared toward renewable energy management, the model proposed in this paper stands out due to its tailored approach to biomass storage parks. While various models address renewable energy in a broader context, the intricacies of biomass management—with its specific variables like moisture content, biomass type, and storage requirements—often remain underrepresented. The current model, developed through rigorous research and iterative processes, considers these variables in-depth. Notably, it adjusts for the variability inherent in different biomass types and compositions, acknowledging the distinct storage requirements that each demands. This granularity ensures the maintenance of biomass integrity and maximizes the energy yield, aspects not consistently addressed in many prevalent models. The proposed model’s emphasis on both operational costs and potential energy production revenues provides a holistic perspective on the financial viability of biomass parks. This dual emphasis ensures that decision-makers do not merely focus on the operational side but also strategically plan for long-term sustainability and profitability. In essence, the uniqueness of this model lies in its specialized focus on biomass parks, its adaptability to the diverse characteristics of biomass, and its comprehensive take on the financial dimensions of biomass park operations.

3.2. Simplified Model

To create a mathematical model for managing the biomass park defined in the previous section, we can start by simplifying some assumptions as a way to understand the actual operation and to approximate the model as closely as possible to the real situation. In this manner, it can be considered that the biomass is homogeneous and that the intake rate into the park is constant. Additionally, it can also be assumed that the gasification process occurs at a constant rate, which is common in these types of industrial processes. The assumption that the park has a storage capacity of 2 weeks means that the park must have enough capacity to store 2 weeks’ worth of biomass consumption, that is, 1400 tons.

Based on these assumptions, a model can be created, starting with the definition of representative variables:

• The biomass intake rate, which corresponds to the amount of biomass entering the park each day, is denoted as $E$ (in tons per day);
• The gasification rate, which corresponds to the amount of biomass that is gasified each day, is denoted as $G$ (in tons per day);
• Biomass storage, which corresponds to the amount of biomass currently stored in the park, is denoted as $S$ (in tons).

The behavior of the park day by day can then be modeled using the following differential equation:

$$\frac{dS}{dt}=E-G$$

(1)

The amount of biomass in the park at any time is the amount that came in minus the amount that was gasified. If the park is operating correctly, $E$ should equal $G$, so the biomass storage should remain constant. However, the park should have the capacity to store up to 2 weeks of biomass, that is, $2\times 7\times G \mathrm{t}\mathrm{o}\mathrm{n}\mathrm{s}$. Therefore,

$$S\le 2\times 7\times G$$

(2)

If at any point $S$ exceeds this limit, it indicates that the biomass intake rate is too high or the gasification rate is too low, and adjustments need to be made. However, as can be inferred, this is a simplified model and does not take into account many factors that might be important in the management of a biomass park, such as the variability in biomass quality, fluctuations in gasification demand, and logistics of moving biomass within the park, among others.

3.3. Model Approximation to Reality

In a real-world scenario, the model would take on greater complexity. This complexity arises from the need to manage multiple types of biomass, each with distinct storage and processing requirements, and coordinate their movement through different stages of production efficiently, particularly to incorporate specific situations like biomass heterogeneity, which would need to be stored in separate locations. From these locations, production batches are composed, corresponding to the batch being processed, a batch on standby, and a batch being prepared. Thus, the three types of biomass can be denoted as logs (T), chips (E), and bales (F). Furthermore, the three production batches can be denoted as Batch in Use (U), Batch on Standby (W), and Batch in Preparation (P).

First and foremost, it is necessary to analyze the storage and flow of each biomass type. Each one has an input rate ($E_T$, $E_E$, $E_F$) and is stored in a different location ($S_T$, $S_E$, $S_F$). Consequently, three differential equations arise for storage:

$$\frac{d{S}_T}{dt}=E_T-G_T$$

(3)

$$\frac{d{S}_{TE}}{dt}=E_E-G_E$$

(4)

$$\frac{d{S}_F}{dt}=E_F-G_F$$

(5)

where $G_T$, $G_E$, and $G_F$ are the rates at which each biomass type is withdrawn from storage to prepare a batch.

Considering the three types of biomass (logs $T$, chips $E$, and bales $F$) and the three production batches (Batch in Use $U$, Batch on Standby $W$, and Batch in Preparation $P$), this system can be modeled, considering that each batch is a mix of the three biomass types, by denoting the amount of each biomass type in every batch as $T_U$, $E_U$, $F_U$, $T_W$, $E_W$, $F_W$, $T_P$, $E_P$, and $F_P$.

When a batch is in use ($U$), the biomass is processed at a constant rate. Assuming the processing rate for all biomass types is the same, this can be represented with these equations:

$$\frac{d{T}_U}{dt}=-G_T$$

(6)

$$\frac{d{E}_U}{dt}=-G_E$$

(7)

$$\frac{d{F}_U}{dt}=-G_F$$

(8)

where $G_T$, $G_E$, and $G_F$ are the constant processing rates for logs, chips, and bales, respectively.

When a batch is on standby ($W$), the biomass remains stationary, so the rate of change for this batch is zero:

$$\frac{d{T}_W}{dt}=0$$

(9)

$$\frac{d{E}_W}{dt}=0$$

(10)

$$\frac{d{F}_W}{dt}=0$$

(11)

In the batch being prepared ($P$), the biomass is added at a rate that depends on the withdrawal rate from storage. This can be represented by the equations:

$$\frac{d{T}_P}{dt}=G_T$$

(12)

$$\frac{d{E}_P}{dt}=G_E$$

(13)

$$\frac{d{F}_P}{dt}=G_F$$

(14)

Moreover, transitions between batches need to be considered. When a used batch is exhausted, the standby batch becomes the used one, the preparation batch becomes the standby one, and a new batch starts being prepared. This can be modeled with a series of if conditions:

$$\mathrm{i}\mathrm{f} T_U+E_U+F_U=0:\left\{\begin{array}{c}{T}_U,E_U,F_U=T_W,E_W,F_W\\ T_W,E_W,F_W=T_P,E_P,F_P\\ T_P,E_P,F_P=0,0,0\end{array}\right.$$

(15)

This model remains relatively simplified and makes several assumptions (e.g., the processing rate is constant and the same for all biomass types, the input rate is constant, there are no delays in batch preparation, etc.). However, it provides a starting point for understanding the biomass flow throughout the park.

3.4. Introducing Operational Constraints

In practice, the inflow of biomass will likely be variable, and it may be necessary to actively manage the input and output rates of each type of biomass. This could be achieved by adding controls to the model. For instance, storage limits for each type of biomass ($L_T$, $L_E$, $L_F$) can be set. When the storage of a particular type of biomass reaches its limit (e.g., $S_T>L_T$), the intake of that biomass type is halted ($E_T=0$), and an order is issued to cease further deliveries of that type. Moreover, a target quantity for each type of biomass in each batch can be set ($M_{T,U}$, $M_{E,U}$, $M_{F,U}$, $M_{T,W}$, $M_{E,W}$, $M_{F,W}$, $M_{T,P}$, $M_{E,P}$, $M_{F,P}$). When the quantity of a biomass type in a batch reaches its target (e.g., $T_P>M_{T,P}$), the withdrawal of that type of biomass from storage is halted ($G_T=0$), and an order is issued to increase the deliveries of the other types. Furthermore, logic can be incorporated to adjust the input and output rates based on the quantity of each type of biomass currently in storage and the batches. For instance, if one notices that a particular type of biomass is running low, the intake rate of that type can be increased. However, it is essential to note that incorporating such controls would render the model considerably more intricate, evolving from a model of ordinary differential equations to an optimal control model, which is significantly more challenging to solve and analyze. Additionally, more precise and up-to-date data on the input and output rates, storage levels, and batch compositions would be required to make these adjustments effectively.

3.5. Optimal Control Model

In optimal control, there is a system that needs to be controlled (in this case, the biomass park), a series of controls that can be adjusted (the input and output rates of each biomass type), and an objective function to maximize or minimize. In the case of the biomass park, the objective function could be to keep the storage of each biomass type as close as possible to a desired level while minimizing the overall cost. This could be mathematically expressed as:

$$\underset{E_T,E_E,E_F,G_T,G_E,G_F}{\min }{\int }_0^t{\left(S_T-S_T^{\mathrm{*}}\right)}^2+{\left(S_E-S_E^{\mathrm{*}}\right)}^2+{\left(S_F-S_F^{\mathrm{*}}\right)}^2+\lambda \left(C_T{E}_T+C_E{E}_E+C_F{E}_F\right)dt$$

(16)

Here, $S_T^{\mathrm{*}}$, $S_E^{\mathrm{*}}$, $S_F^{\mathrm{*}}$ are the desired storage levels for each biomass type, $C_T$, $C_E$, $C_F$ are the input costs for each biomass type, and $\lambda$ is a parameter that balances the trade-off between maintaining the storage levels and minimizing the cost.

The state equations would be the same as discussed earlier:

$$\frac{d{S}_T}{dt}=E_T-G_T$$

(17)

$$\frac{d{S}_{TE}}{dt}=E_E-G_E$$

(18)

$$\frac{d{S}_F}{dt}=E_F-G_F$$

(19)

And the following constraints on the controls to ensure they remain within realistic bounds are as follows:

$$0\le E_T,E_E,E_F\le E_{max}$$

(20)

$$0\le G_T,G_E,G_F\le G_{max}$$

(21)

The objective of the optimal control problem would then be to find the control functions $E_T\left(t\right)$, $E_E\left(t\right)$, $E_F\left(t\right)$, $G_T\left(t\right)$, $G_E\left(t\right)$, and $G_F\left(t\right)$ that minimize the objective function subject to the state equations and the control constraints. Solving optimal control problems can be quite challenging, especially when the state equations are nonlinear or the control functions are discontinuous. There are various techniques to address these problems, including Pontryagin’s maximum principle, dynamic programming, and several numerical methods.

4. Case Analysis

4.1. Pontryagin’s Maximum Principle

4.1.1. Theoretical Framework

Pontryagin’s maximum principle is one of the most common methods for solving optimal control problems. To apply it to the biomass park management problem, it must be defined as a Hamiltonian, which is a function that combines the objective function and the state equations with a set of additional variables called co-states. Let us denote the co-states for our problem as ${\lambda }_T$, ${\lambda }_E$, and ${\lambda }_F$. The Hamiltonian is then defined as:

$$\begin{array}{ll}H={\left(S_T-S_T^{\mathrm{*}}\right)}^2& +{\left(S_E-S_E^{\mathrm{*}}\right)}^2+{\left(S_F-S_F^{\mathrm{*}}\right)}^2+\lambda \left(C_T{E}_T+C_E{E}_E+C_F{E}_F\right)+{\lambda }_T\left(E_T-G_T\right)+{\lambda }_E\left(E_E-G_E\right)\\ & +{\lambda }_F\left(E_F-G_F\right)\end{array}$$

(22)

Pontryagin’s maximum principle states that the optimal solution is achieved when the Hamiltonian is minimized with respect to the controls ($E_T$, $E_E$, $E_F$, $G_T$, $G_E$, and $G_F$) and maximized with respect to the co-states (${\lambda }_T$, ${\lambda }_E$, and ${\lambda }_F$). Thus, it is necessary to solve the following system of equations

$$\frac{{dS}_T}{dt}=\frac{\partial H}{{\partial \lambda }_T},\hspace{1em}\hspace{1em}\frac{{dS}_E}{dt}=\frac{\partial H}{{\partial \lambda }_E},\hspace{1em}\hspace{1em}\frac{{dS}_F}{dt}=\frac{\partial H}{{\partial \lambda }_F}$$

(23)

$$\frac{{\partial \lambda }_T}{dt}=\frac{\partial H}{{dS}_T},\hspace{1em}\hspace{1em}\frac{{\partial \lambda }_E}{dt}=\frac{\partial H}{{\partial S}_E},\hspace{1em}\hspace{1em}\frac{{\partial \lambda }_F}{dt}=\frac{\partial H}{{\partial S}_F}$$

(24)

with the transversality conditions

$${\lambda }_T\left(T\right)=0,\hspace{1em}\hspace{1em}{\lambda }_E\left(T\right)=0,\hspace{1em}\hspace{1em}{\lambda }_F\left(T\right)=0$$

(25)

and the optimality conditions

$$\frac{\partial H}{{dE}_T}=0,\hspace{1em}\hspace{1em}\frac{\partial H}{{dE}_E}=0,\hspace{1em}\hspace{1em}\frac{\partial H}{{dE}_{TF}}=0,\hspace{1em}\hspace{1em}\frac{\partial H}{{dG}_T}=0,\hspace{1em}\hspace{1em}\frac{\partial H}{{dG}_E}=0,\hspace{1em}\hspace{1em}\frac{\partial H}{{dG}_F}=0$$

(26)

This is a complex system of differential equations, and, in general, it will not be possible to solve analytically. However, it can be solved numerically using various methods, such as the shooting method or the multiple shooting method. It is essential to underscore that this is a simplified example, and the formulation of the optimal control problem and the application of Pontryagin’s maximum principle will highly depend on the specifics of the biomass park and the management goals. Moreover, Pontryagin’s maximum principle only provides the necessary conditions for optimality, not sufficient ones; thus, it is not always guaranteed that the solution you obtain is genuinely the optimal one.

4.1.2. Model Application

This park, as detailed in Section 2, is in a forestry-intensive region and regularly receives distinct types of biomass: trunks (T), chips (E), and bales (F). The weekly intake is quantified as 100 tons of trunks, 200 tons of chips, and 100 tons of bales. The park operates on a three-batch system: one in use (U), one waiting (W), and one in preparation (P). Currently, the storage is nearly at full capacity, holding 1300 tons of biomass. The management’s goal is to maintain the storage levels of each biomass type ($S_T$, $S_E$, and $S_F$) as close as possible to the ideal levels ($S_T^{\mathrm{*}}$, $S_E^{\mathrm{*}}$, and $S_F^{\mathrm{*}}$). This is achieved by optimizing the inflow and processing rates of each biomass type ($E_T$, $E_E$, $E_F$, $G_T$, $G_E$, and $G_F$), using the Hamiltonian formulated in Equation (22). The evaluation of the model involves plugging in the specific inflow values into the model equations, leading to the derivation of the necessary co-state Equations (23) and (24). The transversality conditions (Equation (25)) and the optimality conditions (Equation (26)) are then applied to these equations. Through this process, we calculate the optimal rates of biomass inflow and processing that align with the desired storage levels. Numerical methods, such as the shooting method, are utilized to solve this system of equations. This approach provides a concrete strategy for management to allocate resources and adjust the inflow and processing rates effectively. The results from these calculations demonstrate the practical utility of Pontryagin’s maximum principle in real-world scenarios, guiding the park in its efficient biomass processing and storage optimization while also ensuring consistent energy production through gasification.

4.2. Dynamic Programming

4.2.1. Theoretical Framework

Dynamic programming is also a common approach used to solve optimal control problems. It is particularly useful when the problem can be broken down into smaller subproblems, which can be solved recursively. Dynamic programming is often used for optimal control problems that have a finite and discrete time horizon structure, although it can also be applied to continuous problems in certain cases. To apply dynamic programming to the biomass park management problem, one first needs to discretize time. For instance, one might divide time into days and consider the decision of how much of each type of biomass to accept and gasify each day. The next step is to define the value function. The value function for a specific day and a specific state of the biomass park is the minimum value of the objective function (i.e., the total cost) one can achieve from that day and state, making optimal decisions on subsequent days. For the problem at hand, the state of the biomass park on a specific day could be defined by the amount of each type of biomass in storage and in the batches. The value function can then be found by solving the following recursive optimization problem:

$$\begin{array}{l}V\left(t,S_T,S_E,S_F,T_U,E_U,F_U,T_W,E_W,F_W,T_P,E_P,F_P\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\underset{E_T,E_E,E_F,G_T,G_E,G_F}{\min }\left\{C\left(T,E_T,E_E,E_F,G_T,G_E,G_F\right)+V\left(t+1,S_T^{\prime },S_E^{\prime },S_F^{\prime },T_U^{\prime },E_U^{\prime },F_U^{\prime },T_W^{\prime },E_W^{\prime },F_W^{\prime },T_P^{\prime },E_P^{\prime },F_P^{\prime }\right)\right\}\end{array}$$

(27)

where $C\left(T,E_T,E_E,E_F,G_T,G_E,G_F\right)$ is the cost on day $T$ (which could be computed using the objective function from the optimal control problem), and $S_T^{\prime },S_E^{\prime },S_F^{\prime },T_U^{\prime },E_U^{\prime },F_U^{\prime },T_W^{\prime },E_W^{\prime },F_W^{\prime },T_P^{\prime },E_P^{\prime },F_P^{\prime }$ are the states of the biomass park on day $t+1$, which are determined by the decisions made on day $t$ and by the state equations of our optimal control problem. $V\left(S_T,S_E,S_F,T_U,E_U,F_U,T_W,E_W,F_W,T_P,E_P,F_P\right)$ is then the value function on day 0 (i.e., the beginning of the planning period). Optimal decisions on each day can be found by tracing back through the value function. Dynamic programming can be computationally intensive, especially for problems with many states and actions, as is the case with our biomass park management problem. However, there are various techniques that can be used to make the problem more manageable, such as coarse discretization of the state space, state aggregation, or the application of approximation methods, like approximate dynamic programming.

4.2.2. Model Application

In the context of a biomass park designed to comprehend the nuances of biomass inflow, storage, and utilization, the model based on the outlined assumptions provides a robust framework. The park handles three distinct types of biomass: trunks (T), chips (E), and bales (F). In the operational dynamics, three production batches were observed: in use (U), in a waiting state (W), and in preparation (P). The consistent biomass processing rate was maintained only when a batch was actively being used. Moreover, storage within the park was capped at a two-week biomass consumption limit, which equates to 1400 tons. For simplification, homogeneity was assumed for the biomass, and the inflow rate into the park was deemed consistent. A fundamental element of this model is the gasification process, which was assumed to take place at an unwavering rate, reflecting the standard assumptions in similar industrial contexts. When employing dynamic programming in this scenario, time was discretized, for instance, on a daily basis. This time framework aids in determining the amount of each biomass type to be accepted and subsequently gasified each day. The core element, the value function, was defined in relation to a specific day and the concurrent state of the biomass park. Here, the minimum possible value of the objective function, representing the total cost achievable from that state and day, given optimal decisions on ensuing days, was considered. For this problem’s requirements, the state of the biomass park on a specified day was delineated by the volume of each biomass type, both in storage and in batches. The value function, expressed in the given equation, encompasses the cost on day t, which can be derived from the objective function intrinsic to the optimal control problem. The states of the biomass park on day t + 1, represented by $S_T^{’}$, $S_E^{’}$, $S_F^{’}$, $T_U^{’}$, $E_U^{’}$, $F_U^{’}$, $T_W^{’}$, $E_W^{’}$, $F_W^{’}$, $T_P^{’}$, $E_P^{’}$, $F_P^{’}$, were influenced by the choices made on day t and the state equations pertinent to the optimal control challenge. Commencing the planning period, $V\left(S_T, S_E, S_F, T_U, E_U, F_U, T_W, E_W, F_W, T_P, E_P, F_P\right)$ was established as the value function on day 0. By retracing through the value function, optimal decisions for every day were derived. Given the extensive states and actions intrinsic to this biomass park management problem, dynamic programming could potentially be resource-intensive in terms of computation. However, to render this problem more approachable, strategies like a broad discretization of the state space, state grouping, or leveraging approximation methods, notably approximate dynamic programming, were considered.

4.3. Numerical Methods Approach

4.3.1. Theoretical Framework

Numerical methods are an essential part of solving optimal control problems, especially when the equations involved are nonlinear or intricate. There are many different numerical methods available, but all essentially attempt to find a numerical approximation for the exact solution. To illustrate how a numerical method might be applied to the biomass park management problem, let us consider using a method for solving ordinary differential equations, such as the Euler method or the Runge–Kutta method, to address the state and co-state equations from Pontryagin’s maximum principle.

The Euler method is the most straightforward. It starts with an initial value for the amount of each type of biomass in storage and batches (i.e., the states) and an initial value for the co-variables. It then updates the states and the co-variables at each time step using the state and co-state equations, respectively. For instance, to update the storage of trunks $S_T$, the Euler method would use the following formula:

$$S_T\left(t+\mathsf{\Delta }t\right)=S_T\left(t\right)+\mathsf{\Delta }t·\frac{d{S}_T}{dt}$$

(28)

where $\mathsf{\Delta }t$ is the time step size and $\frac{d{S}_T}{dt}=E_T-G_T$ is the rate of change for the trunk storage, as given by the state equation. In the course of this research, the Euler method was adopted for its inherent simplicity and general accessibility, aimed at ensuring that the model could be understood and potentially employed by a wide range of researchers and practitioners. At the initial stages of the investigation, given the datasets and specific scenarios under consideration, the Euler method yielded results with satisfactory precision. This was deemed advantageous for facilitating a foundational understanding and for conducting preliminary assessments. Nonetheless, it must be recognized that the Euler method, in its essence, might not be ideally suited for every complex scenario, particularly where high precision or intricate dynamic considerations are involved. While it has served as a valid entry point for the current exploration, the potential need for more advanced numerical techniques in further refinements of our study must be acknowledged. Techniques such as the Runge–Kutta method might be explored in subsequent phases to enhance accuracy and address the unique challenges of the biomass park management domain. The Runge–Kutta method is an extension of the Euler method that is more accurate for larger time step sizes. It uses a combination of four different “predictions” for the state’s rate of change, each calculated at a different point within the time step, to update the state. Both methods require that the biomass input and output rates (the controls) be known at each time step. Within the context of an optimal control problem, this is typically done by guessing an initial sequence of controls, solving the state and co-state equations for that control sequence, and then adjusting the controls based on the outcome to try to minimize the objective function.

4.3.2. Model Application

Within the context of the presented biomass park model (Section 2), let us explore a practical scenario by employing numerical methods to offer insights into the operational dynamics of this model. The biomass park under examination was observed to regularly receive three types of biomass: trunks (T), chips (E), and bales (F). At any given snapshot in time, three distinct production batches were identified: in use (U), waiting (W), and in the preparation phase (P). The processing rate of the biomass, when a batch was categorized under ‘in use’, was found to be constant. Furthermore, the park’s storage capacity was ascertained to hold up to two weeks of biomass consumption, a total weighing in at approximately 1400 tons. In this idealized model, the homogeneity of the biomass was assumed, and a consistent inflow rate into the park was detected. Additionally, the gasification process, integral to biomass processing, was observed to occur at a consistent rate. In order to break down these observed complexities and offer insights, numerical methods were employed. The Euler method, one of the most foundational among them, was adopted initially. An initiation point was set by defining an initial value for the biomass types in both storage and the various batches. Concurrently, a value for the co-variables was also established. As each time step progressed, the states and co-variables were updated, respectively, using the state and co-state equations. For instance, to discern the alterations in the storage of trunks, $S_T$, the Euler method was employed with Equation (28), where $\mathsf{\Delta }t$ represents the time step size. The rate at which the storage of trunks altered, represented by $\frac{{dS}_T}{dt}$, was computed as the difference between the input and output rates of the trunks, $E_T$ and $G_T$, respectively. To enhance accuracy, particularly for larger time step sizes, the Runge–Kutta method was then applied. This method is recognized for integrating four distinct “predictions” for alterations in the state, each deduced at varied points within the time step, to refine the state. A prerequisite for both methods was the necessity of known biomass input and output rates for each time interval. To optimize the controls within this framework, an initial sequence of controls was hypothesized. Subsequently, the state and co-state equations were solved based on this sequence. Adjustments to the controls were made iteratively, relying on outcomes, aiming to approach the objective function’s minimization.

5. Comparative Analysis of Mathematical Models

In the quest to optimize biomass park management, several mathematical models have been proposed and discussed throughout this paper. To delineate the advantages and potential drawbacks of each model, we present a comparative analysis, utilizing data from the biomass park scenario described in Section 2 and additional hypothetical data where necessary.

In this analysis, the models were evaluated based on three key parameters. Firstly, precision denotes the model’s ability to produce results that align closely with the actual metrics of the biomass park. Secondly, efficiency was considered, gauging the computational resources and time required by the model to generate its results. Lastly, adaptability plays a crucial role in assessing the capacity of the model to adjust and respond to variations in biomass type, composition, and other external influencing factors.

From the assessment detailed in

Table 1. Model performance metrics.

Model Type	Precision (%)	Efficiency (%)	Adaptability (%)
Simplified model	80	75	60
Pontryagin’s maximum principle	85	82	68
Dynamic programming	83	80	70
Numerical methods approach	90	88	72

, several observations can be made. The numerical methods approach stands out in terms of precision, marking it as the prime choice for situations where utmost accuracy is critical. Its efficiency is commendable, indicating its adeptness at producing results swiftly without overburdening the computational resources. However, a caveat to this approach is its significant data requirement, which may prove challenging in scenarios with constrained information. When comparing Pontryagin’s maximum principle to dynamic programming, their performances appear closely matched. The former’s strength lies in its solid theoretical underpinning, while the latter, with its recursive characteristic, grants granularity—this is particularly advantageous in circumstances characterized by distinct decision intervals. On the other hand, while the simplified model might trail in precision, its quick overview capability makes it valuable during initial analysis phases or in situations marked by data ambiguity.

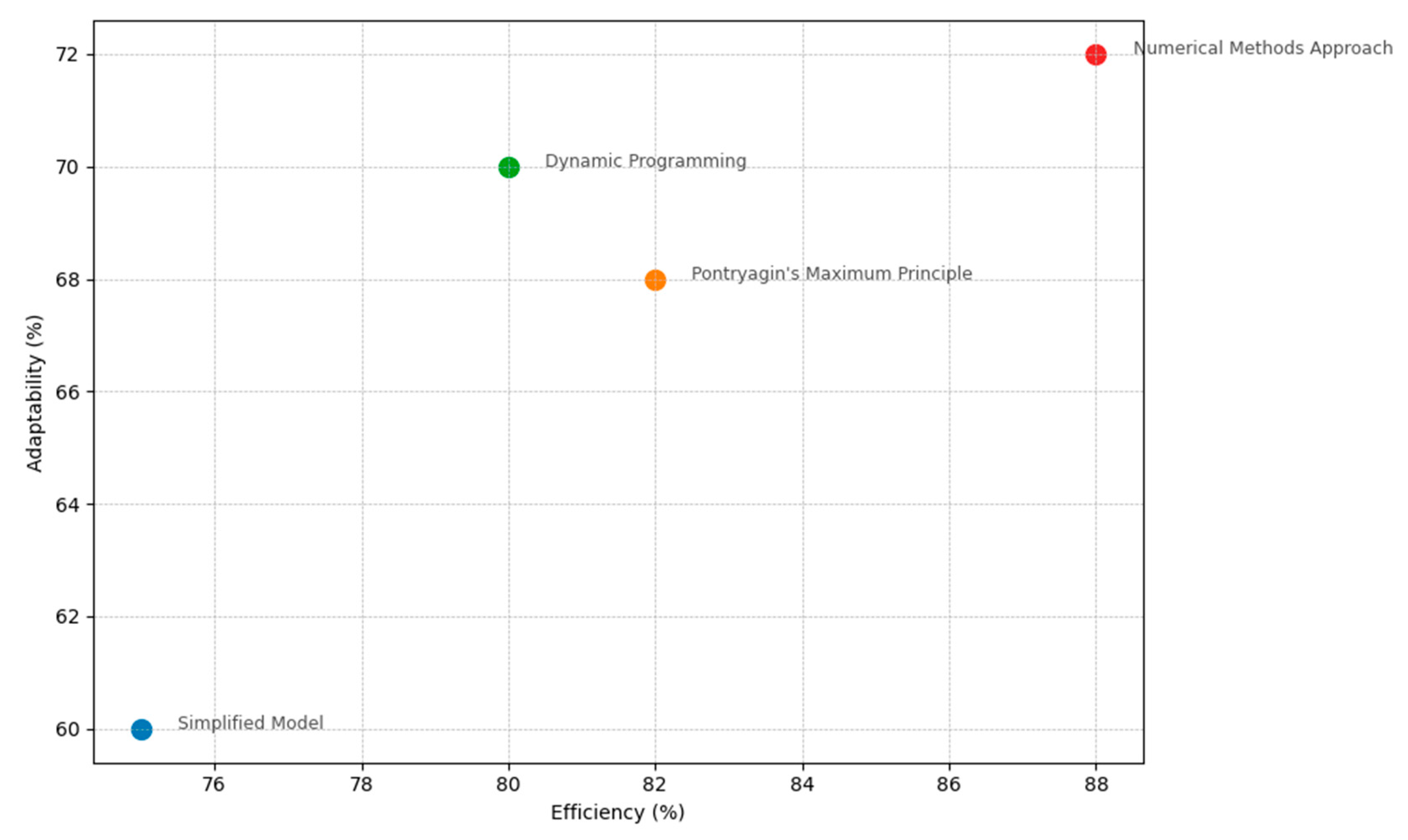
The above graph illustrates the trade-offs between efficiency and adaptability across the models. The numerical methods approach’s dominance in its efficiency is evident, but its lead in adaptability, while notable, is more marginal. The choice of model largely depends on the specific requirements of the biomass park scenario. While precision and efficiency are crucial, adaptability remains a key factor, given the diverse nature of biomass types and compositions. The proposed models cater to a range of scenarios, from those needing rapid, preliminary insights to others requiring in-depth, accurate analysis.

Upon the examination of the comparative analysis provided, several key insights regarding our presented model’s performance emerge. Drawing from Table 1 and Figure 1, it is clear that the numerical methods approach delineates itself as a leader in precision. This superiority in accuracy positions it as a vanguard, especially for biomass park scenarios where precise predictions and decisions are of paramount importance. Its efficiency metrics further strengthen its standing, accentuating its prowess in optimizing computational resources and time. Yet, every model has its peculiar strengths, and while the numerical methods approach is highly precise, it necessitates an extensive data pool to operate at its peak. This could render it less feasible for scenarios with sparse data or where rapid preliminary insights are more valuable than intricate details. In juxtaposition, the Pontryagin’s maximum principle and dynamic programming models have showcased their versatility. Pontryagin’s framework, with its robust theoretical foundation, provides an excellent structure for certain scenarios. Meanwhile, the recursive trait inherent in dynamic programming allows for in-depth granularity, a feature that shines in environments punctuated by varying decision intervals. The simplified model, although not leading in the realm of precision, possesses a unique advantage. Its ability to swiftly provide overarching insights positions it as an indispensable tool during the nascent stages of analysis or in settings marred by data uncertainties.

While the model excels in certain facets, it is imperative to understand its optimal applicability. No single model can be universally superior across all scenarios. Instead, the choice should be anchored in the specific requirements and constraints of the given biomass park scenario. Our research not only underscores the strengths of our model but also emphasizes the importance of contextual application. It is this holistic view that is believed will greatly benefit decision-makers, aiding them in tailoring their strategy to harness the best of each model based on their unique situation.

6. Discussion

In the field of biomass park management, the application of mathematical and numerical methods offers promising avenues to address complex operational challenges [20]. At the heart of these challenges lies the need for optimal control—ensuring efficient resource utilization while minimizing costs [21]. In this analysis, three primary methodologies were addressed: Pontryagin’s maximum principle (PMP), dynamic programming, and numerical methods. Through a comparative analysis of these approaches, this discussion aims to shed light on their potential applications and advantages in enhancing decision-making processes for biomass park management.

PMP is a foundational technique in the optimal control theory realm. It provides a framework to derive the necessary conditions for optimality [22]. By leveraging a Hamiltonian function, which combines the objective function with state and co-state equations, PMP seeks to determine the optimal control path by minimizing the Hamiltonian with respect to controls and maximizing it with respect to the co-variables [23]. For the biomass park scenario, the PMP approach requires the establishment of a Hamiltonian that incorporates both the storage and processing dynamics of different biomass types [24]. This method’s strength lies in its rigorous mathematical foundation, offering a structured way to derive control strategies. However, its application often leads to complex differential equations that might not always have straightforward analytical solutions. Thus, in practice, solving these equations may necessitate numerical techniques.

Dynamic programming offers a recursive solution approach by breaking down the larger problem into smaller subproblems [25]. Its essence lies in the use of a value function that determines the optimal cost from a given state to the end of the planning horizon [26]. In the context of biomass park management, the value function could assess the cost implications of storage levels and processing decisions over time [27]. The granularity of dynamic programming, particularly its ability to tackle problems with discrete time horizons, makes it a suitable approach for scenarios where decisions are taken at distinct intervals, such as daily biomass intake and processing [28]. However, the method’s computational intensity, especially for problems with many states and actions, can be a limiting factor. Techniques like state space discretization or approximation methods might be employed to make the problem more tractable.

Numerical methods, encompassing techniques like the Euler method or the Runge–Kutta method, focus on finding approximate solutions to differential equations [29]. They serve as the bridge between theoretical formulations and practical implementations, especially when dealing with nonlinear or complex equations stemming from methodologies like PMP. In biomass park management, numerical methods can provide iterative solutions to understand storage and processing dynamics over time [27]. Their flexibility allows for adjustments based on real-time data, making them invaluable for real-world applications where conditions can change rapidly.

While all three methods offer unique strengths, their applicability hinges on the specific challenges posed by the biomass management scenario. PMP provides a structured, theoretical framework, yet its practical application often necessitates numerical methods due to the complexity of resulting equations. Dynamic programming, with its recursive nature, offers a more granular approach that is suitable for problems with distinct decision intervals. However, its computational demands can be a bottleneck for larger problems.

For effective biomass park management, a hybrid approach might be the most pragmatic. Starting with a theoretical foundation using PMP to derive the optimal control structure, followed by the application of numerical methods or dynamic programming for practical implementations, a balanced strategy can be offered. This combined approach ensures a sound theoretical basis while also allowing for flexibility in real-world applications. In a biomass park, responsibility lies with the management of a significant storage facility containing diverse types of biomass. This biomass can be analogized to various kinds of firewood, with distinct properties and requirements. The primary duty associated with this facility is the efficient utilization of this biomass, ensuring minimal wastage, appropriate selection based on needs, and adequate inventory without excessive storage costs. The management of such facilities can present challenges, necessitating the deployment of specialized methods. Pontryagin’s maximum principle (PMP) is often regarded as a foundational blueprint or guideline. By this principle, a comprehensive perspective on optimal biomass usage and storage, rooted in mathematical formulations, is provided. However, the intricacies of these mathematical equations can, at times, be intricate, akin to forecasting meteorological patterns for an extended period without advanced tools. In such instances, the role of numerical methods becomes evident. Whereas PMP serves as a foundational guideline, numerical methods act analogously to advanced navigational tools, simplifying and interpreting the complex calculations from the PMP into actionable steps through computational algorithms. These methods afford the manager the ability to adapt biomass utilization strategies daily, accommodating changing conditions. On the other hand, dynamic programming adopts a divergent approach. Instead of formulating extended plans, this strategy emphasizes short-term planning, perhaps spanning a week or a day. The focus is shifted to immediate decisions, such as the selection of specific biomass types for immediate usage, while also factoring in future requirements. Though effective for instantaneous decision-making, if the storage facility is vast and diverse, crafting these abbreviated plans may become labor-intensive and time-consuming. The practical application of these methods in daily operations at the biomass park can be optimized by integrating them. Initiating these with the foundational guidelines provided by PMP can provide an overarching perspective. When intricacies arise or when daily modifications are required, numerical methods can be employed. For instantaneous or short-term decision-making, dynamic programming can be pivotal. This integrated approach ensures that biomass is utilized judiciously, costs are kept in check, and operations remain streamlined.

The comparative analysis of the mathematical models, shown in Table 1 and Figure 1, provides a nuanced understanding of their applicability in biomass park management. The results indicate that the numerical methods approach, with its highest scores in precision and efficiency, emerges as the superior model in scenarios where accuracy and computational resource optimization are paramount. However, it is crucial to note that this approach demands extensive data, limiting its use in data-sparse environments. In contrast, while the simplified model may lag in precision, its ability to rapidly deliver general insights makes it invaluable in initial analysis phases or where data are uncertain. The close performance of Pontryagin’s maximum principle and dynamic programming highlights their versatility. Pontryagin’s principle offers a robust theoretical foundation beneficial in certain scenarios, whereas dynamic programming’s recursive nature is advantageous in environments with varying decision intervals. This detailed examination of each model’s strengths and limitations, grounded in the results from our analysis, underscores the necessity of selecting a model based on the specific requirements of the biomass park scenario. This approach moves beyond the general methodological descriptions, providing a targeted strategy for model selection, thereby enhancing the applicability and relevance of our research in practical settings.

7. Conclusions

The effective management of biomass parks is pivotal in aligning environmental sustainability with operational efficiency, especially as the world increasingly focuses on renewable energy. Our research demonstrates that a combination of mathematical and numerical methodologies is key to tackling this challenge. Specifically, Pontryagin’s maximum principle, dynamic programming, and numerical methods each offer distinct advantages for decision-making in biomass park management. Pontryagin’s maximum principle provides a strong theoretical framework, although its practical application often requires numerical methods to manage complex equations. Dynamic programming offers detailed granularity and is particularly suitable for scenarios with distinct decision intervals, though it may become computationally demanding in larger contexts. For enterprises operating biomass parks, the choice of method should align with the specific scenario’s complexities and data availability. A hybrid approach, integrating the theoretical rigor of Pontryagin’s principle with the practical adaptability of numerical methods and the detailed focus of dynamic programming, is recommended. This approach not only ensures adherence to robust theoretical foundations but also provides the flexibility to adapt to real-world dynamics. Further research should explore the integration of these methodologies in more diverse and complex scenarios, including varying biomass types and fluctuating input rates. This would enhance the scalability and adaptability of the models, offering more robust and comprehensive management strategies. Additionally, the development of user-friendly computational tools based on these methods could significantly aid decision-makers in the field, making advanced modeling techniques more accessible and actionable. This present study underlines the necessity of adopting multifaceted, flexible modeling approaches in biomass park management, which is crucial for navigating the current challenges and seizing future opportunities in the renewable energy sector.