Prediction of China Automobile Market Evolution Based on Univariate and Multivariate Perspectives
Abstract
:1. Introduction
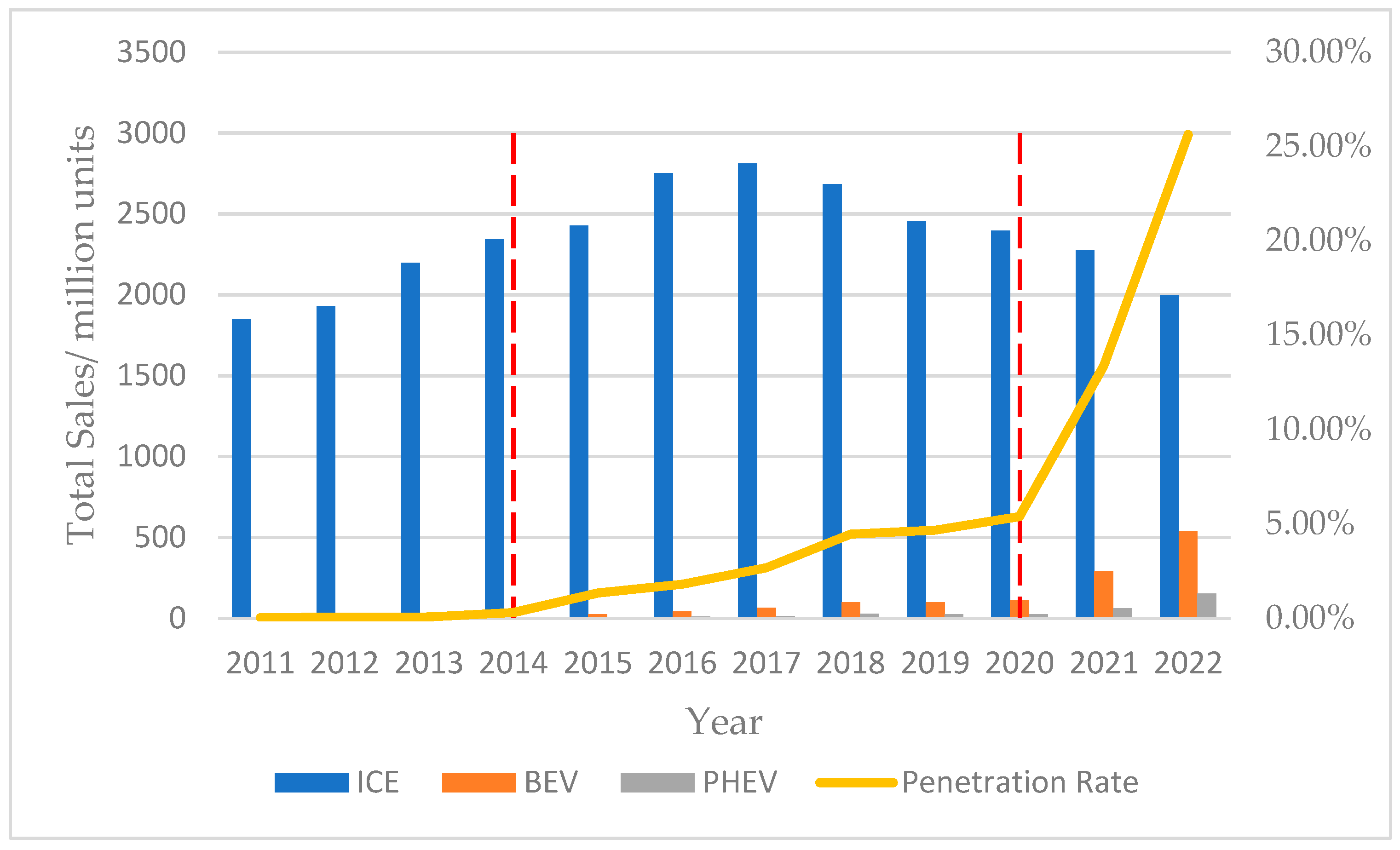
1.1. Background and Motivation
1.2. Literature Review
1.2.1. Influencing Factors of Vehicle Sales
1.2.2. Prediction Models of Vehicle Sales Volume
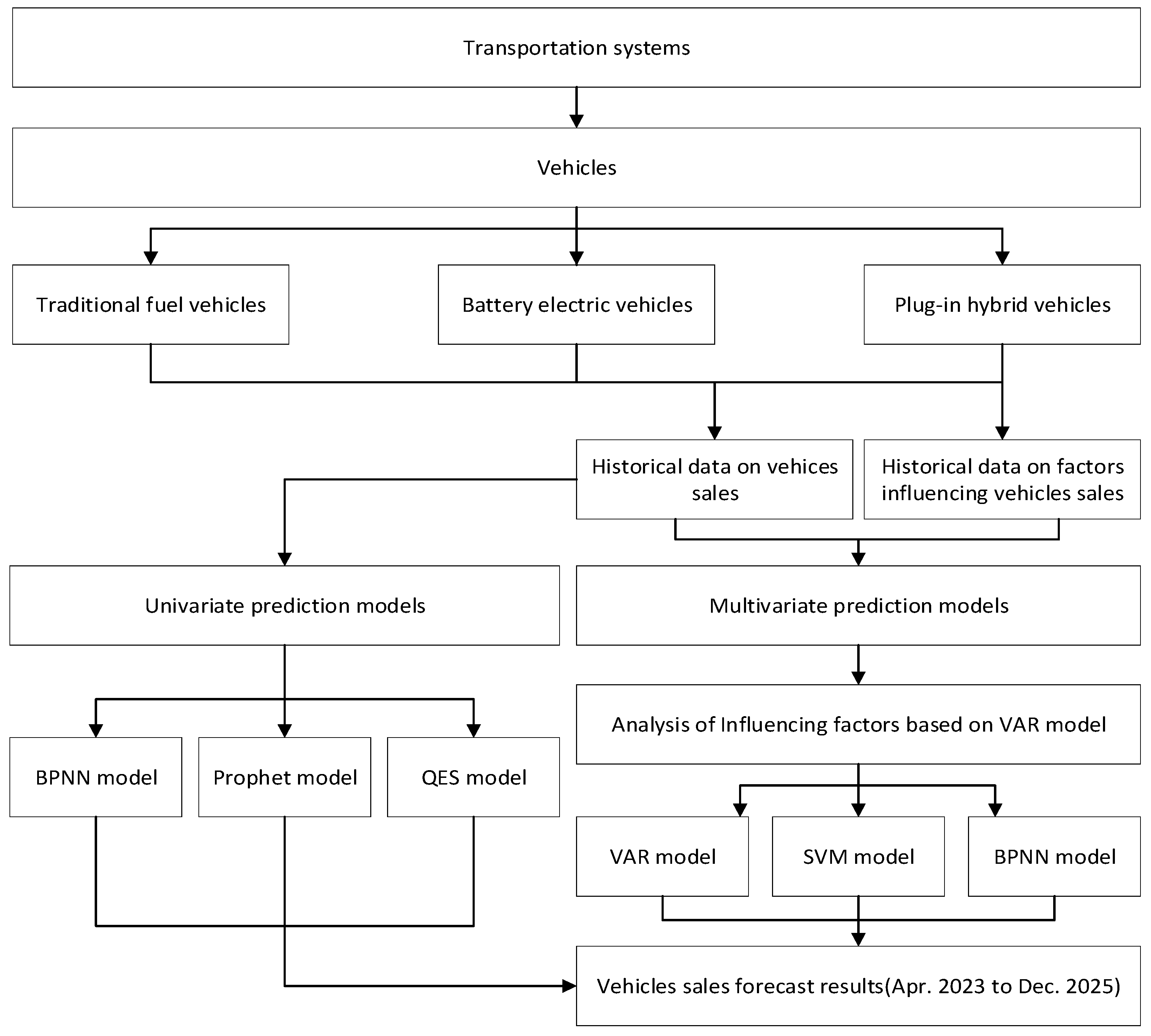
1.3. Contribution and Organization
2. Materials and Methods
2.1. Variable Selection and Data Description
2.2. Methodology
2.2.1. Quadratic Exponential Smoothing Model
2.2.2. Prophet Model
2.2.3. Vector Autoregressive Model
2.2.4. Support Vector Regression Model
2.2.5. BP Neural Network Model
2.3. Model Evaluation Index
3. Results
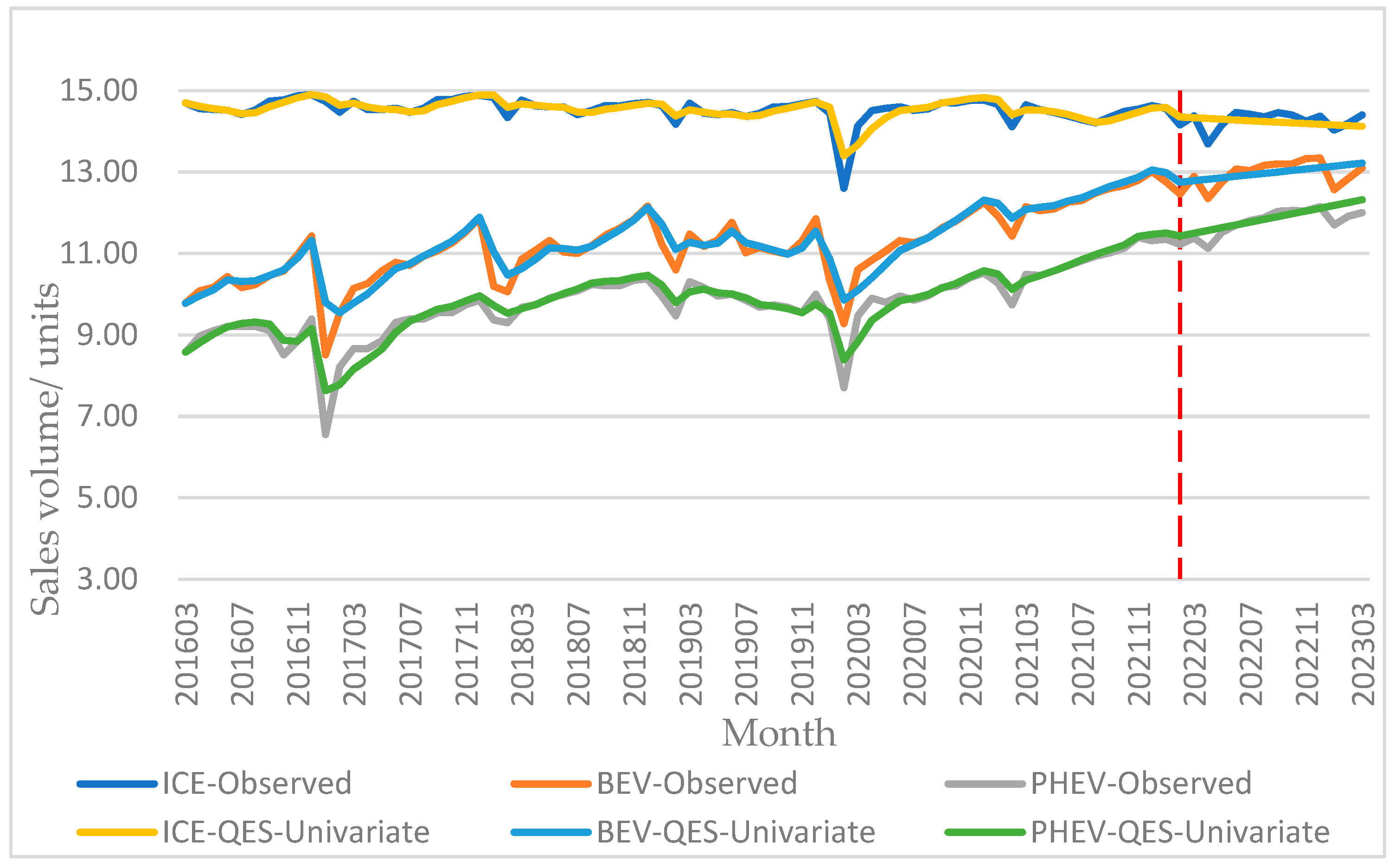
3.1. Comparison of Univariate Prediction Models
3.1.1. Prediction Results of Univariate BP Neural Network
3.1.2. Prediction Results of Quadratic Exponential Smoothing
3.1.3. Prediction Results of Prophet Model
3.1.4. Error Comparison
3.2. Comparison of Multivariate Prediction Models
3.2.1. Analysis of Lag Effect Based on VAR Model
- (1)
- Stationarity test. In order to avoid pseudo-regression, we test the stationarity of the original sales volume and influencing factor series based on the ADF test. In order to eliminate the influence of heteroscedasticity, this paper carries out logarithmic processing on automobile sales data and influencing factors data. As shown in Table 4, at the significance level of 1%, the 17 data series involved in the study are stationary.
- (2)
- Determination of the optimal lag order. The establishment of the VAR model needs to choose the appropriate lag order. In order to fully reflect the dynamic characteristics of the established VAR model, many factors need to be considered when choosing the lag order. Based on LR, FPE, AIC, SC and HQ criteria, the optimal lag order is determined, and the maximum number of * is the optimal lag period. As shown in Table 5, the optimal lag order is 3.
- (3)
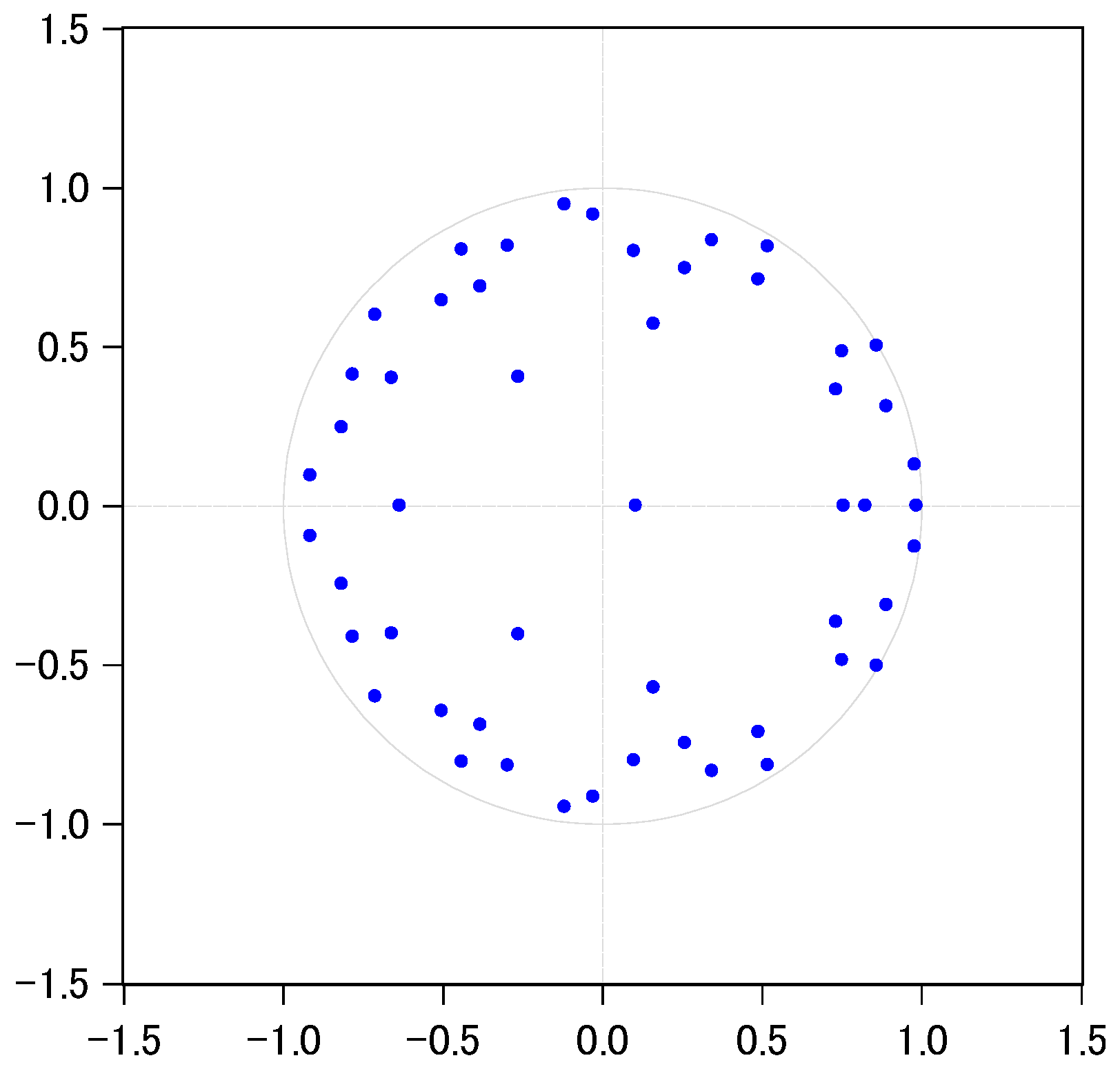
- Stability test of the VAR model. When a pulsating impact is applied to the process of an equation in the VAR model, the system is considered to be stable if the pulse disappears with the passage of time. When the modulus of the reciprocal of the characteristic root is less than 1, it means that the VAR model is stable. As shown in Figure 6, the feature roots are all located in the unit circle, which proves that the VAR (3) model is stable.
- (4)
- The parameters of the unconstrained VAR (3) model constructed in this paper are shown in Table 6:
- (5)
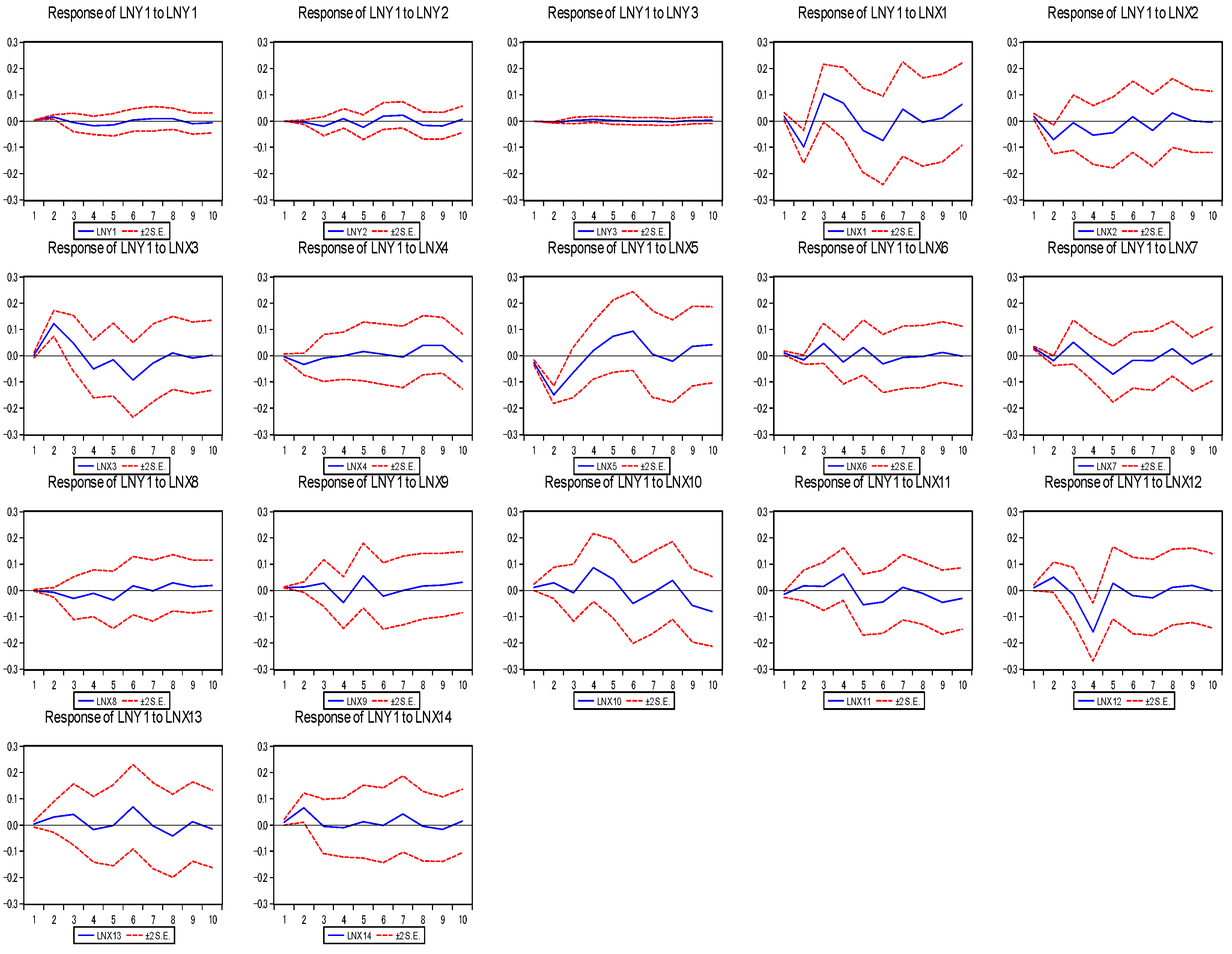
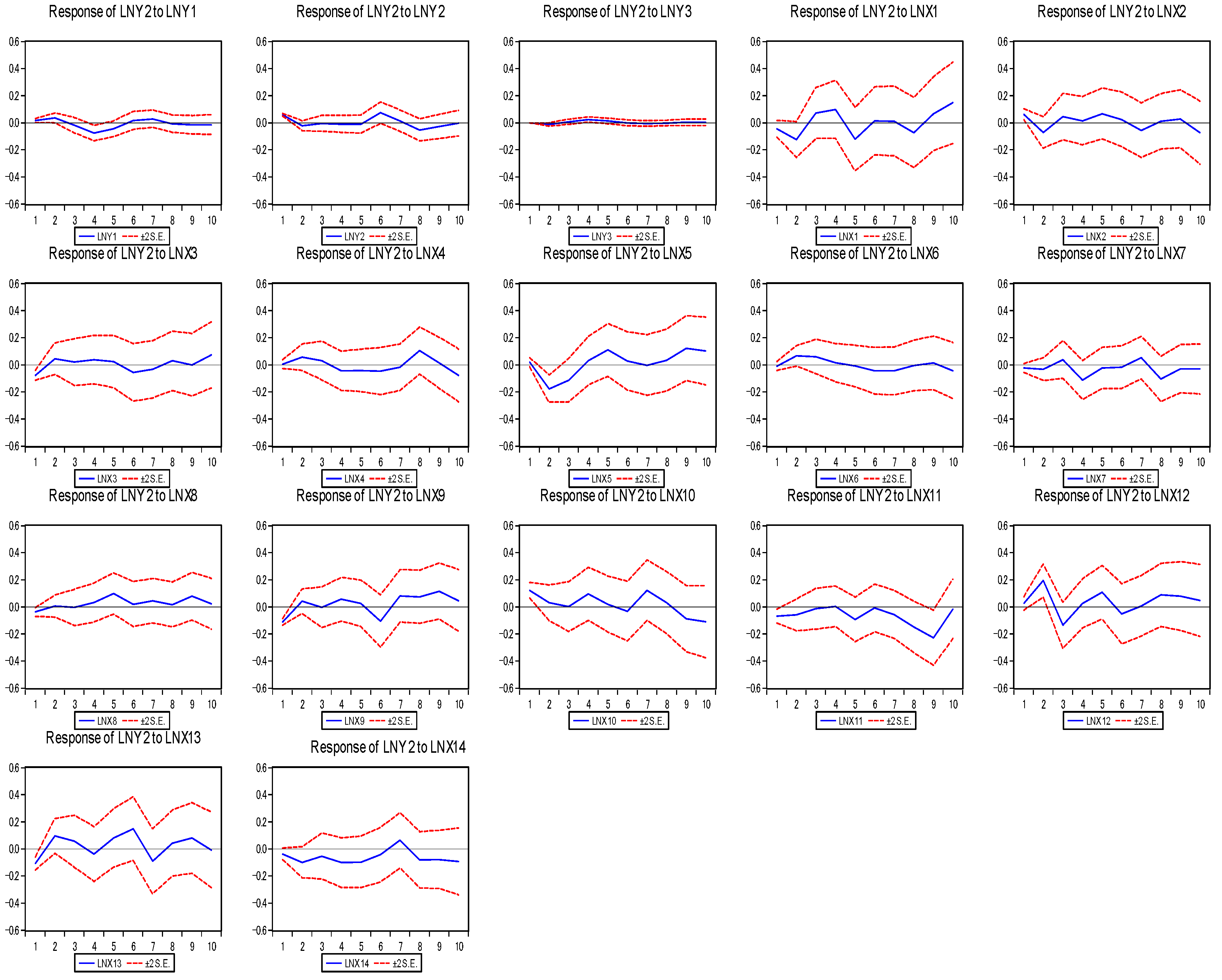
- Impulse response analysis. The impulse response function reflects the dynamic relationship between variables and the dynamic influence path of the impact of one variable on another [42].
3.2.2. Predictive Results of VAR Model
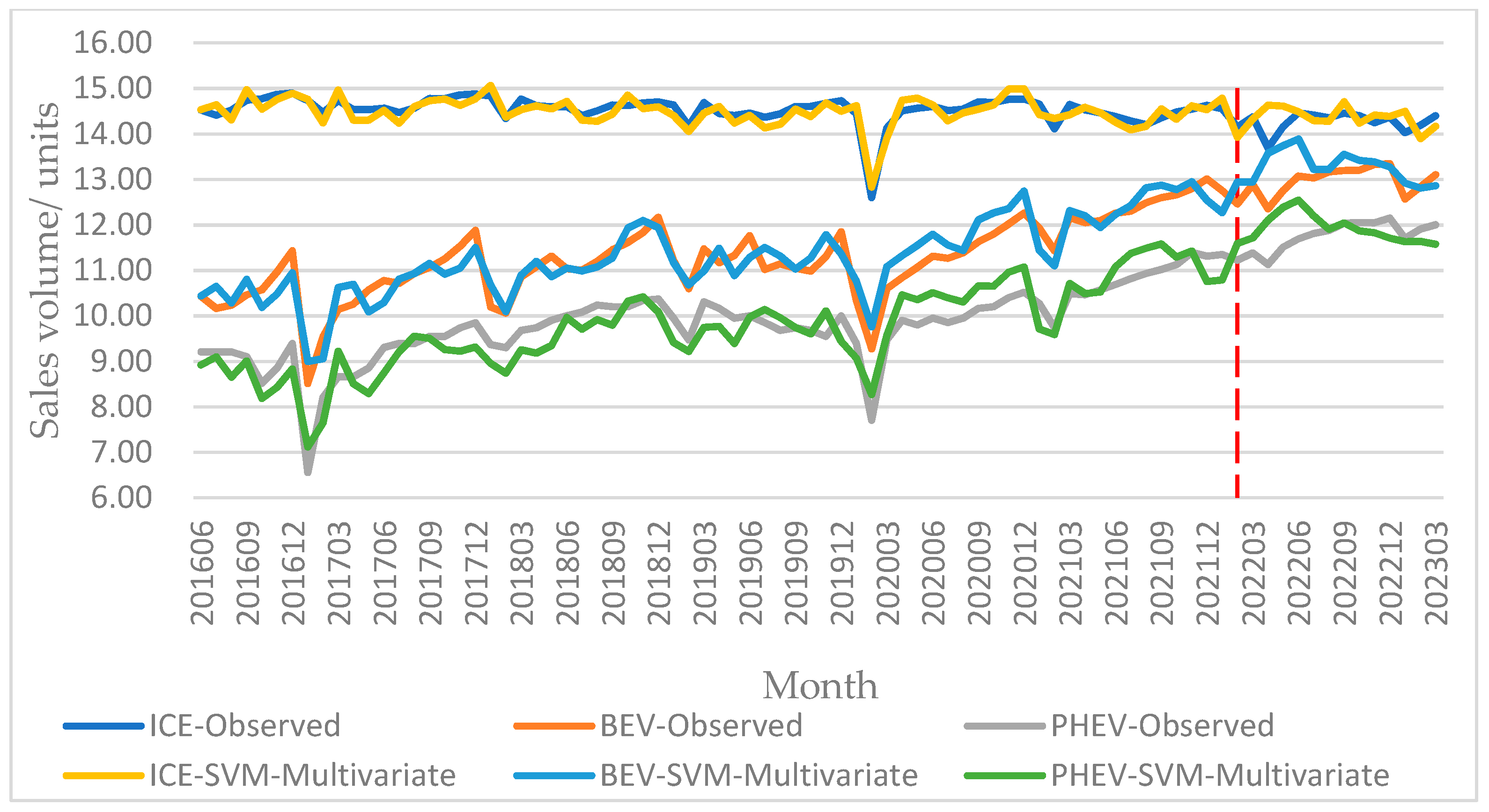
3.2.3. Predictive Results of SVM Model
3.2.4. Prediction Results of Multivariate BP Neural Network Model
3.2.5. Error Comparison
3.3. Comparison and Analysis of Prediction Accuracy
3.3.1. Comparison with Existing Literature
3.3.2. Comparison between Univariate Prediction Models and Multivariate Prediction Models
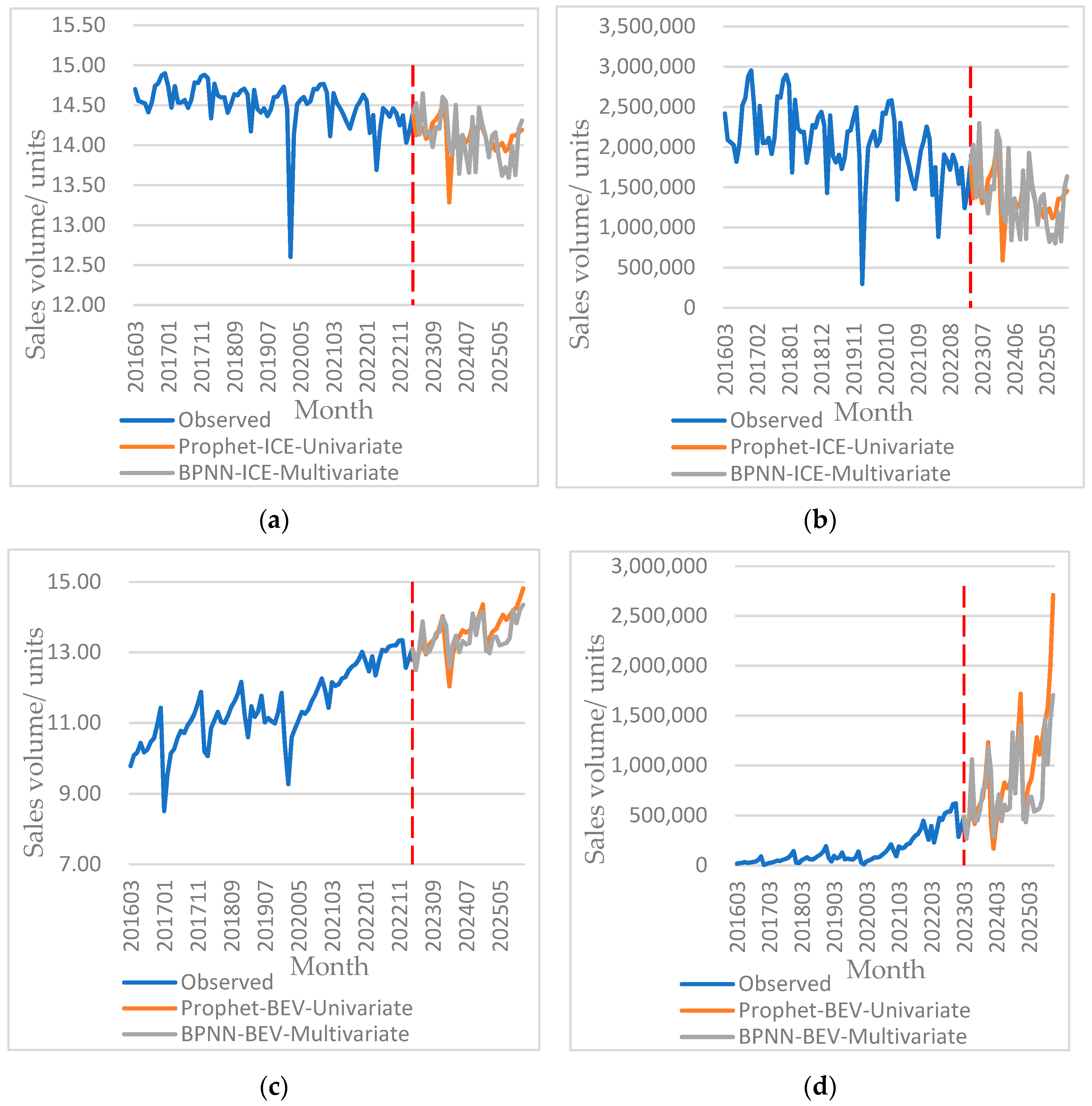
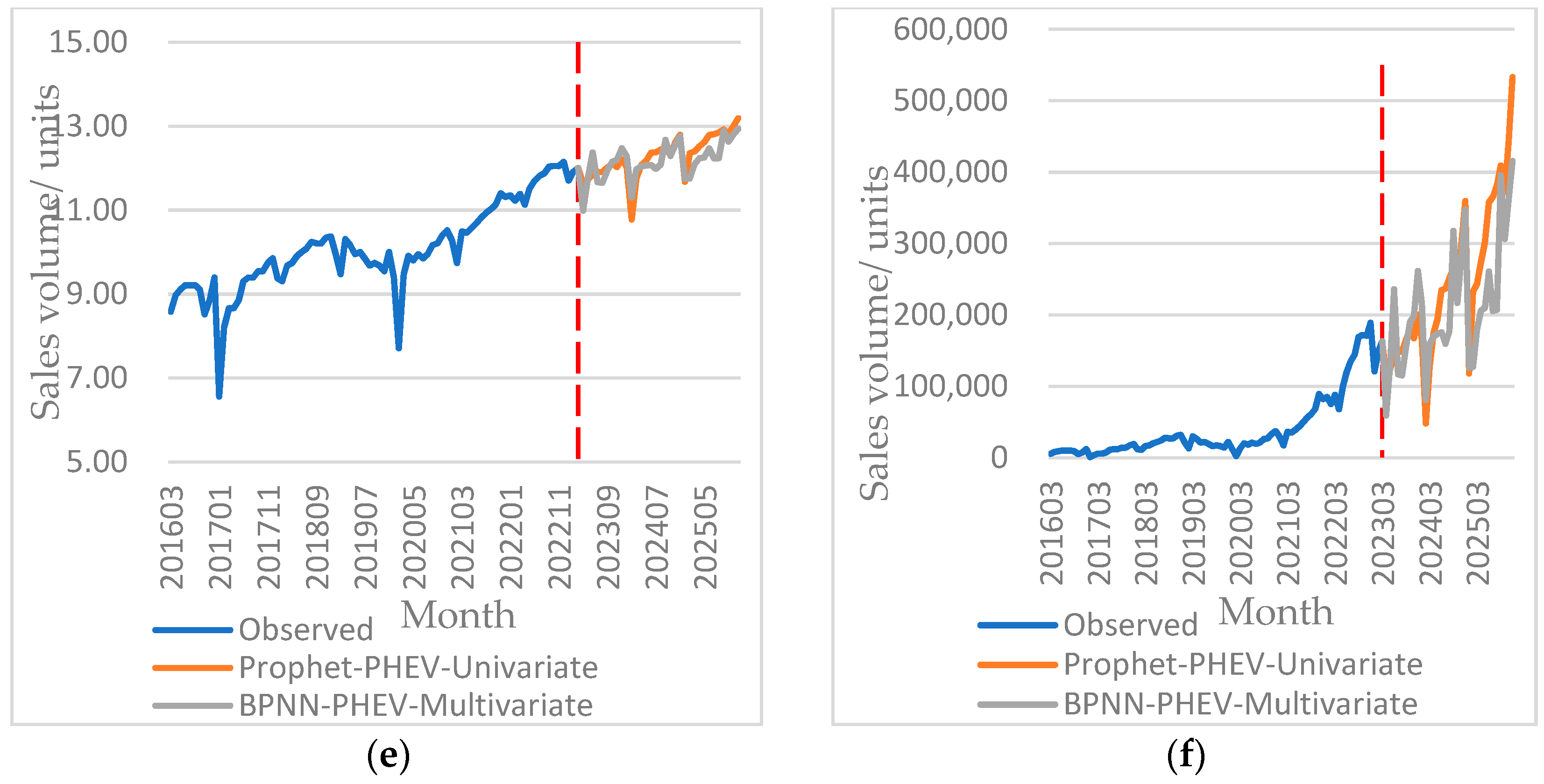
3.4. Extrasample Prediction Result
4. Conclusions
5. Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, L.Y.; Liu, S.F.; Wu, L.F.; Zhu, J.S.; Shang, G. Forecasting the development trend of new energy vehicles in China by an optimized fractional discrete grey power model. J. Clean Prod. 2022, 372, 13. [Google Scholar] [CrossRef]
- Ding, S.; Li, R.J. Forecasting the sales and stock of electric vehicles using a novel self-adaptive optimized grey model. Eng. Appl. Artif. Intell. 2021, 100, 13. [Google Scholar] [CrossRef]
- Lin, B.Q.; Wu, W. Why people want to buy electric vehicle: An empirical study in first-tier cities of China. Energy Policy 2018, 112, 233–241. [Google Scholar] [CrossRef]
- Huang, Y.L.; Qian, L.X. Consumer preferences for electric vehicles in lower tier cities of China: Evidences from south Jiangsu region. Transport. Res. Part D-Transport. Environ. 2018, 63, 482–497. [Google Scholar] [CrossRef]
- Chen, K.; Ren, C.R.; Gu, R.; Zhang, P.D. Exploring purchase intentions of new energy vehicles: From the perspective of frugality and the concept of “mianzi”. J. Clean Prod. 2019, 230, 700–708. [Google Scholar] [CrossRef]
- Zhao, M.; Sun, T.; Feng, Q. Capital allocation efficiency, technological innovation and vehicle carbon emissions: Evidence from a panel threshold model of Chinese new energy vehicles enterprises. Sci. Total Environ. 2021, 784, 11. [Google Scholar] [CrossRef] [PubMed]
- Egbue, O.; Long, S.; Samaranayake, V.A. Mass deployment of sustainable transportation: Evaluation of factors that influence electric vehicle adoption. Clean Technol. Environ. Policy 2017, 19, 1927–1939. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhao, C.Y.; Yin, J.H.; Zhang, B. Purchasing intentions of Chinese citizens on new energy vehicles: How should one respond to current preferential policy? J. Clean Prod. 2017, 161, 1000–1010. [Google Scholar] [CrossRef]
- Yang, Z.L.; Li, Q.; Yan, Y.M.; Shang, W.L.; Ochieng, W. Examining influence factors of Chinese electric vehicle market demand based on online reviews under moderating effect of subsidy policy. Appl. Energy 2022, 326, 120019. [Google Scholar] [CrossRef]
- Wang, N.; Tang, L.H.; Pan, H.Z. Analysis of public acceptance of electric vehicles: An empirical study in Shanghai. Technol. Forecast. Soc. Chang. 2018, 126, 284–291. [Google Scholar] [CrossRef]
- Baur, D.G.; Todorova, N. Automobile manufacturers, electric vehicles and the price of oil. Energy Econ. 2018, 74, 252–262. [Google Scholar] [CrossRef]
- Austmann, L.M.; Vigne, S.A. Does environmental awareness fuel the electric vehicle market? A twitter keyword analysis. Energy Econ. 2021, 101, 105337. [Google Scholar] [CrossRef]
- Ou, S.Q.; Lin, Z.H.; Xu, G.Q.; Hao, X.; Li, H.W.; Gao, Z.M.; He, X.; Przesmitzki, S.; Bouchard, J. The retailed gasoline price in china: Time-series analysis and future trend projection. Energy 2020, 191, 116544. [Google Scholar] [CrossRef]
- Zhuge, C.X.; Wei, B.R.; Shao, C.F.; Dong, C.J.; Meng, M.; Zhang, J. The potential influence of cost-related factors on the adoption of electric vehicle: An integrated micro-simulation approach. J. Clean Prod. 2020, 250, 119479. [Google Scholar] [CrossRef]
- Li, X.; Xiao, X.P.; Guo, H. A novel grey bass extended model considering price factors for the demand forecasting of European new energy vehicles. Neural Comput. Appl. 2022, 34, 11521–11537. [Google Scholar] [CrossRef]
- Hsieh, I.Y.L.; Kishimoto, P.N.; Green, W.H. Incorporating multiple uncertainties into projections of Chinese private car sales and stock. Transp. Res. Rec. 2018, 2672, 182–193. [Google Scholar] [CrossRef]
- Kumar, R.R.; Guha, P.; Chakraborty, A. Comparative assessment and selection of electric vehicle diffusion models: A global outlook. Energy 2022, 238, 16. [Google Scholar] [CrossRef]
- Rietmann, N.; Hugler, B.; Lieven, T. Forecasting the trajectory of electric vehicle sales and the consequences for worldwide CO2 emissions. J. Clean Prod. 2020, 261, 16. [Google Scholar] [CrossRef]
- Zhou, H.M.; Dang, Y.G.; Yang, Y.J.; Wang, J.J.; Yang, S.W. An optimized nonlinear time-varying grey Bernoulli model and its application in forecasting the stock and sales of electric vehicles. Energy 2023, 263, 14. [Google Scholar] [CrossRef]
- Pei, L.L.; Li, Q. Forecasting quarterly sales volume of the new energy vehicles industry in China using a data grouping approach-based nonlinear grey Bernoulli model. Sustainability 2019, 11, 1247. [Google Scholar] [CrossRef]
- Li, S.X.; Chen, H.; Zhang, G.F. Comparison of the short-term forecasting accuracy on battery electric vehicle between modified bass and Lotka-Volterra model: A case study of China. J. Adv. Transp. 2017, 2017, 7801837. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Xu, H.Y.; Ma, N.; Pan, X.L. Intelligent vehicle sales prediction based on online public opinion and online search index. Sustainability 2022, 14, 10344. [Google Scholar] [CrossRef]
- Liu, B.C.; Song, C.Y.; Wang, Q.S.; Zhang, X.M.; Chen, J.L. Research on regional differences of China’s new energy vehicles promotion policies: A perspective of sales volume forecasting. Energy 2022, 248, 13. [Google Scholar] [CrossRef]
- Xia, Z.C.; Xue, S.; Wu, L.B.; Sun, J.X.; Chen, Y.J.; Zhang, R. Forexgboost: Passenger car sales prediction based on XGBoost. Distrib. Parallel Databases 2020, 38, 713–738. [Google Scholar] [CrossRef]
- Wu, M.F.; Chen, W. Forecast of electric vehicle sales in the world and China based on PCA-GRNN. Sustainability 2022, 14, 2206. [Google Scholar] [CrossRef]
- Liu, J.P.; Chen, L.J.; Luo, R.; Zhu, J.M. A combination model based on multi-angle feature extraction and sentiment analysis: Application to EVS sales forecasting. Expert Syst. Appl. 2023, 224, 13. [Google Scholar] [CrossRef]
- Ding, Y.; Wu, P.; Zhao, J.; Zhou, L.G. Forecasting product sales using text mining: A case study in new energy vehicle. Electron. Commer. Res. 2023, 33. [Google Scholar] [CrossRef]
- Sun, S.H.; Wang, W.C. Analysis on the market evolution of new energy vehicle based on population competition model. Transport. Res. Part D-Transport. Environ. 2018, 65, 36–50. [Google Scholar] [CrossRef]
- Guo, D.; Yan, W.; Gao, X.B.; Hao, Y.J.; Xu, Y.; Wenjuan, E.; Tan, X.C.; Zhang, T.Q. Forecast of passenger car market structure and environmental impact analysis in China. Sci. Total Environ. 2021, 772, 17. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.H.; Zhang, Q.; Huang, C.Y. Empirical mode decomposition based hybrid ensemble model for electrical energy consumption forecasting of the cement grinding process. Measurement 2019, 138, 314–324. [Google Scholar] [CrossRef]
- Zhang, C.Q.; Liu, M.; Wang, D.Y.; Ni, A.N.; Xiao, G.N.; Lu, W.T. Linkage mechanism of public transport subsidy: Considering passenger ridership, cost, fare and service quality. Transp. Lett. 2022. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E.; Natarajan, S.; McCullen, N. A comparative assessment of SARIMA, LSTM RNN and Fb prophet models to forecast total and peak monthly energy demand for India. Energy Policy 2022, 168, 113097. [Google Scholar] [CrossRef]
- Guefano, S.; Tamba, J.G.; Azong, T.E.W.; Monkam, L. Forecast of electricity consumption in the Cameroonian residential sector by grey and vector autoregressive models. Energy 2021, 214, 118791. [Google Scholar] [CrossRef]
- Alashari, M.; El-Rayes, K.; Attalla, M.; Al-Ghzawi, M. Multivariate time series and regression models for forecasting annual maintenance costs of EPDM roofing systems. J. Build. Eng. 2022, 54, 104618. [Google Scholar] [CrossRef]
- Maqsood, H.; Maqsood, M.; Yasmin, S.; Mehmood, I.; Moon, J.; Rho, S. Analyzing the stock exchange markets of EU nations: A case study of brexit social media sentiment. Systems 2022, 10, 24. [Google Scholar] [CrossRef]
- Ahmed, Q.I.; Attar, H.; Amer, A.; Deif, M.A.; Solyman, A.A.A. Development of a hybrid support vector machine with grey wolf optimization algorithm for detection of the solar power plants anomalies. Systems 2023, 11, 237. [Google Scholar] [CrossRef]
- Guo, L.; Bai, L.F.; Liu, Y.X.; Yang, Y.Z.; Guo, X.H. Research on the impact of covid-19 on the spatiotemporal distribution of carbon dioxide emissions in China. Heliyon 2023, 9, e13963. [Google Scholar] [CrossRef]
- Ran, Q.Y.; Bu, F.B.; Razzaq, A.; Ge, W.F.; Peng, J.; Yang, X.D.; Xu, Y. When will China’s industrial carbon emissions peak? Evidence from machine learning. Environ. Sci. Pollut. Res. 2023, 30, 57960–57974. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.; Gao, J.X.; Wang, J.J.; Han, J. An empirical study of early warning model on the number of coal mine accidents in China. Saf. Sci. 2020, 123, 104559. [Google Scholar] [CrossRef]
- Li, Y.; Huang, S.Y.; Miao, L.; Wu, Z. Simulation analysis of carbon peak path in China from a multi-scenario perspective: Evidence from random forest and back propagation neural network models. Environ. Sci. Pollut. Res. 2023, 30, 46711–46726. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, M.; Geng, N.N.; Jiang, Y.J. Forecasting electric vehicles sales with univariate and multivariate time series models: The case of China. PLoS ONE 2017, 12, 15. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Yang, D.L.; Dang, Y.G.; Wang, J.J. An enhanced multivariable dynamic time-delay discrete grey forecasting model for predicting China’s carbon emissions. Energy 2022, 249, 123681. [Google Scholar] [CrossRef]
- Liu, B.C.; Song, C.Y.; Liang, X.Q.; Lai, M.Z.; Yu, Z.C.; Ji, J. Regional differences in China’s electric vehicle sales forecasting: Under supply-demand policy scenarios. Energy Policy 2023, 177, 13. [Google Scholar] [CrossRef]
- Pelegov, D.V.; Chanaron, J.J. Electric car market analysis using open data: Sales, volatility assessment, and forecasting. Sustainability 2023, 15, 399. [Google Scholar] [CrossRef]





| Variable | Meaning | Variable | Meaning |
|---|---|---|---|
| Y1 | Sales volume of traditional fuel vehicles (units) | X7 | Average price of new energy vehicles (10,000 CNY) |
| Y2 | Sales volume of battery electric vehicles (units) | X8 | Patents granted for electric vehicles (units) |
| Y3 | Sales volume of plug-in hybrid vehicles (units) | X9 | Effective patents granted for power batteries (units) |
| X1 | Consumer price index (%) | X10 | Output of lithium-ion batteries (million units) |
| X2 | Customs exports (100 million USD) | X11 | Hydroelectric power generation (100 million kWh) |
| X3 | Customs imports (100 million USD) | X12 | Nuclear power generation (100 million kWh) |
| X4 | Total value of imports (1000 USD) | X13 | Employee index (%) |
| X5 | Total export value (1000 USD) | X14 | Highway passenger traffic (ten thousand people) |
| X6 | Average price of traditional fuel vehicles (10,000 CNY) |
| Target Sequence | Number of Plies | Activation Function of Each Layer | Number of Neurons | Training Times | Learning Rate | Loss Function |
|---|---|---|---|---|---|---|
| Traditional fuel vehicle | 3 | ‘relu’, ‘relu’, ‘linear’ | 12 × 6 × 1 | 500 | 0.0001 | MSE |
| Battery electric vehicle | 3 | ‘relu’, ‘relu’, ‘linear’ | 12 × 7 × 1 | 600 | 0.0001 | MSE |
| Plug-in hybrid vehicle | 3 | ‘relu’, ‘relu’, ‘linear’ | 12 × 7 × 1 | 500 | 0.0001 | MSE |
| Model | Error Type | Evaluating Indicator | ICE | BEV | PHEV |
|---|---|---|---|---|---|
| BP Neural Network | Fitting Error | MAPE | 1.042% | 2.488% | 2.214% |
| RMSE | 0.262 | 0.405 | 0.329 | ||
| Predicting Error | MAPE | 0.956% | 1.921% | 2.591% | |
| RMSE | 0.240 | 0.298 | 0.335 | ||
| Quadratic Exponential Smoothing | Fitting Error | MAPE | 0.606% | 1.621% | 1.708% |
| RMSE | 0.150 | 0.276 | 0.241 | ||
| Predicting Error | MAPE | 1.296% | 1.816% | 1.412% | |
| RMSE | 0.234 | 0.274 | 0.231 | ||
| Prophet | Fitting Error | MAPE | 0.688% | 1.715% | 2.842% |
| RMSE | 0.142 | 0.267 | 0.357 | ||
| Predicting Error | MAPE | 2.068% | 3.382% | 1.605% | |
| RMSE | 0.363 | 0.596 | 0.296 |
| Variable | Inspection Type | ADF | 1% Critical Value | 5% Critical Value | 10% Critical Value | Prob | Stationarity |
|---|---|---|---|---|---|---|---|
| LNY1 | (C, T, 0) | −6.3515 | −4.0925 | −3.4744 | −3.1645 | 0.0000 | stationary |
| LNY2 | (C, T, 0) | −4.8055 | −4.0925 | −3.4744 | −3.1645 | 0.0011 | stationary |
| LNY3 | (C, T, 0) | −4.6803 | −4.0925 | −3.4744 | −3.1645 | 0.0017 | stationary |
| LNX1 | (C, T, 1) | −6.6209 | −4.0946 | −3.4753 | −3.1650 | 0.0000 | stationary |
| LNX2 | (C, T, 0) | −5.8395 | −4.0925 | −3.4744 | −3.1645 | 0.0000 | stationary |
| LNX3 | (C, T, 0) | −5.1623 | −4.0925 | −3.4744 | −3.1645 | 0.0003 | stationary |
| LNX4 | (C, T, 0) | −5.2278 | −4.0925 | −3.4744 | −3.1645 | 0.0003 | stationary |
| LNX5 | (C, T, 0) | −5.3067 | −4.0925 | −3.4744 | −3.1645 | 0.0002 | stationary |
| LNX6 | (C, T, 0) | −7.7677 | −4.0925 | −3.4744 | −3.1645 | 0.0000 | stationary |
| LNX7 | (C, T, 0) | −8.2087 | −4.0925 | −3.4744 | −3.1645 | 0.0000 | stationary |
| LNX8 | (C, T, 0) | −8.9109 | −4.0925 | −3.4744 | −3.1645 | 0.0000 | stationary |
| LNX9 | (C, T, 0) | −4.2731 | −4.0925 | −3.4744 | −3.1645 | 0.0059 | stationary |
| LNX10 | (C, T, 5) | −7.5827 | −4.1032 | −3.4794 | −3.1674 | 0.0000 | stationary |
| LNX11 | (C, T, 1) | −5.4392 | −4.0946 | −3.4753 | −3.1650 | 0.0001 | stationary |
| LNX12 | (C, T, 0) | −7.9333 | −4.0925 | −3.4744 | −3.1645 | 0.0000 | stationary |
| LNX13 | (C, T, 0) | −4.1356 | −4.0925 | −3.4744 | −3.1645 | 0.0088 | stationary |
| LNX14 | (C, T, 0) | −6.3515 | −4.0925 | −3.4744 | −3.1645 | 0.0000 | stationary |
| Lag | LogL | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|---|
| 0 | 1109.297 | NA | 1.99 × 10−35 | −31.66079 | −31.11036 | −31.44242 |
| 1 | 1783.608 | 996.8069 | 3.46 × 10−40 | −42.82922 | −32.92144 | −38.89847 |
| 2 | 2195.351 | 405.7754 | 4.64 × 10−41 | −46.38698 | −27.12185 | −38.74386 |
| 3 | 3304.615 | 546.5942 * | 8.68 × 10−49 * | −70.16276 * | −41.54030 * | −58.80728 * |
| Influencing Factors | LNY1 | LNY2 | LNY3 | Influencing Factors | LNY1 | LNY2 | LNY3 | Influencing Factors | LNY1 | LNY2 | LNY3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LNX1 (−1) | −0.631 | 12.767 | 18.913 | LNX7 (−1) | −0.551 | −2.106 | −2.307 | LNX13 (−1) | 3.743 | 13.676 | −1.277 |
| LNX1 (−2) | 3.979 | −8.368 | 10.437 | LNX7 (−2) | −0.342 | −0.884 | 0.000 | LNX13 (−2) | −4.586 | 2.206 | 11.620 |
| LNX1 (−3) | 7.134 | 52.144 | 54.138 | LNX7 (−3) | 0.183 | 1.522 | 0.118 | LNX13 (−3) | 3.248 | 5.035 | 1.930 |
| LNX2 (−1) | −3.008 | 5.272 | 14.088 | LNX8 (−1) | 0.008 | 0.181 | 0.440 | LNX14 (−1) | 0.105 | −2.728 | −2.396 |
| LNX2 (−2) | 3.827 | 12.092 | 11.119 | LNX8 (−2) | 0.088 | 0.352 | 0.280 | LNX14 (−2) | −0.253 | 1.793 | 0.745 |
| LNX2 (−3) | 1.151 | 3.442 | 0.740 | LNX8 (−3) | 0.037 | 0.289 | 0.043 | LNX14 (−3) | −0.373 | 0.274 | 0.061 |
| LNX3 (−1) | 9.710 | 5.202 | 3.057 | LNX9 (−1) | 0.154 | 0.142 | 0.570 | LNY1 (−1) | −0.502 | −0.263 | −0.054 |
| LNX3 (−2) | 0.049 | −34.069 | −60.848 | LNX9 (−2) | 0.176 | 0.533 | 1.072 | LNY1 (−2) | 0.259 | −0.781 | −1.590 |
| LNX3 (−3) | −13.110 | −29.194 | −5.944 | LNX9 (−3) | 0.088 | 0.227 | 0.732 | LNY1 (−3) | −0.006 | −0.619 | 0.135 |
| LNX4 (−1) | 2.084 | −6.401 | −16.612 | LNX10 (−1) | 0.388 | −0.436 | 0.449 | LNY2 (−1) | 0.183 | 0.198 | −0.078 |
| LNX4 (−2) | −5.447 | −13.362 | −13.635 | LNX10 (−2) | −0.272 | −1.021 | −0.649 | LNY2 (−2) | −0.025 | −0.202 | 0.441 |
| LNX4 (−3) | −1.815 | −3.493 | −1.794 | LNX10 (−3) | 0.044 | 1.302 | 0.321 | LNY2 (−3) | 0.118 | 0.461 | 0.089 |
| LNX5 (−1) | −8.802 | −4.380 | −3.387 | LNX11 (−1) | −0.105 | 1.280 | 0.911 | LNY3 (−1) | −0.362 | −0.846 | −0.477 |
| LNX5 (−2) | 0.628 | 34.117 | 60.329 | LNX11 (−2) | 0.133 | −1.581 | −1.070 | LNY3 (−2) | −0.054 | 0.326 | 0.276 |
| LNX5 (−3) | 12.731 | 26.898 | 6.157 | LNX11 (−3) | 0.794 | 0.948 | 0.718 | LNY3 (−3) | 0.163 | 0.933 | 0.736 |
| LNX6 (−1) | −0.149 | 1.526 | 1.468 | LNX12 (−1) | 0.267 | 1.806 | 0.429 | C | −12.037 | −666.481 | −697.181 |
| LNX6 (−2) | −0.169 | 0.634 | 0.759 | LNX12 (−2) | −0.763 | −5.404 | −2.570 | ||||
| LNX6 (−3) | −0.245 | −0.906 | −0.932 | LNX12 (−3) | −0.535 | 2.621 | −1.327 |
| Parameter | Number of Plies | Activation Function of Each Layer | Number of Neurons | Training Times | Learning Rate | Loss Function |
|---|---|---|---|---|---|---|
| Value | 3 | ‘relu’, ‘relu’, ‘linear’ | 51 × 9 × 3 | 500 | 0.0001 | MSE |
| Model | Error Type | Evaluating Indicator | ICE | BEV | PHEV |
|---|---|---|---|---|---|
| VAR | Fitting Error | MAPE | 0.145% | 0.894% | 1.014% |
| RMSE | 0.027 | 0.127 | 0.135 | ||
| Predicting Error | MAPE | 2.565% | 4.190% | 4.863% | |
| RMSE | 0.458 | 0.693 | 0.682 | ||
| SVM | Fitting Error | MAPE | 0.533% | 1.488% | 1.807% |
| RMSE | 0.147 | 0.304 | 0.345 | ||
| Predicting Error | MAPE | 1.280% | 2.389% | 2.168% | |
| RMSE | 0.381 | 0.598 | 0.512 | ||
| BP Neural Network | Fitting Error | MAPE | 0.321% | 1.088% | 1.357% |
| RMSE | 0.068 | 0.169 | 0.179 | ||
| Predicting Error | MAPE | 1.810% | 2.810% | 3.384% | |
| RMSE | 0.324 | 0.482 | 0.496 |
| Authors (Year) | Models | Cases | Performance |
|---|---|---|---|
| Liu et al. (2023) [43] | GRA-DWT-BiLSTM | The electric vehicle sales in China | MAPE: 9.411% |
| Zhang, et al. (2022) [22] | LSTM | The vehicle sales of NIO | MAPE: 9.7718% |
| The vehicle sales of XPeng | MAPE: 5.899% | ||
| Liu et al. (2022) [1] | DWT-BiLSTM | The electric vehicle sales in China | MAPE: 6.04% |
| Ding and Li (2021) [2] | ESOGM (1, 1) | Global electric vehicle sales | MAPE: 6.92% |
| Pei and Li (2022) [20] | DGA-based NGBM (1, 1) | The quarterly sales of new energy vehicles in China | RMSE: 23,907.59 MAPE: 7.26% |
| Advantages and Disadvantages | Univariate Prediction Models | Multivariate Prediction Models |
|---|---|---|
| Advantages | Effectively capture the trends and changing rules contained in the historical sales data of automobiles. | Make full use of the relationship between automobile sales and various factors to improve the generalization ability of the automobile sales forecasting model. |
| Disadvantages | Only one characteristic parameter is considered, and the information extracted is limited, which cannot reflect the influence of other variables in the system on automobile sales. | It is difficult to define the system boundary, and too many influencing factors may affect the extraction of automobile sales trend information. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, D.; Fang, Y.; Wang, S.; Zhao, M. Prediction of China Automobile Market Evolution Based on Univariate and Multivariate Perspectives. Systems 2023, 11, 431. https://doi.org/10.3390/systems11080431
Dai D, Fang Y, Wang S, Zhao M. Prediction of China Automobile Market Evolution Based on Univariate and Multivariate Perspectives. Systems. 2023; 11(8):431. https://doi.org/10.3390/systems11080431
Chicago/Turabian StyleDai, Debao, Yu Fang, Shihao Wang, and Min Zhao. 2023. "Prediction of China Automobile Market Evolution Based on Univariate and Multivariate Perspectives" Systems 11, no. 8: 431. https://doi.org/10.3390/systems11080431
APA StyleDai, D., Fang, Y., Wang, S., & Zhao, M. (2023). Prediction of China Automobile Market Evolution Based on Univariate and Multivariate Perspectives. Systems, 11(8), 431. https://doi.org/10.3390/systems11080431







