Virtual-Simulation-Based Multi-Objective Optimization of an Assembly Station in a Battery Production Factory

Abstract

The planning and design process of manufacturing factory layouts is commonly performed using digital tools, enabling engineers to define and test proposals in virtual environments before implementing them physically. However, this approach often relies on the experience of the engineers involved and input from various cross-disciplinary functions, leading to a time-consuming and subjective process with a high risk of human error. To address these challenges, new tools and methods are needed. The Industry 5.0 initiative aims to further automate and assist human tasks, reinforcing the human-centric perspective when making decisions that influence production environments and working conditions. This includes improving the layout planning process by making it more objective, efficient, and capable of considering multiple objectives simultaneously. This research presents a demonstrator solution for layout planning using digital support, incorporating a virtual multi-objective optimization approach to consider safety regulations, area boundaries, workers’ well-being, and walking distance. The demonstrator provides a cross-disciplinary and transparent approach to layout planning for an assembly station in the context of battery production. The demonstrator solution illustrates how layout planning can become a cross-disciplinary and transparent activity while being automated to a higher degree, providing results that support decision-making and balance cross-disciplinary requirements.

1. Introduction

Digital tools, such as computer-aided technologies (CAx), are widely used to plan, design, and simulate factory layouts in virtual environments before they are physically constructed [1]. These tools enable engineers and designers to identify potential issues and make necessary modifications to ensure that the planned design aligns with the requirements of different stakeholders [2]. The concept of the digital factory encompasses a range of planning activities that enhance product and production design, such as expansion possibilities, material flow and handling, area utilization, safety measures, work environment, and production capacity [3]. Due to the diverse nature of these activities, a variety of software tools are used to perform the different planning activities [4]. The various planning activities are interlinked as the output of one activity often serves as an input for another planning activity and vice versa [5].

However, despite the interdependencies among the various planning activities, they are often executed in isolation and sequentially, leading to slow progress and problematic iterations [6]. The Industry 4.0 initiative aims to automate and assist this kind of manual work, with digitalization to overcome the challenges, and the Industry 5.0 concept extends this initiative to reinforce the human-centric perspective and enable the human workforce to focus on complex tasks [7]. These digitalization concepts are expected to have a significant impact on smart industry and its connected systems [8].

Factory layout planning involves creating a planned description of the arrangement of resources and equipment within a factory, including the spatial positions of artifacts such as resources, equipment, and products that collectively define the factory setup [2].

In many companies, the planning and design of factory layouts is typically assigned to specific expert roles/staff and performed subjectively [9]. This is due to the fact that the staff planning the factory layout typically utilize their own experience and awareness of how layout planning is conducted, in turn meaning that vital information is often missed, such as achieving space claims regarding safety requirements, rules, and regulations.

The planning staff are responsible for defining the spatial positions of geometric descriptions of resources, equipment, and products, which collectively define the configuration of a factory [10]. The layout design must consider the space requirements of equipment setups, which are crucial for realizing the production process. Further it should adhere to design specifications, needed capacity, consumption rate, logistics capabilities, and worker and equipment safety, among other considerations. Consequently, planning and designing future factory setups become multi-criteria activities that require the simultaneous consideration of multiple objectives. In the context of factory layout projects, numerous proposals need to be designed, simulated, and optimized to provide decision-making material. These activities are frequently performed in virtual environments [10].

However, generating the virtual environment and keeping it updated, simulated, and optimal for all planning and design activities often rely on specific expert roles/staff and software tool users, who approach these tasks subjectively, manually, and sequentially, focusing on one objective at a time. This approach carries a significant risk of suboptimal solutions. This way of working highlights a need to enhance today’s manual and subjective process with digital support and multi-objective methods in the planning and design process of factory layouts. However, it should be noted that the planning and design activities are performed in virtual environments using virtual models, and those are meant to replicate, but are still not equivalent to, the real-world implementation of such planned and designed layouts. The current procedure of the real-world implementation depends on the execution ability to follow and verify the installation drawings when setting up the factory according to planned and designed proposals.

Positive attempts using multi-objective methods in manufacturing planning processes have been carried out, e.g., [11], which presents an industrial demonstrator focusing on optimizing a welding station process. However, that work does not consider changing positions of the equipment setup, meaning the layout planning itself is not optimized. There are few studies or demonstrators described in the research literature on the use of multi-objective methods for the optimization of layout design based on real industrial cases, e.g., the setup of equipment. The state-of-the-art method commonly found in the literature for the planning and design process of factory layouts refers to systematic layout planning (SLP) [2]. However, the way SLP is used and described in the literature simplifies the planning and design activities of factory layouts. The focus often revolves around optimizing the positions of rectangular or quadratic resources and equipment in a two-dimensional (2D) environment, e.g., [12,13], and primarily aims to minimize one or two objectives, e.g., area utilization and the distances between these rectangular-shaped equipment.

In a factory, it is not only the actual intended processes, products, and resources that need to claim area and space reservations. In order to be able to produce inside the factory, there also need to be space reservations for staff (this includes the consideration of anthropometric diversity in the workforce) and mobile equipment in order to perform the tasks of realizing the product and manufacturing process, carrying out maintenance tasks, and operating mobile equipment such as tugger trains and forklifts to supply the manufacturing process with material such as parts and consumables. Such space reservations extend beyond just two dimensions (2D), highlighting the need to consider three dimensions (3D) when planning and designing factory layouts. A clear argument for the importance of considering 3D, i.e., to also account for the height dimension, is that height affects the work conditions and worker well-being, e.g., with regard to lifting and picking objects when performing work tasks.

The planning and design of factory layouts need to consider several cross-disciplinary aspects and requirements from several stakeholders. However, there is a research gap in utilizing a multi-objective optimization method within the virtual planning and design process of factory layouts to simultaneously consider requirements related to safety regulations, worker well-being, and worker movements. Therefore, the objective of this work is to investigate, describe, and demonstrate, with an industrial battery production workstation as a use case, how a simulation-based multi-objective optimization method can be used for factory layout planning, by which requirements related to safety regulations, worker well-being for workers of different anthropometry, and distances walked by workers in the layout, can be considered simultaneously. By achieving this, the research seeks to bridge the gap between cross-discipline objectives, handled by different engineering roles, and provide decision-makers with optimized factory layout proposals that comply with rules and regulations, ultimately enhancing the work environment and improving the quality of life for the workers.

2. Materials and Methods

To realize the demonstrator solution, the software Industrial Path Solutions (IPS) was utilized to run series of simulations of differently configured virtual environments. The IPS software is a math-based tool that offers several capabilities including rigid body path planning [14], simulation of flexible components (soft materials capable of bending) [15], digital human modelling (DHM) with ergonomics simulations [16], optimization of robot and multi-robot stations [17], and surface treatment processes [18]. IPS features an application programming interface (API) for the open-source lightweight scripting language LUA [19]. Bespoke LUA scripts were developed to exchange information via JavaScript Object Notation (JSON) [20] files to set up the different virtual environments and run the simulations in IPS, and a bespoke Python (PY) program was developed to run the NSGA-II algorithm, which is an evolutionary algorithm for multi-objective optimization [21]. The development of the LUA and PY script series was essential to establish the communication between the IPS software and the NSGA-II algorithm and to run the optimizations. The NSGA-II algorithm is well-suited for multi-criteria decision-making scenarios where there are more than two objectives that need to be optimized simultaneously. The algorithm facilitates the generation and identification of non-dominated solutions, i.e., the Pareto front, for the defined objectives of the multi-objective optimization [21].

2.1. Use Case Description

In total, four staff members (expert, process, logistic, and layout engineers) were interviewed (semi-structured interviews) at a battery production factory. The details of the use case, a greenfield battery assembly station, were clarified and selected.

The interviewees confirmed that the planning process of a factory layout is a multi-objective optimization activity. For this specific targeted assembly station, several potential simulation-based proposals had already been created for the project and discussions were still in process to decide which of these proposals was to be selected and implemented. The planning staff members wanted to investigate whether multi-objective optimization could be utilized in the factory layout planning process, and in total, 3 objectives (

Table 1. Objectives of the optimization.

Symbol	Description	Unit
AU	Minimize the area utilization of the resources in the material façade.	M2
OWASL-Index	Minimize the musculoskeletal load for the workers.	Index
DW	Minimize the distance walked by the workers.	M

) were decided: the minimization of area utilization (AU), the minimization of musculoskeletal load for the workers (OWAS_L-Index), and the minimization of distance walked by the workers (DW). These are objectives commonly used in layout optimization, e.g., Tsarouchi et al. [22].

The assembly station includes 6 tasks (position a busbar support, mount the busbar support with a bolt, tighten the bolt, position busbars one and two, and mount the busbars with four bolts). To clarify, the assumption for this study is that the task list and the order of the tasks is decided upon, i.e., it is not possible to change.

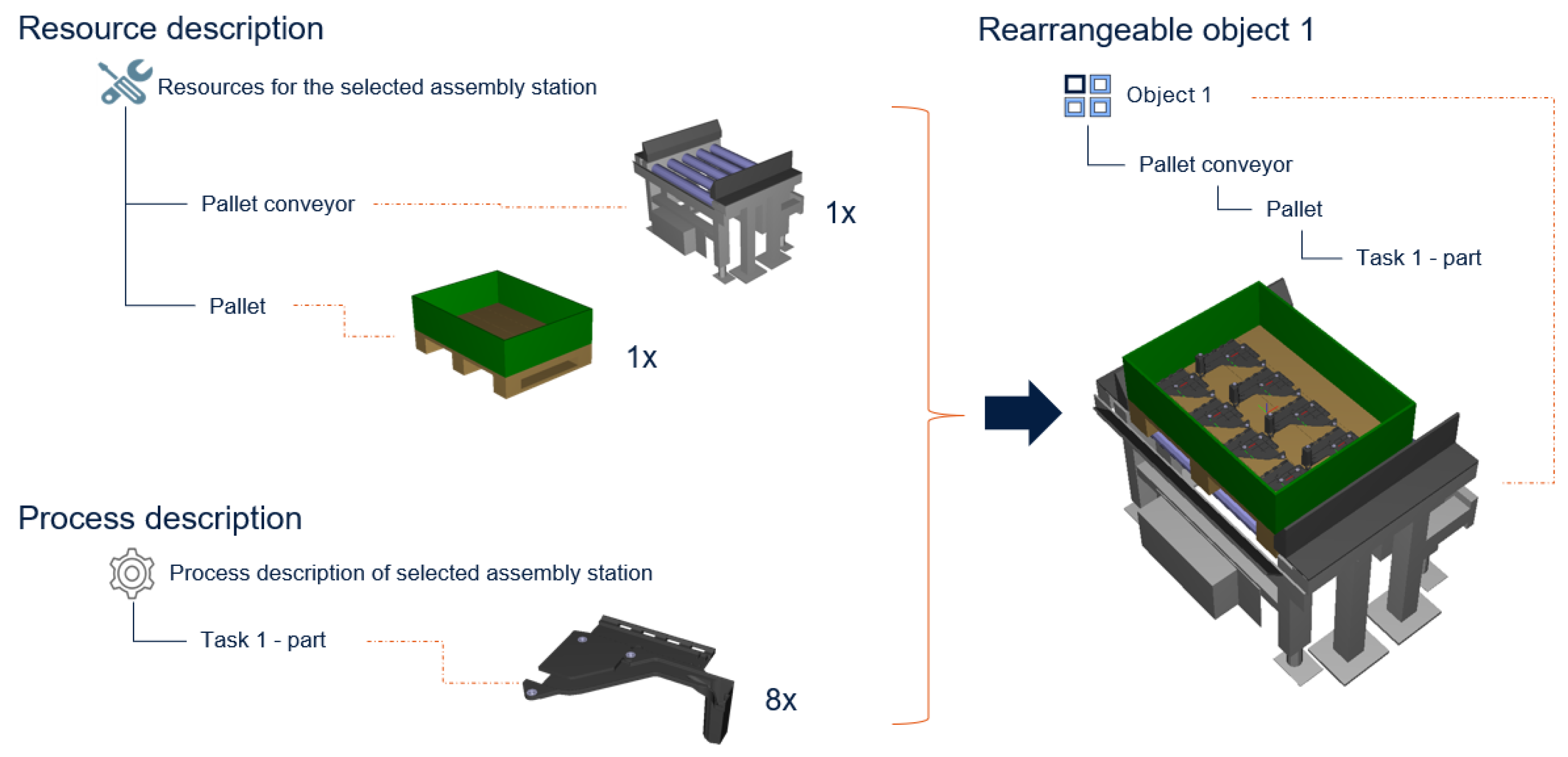
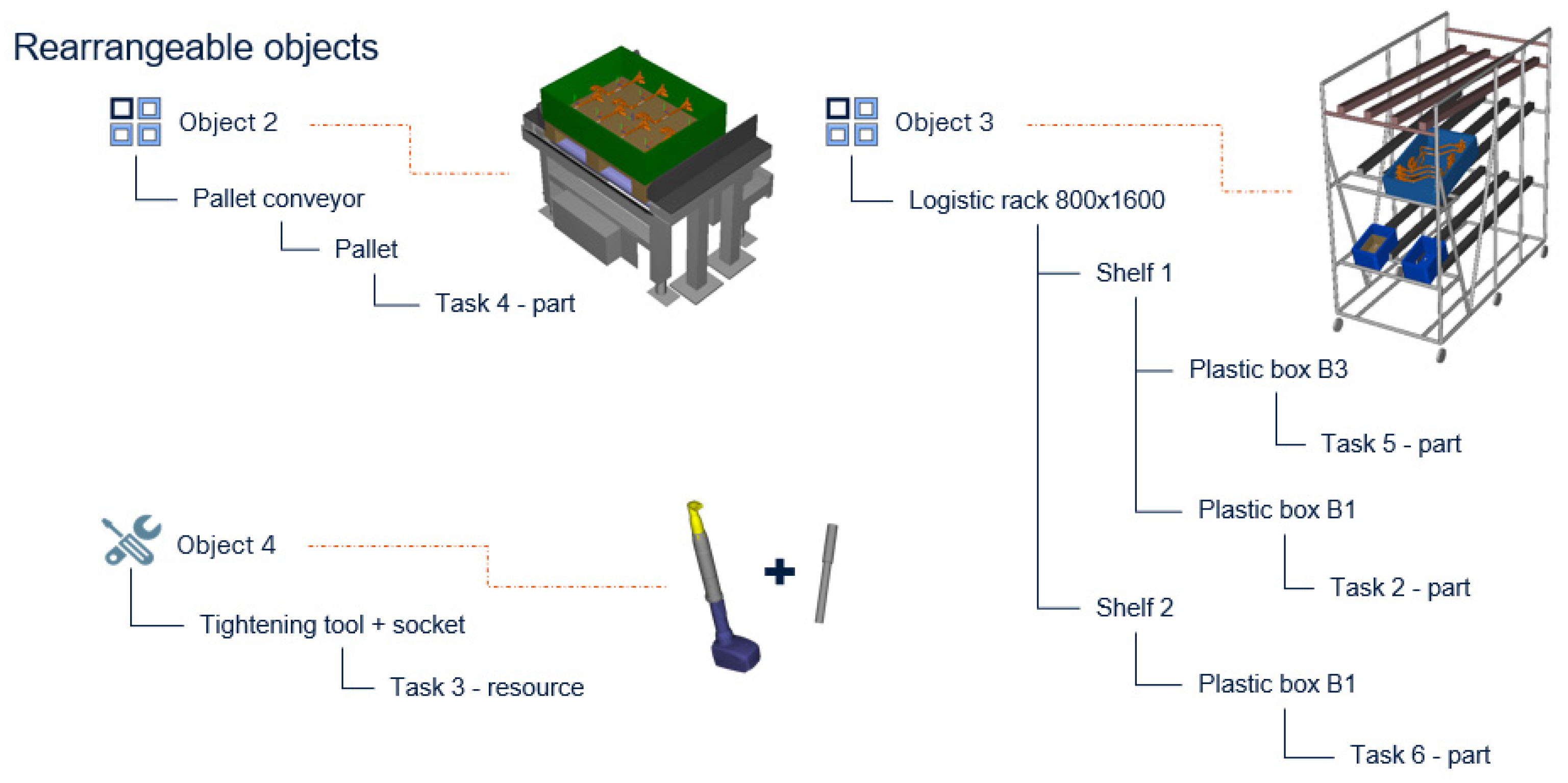
The assembly station consists of two pallet conveyors with one pallet each and one logistic rack containing three plastic boxes used as a material façade. In addition, a tightening tool with a socket is used by the assembly staff, and the two pallet conveyors are refilled by autonomous mobile robots (AMRs). To clarify, the assumption for this study is that the resource description is decided upon, i.e., it is not possible to change.

By combining the resource objects and the assembly task list, the material façade/resource descriptions of the rearrangeable objects of the assembly station were established (objects 1, 2, 3, and 4) (Figure 1 and Figure 2). This also includes the assumed patterns of the parts’ start positions within the rearrangeable objects. Object 1 and object 2 are pallet conveyors, object 3 is a logistic rack with 2 adjustable shelves used to provide parts for the assembly, and object 4 is a tightening tool resource and does not require a pattern. These resources (objects 1, 2, 3, and 4) were decided by the planning staff to be rearrangeable in the assembly station setup. To clarify, the assumption for this study is that the layout performance depends on the spatial position setup of these four objects, i.e., the multi-objective optimization depends on the tested spatial positions of these four objects.

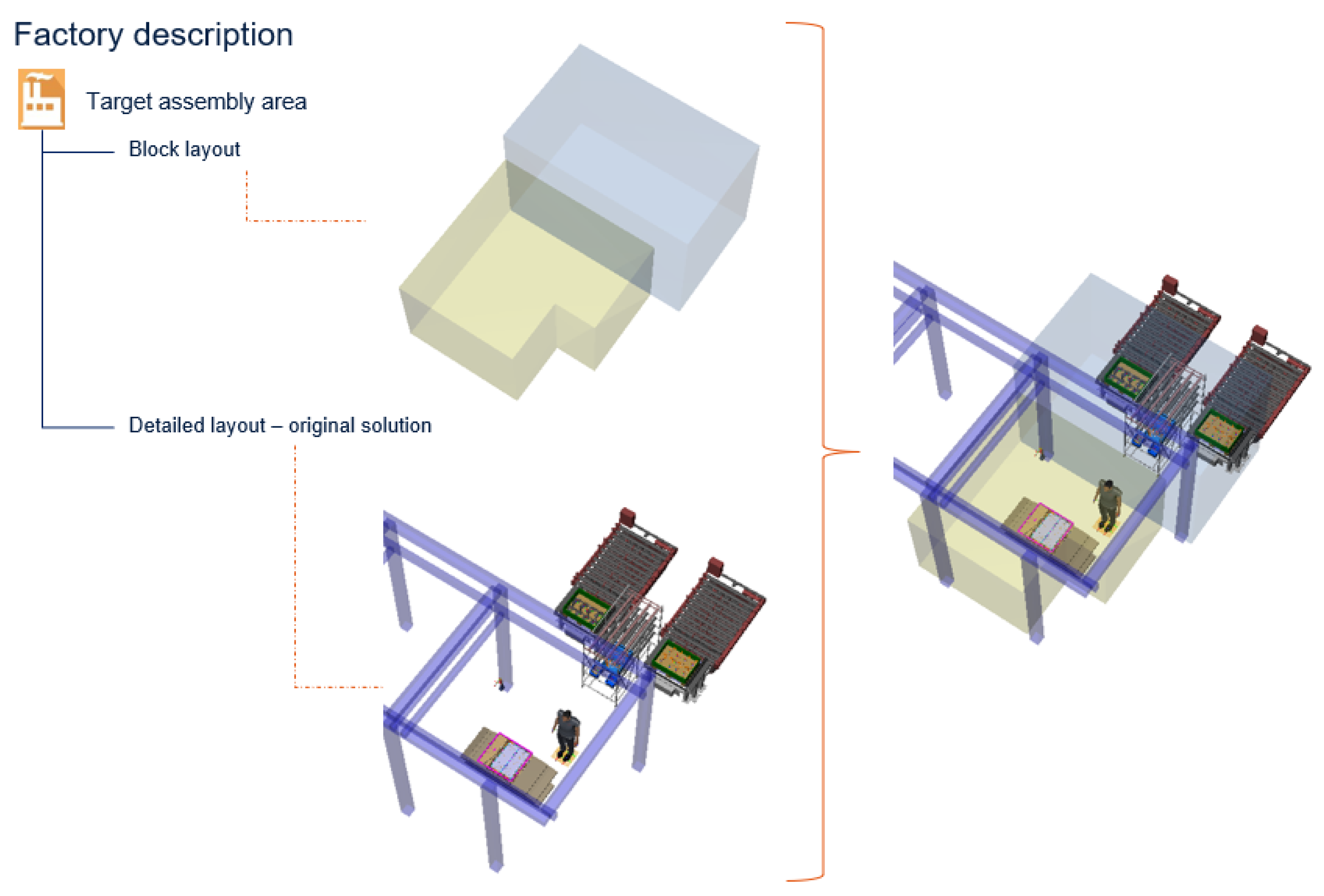
Since the use case deals with an ongoing greenfield (new factory design, development, and construction) project, and with the assumption of a frozen, manually optimized starting proposal of an assembly station (in this work referred to as the original solution) and that there are other adjacent greenfield production areas, the scope was restricted so that the area/volume claims of the potential solutions generated by the optimization algorithm could not exceed the current area/volume claims of the original solution. This means the equipment needs to be positioned within the block layout displayed in Figure 3.

Given this assumption, objects 1, 2, 3, and 4 need to be spatially within the same volume as the block layout of the original solution.

2.2. Definition of the Virtual Environment, Manikins, and Constraints

The virtual environment imported to the DHM module in IPS, i.e., IPS IMMA, consists of the building model and individual models of the resource objects and parts spatially positioned in relation to the building’s point of origin.

When designing a factory layout, it is not only the actual intended processes, products, and equipment (passive and active) geometry that need to claim area/volume reservations [22]. Associated with these objects, there are often different rules, regulations, and requirements, meaning that around the geometry of any object, a layout planner needs to consider additional space claims, e.g., safety distances and spaces needed for equipment to operate.

Therefore, the LUA API of IPS was utilized to create bespoke scripts for the definition and generation of additional space claims for the AMRs and humans accessing the material façade.

With the virtual environment imported to IPS IMMA, a family of 10 manikins (digital human models) consisting of 5 males and 5 females, representing the Swedish population of females and males aged 18–65 [16], with a 95% accommodation level with regard to variability in stature and body weight [16] was instantiated, as given in

Table 2. Manikin family, Swedish female and male population, respectively, with 95% accommodation level.

Manikin, [F = Female, M = Male]	Stature, s [mm]|Percentile	Body Weight, w [kg]|Percentile
F1	1530|1.7	41|1.5
F2	1589|10.9	78|88.5
F3	1673|49.7	64|47.1
F4	1758|89.4	51|10.5
F5	1816|98.2	87|97.8
M1	1639|1.5	47|1.4
M2	1711|12.6	93|86.9
M3	1791|49.7	77|48.5
M4	1871|87.1	61|11.6
M5	1943|98.4	107|98.4

. This manikin family was used to incorporate the consideration of anthropometric diversity among workers in the context of factory layout planning.

In the context of the original solution, as given in Figure 3, and with the assembly task list given, an operation sequence was built into the IPS IMMA software, i.e., defining the tasks that the manikins were to perform in the simulation. The simulation of this sequence is presented with an online animation at https://doi.org/10.5878/gat9-m562. With this operation sequence, the manikin family could simulate the process of collecting parts from the material façade (objects 1, 2, and 3) as well as collecting the tightening tool (object 4) and simulate the assembly.

2.3. Definition of Objectives

The IPS IMMA software offers the possibility to read out parameter values from the simulation. Two values were retrieved: the distance walked (DW) by each manikin in the manikin family and an ergonomics score, representing the workers’ well-being, of each manikin in the manikin family. The ergonomics evaluation method Ovako Working posture Assessment System (OWAS) [23], in combination with the Lundqvist index [24], was used to retrieve scores for the workers’ well-being (OWAS_L-Index). The original OWAS method enables the assessment of aggregated biomechanical load based on four subgroups (back, arms, legs, and lifted weight). However, this aggregated classification is only performed for instances in time, and therefore the OWAS was combined with the Lundqvist index to assess the aggregated biomechanical load over time. The Lundqvist index factor L was classified according to

Table 3. Classification of the Lundqvist index factor.

Lundqvist Index Factor	Description
L = 100 to 120	very little irksome
L = 121 to 140	little irksome
L = 141 to 160	rather irksome
L = 161 to 180	irksome
L = 181 to 200	very irksome
L > 200	very very irksome

[25].

With a virtual scene and a defined operation sequence set up in IPS, the simulation of the operation sequence can be executed. After running a simulation, the resulting values for two of the defined objectives of the virtual scene can be retrieved. This was performed for the original solution, and the results are given in

Table 4. The retrieved values of the original solution for the objectives, OWAS_L-Index and DW.

Manikin	OWASL-Index [Index]	DW [m]
F1	126	38.5
F2	124	38.4
F3	125	37.6
F4	132	38.4
F5	129	39.3
M1	127	38.7
M2	124	38.5
M3	129	39.4
M4	133	40.1
M5	133	42.0

. The retrieved values of OWAS_L-Index and DW vary between the manikins because the manikins represent different physical characteristics, such as variations in stature, leg length, and gait patterns. In turn, these variations affect the distance that each manikin can cover while walking and what postures each manikin assumes while performing work.

Since the optimization is to minimize the values of OWAS_L-Index and DW, the highest value of any manikin in the manikin family was decided to represent two critical values of each layout setup design proposal. In other words, for the original solution, manikin M4 and manikin M5 both give a max. OWAS_L-Index of 133, and manikin M5 gives a max. DW of 42 m. These maximum values represent the worst-case scenario of the layout setup, and the optimization algorithm should minimize these objectives for all iterations.

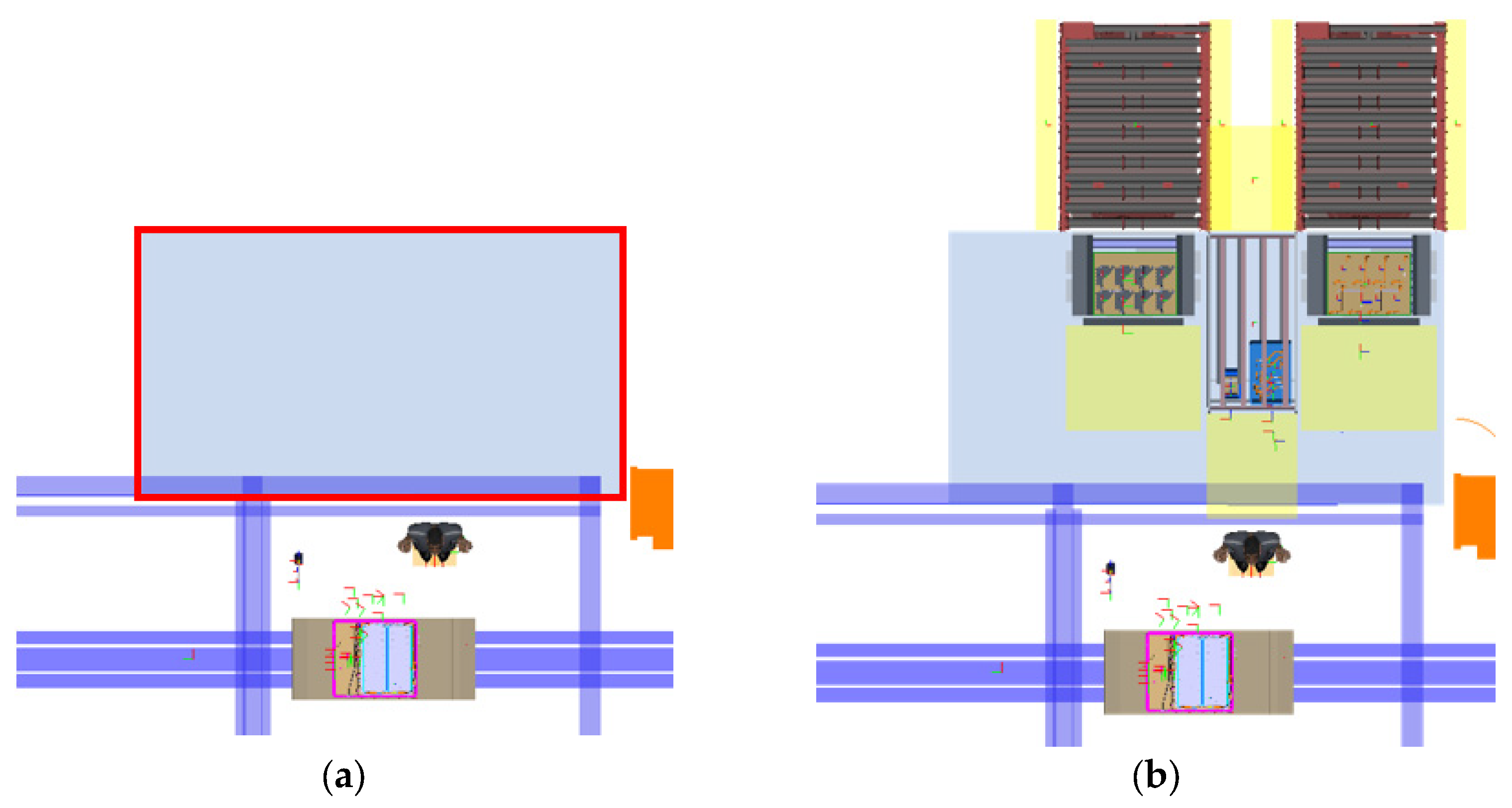
With a defined designated area and a block layout of the assembly station (Figure 4), the third optimization objective, area claim of the layout proposal, can be calculated accordingly.

The used area of the material façade of the layout proposal aligns with all parts of the geometrical sizes of objects 1, 2, and 3 and all additional extra space claims around the equipment inside the designated area of the assembly station, as given in Figure 4. The positions of objects 1, 2, and 3 can be retrieved with LUA scripts executed with the IPS software, and the bounding box of the different space claims, objects, and block layouts (designated areas) can then be retrieved and used to calculate the area utilized within the block layout. The area utilization of the original solution was calculated to 7.1 m². Object 4 and its space claim is neglected since it is a resource (small in comparison to other objects) hanging from a steel construction close to the actual executed assembly.

In addition, the IPS software also facilitates collision detection. LUA scripts were developed to read out information of collision tests, checking whether objects 1, 2, or 3 collide with each other or with any adjacent equipment or fixed equipment such as the steel construction.

2.4. Definition of the Optimization Problem

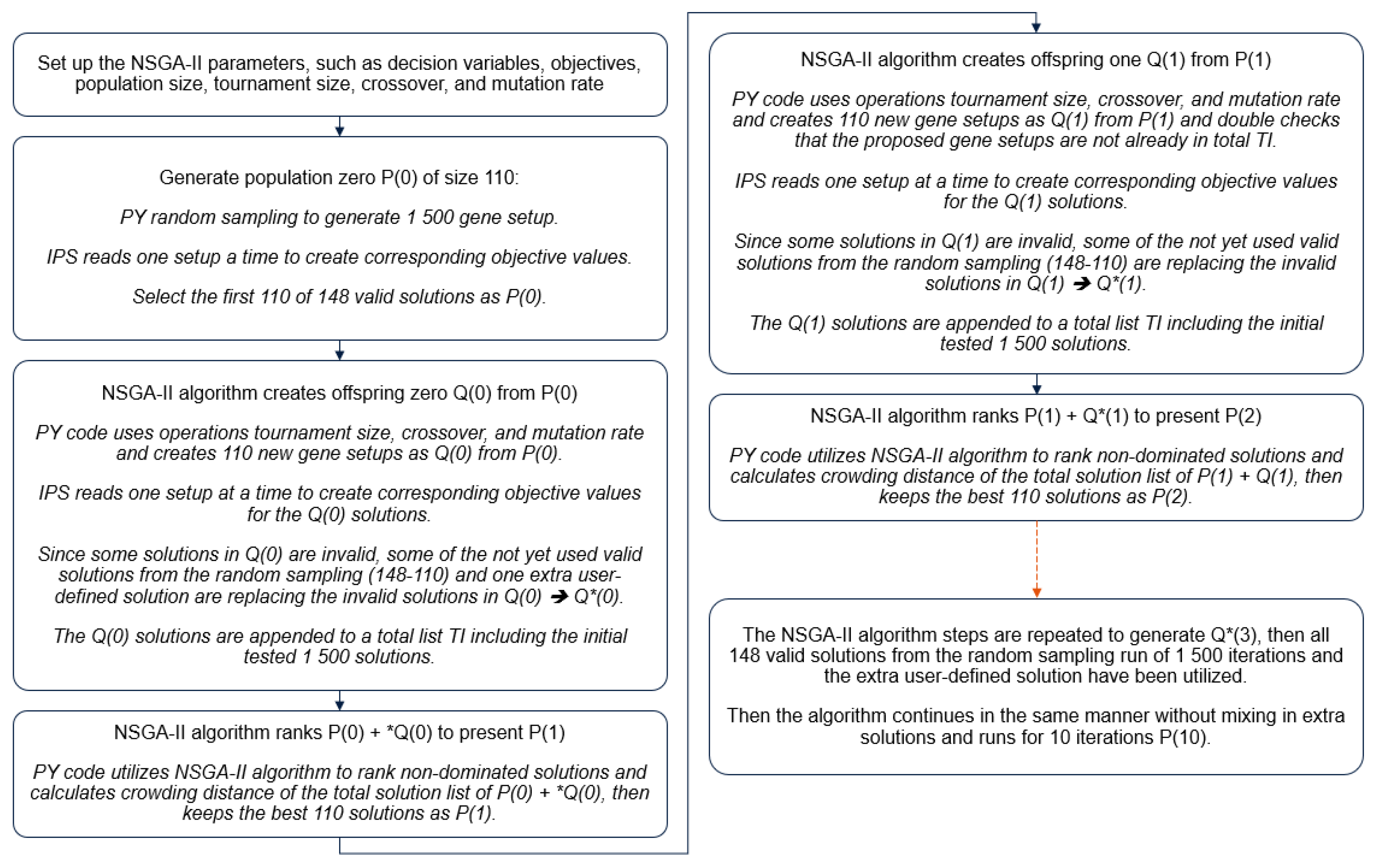
To enable the usage of the NSGA-II algorithm, the optimization problem needs to be defined. This involves specifying the decision variables (also referred to as the genes), objectives, and constraints of the optimization problem. The NSGA-II algorithm also needs parameters such as population size, number of iterations, tournament size, crossover and mutation operation, and selection method.

There are eleven decision variables for this multi-objective optimization of the assembly station, representing the spatial information of objects 1, 2, 3, and 4 (

Table 5. The eleven decision variables.

Decision Variable	Description	Datatype
var 1	Object 1: x coordinate	Float value with 3 decimals [m]
var 2	Object 1: y coordinate	Float value with 3 decimals [m]
var 3	Object 2: x coordinate	Float value with 3 decimals [m]
var 4	Object 2: y coordinate	Float value with 3 decimals [m]
var 5	Object 3: x coordinate	Float value with 3 decimals [m]
var 6	Object 3: y coordinate	Float value with 3 decimals [m]
var 7	Object 3, shelf 1: z coordinate	Float value with 3 decimals [m]
var 8	Object 3, shelf 2: z coordinate	Float value with 3 decimals [m]
var 9	Object 4: x coordinate	Float value with 3 decimals [m]
var 10	Object 4: y coordinate	Float value with 3 decimals [m]
var 11	Object 4: z coordinate	Float value with 3 decimals [m]

).

First, there are six decision variables to define the spatial positions of objects 1, 2, and 3 (Figure 1 and Figure 2) in the xy plane of the designated area (Figure 4). This designated area is considered as a constraint. Then, object 3 has two additional decision variables, i.e., two shelves that are variable in height. The planning staff members (expert, process, and layout engineers) then stated two additional constraints: shelf 1 can be allowed a variance in height between 0.42 and 0.62 m, and shelf 2 can be allowed a variance in height between 1 and 1.2 m. This means that shelf 1 is always beneath shelf 2. Additionally, there are three more decision variables linked to object 4 (the handheld tightening tool, see Figure 2). Object 4 can vary in a decided limited volume (decided by the planning staff member), close to the actual product assembly, hence within the following limits/constraints per direction: x (57.2–57.5 m), y (28.5–31.1 m), and z (1.5–2.2 m). In total, this is, then, eleven decision variables or genes to consider for the NSGA-II algorithm.

The constraints for the NSGA-II algorithm can be summarized to only allow the decision variables to be within set max. and min. values. For objects 1, 2, and 3, this is the designated area (Figure 4), together with max. and min. values of shelf 1 and shelf 2 of object 3 and the limited volume for object 4. In addition to these constraints, the IPS IMMA software has the capability to check collisions between objects and consequently a collision check is performed between objects 1, 2, 3, 4, and adjacent geometry, verifying both that the objects do not collide and that the objects are within the allowed max. and min. values.

2.4.1. Population Zero P(0)

In order to utilize the NSGA-II algorithm, an initial population of candidate solutions (parents) is required, referred to as population zero, P(0). Based on the number of decision variables (11) and the recommendation/rule of thumb to use 10 times the decision variables [21], a population size of 110 individuals was determined. These 110 individuals were created by random sampling via the developed PY code. In addition, one extra user-defined solution was added; see the second and third steps in the optimization procedure flowchart in Figure 5. The random sampling method of the PY script was set to run 1500 iterations, and the IPS software could then compute 148 solutions fulfilling the constraints (without errors) and the extra user-defined solution. The first 110 of the 148 feasible solutions were selected to establish P(0).

This resulting population P(0) then contained individuals, represented by 11 decision variable values and their 3 corresponding objective values. These individuals were then used as the starting point for the NSGA-II algorithm. In other words, the decision variable values and objective values for each individual in P(0) were used as the genes for the NSGA-II algorithm.

The PY code first read the designated area reservation (the min./max. size in the xy plane) of the virtual environment and continued reading out geometrical sizes of objects 1, 2, 3, and 4, the defined constraints of height levels of shelf 1 and shelf 2 (object 3), and the volume limitations for object 4. Then, the PY code used random sampling values for each of the 11 decision variables and proceeded by calculating possible overlapping of the proposed random sampling values of the objects, in other words checking collision detection between proposed solutions and, if collision was detected, disregarding those solutions. If there was no direct overlap of geometry, the 11 decision variables were sent to IPS with JSON format, and IPS rearranged the virtual scene based on the 11 decision variables.

First, IPS rearranged the virtual scene according to the 11 decision variables and also checked the proposed setup, meaning verifying that the objects were within the designated area, height, and volume limits (constraints); if invalid, the simulation did not run and the 11 decision variables were then presented with an error code in JSON format plus a screenshot of the tested layout in PNG format, as given in Figure 6. If the objects were within the designated area, IPS continued to also check if objects were in collision, including the added operation space claims and workspace claims (see definition of constraints in Section 2.2), not just testing whether the geometry collided but also making sure the additional space claims were fulfilled. If IPS found a collision, yet again the 11 decision variables were presented with an error code in JSON format plus a screenshot of the tested layout in PNG format.

If the provided JSON input from PY passed the IPS checks of being within limits and without collision, IPS started to run the simulation for the provided 11 decision variables and computed output for the three objectives (AU, DW, and OWAS_L-Index) plus a screenshot of the tested layout in PNG format. Regardless of whether decision variables are valid or invalid, the PNG allows for visual inspection of the tested setup.

An additional remark: in order to compare OWAS_L-Index, the percentual change (P) between the original solution and the NSGA-II-generated solutions was calculated using Equation (1); see also results in

Table 6. The values of the 3 objectives for the non-dominated individuals of P(10).

Solution Number	Area Utilization, AU [m2]	OWASL-Index,		Distance Walked, DW [m]
		[Index]	Description
Original solution *	7.10	133	little irksome	42.0
Solution nr: 2286	7.22 (+2%)	132 (P = −0.3%)	little irksome	39.8 (−5%)
Solution nr: 2358	7.48 (+5%)	129 (P = −1.3%)	little irksome	36.8 (−12%)
Solution nr: 2051	7.10 (±0%)	130 (P = −1.0%)	little irksome	41.0 (−2%)
Solution nr: 2110	7.23 (+2%)	131 (P = −0.7%)	little irksome	28.4 (−32%)
Solution nr: 2235	7.22 (+2%)	131 (P = −0.7%)	little irksome	40.6 (−3%)
Solution nr: 1501	7.10 (±0%)	133 (P = ±0.0%)	little irksome	40.0 (−5%)
Solution nr: 2217	7.25 (+2%)	131 (P = −0.7%)	little irksome	38.2 (−9%)
Solution nr: 2466	7.82 (+10%)	129 (P = −1.3%)	little irksome	36.3 (−14%)

* Original solution in collision, therefore unfeasible.

. OWAS_L-Index percentual change (P) was calculated as follows:

P [Solution nr] = (X2 − X1) / (b − a) * 100

(1)

where X2 = OWAS_L-Index [Solution nr], X1 = OWAS_L-Index [Original solution]. a = 100 (min. value of OWAS_L-Index), b = 400 (max. value of OWAS_L-Index).

2.4.2. Offspring, Tournament Size, Crossover Rate, and Mutation Rate

In the NSGA-II algorithm, tournament size, crossover rate, and mutation rate are three common operators used to generate new offspring solutions from existing solutions in the population [21]. The tournament size is the number of individuals randomly selected from the population to compete against each other in each generation of a child for the new offspring of the population. The tournament size used in this case was set to 7, which corresponds to a recommended interval of 5–10% of the population size, which was 110 [21]. During the tournament selection process, pairs of individuals are randomly selected from the tournament size, and the one with the best fitness score is selected as a parent for the next generation of a child. The tournament selection process ensures diversity in the creation of offspring and avoids selecting the same individuals as parents in each creation of a child. Then, the crossover rate determines the probability that two parents will produce an offspring with a combination of their genes. For this experiment, the crossover rate was set to 0.8. Furthermore, the actual crossover had one limitation: the genes 2, 4, and 6 (decision variables representing the y coordinates of objects 1, 2, and 3) were selected from one of the parents chosen to reproduce a child. This limitation was noticed after performing initial test runs of the algorithm and, if we had not kept this limitation, the algorithm would have produced many invalid proposals. Therefore, it was believed that this limitation would speed up the NSGA-II algorithm because collisions would occur less frequently. If the algorithm were to propose more mixing in the y direction, objects would be stacked on top of each other more often. However, this does not mean that the y variables could not be changed; the crossover allowed either of the two parents selected to spread the genes 2, 4, and 6; further, the mutation rate, set to 0.01, was added and could be applied to any of the 11 genes to increase diversity in the creation of offspring.

In summary, these parameters are essential in a genetic algorithm to achieve the balance between exploration (introducing new solutions) and exploitation (refining existing solutions) in the population.

Then, with the tournament size, crossover rate, and mutation rate set, a PY script was developed to create the offspring population zero Q(0) from the genes of population zero P(0); see the third step in the flowchart of the optimization procedure in Figure 5.

This PY script started by loading the P(0) and all 110 individuals with all corresponding 11 decision variable values and all 3 objective values. Then it utilized the NSGA-II method to select individuals from the P(0) based on tournament size and objective values, after which it continued with crossover and mutation operators to generate children with new genes. In addition, the PY script also cross-checked that a generated child with genes had not yet been tested in all the already tested solutions including the 1 500 random samples. If the gene setup had not yet been tested, it was added to the offspring list, and finally, 110 new individuals were added to the Q(0) and sent out as a comma-separated values (Q(0).csv) file.

2.4.3. Running of the Q(0) in IPS

The Q(0).csv file contained 110 new individuals with decision variables. Then, each individual needed to be simulated in IPS to retrieve the corresponding 3 objectives. With a similar approach as in Section 2.4.1 Population zero P(0), the solutions were tested to be inside the designated area and not in collision. If this criterion was met, the objective values were calculated and the csv file was appended with the objective values. Then, the tested individuals were added to the total list of tested individuals (total TI) 1500 + 110 new individuals to form a total ledger of tested individuals. See also the third step in the optimization procedure flowchart in Figure 5.

2.4.4. Generation of P(1)

There were solutions in the Q(0) with collisions, and the objectives were set to “inf” by IPS for these solutions. The unfeasible solutions would have been disregarded with the NSGA-II method, but instead they were exchanged with the feasible solutions from the remaining/unused feasible solutions from the initial random sampling of 1500 iterations and the extra user-defined solution. Thus, the Q(0) was modified to *Q(0), adding not yet used solutions from the random sampling + one extra user-defined solution.

With the list of P(0) and *Q(0), a PY script was developed, following the NSGA-II algorithm, combining all individuals and ranking them into Pareto fronts, with the non-dominated solutions, based on the three objectives, in rank 1 and with a calculated crowding distance to keep track of the diversity of the population. The final list of the best 110 individuals from P(0) and *Q(0) was passed to P(1), which then presented iteration one of the NSGA-II method. This is presented in the fourth step in the flowchart of the optimization procedure in Figure 5.

2.4.5. NSGA-II Iterations

The PY scripts described were then reused to generate N iterations of populations with offspring, using the NSGA-II approach, where combining P(N-1) and Q(N-1) will present P(N). If an offspring had unfeasible children after a simulation run in IPS, the extra solutions (148/1500) from the random sampling were mixed into the offspring until all the extra solutions were considered in the NSGA-II evaluation (Figure 5).

Also worth noticing is that the total number of previously tested individuals (total TI) grows by 110 new individuals with each offspring, and consequently, each offspring checked that the genes had not already been tested with the 1500 random samples or the tested offspring, the extra user-defined solution, or previous feasible and unfeasible offspring solutions (in other words, checking that new offspring has not already been tested in the total TI).

3. Results

With the collision detection function of the IPS software it was observed that the original solution was in fact in collision, hence not a feasible solution. Object 3 (the logistics rack where logistics staff are to refill components) in the original solution is positioned so that the additional operation space claim of the AMRs collides with the logistics rack. Therefore, the original solution setup would not enable the AMRs to operate; they would stop before refilling the pallet conveyors (objects 1 and 2).

The NSGA-II algorithm ran for 10 iterations, meaning that 10 populations were created and a total of 2601 solutions (1500 solutions run with random sampling to create the P(0) of the NSGA-II algorithm) were simulated with the IPS software. The developed LUA scripts for IPS read and wrote out (on request by the PY script) in JSON format the tested setup (the 11 genes) and corresponding three objectives values. In addition, the LUA script first checked that objects 1, 2, and 3 were positioned within the designated area (the block layout; this area can be remodelled by user request and therefore the script is generic). Additional LUA scripts then read the collision detection between objects 1, 2, 3, and 4 with regard to each other as well as the surrounding geometry. If any of these constraints were not fulfilled, the LUA script made sure no simulation run/time was spent on calculating the objective values (since violation of these constraints is unfeasible); rather, the objective of such a solution was set to “inf”.

The developed PY scripts could create a JSON file, readable by IPS, with input values of the 11 decision variables. The JSON file was created either with random sampling (the first 1500 solutions) or by utilizing the NSGA-II algorithm to create ranked populations and compute new offspring (solutions) to send via JSON to IPS one solution at a time.

The developed scripts and the DHM tool demonstrate that it is possible to use a simulation-based multi-objective optimization method for factory layout planning, where requirements related to safety regulations, worker well-being for a family of manikins, and distances walked by workers are considered simultaneously.

While the NSGA-II algorithm achieved identifying solutions dominating the original solution, there is no guarantee the real Pareto front has been achieved due to the complexity of the optimization problem. The NSGA-II algorithm includes a sorting process, which checks the current tested individuals (parents and children) and from this individual list sorts out individuals based on dominance; the solutions that are non-dominated are listed with rank 1 and presented as a Pareto front for the ranked solutions.

Population, P(10)

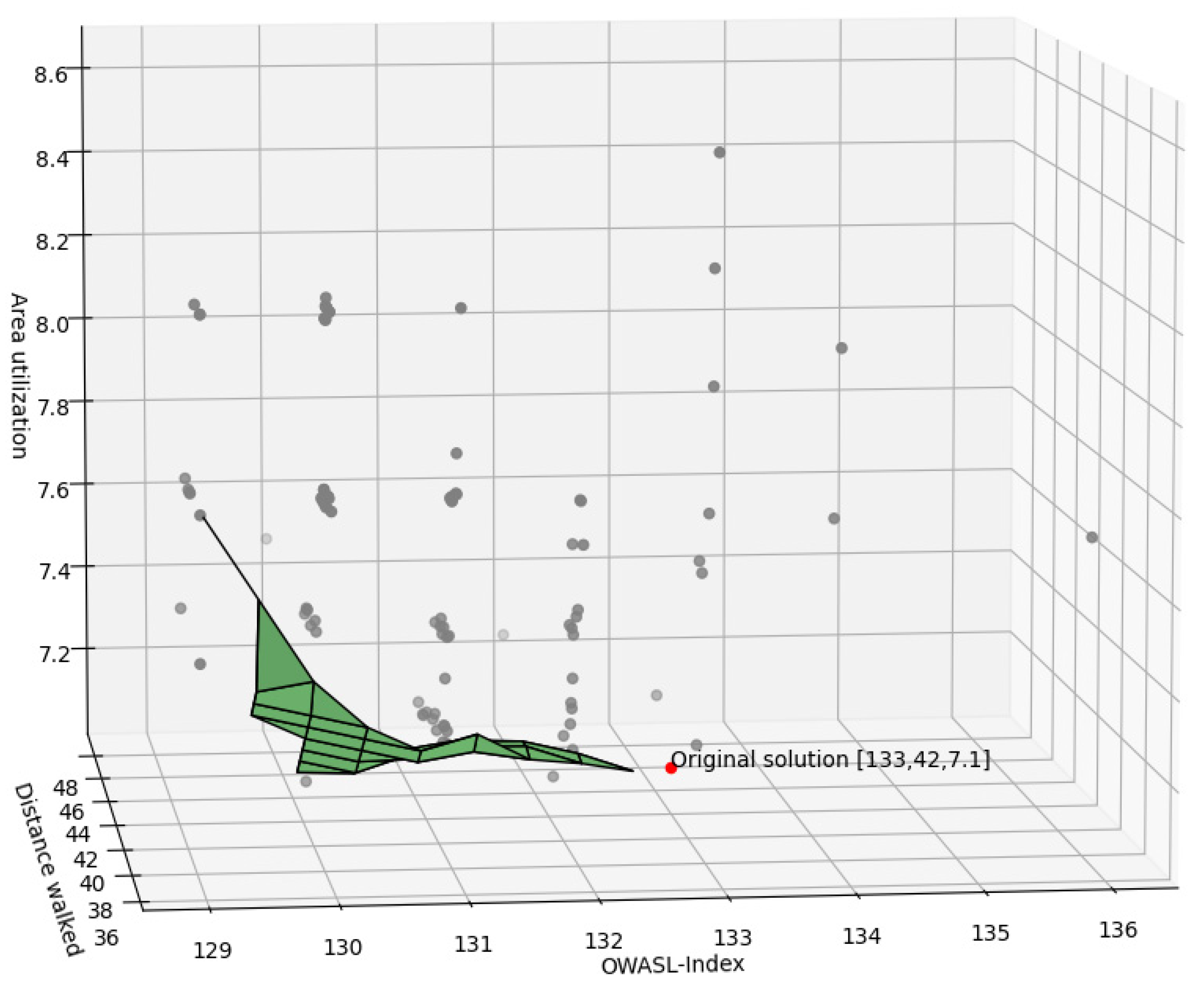
In Figure 7, a 3D plot displays the Pareto front of P(10) as a surface, formed by the eight non-dominated solutions considering the three optimization objectives. In addition, in the 3D plot, the dominated solutions of P(10) are scattered together with a red dot, the original solution (which is not feasible). It is worth pointing out that, if the original solution is not considered to be an unfeasible solution and instead its objective values are tested against the produced Pareto front, the original solution is dominated by two solutions in the Pareto front (solution 1501 and solution 2051 dominated the original solution).

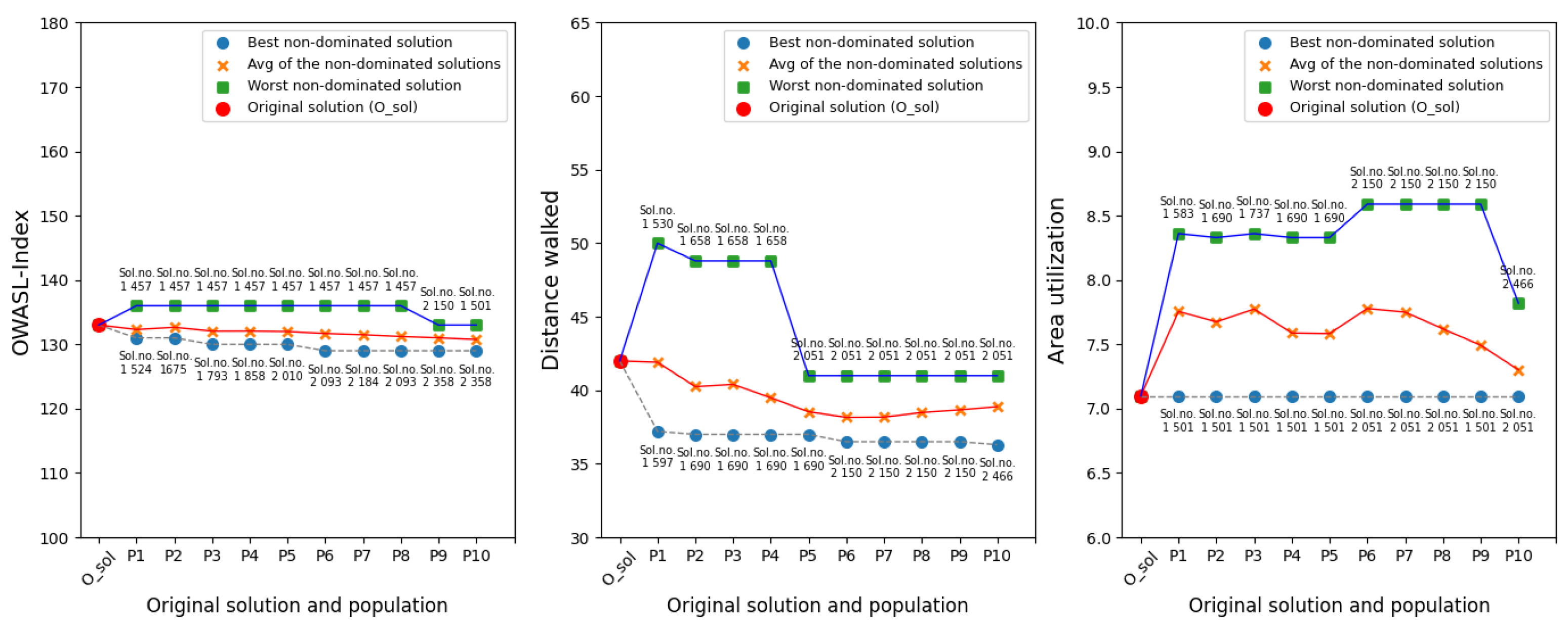
With each iteration/population created with the NSGA-II algorithm, the population was ranked. Then, to test whether convergence was reached with P(10), the best, average, and worst values of the three objectives of the non-dominated solutions of each population were compared (Figure 8). The best produced value for each objective was stable across all populations, the worst non-dominated solution had decreased for the objectives, and for the area utilization it was not possible to reach a lower area utilization than 7.1 m² within the designated area since then the objects sit next to the aisle for the AMRs.

Overall, in a minimization optimization problem, the objective is to find solutions that have lower values for all three objectives. In Figure 9, the box plots visualize the distribution of solutions across all iterated populations and provide insights into the central tendency, spread, outliers, and range of solution performance. A lower median value and smaller box indicates that the NSGA-II algorithm test has better-performing solutions considering the objectives.

From P(10), there were eight solutions defining the Pareto front. These solutions, with their solution numbers, are presented with their values of objectives and the percentage change compared with the original solution in Table 6.

In Table 6, it can be seen that two solutions dominate the original solution, meaning they have better or equal performance for all three objectives. All solutions on the Pareto front have shorter walking distance than the original solution. One solution reduced the distance walked by 32%. Furthermore, all solutions on the Pareto front have an OWAS_L-Index better than or equal to the original solution. Further, the Pareto front solutions have values between 120 and 140, which indicates a work situation being little irksome, Table 3. However, it should be noted that the observed percentual decrease in OWAS_L-Index is not equal to a significant improvement in the workers’ work situation. A qualitative evaluation of the actual index and the classifications of the Lundqvist index in Table 3 represents a clearer understanding of the workers’ work situation for each solution.

The NSGA algorithm was not able to find any solution with lower area utilization than the original invalid solution (however, it is not possible to reach a lower area utilization than 7.1 m² due to the sizes of the objects and the designated area; when a solution reaches 7.1 m², the objects are positioned next to the aisle for the AMRs). Two solutions on the Pareto front had the same area utilization as the original solution.

All the solutions listed in the Pareto front of P(10) are considered optimal. This means that each solution in the Pareto front represents an optimal solution regarding the optimization objectives while also fulfilling the constraints defined. Hence, the findings in Table 6 present possible solutions for which one can proceed with further analyses, in order to better investigate and understand the consequence of the layout proposals and then make informed decisions based on objective values.

The performed multi-objective optimization considers the constraints of the assembly station to position the equipment (objects 1, 2, 3, and 4) within a designated area together with the requirements of workspace and additional operation space claim in front of, behind, and around the equipment. Then, the multi-objective optimization successfully creates solutions and executes simulations to retrieve the specific values for the defined objectives.

When the PY script and IPS do not utilize the algorithm, the decision variables for any solution can be reloaded on request in IPS for visual inspection of such solutions. This means that decisions can be based on both comparing objective values among the solutions and visually comparing the differences between the layout solutions.

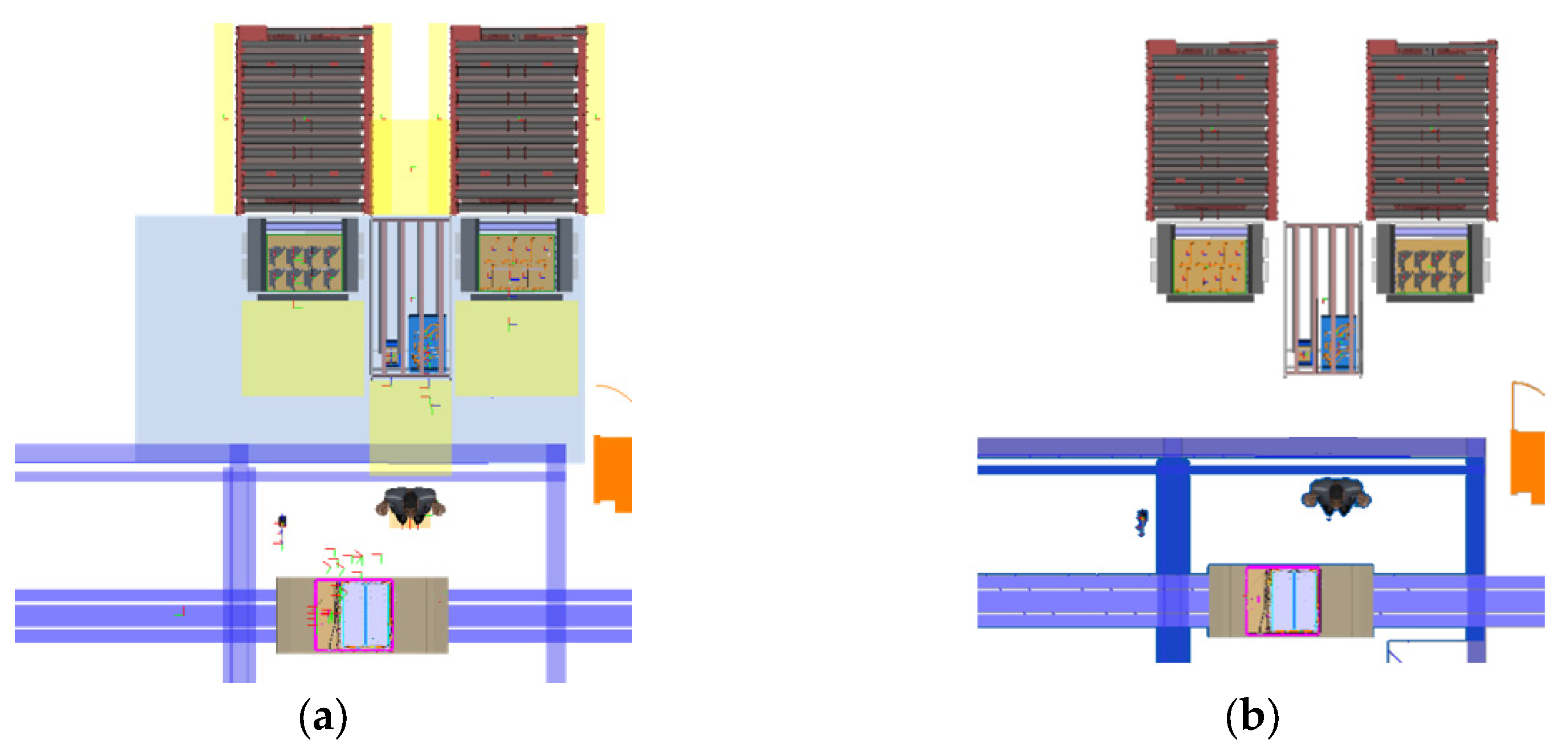
In Figure 10, solution 2051, part of the Pareto front of P(10) (se values of objectives, Table 6), is presented together with the original solution. Solution 2 051 has a slightly improved OWAS_L-Index, (percentual change P = −1.0%, which should correspond to a better situation for the workers’ well-being in the planned and designed work environment); in addition, the distance walked is also slightly decreased, by 2%, and the area utilization is kept at the minimum value of 7.1 m².

It is worth repeating that the NSGA-II algorithm only selects solutions for the iterated populations that comply with rules and regulations for the requirements of the workspace and additional operation space claims in front of, behind, and around the equipment and therefore positions all objects within the designated area.

4. Discussion

The activities involved in the planning and design process of factory layouts are important and have a significant impact on various aspects of manufacturing planning, including processes, resources, capacity, and ergonomics. Since these planning activities are interdependent, the output of one planning activity often serves as an input to another, and the lack of simultaneous consideration of all issues can lead to slow processes and suboptimal outcomes. This paper presents a demonstrator solution that illustrates how layout planning for an industry assembly station can be a transparent and cross-disciplinary activity. The proposed approach utilizes a multi-objective optimization approach to facilitate objective decision-making and display values behind proposed layout solutions.

From a production research and development perspective, the characteristics of the demonstrator solution align with two key focus areas in Industry 4.0: simulation and automation [7]. The approach taken in this study is to take advantage of simulation and combine it with an automated multi-objective optimization approach to generate several solutions and evaluate them in an automated manner. This approach is in line with Industry 4.0 principles and adds new capabilities of industrial development beyond Industry 4.0 potentially towards Industry 5.0 capabilities [7].

It is important to note that the concept of Industry 5.0 is still emerging and there is no universally accepted definition for it yet. However, based on the current discourse on the topic, it could be argued that the approach presented in this paper is in line with the general direction and potential characteristics of Industry 5.0, which is expected to be characterized by even greater automation, integration of digital technologies, and a stronger focus on sustainability and human-centred design.

4.1. Consideration of Results

The multi-objective optimization approach used for the use case of the assembly station presents promising results by providing feasible solutions to handle multiple decision variables, constraints, and objectives simultaneously. The algorithm used can generate several solutions in an automated manner and display corresponding results with numerical values and visual presentations of the layout solutions, making it easier for a development team of production engineers, logistics engineers, and ergonomists to make informed decisions on solutions that balance conflicting objectives.

In previous research, it was observed that the planning and design activities of factory layout areas are frequently associated with specific expert roles/staff and often performed in a subjective manner [9]. The planning staff then utilize their own personal experience and awareness of how to plan and design factory layouts; vital information can often be missed, such as acquiring space claims for safety requirements, rules, and regulations. This is also confirmed by this demonstrator and use case; the requirements for additional operation space claims of the AMR had been missed by the planning staff, meaning that the original solution is unfeasible. However, this demonstrator showcases enhanced digital support to generate and utilize these extra volumes, and by incorporating rules and recommendations into the software, the layout planning process becomes more transparent and traceable. The digital support provides guidance and ensures that important considerations are not overlooked, particularly when compared with manual processes that may be prone to human error or omission. This also enables stakeholders to understand the rationale behind the generated layouts and provides a basis for decision-making, as the software aligns with industry-specific guidelines and best practices.

The presented multi-objective approach encourages improvement and assists in design decisions to find better design solutions, although it should also be noted that the planning and design solutions are performed in virtual environments, and this is not equivalent to the real-world implementation of such planned and designed layout solutions. In order for engineers in the manufacturing development process to make the decision to proceed to execute the construction/setup of real production, usually several design proposals are generated, assessed, and discussed. Engineers typically utilize different tools in the CAx (computer-aided technologies) toolbox, consisting of virtual simulation tools utilized to generate the decision material.

The NSGA-II algorithm, combined with the demonstrator, exhibits advancements in handling and evaluating the work situation of a manikin family while generating layout proposals and rearranging rearrangeable objects within a designated area.

The virtual environments and models are meant to replicate real-world scenarios but are still not equivalent to the real-world implementation of such planned and designed layout. The current procedure of the real-world implementation depends on the execution ability to follow and verify the installation drawings when setting up the factory according to planned and designed proposals.

This approach represents an improvement over previous research that relied on permutations for arranging rearrangeable objects [11]. Unlike those prior methods, the demonstrator in this paper considers the limits of the designated area and can position the rearrangeable objects within the selected area without predefined permutations. This allows for more flexibility and adaptability in generating layout proposals, considering the specific constraints and requirements of the designated area without being locked into predefined arrangements.

Furthermore, this approach provides digital support to the layout planner by facilitating guidance in the planning tool to ensure that rules and regulations are not violated. The developed scripts for this purpose are generalizable and can be used to create volumes based on user-selected geometries in the simulation scene, making them suitable for various use cases. Overall, this multi-objective optimization approach aligns with the trend towards automating processes, supporting digital work with smart solutions for decision-making, and considering large datasets [6].

4.2. Consideration of Method

In this paper, the NSGA-II algorithm was used to demonstrate and conduct a multi-objective optimization of a simulation model of an assembly station in DHM-tool software. The quantitative relation between decision variables and optimization objectives is typically established through the objective function(s) and any constraints present in the problem. However, there was no meta-model/formula of the objective function in this case. The creation of the objective values depends on the simulation run performed by the DHM tool; then, via PY scripts, the values of the objectives are retrieved and evaluated and actions are taken by the NSGA-II algorithm. To complement this explanation, the NSGA-II algorithm proposes decision variables (the spatial positions of the four objects) based on the resulting objectives of the previous simulation runs. These decision variables are sent via PY script and JSON format and then read into the DHM tool, which sets up the spatial positions of the decision variables in the virtual environment and simulates the setup in order to retrieve corresponding objective values. When the DHM tool has retrieved the objective values, they are sent back via JSON format to the NSGA-II algorithm in order for it to proceed with the next decision. The objective to minimize the musculoskeletal load for the workers was evaluated with the OWAS Lundqvist index, which required the generation of the full motion of the manikins with the DHM tool in order to retrieve values of the index. Therefore, the evaluation and the creation of the objectives rely on the simulation results obtained from the DHM tool. The simulation was run in the DHM-tool software and was executed with a developed PY and LUA script series. The simulations and executions of all solutions were performed on a single computer, which required a significant amount of computational power. It took approximately 10–30 min to simulate each feasible solution and to retrieve the results; a total of 110 such solutions were required to generate one population. To make the utilization of multi-objective algorithms more industrialized, one could develop cluster sessions and send solutions/simulation jobs to different parallel computers to speed up the processing time required to generate each population. The generated offspring does not need to be run in sequence; to generate a new population, all offspring must have values for the objectives for each gene setup, and if running these in parallel, it would be expected that one offspring could be generated in 10–30 min for this use case.

Further, the NSGA-II algorithm could be extended to also consider the degree of constraint violation in order to determine the relative quality of infeasible solutions. By assigning constraint-handling techniques based on constraint-violation measures in IPS, NSGA-II can incorporate information about the proximity of solutions to feasibility. This could enable the algorithm to prioritize solutions with less constraint violation, facilitating a more nuanced comparison of infeasible solutions. Constraint violation will let the NSGA-II compare infeasible solutions; it should consider the solution with less violation as better.

The initial population P(0) was selected from the first 110 feasible solutions of a random sampling run of 1500 iterations; one extra user-defined solution was added. Then, during the iterations of the NSGA-II, the extra feasible solutions (after the first 110) from the initial 1500 random sampling run were mixed into the offspring and exchanged the “inf” solutions in the offspring. It could be argued, then, that this is unorthodox and not exclusively depending on the NSGA-II algorithm, but it could also be argued that it can be seen as a pragmatic approach. If the users define solutions and blend them in, the NSGA-II method should be able to rank the provided solutions, and if a user-defined solution can be dominated by an algorithm proposal, then this presents insights for the planning and design of the factory layout. Of course, one can rerun similar experiments and solely rely on the NSGA-II algorithm.

One could also consider other algorithms to explore, utilize, and compare with the NSGA-II algorithm to study the performance of algorithms when conducting multi-objective optimization in future studies. The NSGA-II algorithm was well-suited for this use case, which involved optimizing three objectives simultaneously [21].

In this use case, the OWAS_L-Index was utilized to assess workers’ well-being and evaluate aggregated biomechanical load over time. However, there are other ergonomics evaluation methods available that could be used, depending on the exposures being assessed. The OWAS_L-Index, along with calculating the distance walked for each worker per solution, was utilized as a system (layout) performance indicator. A shorter distance walked by each worker decreases the process time of the action sequence, but additional objectives could be considered in multi-objective optimization of factory layouts, e.g., minimizing material handling costs, optimizing energy consumption, and reducing environmental impact.

Another important aspect to consider is the anthropometric diversity among workers. In this use case, a manikin family representing the Swedish population within a 95% confidence interval was used, which is a step towards achieving Industry 5.0 objectives of more human-centric manufacturing systems in the future [26]. Depending on the use case, future optimization cases could include diversity by representation of other nationalities.

5. Conclusions

The planning and design process of a factory’s layout is a shared challenge for various experts and stakeholders across different fields, as it establishes the basis for the manufacturing potential. Currently, the outcome of a factory layout relies heavily on the communication and combined experience of cross-disciplinary experts, such as engineers and ergonomists, during the design and decision-making processes. This highlights the need for tools and methods that aid in the planning process of factory layouts, enabling informed decisions considering multiple objectives simultaneously. The presented demonstrator solution shows that multi-objective optimization can be utilized to plan factory layouts, evaluate workers’ well-being, and test layout setups of the equipment within a designated area of an assembly station. By providing digital support during the early planning phases of factory layouts, this approach can reduce risk, minimize costly retrospective engineering, and accelerate project completion. The demonstrator also showcases a way of promoting cross-disciplinary, transparent, and collective planning of layouts, which facilitates better-informed decisions during the factory layout planning process.

The general trend within industry is to establish seamless information exchange between users and activities through digitalization. This is an ongoing journey for many companies, and there are many challenges to deal with. The concept of Industry 5.0 builds upon previous digitalization concepts and seeks to automate and enable collaboration between humans and machines in all types of manufacturing activities, including planning and design activities.

This paper proposes an approach to support the users of software tools and automate certain aspects of the planning process, specifically for layout planning. It aims to convert the expertise and knowledge in the relevant field into “smart” solutions within the software tools. The presented study utilizes the NSGA-II algorithm to showcase a demonstrator solution that emphasizes the transformation of layout planning for an assembly station in a battery production factory into a transparent and interdisciplinary activity. The solution highlights the potential for increased automation and incorporates ergonomic evaluation methods and area utilization, resulting in objective proposals for factory layouts that take into account both productivity and worker well-being factors.

The algorithm generates a collection of solutions forming a Pareto front, with each solution representing an optimal outcome based on defined optimization objectives and constraints. However, a critical aspect for future research is addressing the challenge of assisting decision-makers in selecting the most appropriate solution from the various optimal choices during the decision-making process. In addition, regarding some thoughts of repercussion of the proposed approach, there are several considerations related to research ethics when it comes to studying the planning and design process of factory layouts. First, it is important to ensure that the research is conducted in a way that does not disrupt the normal planning and design activities for factory layouts. Use cases should be selected with involvement of end users (layout planners) and with permission from the factory management before experiments are conducted on selected use case datasets to minimize any potential conflicts of competing interests or personal relationships that could appear to influence the research carried out. Further, it is important to respect the way of working of the layout engineers of today, so that proposed solutions do not provide unnecessary workloads on the engineering side. Then, it is important to consider the potential impacts of the research on the workers. For example, if the research involves changing the layout of the factory, it is important to ensure that the changes do not negatively impact the safety or well-being of the workers. Finally, it is important to consider the ethical implications of any conclusions or recommendations that are made based on the research. Researchers should be mindful of the potential consequences of their findings and take care to avoid making recommendations that could have negative impacts on the workers or the factory.

Future Research

The next step in this research is to develop additional methods and demonstrators for various factory layout scenarios involving different manufacturing processes and challenges, for instance in machining manufacturing, human–robot collaboration based assembly, robotic assembly, and hybrid processes. The target is to enhance digital support to assist the planning processes of virtual factory layouts while considering several cross-disciplinary aspects such as worker well-being, productivity, balancing, production sequencing with several product variants, assembly lines in motion, staff safety, and regulations, utilizing a multi-objective approach. Structured evaluations with end users, i.e., engineers potentially using this approach in their daily work, will in the future be carried out to assess the functionality and usability of this enhanced digital support.

Additionally, future research also includes exploring alternative algorithms to assess the effectiveness and efficiency of multi-objective optimizations and address the challenge of assisting decision-makers in selecting the most suitable solution from the various optimal alternatives during the decision-making process.