Comparison of Different Parameters of Feedforward Backpropagation Neural Networks in DEM Height Estimation for Different Terrain Types and Point Distributions
Abstract
1. Introduction
2. Materials and Methods
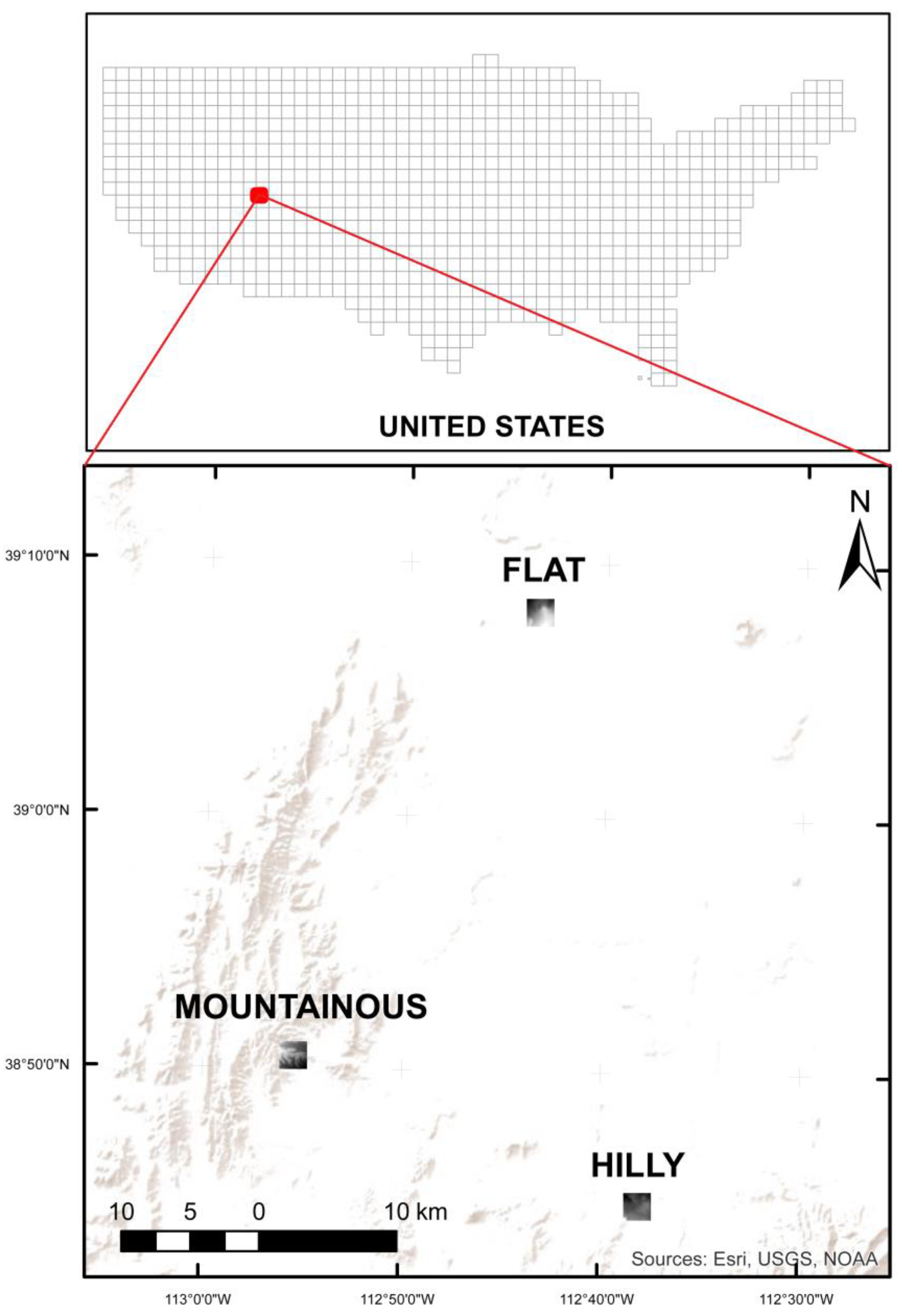
2.1. Experimental Data
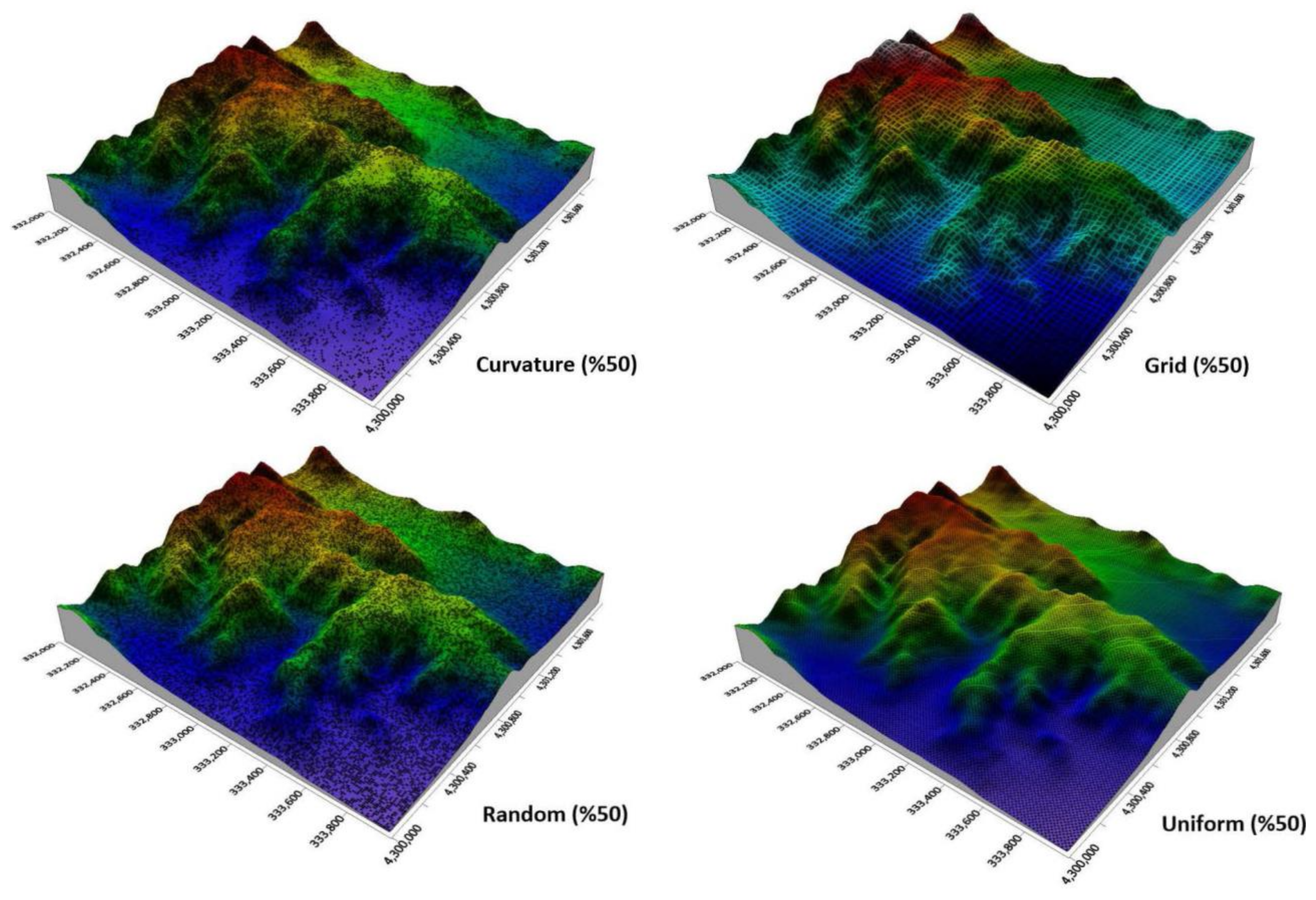
2.2. Point Processing
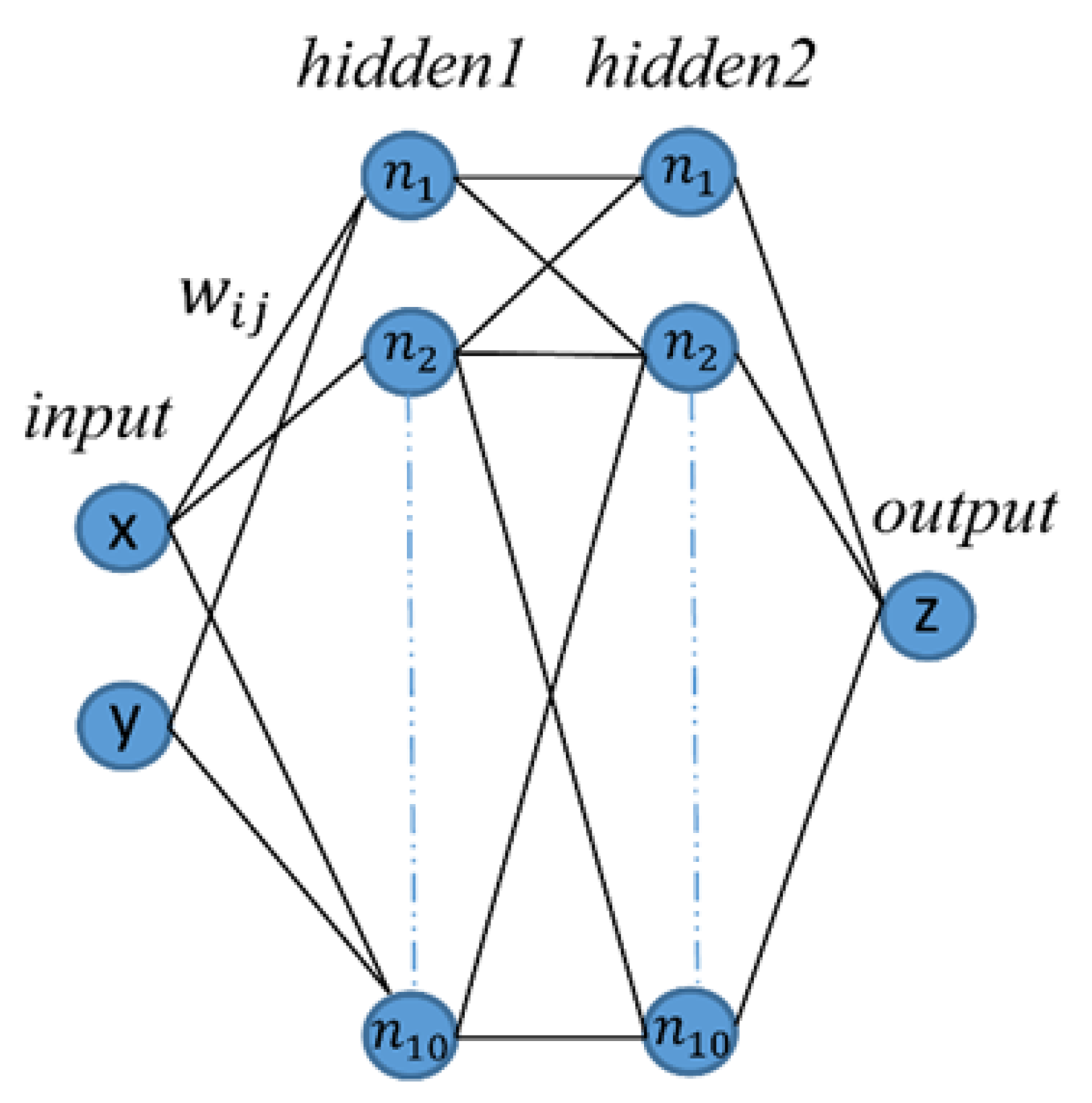
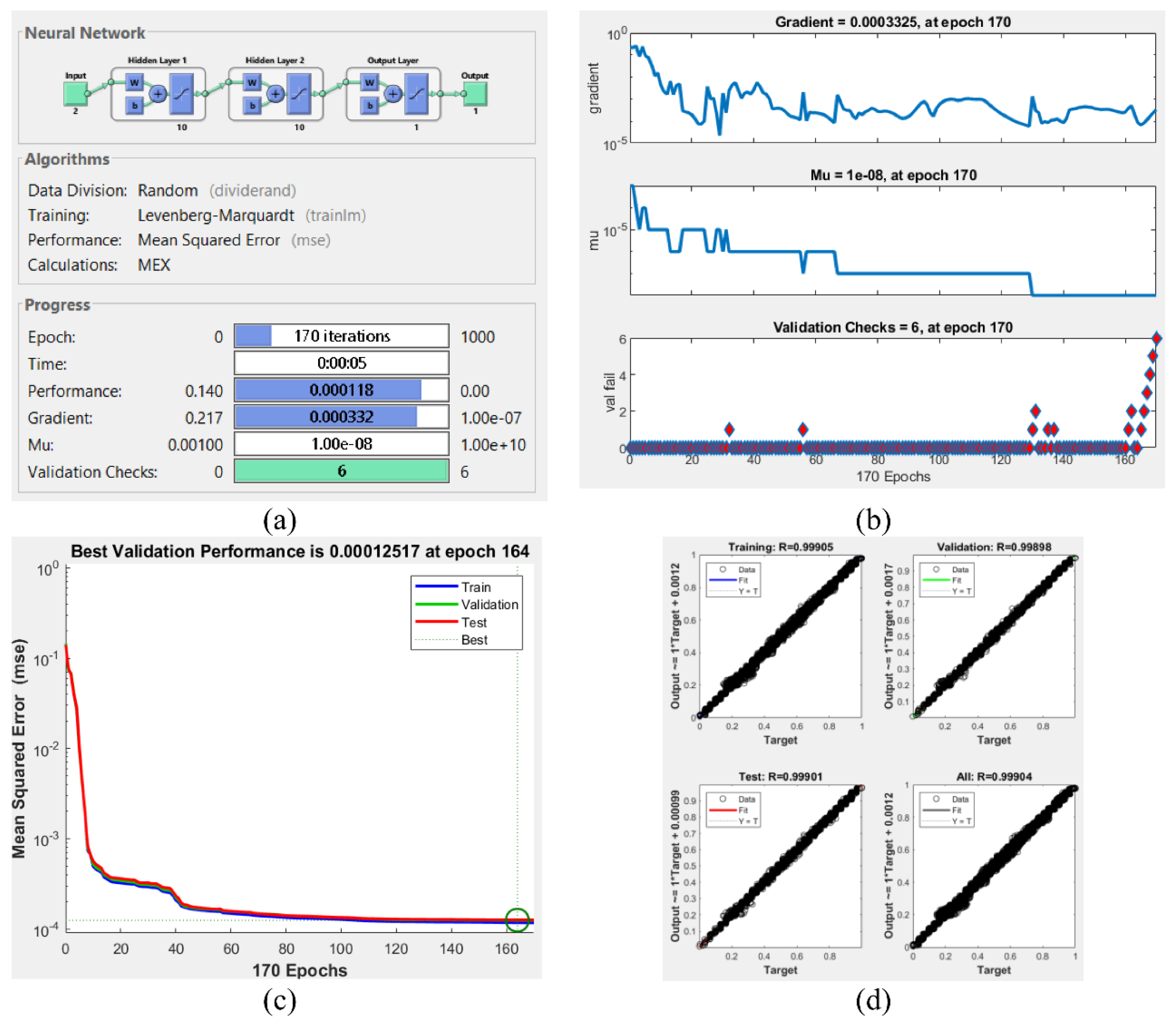
2.3. Feedforward Backpropagation Neural Networks
2.4. Statistical Tests: Analysis of Variance (ANOVA)
2.5. Software
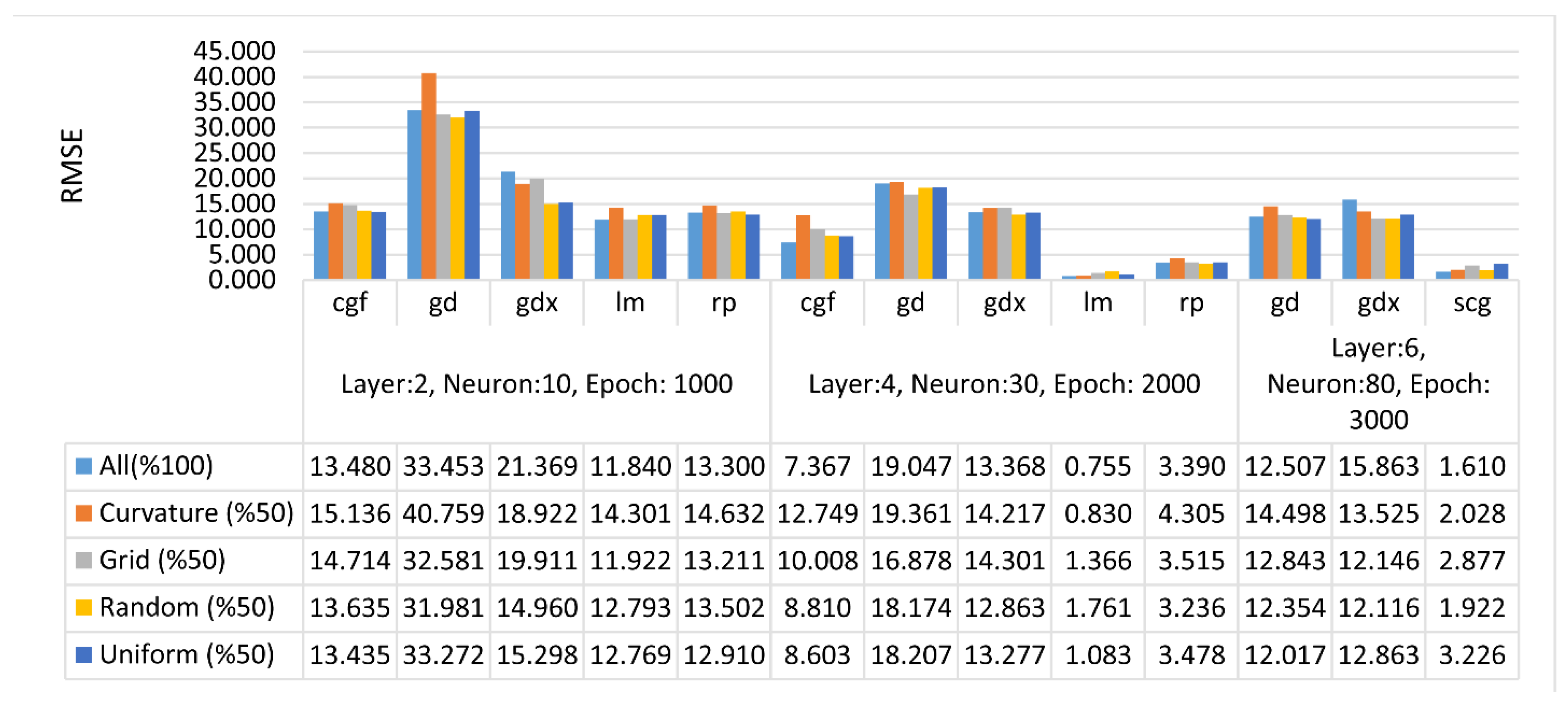
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chaplot, V.; Darboux, F.; Bourennane, H.; Leguédois, S.; Silvera, N.; Konngkeo, P. Accuracy of interpolation techniques for the derivation of digital elevation models in relation to landform types and data density. Geomorphology 2006, 77, 126–141. [Google Scholar] [CrossRef]
- Tu, J.; Yang, G.; Qui, P.; Ding, Z.; Mei, G. Comparative investigation of parallel spatial interpolation algorithms for building large-scale digital elevation models. PeerJ Comput. Sci. 2020, 6, e263. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Tang, X.; Zhang, Y. High Accuracy Interpolation of DEM Using Generative Adversarial Network. Remote Sens. 2021, 13, 676. [Google Scholar] [CrossRef]
- Mitas, L.; Mitasova, H. Spatial interpolarion. In Geographical Information Systems: Principles, Techniques, Management and Applications, 2nd ed.; Longley, P.A., Goodchild, M.F., Maguire, D.J., Rhind, D.W., Eds.; John Wiley & Sons: Chichester, UK, 2005; pp. 481–492. [Google Scholar]
- Hu, P.; Liu, X.; Hu, H. Accuracy Assessment of Digital Elevation Models based on Approximation Theory. Photogramm. Eng. Remote Sens. 2009, 75, 49–56. [Google Scholar] [CrossRef]
- Guo, Q.; Li, W.; Yu, H.; Alvarez, O. Effects of topographic variability and Lidar sampling density on several DEM interpolation methods. Photogramm. Eng. Remote Sens. 2010, 76, 701–712. [Google Scholar] [CrossRef]
- Zhao, M. An indirect interpolation model and its application for digital elevation model generation. Earth Sci. Inform. 2020, 13, 1251–1264. [Google Scholar] [CrossRef]
- Alimissis, A.; Philippopoulos, K.; Tzanis, C.K.; Deligiorgi, D. Spatial estimation of urban air pollution with the use of artificial neural network models. Atmos. Environ. 2018, 191, 205–213. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Appelhans, T.; Mwangomo, E.; Hardy, D.R.; Hemp, A.; Nauss, T. Evaluating machine learning approaches for the interpolation of monthly air temperature at Mt. Kilimanjaro, Tanzania. Spat. Stat. 2015, 14, 91–113. [Google Scholar] [CrossRef]
- Ruiz-Álvarez, M.; Alonso-Sarria, F.; Gomariz-Castillo, F. Interpolation of instantaneous air temperature using geographical and MODIS derived variables with machine learning techniques. ISPRS Int. J. Geo-Inf. 2019, 8, 382. [Google Scholar] [CrossRef]
- Leirvik, T.; Yuan, M. A machine learning technique for spatial Interpolation of solar radiation observations. Earth Sci. Space 2021, 8, e2020EA001527. [Google Scholar] [CrossRef]
- Gumus, K.; Sen, A. Comparison of spatial interpolation methods and multi-layer neural networks for different point distributions on a digital elevation model. Geod. Vestn. 2013, 57, 523–543. [Google Scholar] [CrossRef]
- Snell, S.E.; Gopal, S.; Kaufmann, R.K. Spatial Interpolation of Surface Air Temperatures Using Artificial Neural Networks: Evaluating Their Use for Downscaling GCMs. J. Cliımate 2000, 13, 886–895. [Google Scholar] [CrossRef]
- Charalambous, C. Conjugate gradient algorithm for efficient training of artificial neural networks. IEE Proc. G (Circuits Devices Syst.) 1992, 139, 301–310. [Google Scholar] [CrossRef]
- Moller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Bishop, C. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK, 1995; pp. 116–148. [Google Scholar]
- Tavassoli, A.; Waghei, Y.; Nazemi, A. Comparison of Kriging and artificial neural network models for the prediction of spatial data. J. Stat. Comput. Simul. 2022, 92, 352–369. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining Concepts and Techniques; Elsevier: Waltham, MA, USA, 2012. [Google Scholar]
- Oztopal, A. Artificial neural network approach to spatial estimation of wind velocity data. Energy Convers. Manag. 2006, 47, 395–406. [Google Scholar] [CrossRef]
- Danesh, M.; Taghipour, F.; Emadi, S.M.; Sepanlou, M.G. The interpolation methods and neural network to estimate the spatial variability of soil organic matter affected by land use type. Geocarto Int. 2022, 37, 11306–11315. [Google Scholar] [CrossRef]
- Attoh-Okine, N.O. Analysis of learning rate and momentum term in backpropagation neural network algorithm trained to predict pavement performance. Adv. Eng. Softw. 1999, 30, 291–302. [Google Scholar] [CrossRef]
- Wong, K.; Dornberger, R.; Hanne, T. An analysis of weight initialization methods in connection with different activation functions for feedforward neural networks. Evol. Intell. 2022, 1–9. [Google Scholar] [CrossRef]
- Sharma, B.; Venugopalan, K. Comparison of neural network training functions for hematoma classification in brain CT images. IOSR J. Comput. Eng. 2014, 16, 31–35. [Google Scholar] [CrossRef]
- Kamble, L.; Pangavhane, D.; Singh, T. Neural network optimization by comparing the performances of the training functions -Prediction of heat transfer from horizontal tube immersed in gas–solid fluidized bed. Int. J. Heat Mass Transf. 2015, 83, 337–344. [Google Scholar] [CrossRef]
- Gesch, D. The National Elevation Dataset. Digital Elevation Model Technologies and Applications: The DEM Users Manual. In American Society for Photogrammetry and Remote Sensing; Maune, D., Ed.; Bethesda: Rockville, MD, USA, 2007; pp. 99–118. [Google Scholar]
- Strahler, A. Hypsometric (area-altitude) analysis of erosional topography. Bull. Geol. Soc. Am. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Melton, M. The geomorphic and palaeoclimatic significance of alluvial deposits in Southern Arizona. J. Geol. 1965, 73, 1–38. [Google Scholar] [CrossRef]
- Chorley, R. Spatial Analysis in Geomorphology; Routledge: London, UK, 1972. [Google Scholar]
- Sen, A.; Gumusay, M.U.; Kavas, A.; Bulucu, U. Programming an Artificial Neural Network Tool for Spatial Interpolation in GIS—A case study for indoor radio wave propagation of WLAN. Sensors 2008, 8, 5996–6014. [Google Scholar] [CrossRef] [PubMed]
- Hagan, M.; Menhaj, M. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, Orlando, FL, USA, 27–29 June 1994. [Google Scholar]
- Scales, L. Introduction to Non-Linear Optimization; Springer: New York, NY, USA, 1985. [Google Scholar]
- Hagan, M.; Demuth, H.; Beale, M. Neural Network Design; PWS Publishing: Boston, MA, USA, 1996. [Google Scholar]
- Beale, E. A derivation of conjugate gradients. In Numerical Methods for Nonlinear Optimization; Academic Press: London, UK, 1972; pp. 39–43. [Google Scholar]
- Tukey, J. Comparing individual means in the analysis of variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef]
- Sparks, J. Expository notes on the problem of making multiple comparisons in a completely randomized design. J. Exp. Educ. 1963, 31, 343–349. [Google Scholar] [CrossRef]
- Zhang, Y.; Wenhao, Y. Comparison of DEM Super-Resolution Methods Based on Interpolation and Neural Networks. Sensors 2022, 22, 745. [Google Scholar] [CrossRef]
- Li, M.; Dai, W.; Song, S.; Wang, C.; Tao, Y. Construction of high-precision DEMs for urban plots. Ann. GIS 2023, 1–11. [Google Scholar] [CrossRef]
- Guth, P.L.; Van Niekerk, A.; Grohmann, C.H.; Muller, J.P.; Hawker, L.; Florinsky, I.V.; Gesch, D.; Reuter, H.I.; Herrera-Cruz, V.; Riazanoff, S.; et al. Digital Elevation Models: Terminology and Definitions. Remote Sens. 2021, 13, 3581. [Google Scholar] [CrossRef]




| Morphometric Parameters | Symbol | Description | Flat | Hilly | Mountain |
|---|---|---|---|---|---|
| Area | A | Measure in km2. | 4 km2 | 4 km2 | 4 km2 |
| The total length of 1 m interval contour lines | Measure in km. | 21.489 | 133.993 | 976.09 | |
| Relief [27] | R | The maximum and minimum height differences are given in meters. | 3.12 | 82.21 | 245.29 |
| Melton’s ruggedness number [28] | M | 0.0016 | 0.041 | 0.123 | |
| Slope [29] | S | , is the equidistance (1 m in this study) | 5.37 | 33.5 | 244.02 |
| Acronym | Algorithm | Description |
|---|---|---|
| lm | trainlm | Levenberg–Marquardt [31], |
| rp | trainrp | Resilient Backpropagation [32], |
| scg | trainscg | Scaled Conjugate Gradient [16], |
| cgf | traincgf | Fletcher-Powell Conjugate Gradient [33], |
| gd | traingd | Gradient Descent Backpropagation [34], |
| gdx | traingdx | Gradient descent with momentum and adaptive learning rule backpropagation [35]. |
| Parameters | Values |
|---|---|
| Number of layers | 2, 4, 6 |
| Number of hidden layer nodes | 10, 30, 80 |
| Transfer function | tanh |
| Epoch | 1000, 2000, 3000 |
| Performance function | RMSE |
| Terrain | Distirbution | Layer:2, Neurons:10, Epoch: 1000 | Layer:4, Neurons:30, Epoch: 2000 | Layer:6, Neurons:80, Epoch: 3000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | (%) | cgf | gd | gdx | lm | rp | cgf | gd | gdx | lm | rp | gd | gdx | scg |
| Flat | All | 518 | 1000 | 189 | 265 | 817 | 904 | 2000 | 150 | 536 | 1504 | 3000 | 132 | 672 |
| Curvature (50%) | 255 | 1000 | 182 | 199 | 936 | 439 | 2000 | 161 | 179 | 517 | 3000 | 116 | 209 | |
| Grid (50%) | 482 | 1000 | 184 | 209 | 643 | 437 | 2000 | 144 | 436 | 726 | 3000 | 142 | 203 | |
| Random (50%) | 388 | 1000 | 83 | 79 | 398 | 418 | 2000 | 160 | 705 | 734 | 3000 | 143 | 550 | |
| Uniform (50%) | 293 | 1000 | 178 | 241 | 667 | 340 | 2000 | 143 | 585 | 784 | 3000 | 132 | 550 | |
| Hilly | All | 678 | 1000 | 172 | 787 | 1000 | 774 | 2000 | 143 | 480 | 1000 | 3000 | 128 | 1074 |
| Curvature (50%) | 308 | 1000 | 63 | 989 | 532 | 62 | 2000 | 159 | 429 | 1243 | 3000 | 150 | 948 | |
| Grid (50%) | 141 | 1000 | 171 | 134 | 576 | 932 | 2000 | 161 | 663 | 2000 | 3000 | 22 | 522 | |
| Random (50%) | 277 | 1000 | 63 | 275 | 1000 | 252 | 2000 | 161 | 795 | 1833 | 3000 | 143 | 678 | |
| Uniform (50%) | 156 | 1000 | 172 | 376 | 688 | 482 | 2000 | 161 | 747 | 1493 | 3000 | 142 | 539 | |
| Mountain | All | 279 | 1000 | 173 | 415 | 381 | 825 | 2000 | 152 | 1123 | 1681 | 3000 | 12 | 2755 |
| Curvature (50%) | 263 | 1000 | 163 | 48 | 233 | 278 | 2000 | 154 | 1043 | 2000 | 3000 | 132 | 2998 | |
| Grid (50%) | 337 | 1000 | 169 | 166 | 1000 | 453 | 2000 | 152 | 810 | 1763 | 3000 | 116 | 786 | |
| Random (50%) | 71 | 1000 | 168 | 281 | 220 | 320 | 2000 | 151 | 9 | 2000 | 3000 | 114 | 1800 | |
| Uniform (50%) | 232 | 1000 | 173 | 126 | 677 | 449 | 2000 | 2000 | 319 | 1738 | 3000 | 113 | 646 | |
| Terrain | Distirbution | Layer:2, Neurons:10, Epoch: 1000 | Layer:4, Neurons:30, Epoch: 2000 | Layer:6, Neurons:80, Epoch: 3000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | (%) | cgf | gd | gdx | lm | rp | cgf | gd | gdx | lm | rp | gd | gdx | scg |
| Flat | All | 7 m 38 s | 6 m 6 s | 1 m 5 s | 2 m 58 s | 5 m 16 s | 26 m 19 s | 26 m 35 s | 1 m 56 s | 2 h 4 m 1 s | 30 m 56 s | 2 h 58 m 34 s | 8 m 38 s | 1 h 19 m 45 s |
| Curvature (50%) | 1 m 41 s | 2 m 56 s | 30 s | 1 m 14 s | 4 m 39 s | 5 m 44 s | 14 m 26 s | 51 s | 19 m 43 s | 6 m 21 s | 1 h 8 m 47 s | 4 m 42 s | 10 m 28 s | |
| Grid (50%) | 4 m 04 s | 3 m 33 s | 36 s | 51 s | 2 m 9 s | 6 m 27 s | 15 m 37 s | 1 m 5 s | 46 m 14 s | 5 m 22 s | 2 h 14 m 3 s | 3 m 29 s | 7 m 25 s | |
| Random (50%) | 3 m 39 s | 4 m 16 s | 21 s | 39 s | 2 m 25 s | 9 m 53 s | 23 m 42 s | 1 m 37 s | 2 h 36 m 27 s | 12 m 57 s | 1 h 10 m 18 s | 7 m 46 s | 30 m 0 s | |
| Uniform (50%) | 2 m 24 s | 3 m 26 s | 34 s | 1 m 22 s | 2 m 57 s | 6 m 50 s | 12 m 35 s | 58 s | 1 h 53 m 19 s | 8 m 21 s | 1 h 20 m 3 s | 4 m 26 s | 25 m 36 s | |
| Hilly | All | 12 m 41 s | 6 m 13 s | 1 m 30 s | 6 m 14 s | 6 m 16 s | 21 m 15 s | 41 m 29 s | 3 m 1 s | 51 m 55 s | 13 m 34 s | 2 h 29 m 3 s | 11 m 15 s | 2 h 7 m 12 s |
| Curvature (50%) | 3 m 14 s | 4 m 40 s | 17 s | 3 m 13 s | 1 m 42 s | 8 m 13 s | 21 m 1 s | 1 m 37 s | 40 m 55 s | 9 m 50 s | 1 h 30 m 6 s | 3 m 27 s | 43 m 56 s | |
| Grid (50%) | 2 m 7 s | 5 m 14 s | 59 s | 43 s | 1 m 54 s | 25 m 5 s | 15 m 12 s | 1 m 55 s | 2 h 21 m 51 s | 20 m 51 s | 1 h 45 m 2 s | 48 s | 27 m 26 s | |
| Random (50%) | 2 m 9 s | 3 m 16 s | 12 s | 1 m 1 s | 3 m 8 s | 3 m 47 s | 14 m 35 s | 1 m 7 s | 1 h 30 m 32 s | 12 m 01 s | 1 h 5 m 54 s | 3 m 4 s | 31 m 34 s | |
| Uniform (50%) | 1 m 55 s | 5 m 5 s | 51 s | 2 m 10 s | 3 m 12 s | 12 m 9 s | 24 m 39 s | 1 m 56 s | 2 h 31 m 43 s | 15 m 54 s | 1 h 31 m 45 s | 4 m 48 s | 28 m 15 s | |
| Mountain | All | 4 m 14 s | 12 m 33 s | 1 m 2 s | 2 m 49 s | 6 m 14 s | 24 m 25 s | 28 m 37 s | 4 m 16 s | 4 h 14 m 31 s | 25 m 44 s | 5 h 35 m 10 s | 39 s | 4 h 44 m 44 s |
| Curvature (50%) | 2 m 47 s | 4 m 25 s | 44 s | 11 s | 43 s | 3 m 37 s | 14 m 32 s | 1 m 34 s | 1 h 47 m 40 s | 36 m 5 s | 1 h 24 m 51 s | 2 m 59 s | 2 h 17 m 41 s | |
| Grid (50%) | 3 m 5 s | 3 m 15 s | 33 s | 2 m 4 s | 4 m 30 s | 7 m 51 s | 24 m 55 s | 1 m 4 s | 1 h 30 m 36 s | 22 m 32 s | 1 h 28 m 35 s | 3 m 15 s | 53 m 53 s | |
| Random (50%) | 40 s | 4 m 28 s | 41 s | 1 m 4 s | 41 s | 4 m 36 s | 14 m 55 s | 1 m 30 s | 1 m 19 s | 13 m 40 s | 1 h 43 m 24 s | 2 m 35 s | 1 h 31 m 13 s | |
| Uniform (50%) | 1 m 43 s | 3 m 8 s | 33 s | 30 s | 2 m 16 s | 7 m 17 s | 1 h 50 m 58 s | 25 m 48 s | 35 m 49 s | 12 m 38 s | 1 h 14 m 19 s | 2 m 47 s | 40 m 50 s | |
| Terrain | Distirbution | Layer:2, Neurons:10, Epoch: 1000 | Layer:4, Neurons:30, Epoch: 2000 | Layer:6, Neurons:80, Epoch: 3000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | (%) | cgf | gd | gdx | lm | rp | cgf | gd | gdx | lm | rp | gd | gdx | scg |
| Flat | All | 0.0002 | 0.0295 | 0.0135 | 0.0000 | 0.0004 | 0.0006 | 0.0079 | 0.0256 | 0.0000 | 0.0000 | 0.0054 | 0.0358 | 0.0003 |
| Curvature (50%) | 0.0002 | 0.0296 | 0.0296 | 0.0000 | 0.0003 | 0.0021 | 0.0128 | 0.0163 | 0.0002 | 0.0001 | 0.0041 | 0.0265 | 0.0014 | |
| Grid (50%) | 0.0005 | 0.0501 | 0.0501 | 0.0001 | 0.0002 | 0.0009 | 0.0107 | 0.0250 | 0.0001 | 0.0001 | 0.0053 | 0.0246 | 0.0012 | |
| Random (50%) | 0.0004 | 0.0294 | 0.0294 | 0.0000 | 0.0004 | 0.0009 | 0.0100 | 0.0144 | 0.0003 | 0.0003 | 0.0041 | 0.0134 | 0.0003 | |
| Uniform (50%) | 0.0002 | 0.0351 | 0.0351 | 0.0000 | 0.0005 | 0.0049 | 0.0115 | 0.0182 | 0.0005 | 0.0005 | 0.0051 | 0.0249 | 0.0006 | |
| Hilly | All | 0.0003 | 0.0307 | 0.0122 | 0.0008 | 0.0002 | 0.0003 | 0.0093 | 0.0183 | 0.0001 | 0.0001 | 0.0048 | 0.0009 | 0.0004 |
| Curvature (50%) | 0.0008 | 0.0213 | 0.0633 | 0.0027 | 0.0002 | 0.0004 | 0.0119 | 0.0292 | 0.0000 | 0.0001 | 0.0053 | 0.0276 | 0.0012 | |
| Grid (50%) | 0.0052 | 0.0244 | 0.0230 | 0.0000 | 0.0002 | 0.0009 | 0.0004 | 0.0216 | 0.0001 | 0.0001 | 0.0048 | 0.2390 | 0.0007 | |
| Random (50%) | 0.0005 | 0.0214 | 0.0636 | 0.0001 | 0.0003 | 0.0018 | 0.0117 | 0.0200 | 0.0000 | 0.0001 | 0.0046 | 0.0340 | 0.0004 | |
| Uniform (50%) | 0.0015 | 0.0240 | 0.0080 | 0.0002 | 0.0002 | 0.0006 | 0.0022 | 0.0218 | 0.0000 | 0.0001 | 0.0048 | 0.0510 | 0.0004 | |
| Mountain | All | 0.0011 | 0.0214 | 0.0190 | 0.0005 | 0.0003 | 0.0080 | 0.0110 | 0.0243 | 0.0002 | 0.0001 | 0.0064 | 0.9680 | 0.0003 |
| Curvature (50%) | 0.0011 | 0.0326 | 0.0258 | 0.0001 | 0.0053 | 0.0195 | 0.0114 | 0.0314 | 0.0000 | 0.0002 | 0.0074 | 0.0659 | 0.0005 | |
| Grid (50%) | 0.0008 | 0.0341 | 0.0198 | 0.0001 | 0.0006 | 0.0101 | 0.0090 | 0.0343 | 0.0003 | 0.0001 | 0.0064 | 0.0949 | 0.0009 | |
| Random (50%) | 0.0008 | 0.0226 | 0.0203 | 0.0000 | 0.0007 | 0.0052 | 0.0117 | 0.0409 | 0.0072 | 0.0002 | 0.0059 | 0.0804 | 0.0009 | |
| Uniform (50%) | 0.0004 | 0.0391 | 0.0099 | 0.0000 | 0.0003 | 0.0033 | 0.0117 | 0.0197 | 0.0000 | 0.0002 | 0.0061 | 0.0742 | 0.0019 | |
| Terrain | Distirbution | Layer:2, Neurons:10, Epoch: 1000 | Layer:4, Neurons:30, Epoch: 2000 | Layer:6, Neurons:80, Epoch: 3000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | (%) | cgf | gd | gdx | lm | rp | cgf | gd | gdx | lm | rp | gd | gdx | scg |
| Flat | All | 0.0008 | 0.0117 | 0.0019 | 0.0006 | 0.0009 | 0.0001 | 0.0033 | 0.0014 | 0.0000 | 0.0001 | 0.0012 | 0.0008 | 0.0001 |
| Curvature (50%) | 0.0008 | 0.0118 | 0.0048 | 0.0007 | 0.0009 | 0.0003 | 0.0046 | 0.0015 | 0.0000 | 0.0001 | 0.0009 | 0.0085 | 0.0002 | |
| Grid (50%) | 0.0012 | 0.0246 | 0.0039 | 0.0007 | 0.0008 | 0.0002 | 0.0042 | 0.0015 | 0.0000 | 0.0001 | 0.0011 | 0.0008 | 0.0001 | |
| Random (50%) | 0.0008 | 0.0117 | 0.0252 | 0.0010 | 0.0008 | 0.0002 | 0.0032 | 0.0013 | 0.0000 | 0.0001 | 0.0009 | 0.0008 | 0.0001 | |
| Uniform (50%) | 0.0007 | 0.0164 | 0.0029 | 0.0006 | 0.0007 | 0.0004 | 0.0040 | 0.0009 | 0.0000 | 0.0001 | 0.0011 | 0.0008 | 0.0001 | |
| Hilly | All | 0.0005 | 0.0242 | 0.0031 | 0.0004 | 0.0007 | 0.0001 | 0.0024 | 0.0011 | 0.0000 | 0.0000 | 0.0010 | 0.0393 | 0.0000 |
| Curvature (50%) | 0.0010 | 0.0112 | 0.0276 | 0.0005 | 0.0007 | 0.0001 | 0.0043 | 0.0012 | 0.0000 | 0.0000 | 0.0013 | 0.0012 | 0.0000 | |
| Grid (50%) | 0.0031 | 0.0121 | 0.0047 | 0.0009 | 0.0007 | 0.0001 | 0.0001 | 0.0012 | 0.0000 | 0.0000 | 0.0010 | 0.0594 | 0.0000 | |
| Random (50%) | 0.0009 | 0.0112 | 0.0271 | 0.0010 | 0.0008 | 0.0003 | 0.0041 | 0.0011 | 0.0000 | 0.0000 | 0.0012 | 0.0010 | 0.0000 | |
| Uniform (50%) | 0.0008 | 0.0193 | 0.0024 | 0.0005 | 0.0007 | 0.0001 | 0.0078 | 0.0009 | 0.0000 | 0.0000 | 0.0010 | 0.0009 | 0.0000 | |
| Mountain | All | 0.0030 | 0.0186 | 0.0076 | 0.0023 | 0.0029 | 0.0009 | 0.0060 | 0.0030 | 0.0000 | 0.0002 | 0.0026 | 0.0721 | 0.0000 |
| Curvature (50%) | 0.0038 | 0.0277 | 0.0060 | 0.0034 | 0.0036 | 0.0027 | 0.0063 | 0.0034 | 0.0000 | 0.0003 | 0.0035 | 0.0031 | 0.0001 | |
| Grid (50%) | 0.0036 | 0.0177 | 0.0066 | 0.0024 | 0.0029 | 0.0017 | 0.0048 | 0.0034 | 0.0000 | 0.0002 | 0.0028 | 0.0025 | 0.0001 | |
| Random (50%) | 0.0031 | 0.0170 | 0.0037 | 0.0027 | 0.0030 | 0.0013 | 0.0055 | 0.0028 | 0.0634 | 0.0002 | 0.0025 | 0.0024 | 0.0001 | |
| Uniform (50%) | 0.0030 | 0.0184 | 0.0039 | 0.0027 | 0.0028 | 0.0012 | 0.0055 | 0.0029 | 0.0000 | 0.0002 | 0.0024 | 0.0028 | 0.0002 | |
| Levene Statistic | df1 | df2 | Sig. | ||
|---|---|---|---|---|---|
| Training Functions | mountain | 15.108 | 5 | 59 | 0.000 |
| flat | 11.258 | 5 | 59 | 0.000 | |
| hilly | 13.249 | 5 | 59 | 0.000 | |
| Sum of Squares | df | Mean Square | F | Sig. | ||
|---|---|---|---|---|---|---|
| mountain | Between Groups | 2275.565 | 5 | 455.113 | 12.921 | 0.000 |
| Within Groups | 2078.207 | 59 | 35.224 | |||
| Total | 4353.772 | 64 | ||||
| flat | Between Groups | 0.286 | 5 | 0.057 | 13.894 | 0.000 |
| Within Groups | 0.243 | 59 | 0.004 | |||
| Total | 0.529 | 64 | ||||
| hilly | Between Groups | 229.796 | 5 | 45.959 | 11.282 | 0.000 |
| Within Groups | 240.348 | 59 | 4.074 | |||
| Total | 470.144 | 64 |
| (I) Functions | (J) Functions | Mean Difference (I–J) | Std. Error | Sig. | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | |||||
| traincgf | traingd | −10.069 | 2.656 | 0.021 | −19.071 | −1.067 |
| trainscg | 9.461 | 0.942 | 0.000 | 5.954 | 12.967 | |
| traingd | traincgf | 10.069 | 2.656 | 0.021 | 1.067 | 19.071 |
| trainlm | 13.920 | 3.143 | 0.003 | 3.658 | 24.182 | |
| trainrp | 13.314 | 3.005 | 0.003 | 3.474 | 23.155 | |
| trainscg | 19.530 | 2.521 | 0.000 | 10.710 | 28.349 | |
| traingdx | trainscg | 12.667 | 0.802 | 0.000 | 9.951 | 15.384 |
| trainlm | traingd | −13.920 | 3.143 | 0.003 | −24.182 | −3.658 |
| trainrp | traingd | −13.314 | 3.005 | 0.003 | −23.155 | −3.474 |
| trainscg | traincgf | −9.461 | 0.942 | 0.000 | −12.967 | −5.954 |
| traingd | −19.530 | 2.521 | 0.000 | −28.349 | −10.710 | |
| traingdx | −12.667 | 0.802 | 0.000 | −15.384 | −9.951 | |
| Trainings Functions | N | Mountain | Flat | Hilly | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| Tukey HSD a | trainscg | 5 | 2.333 | 0.034 | 0.457 | ||||||
| trainlm | 10 | 7.942 | 7.942 | 0.051 | 0.051 | 1.134 | 1.134 | ||||
| trainrp | 10 | 8.548 | 8.548 | 0.061 | 0.061 | 1.363 | 1.363 | ||||
| traincgf | 10 | 11.794 | 0.068 | 0.068 | 1.809 | 1.809 | |||||
| traingdx | 15 | 15.000 | 15.000 | 0.133 | 0.133 | 3.664 | 3.664 | ||||
| traingd | 15 | 21.862 | 0.218 | 5.781 | |||||||
| Sig. | 0.219 | 0.116 | 0.136 | 0.847 | 0.079 | 0.059 | 0.692 | 0.085 | 0.217 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sen, A.; Gumus, K. Comparison of Different Parameters of Feedforward Backpropagation Neural Networks in DEM Height Estimation for Different Terrain Types and Point Distributions. Systems 2023, 11, 261. https://doi.org/10.3390/systems11050261
Sen A, Gumus K. Comparison of Different Parameters of Feedforward Backpropagation Neural Networks in DEM Height Estimation for Different Terrain Types and Point Distributions. Systems. 2023; 11(5):261. https://doi.org/10.3390/systems11050261
Chicago/Turabian StyleSen, Alper, and Kutalmis Gumus. 2023. "Comparison of Different Parameters of Feedforward Backpropagation Neural Networks in DEM Height Estimation for Different Terrain Types and Point Distributions" Systems 11, no. 5: 261. https://doi.org/10.3390/systems11050261
APA StyleSen, A., & Gumus, K. (2023). Comparison of Different Parameters of Feedforward Backpropagation Neural Networks in DEM Height Estimation for Different Terrain Types and Point Distributions. Systems, 11(5), 261. https://doi.org/10.3390/systems11050261






