Abstract
Digital Elevation Models (DEMs) are commonly used for environment, engineering, and architecture-related studies. One of the most important factors for the accuracy of DEM generation is the process of spatial interpolation, which is used for estimating the height values of the grid cells. The use of machine learning methods, such as artificial neural networks for spatial interpolation, contributes to spatial interpolation with more accuracy. In this study, the performances of FBNN interpolation based on different parameters such as the number of hidden layers and neurons, epoch number, processing time, and training functions (gradient optimization algorithms) were compared, and the differences were evaluated statistically using an analysis of variance (ANOVA) test. This research offers significant insights into the optimization of neural network gradients, with a particular focus on spatial interpolation. The accuracy of the Levenberg–Marquardt training function was the best, whereas the most significantly different training functions, gradient descent backpropagation and gradient descent with momentum and adaptive learning rule backpropagation, were the worst. Thus, this study contributes to the investigation of parameter selection of ANN for spatial interpolation in DEM height estimation for different terrain types and point distributions.
1. Introduction
A Digital Elevation Model (DEM) is a representation of the earth’s surface composed of equal-sized grid cells with a specific height assigned to each [1,2]. DEMs are commonly used for environment, engineering, architecture-related studies, and a variety of applications such as mapping, geographic information systems, remote sensing, geology, hydrology, and meteorology [3]. A DEM can be generated using photogrammetry (aerial and satellite images), SAR interferometry, radargrammetry, airborne laser scanning (LIDAR), cartographic digitization, and surveying methods. The accuracy of DEMs is influenced by the data source as well as a range of factors such as topographic variability, sample size, interpolation methods, and spatial resolution.
Spatial interpolation is used for the approximation of spatial and spatiotemporal distributions depending on location in a multi-dimensional space [4]. Spatial interpolation is required in DEM generation to determine the height values of grid cells [3,5,6]. Therefore, the model outcome is heavily dependent on the accuracy of the interpolation technique chosen. It is of great importance to determine more accurate interpolation methods for specific purposes, such as the creation of fine-scale DEMs [7]. Current spatial interpolation techniques can be broadly categorized into three traditional groups: (1) Deterministic methods (e.g., Inverse Distance Weighted, Shepard’s method), (2) Geostatistical methods (e.g., Ordinary Kriging), and (3) Combined methods (e.g., Regression Kriging). In addition, the use of machine learning methods and artificial neural networks has been established as an effective solution for spatial interpolation [8].
Notable studies have compared traditional methods, machine learning methods, and artificial neural networks in spatial interpolation. The common feature of these studies is that the use of machine learning methods or the combination of traditional methods and machine methods provides superiority over the sole use of traditional methods. For example, ref. [9] compared traditional and machine learning methods for mud content prediction. The results showed that Random Forest (RF) with Ordinary Kriging (OK) or Inverse Distance Squared (IDS) combination was the most effective and sensitive to input variables. Ref. [10] used several machine learning algorithms and evaluated against the Kriging approach for the prediction of spatial temperature patterns, and a combined Cubist and residual Kriging approach was considered the best solution. Ref. [11] compared two machine learning algorithms, Support Vector Machines (SVM) and RF, with Multiple Linear Regression (MLR) and OK to estimate the air temperature using satellite imagery. Machine learning algorithms, especially RF, reached significantly higher accuracy values. RF with OK obtained the most accurate results. Ref. [12] applied RF and seven other conventional spatial interpolation models to a surface solar radiation dataset. RF outperformed the traditional spatial interpolation models. As a result, the use of machine learning methods for spatial interpolation contributes to spatial interpolation with more accuracy.
Artificial Neural Networks (ANN) can approximate non-linear relationships and their derivatives, even without an understanding of the exact non-linear function, allowing them to make accurate predictions in highly complex non-linear problems such as the estimation of height values in DEM generation [13,14]. The Feedforward Backpropagation Neural Network (FBNN), a type of ANN, is used for supervised learning tasks such as classification and regression. It has one or more layers of interconnected neurons, called hidden layers, between the input and output layers. Each neuron produces its output through a non-linear process called an activation function based on the weighted sum of its input. A learning algorithm called backpropagation iteratively modifies the connections between neurons (the weights) to minimize the least square error objective function, which is defined by the differences between the network’s predictions for each tuple with the actual known target value. This iterative process continues until the error reaches an acceptable threshold [15,16,17,18]. Estimation of height values of DEM using FBNNs is very efficient for two reasons. First, FBNNs can learn non-linear relationships (non-linearity) between input variables and outputs (performing non-linear regression from a statistical perspective); the determination of height values of DEM is also inherently a non-linear process. Second, they can handle a wide array of real-world data, making them suitable for dealing with large-scale spatial datasets [19].
FBNNs outperform traditional methods for spatial interpolation in several studies. For example, the wind speed prediction using an FBNN was compared with measured values at a pivot station. It was shown that the use of a suitable FBNN architecture leads to better predictions than the traditional methods used in the literature [20]. Ref. [13] used Inverse Distance Weighted (IDW), OK, Modified Shepard’s (MS), Multiquadric Radial Basis Function (MRBF), Triangulation with Linear (TWL), and FBNN to predict height for different point distributions such as curvature, grid, random and uniform on a DEM. FBNN was a satisfactory predictor for curvature, grid, random, and uniform distributions. Ref. [8] compared the performance of two interpolation methods, FBNN and MLR, utilizing data from an urban air quality monitoring network. The results showed that FBNN was significantly superior in most cases. Ref. [21] compared traditional methods such as Kriging, Co-Kriging, and IDW with FBNN to predict the spatial variability of soil organic matter. FBNN is the most accurate method via the cross-validation results.
The use of FBNNs in spatial interpolation is highly efficient [8,13,20,21]. Despite the efficiency of FBNNs in spatial interpolation, there are still some research gaps that need to be addressed to optimize the performance of FBNNs for this task. One of the major research gaps is the selection of optimal parameters for FBNNs in spatial interpolation, including the determination of the appropriate number of hidden layers and neurons (nodes), the activation function to use, the learning rate and momentum constant, and the weight initialization method [22,23]. The optimal values for these parameters can vary greatly depending on the specific dataset and spatial interpolation task, and there is still much research needed to determine the optimal parameters for different cases. Another research gap is the comparison of training (gradient optimization) functions of FBNNs for spatial interpolation. A gradient optimization method is used to find the set of weights that minimizes the cost function (a measure of the difference between the network’s predicted output and the target output), which corresponds to the global minimum error in the neural network. The global minimum error represents the best possible performance that the neural network can achieve, and it is the target that we aim to reach through training the network. The cost function is often a non-linear, multivariate function, and finding the global minimum of the cost function is a difficult optimization problem. Therefore, there is still much work needed to optimize their performance for spatial interpolation [15,16,24,25].
This study aims (1) to evaluate the height estimation accuracy of the FBNN for generating the DEM in terms of different parameters and training functions for different point distributions and terrain types, which is important for the generation of high-quality DEMs, and (2) to statistically evaluate the differences between the height estimation of FBNN using different training functions. In this study, we evaluated the FBNN method considering different parameters (the number of hidden layers and neurons, epoch number, and processing time) and training functions (gradient optimization algorithms) for DEM height estimation through different point distributions (curvature, grid, random, uniform) and terrain types (flat, hilly, mountainous). Furthermore, an analysis of variance (ANOVA) test was conducted to investigate the differences between the training functions of FBNNs for height estimation in DEM generation for different terrain types. This study offers significant insights into the optimization of neural network gradients, with a particular focus on spatial interpolation. In this study, the accuracy of Levenberg–Marquardt function was the best, whereas the most significantly different training functions, gradient descent backpropagation and gradient descent with momentum and adaptive learning rule backpropagation, were the worst. In addition, the accuracy of the height estimation using FBNN for the flat terrain was the best, whereas the mountainous terrain was the worst. In terms of point distributions, the accuracy of distributions was similar based on the RMSE values of height estimation.
2. Materials and Methods
A general flowchart of the FBNN pipeline for DEM height estimation and evaluation is shown in Figure 1. Section 2.1 describes input data. Section 2.2 describes the point processing to create different distributions. Section 2.3 describes the normalization of the input parameters, FBNN training, testing and validation, DEM height estimation using different FBNN parameters and training functions, and evaluation of FBNN models using RMSE calculation. Section 2.4 describes a statistical test (ANOVA) for the determination of the effect of six different training functions for different terrain types. Finally, Section 2.5 describes the software used in this study.
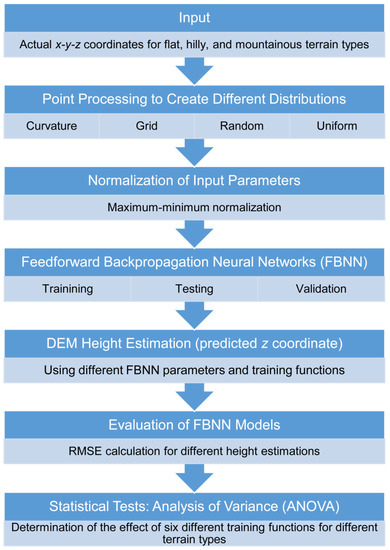
Figure 1.
Flowchart of the FBNN pipeline used in this study.
2.1. Experimental Data
In this study, we used a 1/3 arc-second DEM, approximately 10 m grid spacing, from the USGS (United States Geological Survey) National Elevation Dataset (NED). The production method of the DEM is an improved contour-to-grid interpolation. The vertical accuracy expressed as RMSE is 2.17 m [26].
Morphometric parameters are important for the comparison of different surfaces. Surfaces such as flat, hilly, and mountainous can be classified according to the ruggedness and slope of the terrain. The study area is Lower Beaver in Colorado, USA (see Figure 2). In this study, regarding these morphometric parameters, three different areas (2 km × 2 km), flat, hilly, and mountainous, were chosen by the ruggedness and slope values. The morphometric parameters of these areas were calculated and given in Table 1. The area with the highest ruggedness and slope values refers to mountainous, the area with the least ruggedness and slope values refers to flat, and the area with the average values refers to hilly. The 3D models of these study areas are illustrated in Figure 3. The same exaggeration value, which is 2 inches, was used in 3D models.
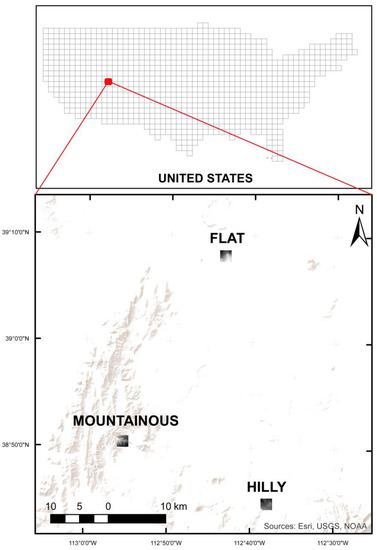
Figure 2.
Geographic location of three different DEMs used in this study for flat, hilly, and mountainous terrains in the United States.

Table 1.
Morphometric parameters for the three different study areas.
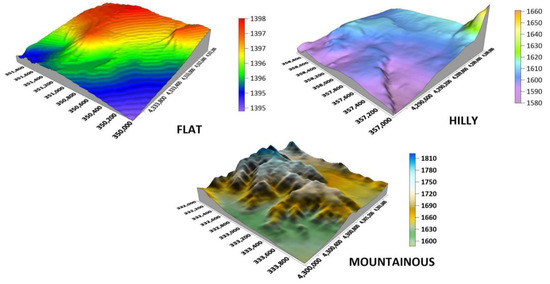
Figure 3.
The 3D Models of the study areas (Top left: hilly, Top right: flat, and Bottom: mountainous).
2.2. Point Processing
In this study, the effect of different point distributions (grid, curvature, random, and uniform) of the 3D data sets representing different topographies, such as flat, hilly, and mountainous areas, in the height estimation using FBNN was determined. The total number of points in the 3D datasets representing flat, hilly, and mountainous areas was reduced by 50% to generate grid, curvature, random, and uniform distributions. Thus, the effect of point reduction on spatial interpolation was also investigated.
The grid distribution reduces the number of points in an irregular point space without considering the curvature and the original density of the pattern. However, the curvature distribution reduces the number of points on surfaces that are very close in height but preserves the detail in areas of high slope. The uniform distribution evenly reduces the number of points on surfaces whose heights are very close to each other but reduces the number of points on curved surfaces to a certain density. Random distribution removes a random percentage of points from an irregular point space. A 3D model of the grid, curvature, random, and uniform distributions of the points of the mountainous area is given in Figure 4.
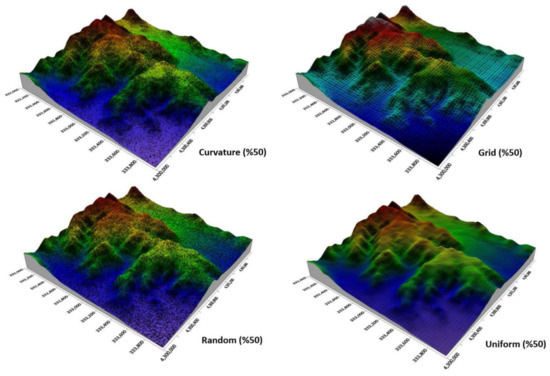
Figure 4.
The 3D model of curvature, grid, random, and uniform distributions of the points for the mountainous area (top left: curvature, top right: Grid, bottom left: random, and bottom right: uniform).
2.3. Feedforward Backpropagation Neural Networks
A feedforward backpropagation neural network is composed of three layers: the input layer, one or more hidden layers, and the output layer. A layer consists of units. The network uses the attributes (features) measured for each training tuple as inputs. In this study, the attributes of the input are the x-y coordinates of the points (see Figure 5).
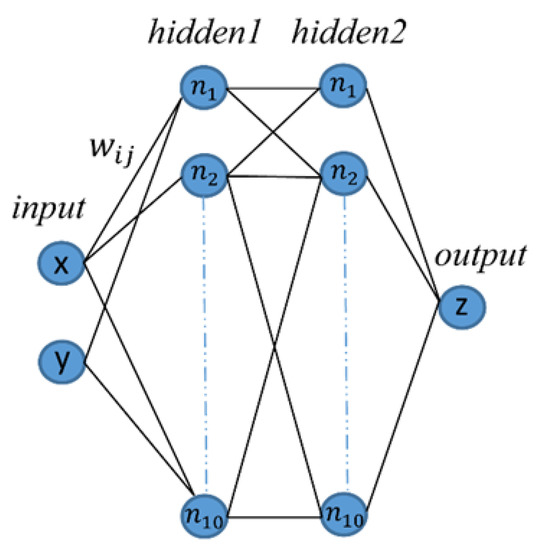
Figure 5.
A FBNN architecture (input: x, y; 2 hidden layers each have 10 neurons; output: z).
Since the mean and variance of input attributes are significantly different from each other, attributes with large averages and variances have a greater impact on others and significantly reduce their roles. Therefore, for the preprocessing step, the input values for each attribute measured in the training tuples are normalized. In this study, input values were normalized to the range of 0.0 and 1.0 using maximum-minimum normalization. For the normalized value of coordinate, :
where is the minimum x coordinate value and is the maximum x coordinate value in the study area. Additionally, the attribute y coordinate values are normalized.
In the feedforward step, the inputs pass through the input layer, they are weighted and fed concurrently to a second layer of units called the hidden layer. A nonlinear (activation) function is implemented to the sum of weighted input in the units. There can be one or more than one hidden layer. Therefore, the outputs of the hidden layer can be the input of the next hidden layer. The sum of weighted input from the last hidden layer is transmitted to the output layer, which emits the network’s prediction for each tuple [17,19,30]. In this study, the predicted output value is the height value (z coordinate) of the points.
Each input connected to the unit is multiplied by its corresponding weight, and this is added up to calculate the net input. The net input of unit j in a hidden or output layer, Ij:
where is the weight of the connection from unit i in the previous layer to unit j; Oi is the output of unit i from the previous layer; and is the bias of the unit.
Each hidden and output layer unit applies an activation function to its net input. In this study, the tangent-sigmoid (tanh) activation function was used. It converts net input to the range [–1, 1]. The actual output ;
In the backpropagation step, to propagate the error of the network’s prediction, weights and biases are updated backwards. Various optimization algorithms can be used to minimize the error between the expected output and the FBNN output. The gradient optimization algorithm finds local minima by calculating the gradient of the minimized function. The global minimum can be reached by considering multiple gradient optimization results. Gradient optimization algorithms vary in performance efficiency and speed [13]. In this study, six different gradient optimization algorithms (training functions) were used (see Table 2). In addition, different layer, neuron, and epoch numbers were used in the height estimation (see Table 3), and RMSE values (see Equation (4)) were determined by comparing the predicted heights and target heights. One of the architectures of the FBNN for predicting the heights in DEM is given in Figure 5 (input: x, y; 2 hidden layers each have 10 neurons; output: z).
where is the number of samples, is the target height value, and is the predicted height value.

Table 2.
Training functions used for the training.

Table 3.
FBNN parameters used for the training.
When training multilayer networks, the data can be partitioned into three different subsets. The first subset, referred to as the training set, is used to calculate the gradient and update the network weights and biases. The second subset, known as the validation set, is used to monitor the error during the training process. Typically, the validation error decreases initially, along with the training set error. However, when the network starts to overfit the data, the validation error can begin to rise. The third subset called the test set, is not used during training, but instead, it is utilized to compare different models. The test error is not backpropagated from the FBNN outputs to the input. In this study, the percentage of training, testing, and validation subsets were 70%, 15%, and 15%, respectively.
2.4. Statistical Tests: Analysis of Variance (ANOVA)
Analysis of variance (ANOVA) was carried out to determine the effect of the six different training functions in FBNN for spatial interpolation in generating the digital terrain models for different terrain types. In statistical tests, ANOVA is used to determine whether there is a significant difference between two means or more than two means. In ANOVA, the effect of independent variables on dependent variables is investigated. It is required that all the groups be normally distributed with homogenous variances. F-test is used in variance analysis. If the F-test statistic (p-value or Sig.) is less than 0.05, the Ho hypothesis is rejected, which means there is a significant difference between the groups. If there is a significant difference between groups, Post Hoc tests are used to determine which groups differ from each other. To determine which groups differ from each other, the Tukey test is used if variance homogeneity is ensured, and Tamhane’s T2 test is used if variance homogeneity is not ensured [36,37]. In this study, the RMSE values calculated from the differences between the target and predicted heights are used as the dependent variable, while the training functions in artificial neural networks (trainlm, traincgf, traingd, traingdx, trainrp, and trainscg) based on different terrain types (hilly, flat, and mountainous) are used as independent variables. An ANOVA test was performed for these dependent and independent variables and their subsets to determine whether there is a statistical difference between the height estimation obtained from the variables.
2.5. Software
We used Matlab neural network toolbox and SPSS to implement FBNN and ANOVA tests, respectively. In addition, we used ArcMap 10.5 for the map visualization. The performance of different FBNN parameters was observed using the neural network toolbox graphical user interface (GUI) for the height estimation for different terrains with different distributions. For example, the Matlab graphic interfaces of the height estimation for the flat area with grid distribution (sample size: 50%) using the FBNN including 2 layers with 10 neurons using trainlm function with 170 epochs are illustrated in Figure 6. In Figure 6a, neural network architecture, training function, training time, performance, and epoch number are monitored. In Figure 6b,c, gradient descent and mean squared error graphics can be observed, respectively. In Figure 4d, regression graphics of the predicted and target values of training, validation, test, and all sets are given.
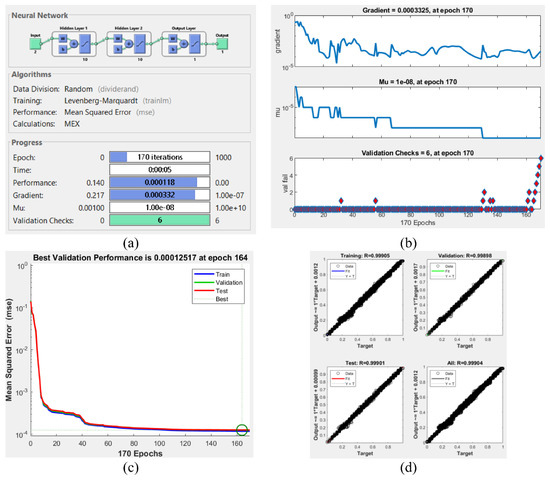
Figure 6.
The FBNN training of the flat area with grid distribution (sample size: 50%) to predict the height values. Neural network tool (a), gradient descent optimization graphic (b), best validation performance shown by a green circle on mean squared error graphics (c), correlation graphics between output and target values for the training, validation, testing, and all data (d).
3. Results and Discussion
The term epoch in ANNs refers to an iteration during the training process that corresponds to the complete processing of the entire training dataset by the network. In each epoch, the training data are presented to the network repeatedly, and the performance of the network is evaluated using a criterion such as error function or accuracy value. As the number of epochs increases, the network generally performs better, but the training time also increases. The number of epochs is important for learning and preventing overfitting. Epoch values obtained from different FBNNs are given in Table 4. In this study, the network was trained with 1000, 2000, and 3000 epochs for different FBNN parameters. Performing too many epochs on training can cause the network to memorize the data and negatively affect its overall performance (overfitting). However, not performing enough epochs can lead to the network not learning the data well enough and performing weakly (underfitting). Generally, the number of epochs is adjusted based on the size of the training data and the complexity of the network. In this study, the maximum number of iterations (1000, 2000, and 3000) was performed for the training function traingd, whereas the minimum number of iterations was performed using the training function traingdx.

Table 4.
Number of epochs for the FBNNs to predict the height values for each parameter, terrain type, and point distribution in DEM.
The processing time of ANN solutions is important in the training of the model, especially for real-time applications. ANNs usually operate on large data sets, and processing these data sets can be time-consuming. The training of ANN models involves many iterative calculation processes, which can extend the processing time. In addition, an efficient processing time is also useful when the model needs to be retrained or adjusted. The processing speed also reduces processing costs. Especially when processing large data sets, a faster model may require less computer memory and be less costly. The processing times of FBNN height estimation for different terrain types and point distributions based on different parameters such as transfer function (trainlm, traincgf, traingd, traingdx, trainrp, and trainscg), number of epochs, layers, and neurons are given in Table 5. In this study, an increase in the number of layers, neurons, and epochs led to an increase in processing time, while a decrease in point density resulted in a decrease in processing time. In addition, the training functions traingd and trainlm required a long time to the process, whereas the training function traingdx required the least time. This study found a direct correlation between processing time and epoch number.

Table 5.
Processing time values for the FBNNs to predict the height values for each parameter, terrain type, and point distribution in DEM.
The gradient value in ANN models is a value calculated by optimization algorithms during the training of the model. The gradient is obtained by calculating the derivatives of an error function concerning the weights and threshold values. Optimization algorithms use the gradient value to minimize the error function and thus improve the performance of the model. The gradient value is used to prevent overfitting in the training. High gradient values indicate that the network is progressing rapidly during training but may be at risk of overfitting. A low gradient indicates a slow training process and requires more time. The gradient values obtained from FBNNs with different parameters are given in Table 6. In this study, generally, as the number of layers, neurons, and epochs increased, the gradient values decreased, and as the point density decreased, the gradient values increased. The gradient values of the training function trainlm were lower than the other functions, and a longer duration of the training occurred. In addition, gradient values for the training function traingdx were higher, and the duration of the training was lower.

Table 6.
Gradient values for the FBNNs to predict the height values for each parameter, terrain type, and point distribution in DEM.
In ANNs, the best validation performance value represents the validation performance of the network at the point where it achieves the best performance during training. An ANN model typically uses a portion for the training data and another portion for validation. While the training data are used to adjust the model’s weights, the best validation performance value is also a measure used to prevent the overfitting of the model. Overfitting refers to the model fitting to the training data but performing weakly on test datasets. The best validation performance measures the ability of the ANN model to make accurate predictions, determines the overall performance of the model, and can be used to compare it with other models. It can also be used to optimize the model’s hyperparameters (such as learning rate, number of epochs, etc.). The best validation performance refers to the lowest error rate or highest accuracy rate on the validation dataset. The best validation performance values obtained from the FBNN based on different FBNN parameters for different terrain types and point distributions are given in Table 7. Note that since the best validation values are normalized, the value range is between 0 and 1. In this study, it was observed that the best validation performance generally improved as the number of layers, neurons, and epochs increased. Additionally, the best validation performance of the training function trainlm was better than the results obtained by other training functions. Furthermore, the performance of interpolation for flat terrain was the best, whereas the mountainous was the worst. In addition, the performance of interpolation for uniform distribution was the best, whereas the random distribution was the worst.

Table 7.
Best validation performances for the FBNNs to predict the height values for each parameter, terrain type, and point distribution in DEM.
In this study, RMSE values were calculated based on the differences between the predicted height of the FBNN and the target output height. Specifically, comparisons were made to determine the performance of the FBNNs in the height estimation for different terrain types and distributions with different ANN parameters. Figure 7, Figure 8 and Figure 9 present comparisons of RMSE values obtained from different FBNN parameters based on different terrain types and point distributions. For flat terrain, the RMSE was within a centimeter, and for hilly or mountainous terrain, within a meter. It was observed that as the number of layers, neurons, and epochs increased in different terrain types and distributions, the RMSE values decreased. Generally, the training function trainlm gave the best result, whereas traingd and traingdx functions gave the worst results. Furthermore, the accuracy of the interpolation for flat terrain was the best, whereas the mountainous was the worst. In the comparisons of RMSE values, the performance of both traingd and traingdx was lower than the others. However, for the training function traingd, the maximum number of iterations was performed, whereas the minimum number of iterations was performed using the training function traingdx. Therefore, the optimum number of epochs can vary depending on the complexity of the network or the size of the training data set.
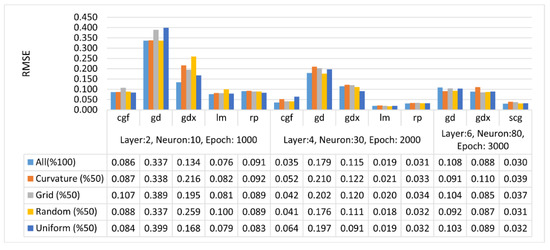
Figure 7.
RMSE values of the flat terrain in meters.
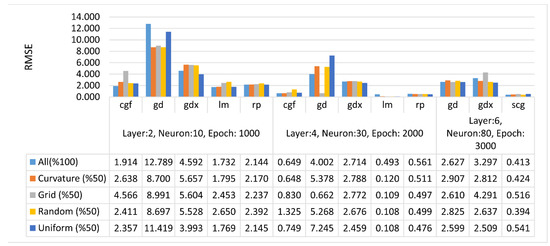
Figure 8.
RMSE values for the hilly terrain in meters.
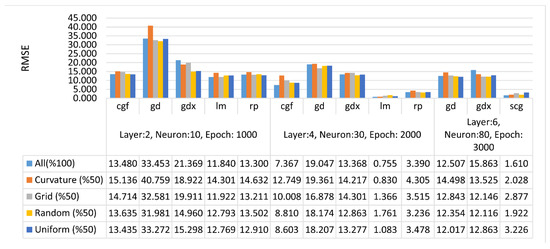
Figure 9.
RMSE values of the mountainous terrain in meters.
For example, the RMSEs for the FBNN model using trainlm training function, which has four hidden layers with 30 neurons each, were 0.02 m, 0.13 m, and 1.45 m, for the grid point distributions on flat, hilly, and mountainous terrains, respectively. The contours obtained from ground truth and spatial distributions of height errors in meters have been illustrated in Figure 10. It was observed that elevation errors increase dramatically on the skeleton lines of the terrain (ridges and drainage lines), as well as at sink and peak points. Since the mountainous terrain has more ridges and drainage lines than the flat terrain, RMSE for the mountainous terrain were higher than that of the flat terrain.
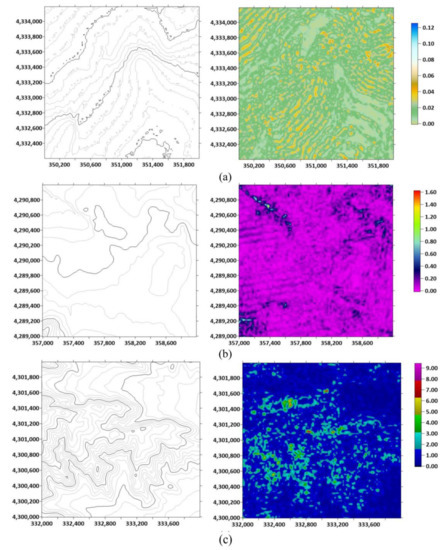
Figure 10.
The contours obtained from ground truth and spatial distributions of errors (in meters) for the estimated heights of grid point distributions on flat (a), hilly (b), and mountainous (c) terrains.
In addition, the ANOVA test was utilized to determine whether there was a significant difference between the RMSE values of FBNN using different learning functions (trainlm, traincgf, traingd, traingdx, trainrp, and trainscg) for the height estimation on different terrain types. If there is a significant difference, it is determined between which learning algorithms this difference is. In the test of homogeneity variance, the significance (sig.) value was less than 0.05. Since the variance homogeneity was not ensured, Tamhane’s T2 was used to determine the differences between groups. The test of homogeneity of variances based on different learning algorithms of FBNN is given in Table 8.

Table 8.
The test of homogeneity of variances based on different learning algorithms of FBNN.
The statistics of the ANOVA test for determining the difference between the groups of different training functions for different terrain types are given in Table 9. If the sig. value is less than 0.05, there is a significant difference between groups. In this study, there were significant differences between the groups of each terrain type.

Table 9.
ANOVA statistics based on different training functions and terrain types.
As a result of the analysis of variance, the Post Hoc Test was applied to determine which training functions are different for different terrain types. Therefore, pairwise comparisons were conducted between FBNN applications. In Table 10, the results of pairwise comparison for the mountainous terrain are given as an example, where the differences are significant (sig. < 0.05). For example, the traingd is significantly different from the traincgf, trainlm, trainrp, and trainscg regarding the RMSE values, which is the most different function.

Table 10.
Pairwise comparisons for training functions for the mountainous dataset.
In addition, in Table 11, subsets were formed to determine whether different training functions have similar results compared to each other and to make statistical evaluations for the height estimation obtained with different training functions for mountainous, hilly, and flat terrain types. In Table 11, training functions gave similar results in the subsets generated for the mountainous, hilly, and flat datasets. The training functions were divided into three subsets for each different terrain dataset. For example, in the mountainous dataset, trainscg, trainlm, and trainrp were similar in estimating the heights in the first subset, while traingdx and traingd were similar in the third group. It has been determined that the results of the training functions in these two subsets differ from each other in height estimation.

Table 11.
Subsets created for different training functions regarding different terrain types.
It is crucial to investigate other factors that may potentially influence the results, such as the resolution of the DEM, which was used 1/3 arc-second in this study. The resolution of the DEM plays a significant role in the performance of the FBNN estimation for spatial interpolation. Comparison of the interpolation performances obtained from different DEM sources, such as ASTER GDEM (1 arc-second), can provide insights into the robustness of the FBNN method. Additionally, the process of DEM super-resolution allows high-resolution DEMs to be economically obtained by recovering from easily obtainable low-resolution DEMs [38]. Considering the accuracy achieved in this study, it is assumed that high-resolution DEMs can be generated from low-resolution DEMs using the FBNN method.
To generate high precision DEMs in urban areas, which encompass numerous surface elements such as buildings, roads, etc., the classification and extraction of the earth surface elements are needed to fuse to complete the DEM of urban plots [39]. Therefore, since the surface elements are dense in urban areas, generating DEMs for urban areas is more complex compared to rural areas. In this study, we used DEMs of USGS, which produces a Digital Terrain Model but calls it a bare-earth DEM [40]. In other words, USGS DEMs are generated based on the bare-earth surface without earth surface elements. Note that the evaluation of DEM height estimation using FBNN in this study encompasses the bare-earth surface.
4. Conclusions
A crucial component in the creation of DEMs is spatial interpolation. This requirement has encouraged researchers to enhance current interpolation methods and improve DEM construction as much as possible. Hence, it is of utmost importance to identify interpolation methods that are more accurate for specific purposes, such as generating fine-scale DEMs. The accuracy of DEM construction is significantly affected by variations in terrain types and point distributions. To determine the accuracy of the spatial interpolation using our method, we selected areas with diverse geomorphic features with different point distributions to construct the DEM and then compared the results with the accuracy obtained. The use of ANN models has been established as an effective solution for interpolating non-linear problems, such as height estimation of grid cells of a DEM. In this study, we used FBNN with different parameters (numbers of epochs, layers, neurons) and different transfer functions (gradient optimization algorithms) to predict the height values for different terrain types and point distributions. Processing time increased with an increase in layers, neurons, and epochs, whereas processing time decreased with a decrease in point density. The interpolation accuracy for flat terrain was the best, while the accuracy for mountainous terrain was the worst. Significant increases in elevation errors were observed along the skeleton lines of the terrain, including ridge and drainage lines, as well as at sink and peak points for terrain types used in this study. This research offers significant insights into the optimization of neural network gradients, with a particular focus on spatial interpolation. Generally, the training function trainlm (which required a long processing time) gave the best result, whereas the most significantly different training functions traingd and traingdx (which required a short processing time) gave the worst result. In a future study, the performance of FBNN can be utilized to generate high-resolution DEMs from low-resolution DEMs. Spatial interpolation for a high-quality DEM generation is still challenging. The investigation of performances of machine learning/deep learning-based approaches in spatial interpolation seems to continue to contribute to this important research topic.
Author Contributions
Conceptualization, A.S. and K.G.; methodology, A.S. and K.G.; software, A.S. and K.G.; validation, A.S. and K.G.; formal analysis, A.S. and K.G.; investigation, A.S. and K.G.; resources, A.S. and K.G.; data curation, A.S. and K.G.; writing—original draft preparation, A.S. and K.G.; writing—review and editing, A.S. and K.G.; visualization, A.S. and K.G.; supervision, A.S. and K.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chaplot, V.; Darboux, F.; Bourennane, H.; Leguédois, S.; Silvera, N.; Konngkeo, P. Accuracy of interpolation techniques for the derivation of digital elevation models in relation to landform types and data density. Geomorphology 2006, 77, 126–141. [Google Scholar] [CrossRef]
- Tu, J.; Yang, G.; Qui, P.; Ding, Z.; Mei, G. Comparative investigation of parallel spatial interpolation algorithms for building large-scale digital elevation models. PeerJ Comput. Sci. 2020, 6, e263. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Tang, X.; Zhang, Y. High Accuracy Interpolation of DEM Using Generative Adversarial Network. Remote Sens. 2021, 13, 676. [Google Scholar] [CrossRef]
- Mitas, L.; Mitasova, H. Spatial interpolarion. In Geographical Information Systems: Principles, Techniques, Management and Applications, 2nd ed.; Longley, P.A., Goodchild, M.F., Maguire, D.J., Rhind, D.W., Eds.; John Wiley & Sons: Chichester, UK, 2005; pp. 481–492. [Google Scholar]
- Hu, P.; Liu, X.; Hu, H. Accuracy Assessment of Digital Elevation Models based on Approximation Theory. Photogramm. Eng. Remote Sens. 2009, 75, 49–56. [Google Scholar] [CrossRef]
- Guo, Q.; Li, W.; Yu, H.; Alvarez, O. Effects of topographic variability and Lidar sampling density on several DEM interpolation methods. Photogramm. Eng. Remote Sens. 2010, 76, 701–712. [Google Scholar] [CrossRef]
- Zhao, M. An indirect interpolation model and its application for digital elevation model generation. Earth Sci. Inform. 2020, 13, 1251–1264. [Google Scholar] [CrossRef]
- Alimissis, A.; Philippopoulos, K.; Tzanis, C.K.; Deligiorgi, D. Spatial estimation of urban air pollution with the use of artificial neural network models. Atmos. Environ. 2018, 191, 205–213. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Appelhans, T.; Mwangomo, E.; Hardy, D.R.; Hemp, A.; Nauss, T. Evaluating machine learning approaches for the interpolation of monthly air temperature at Mt. Kilimanjaro, Tanzania. Spat. Stat. 2015, 14, 91–113. [Google Scholar] [CrossRef]
- Ruiz-Álvarez, M.; Alonso-Sarria, F.; Gomariz-Castillo, F. Interpolation of instantaneous air temperature using geographical and MODIS derived variables with machine learning techniques. ISPRS Int. J. Geo-Inf. 2019, 8, 382. [Google Scholar] [CrossRef]
- Leirvik, T.; Yuan, M. A machine learning technique for spatial Interpolation of solar radiation observations. Earth Sci. Space 2021, 8, e2020EA001527. [Google Scholar] [CrossRef]
- Gumus, K.; Sen, A. Comparison of spatial interpolation methods and multi-layer neural networks for different point distributions on a digital elevation model. Geod. Vestn. 2013, 57, 523–543. [Google Scholar] [CrossRef]
- Snell, S.E.; Gopal, S.; Kaufmann, R.K. Spatial Interpolation of Surface Air Temperatures Using Artificial Neural Networks: Evaluating Their Use for Downscaling GCMs. J. Cliımate 2000, 13, 886–895. [Google Scholar] [CrossRef]
- Charalambous, C. Conjugate gradient algorithm for efficient training of artificial neural networks. IEE Proc. G (Circuits Devices Syst.) 1992, 139, 301–310. [Google Scholar] [CrossRef]
- Moller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Bishop, C. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK, 1995; pp. 116–148. [Google Scholar]
- Tavassoli, A.; Waghei, Y.; Nazemi, A. Comparison of Kriging and artificial neural network models for the prediction of spatial data. J. Stat. Comput. Simul. 2022, 92, 352–369. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining Concepts and Techniques; Elsevier: Waltham, MA, USA, 2012. [Google Scholar]
- Oztopal, A. Artificial neural network approach to spatial estimation of wind velocity data. Energy Convers. Manag. 2006, 47, 395–406. [Google Scholar] [CrossRef]
- Danesh, M.; Taghipour, F.; Emadi, S.M.; Sepanlou, M.G. The interpolation methods and neural network to estimate the spatial variability of soil organic matter affected by land use type. Geocarto Int. 2022, 37, 11306–11315. [Google Scholar] [CrossRef]
- Attoh-Okine, N.O. Analysis of learning rate and momentum term in backpropagation neural network algorithm trained to predict pavement performance. Adv. Eng. Softw. 1999, 30, 291–302. [Google Scholar] [CrossRef]
- Wong, K.; Dornberger, R.; Hanne, T. An analysis of weight initialization methods in connection with different activation functions for feedforward neural networks. Evol. Intell. 2022, 1–9. [Google Scholar] [CrossRef]
- Sharma, B.; Venugopalan, K. Comparison of neural network training functions for hematoma classification in brain CT images. IOSR J. Comput. Eng. 2014, 16, 31–35. [Google Scholar] [CrossRef]
- Kamble, L.; Pangavhane, D.; Singh, T. Neural network optimization by comparing the performances of the training functions -Prediction of heat transfer from horizontal tube immersed in gas–solid fluidized bed. Int. J. Heat Mass Transf. 2015, 83, 337–344. [Google Scholar] [CrossRef]
- Gesch, D. The National Elevation Dataset. Digital Elevation Model Technologies and Applications: The DEM Users Manual. In American Society for Photogrammetry and Remote Sensing; Maune, D., Ed.; Bethesda: Rockville, MD, USA, 2007; pp. 99–118. [Google Scholar]
- Strahler, A. Hypsometric (area-altitude) analysis of erosional topography. Bull. Geol. Soc. Am. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Melton, M. The geomorphic and palaeoclimatic significance of alluvial deposits in Southern Arizona. J. Geol. 1965, 73, 1–38. [Google Scholar] [CrossRef]
- Chorley, R. Spatial Analysis in Geomorphology; Routledge: London, UK, 1972. [Google Scholar]
- Sen, A.; Gumusay, M.U.; Kavas, A.; Bulucu, U. Programming an Artificial Neural Network Tool for Spatial Interpolation in GIS—A case study for indoor radio wave propagation of WLAN. Sensors 2008, 8, 5996–6014. [Google Scholar] [CrossRef] [PubMed]
- Hagan, M.; Menhaj, M. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, Orlando, FL, USA, 27–29 June 1994. [Google Scholar]
- Scales, L. Introduction to Non-Linear Optimization; Springer: New York, NY, USA, 1985. [Google Scholar]
- Hagan, M.; Demuth, H.; Beale, M. Neural Network Design; PWS Publishing: Boston, MA, USA, 1996. [Google Scholar]
- Beale, E. A derivation of conjugate gradients. In Numerical Methods for Nonlinear Optimization; Academic Press: London, UK, 1972; pp. 39–43. [Google Scholar]
- Tukey, J. Comparing individual means in the analysis of variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef]
- Sparks, J. Expository notes on the problem of making multiple comparisons in a completely randomized design. J. Exp. Educ. 1963, 31, 343–349. [Google Scholar] [CrossRef]
- Zhang, Y.; Wenhao, Y. Comparison of DEM Super-Resolution Methods Based on Interpolation and Neural Networks. Sensors 2022, 22, 745. [Google Scholar] [CrossRef]
- Li, M.; Dai, W.; Song, S.; Wang, C.; Tao, Y. Construction of high-precision DEMs for urban plots. Ann. GIS 2023, 1–11. [Google Scholar] [CrossRef]
- Guth, P.L.; Van Niekerk, A.; Grohmann, C.H.; Muller, J.P.; Hawker, L.; Florinsky, I.V.; Gesch, D.; Reuter, H.I.; Herrera-Cruz, V.; Riazanoff, S.; et al. Digital Elevation Models: Terminology and Definitions. Remote Sens. 2021, 13, 3581. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).