A Change-Sensitive Complexity Measurement for Business Process Models Based on Control Structure

Abstract

The analysis of the process model complexity has significant implications for the operation, maintenance, and optimization of processes. As process models consist of control structures with specific repetitive patterns, the complexity of the control structures often determines the process model complexity. While the existing methods for measuring the process model complexity consider most control structure complexity, some changes in branch structures cannot be reflected in the process model complexity. To address this issue, this paper considers the impact of the number and position of activities in branching structures on the process model complexity, distinguishes the connection forms between branch structures, and defines the complexity of the branching structures. We propose a new complexity measurement (CP) based on the control structures. The theoretical validity of CPs was confirmed using Weyuker’s properties, and the process structure variant model was used to experiment with its sensitivity. The findings indicate that the CP satisfies eight out of the nine properties proposed by Weyuker. Compared with the other complexity measurement methods of the process model, the CP is more sensitive to some structural changes in the process model. Therefore, when the structure of the process model changes, the CP reflects the changes in the process model complexity more accurately.

1. Introduction

A business process is composed of a series of structured activities or tasks [1] aimed at providing specific products or services to customers, thereby creating value and revenue for the enterprise [2]. A business process model is the direct representation of the function and structure of the business process [3]. The complexity of a process model is measured to evaluate its quality, identify the structures suitable for improvement and simplification, guide optimization and the design of processes in business process management, and achieve simpler, more reliable, and robust process models [4]. Process models are usually expressed graphically using Petri nets [5], Event Driven Process Chains (EPCs) [6], and Business Process Model and Notation (BPMN) [7]. Business process complexity involves multiple aspects such as activity complexity [8], control structure complexity [9], resource complexity [10], cognitive complexity [11], etc. In addition, control structure complexity is a hot research topic and an important prerequisite for optimizing business processes. The complexity of process control structures mainly considers the impact of activities and their connection relationships on the process complexity. A BPMN is chosen to model processes in the paper, which includes various elements such as events, gateways, activities, control flows, swimlanes, and pools [12]. Considering that the current focus on the complexity of process control structures is on activities and the connectivity between activities, this article only considers the three basic elements of activities, control flow, and gateways in BPMN. For gateways, we only consider AND, XOR, and OR gateways.

The current methods used to measure the complexity of process models fail to take into account the impact of activity quantity and location, resulting in a lack of sensitivity in detecting changes in the process structure. This, in turn, leads to inaccurate representations of the complexity changes. In our paper, we propose a new approach to address this issue by considering the activity quantity and location in branching structures, distinguishing complex relationships generated by different connection forms between branching structures, and defining a new measurement method for their complexity. We further introduce a complexity measurement method (CP) based on the control structure, which comprehensively considers the complexity of branching, sequential, and cyclic structures. To validate the effectiveness of CPs for measuring the process model complexity, we use Weyuker’s properties [13] and construct the process structure variant models to verify its ability to sensitively detect changes in the process model structures.

The remainder of this paper is structured as follows: Section 2 introduces the work related to the process model complexity. Section 3 describes the relevant theoretical foundations of the study. Section 4 presents some problems with the current study and proposes a complexity measurement method for the process model based on the control structures. Section 5 validates the proposed method theoretically and designs the process structure variant models to verify the sensitivity of our method. Section 6 conducts experimental analysis to validate the sensitivity of our method to changes in the process model. Finally, Section 7 summarizes the work of our study.

2. Related Work

The complexity of control structures is an important factor affecting process model complexity and has been extensively studied. Cardoso proposed the Control Flow Complexity (CFC) to describe the impact of the three branch structures (AND, XOR, OR) on the complexity of process models [8]. However, CFC only calculates the number of possible paths generated by branch structures, without considering the impact of other control structures such as sequences and loops. Gruhn and Laue argued that CFC cannot provide a better understanding of business process models and assigned the cognitive weight (CW) to control structures from the perspective of cognitive dimensions to quantify the difficulty of people’s understanding of control structures [11]. Rolon used the Connectivity Level Between Activities (CLA) [14] to measure the degree of connectivity between activities in a process. The more the number of sequence flows between activities is, the lower the activity connectivity is, and the higher the process complexity is. Vanderfeesten introduced Cross-Connectivity (CC) [15] to analyze the impact of the closeness between activities on the understandability of process models. The higher the connection strength between activities, the easier the process model is to understand. Mendling proposed a set of complexity measures (Average Connector Degree, Maximum Connector Degree, etc.) to analyze the impact of control structure complexity on the probability of process errors [9]. He employed numerous EPC models to examine the statistical correlation between these measures and the likelihood of errors in process models. The findings indicated that the majority of these measures have the anticipated effect of either elevating or reducing the probability of process errors. In addition, Sanchez-Gonzalez analyzes the impact of gateway complexity on the understandability and maintainability of process models based on a Gateway Complexity Indicator (GCI) [16], and extracted the threshold in the experiment. When the GCI value exceeds the predetermined value, the process understandability and maintainability will be affected. Yaqin has enhanced the study of process model complexity by incorporating the influence of activity and arc numbers and introduced the Scale complexity measurement method [17]. Later, in response to the inadequate comprehensiveness and sensitivity of CADAC [18] in assessing process model complexity, Yaqin proposed the complexity measurement formula YC [19], which offers a comprehensive and sensitive analysis of the process model complexity.

Although the current complexity measures for process models are capable of measuring the complexity of control structures, they may not be sensitive to certain changes in control structures. This insensitivity can result in inaccuracies in detecting changes in the complexity of process models. For instance, the three process models represented by BPMN, as shown in Figure 1, contain an AND structure with two branches. In process model P1, one branch contains activity A, while the other branch contains activity B. In process model P2, one branch contains activities A and B, while the other branch contains activities C and D. In process model P3, one branch contains activities A, B, and C, while the other branch contains activity D. Despite having the same number of branches, the number of activities and their positions on each branch differ among the three process models. These existing methods measure the complexity of the three branching structures in the same way, without taking into account the impact of the number and position of activities on the complexity of process models, which leads to inaccurate measurements of complexity.

As is commonly understood, the addition of activities to a process can increase its workload. Process models with few activities in branching structures are less complex than those with many activities. For example, the P1 process model in Figure 1 generates two activity sequences (AB and BA), whereas P2 generates six activity sequences (ABCD, ACDB, ACBD, CADB, CABD, and CDAB). This indicates that P2 is more complex than P1. Therefore, when assessing process model complexity, the variations in complexity caused by the different numbers of activities must be taken into consideration. Moreover, P2 and P3 have the same number of branches and activities, but the locations of the activities differ. P3 generates four activity sequences (ABCD, ADBC, ABDC, and DABC), which are less complex than P2. Thus, the changes in complexity resulting from different activity positions should also be taken into account. Overall, the complexity of a process model should consider both the number and position of activities.

3. Basic Theories

In this section, we will introduce the relevant theoretical foundations, including an overview of BPMN, basic control structures, and the complexity measurement of process models.

3.1. BPMN

Business Process Model and Notation (BPMN) is a standardized language used for describing and visualizing business processes [20]. Its notations encompass events, activities, gateways, and data objects, which can depict tasks, decisions, parallel processes, and messaging in business processes [21]. BPMN employs easily understood symbols and graphics to represent business processes, thereby enabling the communication, comprehension, optimization, and enhancement of business processes within an organization [22]. Moreover, it facilitates workflow automation. Due to its usefulness, BPMN has become a widely adopted modeling language for constructing business process models [23]. In this paper, we aim to experiment with the process structure variant models represented by BPMN to validate the advantages of our proposed complexity measurement method.

3.2. Basic Control Structures

The business process model comprises Basic Control Structures (BCSs) [24], which represent fundamental flow control mechanisms utilized to establish the logical framework of a process model [25]. BCSs encompass three control structures: sequence, branching, and looping. A sequential structure executes steps in the order presented in the process diagram. In a branching structure, specific conditions determine the execution path to be taken. A looping structure repeats the same step until a specific condition is met before exiting the loop. A BCS is regarded as a component of workflow based on cognitive patterns [26], where cognitive weights are employed to describe the difficulty of understanding different control structures. This paper adheres to Yaqin’s definition of a BCS [19].

• BCS = {seq, AND, OR, XOR, cyc}
• BCS is defined as seq if t₀ → t_k, where t ∈ Ac
• BCS is defined as AND if t₀ has branch t₀₁, t₀₂ …, t_0S, where t ∈ Ac
• BCS is defined as OR if t₀ has branch t₀₁, t₀₂ …, t_0S, where t ∈ Ac
• BCS is defined as XOR if t₀ has branch t₀₁, t₀₂ …, t_0S, where t ∈ Ac
• BCS is defined as cyc if t_k has a loop branch, where t ∈ Ac

3.3. Process Model Complexity Based on the Control Structure

Process complexity is defined as the degree to which a process is difficult to analyze, understand, or explain [27]. A process model is a visual representation of an abstract process that facilitates the design, management, maintenance, and optimization of processes [28]. The process model complexity can be measured in terms of activities, control flow, data flow, and resources [8]. Control structures, in particular, play a critical role in determining the complexity of process models owing to their intricate relationships. To describe the effort required to comprehend them, cognitive weights were established for control structures in process models [29].

In this study, we analyze the process model complexity through the lens of control structures, define the complexity of different control structures based on cognitive weights, and ultimately introduce a control-structure-based approach to measure the complexity of process models.

Table 1. Cognitive weight for control structures.

Control Structure	Weight	Source
Sequence	1	[11]
Parallel Split (AND)	4
Exclusive Choice (XOR)	3
Multiple Choice (OR)	7
Looping (Cyclic)	3	[19]

displays the weight values of control structures.

4. The Process Model Complexity Measurement

In business process modeling, the branching structure is a fundamental component of control structures that govern the direction of process flow. The current methods for measuring the complexity of branching structures are not sensitive enough to the changes in the structure of process models. Consequently, our research aims to enhance the structural sensitivity of complexity measures in process models by taking the branching structure as a starting point.

4.1. Measuring the Branching Structure Complexity

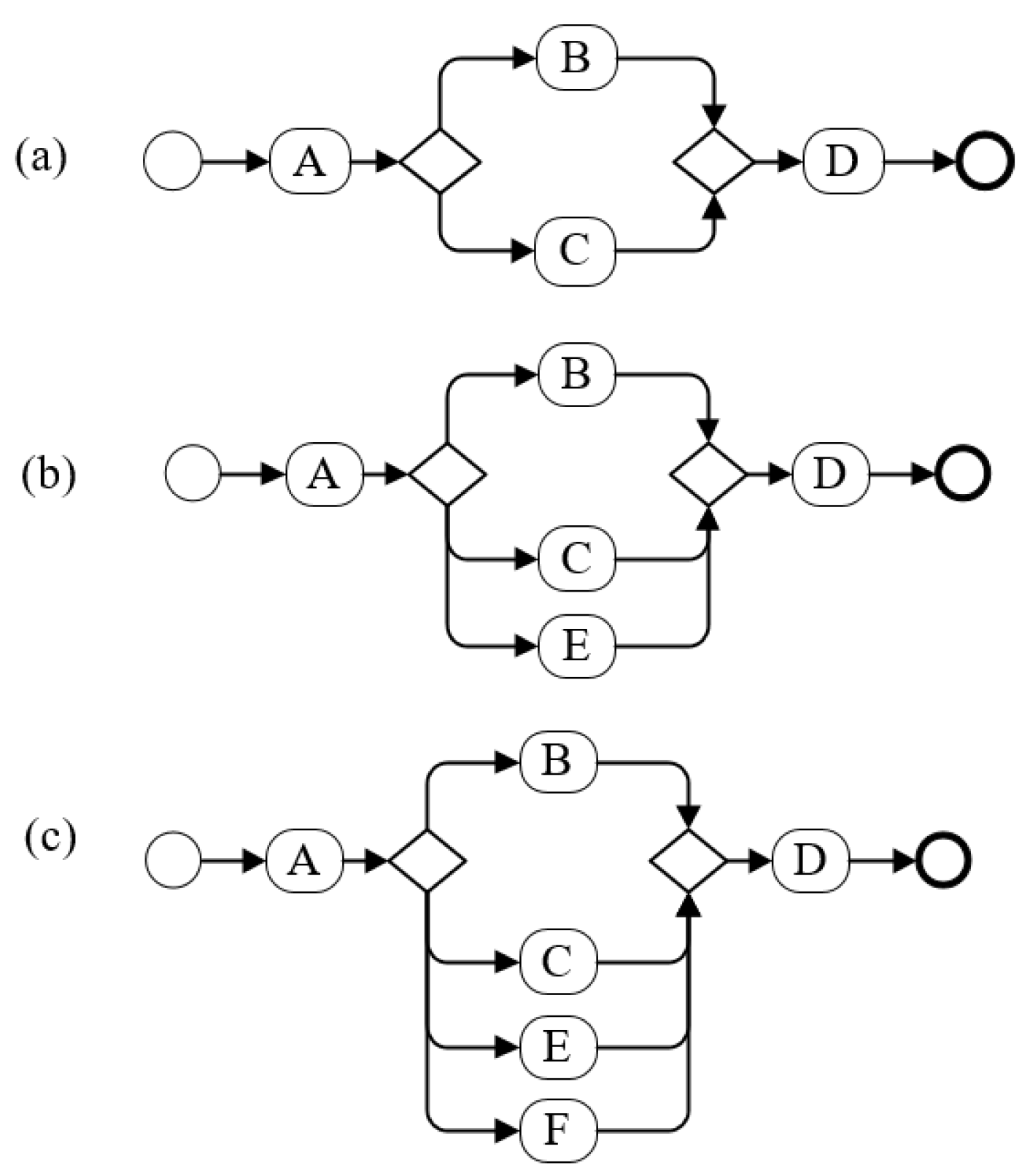
4.1.1. The Branching Structure Complexity

In BPMN process models, there are three common types of branching structures (AND, XOR, OR) [30], each with varying degrees of complexity. However, existing complexity measurement methods for process models [8,9,11,17,18,19] only take into account the number of branches, disregarding the effect of the number and placement of activities within the branching structures. In light of this, we propose a novel definition of the complexity for the three branching structures, which considers the different activity sequences that can be generated by each structure. The core idea is that the more diverse activity sequences a branching structure can produce, the more complex it is. To distinguish the complexity degrees of different types of branching structures, we assign a cognitive weight to each type of structure. If two branching structures can generate the same number of activity sequences, their different weights lead to different levels of complexity. Therefore, our approach accounts for the impact of the number and location of activities on the process model complexity and effectively distinguishes the difficulty of understanding the different types of branching structures.

Definition 1.

AND branching structure complexity.

The AND branching structure is designed to execute all of its branches during the process. To calculate the number of different activity sequences generated by the AND structure, the first branch is assumed to have the most activities, and the number of sequences is calculated accordingly. If multiple branches have the same maximum number of activities, any one of them can be selected as the first branch. The formula for calculating the number of activity sequences for the AND structure is represented by the symbol $L_{{AND}_i}$, defined as follows:

$$L_{{AND}_i}=\prod _{j=1}^{n-1}\left[\sum _{i=1}^{m_{j+1}}\left(C_{\left(\sum _{k=1}^j{m}_k\right)+1}^i\cdot C_{m_{j+1}-1}^{i-1}\right)\right]$$

(1)

where n represents the number of branches, $C_n^m$ is mathematical combination formula, and m_j represents the number of activities on the jth branch. Since intermediate events and activities are elements at the same level, we consider that they have the same impact on the process complexity. If there is an intermediate event, it is added to m_j as an activity. When combined with the weight CW_AND = 4 shown in Table 1, the complexity of an AND branching structure is represented by the symbol $C_{{AND}_i},$ defined as follows:

$$C_{{AND}_i}={CW}_{AND}·L_{{AND}_i}=4L_{{AND}_i}$$

(2)

where $L_{{AND}_i}$ is the activity sequences of the AND_i branching structure, CW_AND is the weight of the AND branching structure. For example, to calculate the branching structure complexity of model P3 in Figure 1, where the AND branching structure has two branches n = 2, the number of activities on the first branch m₁ = 3, AND the number of activities on the second branch m₂ = 1, the number of activity sequences $L_{{AND}_{P3}}$ = 4, the weight CW_AND = 4, so the complexity is $C_{{AND}_{P3}}$ = 16.

Definition 2.

XOR branching structure complexity.

The XOR branching structure executes only one of its branches, each of which generates a set of activity sequences. Therefore, the total number of different activity sequences represented by the symbol $L_{{XOR}_i}$, that can be produced by the XOR branching number as follows:

$$L_{{XOR}_i}=n$$

(3)

where n is the number of branches. When combined with the weight CW_XOR = 3 shown in Table 1, the complexity of an XOR branching structure represented by the symbol $C_{{XOR}_i}$ can be calculated as:

$$C_{{XOR}_i}={CW}_{XOR}·L_{{XOR}_i}=3·L_{{XOR}_i}$$

(4)

where CW_XOR is the weight of the XOR branching structure, $L_{{XOR}_i}$ is the activity sequences of the XOR_i branching structure. As shown in Figure 2, the process model P4 includes an XOR branching structure with two branches n = 2, which generates two different activity sequences $L_{{XOR}_{P4}}$= 2. The XOR structure has the weight CW_XOR = 3, so its complexity $C_{{XOR}_{P4}}$= 6.

Definition 3.

OR branching structure complexity.

The OR branching structure executes one or more of its branches. For an OR structure with n branches, there are 2ⁿ − 1 possible combinations of branches that can be executed simultaneously. One combination executes all the branches with a probability of $\frac{1}{2^n-1}$, which is similar to an AND structure executing all of its branches (with a probability of 1). The total probability of executing the remaining combinations is $\frac{2^n-2}{2^n-1}$, and each combination can be viewed as an XOR structure executing one of its branches (with a probability of 1/n). The number of different activity sequences generated by an OR branching structure can be represented by the symbol $L_{{OR}_i},$ defined as follows:

$$L_{{OR}_i}=\left(\frac{1}{2^n-1}\cdot 1\right)L_{{AND}_i}+\left(\frac{2^n-2}{2^n-1}\cdot \frac{1}{n}\right)L_{{XOR}_i}$$

(5)

where n is the number of branches, $L_{{AND}_i}$ is the number of activity sequences for the corresponding AND branching structure, and L_XOR is the number of activity sequences for the corresponding XOR branching structure. When combined with the CW_OR = 7 shown in Table 1, an OR branching structure complexity can be represented by the symbol $C_{{OR}_i}$ as:

$$C_{{OR}_i}={CW}_{OR}·L_{{OR}_i}=7·L_{{OR}_i}$$

(6)

where CW_OR is the weight of the OR branching structure, $L_{{OR}_i}$ is the activity sequences of the OR_i branching structure. As shown in Figure 2, the process model P5 has an OR branching structure. The number of different activity sequences $L_{{OR}_{P5}}=(\frac{1}{3}\cdot 1)\cdot 4+(\frac{2}{3}\cdot \frac{1}{2})\cdot 2=2$, the weight CW_XOR = 7, so we find its complexity $C_{{OR}_{P5}}=14$.

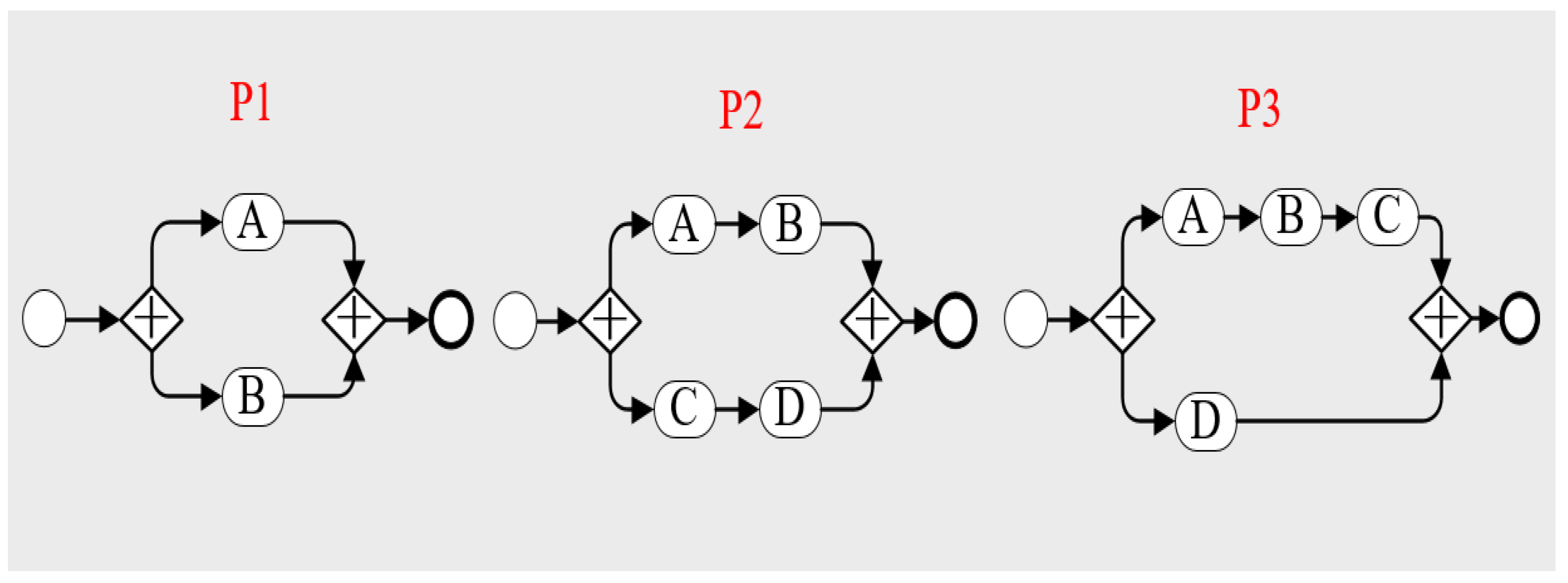
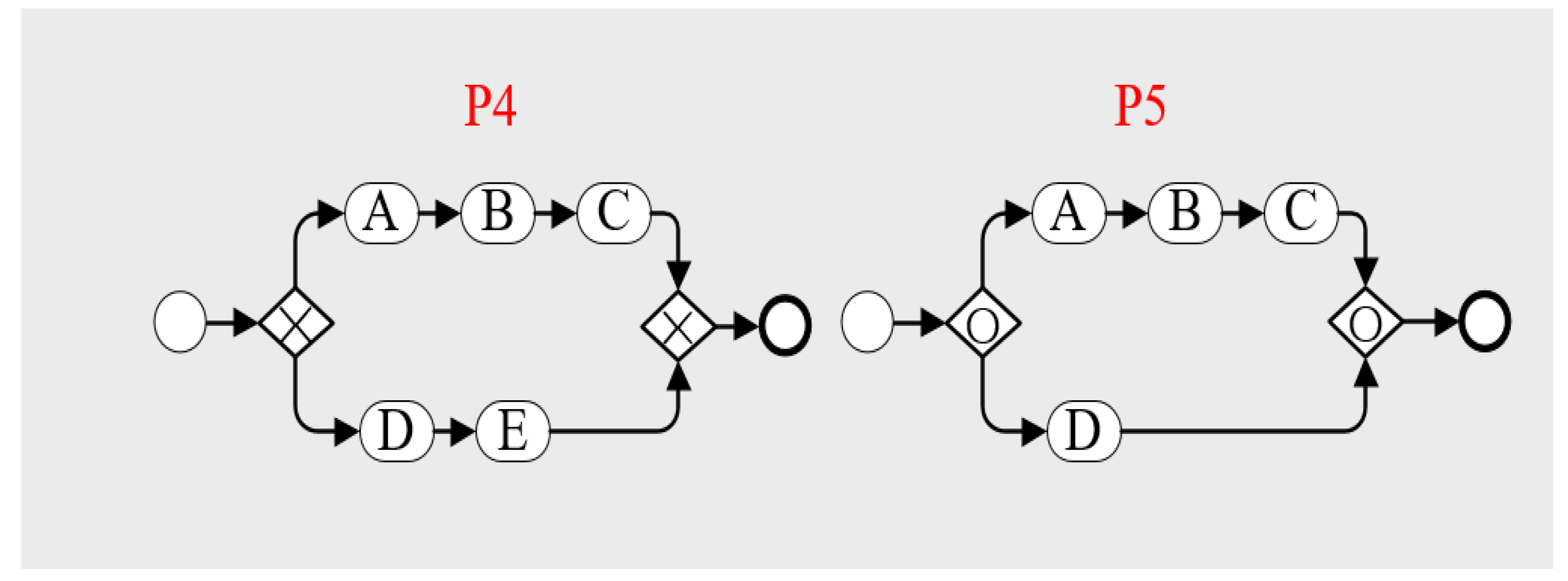
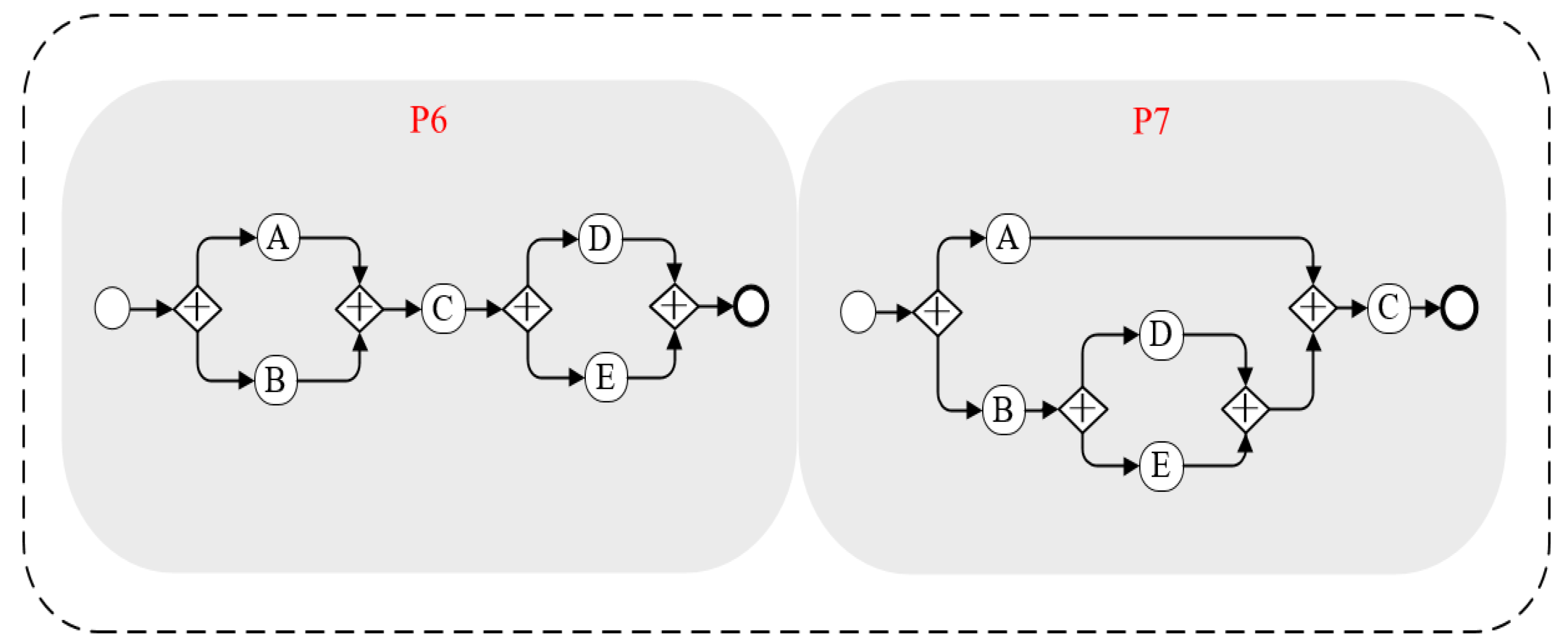
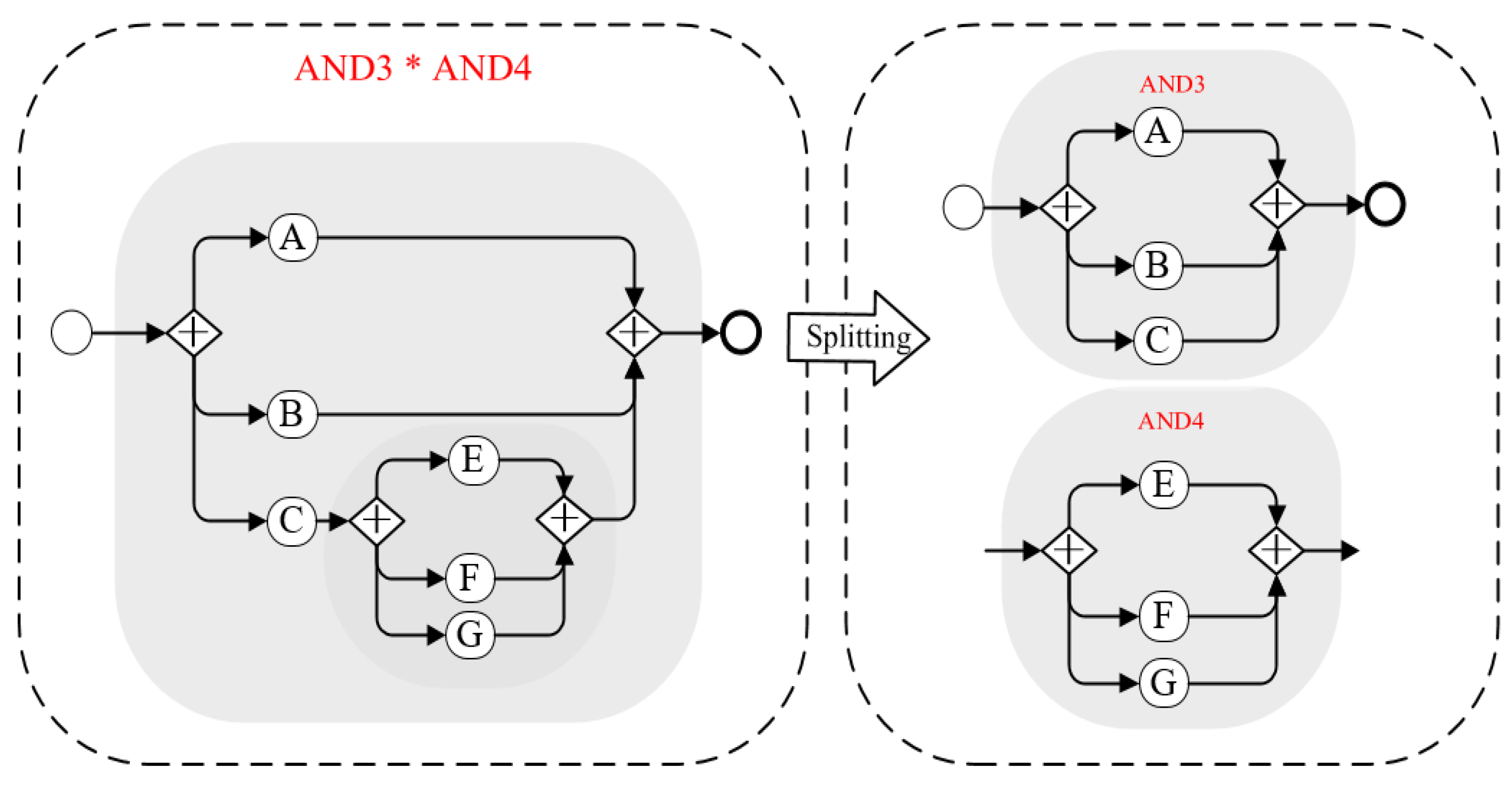
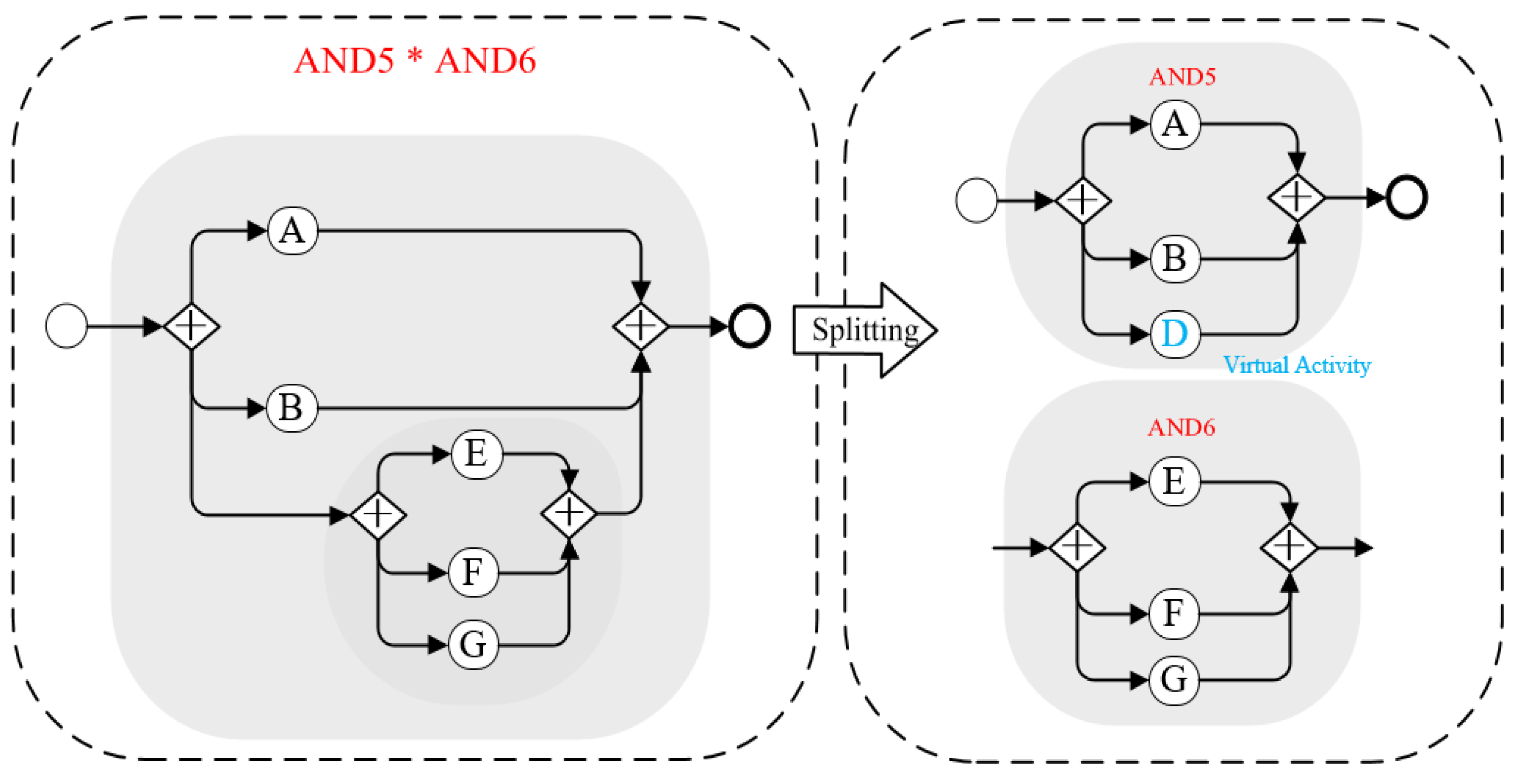
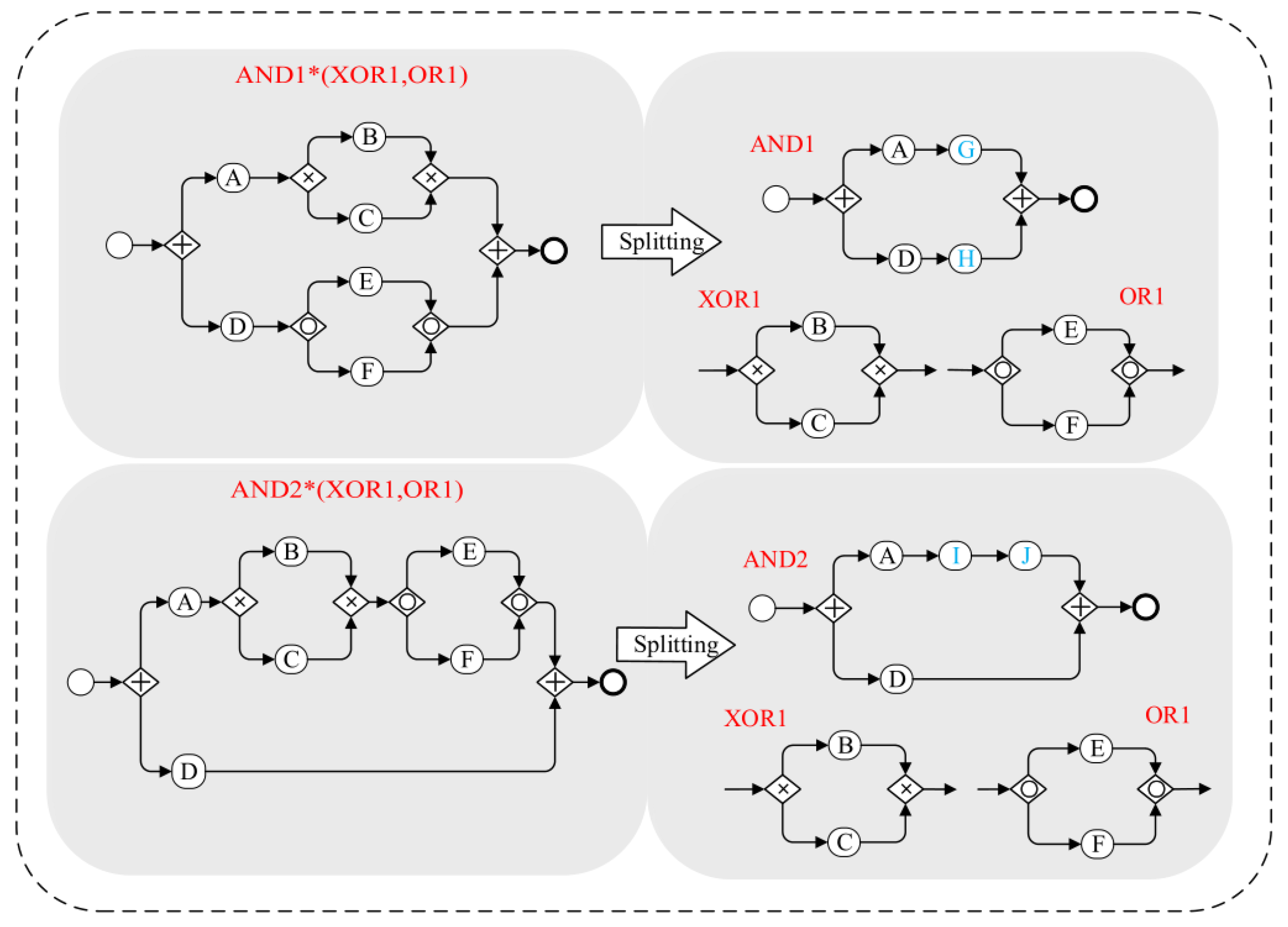
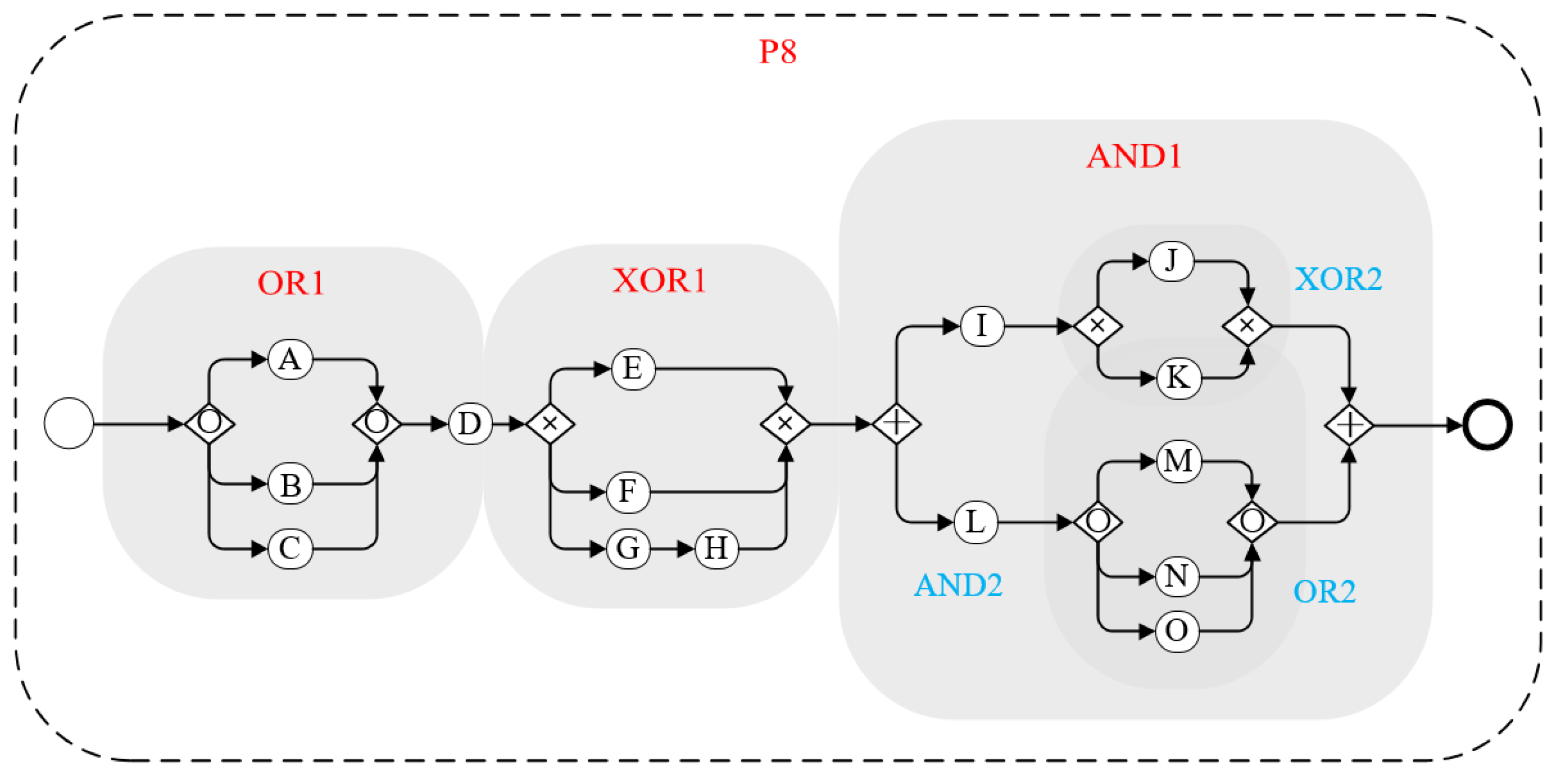
4.1.2. The Connection Forms between the Branching Structures

The connections between branching structures in a process model can be classified as either sequential or nested. As illustrated in Figure 3, both P6 and P7 contain two identical AND branching structures. In P6, these two structures are connected sequentially, leading to four different activity sequences: ABCDE, ABCED, BACDE, and BACED. In contrast, in P7, the two structures are nested, resulting in eight different activity sequences: ABDEC, ABEDC, BADEC, BAEDC, BDAEC, BEADC, BDEAC, and BEDAC. The nested connections between the branching structures create a more complex overall structure than the sequential connections.

When two independent branching structures are integrated into a unified structure, the overall complexity is not less than the sum of the complexity of each branching structure [18]. The current complexity measurement methods for process models merely sum up the complexities of the individual branching structures, without taking into account the impact of their connection forms on the overall complexity. Thus, this paper proposes a novel approach to differentiate the complexity of process models resulting from the diverse forms of connection between the branching structures.

Definition 4.

The complexity of the sequential connection.

When multiple branching structures are connected in sequence to form a unified structure (AND/XOR/OR-AND/XOR/OR), the overall complexity is equal to the sum of the complexities of each branching structure. The formula for calculating complexity is as follows:

$$C_{branch1-branch2}=C_{branch1}+C_{branch2}$$

(7)

where the branch can be an AND/XOR/OR branching structure. In Figure 4, the two branching structures AND1 and AND2 are sequentially connected to form the structure AND1-AND2. The complexity of the entire And1-And2 structure is determined as C_AND1-AND2 = C_AND1 + C_AND2.

Definition 5.

The complexity of the nested connection.

The nested structure resulting from the branching structures is more intricate than that formed through the sequential connections. When multiple branches are nested (AND/XOR/OR * AND/XOR/OR), the complexity of the nested structure is the product of the outer branching structure’s complexity and the sum of the inner branching structures’ complexity. The formula for computing this complexity is as follows:

$$C_{branch1\ast branch2}=C_{branch1}·C_{branch2}$$

(8)

where the branch can be an AND/XOR/OR branching structure. In Figure 5, the branching structures AND3 and AND4 are connected in a nested way to form the structure AND3*AND4, where the AND3 structure is the outer nested layer and the AND4 structure is the inner nested layer, and the complexity of the nested structure is calculated as C_AND3∗AND4 = C_AND3 · C_AND4.

Furthermore, a unique scenario must be taken into consideration. If activity C is removed from Figure 5, the third branch of the outer nested AND3 branching structure will become inactive, rendering its complexity impossible to calculate. When multiple branching structures are nested to form an overall structure, but the outer branching structure has no activity on its branches, the current methods of measuring complexity are inadequate for determining the structure’s complexity. As shown in Figure 6, the current methods calculate the complexity of the AND5*AND6 structure by separately determining the complexities of the AND5 and AND6 branching structures and summing them. However, since there is no activity on the branches of the AND5 structure, its complexity cannot be measured. To address the issue of the unmeasurable complexity of branching structures caused by the absence of activity on the branches, we propose considering the internally nested AND6 structure as a virtual activity (i.e., activity D in Figure 6). When calculating the complexity of the outer AND5 branching structure, we must account for the impact of the virtual activity on complexity.

The addition of virtual activities enables the differentiation of cases in which different nested structures are formed by the same branching structure, but exhibit varying levels of complexity due to the positions of the internal branching structures. Figure 7 illustrates that both AND1*(XOR1, OR1) and AND2*(XOR1, OR1) are constructed by the same branching structure, but have different complexities because of the differences in the number of activity sequences that can be generated. The current complexity measures cannot distinguish between these two nested structures, but virtual activities can. By splitting the nested structure AND1*(XOR1, OR1), it becomes apparent that the virtual activities G and H on the outer branching structure AND1 represent the internal branching structures XOR1 and OR1, respectively. The complexity of the outer branching structure AND1 is calculated as C_AND1 = 24, and the complexity of the entire nested structure AND1*(XOR1, OR1) is calculated as C_{AND1*(XOR1,OR1)} = C_AND1(C_XOR1 + C_OR1) = 368. Likewise, for the nested structure AND2*(XOR1, OR1), the virtual activities I and J on the outer branching structure AND2 represent the branching structures XOR1 and OR1, respectively. The complexity of the outer branching structure AND2 is calculated as C_AND2 = 16, and the complexity of the entire nested structure AND2*(XOR1, OR1) is calculated as C_{AND2*(XOR1,OR1)} = C_AND2 (C_XOR1 + C_OR1) = 736/3.

When confronted with multiple layers of nesting, the complexity can be calculated by working from the inside out. In Figure 8, the branching structures AND1, AND2, and XOR1 form a multi-layer nested structure AND1*(XOR1*AND2). To calculate the complexity, we first determine the complexity of the inner nested structure XOR1*AND2 as C_XOR1*AND2 = C_XOR1·C_AND2. We then calculate the complexity of the outer nested structure AND1*(XOR1*AND2) as C_{AND1*(XOR1*AND2)} = C_AND1 C_XOR1*AND2. Thus, the complexity of the entire multi-layer nested structure can be expressed as C_{AND1*(XOR1*AND2)} =C_AND1·C_XOR1·C_AND2.

4.1.3. The Complexity Measurement for Branching Structures

With the definitions of the three types of branching structures outlined above, it is possible to assess the complexity of each branching structure within a given process. By analyzing the connections between the branching structures, we can calculate the complexity of both the nested and sequential structures, and then calculate the overall complexity generated by all branching structures in the process model.

Definition 6.

The branching structure complexity in the process model.

The branching structure complexity of a process model is determined by the complexities of its AND, XOR, and OR branching structures. Therefore, the formula for determining the branching structure complexity of a process model is represented by the symbol $C_B$, defined as follows:

$$C_B=\sum {\left(C_{AND}\right)}_i+\sum {\left(C_{OR}\right)}_i+\sum {\left(C_{XOR}\right)}_i$$

(9)

Figure 9 shows that the process model P8 comprises three separate branching structures, OR1, XOR1, and AND1, connected sequentially. AND1 is represented by the nested structure AND2*(XOR2, OR2), which is composed of AND2, XOR2, and OR2. The complexity of OR1 is C_OR1 = 12, while the complexity of XOR1 is C_XOR1 = 9. In the nested structure AND2*(XOR2, OR2), the outer layer nested structure AND2 has a complexity of C_AND2 = 24, while the inner layer nested structures OR2 and XOR2 have complexities of C_OR2 = 12 and C_XOR2 = 6, respectively. Consequently, the complexity of AND1 is C_AND1 = C_{AND2*(XOR2,OR2)} = C_AND2·(C_XOR2 + C_OR2) = 432. The total complexity resulting from the branching structures in the process model is C_B = C_AND1 + C_XOR1 + C_OR1 = 453.

4.2. The Change-Sensitive Complexity Measurement for the Process Model Based on the Control Structure

To comprehensively measure the complexity of a process model, we define the complexity of its sequence and loop structures and formulate a complexity measurement formula based on the control structure of the process model.

Definition 7.

The sequence structure complexity.

In conjunction with the weight CW_seq = 1 as presented in Table 1, the formula for calculating the complexity of the sequence structure in the process model is represented by the symbol $C_{seq}$, defined as follows:

$$C_{seq}={CW}_{seq}·N_{seq}=N_{seq}$$

(10)

where CW_seq is the weight of the sequence structure, the number of sequential nodes N_seq includes all nodes in the sequential structure, such as the start nodes, end nodes, activity nodes, and gateway nodes.

Definition 8.

The loop structure complexity.

Combined with the weight CW_cyc = 3 outlined in Table 1, the formula for calculating the complexity of the loop structure denoted by $C_{cyc}$ in the process model is defined as follows:

$$C_{cyc}={CW}_{cyc}·\frac{N_{cyc}}{N}=3·\frac{N_{cyc}}{N}$$

(11)

where CW_cyc is the weight of the cyclic structure, N is the total number of nodes in the process model, the number of nodes in the loop N_cyc includes all nodes in the loop, such as the start nodes, end nodes, activity nodes, and gateway nodes.

Definition 9.

The change-sensitive process model complexity measurement based on the control structure.

Based on the control structure complexity formulas mentioned above, the complexity of the process model can be represented by the symbol CP, defined as the sum of the complexities arising from the sequence, branching, and loop structures.

$$CP={{C_{AND}+C_{XOR}+C_{OR}+C}_{seq}+C}_{cyc}$$

(12)

5. Experiment Design and Theoretical Validation

In this section, we construct the process structure variant models to test the sensitivity of CPs in identifying specific changes in the process model. We also demonstrate the effectiveness of CPs in measuring the process model complexity by validating it through Weyuker’s properties [13].

5.1. Experiment Models

As illustrated in the following figures, this section constructs the process structure variant models [31] to show some of the structural changes that may occur in the process models. The baseline for the construction of the model is to consider the five control structures (sequence, three branching structures, and loop structures). Each control structure causes a different activity sequence by changing the number and position of the activities. The branching structures are separately considered by exchanging the gateway types in nested structures, increasing the number of branches, and changing the connection method to discover the differences in the model structure complexity caused by the differences in the execution sequence. Table 2 elaborates on the purpose of designing the process models in these figures and groups them according to their different applications. Each group represents a structural change that may occur in the process model. In the following process models, if the gateway is not marked with a type and represented as an empty diamond, it can be an AND, XOR, or OR gateway.

Table 2. The purpose of business process models.

Group	Purpose	Business Process Model	Figure
1	This group is intended to show the effect of adding new elements on the process model complexity.	In the first case, as shown in Figure 10, process models b and c are obtained by sequentially adding the activities to the base process model a.	Figure 10
2	This group is intended to show the effect of changes in the number of branches on the complexity of the process model.	In the first case, as shown in Figure 11, process models b and c are obtained by gradually adding activities to the branching structure based on process model a.	Figure 11, Figure 12 and Figure 13
		In the second case, as shown in Figure 12, process models b and c are obtained by moving sequential activities to the branching structure based on process model a.
		In the third case, as shown in Figure 13, process models b and c are obtained by changing the positions of activities in the branching structure based on process model a.
3	This group is intended to show the effect of shifting branching locations on the business process complexity.	As shown in Figure 14, process models b and c are obtained by shifting the branching structure based on process model a.	Figure 14
4	This group is intended to show the effect of changes in the number of activities on the branch structure on the process model complexity.	In the first case, as shown in Figure 15, process models b and c are obtained by gradually adding new activities to the branching structure based on process model a.	Figure 15 and Figure 16
		In the second case, as shown in Figure 16, process models b and c are obtained by gradually moving the sequential activities to the branching structure based on process model a.
5	This group is intended to show the effect of changing the location of activities on the branches on the business process complexity.	As shown in Figure 17, process models b and c are obtained by changing the positions of activities in the branching structure based on process model a.	Figure 17
6	This group is intended to show the effect of the change of branch logic type on the process model complexity.	As shown in Figure 18, process models b and c are obtained by changing the branch logic type based on process model a.	Figure 18
7	This group is intended to show the effect of exchanging the branch logic type on the process model complexity.	As illustrated in Figure 19, process models b and c are obtained by exchanging the branch logic types based on process model a.	Figure 19
8	This group is intended to show the effect of changing the connection forms between the branching structures on the process model complexity.	As shown in Figure 20, process models b and c are obtained by changing the connection form between branching structures based on process model a.	Figure 20
9	This group is intended to show the effect of changing the number of cycles and activities in the loop on the process model complexity.	As shown in Figure 21, process models b, c, and d are obtained by changing the number of activities in the loop and the number of loops based on process model a.	Figure 21

Table 2. The purpose of business process models.

Group	Purpose	Business Process Model	Figure
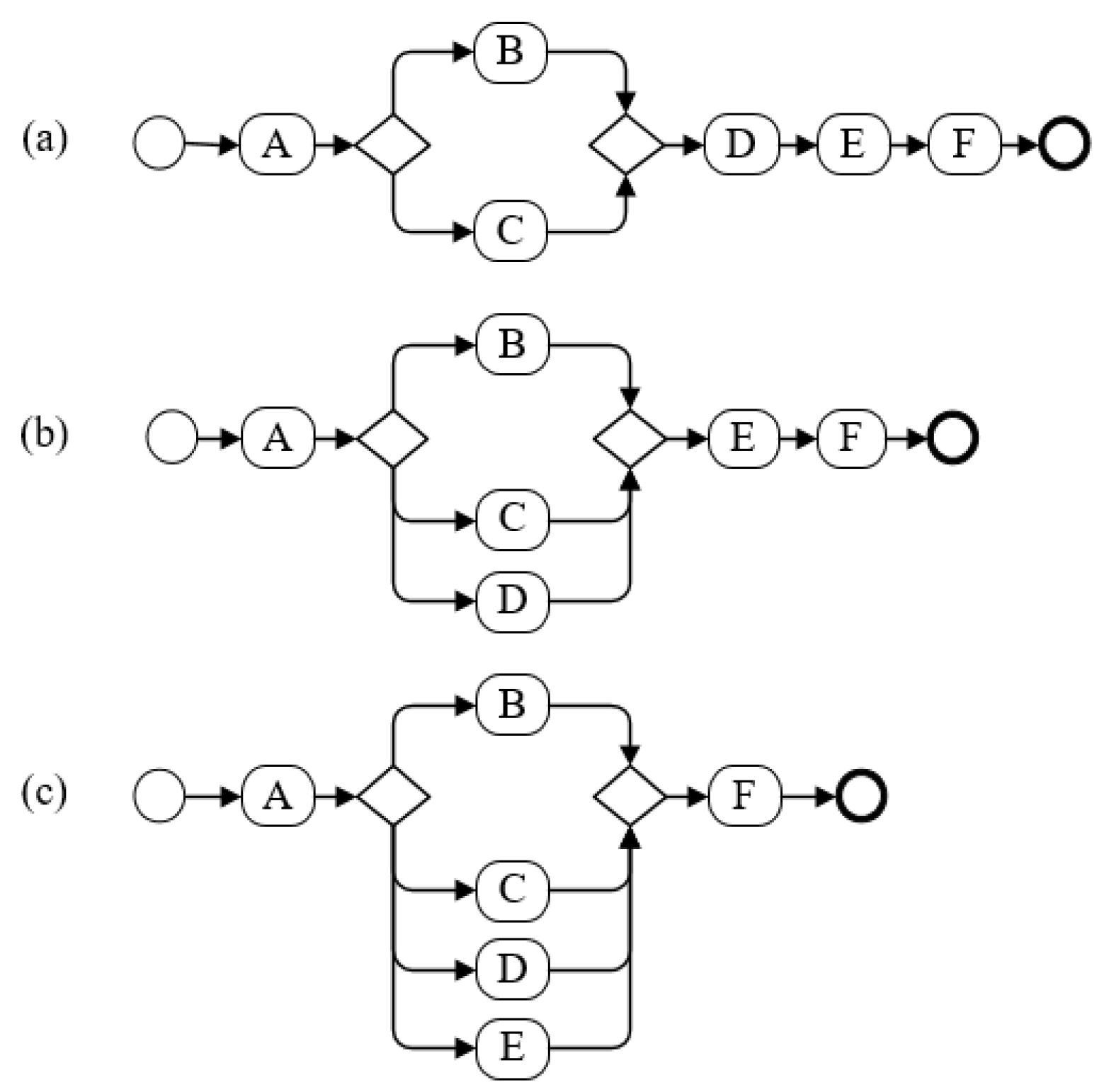
1	This group is intended to show the effect of adding new elements on the process model complexity.	In the first case, as shown in Figure 10, process models b and c are obtained by sequentially adding the activities to the base process model a.	Figure 10
2	This group is intended to show the effect of changes in the number of branches on the complexity of the process model.	In the first case, as shown in Figure 11, process models b and c are obtained by gradually adding activities to the branching structure based on process model a.	Figure 11, Figure 12 and Figure 13
		In the second case, as shown in Figure 12, process models b and c are obtained by moving sequential activities to the branching structure based on process model a.
		In the third case, as shown in Figure 13, process models b and c are obtained by changing the positions of activities in the branching structure based on process model a.
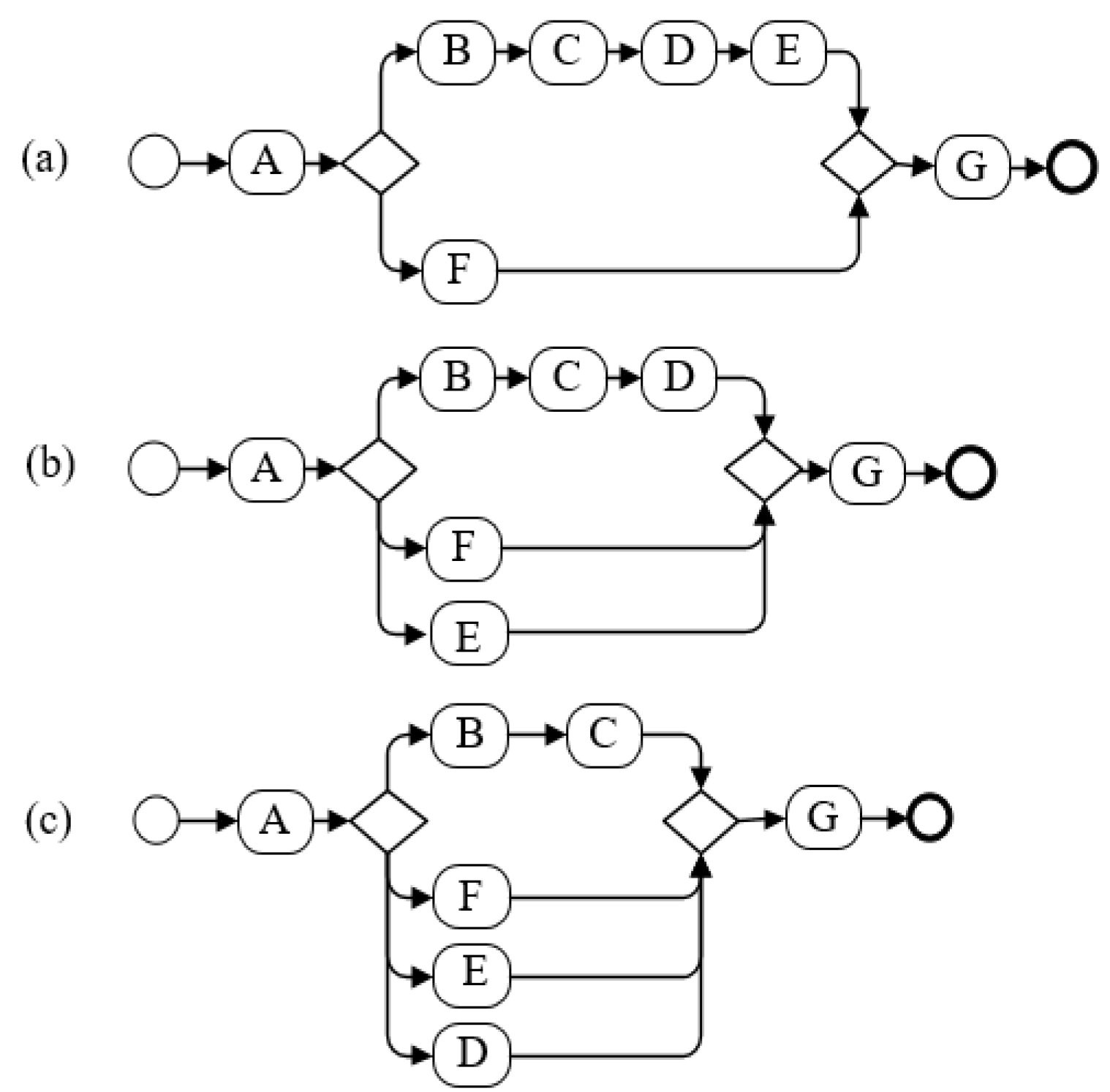
3	This group is intended to show the effect of shifting branching locations on the business process complexity.	As shown in Figure 14, process models b and c are obtained by shifting the branching structure based on process model a.	Figure 14
4	This group is intended to show the effect of changes in the number of activities on the branch structure on the process model complexity.	In the first case, as shown in Figure 15, process models b and c are obtained by gradually adding new activities to the branching structure based on process model a.	Figure 15 and Figure 16
		In the second case, as shown in Figure 16, process models b and c are obtained by gradually moving the sequential activities to the branching structure based on process model a.
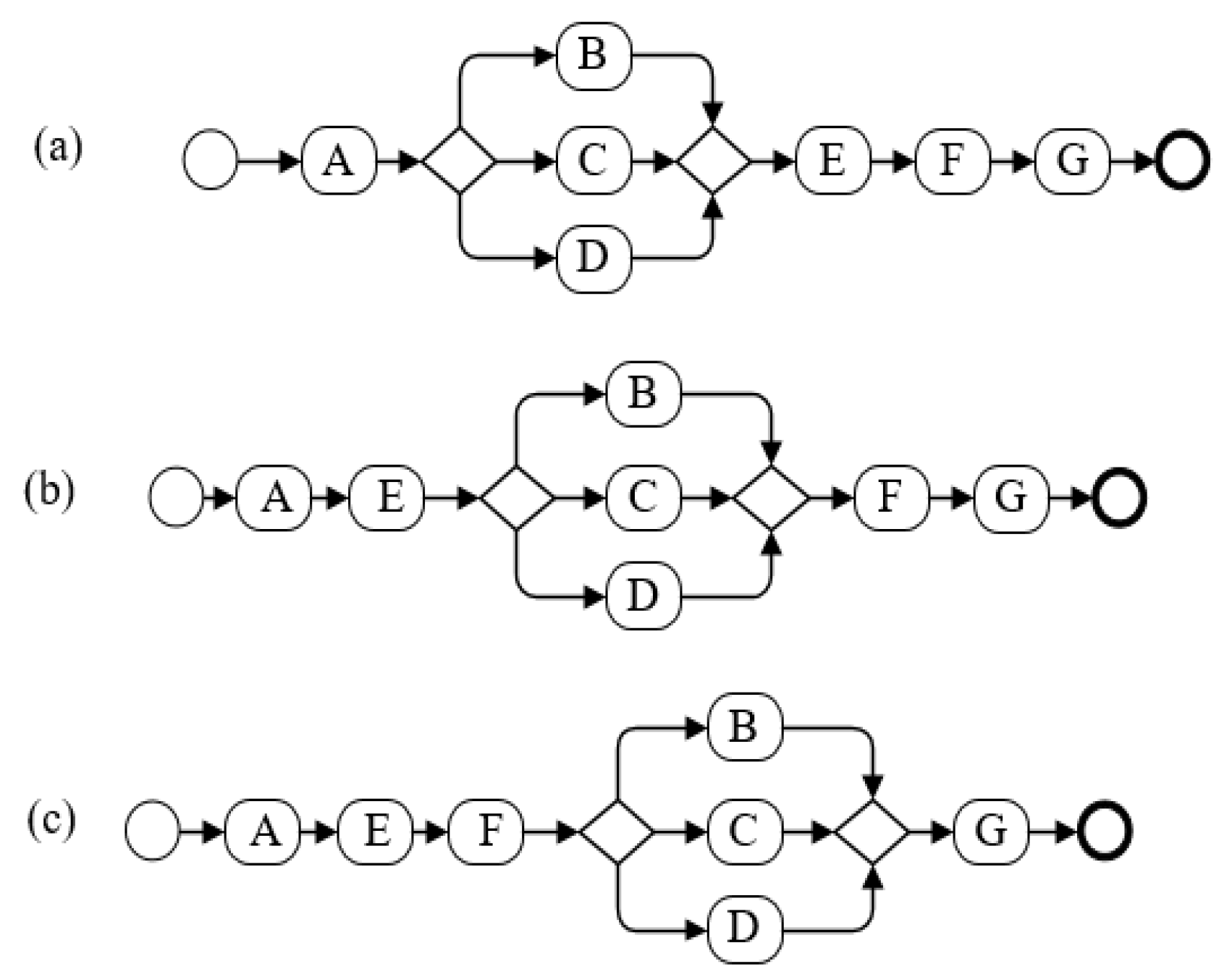
5	This group is intended to show the effect of changing the location of activities on the branches on the business process complexity.	As shown in Figure 17, process models b and c are obtained by changing the positions of activities in the branching structure based on process model a.	Figure 17
6	This group is intended to show the effect of the change of branch logic type on the process model complexity.	As shown in Figure 18, process models b and c are obtained by changing the branch logic type based on process model a.	Figure 18
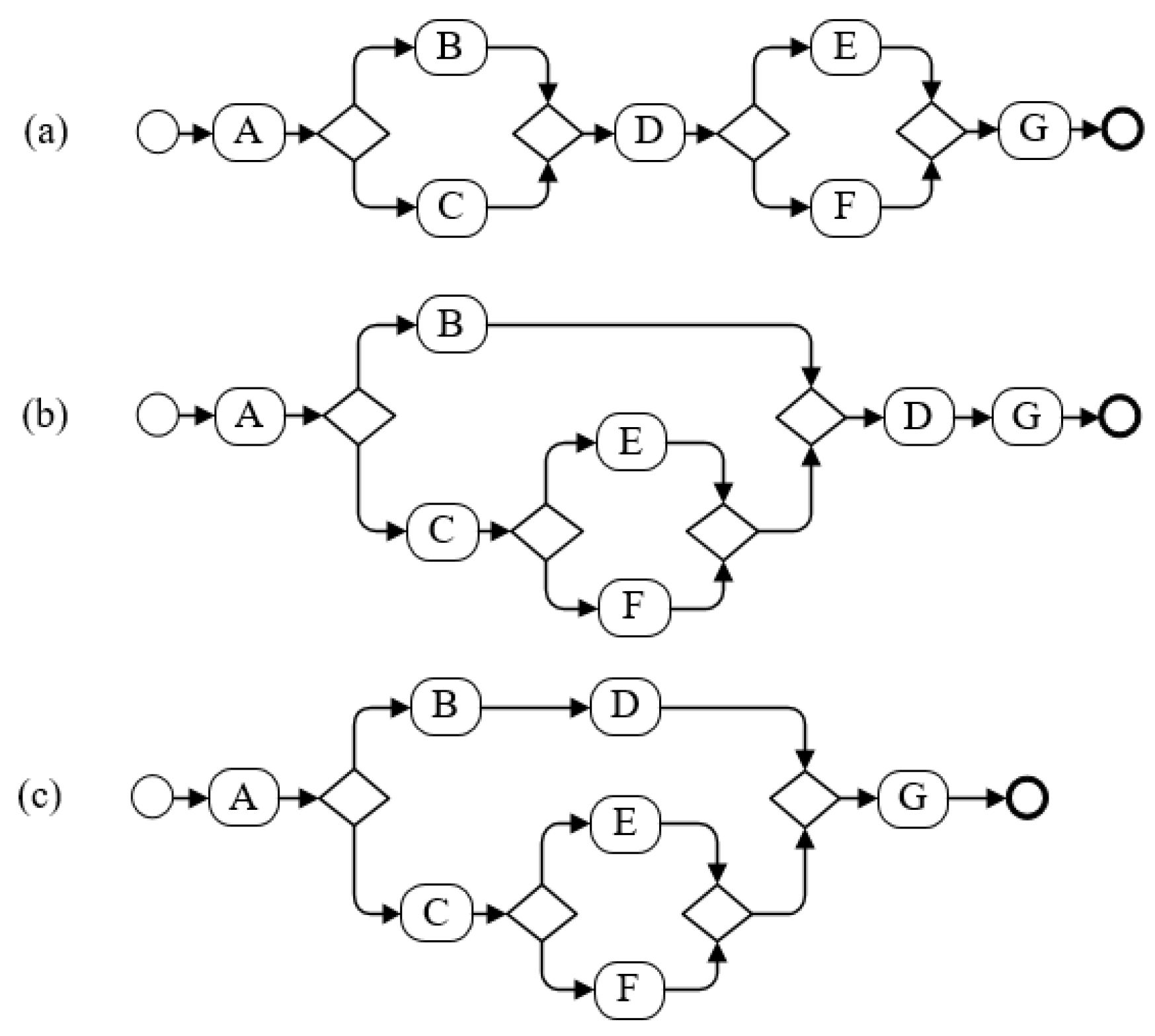
7	This group is intended to show the effect of exchanging the branch logic type on the process model complexity.	As illustrated in Figure 19, process models b and c are obtained by exchanging the branch logic types based on process model a.	Figure 19
8	This group is intended to show the effect of changing the connection forms between the branching structures on the process model complexity.	As shown in Figure 20, process models b and c are obtained by changing the connection form between branching structures based on process model a.	Figure 20
9	This group is intended to show the effect of changing the number of cycles and activities in the loop on the process model complexity.	As shown in Figure 21, process models b, c, and d are obtained by changing the number of activities in the loop and the number of loops based on process model a.	Figure 21

5.2. Experiment Data

The complexity analysis of the experimental model was measured using a CP, CFC [8], CW [11], Scale [17], CADAC [18], and YC [19]. The measurement results are shown in

Table 3. Complexity measurement results of the business process models.

Process Models	CP	YC	CFC	CADAC	Scale	CW
	AND/XOR/OR	AND/XOR/OR	AND/XOR/OR	AND/XOR/OR	AND/XOR/OR	AND/XOR/OR
Figure 10a	3.00	19.00	0	21	0	1
Figure 10b	4.00	21.00	0	23	0	1
Figure 10c	5.00	23.00	0	25	0	1
Figure 11a	12.00/10.00/13.33	45.00/43.00/51.00	1/2/3	48/46/51	16/32/48	5/4/8
Figure 11b	29.00/14.00/17.00	65.40/50.40/104.40	1/3/7	51/49/54	19/57/133	5/4/8
Figure 11c	102.00/18.00/23.73	141.33/57.33/325.33	1/4/15	54/52/57	22/88/130	5/4/8
Figure 12a	14.00/12.00/15.33	46.67/44.67/52.67	1/2/3	52/50/55	20/40/60	5/4/8
Figure 12b	29.00/14.00/17.00	66.00/51.00/105.00	1/3/7	48/46/51	21/63/147	5/4/8
Figure 12c	100.00/16.00/21.73	141.33/57.33/325.33	1/4/15	51/49/54	22/88/330	5/4/8
Figure 13a	24.00/10.00/20.33	54.00/52.00/60.00	1/2/3	54/52/57	22/44/66	5/4/8
Figure 13b	84.00/13.00/30.00	71.00/56.00/110.00	1/3/7	55/53/58	23/69/161	5/4/8
Figure 13c	244.00/16.00/38.53	144.00/60.00/328.00	1/4/15	56/54/59	24/96/360	5/4/8
Figure 14a	30.00/15.00/18.00	46.67/31.67/85.67	1/3/7	52/50/55	20/60/140	5/4/8
Figure 14b	30.00/15.00/18.00	46.67/31.67/85.67	1/3/7	52/50/55	20/60/140	5/4/8
Figure 14c	30.00/15.00/18.00	46.67/31.67/85.67	1/3/7	52/50/55	20/60/140	5/4/8
Figure 15a	12.00/10.00/13.33	45.00/43.00/51.00	1/2/3	48/46/51	16/32/48	5/4/8
Figure 15b	17.00/11.00/16.67	49.40/47.40/55.40	1/2/3	50/48/53	18/36/54	5/4/8
Figure 15c	30.00/12.00/24.67	51.33/49.33/57.33	1/2/3	52/50/55	20/40/60	5/4/8
Figure 16a	14.00/12.00/15.33	46.67/44.67/52.67	1/2/3	52/50/55	20/40/60	5/4/8
Figure 16b	17.00/11.00/16.67	46.67/44.67/52.67	1/2/3	52/50/55	20/40/60	5/4/8
Figure 16c	28.00/10.00/22.67	46.67/44.67/52.67	1/2/3	52/50/55	20/40/60	5/4/8
Figure 17a	124.00/13.00/40.00	73.50/58.50/112.50	1/3/7	57/55/60	25/75/175	5/4/8
Figure 17b	244.00/13.00/70.00	73.50/58.50/112.50	1/3/7	57/55/60	25/75/175	5/4/8
Figure 17c	364.00/13.00/100.00	73.50/58.50/112.50	1/3/7	57/55/60	25/75/175	5/4/8
Figure 18a	28.00	65.40	1	51	19	5
Figure 18b	13.00	40.50	3	49	57	4
Figure 18c	4.00	104.50	7	54	133	8
Figure 19a	372.00	93.50	6	85	204	15
Figure 19b	108.00	93.50	6	85	204	15
Figure 19c	4.00	93.50	6	85	204	15
Figure 20a	21.00/17.00/23.67	65.00/61.00/77.00	2/4/6	61/57/67	54/108/162	9/7/15
Figure 20b	101.00/41.00/113.89	69.00/65.00/81.00	2/4/6	75/71/81	54/108/162	9/7/15
Figure 20c	196.00/40.00/178.22	71.00/67.00/83.00	2/4/6	75/71/81	54/108/162	9/7/15
Figure 21a	7.20/7.20/7.20	39.42/39.42/39.42	1/2/3	48/46/51	20/40/60	4/4/4
Figure 21b	6.50/6.50/6.50	42.13/42.13/42.13	1/2/3	48/46/51	20/40/60	4/4/4
Figure 21c	5.80/5.80/5.80	44.83/44.83/44.83	1/2/3	48/46/51	20/40/60	4/4/4
Figure 21d	6.75/6.75/6.75	47.50/47.50/47.50	2/4/6	51/47/57	50/100/150	7/7/7

. In the table below, the three complexity values represent the complexity of process models for the different gateway types. In Figure 10, Figure 18 and Figure 19, the gateway types of the process models have been determined so that the models have only one complex value.

5.3. Theoretical Validation

Proposing a new complexity measure requires theoretical validation [32]. Theoretical validation evaluates the proposed complexity measure by verifying that it satisfies some widely recognized properties. Only validated measures can produce convincing and effective results. Next, we will perform theoretical validation of CPs using the nine properties proposed by Weyuker [13], to determine if it possesses some properties of a good complexity measure. The validation results will then be compared to those of validated measures such as YC, CADAC, CFC, CW, and Scale.

• Property 1: (∃P) (∃Q) (|P|≠|Q|). There exist two distinct processes of P and Q, which are not of the same complexity. This property requires that the measure can distinguish at least two different complexity process models, meaning that all process models cannot be considered the same complexity. The CP can differentiate the complexity of the different process models. As shown in Table 3, the results of the complexity measurements of CPs are not the same. Therefore, the CP satisfies property 1.
• Property 2: Let c be a non-negative number. Then there are only finite processes for which |P| = c. This property requires that the result of the complexity measurement must be non-negative. As shown in Table 3, the measurement values of CPs are positive for different process models. Therefore, the CP satisfies Property 2.
• Property 3: There are distinct processes P and Q such that |P| = |Q|. There exist distinct process models P and Q, and their complexity measurements are equal. This property requires that different process models can have the same complexity. As shown in Table 3, the CP measure yields the same complexity for different process models Figure 13a–c. Therefore, the CP satisfies property 3.
• Property 4: (∃P) (∃Q) (P ≡ Q & |P| ≠ |Q|). There exist two process models P and Q with the same function but different structural designs, such that their complexity measurements are not equal. This property requires that the complexity measurement method can distinguish between two process models with the same functionality but different structural designs. The CP describes a process model complexity by analyzing the complexity of its structural design. Thus, the CP can distinguish between two process models with the same functionality but different structural designs. Therefore, the CP satisfies this property.
• Property 5: (∀P) (∀Q); (|P| ≤ |P; Q| &|Q| ≤ |P; Q|). For any two process models P and Q, if they are combined to form a new process model, then the complexity of the combined process model is not less than the complexity of each process model. When two process models are combined in sequence to form a new process model, the CP describes the complexity of the combined process model as the sum of the complexities of the two individual process models. Therefore, the CP satisfies property 5.
• Property 6:
  a. (∃P) (∃Q) (∃R) (|P| = |Q| & |P; R| ≠ |Q; R|);
  b. (∃P) (∃Q) (∃R) (|P| = |Q| & | R; P| ≠ |R; Q|)
• Two processes P and Q with the same complexity are combined with process R in the same way to form a new process. The measure can distinguish the complexity of the two process models obtained after composition. When P and Q are sequentially connected to R to form a new process, the CP measures that the complexity of the two resulting process models is the same, meaning that it is impossible to distinguish between the complexity of the two combined process models. Therefore, the CP does not satisfy this property.
• Property 7: If Q is formed by permuting the order of the activities of P, then the complexity of P and Q may be different, |P|≠|Q|. Changes to the position of elements in the process (such as activities) may affect the complexity of the process model. As shown in Table 3, the complexity values of the process models Figure 15a,b change as the positions of the activities are altered. Therefore, the CP satisfies this property.
• Property 8: If P is a renaming of Q, then |P| = |Q|. Changing the names of the components of a process model does not affect its complexity. This property requires that renaming the activity or any other structural components of a model should not change the complexity. The CP describes the complexity of a process model based on its structure, and the measurement results are not affected by changes in the structure’s names. Therefore, the CP satisfies the property.
• Property 9: (∃P) (∃Q); (|P| + |Q| < |P; Q|). There are two processes P and Q, whose complexity when combined into a process model is greater than the sum of the complexities of each process model. This means that the complexity of a whole process model is at least equal to the sum of the complexities of all its local components. When two processes are combined by nesting, the CP describes their complexity to be greater than the sum of their complexities. Therefore, the CP satisfies property 9.

In summary, the CP satisfies eight out of the nine properties proposed by Weyuker. The results of validating the YC, CADAC, CFC, CW, and Scale using Weyuker’s properties are shown in

Table 4. Weyuker’s properties comparison.

Properties	CP	YC	Scale	CADAC	CFC	CW
1	√	√	√	√	√	√
2	√	√	√	√	×	√
3	√	√	√	√	√	√
4	√	√	√	√	√	√
5	√	√	√	√	√	√
6	×	×	×	×	×	×
7	√	√	×	×	√	√
8	√	√	√	√	√	√
9	√	√	√	√	√	√

.

6. Results and Discussion

In this section, we discuss the nine groups of changes that may occur in the process model shown in Table 2. We analyze and compare the measurement results of various complexity measures, and verify whether the CP is more sensitive than the YC, CADAC, CFC, CW, and Scale in detecting the impact of certain structural changes in the process model on its complexity.

• Group 1: Adding new elements to the process model

The complexity value of a CP increases with the number of activities in the process model. Changes in the number of activities in the process model affect its complexity. As the models are shown in Figure 10, the gradual addition of sequential activities to the process model resulted in differences in the CP, YC, and CADAC values in Table 3. In Figure 15, the gradual addition of activities to the branch resulted in differences in the CP, YC, CADAC, and Scale values in Table 3. Based on the above analysis, it can be concluded that compared to the CFC, CW, and Scale, the CP, YC, and CADAC are more sensitive to changes in the process model complexity resulting from the addition of new elements. Additionally, when there is no branching structure in the process model, Scale cannot measure changes in the complexity value resulting from the addition of new elements.

• Group 2: Adding branches to the process model

The complexity value of a CP increases with the number of branches in the process model. Changes in the number of branches in the process model affect its complexity. In Figure 11, as the number of branches and activities gradually increased, the values of the CP, YC, CADAC, and Scale in Table 3 increased. In Figure 12 and Figure 13, moving activities increased the number of branches in the process model, which affected the CP, YC, CADAC, and Scale values in Table 3. However, the results of the CFC and CW did not change. In conclusion, the CP, YC, CADAC, and Scale are more sensitive than the CFC and CW in detecting the impact of changes in the number of branches on the process model complexity.

• Group 3: Shifting the location of the branching structure

Shifting the location of the branching structure in a process model does not affect the complexity value of the CP. As the models are shown in Figure 14, the three process models have the same AND branching structure, but the location of the AND branching structure differs in each model. The measurement results of the various complexity measures in Table 3 did not change. Thus, the CP, YC, CADAC, Scale, CFC, and CW cannot distinguish between these three process models. Therefore, based on the measurement results of the CP, YC, CADAC, Scale, CFC, and CW, it can be concluded that shifting the location of the branching structure in the process model does not affect the process model complexity.

• Group 4, 5, 7: Changing the number of activities, activity position, and exchanging branch logic type

The complexity value of the CP changes with changes in the number of activities, activity position, and the exchange of the branch logic type in the branching structure. In group 4: as shown in Figure 15, adding activities to the branching structure causes differences in the CP, YC, CADAC, and Scale values in Table 3. In Figure 16, moving the sequential activities to the branching structure only changes the CP value in Table 3. In group 5: as shown in Figure 17, moving the activities in the branching structure causes differences in the CP value in Table 3, and the YC, CFC, CW, Scale, and CADAC values do not change. In group 7: as shown in Figure 19, exchanging the branch logic type in the process model causes differences in the CP value in Table 3. Because only the branch logic type in the process model is exchanged without changing the number of the branches, the YC, CFC, CW, Scale, and CADAC values in Table 3 do not change. It should be noted that the measurement results of the YC only change when two branching structures with different numbers of branches exchange their logic types. In summary, compared to the YC, CFC, CW, Scale, and CADAC, the CP is more sensitive in detecting the impact of changes in the number of activities, activity position, and the exchange of branch logic type on the process model complexity.

• Group 6: Changing the logic type of the branching structure

The complexity value of the CP varies with the changes in the branching logic types in the process model. Changing the branch logic types affects the process model complexity. As shown in Figure 18, changing the branch logic type resulted in differences in the CP value in Table 3. Since the YC, CFC, CW, Scale, and CADAC differentiate the complexity between the different types of branching structures, the values of YC, CFC, CW, Scale, and CADAC in Table 3 also had differences. Therefore, when the branching structure type in the process model changes, the CP, YC, CFC, CW, Scale, and CADAC can detect the changes in the process model complexity sensitively.

• Group 8: Changing the connection form between the branching structures

Changing the connection form between the branching structures affects the complexity value of the CP. The occurrence of nesting between the branch structures will affect the process model complexity. In Figure 20, changing the connection form between branching structures makes the appearance of nested branching structures in the process model. Then the CP value in Table 3 changed. Due to the change in the depth of the nested activities in the process model, the values of YC and CADAC in Table 3 also changed, while the results of the CFC, CW, and Scale remained the same. Therefore, the CP, YC, and CADAC are more sensitive than the CFC, CW, and Scale in detecting the impact of changes in the connection form of the branching structures on the process model complexity.

• Group 9: Changing the number of loop nodes and loop in the process model

According to the CP, changing the number of nodes on the loop and loop in the process model affects the process model complexity. As the models Figure 21a–c, the number of activities in the loop structure of the process model gradually increases, resulting in differences in the CP value in Table 3. The YC value also changes, but the CFC, CW, CADAC, and Scale values remain the same. Furthermore, as the models Figure 21a,d, when the number of the loop in the process model gradually increases, the CP, YC, CFC, Scale, CADAC, and CW values in Table 3 changed. Therefore, the CP and YC are more sensitive than the CFC, CW, CADAC, and Scale in detecting the impact of changes in the number of loop nodes on the complexity of the process model. Moreover, the CP, YC, CFC, CW, CADAC, and Scale can all measure the changes in the process model complexity resulting from changes in the number of the loop.

Based on the analysis of the nine groups above, it can be concluded that the CP is sensitive to changes in the structure of process models, accurately reflecting the changes in the complexity of process models. Compared with the YC, CADAC, ACD, MCD, CFCS, and CW, the CP has significant advantages for detecting the changes in the number of activities on branches, the changes in activity positions on branch structures, and the exchange of branch logic types in the process model. When the number of branches and elements in the process model changes, its complexity also changes. For different changes in the structure of process models, the CP measures different complexity values as shown in

Table 5. Comparison of the process model complexity analysis.

Groups	CP	YC	Scale	CADAC	CFC	CW
1	√	√	×	√	×	×
2	√	√	√	√	×	×
3	×	×	×	×	×	×
4	√	√	×	×	×	×
5	√	×	×	×	×	×
6	√	√	√	√	√	√
7	√	×	×	×	×	×
8	√	√	×	√	×	×
9	√	√	×	×	×	×

. It should be noted that all the complexity measures did not change their measurements for group 3. This is because the complexity measurement methods reflect the process model complexity based on their structural composition. When there is no structural change in the process model, the complexity measures consider that its complexity has not changed.

7. Conclusions

As external demands continue to increase, enterprises require high-quality business processes to provide satisfactory products and services to their customers [33]. The process model complexity is an important factor that affects the process quality [34]. Therefore, enterprises need to use complexity metrics to measure the structural changes in process models, and continuously optimize the gradually growing business process framework. By analyzing the process model complexity, enterprises can predict the workload required to complete new process instances and clarify the configuration of information systems. Understanding and controlling the structure complexity of business process models is crucial for enterprises.

This paper considers the impact of the number and location of activities in branching structures on the process model complexity, distinguishes the connection forms between the branching structures, and defines the complexity of the branching structures. Based on the control structures, we propose the complexity measurement formula CP. The CP satisfies eight out of nine properties proposed by Weyuker. In addition, compared to other complexity measurement methods, the CP offers significant advantages in detecting changes in the number and position of activities on the branches, as well as the exchange of the branch logic types in our constructed dataset. When some structural changes occur in the process model, the CP is more sensitive in detecting the changes, thus accurately describing the changes in the complexity of the model.

Our study analyzes the influence of some structural changes such as the number and location of activities on the process model complexity from the perspective of the control structure. In the future, process complexity analysis can consider other process elements such as events, actors, and messages, and discuss the influence of other elements on the process model complexity.