Abstract
In order to ensure a smooth construction project, it is necessary to select an appropriate contractor. However, traditional bid evaluation methods are highly subjective in determining weights. Data envelopment analysis (DEA), a comprehensive bid evaluation method that considers multiple factors, was introduced to reduce subjectivity and provide a simple yet comprehensive method for evaluating bids. Based on the existing cross-evaluation and balance index models, this research proposed a new DEA ranking model—the comprehensive input efficiency model, as well as its specific application steps. Additionally, a case study on selecting contractors for a water engineering project was presented to demonstrate the effectiveness of this model. The results indicated that the comprehensive input efficiency model could achieve the same ranking function as the balance index and was suitable for assessing bidders’ relative efficiency. Moreover, the comprehensive input efficiency model proposed in this research is more simplified. Thus, this research compensates for the drawbacks of the existing comprehensive evaluation models in that the bid evaluation process is cumbersome, thereby extending the research on DEA methods in bid evaluation. Additionally, the model provides tenderers with a more efficient and effective bid evaluation method to select the most appropriate contractor. In the future, research may be conducted to apply DEA to other types of projects, including service projects, real estate, and consulting services.
1. Introduction
The construction industry is characterized by complex environments, adversity, intense competition, heavy construction tasks, and the high number of fixed assets required. Given these factors, it has become increasingly challenging to select reputable construction contractors who are capable of providing quality, streamlining the construction process, and reducing project costs [1,2,3,4]. Generally, tending and bidding remain the most common methods for hiring qualified contractors. Therefore, to ensure that selected contractors can deliver the project smoothly following the contract requirements, careful evaluation is exceptionally essential during the bidding process [5].
The lowest bid price is traditionally used to select contractors for construction projects [6,7]. The emphasis on price as the sole criterion for selection may result in many drawbacks, such as poor quality, delays, and additional costs resulting from rework, claims, and disputes [8,9,10,11]. Thus, contractors should be evaluated comprehensively using quantitative and qualitative criteria [12], called comprehensive bid evaluation, which considers the weights of multiple factors. For instance, weights should be determined by considering not only the project’s characteristics but also the tenderer’s requirements in selecting the contractor [13,14,15]. However, in the practice of comprehensive bid evaluation, it has been noted that the weight of the evaluation index is clearly subjective, and most quantitative methods cannot alter this element.
DEA, an effective non-parametric method to evaluate the relative effectiveness of DMUs with the same structure [16], has been introduced into the construction industry as a comprehensive evaluation method. In some research, DEA methods have been applied to assess the safety performance of contractors. For example, Nahangi, et al. [17] used DEA to conduct a safety-based efficiency evaluation of construction sites. DEA was used by El-Mashaleh, et al. [18] to benchmark construction contractors’ safety performance. Additionally, some research has combined DEA with other methods to assess and select bidders. In particular, Cheaitou, Larbi and Al Housani [8] combined DEA, fuzzy logic, and mixed integer linear programming to assist public organizations in selecting the most appropriate construction contractor(s). Other methodologies are also discussed, such as the analytical hierarchy process (AHP) [19,20,21], the analytic network process (ANP) [22,23], partial least squares [14], fuzzy set theory [24,25], and fuzzy analytic hierarchy process [26,27]. However, these methods and model operations, coupled with modern mathematical theories, are complex and poorly defined in terms of their application. Specifically, they cannot systematically deal with uncertainty and certainty in objective things and subjective consciousness during the bid evaluation process. Therefore, they are rarely used in practical evaluating bids [26]. Furthermore, most existing research combines DEA with other methods to develop improved models instead of using the basic DEA model.
As a result, in order to fill this gap, this research introduced the DEA method into comprehensive bid evaluation and discussed its basic model first. Considering the DEA cross-evaluation model requires multiple cross-evaluations to achieve a complete ranking, the balance index model was then analyzed. Based on this, this research proposed an improved DEA ranking model—comprehensive input efficiency. Additionally, through analysis and comparison, it is demonstrated that the balance index and comprehensive input efficiency models can provide reasonable evaluation results and are more effective in ranking DMUs. Finally, a case study of selecting contractors for a water construction project in China is presented to illustrate the effectiveness of the model proposed. Through sorting out the bid evaluation indexes and methods, this research established a comprehensive, objective, understandable, and impartial comprehensive input efficiency model. Besides overcoming the shortcomings of the traditional comprehensive bid evaluation method, this model is more practical and simplified as well. Furthermore, this model enhances bid evaluation efficiency, is suitable for sectoral application and grassroots promotion, and ultimately provides a relatively objective evaluation basis for tenderers. Accordingly, the comprehensive input efficiency model contributes to the comprehensive evaluation of bidders in both theory and practice.
2. Literature Review
2.1. Application Research of DEA in Bid Evaluation
DEA is an effective non-parametric method to evaluate the relative effectiveness of DMUs with the same structure [16]. The input–output efficiency analysis is the original type of DEA analysis. However, as a system analysis method, unlike other system methods dealing with complex systems with multiple inputs and multiple outputs, the DEA method does not require providing functional relationships between inputs and outputs, nor weightings between input indicators and output indicators. Only input and output observations are required to evaluate the relative efficiency of different DMUs. For instance, according to Guo and Wu [28], cost indicators are regarded as the input index, and efficiency indicators are regarded as the output index of the DMU, which has been transformed into the input–output evaluation and assessed by the DEA method. Further, the principles of the DEA method are the same regardless of whether it is applied to input–output analysis or the evaluation of comprehensive indicators. Inti and Tandon [29] calculated the index value through AHP to obtain the index value of the evaluation object and processed the second relative evaluation using the DEA method.
The traditional DEA methods consist of a self-evaluation of DMUs, which can only be used for determining whether they are relatively efficient but not for ranking them. In various fields, improved DEA evaluation ranking models have been developed [30,31,32]. Talluri [33] first introduced the DEA model based on a game model of buyers and sellers in auctions and established an auction evaluation model. Chetan, et al. [34] present an iterative multi-attribute reverse auction mechanism based on integrated data envelopment analysis (DEA) and the best–worst method (BWM). As well, DEA methods have been used to evaluate all bidders fairly and comprehensively. Zhao, et al. [35] present a novel model integrating an analytical hierarchy process and data envelopment analysis (AHP/DEA) to evaluate bids for major construction projects. Yang, et al. [36] used DEA to support best-value contractor selection. Thus, it has been demonstrated that DEA is an effective tool for objectively generating a list of bidders with comprehensive expertise. However, existing DEA evaluation models mainly combined DEA with other methods. Few research studies have proposed an improved comprehensive bid evaluation model that is directly based on the DEA basic model. Moreover, most existing models, in conjunction with modern mathematical theories, have a complex application in practice. Consequently, tenderers do not have the capacity to apply these models systematically to evaluate bidders, resulting in their rare use in practice.
By considering the comprehensive evaluation mechanism as a mixed linear multi-criteria optimization problem, this research proposed a comprehensive input efficiency model and intended to solve it using an optimization algorithm. It is believed that the comprehensive input efficiency model could simplify the bid evaluation process, extending research on DEA models in evaluating construction bids. Furthermore, this model has the potential to increase the operability of existing DEA bidding models, enhance the bidding efficiency, and provide tenderers with a fairly objective evaluation basis.
2.2. Contractor Selection Criteria
Choosing responsive and responsible contractors can ensure smooth project delivery and a reduction in costs. Thus, the selection criteria are essential research subjects [37]. For construction projects, contractors are typically selected based on their lowest bid price [7,38]. It is possible, however, that this may result in eliminating qualified contractors and accepting others who cannot complete the project successfully. In view of this, using price as the sole selection criterion is not advisable [12]. Rather, both quantitative and qualitative criteria should be used to make a comprehensive selection of contractors. During the comprehensive tender evaluation process, the owner must evaluate the most suitable overall bidder based on a combination of factors (price, quality, duration, etc.) to maximize the overall benefit to the bidder (minimizing costs). Over the past few years, a growing body of literature has been developed for evaluating contractors [39,40]. For instance, to address the issue that the bid evaluation process is imprecise and uncertain regarding alternative-criterion decision appraisals, Chen, et al. [41] developed a novel ELECTRE III-based MCGDM approach for bid evaluation, in which generalized comparative linguistic expressions (GCLEs) are used to evaluate bidder performance. Based on the logic pattern of the human cognition process and the compensatory relation among attributes, Chen, et al. [42] established a two-stage logic scoring of preference—an ELECTRE III-based approach for managing and manipulating bidder selection. Given that CO2 emissions need to be prioritized in traditional bid evaluation, Liu, Yang, Huo, Shen and Wang [15] developed a conceptual, computational model for CO2 emissions, as well as a linguistic group decision-making framework for evaluating bids in mega projects that aim to reduce CO2 emissions. Thus, the establishment of standards may depend on the type of project and local norms (e.g., the local legal and industrial ecosystem). Additionally, the indicator system may be established based on the owner’s requirements for the project objectives, the project conditions, and the construction conditions. However, few research studies provide a comprehensive analysis and systematic summary of evaluation indicators. Therefore, by reviewing existing research, the indicator system for the comprehensive evaluation of bids summarized in this study is shown in Table 1.

Table 1.
The indicator system for comprehensive bid evaluation.
3. Methodology
3.1. Basic Model of DEA
The DEA method requires finding an optimal set of input–output weights. The basic model of the DEA method is as follows:
and represent unknown output and input weights; represents a specific bidder in bidders (); and each bidder has input metrics () and output indicators ().
The DEA method aims to determine the optimal output and input weights for the owner to achieve the desired target. This target represents the optimal benefit between each input and each output of all bidders (for example, the smallest input gets the largest output). This problem can be converted into a linear programming problem:
Through solving the above linear programming problem, the optimal solution of and (call it and ) can be obtained. Therefore, the efficiency value of each bidder, named self-evaluation value, can be calculated as follows:
Using (3), the efficiency value of each bidder can be calculated; (1) indicates the bidder is valid, and (2) indicates the bidder is invalid. Under normal conditions, multiple bidders exist whose reaches 1. Therefore, constraints must be added to further evaluate the bidders.
This research will further analyze several methods which improve the relative optimal efficiency DEA evaluation model, including cross-evaluation mechanism, balance index, and comprehensive input efficiency.
3.2. Cross-Evaluation Mechanism
The basic idea of cross-evaluation mechanism is as follows: the optimal solutions and of each bidder are used to calculate the efficiency value of other bidders, obtaining cross-evaluation values:
For the above issues, the higher the cross-evaluation value , the more favorable it is for bidder , and the more unfavorable for bidder . The above questions can be converted into
Through solving the above linear programming problem, a new set of optimal solutions for and (call them and ) can be obtained. The cross-evaluation value and cross-evaluation matrix are obtained by using the optimal solution:
The relative efficiency value of the bidder obtained above is the value on the diagonal in the cross-evaluation matrix , which serves as the first evaluation index. The second evaluation index is divided into two kinds. Many researchers use the average value of off-diagonal elements in line as the second index of evaluation. Additionally, the smaller the , the better. Additionally, much research uses the average value of the element in column as the second index of evaluation. Additionally, the bigger the , the better. In the evaluation process of DEA, the first evaluation index is compared first. If is the same, then the second evaluation index is compared. This research takes the average value of non-diagonal elements in column as the second index of evaluation. The calculation formula of and are as follows:
In the process of bid evaluation, the efficiency of bidders is compared first. Additionally, bigger is prioritized. If is identical, or is compared, with bigger or smaller being given priority. For the second evaluation index , it takes the average value of off-diagonal elements in line as the evaluation index. However, in the calculation process of DEA evaluation method, all calculations are carried out for each column of data, aiming to find the optimal weight distribution between input and output of each column. If is used as the second evaluation index, reasonable results cannot be obtained in most cases. Thus, it is not suitable to use as the second evaluation index. Thus, , which takes the average value of non-diagonal elements in column, should be the second evaluation index.
When is the evaluation index, in most cases, relatively complete evaluation results can be obtained. However, in special situations, the same value of may also occur, which cannot offer complete evaluation results. As a result, should be chosen as the second evaluation index. In view of the possibility that may have the same value, another cross-evaluation should be conducted. The new optimal solutions and should be used to calculate the efficiency value of other bidding units to obtain a new cross-evaluation matrix. The second cross-evaluation is referred that the average value of non-diagonal elements in column is used as the evaluation index (the evaluation index of the second cross-evaluation is expressed by ). The calculation process of DEA model with cross-evaluation mechanism is shown in Figure 1.
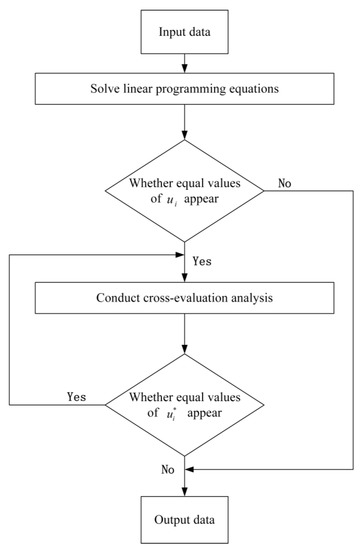
Figure 1.
Calculation process of DEA model with cross-evaluation.
The complete evaluation can be completed after a cross-evaluation process or after a second cross-evaluation process if the number of bidders i is relatively small. However, if there are a large number of bidders, a second cross-evaluation process may not be able to provide a complete judgment. Therefore, to obtain a comprehensive evaluation report, multiple cross-evaluation methods must be employed.
Based on the above analysis, it appears that the cross-evaluation mechanism can assist in evaluating and ranking bidders (DMUs) more accurately. It is important to note, however, that for large numbers of bidders, DEA evaluation with the cross-evaluation mechanism may require multiple cross-evaluations to produce reasonable results.
3.3. Balance Index Model
For the above DEA bid evaluation model, it can be known that is the total output of the bidder and is the total input of the bidder. Then, the interest constraint conditions of the bidder are as follows.
Assuming that is an efficiency function, then
In addition, under the condition of maximizing competitive interests, the input of the bidder is proportional to , and the output of the bidder is proportional to . That the input of the bidder is zero is called the ideal optimum.
In the process of bid evaluation, when the interest constraint condition of the bidder is zero, it is said to be valid; otherwise, it is said to be invalid. If the interest constraints of other bidders are not equal to zero, then the bidder wins. If the interest constraints of several bidders are equal to zero, it is necessary to introduce “balance index” [61] for further evaluation and analysis. Balance index of each bidder refers to the sum of all other bidders’ interest constraints. In the process of bid evaluation, the smaller the balance index is, the better. The balance index is expressed by :
where is the optimal input weight of the bidder; is the input of bidder . The indicators for the other parameters are as described previously.
In DEA evaluation model, which introduces balance index, the efficiency value of each bidder is compared first. Additionally, the higher the , the higher the priority. If is identical, then the balance index is compared. Additionally, the smaller is, the higher priority will be given. In this method, complete evaluation results can be well given even if the number of bidders is relatively large. The advantage of this method is that it is only necessary to calculate the balance index of the bidder (DMU) once to obtain a reasonable evaluation result.
3.4. Comprehensive Input Efficiency Model
By referring to the principle of cross-evaluation mechanism, the optimal input weight of each bidder is used to calculate the cross-evaluation value and cross-evaluation matrix of input efficiency of other bidders:
The efficiency value of the bidder was obtained previously. In Equation (13), all the diagonal elements in the cross-evaluation matrix are 1. The efficiency value of each bidder is the minimum value of all elements in column , denoted by , which is equal to the efficiency value calculated above:
If only self-evaluation value is used for evaluation, the same situation may occur in , which will lead to failure to evaluate all bidders completely. Thus, this study presents the concept of comprehensive input efficiency, which is expressed by :
Through the DEA evaluation model, which introduces comprehensive input efficiency, in most cases, the bidder can be completely evaluated. The priority order of each bidder can be obtained by comparing the size of directly. However, in special cases, and can be combined to evaluate bidders. First, is compared. If has the same value, then is compared. Additionally, the bigger , the more priority it has. Comprehensive input efficiency requires only one linear programming calculation to rank the efficacy of all bidders. Multiple cross-evaluations are not required. Moreover, this model is more efficient in its evaluation and will not be affected by the number of bidders .
The calculation process of DEA model that introduces difference index or comprehensive input efficiency is shown in Figure 2.
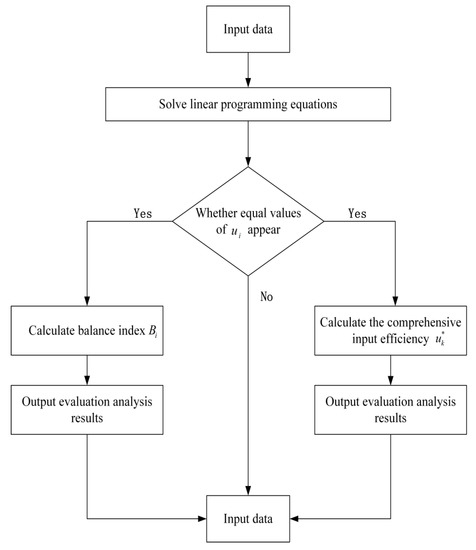
Figure 2.
Calculation process of DEA model with balance index or comprehensive input efficiency.
In this section, the DEA basic model is introduced first. Then, cross-evaluation model and balance index model were analyzed. Finally, based on the above analysis, a new DEA ranking model, the comprehensive input efficiency model, is proposed. As a result of the analysis, it is evident that in the cross-evaluation model, multiple evaluation processes are required to achieve a complete ranking. However, the balance index model and the comprehensive input efficiency model only need to calculate one linear programming equation and the second evaluation index or to obtain more complete ranking results. Thus, the bid evaluation efficiency of the latter two models is higher.
4. Case Study
4.1. General Information of the Bidding Project
In the first phase of the eastern route of the south-to-north water diversion project, the civil and construction engineering of the Huai’an pumping station was considered as an example. This project is located in Sanbao township, Chuzhou District, Huai’an City, Jiangsu Province, at the intersection of an irrigation canal and a canal, with a design flow of 100 m3/s. In conjunction with the completed stations, it was the second step of the first phase of the south-to-north water diversion project. The overall design flow for this step is 300 m3/s, and the total installed capacity, including standby machines, is 340 m3/s. This station is expected to be built on the west side of Huai’an II Station. A distance of 340 m separates the center line of the diversion river from the diversion river of Huai’an II Station, and a distance of 300 m separates the center line of the bottom plate of the pumping station from the center line of Xinhe Station.
The scope of the bidding includes excavation of the upper and lower river diversion, civil construction of the bridge under the station, procurement, and installation of the metal structure of the pump station, hydraulic hoist, and bridge crane. The main works include 650,000 m3 of earth excavation and filling; 16,500 m3 of concrete and reinforced concrete; 19,000 m3 of masonry; 298 t of fabrication and installation of metal structures; four sets of main pump and corresponding equipment installation; eight sets of hydraulic hoist procurement and installation; and one bridge crane procurement and installation. It will take approximately 24 months to complete the construction.
The bidding process for the pump station project is more complicated than that for the river project, based on the general situation of the project. Therefore, there are relatively high requirements for bidders in the bidding process. In general, the requirements are as follows. It is necessary for the bidder to possess a certificate of qualification of grade I or higher of general contracting for water conservancy and hydropower projects, and for the enterprise legal representative to possess at least five years of construction experience in the field of water conservancy and hydropower projects.
4.2. Implementation of Comprehensive Bid Evaluation Mechanism
Since the pump station project is a complex water conservation project, it involves multiple construction management interfaces, which include the installation and debugging of pump station equipment, instruments, and an uncertain construction environment. All of these factors may contribute to an increase in transaction costs. As a result, it is imperative to evaluate the bidders from a variety of perspectives in order to select an excellent winning bidder.
- (1)
- Comprehensive evaluation index system
In addition to the tender offer, the bidder’s construction organization design, ability, performance, and credit should also be evaluated. Specific evaluation indicators are shown in Table 2.

Table 2.
Evaluation index of bidders.
- (2)
- Comprehensive scoring mechanism and evaluation results
In total, nine bidders participated in the bidding process. All of their bid documents met the requirements of the bidding documents and passed the prequalification phase, entering into the second phase of the review process.
The bid evaluation committee is composed of nine experts, who respectively score the bidders’ evaluation indexes and take the average value as the final score. The total price of the pre-tender estimate is RMB 4,602,000.00, and the composite pre-tender estimate is RMB 4,639,8032.17. The owner’s pre-tender estimate has a weight coefficient of 0.60. Expert ratings are shown in Table 3.

Table 3.
Experts’ scores.
- (3)
- Comprehensive score result
According to the bid evaluation method, bidder B is selected as the first winning candidate and G as the second winning candidate. Comprehensive scoring results of nine bidders are shown in the Table 4.

Table 4.
Comprehensive scoring results.
4.3. Improvement of Comprehensive Bid Evaluation Mechanism
In this tender, scoring quotations based on the base bid was an unreasonable aspect of comprehensive scoring. Moreover, the bid evaluation results obtained by setting weights are not necessarily appropriate for the comprehensive scoring of the project bid. Therefore, this construction example is analyzed below using an improved DEA evaluation method.
- (1)
- Index system conversion and data process
Due to the large number of evaluation indicators in this engineering example, they are grouped together here as follows: are combined into ; are combined into ; are combined into ; are combined into ; , , , and are taken as input indices; and and are taken as the output indicators and .
For data processing, the largest output with the smallest input is obtained; therefore, the above input indicators should be converted into a minimal indicator, while the output index is converted into a maximal index.
If it is determined by the expert scoring system, most input indexes are qualitative. Suppose there are bidders, and experts scored each indicator of the bidders. Each index can be represented by an scoring matrix :
where is the expert’s score for the bidder; means that the score of experts on the th bidder is averaged. According to the previous analysis, input indicators are processed as minimal indicator data:
is the processed data; and are the maximum and minimum values in the expert rating matrix; and is the average of the original expert scores.
The rationality of the quotation in the output index O2 is a qualitative indicator, which is determined by the expert rating system. According to the previous analysis, the more reasonable the quotation, the higher the score. Thus, it is a maximal index. Suppose there are experts to evaluate this index of these bidders; the expert scoring matrix and mean scoring matrix are shown in Equations (17) and (18):
where is the processed data; is the average of the original expert scores; and is the maximum value in the expert average score matrix .
The bid price indicator in the output indicator no longer uses the method that tender evaluation experts score quotations in engineering tenders based on the base bid. Rather, it evaluates whether a bidder’s price is lower than its individual costs based on the level of individual costs determined by the evaluation experts. If less, the bid is rejected. For the bidder whose quotation is judged to be reasonable, the transformation of its quotation index should reflect the principle of market competition, that is, the idea of the lowest-bid mechanism. Additionally, the lower the quotation, the higher the index value. Quotation (bidding period) sequence (), the processing method is as follows:
where is the processed value; and are the maximum and minimum values in the bidding sequence; and is the original bidding sequence, converted to maximal indicators. Evaluation index and data disposed of bidders are shown in Table 5.

Table 5.
Evaluation index and data disposed of bidders.
- (2)
- Comprehensive bid evaluation analysis based on DEA
Four DEA models with self-efficiency evaluation, cross-evaluation mechanism, balance index model, and comprehensive input efficiency were analyzed and compared. The calculation and ranking results of different models are shown in Table 6.

Table 6.
Results of different DEA evaluation models.
It can be seen that the top three bidders with better self-evaluation efficiency are B, F, and G (relative efficiency value reaches 1). In the cross-evaluation model and margin (balance) index models, such results were not obtained; however, they were obtained in the comprehensive input efficiency model analysis. As a result, the comprehensive input efficiency model proposed in this research is more scientific and reasonable than the other three models.
- (3)
- Analysis of evaluation results
The evaluation results in comprehensive scoring bidding and under different bid evaluation models are shown in Table 7.

Table 7.
Result under different bidding evaluation methods.
It can be seen that the quantitative model evaluation is consistent with quantitative scoring. The results of the comprehensive input efficiency model are consistent with those of the integrated score. Additionally, the first winning bidder and the second winning bidder are the same. It indicates that the scoring weight adopted in the bidding process of this project is relatively reasonable, evaluating the outstanding winning bidder. Through this case, the rationality of the comprehensive input efficiency model is demonstrated in practice. Additionally, the results indicate that the comprehensive input efficiency model is a simple, operational model that project tenderers can use to evaluate bidders efficiently and accurately.
5. Conclusions and Discussions
By incorporating the DEA method into comprehensive bid evaluation, this research also proposed a comprehensive input efficiency model based on the existing cross-evaluation ranking mechanisms and difference index model. Additionally, through a case study, this research explores the application of the bid evaluation model systematically and further proves the scientific validity and applicability of the model.
First, this research introduces the basic DEA model. In light of the differences between the engineering bid evaluation process and the DEA method evaluation process, it is necessary to process the input and output index data before applying the DEA method to construction project evaluation. Considering this difference, this research proposed that different data processing methods should be adapted to ensure the feasibility of the DEA method based on the different characteristics of each input and output index in the bid evaluation process. As a result, a new DEA model, namely the comprehensive input efficiency model, was developed. This model extends the research on DEA bid evaluation models, which mainly use a one-input and multiple-output model to assess bidders.
Second, it is impossible to make a complete evaluation of all DMUs if only self-evaluation values were considered in the course of the DEA model calculation. Thus, this research analyzed and compared three DEA evaluation models in detail. Results showed that to obtain complete evaluation results, the cross-evaluation ranking mechanism needed to conduct further cross-evaluation. In contrast, the difference index and comprehensive input efficiency model only needed to solve linear programming equations and calculate the second evaluation index or . Thus, the latter two models were more effective, which extends the comprehensive bid evaluation model based on the DEA method theoretically. These findings address the shortcoming of how the evaluation process of the cross-evaluation mechanism is too cumbersome. Furthermore, the comprehensive input efficiency model simplifies and streamlines the evaluation process compared to previous evaluation models that incorporated DEA and other methods.
The civil and construction engineering of the Huai’an pumping station in the first phase of the eastern route of the south-to-north water diversion project was taken as an example. As a result of applying the theories and methods proposed in this research comprehensively, the results indicate that the comprehensive input efficiency model is more scientifically sound and reasonable than the other three models (self-evaluation efficiency model, cross-evaluation mechanism, and balance indicator model). It is further demonstrated that the model is scientifically valid and practical from a practical point of view.
This article can provide some insightful information for tenderers who assess bidders. First, this research summarized and proposed the bid evaluation indexes and methods which can be used to reflect the contractors’ capabilities. Moreover, these indexes and methods are suitable for application and grassroots promotion. Therefore, tenderers can use this template to determine the bidder evaluation indicators for the actual projects. In addition, the traditional comprehensive bid evaluation method is highly subjective, and the application of existing bid evaluation models is complex and impractical. Therefore, this research presented a comprehensive input efficiency model based on the cross-evaluation ranking mechanism and balance index models. Through practical examples, the comprehensive input efficiency model has also been demonstrated to simplify bid evaluation, improve bid evaluation efficiency, reduce subjectivity in weight determination, and provide a more comprehensive and credible ranking of bidders.
Further research can be conducted in the following directions. First, the input values of DEA are set to 1.0 to simplify the assumption that all bidders will do their best to prepare their proposals for the competition. It would be beneficial to explore a new model to overcome this simplification. Additionally, the case studies here are limited to construction work. In the future, research may be conducted to apply DEA to other types of projects, including service projects, real estate, and consulting services.
Author Contributions
Conceptualization, X.L., S.C. and Z.D.; methodology, X.L., S.C. and B.X.; formal analysis, X.L. and S.C.; investigation, S.C., Z.D. and B.X.; data curation, X.L.; writing—original draft preparation, S.C.; writing—review and editing, X.L.; supervision, Z.D. and B.X. All authors have read and agreed to the published version of the manuscript.
Funding
Philosophy and Social Science Research in Colleges and Universities in Jiangsu Province (No. 2020SJA1394), Postgraduate Research & Practice Innovation Program of Jiangsu Province (SJCX22_1568), Postgraduate Research & Practice Innovation Program of Jiangsu Province (A study on the mechanism of the impact of empowering leadership on organizational members’ engineering ethical behaviors).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to appreciate the reviewers for all their helpful comments and thank the Foundation of Philosophy and Social Science Research in Colleges and Universities in Jiangsu Province (No. 2020SJA1394), Postgraduate Research & Practice Innovation Program of Jiangsu Province (SJCX22_1568), and Postgraduate Research & Practice Innovation Program of Jiangsu Province (a study on the mechanism of the impact of empowering leadership on organizational members’ engineering ethical behaviors).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ye, K.; Li, B.; Shen, L. Key Factors Considered in Compiling Tender Prices for China’s Public Works Projects. J. Manag. Eng. 2013, 29, 206–215. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Watanabe, T. The Impact of Project Organizational Culture on the Performance of Construction Projects. Sustainability 2017, 9, 781. [Google Scholar] [CrossRef]
- Birjandi, A.K.; Akhyani, F.; Sheikh, R.; Sankar Sana, S. Evaluation and selecting the contractor in bidding with incomplete information using MCGDM method. Soft Comput. 2019, 23, 10569–10585. [Google Scholar] [CrossRef]
- Yu, W.-D.; Chang, H.-K.; Hsu, Y.-Y.; Cheng, S.T. Pretendering decision model for contractor selection of public procurement projects. J. Constr. Eng. Manag. 2020, 146, 04020126. [Google Scholar] [CrossRef]
- Radzi, A.R.; Rahman, R.A.; Doh, S.I.; Esa, M. Construction Readiness for Highway Projects: Key Decision Criteria. J. Constr. Eng. Manag. 2022, 148, 04021196. [Google Scholar] [CrossRef]
- Idrees, S.M.; Eid, M.S.; Awwad, R. Impact of Altering the Bid Selection Method to Below-Average Method: An Agent-Based Modeling Approach. J. Manag. Eng. 2023, 39, 04023003. [Google Scholar] [CrossRef]
- Yu, W.-D.; Wang, K.-W. Best Value or Lowest Bid? A Quantitative Perspective. J. Constr. Eng. Manag. 2012, 138, 128–134. [Google Scholar]
- Cheaitou, A.; Larbi, R.; Al Housani, B. Decision making framework for tender evaluation and contractor selection in public organizations with risk considerations. Socio-Econ. Plan. Sci. 2018, 68, 100620. [Google Scholar] [CrossRef]
- Mbachu, J. Conceptual framework for the assessment of subcontractors’ eligibility and performance in the construction industry. Constr. Manag. Econ. 2008, 26, 471–484. [Google Scholar] [CrossRef]
- Horta, I.M.; Camanho, A.S.; Lima, A.F. Design of Performance Assessment System for Selection of Contractors in Construction Industry E-Marketplaces. J. Constr. Eng. Manag. 2013, 139, 910–917. [Google Scholar] [CrossRef]
- Lee, H.-Y.; Shiue, F.-J.; Zheng, M.-C.; Chang, Y.-C. Integrating value estimation and simulation for contractor selection. Autom. Constr. 2020, 119, 103340. [Google Scholar] [CrossRef]
- Semaan, N.; Salem, M. A deterministic contractor selection decision support system for competitive bidding. Eng. Constr. Archit. Manag. 2017, 24, 61–77. [Google Scholar] [CrossRef]
- Liu, B.; Huo, T.; Liao, P.; Gong, J.; Xue, B. A Group Decision-Making Aggregation Model for Contractor Selection in Large Scale Construction Projects Based on Two-Stage Partial Least Squares (PLS) Path Modeling. Group Decis. Negot. 2015, 24, 855–883. [Google Scholar] [CrossRef]
- Liu, B.; Huo, T.; Liao, P.; Yuan, J.; Sun, J.; Hu, X. A special Partial Least Squares (PLS) path decision modeling for bid evaluation of large construction projects. KSCE J. Civ. Eng. 2017, 21, 579–592. [Google Scholar] [CrossRef]
- Liu, B.; Yang, X.; Huo, T.; Shen, G.Q.; Wang, X. A linguistic group decision-making framework for bid evaluation in mega public projects considering carbon dioxide emissions reduction. J. Clean. Prod. 2017, 148, 811–825. [Google Scholar] [CrossRef]
- Aldamak, A.; Zolfaghari, S. Review of efficiency ranking methods in data envelopment analysis. Measurement 2017, 106, 161–172. [Google Scholar] [CrossRef]
- Nahangi, M.; Chen, Y.T.; McCabe, B. Safety-based efficiency evaluation of construction sites using data envelopment analysis (DEA). Saf. Sci. 2019, 113, 382–388. [Google Scholar] [CrossRef]
- El-Mashaleh, M.S.; Rababeh, S.M.; Hyari, K.H. Utilizing data envelopment analysis to benchmark safety performance of construction contractors. Int. J. Proj. Manag. 2010, 28, 61–67. [Google Scholar] [CrossRef]
- Martin, H.; Koylass, J.; Welch, F. An exploration of the consistency limits of the analytical hierarchy process and its impact on contractor selection. Int. J. Constr. Manag. 2018, 18, 14–25. [Google Scholar] [CrossRef]
- Koc, K.; Okudan, O. Assessment of Life Cycle Risks of Deconstruction in Urban Regeneration Projects. J. Constr. Eng. Manag. 2021, 147, 04021137. [Google Scholar] [CrossRef]
- Elsayegh, A.; El-adaway, I.H. Collaborative Planning Index: A Novel Comprehensive Benchmark for Collaboration in Construction Projects. J. Manag. Eng. 2021, 37, 04021057. [Google Scholar] [CrossRef]
- Hasnain, M.; Thaheem, M.J.; Ullah, F. Best Value Contractor Selection in Road Construction Projects: ANP-Based Decision Support System. Int. J. Civ. Eng. 2018, 16, 695–714. [Google Scholar] [CrossRef]
- Al Subaie, A.A.; Faisal, M.N.; Sabir, L.B. ISO 21500 and the Sustainability Focused ANP-BOCR Framework for Subcontractor Selection in Megaprojects. Proj. Manag. J. 2023, 17. [Google Scholar] [CrossRef]
- Tomczak, M.; Jaśkowski, P. Application of Type-2 Interval Fuzzy Sets to Contractor Qualification Process. KSCE J. Civ. Eng. 2018, 22, 2702–2713. [Google Scholar] [CrossRef]
- Martin, H.; Ramjarrie, K. Cloud Contractor Selection Model for Design-Build Open Tender. J. Constr. Eng. Manag. 2021, 147, 04021020. [Google Scholar] [CrossRef]
- Taylan, O.; Kabli, M.R.; Porcel, C.; Herrera-Viedma, E. Contractor Selection for Construction Projects Using Consensus Tools and Big Data. Int. J. Fuzzy Syst. 2018, 20, 1267–1281. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Kubek, D. Multicriteria Selection of the Building Material Supplier Using AHP and Fuzzy AHP. J. Constr. Eng. Manag. 2016, 142, 04015057. [Google Scholar] [CrossRef]
- Guo, D.; Wu, J. A complete ranking of DMUs with undesirable outputs using restrictions in DEA models. Math. Comput. Model. 2013, 58, 1102–1109. [Google Scholar] [CrossRef]
- Inti, S.; Tandon, V. Integration of Data Envelopment Analysis-Based Preference Aggregation Method and α Particle Swarm Optimization Technique into Group Decision Model. J. Comput. Civ. Eng. 2017, 31, 1–12. [Google Scholar] [CrossRef]
- Liu, S.-T. A DEA ranking method based on cross-efficiency intervals and signal-to-noise ratio. Ann. Oper. Res. 2018, 261, 207–232. [Google Scholar] [CrossRef]
- Wen, Y.; An, Q.; Xu, X.; Chen, Y. Selection of Six Sigma project with interval data: Common weight DEA model. Kybernetes 2018, 47, 1307–1324. [Google Scholar] [CrossRef]
- Ang, S.; Chen, M.; Yang, F. Group cross-efficiency evaluation in data envelopment analysis: An application to Taiwan hotels. Comput. Ind. Eng. 2018, 125, 190–199. [Google Scholar] [CrossRef]
- Talluri, S. A buyer–seller game model for selection and negotiation of purchasing bids. Eur. J. Oper. Res. 2002, 143, 171–180. [Google Scholar] [CrossRef]
- Chetan, T.G.; Jenamani, M.; Sarmah, S.P. Iterative Multi-Attribute Procurement Auction with Decision Support for Bid Formulation. Asia-Pac. J. Oper. Res. 2022, 39, 2150036. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, W.G.; Wu, Y. Bid evaluation decision for major project based on analytic hierarchy process and data envelopment analysis cross-efficiency model. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 3639–3647. [Google Scholar] [CrossRef]
- Yang, J.B.; Wang, H.-H.; Wang, W.-C.; Ma, S.-M. Using Data Envelopment Analysis to Support Best-Value Contractor Selection. J. Civ. Eng. Manag. 2016, 22, 199–209. [Google Scholar] [CrossRef]
- Watt, D.J.; Kayis, B.; Willey, K. The relative importance of tender evaluation and contractor selection criteria. Int. J. Proj. Manag. 2010, 28, 51–60. [Google Scholar] [CrossRef]
- Cristóbal, J.R.S. Contractor Selection Using Multicriteria Decision-Making Methods. J. Constr. Eng. Manag. 2012, 138, 751–758. [Google Scholar] [CrossRef]
- Alhumaidi, H.M. Construction Contractors Ranking Method Using Multiple Decision-Makers and Multiattribute Fuzzy Weighted Average. J. Constr. Eng. Manag. 2015, 141, 04014092. [Google Scholar] [CrossRef]
- El-Abbasy, M.S.; Zayed, T.; Ahmed, M.; Alzraiee, H. Contractor Selection Model for Highway Projects Using Integrated Simulation and Analytic Network Process. J. Constr. Eng. Manag. 2013, 139, 755–767. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhang, X.; Rodríguez, R.M.; Pedrycz, W.; Martínez, L. Expertise-based bid evaluation for construction-contractor selection with generalized comparative linguistic ELECTRE III. Autom. Constr. 2021, 125, 103578. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhang, X.; Pedrycz, W.; Wang, X.-J.; Skibniewski, M.J. Bid evaluation in civil construction under uncertainty: A two-stage LSP-ELECTRE III-based approach. Eng. Appl. Artif. Intell. 2020, 94, 103835. [Google Scholar] [CrossRef]
- Watt, D.J.; Kayis, B.; Willey, K. Identifying key factors in the evaluation of tenders for projects and services. Int. J. Proj. Manag. 2009, 27, 250–260. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, H.; He, Y. A System for Tender Price Evaluation of Construction Project Based on Big Data. Procedia Eng. 2015, 123, 606–614. [Google Scholar] [CrossRef]
- Hatush, Z.; Skitmore, M. Contractor selection using multicriteria utility theory: An additive model. Build. Environ. 1998, 33, 105–115. [Google Scholar] [CrossRef]
- Jaskowski, P.; Biruk, S.; Bucon, R. Assessing contractor selection criteria weights with fuzzy AHP method application in group decision environment. Autom. Constr. 2010, 19, 120–126. [Google Scholar] [CrossRef]
- Marzouk, M.M.; El Kherbawy, A.A.; Khalifa, M. Factors influencing sub-contractors selection in construction projects. HBRC J. 2013, 9, 150–158. [Google Scholar] [CrossRef]
- Lai, K.K.; Liu, S.L.; Wang, S.Y. A method used for evaluating bids in the chinese construction industry. Int. J. Proj. Manag. 2004, 22, 193–201. [Google Scholar] [CrossRef]
- El-Sayegh, S.M. Multi-criteria decision support model for selecting the appropriate construction management at risk firm. Constr. Manag. Econ. 2009, 27, 385–398. [Google Scholar] [CrossRef]
- Hosseini Nasab, H.; Ghamsarian, M.M. A fuzzy multiple-criteria decision-making model for contractor prequalification. J. Decis. Syst. 2015, 24, 433–448. [Google Scholar] [CrossRef]
- Afshar, M.R.; Alipouri, Y.; Sebt, M.H.; Chan, W.T. A type-2 fuzzy set model for contractor prequalification. Autom. Constr. 2017, 84, 356–366. [Google Scholar] [CrossRef]
- Singh, D.; Tiong, R.L.K. Contractor Selection Criteria: Investigation of Opinions of Singapore Construction Practitioners. J. Constr. Eng. Manag. 2006, 132, 998–1008. [Google Scholar] [CrossRef]
- Hatush, Z.; Skitmore, M. Evaluating contractor prequalification data: Selection criteria and project success factors. Constr. Manag. Econ. 1997, 15, 129–147. [Google Scholar] [CrossRef]
- Rashvand, P.; Majid, M.Z.A.; Pinto, J.K. Contractor management performance evaluation model at prequalification stage. Expert Syst. Appl. 2015, 42, 5087–5101. [Google Scholar] [CrossRef]
- Tiong, R.L.K.; Alum, J. Evaluation of proposals for BOT projects. Int. J. Proj. Manag. 1997, 15, 67–72. [Google Scholar] [CrossRef]
- Holt, G.D.; Olomolaiye, P.O.; Harris, F.C. Factors influencing U.K. construction clients’ choice of contractor. Build. Environ. 1994, 29, 241–248. [Google Scholar]
- Nieto-Morote, A.; Ruz-Vila, F. A fuzzy multi-criteria decision-making model for construction contractor prequalification. Autom. Constr. 2012, 25, 8–19. [Google Scholar] [CrossRef]
- Mahdi, I.M.; Riley, M.J.; Fereig, S.M.; Alex, A.P. A multi-criteria approach to contractor selection. Eng. Constr. Archit. Manag. 2002, 9, 29–37. [Google Scholar]
- Sarkis, J.; Meade, L.M.; Presley, A.R. Incorporating sustainability into contractor evaluation and team formation in the built environment. J. Clean. Prod. 2012, 31, 40–53. [Google Scholar] [CrossRef]
- Alsugair, A.M. Framework for Evaluating Bids of Construction Contractors. J. Manag. Eng. 1999, 15, 72–78. [Google Scholar] [CrossRef]
- Alirezaee, M.R.; Afsharian, M. A complete ranking of DMUs using restrictions in DEA models. Appl. Math. Comput. 2007, 189, 1550–1559. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).