Abstract
Permutation flow-shop scheduling is the strategy that ensures the processing of jobs on each subsequent machine in the exact same order while optimizing an objective, which generally is the minimization of makespan. Because of its NP-Complete nature, a substantial portion of the literature has mainly focused on computational efficiency and the development of different AI-based hybrid techniques. Particle Swarm Optimization (PSO) has also been frequently used for this purpose in the recent past. Following the trend and to further explore the optimizing capabilities of PSO, first, a standard PSO was developed during this research, then the same PSO was hybridized with Variable Neighborhood Search (PSO-VNS) and later on with Simulated Annealing (PSO-VNS-SA) to handle Permutation Flow-Shop Scheduling Problems (PFSP). The effect of hybridization was validated through an internal comparison based on the results of 120 different instances devised by Taillard with variable problem sizes. Moreover, further comparison with other reported hybrid metaheuristics has proved that the hybrid PSO (HPSO) developed during this research performed exceedingly well. A smaller value of 0.48 of ARPD (Average Relative Performance Difference) for the algorithm is evidence of its robust nature and significantly improved performance in optimizing the makespan as compared to other algorithms.
1. Introduction
Scheduling is a fundamental component of advanced manufacturing processes and systems. It efficiently utilizes resources to maximize objectives, e.g., makespan, flow time, average tardiness, etc. It plays a significant role in modern production facilities by optimally organizing and controlling the work and workloads in a manufacturing process, resulting in minimal inventory, processing time, idle time, and product cost [1]. In scheduling resources, such as machines, are allocated to tasks, such as jobs, to ensure the completion of these tasks in a limited amount of time. Scheduling while manufacturing, is basically the arrangement of jobs that can be processed on available machines subjected to different constraints.
Some of the classical models used to solve scheduling problems are job-shop, flow-shop, and open-shop. The Permutation Flow-shop Scheduling Problem (PFSP) addresses the most important problems related to machine scheduling and involves the sequential processing of n jobs on m machines [2]. Flow-Shop scheduling problems are NP-complete [3,4], for which complete enumeration requires considerable computational effort and time exponentially increasing with the problem size. The intricate nature of these problems renders exact solution methods impractical when dealing with numerous jobs and/or machines. This is the primary rationale behind the utilization of various heuristics, found in the literature.
2. Literature Review
Pioneering efforts by Johnson [5] concluded that PFSP with more than two machines could not be solved analytically. Consequently, researchers focused on other heuristic-based approaches to handle the PFSP of more than two machines. Some notable examples include Palmer’s heuristic [6], CDS (Campbell, Dudek & Smith) [7], VNS (Variable Neighborhood Search) [8], Branch & Bound [9], etc. However, with the increase in problem size, even the best heuristics tend to drift away from the optimal solutions and converge to suboptimal solutions. Therefore, the focus of research shifted towards meta-heuristics. Many such approaches, as viable solutions to PFSP, have already been reported in the literature, which includes GA (Genetic Algorithms) [10,11], PSO (Particle Swarm Optimization) [12,13] and ACO (Ant Colony Optimization) [14], Q-Learning algorithms [15], HWOA (Hybrid Whale Optimization Algorithms) [16], CWA (Enhanced Whale Optimization Algorithms) [17], and BAT-algorithms [18]. Metaheuristic-based approaches start with sequences generated randomly by a heuristic and then iterate until a stopping criterion is satisfied [19]. These approaches have been extensively applied to find optimal solutions to flow-shop scheduling problems [20]. Goldberg et al. [21] proposed GA-based algorithms as viable solutions to scheduling problem. A GA-based heuristic for flow-shop scheduling, with makespan minimization as the objective, was presented by Chen et al. [22]. The authors utilized a partial crossover, no mutation, and a different heuristic for the random generation of the initial population. A comparative analysis showed no improvement in results for a population size of more than 60. However, hybrid GA-based approaches have significantly improved results [23,24,25,26,27]. Despite this, the increased computational cost of such approaches is a major limitation. Therefore, comparatively more efficient algorithms such as PSO have recently been opted for more frequently [28].
PSO, initially proposed by Kennedy and Eberhart [29], is based on the “collective intelligence” exhibited by swarms of animals. In PSO, a randomly generated initial population of solutions iteratively propagates toward the optimal solution. PSO has been extensively applied to flow-shop scheduling problems. Tasgetiren et al. [30] implemented the PSO algorithm on a single machine while optimizing the total weighted tardiness problem and developed the SPV (Smallest Position Value) heuristic-based approach for solving a wide range of scheduling and sequencing problems. The authors hybridized PSO with VNS to obtain better results by avoiding local minima. Improved performance of the PSO was reported in comparison to ACO, with ARPD (average relative percent deviation) as the evaluation criteria. Another approach, presented by Tasgetiren et al. [31], utilized PSO with SPV and VNS for solving Taillard’s [32] benchmark problems and concluded that PSO with VNS produced the same results as GA with VNS. Moslehi et al. [33] conducted a study on the challenges of a Limited Buffer PSFP (LBPSFP) using a hybrid VNS (HVNS) algorithm combined with SA. Despite the similar performance, the computational efficiency of PSO was found to be exceedingly better than GA [28,34,35]. In addition, Fuqiang et al. [36] proposed a Two Level PSO (TLPSO) to solve the management problem related to credit portfolio. TLPSO included internal search and external search processes, and the experimental results show that the TLPSO is more reliable than the other tested methods.
Horng et al. [37] presented a hybrid metaheuristic by combining SA (Simulated Annealing) with PSO and compared their results with that of simple GA and PSO. The results for 20 different mathematical optimization functions confirmed the quick convergence and good optimality of SA-PSO compared to standalone GA and PSO. A similar but slightly different metaheuristic compounding PSO, SA, and TS (Tabu Search) was developed by Zhang et al. [38]. The algorithm obtained quality solutions while consuming lesser computational time when tested with 30 instances of 10 different sizes taken from Taillard’s [39] benchmark problems for PFSP and performed significantly better than NPSO (Novel PSO) and GA. Given the optimizing capabilities of hybrid approaches, recently, researchers have focused even more on applying hybrid metaheuristics to PFSP to improve the global and local neighborhood search capabilities of the standard algorithms. The optimizing capabilities of the hybrid approaches have invigorated the researchers to apply these techniques to the global and localneighborhood search algorithms. Yannis et al. [40] hybridized his PSO-VNS algorithm with PR (Path Relinking Strategy). A comparative analysis of the technique while solving Taillard’s [32] problems yielded a significantly better PSO-VNS-PR algorithm performance than PSO with constant global and local neighborhood searches. The effects of population initialization on PSO performance were studied by Laxmi et al. [41]. The authors hybridized standard PSO with a NEH (Nawaz, Enscore & Ham) heuristic for population initialization and SA for enhanced local neighborhood search. A significantly improved performance of the algorithm was reported compared to other competing algorithms. Fuqiang et al. [42] developed a technique including SA and GA for scheduled risk management of IT outsourcing projects. They concluded that SA, in combination with GA, is the superior algorithm in terms of stability and convergence.
From the literature review presented above, it can be evidently concluded that metaheuristics have the increased the capability of handling NP-hard problems. Furthermore, PSO, combined with other heuristics, have performed better than other tools, e.g., GA, ACO, etc. Therefore, to further validate this conclusion, a PSO-based approach was developed during this research in a stepwise manner. First, a standard PSO was developed and validated through Taillard’s [32] suggested benchmark problems. This was followed by its gradual hybridization with VNS only and then both with VNS & SA while observing the initial temperature’s effect on SA optimality [43]. An internal comparison based on Taillard’s benchmark problems was also carried out to justify the effect of hybridization. After validation, the hybrid PSO (HPSO)—developed during this research—was also compared with a recently reported Hybrid Genetic Simulated Annealing Algorithm (HGSA) [26] and other famous techniques based on the ARPD values. The comparison showed the effectiveness and the robust nature of the HPSO (PSO—VNS—SA), developed during this research, as it outperformed all its competitors.
3. Methodology
To execute the proposed research, a stepwise methodology adopted during this research is as follows:
- (1)
- Formulation of an optimization model for the PFSP.
- (2)
- Development of standard PSO.
- (3)
- Hybridization of standard PSO with VNS.
- (4)
- Further hybridization of PSO—VNS with SA.
3.1. Optimization Model
An optimization model is formulated for n–jobs and m–machines PFSP while having minimization of makespan (Cmax) as the objective function so that its results can be easily compared with other approaches. To optimize Cmax, the model needs to fulfill several constraints listed as follows:
- Each job (j) must start its next operation on the next machine (i + 1) in sequence after its previous operation on the previous machine (i) is completed.
- Each job (j) has an operation scheduled on each machine (i), i.e., each job must visit each machine only once
- Jobs must not overtake each other in between machines, and the permutation remains the same on each subsequent machine.
The formulated model is presented in Equation (1)
where Cmax = max (CTj); CTj is the completion time of job j and j = 1, 2, 3……., n; where n is the total number of jobs. In PFSP, the value of makespan is always defined by the last job in each permutation; therefore, to reduce the computational effort, Cmax is determined only for the last job (j = L) and is given by Equation (2).
where:
- = Completion time of the last job (j = L) in a permutation on machine1.
- = Start time of the last job on the next machine.
- = Waiting time of the last job (j = L) in a permutation on the next machine.
- = Processing time of the last job in a permutation on the next machine.
Subject to:
Job (j) must start its next operation on the next machine (i + 1) after its previous operation on the previous machine (i) is completed.
This constraint ensures that the processing time of each job must be positive, i.e., each job has an operation scheduled on each machine.
This ensures that jobs do not overtake each other in between machines, and the permutation remains the same on each subsequent machine.
3.2. Solution Representation
Since PSO is domain-independent, the most complicated step is the solution representation. There is n number of coordinates or positions for n number of jobs, representing the direct relationship between the problem domain and the PSO particles. In parallel, the particle represents the continuous values of positions for n number of jobs in the flow-shop problems. For the determination of sequencing, the smallest position value (SPV) was embedded in the algorithm for finding the position values of the particle proposed by Tasgetiren et al. [31]. The solution representation of particle with its positions and velocity values, and the sequence, according to the SPV rule, is shown in Table 1.

Table 1.
Solution representation of a particle.
is the minimum value in the position row, so the first job assigned in the permutation j = 5; the second minimum position value is . Therefore, j = 2 is assigned to the next job, and so on. Otherwise stated, permutation is constructed by using the sorted value of positions.
3.3. Algorithm Implementation
The approach is implemented in three different stages using MATLAB programming. Firstly, a standard PSO is encoded, as shown in Figure 1, Part (a). To test its performance, a total number of 120 benchmark problems, devised by Taillard [32], are handled, and their respective outcomes are listed in Table 1. Later on, the same standard PSO is hybridized with VNS by allowing the best solution in each iteration of standard PSO to receive further improvements under the procedure devised by VNS. PSO is a global search algorithm and thus explores the larger search space and identifies the potential region where the optimum may exist. VNS, on the other hand, searches inside this potential space and narrows down the location of a possible optimum. In each iteration this process is repeated until the best solution is identified. This combination of standard PSO with VNS is presented in Figure 1, combination of Parts (a) and (b). The performance of hybridized PSO-VNS is also validated through the same 120 benchmark problems, and the results are listed in Table 1.
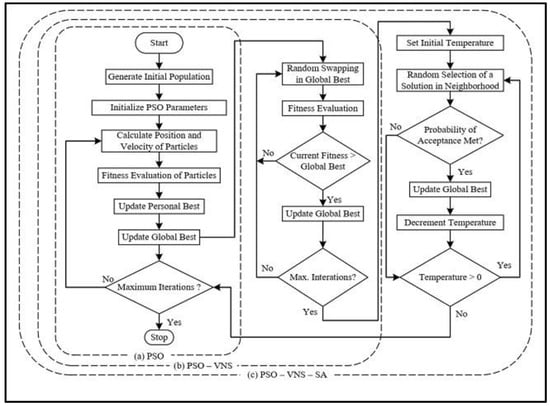
Figure 1.
Flow diagram of PSO, PSO-VNS and PSO-VNS-SA.
Finally, the hybrid version of PSO-VNS is further hybridized with SA to intensify local improvement and give further chance to the best solution in each iteration of the standard PSO by searching in its neighborhood for an even better option. The evolution part of the search is taken care of by the PSO whereas both VNS and SA help in locally improving the solution (Best) identified by PSO. VNS, by nature, is a greedy search algorithm and selects only better solutions whereas SA chooses even a slightly inferior solution if it falls within an already calculated range of probability. This helps the overall algorithm in avoiding local minima, reaching global optimum, and maintaining diversity in the population as well. The combined operating strategy of HPSO is shown in Figure 1. Its performance has also been confirmed through the same 120 benchmark problems. All the algorithms were run on a Core-i7 processor with 8 Gb of RAM using Windows 10 as the operating system. For comparison, the results are also listed in Table 1. The statistical comparison of the algorithms was based on a t-test, and the level of significance was set to p = 0.05.
3.4. Sensitivity Analysis
Like other evolutionary computational algorithms, particle swarm optimization is sensitive to hyperparameters and may suffer from premature convergence due to poorly selected control parameters. This may result in suboptimal performance and convergence at a local minimum. Extensive research has been conducted to characterize the influence of various control parameters on the performance of PSO. Isiet et al. [44] studied the effect of individual parameter variation on the performance of a standard benchmark problem. The authors testified a profound impact of inertia weight and acceleration coefficients on algorithm performance and reported a range of [0, 0.5] for the inertia weight matrix contrary to the previously reported [45,46] range of [0.9, 1.2]. More recent studies have proposed a dynamically changing inertia matrix approach [47] for increased exploration at the initial stage and reduced randomness at the converging stage of the algorithm. The algorithm developed in this research followed a similar approach with an inertia matrix in the range of [0.4, 1.2] and a decrement factor of 0.975. In addition to the inertia matrix, C1 (self-adjustment) and C2 (social adjustment) learning factors significantly impact algorithm’s performance. Previous studies have experimented with contrasting values of C1 and C2 and have suggested that the sum of the two variables should not be more than 4 [48], as proposed by [29]. The algorithm, developed during this research, exhibited similar behavior, which utilized a value of 2 for both the social coefficients. The main PSO algorithm was hybridized with Simulated Annealing (SA) to improve its performance against local minima. The computational procedure of SA is analogous to the positioning of molecules to the lowest state of energy as well as the constancy state through a controlled cooling rate for improving material properties. SA’s behavior depends on hyperparameters too. These include initial temperature, acceptance criteria, and cooling rate. The cooling rate is dynamically adjusted, starting with a higher value and decreasing it with increasing iterations. The initial temperature is kept at a higher value to ensure maximum variation and is slowly cooled with a specific cooling rate to the final temperature, which is also the stopping criterion for the algorithm. The approach developed during this research utilizes an initial temperature of 100 cooled to a final temperature of 0.5 with a final cooling rate of 0.99.
4. Results and Discussion
The sizes of Taillard’s benchmark problems, used for validation of the three algorithms presented in Figure 1, ranged from 20 × 5 (n × m) to 500 × 20. Each problem was given ten runs while using a swarm size of twice the number of jobs, and the inertial weights used, ranged from 1.2 to 0.4, with a decrement factor of 0.975. The cognitive and social acceleration coefficients (C1 and C2) were initialized with a value of 2, and the maximum iterations were kept limited to 100. The results obtained are listed in Table 2, Table 3, Table 4 and Table 5 and presented in Figure 2, Figure 3, Figure 4 and Figure 5. The recently reported results of the Q-Learning algorithm [15], though limited to a maximum problem size of 50 × 20, have also been analyzed for performance comparisons. The data in Table 2 and Figure 2 show that the algorithm achieved the upper bound in all instances of the 20-job problems resulting in an ARPD value of zero. A similar trend can be observed for the 50-job problems (Table 3, Figure 3), where the HPSO results in an ARPD value of 0.80, which is significantly better than the PSO-VNS and PSO with ARPD values of 3.21 and 4.20, respectively. The performance consistency is also apparent from the 100- and 200-job instances results, where the HPSO achieved ARPD values of 0.48 and 0.63 compared to 3.03 and 3.06 for PSO-VNS and 6.30 and 8.49 for the PSO. Figure 2, Figure 3, Figure 4 and Figure 5 clearly depict that the performance of HPSO in comparison to standard PSO and PSO–VNS was consistently superior as it returned improved solutions for the entire set of 120 benchmark problems.

Table 2.
Results of PSO, PSO-VNS, and HPSO for Taillard’s benchmark problems.

Table 3.
Results of PSO, PSO-VNS, and HPSO for Taillard’s 50-job benchmark problems.

Table 4.
Results of PSO, PSO-VNS and HPSO for Taillard’s 100 job benchmark problems.

Table 5.
Results of PSO, PSO-VNS, and HPSO for Taillard’s 200- and 500-job benchmark problems.
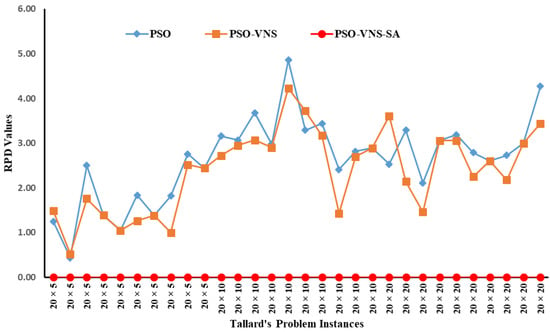
Figure 2.
Performance comparison of the three algorithms for the 20-Job.
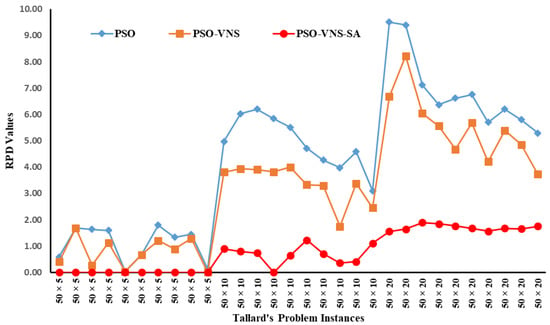
Figure 3.
Performance comparison of the three algorithms for the 50-Job.
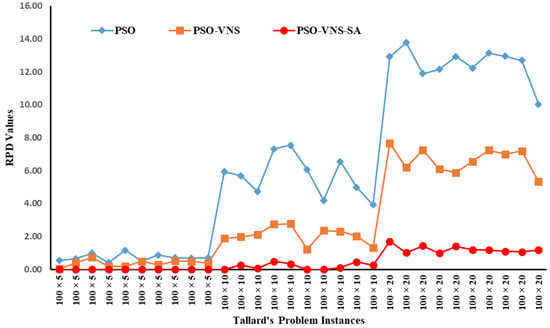
Figure 4.
Performance comparison of the three algorithms for the 100-Job Taillard’s instances.
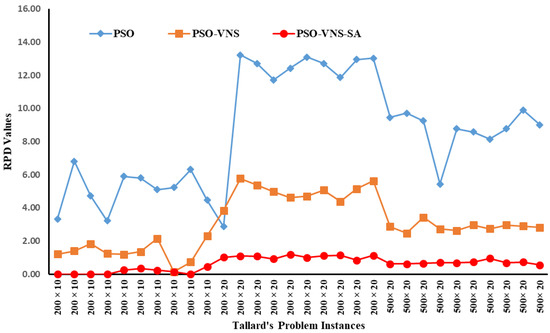
Figure 5.
Performance comparison of the RPD values of the three PSO algorithms for the 200- and 500-Job Taillard’s instances.
It can be concluded that the assimilation of VNS and SA significantly improved the convergence ability of standard PSO, which is evident from the results of the three PSO-based algorithms. The performance difference among the three variants of the PSO was significant (p << 0.05) for problem sizes up to 50 × 5 (Figure 4). However, the deviation of the results became more pronounced with the increasing problem size, as is evident from Figure 4 and Figure 5. Zhang et al. [49] conveyed a similar pattern of results for a hybrid metaheuristic-based approach they developed by combining PSO and SA with a stochastic variable neighborhood search. Researchers have mostly reported a significantly improved performance of SA with an initial temperature setting of 5°. However, the HPSO algorithm presented in this paper performed comparatively better with an initial temperature setting of 100° and a cooling rate of 0.95°. A possible reason for this deviation from other algorithms is the comparatively wider initial search space that increased the probability acceptance level of SA.
To further elaborate on the HPSO’s effectiveness, its performance has also been compared against hybrid GA (HGA)-based approaches. Since HGAs have been extensively reported in the literature and are widely regarded as the best metaheuristic for these sorts of problems, to justify the robust behavior of HPSO developed during this research, its performance was also compared with HGA by Tseng et al. [27] and HGSA by Wei et al. [26] (hybrid GA with SA). The algorithm performed significantly better than HGA (p = 0.05) and HGSA (p = 0.05), as evident from Figure 6.
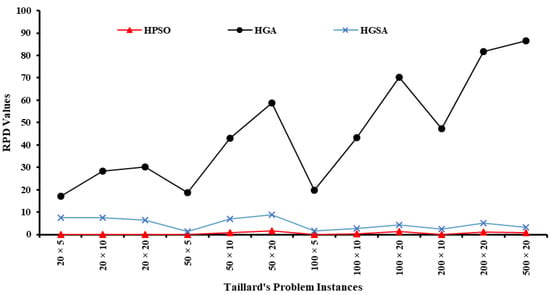
Figure 6.
Comparison of HPSO with HGA and HGSA heuristics for 120 Taillard’s instances.
Comparisons were also carried out with four different versions of GA, i.e., SGA (Simple Genetic Algorithm) [24], MGGA (Mining Gene Genetic Algorithm) [23], ACGA (Artificial Chromosome with Genetic Algorithm) [23], and SGGA (Self-Guided Genetic Algorithm) [24], as presented in Figure 7. The deviation of the GA from the upper bound, which increases in magnitude with the increasing problem size, was significantly more than HPSO. Thus, it can be concluded that the algorithm developed during this research is comparatively more robust and performs better than other hybrid GA techniques even while handling larger problem sizes.
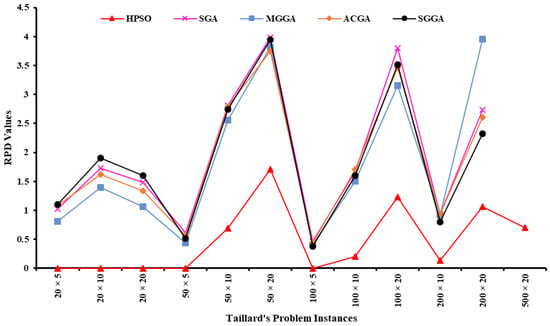
Figure 7.
Comparison of HPSO with hybrid GA-based heuristics.
Once the internal comparison of HPSO with standard PSO, PSO-VNS, and validation against HGA and HGSA was completed, the last part of validation was against other notable techniques already reported in the literature. For this purpose, a more detailed comparison was carried out with WOA [16], Chaotic Whale Optimization (CWA) [17], the BAT-algorithm [18], NEHT (NEH algorithm together with the improvement presented by Taillard) [31], ACO [50], CPSO (Combinatorial PSO) [51], PSOENT (PSO with Expanding Neighborhood Topology) [40], and HAPSO (Hybrid Adaptive PSO) [52]. This comparison was solely based on ARPD values and is shown in Table 6 and graphically illustrated in Figure 8. The improved performance of HPSO, developed during this research, is evident as compared to other reported hybrid heuristics.

Table 6.
Comparison of ARPD values of different metaheuristics with the algorithm developed during this research.
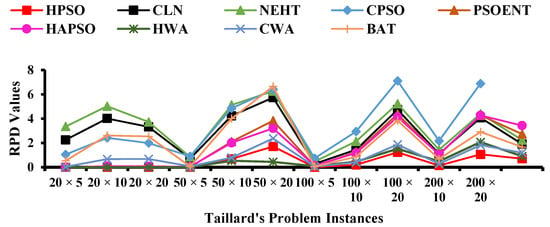
Figure 8.
Comparison of HPSO with CLS, NEHT, and three other hybridized PSO techniques.
The results of the Q-Learning algorithm [15] have not been shown in Table 6 due to the limited results reported by the author, as only 30 out of the 120 problems limited to a maximum problem size of 50 × 20 were analyzed. However, a comparison was performed for ARPD values for the limited number of problems for both HPSO and Q-learning. The results show a superior performance of the HPSO compared to the Q-Learning algorithm.
A row-wise comparison yields the performance variation of different approaches for individual problem groups. It is important to note that the technique developed during this research (HPSO) outperformed the other algorithms for each problem set. Although there is a performance variation across the techniques for different problem sizes, the algorithm was consistently better than all the other techniques. A smaller ARPD value in each problems group resulted in an overall smallest average ARPD value of 0.48, significantly better than the closest value of 0.85 for the HWA algorithm. It validates the claim that the HPSO approach, developed during this research, is comparatively more robust and remains consistent even while handling large sized problems. Furthermore, the average computation time of HPSO is reported in Table 7.

Table 7.
Comparison of Average Computation time in seconds of PSO, PSO-VNS, and HPSO.
5. Conclusions
As a member of the class of NP-complete problems, PFSP has been regularly researched and reported in the literature. Several heuristic-based approaches in the literature can efficiently handle this problem. However, for the larger problem sizes, most of the researchers focused on hybridized metaheuristics due to their ability to produce quality results in polynomial time, even for large-sized problems. Following this trend, a PSO-based approach was developed during this research in a stepwise manner. First, a standard PSO was developed, then it was hybridized with VNS, and finally, with SA. The final version, HPSO, outperformed not just standard PSO and PSO-VNS, but it also performed exceedingly well against other algorithms, including HGA, HGSA, ACO, BAT, WOA, and CWA. Comparisons based on the ARPD values showed that the performance of HPSO remained comparatively consistent, as evidenced by its small overall ARPD value of 0.48.
Author Contributions
Conceptualization, I.H. and W.S.; data curation, I.H.; formal analysis, W.S.; investigation, M.U.A.; methodology, I.H. and A.T.; project administration, A.Z.; supervision, S.A.; validation, A.T.; writing—original draft, I.H.; writing—review & editing, A.T., M.M., S.A., M.U.A. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data that support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arora, D.; Agarwal, G. Meta-Heuristic Approaches for Flowshop Scheduling Problems: A Review. Int. J. Adv. Oper. Manag. 2016, 8, 1–16. [Google Scholar] [CrossRef]
- Khurshid, B.; Maqsood, S.; Omair, M.; Sarkar, B.; Ahmad, I.; Muhammad, K. An Improved Evolution Strategy Hybridization With Simulated Annealing for Permutation Flow Shop Scheduling Problems. IEEE Access 2021, 9, 4505–94522. [Google Scholar] [CrossRef]
- Book, R.V. Book Review: Computers and Intractability: A Guide to the Theory of $NP$-Completeness. Bull. Am. Math. Soc. 1980, 3, 898–905. [Google Scholar] [CrossRef]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.H.G.R. Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey. In Discrete Optimization II; Annals of Discrete Mathematics; Hammer, P.L., Johnson, E.L., Korte, B.H., Eds.; Elsevier: Amsterdam, The Netherlands, 1979; Volume 5, pp. 287–326. [Google Scholar]
- Johnson, S.M. Optimal Two- and Three-Stage Production Schedules with Setup Times Included. Nav. Res. Logist. Q. 1954, 1, 61–68. [Google Scholar] [CrossRef]
- Hundal, T.S.; Rajgopal, J. An Extension of Palmer’s Heuristic for the Flow Shop Scheduling Problem. Int. J. Prod. Res. 1988, 26, 1119–1124. [Google Scholar] [CrossRef]
- Campbell, H.G.; Dudek, R.A.; Smith, M.L. A Heuristic Algorithm for the n Job, m Machine Sequencing Problem. Manag. Sci. 1970, 16, B-630–B-637. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, L.; Song, X.; Wang, Y.; Zhou, C. A Variable Neighborhood Search Based Genetic Algorithm for Flexible Job Shop Scheduling Problem. Clust. Comput. 2019, 22, 11561–11572. [Google Scholar] [CrossRef]
- Ruiz, R.; Maroto, C. A Comprehensive Review and Evaluation of Permutation Flowshop Heuristics. Eur. J. Oper. Res. 2005, 165, 479–494. [Google Scholar] [CrossRef]
- Mumtaz, J.; Zailin, G.; Mirza, J.; Rauf, M.; Sarfraz, S.; Shehab, E. Makespan Minimization for Flow Shop Scheduling Problems Using Modified Operators in Genetic Algorithm. Adv. Transdiscipl. Eng. 2018, 8, 435–440. [Google Scholar] [CrossRef]
- Umam, M.S.; Mustafid, M.; Suryono, S. A Hybrid Genetic Algorithm and Tabu Search for Minimizing Makespan in Flow Shop Scheduling Problem. J. King Saud. Univ. Comput. Inf. Sci. 2022, 34, 7459–7467. [Google Scholar] [CrossRef]
- Radha Ramanan, T.; Iqbal, M.; Umarali, K. A Particle Swarm Optimization Approach for Permutation Flow Shop Scheduling Problem. Int. J. Simul. Multidiscip. Des. Optim. 2014, 5, A20. [Google Scholar] [CrossRef]
- Marichelvam, M.K.; Geetha, M.; Tosun, Ö. An Improved Particle Swarm Optimization Algorithm to Solve Hybrid Flowshop Scheduling Problems with the Effect of Human Factors—A Case Study. Comput. Oper. Res. 2020, 114, 104812. [Google Scholar] [CrossRef]
- Shen, C.; Chen, Y.L. Blocking Flow Shop Scheduling Based on Hybrid Ant Colony Optimization. Int. J. Simul. Model. 2020, 19, 313–322. [Google Scholar] [CrossRef]
- He, Z.; Wang, K.; Li, H.; Song, H.; Lin, Z.; Gao, K.; Sadollah, A. Improved Q-Learning Algorithm for Solving Permutation Flow Shop Scheduling Problems. IET Collab. Intell. Manuf. 2022, 4, 35–44. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; El-Shahat, D.; Mirjalili, S. A Hybrid Whale Optimization Algorithm Based on Local Search Strategy for the Permutation Flow Shop Scheduling Problem. Future Gener. Comput. Syst. 2018, 85, 129–145. [Google Scholar] [CrossRef]
- Li, J.; Guo, L.; Li, Y.; Liu, C.; Wang, L.; Hu, H. Enhancing Whale Optimization Algorithm with Chaotic Theory for Permutation Flow Shop Scheduling Problem. Int. J. Comput. Intell. Syst. 2021, 14, 651–675. [Google Scholar] [CrossRef]
- Bellabai, J.R.; Leela, B.N.M.; Kennedy, S.M.R. Testing the Performance of Bat-Algorithm for Permutation Flow Shop Scheduling Problems with Makespan Minimization. Braz. Arch. Biol. Technol. 2022, 65. [Google Scholar] [CrossRef]
- Liao, C.-J.; Tseng, C.-T.; Luarn, P. A Discrete Version of Particle Swarm Optimization for Flowshop Scheduling Problems. Comput. Oper. Res. 2007, 34, 3099–3111. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M.; Chakrabortty, R.K.; Ryan, M.J. A Simple and Effective Approach for Tackling the Permutation Flow Shop Scheduling Problem. Mathematics 2021, 9, 270. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Chen, C.-L.; Vempati, V.S.; Aljaber, N. An Application of Genetic Algorithms for Flow Shop Problems. Eur. J. Oper. Res. 1995, 80, 389–396. [Google Scholar] [CrossRef]
- Chang, P.-C.; Chen, S.-H.; Fan, C.-Y.; Chan, C.-L. Genetic Algorithm Integrated with Artificial Chromosomes for Multi-Objective Flowshop Scheduling Problems. Appl. Math. Comput. 2008, 205, 550–561. [Google Scholar] [CrossRef]
- Chen, S.-H.; Chang, P.-C.; Cheng, T.C.E.; Zhang, Q. A Self-Guided Genetic Algorithm for Permutation Flowshop Scheduling Problems. Comput. Oper. Res. 2012, 39, 1450–1457. [Google Scholar] [CrossRef]
- Chen, W.; Hao, Y.F. Genetic Algorithm-Based Design and Simulation of Manufacturing Flow Shop Scheduling. Int. J. Simul. Model. 2018, 17, 702–711. [Google Scholar] [CrossRef]
- Wei, H.; Li, S.; Jiang, H.; Hu, J.; Hu, J. Hybrid Genetic Simulated Annealing Algorithm for Improved Flow Shop Scheduling with Makespan Criterion. Appl. Sci. 2018, 8, 2621. [Google Scholar] [CrossRef]
- Tseng, L.-Y.; Lin, Y.-T. A Hybrid Genetic Algorithm for No-Wait Flowshop Scheduling Problem. Int. J. Prod. Econ. 2010, 128, 144–152. [Google Scholar] [CrossRef]
- Hassan, R.; Cohanim, B.; de Weck, O.; Venter, G. A Comparison of Particle Swarm Optimization and the Genetic Algorithm. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2015; American Institute of Aeronautics and Astronautics: Reston, Virigina, 2005. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Tasgetiren, M.F.; Sevkli, M.; Liang, Y.-C.; Gencyilmaz, G. Particle Swarm Optimization Algorithm for Single Machine Total Weighted Tardiness Problem. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2014; pp. 1412–1419. [Google Scholar]
- Tasgetiren, M.F.; Sevkli, M.; Liang, Y.-C.; Gencyilmaz, G. Particle Swarm Optimization Algorithm for Permutation Flowshop Sequencing Problem. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; pp. 382–389. [Google Scholar]
- Taillard, E. Benchmarks for Basic Scheduling Problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Moslehi, G.; Khorasanian, D. A Hybrid Variable Neighborhood Search Algorithm for Solving the Limited-Buffer Permutation Flow Shop Scheduling Problem with the Makespan Criterion. Comput. Oper. Res. 2014, 52, 260–268. [Google Scholar] [CrossRef]
- Lian, Z.; Gu, X.; Jiao, B. A Similar Particle Swarm Optimization Algorithm for Permutation Flowshop Scheduling to Minimize Makespan. Appl. Math. Comput. 2006, 175, 773–785. [Google Scholar] [CrossRef]
- Singh, M.R.; Mahapatra, S.S. A Swarm Optimization Approach for Flexible Flow Shop Scheduling with Multiprocessor Tasks. Int. J. Adv. Manuf. Technol. 2012, 62, 267–277. [Google Scholar] [CrossRef]
- Lu, F.-Q.; Huang, M.; Ching, W.-K.; Siu, T.K. Credit Portfolio Management Using Two-Level Particle Swarm Optimization. Inf. Sci. 2013, 237, 162–175. [Google Scholar] [CrossRef]
- Shieh, H.-L.; Kuo, C.-C.; Chiang, C.-M. Modified Particle Swarm Optimization Algorithm with Simulated Annealing Behavior and Its Numerical Verification. Appl. Math. Comput. 2011, 218, 4365–4383. [Google Scholar] [CrossRef]
- Zhang, X.-F.; Koshimura, M.; Fujita, H.; Hasegawa, R. Hybrid Particle Swarm Optimization and Convergence Analysis for Scheduling Problems. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; ACM: New York, NY, USA, 2012; pp. 307–314. [Google Scholar]
- Taillard, E. Some Efficient Heuristic Methods for the Flow Shop Sequencing Problem. Eur. J. Oper. Res. 1990, 47, 65–74. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M. Particle Swarm Optimization with Expanding Neighborhood Topology for the Permutation Flowshop Scheduling Problem. Soft Comput. 2013, 17, 1159–1173. [Google Scholar] [CrossRef]
- Bewoor, L.; Chandra Prakash, V.; Sapkal, S. Evolutionary Hybrid Particle Swarm Optimization Algorithm for Solving NP-Hard No-Wait Flow Shop Scheduling Problems. Algorithms 2017, 10, 121. [Google Scholar] [CrossRef]
- Lu, F.; Bi, H.; Huang, M.; Duan, S. Simulated Annealing Genetic Algorithm Based Schedule Risk Management of IT Outsourcing Project. Math. Probl. Eng. 2017, 2017, 6916575. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Gao, L.; Song, Y.; Li, X. An Improved Simulated Annealing Algorithm Based on Residual Network for Permutation Flow Shop Scheduling. Complex. Intell. Syst. 2021, 7, 1173–1183. [Google Scholar] [CrossRef]
- Isiet, M.; Gadala, M. Sensitivity Analysis of Control Parameters in Particle Swarm Optimization. J. Comput. Sci. 2020, 41, 101086. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998; IEEE World Congress on Computational Intelligence (Cat. No.98TH8360). pp. 69–73. [Google Scholar]
- Bansal, J.C.; Singh, P.K.; Saraswat, M.; Verma, A.; Jadon, S.S.; Abraham, A. Inertia Weight Strategies in Particle Swarm Optimization. In Proceedings of the 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; pp. 633–640. [Google Scholar]
- Zhu, X.; Wang, H. A New Inertia Weight Control Strategy for Particle Swarm Optimization. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2018; Volume 1955. [Google Scholar]
- Ozcan, E.; Mohan, C.K. Particle Swarm Optimization: Surfing the Waves. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1939–1944. [Google Scholar]
- Zhang, L.; Wu, J. A PSO-Based Hybrid Metaheuristic for Permutation Flowshop Scheduling Problems. Sci. World J. 2014, 2014, 902950. [Google Scholar] [CrossRef]
- Ying, K.-C.; Liao, C.-J. An Ant Colony System for Permutation Flow-Shop Sequencing. Comput. Oper. Res. 2004, 31, 791–801. [Google Scholar] [CrossRef]
- Jarboui, B.; Ibrahim, S.; Siarry, P.; Rebai, A. A Combinatorial Particle Swarm Optimisation for Solving Permutation Flowshop Problems. Comput. Ind. Eng. 2008, 54, 526–538. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M. An Adaptive Parameter Free Particle Swarm Optimization Algorithm for the Permutation Flowshop Scheduling Problem. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11943, pp. 168–179. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).