Abstract
Online customer reviews (OCRs) are the real feelings of customers in the process of using products, which have great reference value for potential customers’ purchase decisions. However, it is difficult for consumers to extract helpful information from very large numbers of OCRs. To support consumers’ purchase decisions, this paper proposes a hybrid method to rank alternative products through OCRs. In this method, we use the fine-grained Bidirectional Encoder Representation from Transformers (BERT) model for aspect-level sentiment analysis (SA) and convert SA results of sub-criteria into a corresponding interval intuitionistic fuzzy number, accurately extracting customer satisfaction in OCRs and reducing the errors caused by different amounts of OCRs. Furthermore, in order to obtain the ranking results of products, the subjective and objective weights are combined to determine weight of feature. Subsequently, an improved interval intuitionistic fuzzy VIKOR method is proposed to rank mobile games. Finally, we conduct a case study and make some comparisons, which show that our method can reduce the complexity of accurately obtaining consumers’ personal preferences and help consumers make more accurate decisions.
1. Introduction
With the wide application of the Internet and social media, more and more people share their experiences of purchasing or using products on social networks. Through online customer reviews (OCRs), potential consumers can gain a deeper understanding of product performance and quality, which can help them to make better purchase decisions to a certain extent [1]. In addition, enterprise managers can better understand the quality of products, master users’ preferences and purchase desires for products to better improve product design and plan future development strategies of products [2]. Therefore, OCRs have become a significant information carrier of user needs [3].
However, with the surge in OCRs, the number of product categories and related OCRs has become enormous. Relevant product information has become more complicated and chaotic, which has exceeded the scope that consumers can accept and effectively process [4,5,6,7]. Therefore, this paper proposes a hybrid method that combines a fine-grained Bidirectional Encoder Representation from Transformers (BERT) model and weight fusion interval intuitionistic fuzzy number to solve the above problems.
Traditional sentiment analysis (SA) research only considers the local information of a text and does not consider the influence of global information on word vector training [8,9,10,11,12,13]. Only considering local information, it often obtains biased information, and leads to wrong decisions. Araci et al. [14] introduce the BERT model in financial SA, combining the global information of target words to conduct sentiment analysis. The classification result is 15% more accurate than the top result of the two financial sentiment analysis data sets. Therefore, this paper uses the fine-grained BERT model to learn a better text feature from the sub-feature layer of the product, changing the unidirectional training mode of traditional language models. By integrating the text’s upper and lower semantic information to encode and fine-tune the model’s hyperparameters, we can better understand the semantic information of sentences and articles.
The existing research of feature weight mainly divides the determination into two parts: (1) only use collective attribute weight [15,16]; and (2) only use personal attribute preference [17]. However, only collective attribute preference or individual attribute preference is used when calculating the feature weight, which makes it easy to lose individual preference information and renders the feature weight subject to external interference, resulting in large experimental errors. Therefore, both subjective preference and objective preference are considered when calculating the feature weight in this paper, and an improved VIKOR method is established based on this. While considering the collective preferences, it also refers to the objective preferences of potential consumers to better support the purchase decisions of potential consumers.
Nowadays, scholars have realized that, due to the complexity and uncertainty in OCRs, it is challenging to represent the information carried in OCRs with accurate real values. Therefore, a few studies have applied intuitionistic fuzzy set theory for product ranking problems [18,19]. Studies have constructed an intuitionistic fuzzy number (IFN) based on OCR sentiment analysis results. Furthermore, these studies have uses membership degree, non-membership degree and hesitation degree in the IFN to reflect the positive, negative and neutral attitudes of online reviews related to product features [20]. However, they did not consider the effect of the number of OCRs on the consistency of the decision data obtained from online reviews. The higher the number of OCRs is, the higher the consistency of decision data obtained from online reviews is; the lower the number of OCRs is, the lower the consistency of decision data obtained from OCRs is. Therefore, we construct an interval-valued intuitionistic fuzzy number to represent the product performance of alternative products and eliminate the influence of the number of OCRs on the consistency of decision data.
The objective of this paper is to propose a hybrid method based on the fine-grained BERT model, subjective weight and objective weight to rank products through OCRs. First, we classify target products to determine alternative products and obtain OCRs. Then, we extract the product features concerning consumers from a large number of OCRs and construct the evaluation system of the target, standard and sub-standard layers. After that, we use the fine-grained BERT model for SA and to score OCRs. Finally, according to the interval intuitionistic fuzzy theory, we use a constructed IFN to represent the feature performance of the alternative products and use the weight fusion VIKOR method to rank all the alternative products. So far, few studies have combined the BERT model with subjective and objective weights to deal with product ranking. Our method provides a new process for product ranking through OCRs in the future.
The main contributions of this paper are as follows:
- Classify products and analyze them at a more fine-grained level. Previous studies have rarely considered the classification of products, ignoring the error caused by product classification, which makes it easy to mislead consumers into making wrong decisions;
- Integrate subjective weight and objective weight into the VIKOR method, correct the deviation caused by the traditional method that only considers subjective or objective weight and help consumers choose more satisfactory and suitable products;
- Verify the effectiveness of the method via an example analysis. A mobile game case study shows that our method can reduce the complexity of accurately obtaining consumers’ personal preferences and help consumers make more accurate decisions.
The rest of this paper is structured as follows: In Section 2, the related literature is reviewed. Section 3 describes the product ranking problem and introduces the approach of this article. Section 4 describes case studies of mobile game ranking and how the proposed approach and sensitivity analysis can be used. Section 5 presents the conclusions and limitations of this study and puts forward future research directions.
2. Literature Review
This paper is related to two streams of the literature: (1) the studies on sentiment analysis, and (2) the studies on ranking products through OCRs.
2.1. Studies on Sentiment Analysis
Sentiment analysis is a process of analyzing, processing and extracting subjective text with sentiment colors by using natural language processing and text mining technology [21]; it covers many fields, such as natural language processing, text mining and machine learning. In recent years, it has become the primary concern in natural language processing and text mining [22,23,24].
According to the granularity of analysis objects, SA can be divided into three research levels: document-level, sentence-level and aspect-level [21]. The document-level identifies the sentiment polarity of the whole document, and it is considered the most basic task [25]. The sentence-level SA is regarded as a subtask of document-level SA, which identifies the sentiment polarity of each sentence in the document [26]. The aspect-level SA determines the corresponding sentiment intensity of each aspect from the fine-grained level of the document [27]. In order to obtain more accurate information from OCRs, aspect-level SA is utilized in this paper.
Li et al. [28], through a summary of multimodal emotional analysis research on existing multiple media channels, discussed future research trends and potential directions of multimedia emotional analysis. Anastasiei et al. [29], through an online survey, have proved that rational information is more persuasive than emotional information, which is conducive to a deeper understanding of the impact of rational and emotional information on consumer decision-making in social media. Kauffmann et al. [30] studied the impact of online reviews on brand image and positioning to classify customers and improve recommendation systems. Yuan et al. [31], based on real data from Amazon.cn, have revealed why useful comments can help consumers.
According to the existing SA research, the main sentiment classification methods are divided into three categories: lexicon-based [8,9,10], traditional machine learning [11,12] and deep learning [32,33,34]. However, lexicon-based SA technology cannot analyze sentiments in the contextual semantic environment of sentiment words, nor can it analyze the semantic similarity of the same word in a text [35]. This dramatically reduces SA accuracy and makes it challenging to process sentiment classification in long texts. Meanwhile, traditional machine learning SA technology cannot learn the sequential dependence of texts and analyze the semantic information of words in different contexts. Therefore, to ensure the accuracy of sentiment analysis results, this paper utilizes aspect-level SA technology based on fine-grained BERT in deep learning. Compared to traditional methods, this method has strong discrimination ability and feature self-learning ability, enabling it to automatically learn a text’s deep semantic and syntactic features. Through the fine-grained BERT model, connection with the target word’s context to semantic analysis can maintain a high effect even in long texts without data annotation.
2.2. Studies on Ranking Products through Online Reviews
Text mining of OCRs has been studied for a long time, but no research has combined it with fine-grained sentiment analysis and subjective and objective weights. Current studies mainly include [17,36,37,38,39].
Najmi et al. [36] proposed a new method of online product ranking combining OCR usefulness analysis, sentiment analysis and product brand ranking. Their dataset included 197 products in the TV and camera categories and 56,368 OCRs of Amazon-related products. Experiments show that this method can provide better product suggestions when inquiring with consumers about relevant products. Liu et al. [17] proposed a novel approach combining intuitionistic fuzzy theory with SA techniques. The method consisted of two stages: first, it used SA technology to determine online review sentiment orientation, and second, it used intuitionistic fuzzy theory to determine product ranking. This method developed an algorithm to classify the characteristics of each review as positive, negative or neutral. Next, the method transformed the identified emotional orientations into intuitionistic fuzzy numbers to represent the performance of the product features. Finally, it used a fuzzy PROMETHEE II method to calculate the final product ranking.
Wu et al. [37] proposed a comprehensive method for ranking products through online reviews. The method proposed a new framework and corresponding calculation rules based on intuitionistic fuzzy theory for expressing sentiment orientation and intensity. Then, the weight of features was determined through feature occurrence frequency and attention degree, so different features’ weights were more reasonable. Finally, it combined multi-attribute decision theory and the TODIM method to determine the final product ranking result. Chen et al. [38] proposed a framework for visualizing market structures via integrating online reviews with topic modeling, MDS and TOPSIS techniques. In the approach, they first separated the polarity of OCRs into positive and negative evaluations. Then, they extracted the critical attribute characteristics of the product from the positive and negative evaluations, respectively, and determined the weight matrix and significant criteria weight of each brand. Finally, they derived the market structure from the product attributes. Peng et al. [39] proposed a fuzzy MCDM method for evaluation and ranking products through OCRs. First, they calculated the similarity between words, regarded Chinese characters with word similarity greater than 0.5 as synonyms and found synonyms for all the words. Then, based on the frequency of each word and its synonyms, they determined the main characteristic criteria of the products. Finally, the fuzzy decision matrix of products was obtained, and they determined the ranking of all alternative products through the fuzzy PROMETHEE method.
This research has made significant contributions to SA and product ranking through online reviews. However, some aspects that need attention have not been considered in these studies. First, selecting alternative products was not classified, thus ignoring the differences among different products. In addition, few studies have paid attention to the combination of objective and subjective weights. Most studies only considered objective or subjective weight, which brings significant deviation to consumer decision-making. Finally, the construction of sentiment dictionaries and pre-training annotation data processing in existing studies is troublesome and consumes many human and material resources. Therefore, to solve these problems to support consumer decisions, we develop a method to select products by combining product classification, the fine-grained BERT model and weight fusion. Table 1 shows the traditional approach compared with our method.

Table 1.
Comparison of previous works with our proposed method.
3. Research Method
The proposed method in this paper consists of three phases. The first phase classifies products to determine alternative products and crawl OCRs of alternative products. Next, the second phase extracts the aspects that concern consumers from the OCRs to construct a three-level evaluation system, using aspect-level SA to identify the sentiment orientations of sub-criteria through the fine-grained BERT model. The third and final phase constructs interval intuitionistic fuzzy numbers (IVIFNs) based on interval intuitionistic fuzzy sets theory to rank the alternative products with the improved IVIFN-VIKOR. The process of this proposed methodology is shown in Figure 1. We combine objective weight with subjective weight. The opinions of consumers who have purchased products also take into account the personal purchase preferences of potential consumers. In addition, the interval-valued intuitionistic fuzzy number is used to represent product performance, which reduces the impact of the number of online comments on the consistency of decision data and makes the results more accurate.
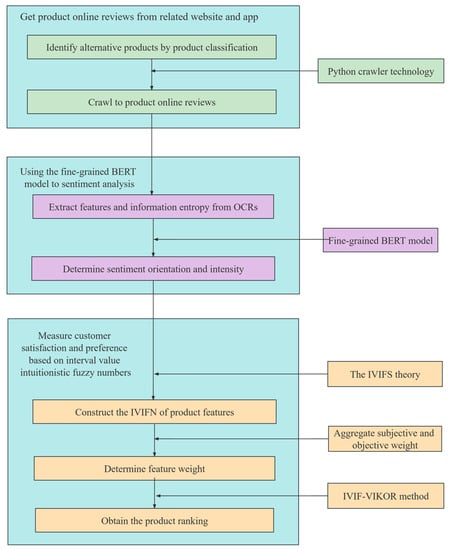
Figure 1.
The process of the proposed methodology.
3.1. Collecting and Processing Online Reviews
3.1.1. Crawling Online Reviews Concerning Alternative Products
According to product attributes, main uses and use status, we classified products in order to determine alternative products. We classified products and determined each category’s most popular alternative products through a questionnaire survey. Then, we used a crawler written in Python 3.8 to crawl a large number of OCRs related to product features from three relevant websites.
3.1.2. Crawling and Preprocessing Data
To identify the sentiment orientations of the online reviews, it was necessary to preprocess the obtained online reviews. The preprocessing included two processes: (1) word segmentation and part-of-speech (POS) tagging and (2) stop words removal. Word segmentation recombined online reviews into word sequences according to certain norms. POS is the correct part of speech for each wordmark in the segmentation result. For example, after processing the Chinese “游戏画面不算差” (graphics are not bad) with word segmentation and POS, the result is “游戏画面/n, 不/v, 算/d,差/a” (i.e., graphics /n, are /v, not /d, bad /a). Where “/n”, “/v”, “/d” and “/a” denote “noun”, “verb”, “adverb” and “adjective”, respectively. Finally, we deleted the stop words. Deleting stop words deletes words that frequently appear in the text but do not carry important information so as to improve the efficiency and effect of sentiment analysis [17].
3.2. Using the Fine-Grained BERT Model for Sentiment Analysis
3.2.1. Extracting Product Aspect Features from Online Reviews
We combined word vectors and K-means clustering to extract product features from online reviews. First, we calculated the Term Frequency-Inverse Document Frequency (TF-IDF) values of OCRs, and selected N product keywords with high TF-IDF values. Then, we used word2Vec to transform the product keywords into word vector form, embedding the words in the high-dimensional word vector space. Finally, we used the K-means clustering method to cluster the product keywords, making the similarity within the group as large as possible, and the similarity between the groups as small as possible [40]. The feature values of the products were extracted from the clustering results. Furthermore, we calculated the information entropy of online reviews according to Equation (1):
where denotes a set of words that appear in a review and denotes the frequency of the th word in review, .
3.2.2. Calculating the Sentiment Orientation
There were many reviews with semantic and scoring ambiguities in the initial OCRs. For example, online reviews containing “这款游戏的画质非常不好,我的体验感非常差” (“The picture quality of this game is very bad, my experience is very bad”) obtained a consumer scoring of 5. It was clear from the semantics of online reviews that consumers felt very poorly about the product they were reviewing, and yet they gave the product the highest possible score of 5 points. So, in the first step, we used Snow NLP to perform sentiment scoring on the initial reviews. We marked the sentiment values less than or equal to 0.5 as 0, and the sentiment values greater than 0.5 as 1. Then, we removed data with a scoring of 3 in the training data. We regarded reviews with scores of 1 and 2 as negative and marked them as 0. We regarded reviews with scores of 4 and 5 as positive and marked them as 1. Finally, we compared the score results with the sentiment scores and deleted the reviews with ambiguous scores. We used the remaining data as training data. We selected 20% of the training data as the test set and used the Adam optimizer to fine-tune the BERT-Base-Chinese model.
We input the data set into the trained BERT-Base-Chinese model. Through multiple Transformer layers, we calculated the similarity between a product feature word and other words in the same sentence and normalized the similarity results into weights through the softmax function. Then, we calculated the sentiment score of product features by integrating the value of the product feature word and the upper and lower words. Finally, we identified the sentiment orientation. Figure 2 shows the BERT model. The following describes the calculation of the Self-Attention mechanism.
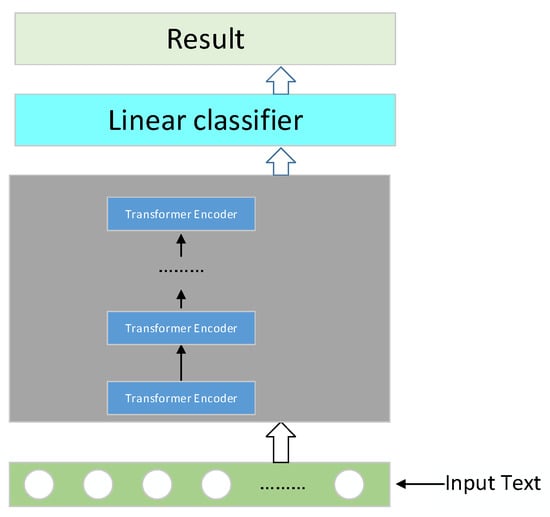
Figure 2.
The BERT model.
Suppose the model input is : , which maps onto the continuous representation sequence : . We produced a linear mapping for each input input and multiplied it by the weight matrix , and , respectively, to obtain the Query vector, Key vector and Value vector of each input (Briefly referred to as , , and vectors):
The similarity between vector and vector was normalized via the softmax function. We then multiplied the calculation results generated by the softmax function by vector to obtain the continuous representation sequence . This is expressed by the following formula:
where is the dimension of vectors and .
The multi-attentional mechanism was adopted in the BERT model; that is, it used different self-attentional modules to calculate the semantic vectors of text in different semantic spaces. For example, the Transformer used eight attention headers, and each attention header was equipped with a Query, Key and Value weight matrix to calculate the semantic vector. Finally, multiple semantic vectors of each word were linearly combined to obtain the final semantic vector.
The process is expressed by the formula:
where , .
We utilized the linear classifier to identify product features’ sentiment orientations. A product feature with a sentiment score less than or equal to 0.35 was considered negative, while a product feature with a sentiment score greater than 0.35 and less than or equal to 0.7 was considered neutral and one with a sentiment score greater than 0.7 was considered positive.
denotes the sentiment orientation concerning feature in the th online review of alternative product . The value of has four cases, i.e., = (1,0,0), = (0,1,0), = (0,0,1) and = (0,0,0), where = (1,0,0), = (0,1,0), = (0,0,1), respectively, denote that the th online review of alternative product expresses the positive, neutral and negative sentiment orientations. Specially, = (0,0,0) denotes that the sentiment orientation does not contain the relevant content of feature in the th online review of alternative product , , , .
3.3. Measure Consumer Satisfaction and Preference Based on Interval Value Intuitionistic Fuzzy Number
3.3.1. Interval Value Intuitionistic Fuzzy Set
Definition 1
([41]). Let be a non-empty finite set, then an interval intuitive fuzzy set on is defined as:
where and represent the ordered interval pairs that element belongs to, respectively, the member interval and the non-member interval of set .
In general, the ordered interval pair composed of membership interval and non-membership interval is called the interval intuitive fuzzy number.
Definition 2
([42]). Let , be a group of interval intuitionistic fuzzy numbers, as follows:
where is the weight of and , . stands for interval intuitionistic fuzzy weighted arithmetic average operator.
Definition 3
([42]). Let and
be two arbitrary interval intuitionistic fuzzy numbers; the scoring functions of and are, respectively, , , and the exact functions of and are, respectively, and , then:
- (1):
- If , then ;
- (2):
- If: , as follows:If , then ;If , then .
The distance formula of two interval intuitive fuzzy numbers and is:
3.3.2. Construct the Interval Value Intuitionistic Fuzzy Number of Product Features
Information entropy is a measure of the amount of information. Online reviews with higher entropy are more helpful to consumers and more critical. To determine the weight of online review based on its information entropy, where denotes the sentence concerning feature in the th OCRs of alternative product , , , :
where denotes the weight of review , denotes the information entropy of review , , .
, and represent the weighted frequencies of positive, neutral and negative online reviews concerning feature for product alternative , respectively. , . , and are computed as follows:
To construct intuitionistic fuzzy numbers: , Where and ,respectively, denote the support and opposition degrees of alternative product concerning feature . and are computed as follows:
According to the method presented in [39], one can calculate , , and by intuitionistic fuzzy number based on consistency interval estimation in probability theory. The calculation process is as follows:
In the above formulas, in order to eliminate the influence of the different number of online reviews, we introduced to express internal sentiment value based on consistency interval estimation in probability theory. represents the confidence level, and the value of can be found in the normal distribution table. However, and might not satisfy the definition of interval-valued intuitionistic fuzzy numbers that . So, we must convert , , and using the following formulas:
Based on , , and , we can construct the intuitionistic fuzzy number of alternative product concerning feature . and denote the lower and upper limits of the membership degree of the attribute in alternative , while and denote the lower and upper limits of the non-membership degree of the attribute in alternative product , .
3.3.3. Use Fuzzy Best–Worst Method (FBWM) to Calculate Product Attribute Weight
The FBWM integrates the traditional fuzzy preference relationship into the BWM, expands the precise integer used for preference comparison to fuzzy number to represent experts’ preference cognitions of alternative schemes and only uses a scale between 0.5 and 0.9 to compare and describe the two schemes. This situation is simpler for decision makers to directly ensure the accuracy and objectivity of information description [43]. The use of the FBWM model to measure index weight is mainly divided into five steps:
- Define the indicator set. A set of indicators is used to describe the target object for evaluation;
- Select the best indicator and the worst indicator. The decision maker selects the best indicator and the worst indicator from the indicator set , according to the actual situation;
- Determine the importance of other indicators relative to the best indicators. Numbers 1–9 were used to represent the importance of other indicators relative to the best indicator, and a comparison vector was constructed, where represented the importance of the best indicator relative to the indicator . A value of 1 means that and are equally important, and 9 means that is extremely important relative to ;
- Determine how important other indicators are relative to the worst indicators. Numbers 1 to 9 are used to represent the importance of other indicators relative to the worst indicator, and a comparison vector is constructed, where represents the importance of the worst indicator relative to the indicator . A value of 1 means that and are equally important, and 9 means that is extremely important relative to ;
- Determine the index weight . A mathematical programming model is constructed and solved:
3.3.4. Ranking Products Based on the Improved Interval Value Intuitionistic Fuzzy VIKOR Method
The attribute weights of traditional VIKORs do not consider the personal preferences of potential consumers. Therefore, we combined the consumer’s attribute preference and collective attribute preference to improve the conventional VIKOR method.
First, we determined the positive-ideal solution and negative ideal solution :
Then, we computed the values and :
where denotes the importance of individual attribute preference, which is the result of decision makers weighing personal attribute preference and collective attribute preference.
Next, we computed the value :
where , , , , is identified as a weight for strategy of maximum group utility.
Finally, we ranked the alternatives, sorting by the values of in decreasing order.
4. Case Study
4.1. Decision-Making Process
This paper selects mobile games from China’s leading mobile phone market for the case study. The reason why we chose mobile games as the research object is not only because mobile games have penetrated people’s lives and become the fastest-growing entertainment product in the field of mobile applications, but also because two-thirds of mobile game consumers provide feedback on online game user platforms [44].
We have divided mobile games into 11 categories by content: Strategy Game (STG), Role-playing Game (RPG), Racing Game (RCG), Puzzle Game (PUZG), Simulation Game (SIMG), First-person Shooting Game (FPS), Card Game (CAG), Music Game (MUG), Tabletop Role-playing Game (TRPG), Sports Game (SPG) and Multiplayer Online Battle Arena (MOBA). Each game category contains five of the most popular games. For example, the RPG category includes Journey to the West, Brawl Stars, Identity V, Onmyoji and Aotu World. Table 2 shows a detailed breakdown of the games.

Table 2.
Game classification.
We took a questionnaire to select the most popular game from each category; the questionnaire was conducted online, with 11 single-choice questions to determine the most popular games in 11 categories. We distributed 515 questionnaires and collected 511 questionnaires, among which 280 male students and 231 female students participated. The results of the alternative game products determined by the questionnaire are: Boom Beach (P1), Identity V (P2), QQ Speed (P3), Hearth Stone: Heroes of Warcraft (P4), Mole’s World (P5), Game For Peace (P6), Clash Royale (P7), QQ Dance (P8) Killers of Three Kingdom (P9), FIFA Mobile (P10) and Honor of Kings (P11). To ensure the rationality of the questionnaire results, we used Cronbach’s alpha to test the reliability of the questionnaire data. We used SPSS 26.0 to study the reliability of experimental data and calculated Cronbach’s alpha to be 0.842. The reliability coefficient value is higher than 0.8, indicating that the reliability is excellent [45].
We used Python 3.8 to write crawler software to obtain 94,395 online reviews of relevant mobile games from the Apple and Huawei mobile app stores, we preprocessed initial online reviews and deleted ambiguous reviews. After the original data were processed, the scores were compared with the scores calculated by SnowNLP, and 4608 online reviews whose semantics and scores differed in snow resolution were deleted to obtain a final dataset containing 89,787 online reviews.
We calculated the TF-IDF value of each OCR after processing and selected the words with high TF-IDF values in the reviews as feature candidates; that is, we selected the words representing the most complete online review content. We screened the candidate words into words with two characters or more, and deleted the words with low frequency and no apparent correlation with product features. After processing, we obtained 200 feature candidate words related to product feature attributes in each mobile game.
Then, we used the Word2Vec tool of Wikipedia Chinese training to calculate the word vector of each feature candidate word. We obtained each candidate word’s similarity by calculating the Euclidean distance of each feature vector and using the K-means clustering algorithm to cluster 200 feature candidate words. We set K to 5 based on recommendations from mobile game industry experts. After obtaining the K-means clustering results of 200 feature candidate words, we deleted those unrelated to feature attributes and SA. We combined them with the frequency of consumers’ reviews on relevant candidate features and selected the product features that most concerned consumers from the remaining candidate features. The product feature clustering results are shown in Table 3.

Table 3.
The product feature clustering results.
Then, we conducted SA of online reviews of mobile games using trained Bert models. We calculated the weighted frequency and of online reviews’ sentiment orientation, . The weighted frequency of sentiment orientation is shown in Table 4. We constructed the interval intuitionistic fuzzy number of features with formulas (17)–(20), and the data are shown in Table 5. According to Formulas (21)–(22), we used interval intuitive fuzzy entropy to calculate the collective attribute preferences of consumers who have experienced the product, and the collective attribute weights are shown in Table 6. The preferences given by customers are shown in Table 7.

Table 4.
The weighted frequency of sentiment orientation.

Table 5.
The interval intuitionistic fuzzy numbers of features.

Table 6.
The collective attribute weights.

Table 7.
The individual preference weights.
Then, given , , we used the improved VIKOR method to calculate the consumer’s . The results are as follows: = 0.3206, = 0.2388, = 0.4127, = 0.4718, = 0.4383, = 0.4043, = 0.4349, = 0.3221, = 0.1515, = 0.4229 and = 0.3852. We determined the order of alternative game products based on the size of the value to be: P4 > P5 > P7 > P10 > P3 > P6 > P11 > P8 > P1 > P2 > P9.
4.2. Sensitivity Analysis
In this research, the subjective and objective weight ratio and the majority importance degree of criteria significantly impacted the ranking results of products. We performed a sensitivity analysis to assess the influence of changes in and values on the ranking. The results are shown in Figure 3 and Figure 4.
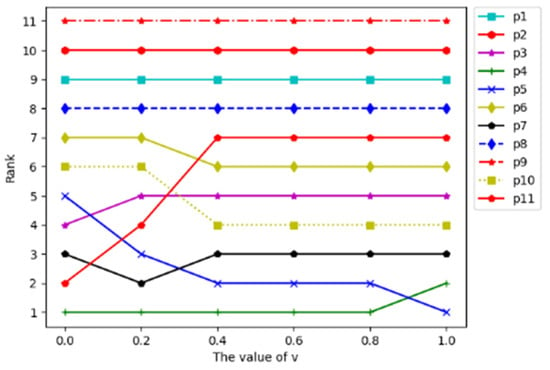
Figure 3.
Sensitivity analysis of .
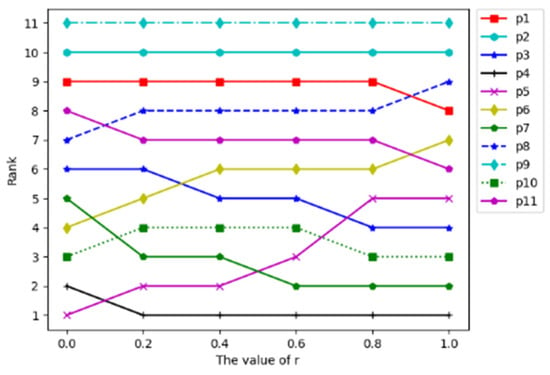
Figure 4.
Sensitivity analysis of .
As shown in Figure 3, the rankings of products P3, P4 and P11 gradually increase with the decrease in decision makers’ risk preference degree value. This indicates that, when decision makers pay more attention to the best interests, they are more satisfied with products P3, P4 and P11. At this time, decision makers are more satisfied with product P11, because product P11 increases more significantly with decision makers favoring group interests. Similarly, the rankings of P5, P6 and P10 increase with the increase in decision makers’ risk preference degree . This means that decision makers are more satisfied with P5, P6 and P10 when they pay more attention to their minimal regrets. In addition, the rankings of products P1, P2, P8 and P9 are not affected by the change in value, which indicates that no matter whether decision makers pay more attention to the maximum benefit of all or the minimum personal regret, they have low satisfaction with P1, P2, P8 and P9.
Figure 4 shows the change in product ranking as the weight fusion coefficient of individual preference weight and collective attribute weight changes from 0 to 1. As shown from Figure 4, the rankings of products P1, P3, P4, P7 and P11 also improve with the increasing value. Similarly, the rankings of P5, P6 and P8 decrease as the value increases. In addition, the rankings of P2 and P9 are not affected by the value, and the rankings of P2 and P9 do not change no matter how the r value changes. This indicates that both individual and collective preferences are dissatisfied with P2 and P9, which means that P2 and P9 are unsatisfactory for all customers. Due to , individual preference plays an increasingly important role with the increase in r. Customers’ personal preference for products has a greater impact on the final ranking result, and the decision result is highly subjective. On the contrary, the opinions of consumers who have purchased products have a greater impact on the final ranking results, and the decision results lack individuation. Hence, we combine objective weight with subjective weight. Considering not only the opinions of consumers who have bought products but also the personal preferences of consumers who want to buy products can help potential consumers choose more satisfactory and suitable products.
To summarize, different and values produce different sorting results. That is to say, the proportion of consumers’ personal attribute preference and collective attribute preference will greatly impact the decision makers’ product ranking and selection results. Therefore, combining consumers’ individual and collective attribute preferences is necessary when ranking products through online reviews.
4.3. Comparative Analysis
We selected five game features common to eleven kinds of mobile games and used the same experimental data comparative test to illustrate the rationality and correctness of the method in this paper. The five game features were picture, optimization, content, lag and experience. Using the same experimental data, the product ranking results are shown in Figure 5.
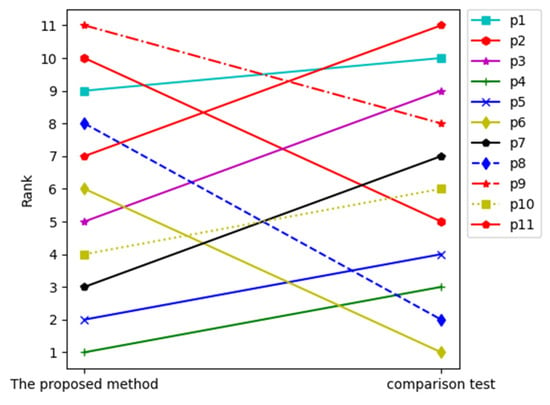
Figure 5.
Product classification comparison test.
As can be seen in Figure 5, there are big differences in the ranking results of products. The reason for this is because the extraction of their common product features ignores the different game characteristics of different categories of mobile games, which are the indicators that consumers care about. As a result, traditional mobile game feature extraction methods extract the game feature results that often miss the most competitive aspects of the games. Therefore, this paper makes a fine-grained summary and grouping according to different categories of mobile games, and finally extracts the features that can more accurately show the features and attributes of mobile game products that affect consumers’ decisions.
We compared the proposed method with the previously designed ones by [46,47,48] to prove the reliability of the proposed method. Using the same data, the product ranking results are shown in Table 8.

Table 8.
Product ranking results.
From the comparison of the ranking results shown in Table 8, we can see that the ranking results of different methods are similar. Compared with the ranking results of the other three methods, products P4 and P5 are ranked first and second, respectively. Products P2 and P9 are the last two products. Our method is similar to the result obtained by using the existing methods; the same product ranking part shows the effectiveness and rationality of our method, and the different product ranking part denotes the advantage of our method.
The first advantage of our method is that it constructs an interval value intuitionistic fuzzy number to evaluate product feature attributes. Sıcakyüz [48] combines the triangular fuzzy logarithm methodology of additive weights and the Fermatean fuzzy weighted aggregated sum product assessment method, but ignores the impact of the number of online reviews on the consistency of decision data. The fewer online reviews there are, the lower the consistency of decision data. Therefore, this paper adopts the form of an interval valued intuitionistic fuzzy number to eliminate the influence of the number of online reviews.
The second advantage of our methods is that it uses the fine-grained BERT model for sentiment analysis. Both [46] and [47] use the lexicon method to conduct sentiment analysis, so the product ranking results are different from [46,47]. We can capture longer-distance semantic information more efficiently and obtain bidirectional text information in the real sense through pre-training and fine-tuning the fine-grained BERT model.
The third advantage of our method is that it combines subjective and objective weights. Only subjective weight or objective weight is used in [46,47,48]. We calculate the collective preference weight of product attributes through interval intuitionistic fuzzy entropy and respect the individual preference of consumers’ attributes, making the ranking method more scientific and personalized.
4.4. Discussion
Before determining mobile game products, we classified different game products according to their characteristics, breaking away from the previous model of lumping all products into one category. The analysis of products at a more fine-grained level corrects the decision errors associated with lumping together different types of products.
We used a fine-grained BERT model for sentiment analysis on online reviews. The fine-grained BERT model had stronger feature extraction abilities that combined with entity naming to extract semantic information of text at a deeper level and improve the accuracy of sentiment analysis.
Our weights were composed of individual and collective preference weights. Consumers determined the weight value of individual preferences according to their personal preferences, and the weight values of collective preferences were calculated with intuitionistic fuzzy entropy. This considers the opinions of consumers who purchased products and the personal preferences of potential consumers. This method can help potential customers purchase satisfactory and more truly desirable products based on their personal preferences.
4.5. Research Hypothesis and Limitations
Our research applies to mobile game ranking issues and is highly portable and can be used with other processes with similar characteristics, such as online shopping, hotel booking, etc. However, there are some limitations to this study. When using a fine-grained BERT model for sentiment analysis, we directly analyzed all online reviews without considering inefficient and useless reviews in online reviews, which increases the complexity of the decision-making process. Therefore, the information load in online reviews needs to be considered in future studies. In addition, with the gradual diversification of the types and structures of information expressed by consumers, accurately describing the ambiguity and complex uncertainty in consumer information is an important research direction for the future.
5. Conclusions
Faced with massive amounts of online review data in the Internet era, it is a real problem to efficiently extract useful information. To this end, this paper proposes a hybrid method to solve this problem. The hybrid method of this paper consists of three stages: The first stage classifies products to identify alternative products and crawls online reviews related to alternative products. In the second stage, the features of game products that consumers care about are extracted through dimension reduction and clustering and a fine-grained BERT model is used for aspect-level sentiment analysis. The third stage identifies each feature’s interval intuitionistic fuzzy information and determines standard weights by combining the preference information of potential customers and experienced customers. Finally, it uses the improved VIKOR method to rank the alternative game products. Our method can reduce the complexity of accurately obtaining consumers’ personal preferences and help consumers make more accurate decisions.
In the face of a large number of OCRs, how to quickly and effectively help potential consumers and business operators to obtain information is a very practical problem. The hybrid method of this paper can provide potential consumers and business operators with useful information from very large numbers of OCRs to make better decisions. This new approach fully integrates the two types of weight, respecting the individual minds of potential consumers while also taking into account the thoughts of past consumers, thus helping consumers to make more authentic choices. In addition, the method proposed in this paper can also effectively help enterprise managers to accurately screen out helpful product information from OCRs, understand the market environment, provide references for enterprise promotion, market development and product development and help merchants to accurately position their products in fiercely competitive markets to gain competitive advantages.
Author Contributions
Conceptualization, Y.J., Y.Z. and S.Q.; data curation, Y.Z. and Z.W.; formal analysis, Y.J. and R.G.; investigation, Y.Z., S.Q. and Z.W.; methodology, Y.J., Y.Z. and S.Q.; resources, Y.J., Y.Z. and Z.W.; software, Z.W.; validation, Y.Z. and R.G.; supervision, Y.J. and S.Q.; project administration, Y.J., Y.Z., S.Q., R.G. and Z.W.; funding acquisition, Y.J. and S.Q.; writing–original draft, Z.W.; writing–review and editing, Y.J. and S.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was jointly supported by the National Natural Science Foundation of China (No. 72171123, 72171149).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are very grateful to the editors and anonymous reviewers for their careful reading and constructive suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, Y.Y.; Liu, T.J.; Teng, L.F.; Zhang, H.; Xie, C.X. The impact of online review variance of new products on consumer adoption intentions. J. Bus. Res. 2021, 136, 209–218. [Google Scholar] [CrossRef]
- Emadi, M.; Rahgozar, M. Twitter sentiment analysis using fuzzy integral classifier fusion. J. Inf. Sci. 2020, 46, 226–242. [Google Scholar] [CrossRef]
- Rana, T.A.; Cheah, Y.N. Sequential patterns rule-based approach for opinion target extraction from customer reviews. J. Inf. Sci. 2019, 45, 643–655. [Google Scholar] [CrossRef]
- Bi, J.W.; Liu, Y.; Fan, Z.P. Representing sentiment analysis results of online reviews using interval type-2 fuzzy numbers and its application to product ranking. Inf. Sci. 2019, 504, 293–307. [Google Scholar] [CrossRef]
- Park, D.H.; Lee, J. eWOM overload and its effect on consumer behavioral intention depending on consumer involvement. Electron. Commer. Res. Appl. 2008, 7, 386–398. [Google Scholar] [CrossRef]
- Wang, X.H.; Dong, S. Users’ sentiment analysis of shopping websites based on online reviews. Appl. Math. Nonlinear Sci. 2020, 5, 493–502. [Google Scholar] [CrossRef]
- Abu-Salih, B.; Wongthongtham, P.; Chan, K.Y.; Zhu, D.Y. CredSaT: Credibility ranking of users in big social data incorporating semantic analysis and temporal factor. J. Inf. Sci. 2019, 45, 259–280. [Google Scholar] [CrossRef]
- Liang, L.; Tian, F. Using normal dictionaries to extract multiple semantic relationships. J. Eng. 2020, 2020, 595–600. [Google Scholar] [CrossRef]
- Zabha, N.I.; Ayop, Z.; Anawar, S.; Hamid, E.; Zainal, Z. Developing cross-lingual sentiment analysis of malay twitter data using lexicon-based approach. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 346–351. [Google Scholar] [CrossRef]
- Moussa, M.E.; Mohamed, E.H.; Haggag, M.H. A generic lexicon-based framework for sentiment analysis. Int. J. Comput. Appl. 2018, 42, 463–473. [Google Scholar] [CrossRef]
- Cyril, C.P.D.; Beulah, J.R.; Subramani, N.; Mohan, P.; Harshavardhan, A.; Sivabalaselvamani, D. An automated learning model for sentiment analysis and data classification of Twitter data using balanced CA-SVM. Concurr. Eng. 2021, 29, 386–395. [Google Scholar] [CrossRef]
- Patil, H.P.; Atique, M. CDNB: CAVIAR-dragonfly optimization with naive bayes for the sentiment and affect analysis in social media. Big Data 2020, 8, 107–124. [Google Scholar] [CrossRef]
- Dogra, V.; Alharithi, F.S.; Alvarez, R.M.; Singh, A.; Qahtani, A.M. NLP-Based application for analyzing private and public banks stocks reaction to news events in the Indian stock exchange. Systems 2022, 10, 233. [Google Scholar] [CrossRef]
- Araci, D. FinBERT: Financial sentiment analysis with pre-trained language models. arXiv 2019, arXiv:1908.10063. [Google Scholar]
- Kumar, G.; Parimala, N. An integration of sentiment analysis and MCDM approach for smartphone recommendation. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 1037–1063. [Google Scholar] [CrossRef]
- Ji, P.; Zhang, H.Y.; Wang, J.Q. A fuzzy decision support model with sentiment analysis for items comparison in e-commerce: The case study of http://PConline.com. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1993–2004. [Google Scholar] [CrossRef]
- Liu, Y.; Bi, J.W.; Fan, Z.P. Ranking products through online reviews: A method based on sentiment analysis technique and intuitionistic fuzzy set theory. Inf. Fusion 2017, 36, 149–161. [Google Scholar] [CrossRef]
- Li, H.M.; Liang, M.X.; Zhang, C.Y.; Cao, Y.C. Risk evaluation of water environmental treatment PPP projects based on the intuitionistic fuzzy MULTIMOORA improved FMEA method. Systems 2022, 10, 163. [Google Scholar] [CrossRef]
- Song, J.K.; Jiang, L.N.; Liu, Z.C.; Leng, X.L.; He, Z.G. Selection of third-party reverse logistics service provider based on intuitionistic fuzzy multi-criteria decision making. Systems 2022, 10, 188. [Google Scholar] [CrossRef]
- Cali, S.; Balaman, S.Y. Improved decisions for marketing, supply and purchasing: Mining big data through an integration of sentiment analysis and intuitionistic fuzzy multi criteria assessment. Comput. Ind. Eng. 2019, 129, 315–332. [Google Scholar] [CrossRef]
- Abdi, A.; Shamsuddin, S.M.; Hasan, S.; Piran, J. Deep learning-based sentiment classification of evaluative text based on multi-feature fusion. Inf. Process. Manag. 2019, 56, 1245–1259. [Google Scholar] [CrossRef]
- Alaei, A.R.; Becken, S.; Stantic, B. Sentiment analysis in tourism: Capitalizing on big data. J. Travel Res. 2019, 58, 175–191. [Google Scholar] [CrossRef]
- Karami, A.; Shah, V.; Vaezi, R.; Bansal, A. Twitter speaks: A case of national disaster situational awareness. J. Inf. Sci. 2020, 46, 313–324. [Google Scholar] [CrossRef]
- Keramatfar, A.; Amirkhani, H. Bibliometrics of sentiment analysis literature. J. Inf. Sci. 2019, 45, 3–15. [Google Scholar] [CrossRef]
- Rhanoui, M.; Mikram, M.; Yousfi, S.; Barzali, S. A CNN-BiLSTM model for document-level sentiment analysis. Mach. Learn. Knowl. Extr. 2019, 1, 832–847. [Google Scholar] [CrossRef]
- Chen, T.; Xu, R.; He, Y.; Wang, X. Improving sentiment analysis via sentence type classification using BiLSTM-CRF and CNN. Expert Syst. Appl. 2017, 72, 221–230. [Google Scholar] [CrossRef]
- Ding, Y.G.; Li, S.J.; Fu, X.; Liu, M.J. Temporal-aware multi-category products recommendation model based on aspect-level sentiment analysis. J. Electron. Inf. Technol. 2018, 40, 1453–1460. [Google Scholar] [CrossRef]
- Li, Z.; Fan, Y.; Jiang, B.; Lei, T.; Liu, W. A survey on sentiment analysis and opinion mining for social multimedia. Multimed. Tools Appl. 2019, 78, 6939–6967. [Google Scholar] [CrossRef]
- Anastasiei, B.; Dospinescu, N.; Dospinescu, O. The impact of social media peer communication on customer behaviour-evidence from romania. Argum. Oeconomica 2022, 48, 247–264. [Google Scholar] [CrossRef]
- Kauffmann, E.; Peral, J.; Gil, D.; Ferrández, A.; Sellers, R.; Mora, H. Managing marketing decision-making with sentiment analysis: An evaluation of the main product features using text data mining. Sustainability 2019, 11, 4235. [Google Scholar] [CrossRef]
- Meng, Y.; Yang, N.; Qian, Z.; Zhang, G. What makes an online review more helpful: An interpretation framework using XGBoost and SHAP values. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 466–490. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, Y.x.; Fan, L.w.; Li, Y.h. Customized ranking for products through online reviews: A method incorporating prospect theory with an improved VIKOR. Appl. Intell. 2020, 50, 1725–1744. [Google Scholar] [CrossRef]
- Liu, Y.; Bi, J.W.; Fan, Z.P. A method for ranking products through online reviews based on sentiment classification and interval-valued intuitionistic fuzzy TOPSIS. Int. J. Inf. Technol. Decis. Mak. 2017, 16, 1497–1522. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Wang, F.; Jia, X.; Rui, G. Applying BERT to analyze investor sentiment in stock market. Neural Comput. Appl. 2020, 33, 4663–4676. [Google Scholar] [CrossRef]
- Khoo, C.S.G.; Johnkhan, S.B. Lexicon-based sentiment analysis: Comparative evaluation of six sentiment lexicons. J. Inf. Sci. 2018, 44, 491–511. [Google Scholar] [CrossRef]
- Najmi, E.; Hashmi, K.; Malik, Z.; Rezgui, A.; Khan, H.U. CAPRA: A comprehensive approach to product ranking using customer reviews. Computing 2015, 97, 843–867. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, D. Ranking products with IF-based sentiment word framework and TODIM method. Kybernetes 2019, 48, 990–1010. [Google Scholar] [CrossRef]
- Chen, K.; Kou, G.; Shang, J.; Chen, Y. Visualizing market structure through online product reviews: Integrate topic modeling, TOPSIS, and multi-dimensional scaling approaches. Electron. Commer. Res. Appl. 2015, 14, 58–74. [Google Scholar] [CrossRef]
- Peng, Y.; Kou, G.; Li, J. A fuzzy PROMETHEE approach for mining customer reviews in Chinese. Arab. J. Sci. Eng. 2014, 39, 5245–5252. [Google Scholar] [CrossRef]
- Mahdiraji, H.A.; Kazimieras Zavadskas, E.; Kazeminia, A.; Abbasi Kamardi, A. Marketing strategies evaluation based on big data analysis: A CLUSTERING-MCDM approach. Econ. Res.-Ekon. Istraživanja 2019, 32, 2882–2898. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Xu, Z.S.; Xia, M.M. Induced generalized intuitionistic fuzzy operators. Knowl. Based Syst. 2011, 24, 197–209. [Google Scholar] [CrossRef]
- Xu, Y.J.; Zhu, X.T.; Wen, X.W.; Herrera-Viedma, E. Fuzzy best-worst method and its application in initial water rights allocation. Appl. Soft Comput. 2021, 101, 107007. [Google Scholar] [CrossRef]
- Jeppesen, L.B.; Frederiksen, L. Why do users contribute to firm-hosted user communities? The case of computer-controlled music instruments. Organ. Sci. 2006, 17, 45–63. [Google Scholar] [CrossRef]
- Bujang, M.A.; Omar, E.D.; Baharum, N.A. A review on sample size determination for cronbach’s alpha test: A simple guide for researchers. Malays. J. Med. Sci. 2018, 25, 85–99. [Google Scholar] [CrossRef]
- Ah, K.H.; Song, H. Constructing sentiment lexicon for subject-specific sentiment analysis. Korean Linguist. 2021, 93, 83–110. [Google Scholar] [CrossRef]
- Liu, H.; Chen, X.; Liu, X.X. A study of the application of weight distributing method combining sentiment dictionary and TF-IDF for text sentiment analysis. IEEE Access 2022, 10, 32280–32289. [Google Scholar] [CrossRef]
- Sıcakyüz, Ç. Analyzing healthcare and wellness products’ Quality embedded in online customer reviews: Assessment with a hybrid fuzzy LMAW and fermatean fuzzy WASPAS method. Sustainability 2023, 15, 3428. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).