The Intersectoral Systemic Risk Shock of Emergency Crisis Events in China’s Financial Market: Nonparametric Methods and Panel Event Study Analyses
Abstract
1. Introduction
2. Methodology and Estimation Framework
2.1. Specification of Sectoral Systemic Risk
2.2. Estimation Framework of Sectoral Systemic Risk
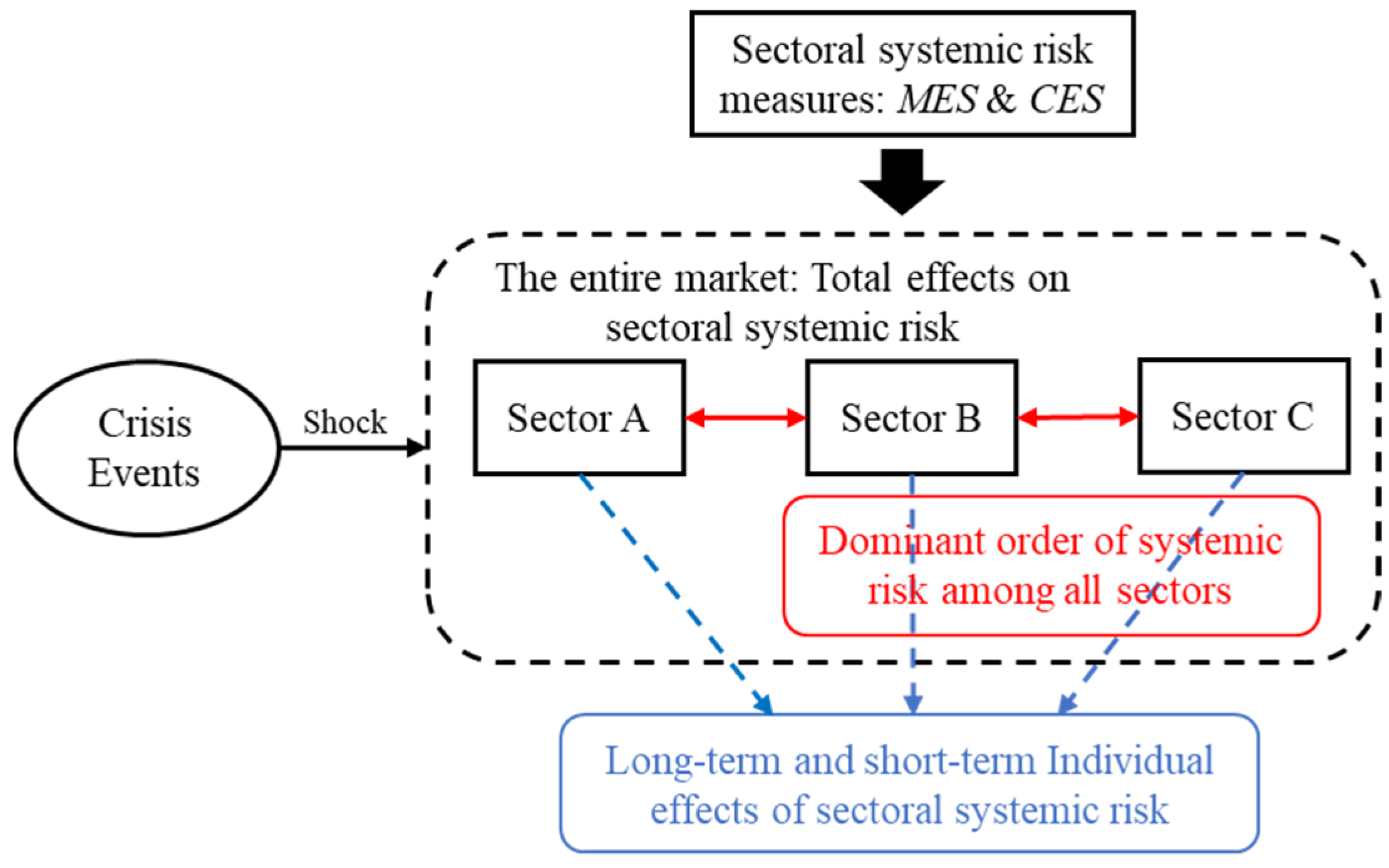
2.3. Testing the Total and Individual Effects of Crisis Events on Sectoral Systemic Risk
2.4. Data and Variables
3. Empirical Results and Analyses
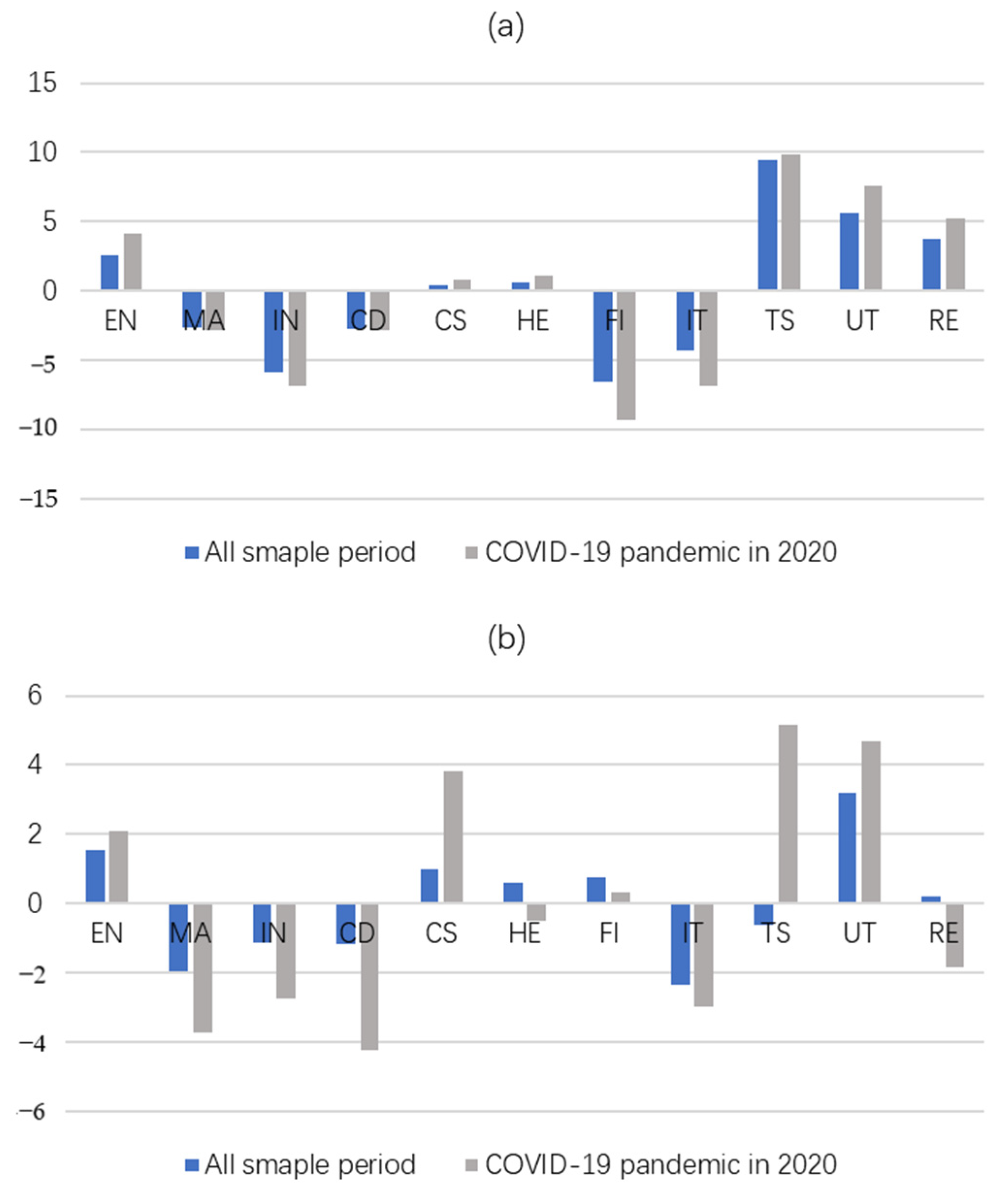
3.1. The Average Effects of Sectoral Systemic Risk during Crisis Periods
3.2. The Total Effects of Crisis Events on Sectoral Systemic Risk
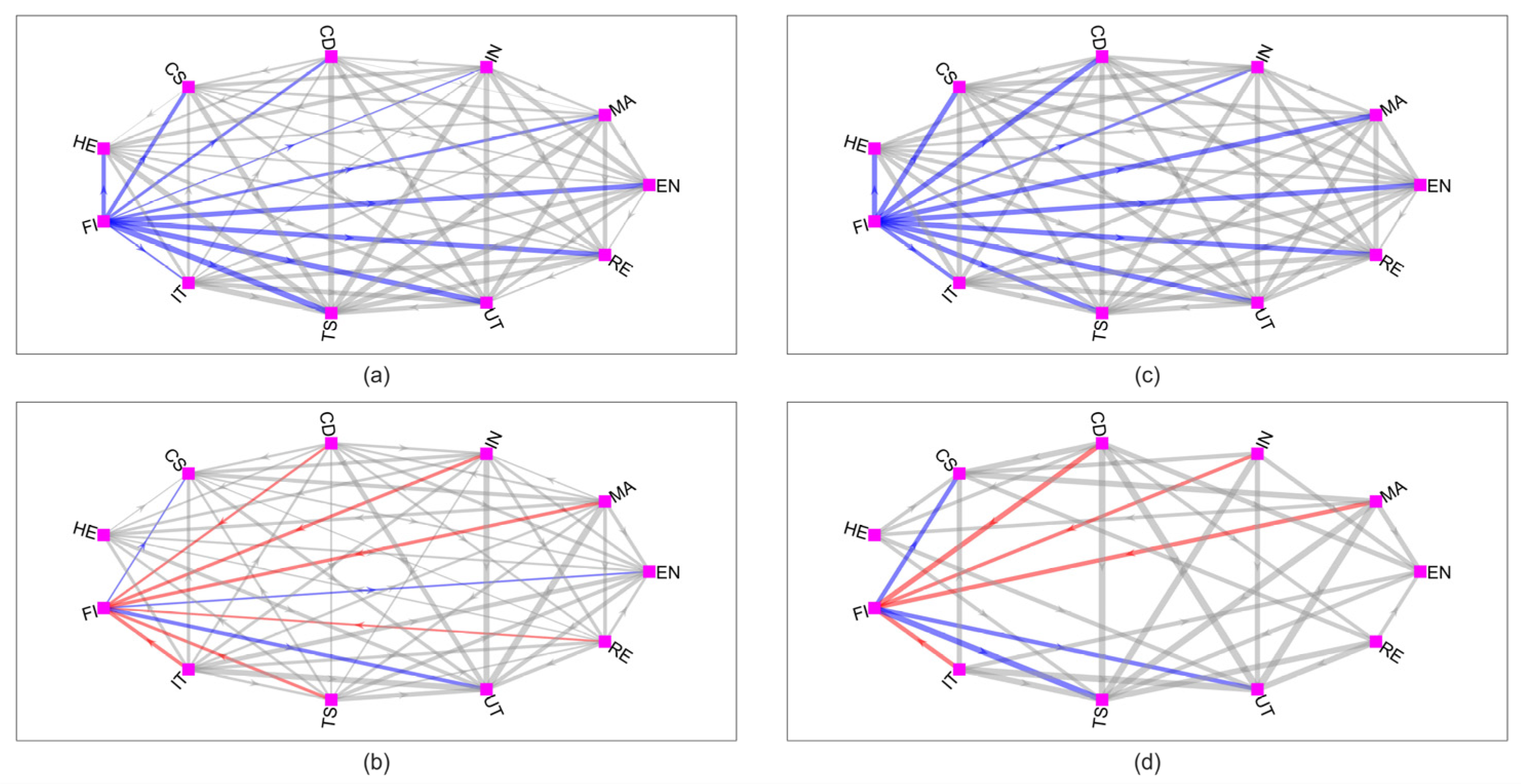
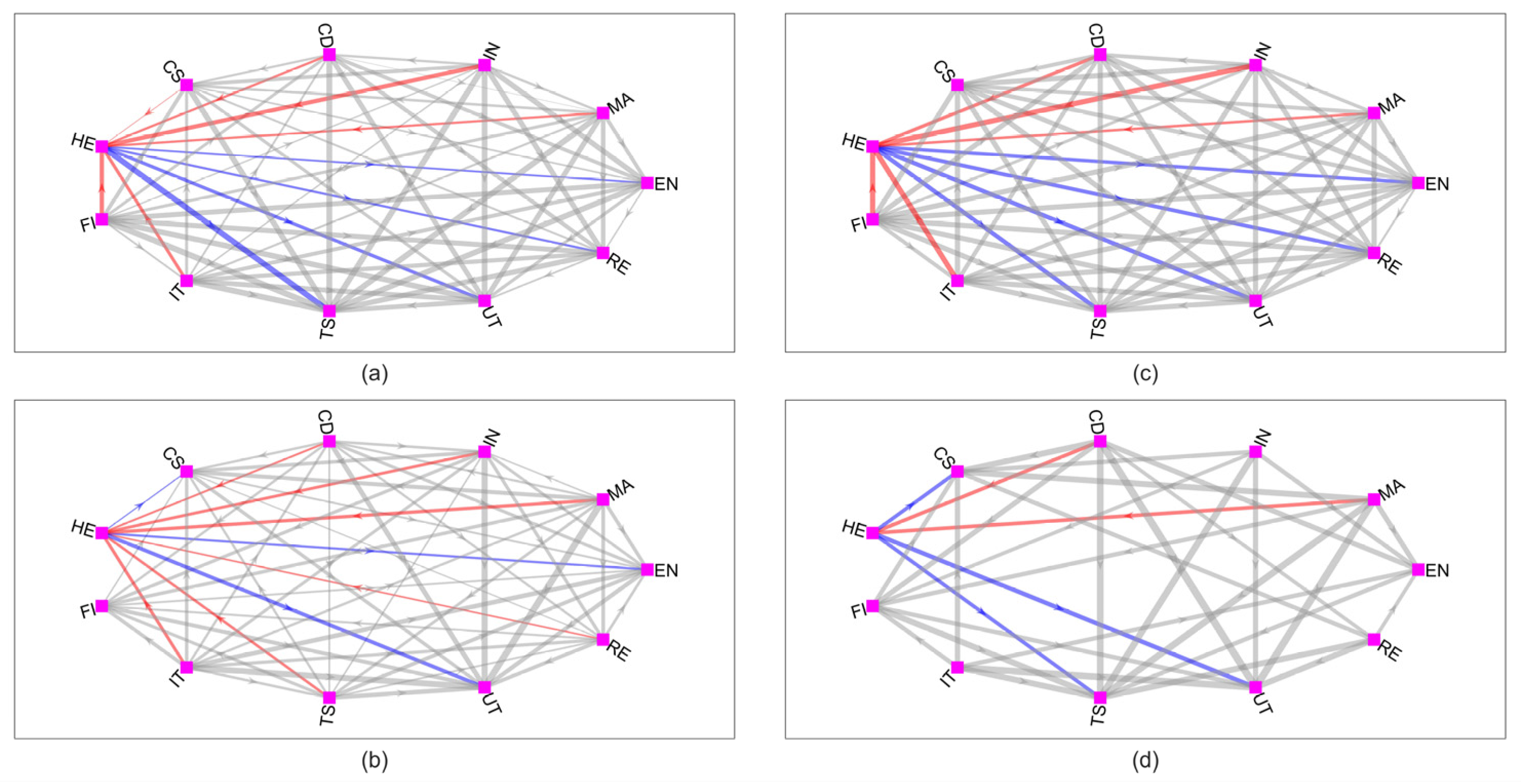
3.3. The Individual Effects of Crisis Events on Sectoral Systemic Risk
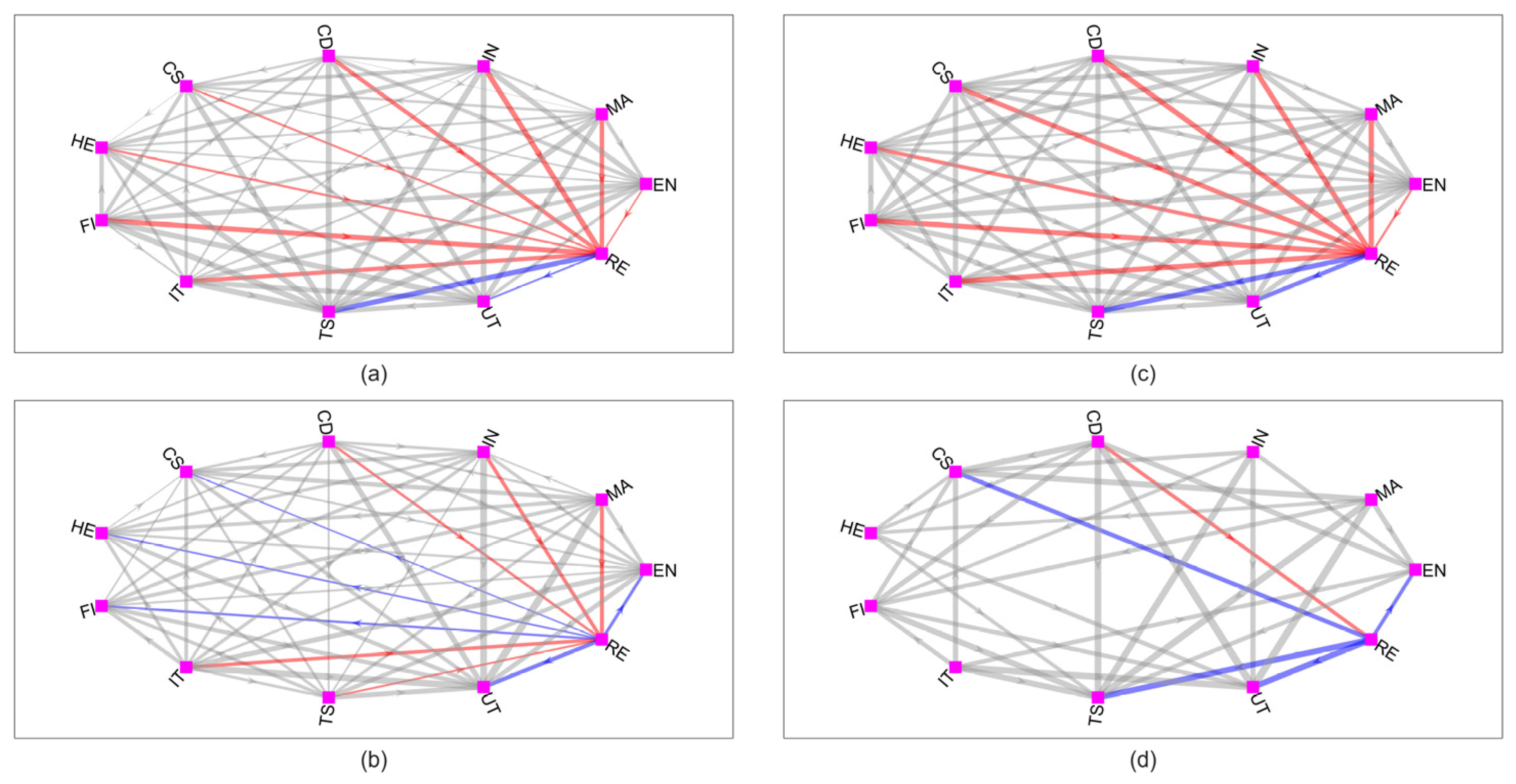
3.4. The Dominant Order of Sectoral Systemic Risk during the COVID-19 Crisis
4. Conclusions and Implications
4.1. Main Conclusions
4.2. Implications
4.3. Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
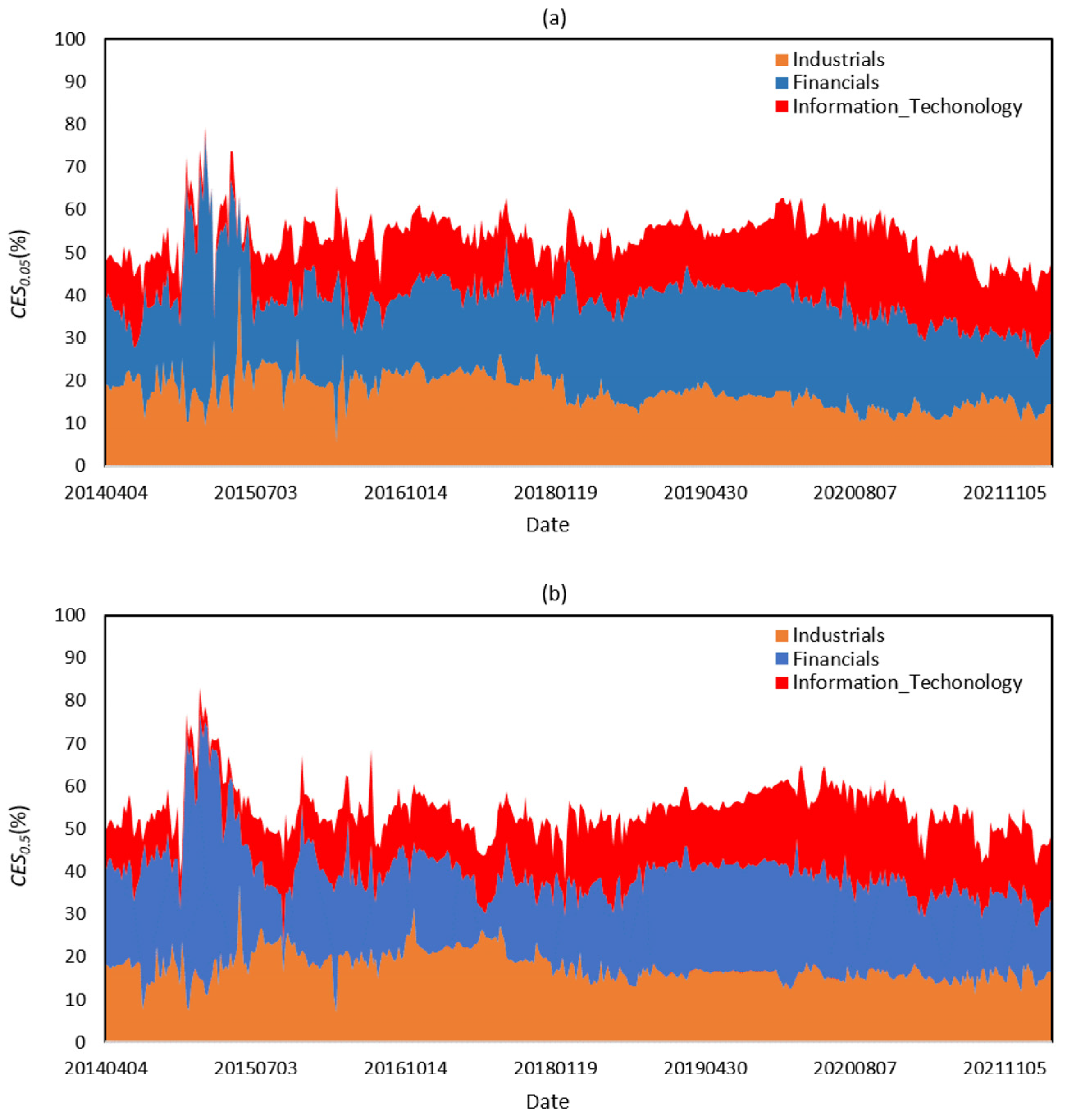

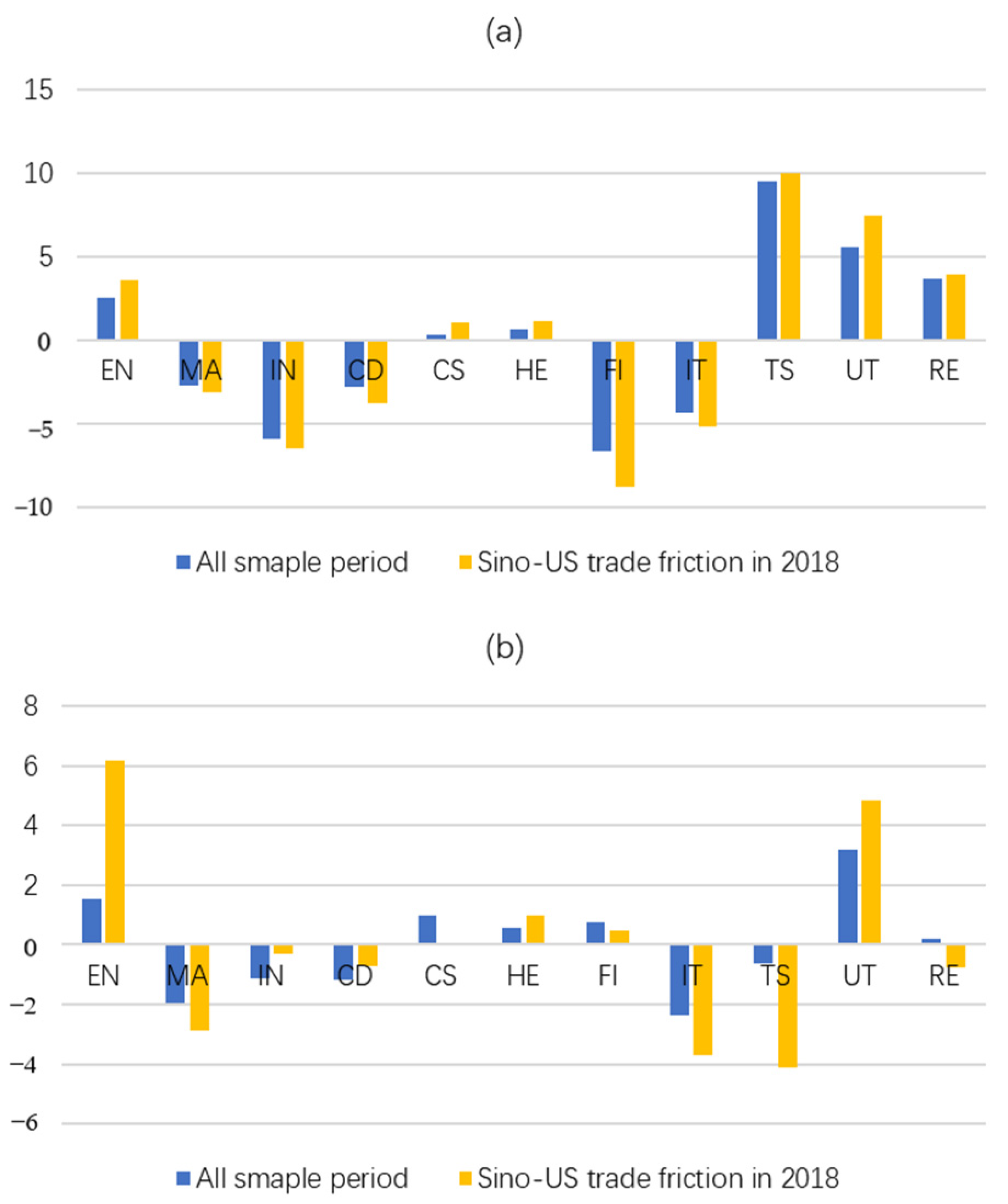
| Panel A: CES0.05 | ||||||||
|---|---|---|---|---|---|---|---|---|
| All Period | Period I | Period II | Period III | |||||
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | |
| Energy | 0.045 | 0.032 | 0.111 | 0.046 | 0.043 | 0.005 | 0.039 | 0.010 |
| Materials | 0.091 | 0.048 | 0.194 | 0.082 | 0.083 | 0.020 | 0.108 | 0.027 |
| Industrials | 0.149 2 | 0.093 2 | 0.385 1 | 0.148 1 | 0.122 2 | 0.034 2 | 0.176 3 | 0.042 3 |
| Consumer_ Discretionary | 0.088 | 0.053 | 0.218 3 | 0.079 | 0.084 | 0.027 | 0.103 | 0.019 |
| Consumer_ Staples | 0.051 | 0.031 | 0.078 | 0.026 | 0.042 | 0.020 | 0.071 | 0.020 |
| Healthcare | 0.049 | 0.027 | 0.089 | 0.033 | 0.053 | 0.021 | 0.055 | 0.032 |
| Financials | 0.185 1 | 0.097 1 | 0.303 2 | 0.084 2 | 0.156 1 | 0.037 1 | 0.242 1 | 0.048 1 |
| Information_ Technology | 0.118 3 | 0.062 3 | 0.217 | 0.083 3 | 0.113 3 | 0.030 3 | 0.185 2 | 0.048 2 |
| Telecom_ Service | 0.003 | 0.002 | 0.007 | 0.003 | 0.003 | 0.001 | 0.005 | 0.001 |
| Utilities | 0.020 | 0.017 | 0.064 | 0.024 | 0.017 | 0.004 | 0.020 | 0.003 |
| Real Estate | 0.032 | 0.024 | 0.088 | 0.026 | 0.037 | 0.022 | 0.033 | 0.011 |
| Panel B: MES0.05 | ||||||||
| All Period | Period I | Period II | Period III | |||||
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | |
| Energy | 0.748 | 0.402 | 1.586 | 0.572 | 0.666 | 0.055 | 0.951 | 0.247 |
| Materials | 0.926 2 | 0.507 | 2.056 | 0.871 2 | 0.860 | 0.216 | 1.220 1 | 0.305 3 |
| Industrials | 0.896 3 | 0.501 | 2.107 2 | 0.799 3 | 0.757 | 0.217 | 1.145 3 | 0.264 |
| Consumer_ Discretionary | 0.848 | 0.484 | 1.963 | 0.754 | 0.786 | 0.248 | 1.144 | 0.219 |
| Consumer_ Staples | 0.721 | 0.425 | 1.631 | 0.576 | 0.653 | 0.313 | 0.844 | 0.245 |
| Healthcare | 0.769 | 0.464 | 1.809 | 0.695 | 0.786 | 0.309 3 | 0.698 | 0.408 1 |
| Financials | 0.730 | 0.330 | 1.142 | 0.306 | 0.598 | 0.115 | 0.964 | 0.187 |
| Information_ Technology | 1.024 1 | 0.599 1 | 2.316 1 | 1.017 1 | 1.056 1 | 0.276 | 1.203 2 | 0.304 |
| Telecom_ Service | 0.888 | 0.528 3 | 1.842 | 0.690 | 0.954 3 | 0.347 2 | 1.128 | 0.281 |
| Utilities | 0.610 | 0.432 | 1.693 | 0.586 | 0.565 | 0.145 | 0.742 | 0.126 |
| Real Estate | 0.877 | 0.532 2 | 2.064 3 | 0.638 | 0.959 2 | 0.545 1 | 1.074 | 0.339 2 |
| Sectoral Systemic Risk CES0.05 | Sectoral Systemic Risk MES0.05 | |||||
|---|---|---|---|---|---|---|
| Event I | Event II | Event III | Event I | Event II | Event III | |
| Lead10 | −0.163 (0.257) | 0.037 ** (0.038) | 0.037 ** (0.041) | −0.845 (0.238) | 0.552 ** (0.016) | 0.351 * (0.056) |
| Lead9 | −0.223 (0.158) | 0.028 (0.129) | 0.045 ** (0.027) | −1.790 ** (0.044) | 0.309 (0.101) | 0.375 ** (0.046) |
| Lead8 | −0.254 * (0.062) | 0.042 * (0.094) | 0.015 (0.273) | −2.088 *** (0.007) | 0.732 ** (0.030) | 0.019 (0.883) |
| Lead7 | −0.203 (0.103) | 0.011 (0.509) | 0.017 (0.176) | −1.678 ** (0.023) | 0.334 (0.152) | 0.025 (0.844) |
| Lead6 | −0.105 (0.336) | −0.003 (0.884) | 0.013 (0.338) | −0.695 (0.304) | 0.214 (0.416) | 0.034 (0.777) |
| Lead5 | 0.057 (0.655) | 0.010 (0.690) | 0.011 (0.374) | 0.737 (0.400) | 0.328 (0.196) | 0.085 (0.500) |
| Lead4 | −0.117 (0.150) | 0.005 (0.776) | 0.012 (0.450) | −0.591 (0.115) | 0.164 (0.346) | 0.029 (0.847) |
| Lead3 | −0.076 (0.258) | 0.007 (0.526) | 0.010 (0.476) | −0.477 (0.131) | 0.076 (0.619) | 0.186 (0.280) |
| Lead2 | −0.061 (0.108) | 0.025 (0.140) | 0.009 (0.511) | −0.323 (0.149) | 0.363 * (0.094) | 0.171 (0.258) |
| Lag0 | 0.221 ** (0.039) | 0.038 * (0.067) | −0.005 (0.800) | 2.486 ** (0.015) | 0.236 * (0.059) | 0.007 (0.971) |
| Lag1 | 0.359 *** (0.006) | 0.106 ** (0.014) | −0.048 * (0.085) | 4.378 *** (0.001) | 1.095 *** (0.000) | −0.433 * (0.075) |
| Lag2 | −0.079 (0.639) | 0.075 * (0.078) | −0.060 * (0.062) | 0.079 (0.954) | 0.771 ** (0.037) | −0.670 ** (0.025) |
| Lag3 | 0.232 * (0.072) | 0.075 * (0.055) | 0.009 (0.388) | 3.809 *** (0.001) | 1.002 ** (0.027) | −0.057 (0.723) |
| Lag4 | 0.210 * (0.077) | 0.054 * (0.095) | 0.019 (0.345) | 3.822 *** (0.000) | 0.549 ** (0.011) | −0.013 (0.955) |
| Lag5 | 0.287 ** (0.033) | 0.023 (0.427) | 0.029 (0.324) | 4.292 *** (0.000) | 0.246 (0.251) | 0.311 (0.291) |
| Lag6 | 0.127 (0.316) | 0.049 (0.154) | 0.060 * (0.050) | 1.929 (0.102) | 0.227 (0.169) | 0.569 * (0.084) |
| Lag7 | 0.219 * (0.075) | 0.130 ** (0.014) | 0.086 ** (0.013) | 3.395 *** (0.001) | 1.464 ** (0.019) | 0.852 ** (0.015) |
| Lag8 | 0.194 * (0.097) | 0.098 * (0.060) | 0.024 (0.247) | 3.113 *** (0.001) | 0.679 * (0.056) | 0.159 (0.550) |
| Lag9 | −0.039 (0.758) | 0.117 ** (0.042) | 0.003 (0.893) | 0.153 (0.896) | 1.142 ** (0.033) | −0.089 (0.714) |
| Lag10 | 0.049 (0.756) | 0.103 * (0.099) | −0.011 (0.601) | 1.094 (0.371) | 0.778 * (0.064) | −0.169 (0.478) |
| Period I: A-Share Market Crash in 2015 () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 0.471 *** (0.000) | 0.853 *** (0.000) | 0.559 *** (0.000) | 0.059 (0.882) | 0.147 (0.454) | 0.853 *** (0.000) | 0.588 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.118 (0.604) | |
| MA | 0.000 (1.000) | 0.500 *** (0.000) | 0.265 * (0.077) | 0.000 (1.000) | 0.000 (1.000) | 0.500 *** (0.000) | 0.265 * (0.077) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IN | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.118 (0.604) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CD | 0.000 (1.000) | 0.000 (1.000) | 0.500 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.471 *** (0.000) | 0.118 (0.604) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CS | 0.382 *** (0.005) | 0.676 *** (0.000) | 0.971 *** (0.000) | 0.794 *** (0.000) | 0.235 (0.133) | 0.971 *** (0.000) | 0.794 *** (0.000) | 0.000 (1.000) | 0.029 (0.969) | 0.294 ** (0.043) | |
| HE | 0.353 ** (0.011) | 0.647 *** (0.000) | 0.912 *** (0.000) | 0.764 *** (0.000) | 0.059 (0.882) | 0.912 *** (0.000) | 0.029 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.088 (0.753) | |
| FI | 0.000 (1.000) | 0.029 (0.969) | 0.324 ** (0.022) | 0.029 (0.969) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (0.969) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IT | 0.000 (1.000) | 0.088 (0.753) | 0.500 *** (0.000) | 0.147 (0.454) | 0.000 (1.000) | 0.000 (1.000) | 0.588 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| TS | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.971 *** (0.000) | 1.000 *** (0.000) | |
| UT | 0.412 *** (0.002) | 0.676 *** (0.000) | 1.000 *** (0.000) | 0.882 *** (0.000) | 0.206 (0.213) | 0.382 *** (0.005) | 0.971 *** (0.000) | 0.882 *** (0.000) | 0.000 (1.000) | 0.412 *** (0.002) | |
| RE | 0.382 *** (0.005) | 0.676 *** (0.000) | 0.971 *** (0.000) | 0.853 *** (0.000) | 0.118 (0.604) | 0.118 (0.604) | 0.941 *** (0.000) | 0.853 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | |
| Period II: Sino-US Trade Friction in 2018 () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 0.979 *** (0.000) | 1.000 *** (0.000) | 0.914 *** (0.000) | 0.553 *** (0.000) | 0.574 *** (0.000) | 1.000 *** (0.000) | 0.979 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.191 (0.161) | |
| MA | 0.000 (1.000) | 0.532 *** (0.000) | 0.298 ** (0.012) | 0.000 (1.000) | 0.000 (1.000) | 0.936 *** (0.000) | 0.426 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IN | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.511 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CD | 0.000 (1.000) | 0.149 (0.331) | 0.404 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.766 *** (0.000) | 0.255 ** (0.039) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CS | 0.085 (0.697) | 0.723 *** (0.000) | 0.894 *** (0.000) | 0.617 *** (0.000) | 0.064 (0.816) | 0.979 *** (0.000) | 0.745 *** (0.000) | 0.000 (1.000) | 0.000 (0.969) | 0.043 (0.914) | |
| HE | 0.191 (0.161) | 0.745 *** (0.000) | 0.936 *** (0.000) | 0.617 *** (0.000) | 0.128 (0.441) | 0.979 *** (0.000) | 0.766 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.043 (0.914) | |
| FI | 0.000 (1.000) | 0.000 (1.000) | 0.021 (0.978) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IT | 0.000 (1.000) | 0.021 (0.978) | 0.255 ** (0.039) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.617 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| TS | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | |
| UT | 0.979 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.894 *** (0.000) | 0.915 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.000 (1.000) | 0.702 *** (0.000) | |
| RE | 0.447 *** (0.000) | 0.851 *** (0.000) | 0.936 *** (0.000) | 0.766 *** (0.000) | 0.447 *** (0.000) | 0.426 *** (0.000) | 0.957 *** (0.000) | 0.851 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | |
| Period I: A-Share Market Crash in 2015 () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 0.294 ** (0.043) | 0.353 ** (0.011) | 0.324 ** (0.022) | 0.176 (0.321) | 0.294 ** (0.043) | 0.088 (0.753) | 0.412 *** (0.002) | 0.235 (0.133) | 0.265 * (0.078) | 0.441 *** (0.001) | |
| MA | 0.000 (1.000) | 0.147 (0.455) | 0.117 (0.604) | 0.000 (1.000) | 0.088 (0.753) | 0.000 (1.000) | 0.206 (0.213) | 0.058 (0.882) | 0.088 (0.753) | 0.235 (0.133) | |
| IN | 0.000 (1.000) | 0.058 (0.882) | 0.088 (0.753) | 0.000 (1.000) | 0.059 (0.882) | 0.000 (1.000) | 0.176 (0.321) | 0.029 (0.969) | 0.029 (0.969) | 0.118 (0.604) | |
| CD | 0.000 (1.000) | 0.117 (0.604) | 0.147 (0.455) | 0.000 (1.000) | 0.118 (0.604) | 0.000 (1.000) | 0.206 (0.213) | 0.058 (0.882) | 0.058 (0.882) | 0.206 (0.213) | |
| CS | 0.058 (0.881) | 0.264 * (0.078) | 0.265 * (0.078) | 0.265 * (0.078) | 0.206 (0.213) | 0.088 (0.753) | 0.324 ** (0.022) | 0.176 (0.321) | 0.206 (0.213) | 0.324 ** (0.022) | |
| HE | 0.088 (0.753) | 0.235 (0.133) | 0.235 (0.133) | 0.265 * (0.078) | 0.117 (0.604) | 0.000 (1.000) | 0.324 ** (0.022) | 0.088 (0.753) | 0.176 (0.321) | 0.206 (0.213) | |
| FI | 0.382 *** (0.005) | 0.588 *** (0.000) | 0.588 *** (0.000) | 0.559 *** (0.000) | 0.441 *** (0.001) | 0.500 *** (0.000) | 0.647 *** (0.000) | 0.500 *** (0.000) | 0.382 *** (0.005) | 0.559 *** (0.000) | |
| IT | 0.000 (1.000) | 0.059 (0.882) | 0.059 (0.882) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.059 (0.882) | |
| TS | 0.088 (0.753) | 0.264 * (0.078) | 0.264 * (0.078) | 0.206 (0.213) | 0.088 (0.213) | 0.147 (0.455) | 0.059 (0.882) | 0.294 ** (0.043) | 0.176 (0.321) | 0.206 (0.213) | |
| UT | 0.029 (0.969) | 0.206 (0.213) | 0.235 (0.133) | 0.206 (0.213) | 0.088 (0.213) | 0.176 (0.321) | 0.000 (1.000) | 0.294 ** (0.043) | 0.147 (0.454) | 0.235 (0.133) | |
| RE | 0.000 (1.000) | 0.176 (0.321) | 0.147 (0.455) | 0.117 (0.604) | 0.000 (0.604) | 0.058 (0.882) | 0.000 (1.000) | 0.206 (0.213) | 0.058 (0.882) | 0.088 (0.753) | |
| Period II: Sino-US Trade Friction in 2018 () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 0.894 *** (0.000) | 0.574 *** (0.000) | 0.659 *** (0.000) | 0.596 *** (0.000) | 0.553 *** (0.000) | 0.638 *** (0.000) | 0.872 *** (0.000) | 0.894 *** (0.000) | 0.277 ** (0.022) | 0.617 *** (0.001) | |
| MA | 0.000 (1.000) | 0.043 (0.914) | 0.191 (0.161) | 0.106 (0.569) | 0.064 (0.816) | 0.000 (1.000) | 0.319 *** (0.006) | 0.234 * (0.065) | 0.000 (1.000) | 0.213 (0.105) | |
| IN | 0.000 (1.000) | 0.340 *** (0.003) | 0.191 (0.161) | 0.085 (0.697) | 0.064 (0.816) | 0.085 (0.697) | 0.319 *** (0.006) | 0.362 *** (0.002) | 0.000 (1.000) | 0.191 (0.161) | |
| CD | 0.085 (0.697) | 0.255 ** (0.039) | 0.106 (0.569) | 0.021 (0.978) | 0.043 (0.914) | 0.106 (0.569) | 0.234 * (0.065) | 0.255 ** (0.039) | 0.021 (0.978) | 0.149 (0.331) | |
| CS | 0.128 (0.443) | 0.319 *** (0.006) | 0.170 (0.236) | 0.170 (0.236) | 0.043 (0.914) | 0.149 (0.331) | 0.277 ** (0.022) | 0.383 *** (0.000) | 0.021 (0.978) | 0.170 (0.236) | |
| HE | 0.213 (0.105) | 0.362 *** (0.002) | 0.277 ** (0.022) | 0.191 (0.161) | 0.128 (0.443) | 0.255 ** (0.039) | 0.340 *** (0.003) | 0.404 *** (0.000) | 0.064 (0.816) | 0.255 ** (0.038) | |
| FI | 0.043 (0.914) | 0.340 *** (0.003) | 0.170 (0.236) | 0.298 ** (0.012) | 0.170 (0.234) | 0.128 (0.443) | 0.404 *** (0.000) | 0.489 *** (0.000) | 0.021 (0.978) | 0.298 ** (0.012) | |
| IT | 0.000 (1.000) | 0.043 (0.914) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.149 (0.331) | 0.000 (1.000) | 0.064 (0.816) | |
| TS | 0.000 (1.000) | 0.021 (0.977) | 0.000 (1.000) | 0.043 (0.914) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.191 (0.161) | 0.000 (1.000) | 0.127 (0.443) | |
| UT | 0.426 *** (0.000) | 0.638 *** (0.000) | 0.489 *** (0.000) | 0.489 *** (0.000) | 0.404 *** (0.000) | 0.383 *** (0.000) | 0.447 *** (0.000) | 0.617 *** (0.000) | 0.744 *** (0.000) | 0.489 *** (0.000) | |
| RE | 0.000 (1.000) | 0.277 ** (0.022) | 0.043 (0.914) | 0.106 (0.569) | 0.043 (0.914) | 0.000 (1.000) | 0.085 (0.697) | 0.298 ** (0.012) | 0.340 *** (0.003) | 0.000 (1.000) | |
References
- Acemoglu, D.; Ozdaglar, A.; Tahbaz-Salehi, A. Systemic Risk and Stability in Financial Networks. Am. Econ. Rev. 2015, 105, 564–608. [Google Scholar] [CrossRef]
- Huang, C.X.; Deng, Y.K.; Yang, X.; Yang, X.G.; Cao, J.D. Can financial crisis be detected? Laplacian energy measure. Eur. J. Financ. 2022, in press. [Google Scholar] [CrossRef]
- Pan, Q.X.; Mei, X.W.; Gao, T.Q. Modeling dynamic conditional correlations with leverage effects and volatility spillover effects: Evidence from the Chinese and US stock markets affected by the recent trade friction. N. Am. J. Econ. Financ. 2022, 59, 101591. [Google Scholar] [CrossRef]
- Huang, C.X.; Liu, S.J.; Yang, X.G.; Yang, X. Identification of crisis in the Chinese stock market based on complex network. Appl. Econ. Lett. 2022, in press. [Google Scholar] [CrossRef]
- Liu, D.H.; Gu, H.M.; Xing, T.C. The meltdown of the Chinese equity market in the summer of 2015. Int. Rev. Econ. Financ. 2016, 45, 504–517. [Google Scholar] [CrossRef]
- Fang, L.B.; Sun, B.Y.; Li, H.J.; Yu, H.H. Systemic risk network of Chinese financial institutions. Emerg. Mark. Rev. 2018, 35, 190–206. [Google Scholar] [CrossRef]
- Xu, G.X.; Gao, W.F. Financial Risk Contagion in Stock Markets: Causality and Measurement Aspects. Sustainability 2019, 11, 296. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhuang, X.T.; Wang, J.; Zhang, W.P. Analysis of the impact of Sino-US trade friction on China’s stock market based on complex networks. N. Am. J. Econ. Financ. 2020, 52, 101185. [Google Scholar] [CrossRef]
- Altig, D.; Baker, S.; Barrero, J.M.; Bloom, N.; Bunn, P.; Chen, S.; Davis, S.J.; Leather, J.; Meyer, B.; Mihaylov, E.; et al. Economic uncertainty before and during the COVID-19 pandemic. J. Public Econ. 2020, 191, 104274. [Google Scholar] [CrossRef]
- Grundke, P.; Tuchscherer, M. Global systemic risk measures and their forecasting power for systemic events. Eur. J. Financ. 2019, 25, 205–233. [Google Scholar] [CrossRef]
- Avramidis, P.; Pasiouras, F. Calculating systemic risk capital: A factor model approach. J. Financ. Stab. 2015, 16, 138–150. [Google Scholar] [CrossRef]
- Zhang, D.Y.; Hu, M.; Ji, Q. Financial markets under the global pandemic of COVID-19. Financ. Res. Lett. 2020, 36, 101528. [Google Scholar] [CrossRef]
- Guo, Y.H.; Li, P.; Li, A.H. Tail risk contagion between international financial markets during COVID-19 pandemic. Int. Rev. Financ. Anal. 2021, 73, 101649. [Google Scholar] [CrossRef]
- Samitas, A.; Kampouris, E.; Polyzos, S. COVID-19 pandemic and spillover effects in stock markets: A financial network approach. Int. Rev. Financ. Anal. 2022, 80, 102005. [Google Scholar] [CrossRef]
- Liu, S.T.; Xu, Q.F.; Jiang, C.X. Systemic risk of China’s commercial banks during financial turmoils in 2010–2020: A MIDAS-QR based CoVaR approach. Appl. Econ. Lett. 2021, 28, 1600–1609. [Google Scholar] [CrossRef]
- Cincinelli, P.; Pellini, E.; Urga, G. Systemic risk in the Chinese financial system: A panel Granger causality analysis. Int. Rev. Financ. Anal. 2022, 82, 102179. [Google Scholar] [CrossRef]
- So, M.K.P.; Chu, A.M.Y.; Chan, T.W.C. Impacts of the COVID-19 pandemic on financial market connectedness. Financ. Res. Lett. 2021, 38, 101864. [Google Scholar] [CrossRef]
- Lai, Y.J.; Hu, Y.B. A study of systemic risk of global stock markets under COVID-19 based on complex financial networks. Phys. A 2021, 566, 125613. [Google Scholar] [CrossRef]
- Kanno, M. Risk contagion of COVID-19 in Japanese firms: A network approach. Res. Int. Bus. Financ. 2021, 58, 101491. [Google Scholar] [CrossRef]
- Dai, Z.F.; Peng, Y.X. Economic policy uncertainty and stock market sector time-varying spillover effect: Evidence from China. N. Am. J. Econ. Financ. 2022, 62, 101745. [Google Scholar] [CrossRef]
- Aloui, R.; Ben Jabeur, S.; Mefteh-Wali, S. Tail-risk spillovers from China to G7 stock market returns during the COVID-19 outbreak: A market and sectoral analysis. Res. Int. Bus. Financ. 2022, 62, 101709. [Google Scholar] [CrossRef] [PubMed]
- Costa, A.; Matos, P.; Da Silva, C. Sectoral connectedness: New evidence from US stock market during COVID-19 pandemics. Financ. Res. Lett 2022, 45, 102124. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.Y. Dynamic volatility spillovers between industries in the US stock market: Evidence from the COVID-19 pandemic and Black Monday. N. Am. J. Econ. Financ. 2022, 59, 101614. [Google Scholar] [CrossRef]
- Alomari, M.; Al Rababa’A, A.R.; Rehman, M.U.; Power, D.M. Infectious diseases tracking and sectoral stock market returns: A quantile regression analysis. N. Am. J. Econ. Financ. 2022, 59, 101584. [Google Scholar] [CrossRef]
- Nguyen, K.H. A coronavirus outbreak and sector stock returns: A tale from the first ten weeks of 2020. Appl. Econ. Lett. 2022, 29, 1730–1740. [Google Scholar] [CrossRef]
- Acharya, V.; Engle, R.; Richardson, M. Capital Shortfall: A New Approach to Ranking and Regulating Systemic Risks. Am. Econ. Rev. 2012, 102, 59–64. [Google Scholar] [CrossRef]
- Banulescu, G.D.; Durnitrescu, E.I. Which are the SIFIs? A Component Expected Shortfall approach to systemic risk. J. Bank Financ. 2015, 50, 575–588. [Google Scholar] [CrossRef]
- Harjoto, M.A.; Rossi, F.; Paglia, J.K. COVID-19: Stock market reactions to the shock and the stimulus. Appl. Econ. Lett. 2021, 28, 795–801. [Google Scholar] [CrossRef]
- He, P.L.; Sun, Y.L.; Zhang, Y.; Li, T. COVID-19’s Impact on Stock Prices Across Different Sectors—An Event Study Based on the Chinese Stock Market. Emerg. Mark Financ. Trade 2020, 56, 2198–2212. [Google Scholar] [CrossRef]
- Liu, J.X.; Cheng, Y.N.; Zhou, Y.F.; Li, X.Q.; Kang, H.Y.; Sriboonchitta, S. Systemic Risk Contribution and Contagion of Industrial Sectors in China: From the Global Financial Crisis to the COVID-19 Pandemic. J. Math. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Freyaldenhoven, S.; Hansen, C.; Shapiro, J.M. Pre-Event Trends in the Panel Event-Study Design. Am. Econ. Rev. 2019, 109, 3307–3338. [Google Scholar] [CrossRef]
- Ouyang, Z.S.; Chen, S.L.; Lai, Y.Z.; Yang, X.T. The correlations among COVID-19, the effect of public opinion, and the systemic risks of China’s financial industries. Phys. A 2022, 600, 127518. [Google Scholar] [CrossRef] [PubMed]
- Goodman-Bacon, A. Difference-in-differences with variation in treatment timing. J. Econ. 2021, 225, 254–277. [Google Scholar] [CrossRef]
- Tian, M.X.; Guo, F.; Niu, R. Risk spillover analysis of China’s financial sectors based on a new GARCH copula quantile regression model. N. Am. J. Econ. Financ. 2022, 63, 101817. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Hoang, T.H.V.; Bouri, E. From pandemic to systemic risk: Contagion in the US tourism sector. Curr. Issues Tour. 2022, 25, 34–40. [Google Scholar] [CrossRef]
- Zou, Z.H.; Wang, X.P. Research on the investment value of China’s medical sector in the context of COVID-19. Ekon. Istraz. 2023, 1, 614–633. [Google Scholar] [CrossRef]
- Ahnert, T.; Georg, C.P. Information contagion and systemic risk. J. Financ. Stab. 2018, 35, 159–171. [Google Scholar] [CrossRef]
- Morelli, D.; Vioto, D. Assessing the contribution of China’s financial sectors to systemic risk. J. Financ. Stab. 2020, 50, 100777. [Google Scholar] [CrossRef]
- Bernal, O.; Gnabo, J.Y.; Guilmin, G. Assessing the contribution of banks, insurance and other financial services to systemic risk. J. Bank Financ. 2014, 47, 270–287. [Google Scholar] [CrossRef]
- Wen, F.H.; Weng, K.Y.; Zhou, W.X. Measuring the contribution of Chinese financial institutions to systemic risk: An extended asymmetric CoVaR approach. Risk Manag. 2020, 22, 310–337. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Engle, R.F. Dynamic Conditional Beta. J. Financ. Econ. 2016, 14, 643–667. [Google Scholar] [CrossRef]
- Scaillet, O. Nonparametric estimation and sensitivity analysis of expected shortfall. Math. Financ. 2004, 14, 115–129. [Google Scholar] [CrossRef]
- Raftopoulou, A.; Giannakopoulos, N. Unemployment and health: A panel event study. Appl. Econ. Lett. 2022, in press. [Google Scholar] [CrossRef]
- Clarke, D.; Tapia-Schythe, K. Implementing the panel event study. Stat. J. 2021, 21, 853–884. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods, 3rd ed.; Wiley: New York, NY, USA, 2015; pp. 118–120. [Google Scholar]
- Abadie, A. Bootstrap tests for distributional treatment effects in instrumental variable models. J. Am. Stat. Assoc. 2002, 97, 284–292. [Google Scholar] [CrossRef]
- Tan, X.Y.; Ma, S.Q.; Wang, X.T.; Feng, C.; Xiang, L.J. The impact of the COVID-19 pandemic on the global dynamic spillover of financial market risk. Front. Public Health 2022, 10, 963620. [Google Scholar] [CrossRef]
- Tian, J.; Wang, X.X.; Wei, Y.Q. Does CSR performance improve corporate immunity to the COVID-19 pandemic? Evidence from China’s stock market. Front. Public Health 2022, 10, 956521. [Google Scholar] [CrossRef]
- Chen, N.; Jin, X. Industry risk transmission channels and the spillover effects of specific determinants in China’s stock market: A spatial econometrics approach. N. Am. J. Econ. Financ. 2020, 52, 101137. [Google Scholar] [CrossRef]
- Yang, H.F.; Liu, C.L.; Chou, R.Y. Bank diversification and systemic risk. Q Rev. Econ. Financ. 2020, 77, 311–326. [Google Scholar] [CrossRef]
- Amihud, Y.; Noh, J. Illiquidity and Stock Returns II: Cross-section and Time-series Effects. Rev. Financ. Stud. 2021, 34, 2101–2123. [Google Scholar] [CrossRef]
- Rehman, F.; Islam, M.M. Financial infrastructure—Total factor productivity (TFP) nexus within the purview of FDI outflow, trade openness, innovation, human capital and institutional quality: Evidence from BRICS economies. Appl. Econ. 2023, 55, 783–801. [Google Scholar] [CrossRef]
- Drakos, A.A.; Kouretas, G.P. Bank ownership, financial segments and the measurement of systemic risk: An application of CoVaR. Int. Rev. Econ. Financ. 2015, 40, 127–140. [Google Scholar] [CrossRef]
- Laeven, L.; Ratnovski, L.; Tong, H. Bank size, capital, and systemic risk: Some international evidence. J. Bank. Financ. 2016, 69, S25–S34. [Google Scholar] [CrossRef]
- Kamani, E.F. Revisiting the effects of banks’ size on systemic risk: The role of banking sector concentration in the European Banking Union. Appl. Econ. Lett. 2022, 29, 817–821. [Google Scholar] [CrossRef]
- Olabisi, M. Input-Output Linkages and Sectoral Volatility. Economica 2020, 87, 713–746. [Google Scholar] [CrossRef]
- Yin, K.; Liu, Z.; Jin, X. Interindustry volatility spillover effects in China’s stock market. Phys. A 2020, 539, 122936. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, D.; Zhang, Z. Connectedness and risk spillovers in China’s stock market: A sectoral analysis. Econ. Syst. 2019, 43, 100718. [Google Scholar] [CrossRef]
- Louhichi, W.; Saghi, N.; Srour, Z.; Viviani, J.L. The effect of liquidity creation on systemic risk: Evidence from European banking sector. Ann. Oper. Res. 2022, in press. [Google Scholar] [CrossRef]
- Zhang, W.P.; Zhuang, X.T.; Wang, J.; Lu, Y. Connectedness and systemic risk spillovers analysis of Chinese sectors based on tail risk network. N. Am. J. Econ. Financ. 2020, 54, 101248. [Google Scholar] [CrossRef]
- Rehman, F.; Sohag, K. Does transport infrastructure spur export diversification and sophistication in the G-20 economies? An application of CS-ARDL. Appl. Econ. Lett. 2023, in press. [Google Scholar] [CrossRef]
- International Labor Organization. Available online: https://www.ilo.org/global/topics/coronavirus/impacts-and-responses/WCMS_824092 (accessed on 30 January 2023).
- Mahmoud, A.B.; Reisel, W.D.; Fuxman, L.; Hack-Polay, D. Locus of control as a moderator of the effects of COVID-19 perceptions on job insecurity, psychosocial, organisational, and job outcomes for MENA region hospitality employees. Eur. Manag. Rev. 2022, 19, 313–332. [Google Scholar] [CrossRef]
- Deng, H.; Wu, W.B.; Zhang, Y.H.; Zhang, X.Y.; Ni, J. The Paradoxical Effects of COVID-19 Event Strength on Employee Turnover Intention. Int. J. Environ. Res. Public Health 2022, 19, 8434. [Google Scholar] [CrossRef]
- Wu, W.M.; Lee, C.C.; Xing, W.W.; Ho, S.J. The impact of the COVID-19 outbreak on Chinese-listed tourism stocks. Financ. Innov. 2021, 7, 22. [Google Scholar] [CrossRef]
- Liu, H.Y.; Wang, Y.L.; He, D.M.; Wang, C.Y. Short term response of Chinese stock markets to the outbreak of COVID-19. Appl. Econ. 2020, 52, 5859–5872. [Google Scholar] [CrossRef]
- Feng, S.; Huang, S.; Qi, Y.; Liu, X.; Sun, Q.; Wen, S. Network features of sector indexes spillover effects in China: A multi-scale view. Phys. A 2018, 496, 461–473. [Google Scholar] [CrossRef]
- Hoque, M.E.; Zaidi, M.A.S. The impacts of global economic policy uncertainty on stock market returns in regime switching environment: Evidence from sectoral perspectives. Int. J. Financ. Econ. 2019, 24, 991–1016. [Google Scholar] [CrossRef]
- Shen, Y.; Jiang, Z.; Ma, J.; Wang, G.; Zhou, W. Sector connectedness in the Chinese stock markets. Empir. Econ. 2021, 62, 825–852. [Google Scholar] [CrossRef]
- Egger, P.H.; Zhu, J. The US–Chinese trade war: An event study of stock-market responses. Econ. Policy 2020, 35, 519–559. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Niu, T. Two-Way Risk Spillover of Financial and Real Sectors in the Presence of Major Public Emergencies. Sustainability 2022, 14, 12571. [Google Scholar] [CrossRef]
- Mensi, W.; Hammoudeh, S.; Shahzad, S.J.H.; Shahbaz, M. Modeling systemic risk and dependence structure between oil and stock markets using a variational mode decomposition-based copula method. J. Bank. Financ. 2017, 75, 258–279. [Google Scholar] [CrossRef]
- Ji, Q.; Liu, B.Y.; Nehler, H.; Uddin, G.S. Uncertainties and extreme risk spillover in the energy markets: A time-varying copula-based CoVaR approach. Energy Econ. 2018, 76, 115–126. [Google Scholar] [CrossRef]
- Luo, C.Q.; Liu, L.; Wang, D. Multiscale financial risk contagion between international stock markets: Evidence from EMD-Copula-CoVaR analysis. N. Am. J. Econ. Financ. 2021, 58, 101512. [Google Scholar] [CrossRef]

| Mean | Max. | Min. | Stand. Dev. | Skewness | Kurtosis | J.B. Test | L.B. Q-Test | |
|---|---|---|---|---|---|---|---|---|
| Energy | 0.028 | 6.219 | −7.759 | 1.592 | −0.687 | 6.774 | 285.101 *** | 235.701 *** |
| Materials | 0.103 | 5.434 | −11.470 | 1.774 | −1.134 | 8.397 | 605.620 *** | 317.333 *** |
| Industrials | 0.071 | 5.220 | −11.135 | 1.714 | −1.245 | 9.522 | 861.130 *** | 363.099 *** |
| Consumer_ Discretionary | 0.056 | 5.109 | −9.316 | 1.640 | −1.135 | 8.044 | 540.778 *** | 415.668 *** |
| Consumer_ Staples | 0.136 | 4.560 | −8.704 | 1.579 | −1.106 | 6.812 | 343.353 *** | 165.745 *** |
| Healthcare | 0.086 | 5.663 | −7.218 | 1.653 | −0.763 | 5.833 | 182.998 *** | 340.142 *** |
| Financials | 0.083 | 6.878 | −5.882 | 1.461 | 0.094 | 5.785 | 137.714 *** | 112.688 *** |
| Information_ Technology | 0.095 | 7.668 | −10.040 | 2.057 | −0.807 | 6.715 | 289.910 *** | 474.665 *** |
| Telecom_ Service | 0.009 | 7.453 | −9.661 | 1.933 | −0.573 | 6.623 | 255.178 *** | 258.119 *** |
| Utilities | 0.064 | 5.127 | −11.948 | 1.488 | −1.576 | 14.531 | 252.480 *** | 172.600 *** |
| Real Estate | 0.065 | 5.916 | −9.520 | 1.786 | −0.660 | 6.208 | 212.681 *** | 233.441 *** |
| Variables | Descriptions | Measurements |
|---|---|---|
| Dependent variable | ||
| CES0.05/MES0.05 | The level of sectoral systemic risk | The approaches to Component Expected Shortfall and Marginal Expected Shortfall, which measure the magnitude of systemic risk, are shown in Section 2.1 |
| Explanatory variables | ||
| Lead/Lag | Temporal dummy variables | The binary variables indicate the given states in the pre-event or post-event periods |
| Control variables | ||
| Returns | Sectoral profitability | Total average return of sectoral index within one week |
| Volatility | Sectoral volatility | The percent of rise or fall of sectoral index within one week |
| Size | Sectoral market size | The logarithm scale of the average amount of market capitalization of the sectoral index within one week |
| Liquidity | Sectoral liquidity | The liquidity level of a sector within one week, measured by ILLIQ (Amihud and Noh (2021) [53]) |
| Variables | Observations | Mean | Std. Dev. | Min. | Max. |
|---|---|---|---|---|---|
| CES0.05 | 4521 | 0.194 | 0.197 | 0.003 | 2.097 |
| MES0.05 | 4521 | 2.177 | 1.363 | 0.001 | 13.849 |
| Returns | 4521 | 0.077 | 1.717 | −11.948 | 7.668 |
| Volatility | 4521 | 0.256 | 3.903 | −24.051 | 19.311 |
| Size | 4521 | 3.564 | 0.490 | 2.009 | 4.291 |
| Liquidity | 4521 | 0.022 | 0.068 | 0.001 | 1.461 |
| Panel A: CES0.05 | ||||||||
|---|---|---|---|---|---|---|---|---|
| All Period | Period I | Period II | Period III | |||||
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | |
| Energy | 0.111 | 0.082 | 0.273 | 0.143 | 0.130 | 0.020 | 0.088 | 0.021 |
| Materials | 0.230 | 0.129 | 0.505 | 0.232 3 | 0.290 | 0.065 | 0.250 | 0.057 |
| Industrials | 0.382 2 | 0.264 1 | 0.986 1 | 0.415 1 | 0.430 2 | 0.122 2 | 0.386 3 | 0.077 |
| Consumer_ Discretionary | 0.239 | 0.147 | 0.569 3 | 0.229 | 0.311 | 0.102 | 0.251 | 0.045 |
| Consumer_ Staples | 0.139 | 0.091 | 0.204 | 0.088 | 0.171 | 0.063 | 0.156 | 0.034 |
| Healthcare | 0.134 | 0.078 | 0.228 | 0.086 | 0.167 | 0.062 | 0.151 | 0.083 3 |
| Financials | 0.464 1 | 0.245 2 | 0.794 2 | 0.253 2 | 0.651 1 | 0.195 1 | 0.539 1 | 0.098 1 |
| Information_ Technology | 0.299 3 | 0.165 3 | 0.566 | 0.229 | 0.370 3 | 0.119 3 | 0.402 2 | 0.088 2 |
| Telecom_ Service | 0.008 | 0.005 | 0.016 | 0.008 | 0.012 | 0.003 | 0.007 | 0.002 |
| Utilities | 0.051 | 0.049 | 0.174 | 0.082 | 0.058 | 0.017 | 0.049 | 0.008 |
| Real Estate | 0.081 | 0.068 | 0.218 | 0.068 | 0.129 | 0.081 | 0.077 | 0.023 |
| Panel B: MES0.05 | ||||||||
| All Period | Period I | Period II | Period III | |||||
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | |
| Energy | 1.869 | 1.069 | 3.851 | 1.709 | 1.997 | 0.241 | 2.162 | 0.492 |
| Materials | 2.345 | 1.370 | 5.332 3 | 2.390 2 | 2.990 | 0.694 | 2.831 1 | 0.650 3 |
| Industrials | 2.287 2 | 1.435 3 | 5.391 2 | 2.215 3 | 2.678 | 0.785 | 2.515 | 0.480 |
| Consumer_ Discretionary | 2.315 | 1.369 | 5.134 | 2.152 | 2.936 | 1.057 3 | 2.806 2 | 0.500 |
| Consumer_ Staples | 1.957 | 1.268 | 4.297 | 1.933 | 2.638 | 0.970 | 1.863 | 0.428 |
| Healthcare | 2.028 | 1.266 | 4.661 | 1.861 | 2.514 | 0.944 | 1.919 | 1.054 1 |
| Financials | 1.841 | 0.876 | 3.002 | 0.984 | 2.496 | 0.645 | 2.147 | 0.381 |
| Information_ Technology | 2.608 1 | 1.601 1 | 5.941 1 | 2.424 1 | 3.485 1 | 1.176 2 | 2.616 | 0.546 |
| Telecom_ Service | 2.265 3 | 1.391 | 4.522 | 2.177 | 3.376 2 | 0.883 | 1.761 | 0.476 |
| Utilities | 1.564 | 1.319 | 4.611 | 2.086 | 1.897 | 0.535 | 1.805 | 0.297 |
| Real Estate | 2.179 | 1.592 2 | 5.113 | 1.732 | 3.311 3 | 2.042 1 | 2.539 3 | 0.754 2 |
| Panel A: Sectoral Systemic Risk CES0.05 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Event I: CSRC’s Deleveraging Policy in 12 June 2015 | Event II: US’s Additional Trade Tariffs in 15 June 2018 | Event III: COVID-19 Outbreak in 20 January 2020 | |||||||
| Constant | 2.915 ** (0.015) | 2.088 *** (0.003) | 3.107 (0.302) | 2.118 *** (0.002) | 1.983 *** (0.000) | 1.177 (0.555) | 0.225 (0.554) | 0.228 *** (0.000) | 0.193 (0.348) |
| Leads /Lags | Yes | Yes | Yes | Yes | Yes | Yes | |||
| Returns | −0.412 *** (0.002) | −0.463 *** (0.001) | −0.192 * (0.085) | −0.258 * (0.089) | −0.237 ** (0.010) | −0.249 *** (0.003) | |||
| Volatility | 0.176 *** (0.002) | 0.201 *** (0.000) | 0.091 * (0.091) | 0.116 * (0.095) | 0.101 ** (0.011) | 0.108 *** (0.003) | |||
| Size | −0.712 (0.136) | −0.818 (0.336) | −1.378 (0.427) | −0.273 (0.622) | −0.004 (0.971) | 0.326 (0.248) | |||
| Liquidity | −1.505 *** (0.002) | −2.462 *** (0.002) | −0.047 (0.348) | −0.016 (0.468) | −0.038 * (0.051) | −0.071 * (0.082) | |||
| Sector-fixed | Control | Control | Control | Control | Control | Control | Control | Control | Control |
| Time-fixed | Control | Control | Control | Control | Control | Control | Control | Control | Control |
| L-likelihood | −2.503 | 65.813 | 82.031 | 341.149 | 368.109 | 372.024 | 381.378 | 427.016 | 434.916 |
| AIC | 13.006 | −111.626 | −144.063 | −674.298 | −716.219 | −724.049 | −754.757 | −834.033 | −849.831 |
| BIC | 26.775 | −77.201 | −109.639 | −660.528 | −681.795 | −689.624 | −740.987 | −799.609 | −815.407 |
| R-squared | 0.177 | 0.545 | 0.604 | 0.361 | 0.493 | 0.511 | 0.156 | 0.364 | 0.406 |
| Observations | 231 | 231 | 231 | 231 | 231 | 231 | 231 | 231 | 231 |
| Panel B: Sectoral Systemic Risk MES0.05 | |||||||||
| Event I: CSRC’s Deleveraging Policy in 12 June 2015 | Event II: US’s Additional Trade Tariffs 15 June 2018 | Event III: COVID-19 Outbreak in 20 January 2020 | |||||||
| Constant | 3.102 *** (0.008) | 2.420 *** (0.000) | 1.528 (0.337) | 6.002 *** (0.000) | 2.257 *** (0.000) | 5.145 (0.105) | 1.938 ** (0.025) | 2.535 *** (0.000) | 1.011 (0.469) |
| Leads /Lags | Yes | Yes | Yes | Yes | Yes | Yes | |||
| Returns | −4.146 *** (0.000) | −4.267 *** (0.001) | −2.863 ** (0.024) | −3.764 *** (0.000) | −3.074 *** (0.009) | −3.567 ** (0.013) | |||
| Volatility | 1.770 *** (0.000) | 1.825 *** (0.001) | 1.322 ** (0.019) | 1.675 *** (0.000) | 1.323 *** (0.009) | 1.566 ** (0.012) | |||
| Size | −7.528 (0.317) | −3.624 (0.415) | −1.618 (0.517) | −1.373 (0.489) | −4.784 (0.441) | −2.134 (0.581) | |||
| Liquidity | −3.361 * (0.068) | −1.158 *** (0.009) | −0.982 (0.558) | −1.130 (0.694) | −2.701 *** (0.000) | −2.210 *** (0.009) | |||
| Sector-fixed | Control | Control | Control | Control | Control | Control | Control | Control | Control |
| Time-fixed | Control | Control | Control | Control | Control | Control | Control | Control | Control |
| L-likelihood | −526.357 | −383.974 | −362.676 | −207.843 | −202.217 | −185.305 | −150.801 | −111.089 | −98.567 |
| AIC | 1060.714 | 787.949 | 745.352 | 423.687 | 424.433 | 390.610 | 309.602 | 242.178 | 217.135 |
| BIC | 1074.484 | 822.373 | 779.776 | 437.457 | 458.857 | 425.035 | 323.372 | 276.602 | 251.560 |
| R-squared | 0.231 | 0.775 | 0.813 | 0.401 | 0.429 | 0.506 | 0.131 | 0.383 | 0.446 |
| Observations | 231 | 231 | 231 | 231 | 231 | 231 | 231 | 231 | 231 |
| Panel A: CES0.05 | ||||||
|---|---|---|---|---|---|---|
| Event I: CSRC’s Deleveraging Policy in 12 June 2015 | Event II: US’s Additional Trade Tariffs in 15 June 2018 | Event III: COVID-19 Outbreak in 20 January 2020 | ||||
| Short Term | Long Term | Short Term | Long Term | Short Term | Long Term | |
| Energy | −0.168 *** (0.002) | −0.219 *** (0.000) | −0.018 *** (0.004) | −0.023 *** (0.000) | −0.014 ** (0.041) | −0.009 * (0.086) |
| Materials | −0.555 *** (0.002) | −0.589 *** (0.000) | −0.042 ** (0.041) | −0.033 * (0.054) | −0.032 (0.484) | −0.048 * (0.076) |
| Industrials | −0.678 * (0.064) | −0.859 *** (0.003) | −0.099 ** (0.026) | −0.107 *** (0.002) | 0.021 (0.588) | 0.004 (0.850) |
| Consumer_ Discretionary | −0.698 *** (0.002) | −0.657 *** (0.000) | −0.134 *** (0.002) | −0.152 *** (0.000) | 0.029 (0.132) | 0.006 (0.191) |
| Consumer_ Staples | −0.251 *** (0.002) | −0.249 *** (0.000) | −0.048 * (0.065) | −0.089 *** (0.001) | −0.053 ** (0.015) | −0.043 ** (0.031) |
| Healthcare | −0.269 *** (0.002) | −0.254 *** (0.000) | −0.054 *** (0.009) | −0.077 *** (0.000) | −0.002 (0.394) | −0.048 ** (0.045) |
| Financials | −0.275 ** (0.026) | −0.283 *** (0.009) | −0.123 *** (0.002) | −0.147 *** (0.001) | 0.049 (0.179) | 0.033 (0.162) |
| Information_ Technology | −0.868 *** (0.002) | −0.744 *** (0.000) | −0.184 *** (0.004) | −0.161 *** (0.001) | 0.060 (0.394) | 0.047 * (0.075) |
| Telecom_ Service | −0.011 *** (0.002) | −0.009 *** (0.001) | −0.001 (0.179) | 0.001 (0.623) | 0.003 * (0.065) | 0.003 *** (0.005) |
| Utilities | −0.148 *** (0.002) | −0.177 *** (0.000) | −0.020 *** (0.004) | −0.009 (0.104) | 0.010 * (0.065) | 0.009 *** (0.009) |
| Real Estate | −0.129 *** (0.002) | −0.152 *** (0.000) | −0.030 (0.699) | −0.037 (0.212) | 0.007 (0.394) | 0.004 (0.273) |
| Panel B: MES0.05 | ||||||
| Event I: CSRC’s Deleveraging Policy in 12 June 2015 | Event II: US’s Additional Trade Tariffs in 15 June 2018 | Event III: COVID-19 Outbreak in 20 January 2020 | ||||
| Short Term | Long Term | Short Term | Long Term | Short Term | Long Term | |
| Energy | −1.899 *** (0.002) | −2.818 *** (0.000) | −0.286 *** (0.004) | −0.292 *** (0.000) | −0.520 *** (0.004) | −0.469 ** (0.014) |
| Materials | −5.839 *** (0.002) | −6.151 *** (0.000) | −0.499 ** (0.041) | −0.399 ** (0.045) | −0.371 (0.588) | −0.530 * (0.074) |
| Industrials | −3.948 *** (0.065) | −4.759 *** (0.003) | −0.658 ** (0.026) | −0.726 *** (0.002) | 0.234 (0.588) | −0.131 * (0.077) |
| Consumer_ Discretionary | −6.481 *** (0.002) | −5.998 *** (0.000) | −1.222 *** (0.002) | −1.463 *** (0.000) | 0.249 (0.309) | −0.302 * (0.089) |
| Consumer_ Staples | −5.393 *** (0.002) | −5.265 *** (0.000) | −0.625 * (0.093) | −1.242 *** (0.002) | −0.660 ** (0.015) | −0.530 ** (0.011) |
| Healthcare | −5.798 *** (0.002) | −5.377 *** (0.000) | −0.709 *** (0.009) | −1.087 *** (0.000) | 0.094 (0.588) | −0.477 * (0.076) |
| Financials | −0.877 * (0.079) | −0.882 ** (0.021) | −0.467 *** (0.002) | −0.536 *** (0.001) | 0.042 (0.692) | −0.032 (0.850) |
| Information_ Technology | −9.193 *** (0.002) | −7.921 *** (0.000) | −1.651 *** (0.004) | −1.484 *** (0.001) | 0.763 (0.179) | 0.682 *** (0.009) |
| Telecom_ Service | −3.844 *** (0.002) | −3.028 *** (0.000) | −0.435 * (0.065) | −0.203 (0.521) | 0.957 * (0.065) | 0.887 *** (0.002) |
| Utilities | −3.627 *** (0.002) | −4.302 *** (0.000) | −0.665 *** (0.004) | −0.275 (0.307) | 0.228 (0.179) | 0.176 ** (0.037) |
| Real Estate | −3.478 *** (0.002) | −3.755 *** (0.000) | −0.924 (0.485) | −1.168 (0.121) | 0.034 (0.394) | −0.085 * (0.077) |
| All Sample Periods () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 0.642 *** (0.000) | 0.886 *** (0.000) | 0.630 *** (0.000) | 0.304 *** (0.000) | 0.316 *** (0.000) | 0.849 *** (0.000) | 0.667 *** (0.000) | 0.002 (0.997) | 0.000 (1.000) | 0.010 (0.961) | |
| MA | 0.000 (1.000) | 0.411 *** (0.000) | 0.095 ** (0.023) | 0.000 (1.000) | 0.000 (1.000) | 0.521 *** (0.000) | 0.370 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IN | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.246 *** (0.000) | 0.061 (0.213) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CD | 0.000 (1.000) | 0.071 (0.125) | 0.394 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.506 *** (0.000) | 0.341 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CS | 0.066 (0.164) | 0.436 *** (0.000) | 0.640 *** (0.000) | 0.377 *** (0.000) | 0.061 (0.213) | 0.655 *** (0.000) | 0.499 *** (0.000) | 0.005 (0.990) | 0.002 (0.997) | 0.005 (0.990) | |
| HE | 0.046 (0.409) | 0.384 *** (0.000) | 0.710 *** (0.000) | 0.397 *** (0.000) | 0.107 *** (0.008) | 0.720 *** (0.000) | 0.543 *** (0.000) | 0.005 (0.990) | 0.002 (0.997) | 0.005 (0.990) | |
| FI | 0.000 (1.000) | 0.000 (1.000) | 0.044 (0.448) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IT | 0.002 (0.997) | 0.046 (0.409) | 0.260 *** (0.000) | 0.029 (0.700) | 0.002 (0.997) | 0.005 (0.990) | 0.326 *** (0.000) | 0.002 (0.997) | 0.002 (0.997) | 0.005 (0.990) | |
| TS | 0.944 *** (0.000) | 0.985 *** (0.000) | 1.000 *** (0.000) | 0.988 *** (0.000) | 0.949 *** (0.000) | 0.949 *** (0.000) | 0.998 *** (0.000) | 0.968 *** (0.000) | 0.815 *** (0.000) | 0.886 *** (0.000) | |
| UT | 0.545 *** (0.000) | 0.869 *** (0.000) | 0.949 *** (0.000) | 0.847 *** (0.000) | 0.543 *** (0.000) | 0.572 *** (0.000) | 0.929 *** (0.000) | 0.835 *** (0.000) | 0.019 (0.853) | 0.314 *** (0.000) | |
| RE | 0.265 *** (0.000) | 0.759 *** (0.000) | 0.891 *** (0.000) | 0.696 *** (0.000) | 0.350 *** (0.000) | 0.384 *** (0.000) | 0.854 *** (0.000) | 0.723 *** (0.000) | 0.002 (0.997) | 0.000 (1.000) | |
| Period III: COVID-19 Pandemic () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.833 *** (0.000) | 0.667 *** (0.002) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.083 (0.909) | |
| MA | 0.000 (1.000) | 0.667 *** (0.002) | 0.167 (0.684) | 0.000 (1.000) | 0.000 (1.000) | 1.000 *** (0.000) | 0.750 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IN | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.583 *** (0.009) | 0.250 (0.426) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CD | 0.000 (1.000) | 0.167 (0.684) | 0.750 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 1.000 *** (0.000) | 0.833 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| CS | 0.000 (1.000) | 0.750 *** (0.000) | 1.000 *** (0.000) | 0.750 *** (0.000) | 0.333 (0.219) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| HE | 0.167 (0.684) | 0.500 ** (0.033) | 1.000 *** (0.000) | 0.667 *** (0.002) | 0.333 (0.219) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.167 (0.684) | 0.167 (0.684) | 0.167 (0.684) | |
| FI | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| IT | 0.000 (1.000) | 0.000 (1.000) | 0.167 (0.684) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.750 *** (0.005) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | |
| TS | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.833 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | |
| UT | 0.917 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.833 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.000 (1.000) | 0.833 *** (0.000) | |
| RE | 0.417 * (0.093) | 1.000 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.917 *** (0.000) | 0.750 *** (0.000) | 1.000 *** (0.000) | 1.000 *** (0.000) | 0.000 (1.000) | 0.000 (1.000) | |
| All Sample Period () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 0.243 *** (0.000) | 0.199 *** (0.000) | 0.219 *** (0.000) | 0.136 *** (0.000) | 0.151 *** (0.000) | 0.131 *** (0.000) | 0.311 *** (0.000) | 0.258 *** (0.000) | 0.019 (0.853) | 0.187 *** (0.001) | |
| MA | 0.000 (1.000) | 0.039 (0.531) | 0.088 (0.340) | 0.002 (0.997) | 0.002 (0.997) | 0.005 (0.990) | 0.170 *** (0.000) | 0.087 (0.340) | 0.000 (1.000) | 0.039 (0.531) | |
| IN | 0.000 (1.000) | 0.105 ** (0.010) | 0.180 *** (0.000) | 0.044 (0.448) | 0.085 (0.148) | 0.061 (0.213) | 0.209 *** (0.000) | 0.073 (0.108) | 0.000 (1.000) | 0.044 (0.448) | |
| CD | 0.000 (1.000) | 0.153 *** (0.000) | 0.095 (0.125) | 0.002 (0.997) | 0.000 (1.000) | 0.005 (0.990) | 0.170 *** (0.000) | 0.090 (0.134) | 0.005 (0.990) | 0.034 (0.615) | |
| CS | 0.138 (0.378) | 0.275 *** (0.000) | 0.243 *** (0.000) | 0.163 *** (0.000) | 0.078 * (0.079) | 0.107 *** (0.008) | 0.231 *** (0.000) | 0.165 *** (0.000) | 0.012 (0.940) | 0.092 ** (0.028) | |
| HE | 0.092 (0.128) | 0.226 *** (0.000) | 0.197 *** (0.000) | 0.138 *** (0.000) | 0.029 (0.700) | 0.036 (0.573) | 0.214 *** (0.000) | 0.182 *** (0.000) | 0.015 (0.915) | 0.112 *** (0.005) | |
| FI | 0.112 (0.105) | 0.236 *** (0.000) | 0.226 *** (0.000) | 0.170 *** (0.000) | 0.066 (0.164) | 0.066 (0.164) | 0.246 *** (0.000) | 0.214 *** (0.000) | 0.034 (0.615) | 0.143 *** (0.000) | |
| IT | 0.012 (0.940) | 0.071 (0.125) | 0.044 (0.448) | 0.022 (0.818) | 0.015 (0.915) | 0.010 (0.961) | 0.017 (0.886) | 0.012 (0.940) | 0.000 (1.000) | 0.019 (0.853) | |
| TS | 0.024 (0.781) | 0.197 *** (0.000) | 0.114 *** (0.004) | 0.126 *** (0.001) | 0.010 (0.961) | 0.029 (0.700) | 0.041 (0.488) | 0.175 *** (0.000) | 0.015 (0.915) | 0.027 (0.741) | |
| UT | 0.289 *** (0.000) | 0.450 *** (0.000) | 0.408 *** (0.000) | 0.331 *** (0.000) | 0.236 *** (0.000) | 0.255 *** (0.000) | 0.265 *** (0.000) | 0.404 *** (0.000) | 0.309 *** (0.000) | 0.253 *** (0.000) | |
| RE | 0.107 (0.108) | 0.246 *** (0.000) | 0.226 *** (0.000) | 0.163 *** (0.000) | 0.017 (0.886) | 0.065 (0.164) | 0.085 (0.148) | 0.219 *** (0.000) | 0.124 *** (0.002) | 0.002 (0.996) | |
| Period III: COVID-19 Pandemic () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EN | MA | IN | CD | CS | HE | FI | IT | TS | UT | RE | |
| EN | 0.583 *** (0.009) | 0.500 ** (0.033) | 0.583 *** (0.009) | 0.000 (1.000) | 0.250 (0.425) | 0.167 (0.684) | 0.500 ** (0.033) | 0.000 (1.000) | 0.000 (1.000) | 0.417 * (0.093) | |
| MA | 0.000 (1.000) | 0.000 (1.000) | 0.167 (0.684) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.083 (0.909) | 0.000 (1.000) | 0.000 (1.000) | 0.083 (0.909) | |
| IN | 0.000 (1.000) | 0.250 (0.425) | 0.333 (0.219) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.250 (0.425) | 0.000 (1.000) | 0.000 (1.000) | 0.167 (0.684) | |
| CD | 0.000 (1.000) | 0.167 (0.684) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.083 (0.909) | 0.000 (1.000) | 0.000 (1.000) | 0.083 (0.909) | |
| CS | 0.333 (0.219) | 0.667 *** (0.002) | 0.500 ** (0.033) | 0.667 *** (0.002) | 0.417 * (0.093) | 0.500 ** (0.033) | 0.583 *** (0.009) | 0.167 (0.684) | 0.250 (0.425) | 0.500 ** (0.033) | |
| HE | 0.333 (0.219) | 0.417 * (0.093) | 0.333 (0.219) | 0.417 * (0.093) | 0.167 (0.684) | 0.333 (0.219) | 0.333 (0.219) | 0.250 (0.425) | 0.250 (0.425) | 0.333 (0.219) | |
| FI | 0.250 (0.425) | 0.500 ** (0.033) | 0.417 * (0.093) | 0.583 *** (0.009) | 0.000 (1.000) | 0.333 (0.219) | 0.500 ** (0.033) | 0.000 (1.000) | 0.000 (1.000) | 0.333 (0.219) | |
| IT | 0.000 (1.000) | 0.250 (0.423) | 0.083 (0.909) | 0.250 (0.425) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.000 (1.000) | 0.083 (0.909) | |
| TS | 0.500 ** (0.033) | 0.750 *** (0.000) | 0.750 *** (0.000) | 0.750 *** (0.000) | 0.250 (0.426) | 0.417 * (0.093) | 0.667 *** (0.002) | 0.667 *** (0.000) | 0.333 (0.219) | 0.667 *** (0.002) | |
| UT | 0.333 (0.219) | 0.833 *** (0.000) | 0.583 *** (0.009) | 0.833 *** (0.000) | 0.250 (0.426) | 0.500 ** (0.033) | 0.500 ** (0.033) | 0.750 *** (0.001) | 0.250 (0.425) | 0.667 *** (0.002) | |
| RE | 0.083 (0.909) | 0.333 (0.219) | 0.167 (0.684) | 0.417 * (0.093) | 0.000 (1.000) | 0.167 (0.684) | 0.083 (0.909) | 0.250 (0.425) | 0.000 (1.000) | 0.000 (1.000) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, A.; Zhao, H.; Tian, Y. The Intersectoral Systemic Risk Shock of Emergency Crisis Events in China’s Financial Market: Nonparametric Methods and Panel Event Study Analyses. Systems 2023, 11, 147. https://doi.org/10.3390/systems11030147
Lei A, Zhao H, Tian Y. The Intersectoral Systemic Risk Shock of Emergency Crisis Events in China’s Financial Market: Nonparametric Methods and Panel Event Study Analyses. Systems. 2023; 11(3):147. https://doi.org/10.3390/systems11030147
Chicago/Turabian StyleLei, Ao, Hui Zhao, and Yixiang Tian. 2023. "The Intersectoral Systemic Risk Shock of Emergency Crisis Events in China’s Financial Market: Nonparametric Methods and Panel Event Study Analyses" Systems 11, no. 3: 147. https://doi.org/10.3390/systems11030147
APA StyleLei, A., Zhao, H., & Tian, Y. (2023). The Intersectoral Systemic Risk Shock of Emergency Crisis Events in China’s Financial Market: Nonparametric Methods and Panel Event Study Analyses. Systems, 11(3), 147. https://doi.org/10.3390/systems11030147






