Ramp Spacing Evaluation of Expressway Based on Entropy-Weighted TOPSIS Estimation Method
Abstract
1. Introduction
2. Problem Statement and Evaluation Indicators
2.1. Problem Statement
2.2. Evaluation Indicator System
2.2.1. Traffic Efficiency
2.2.2. Safety
2.2.3. Traffic Accessibility
2.2.4. Economy
3. Methodology
3.1. Entropy Weight Method
3.2. TOPSIS Method
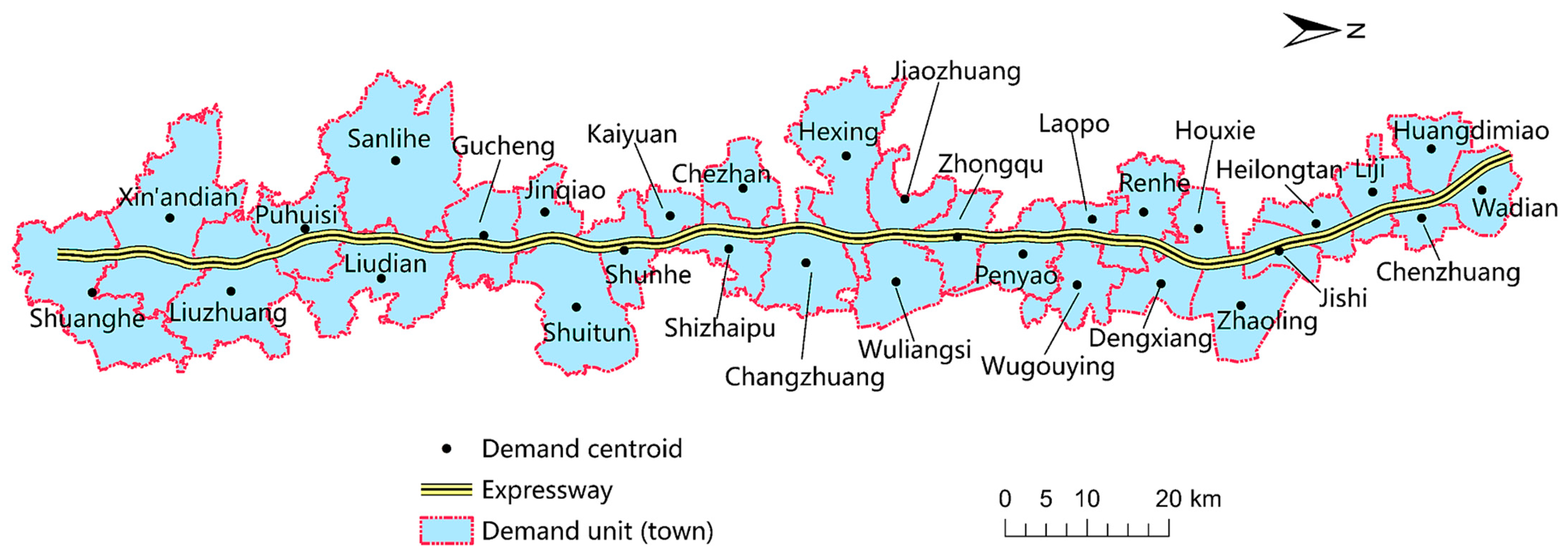
4. Case Study
4.1. Study Area
4.2. Results and Discussions
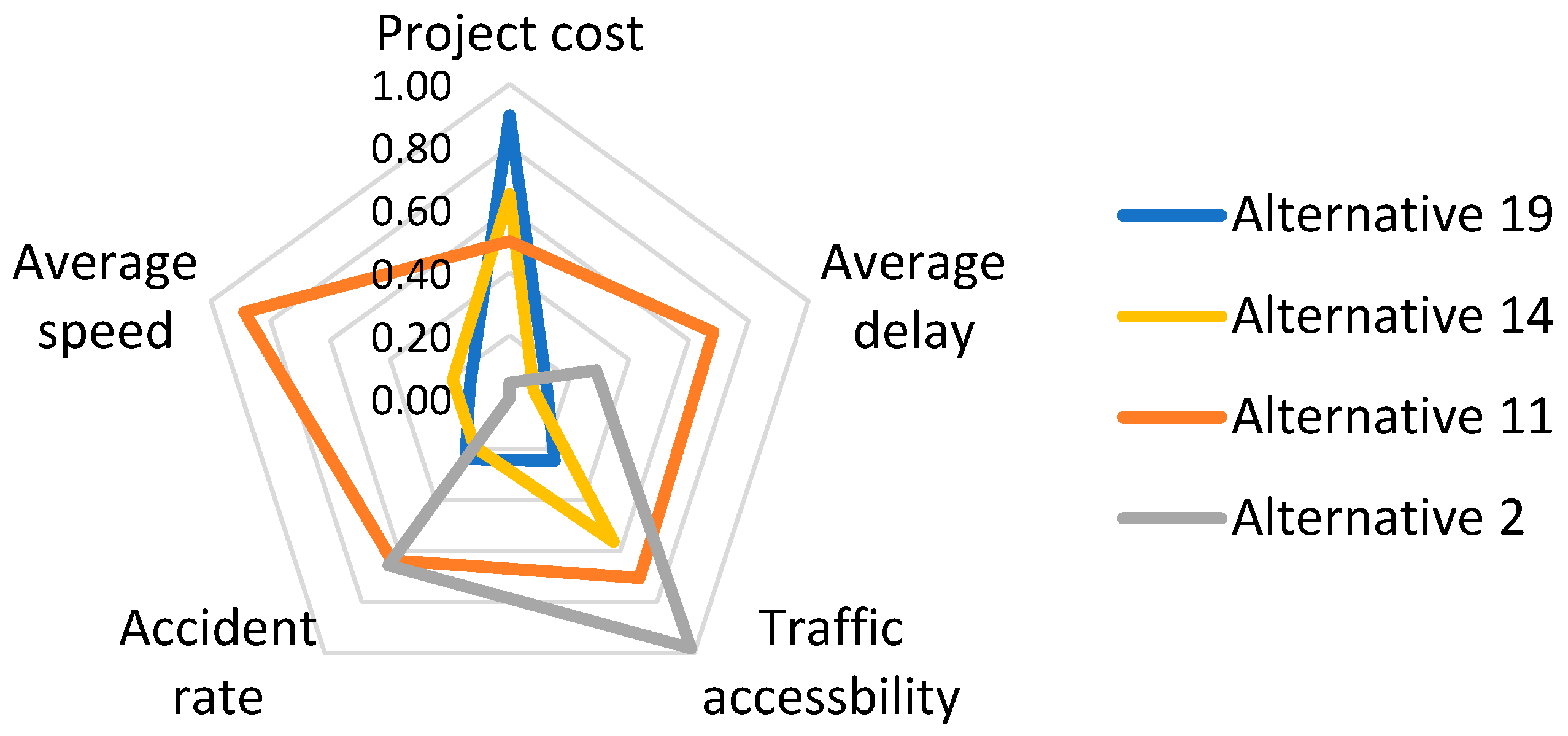
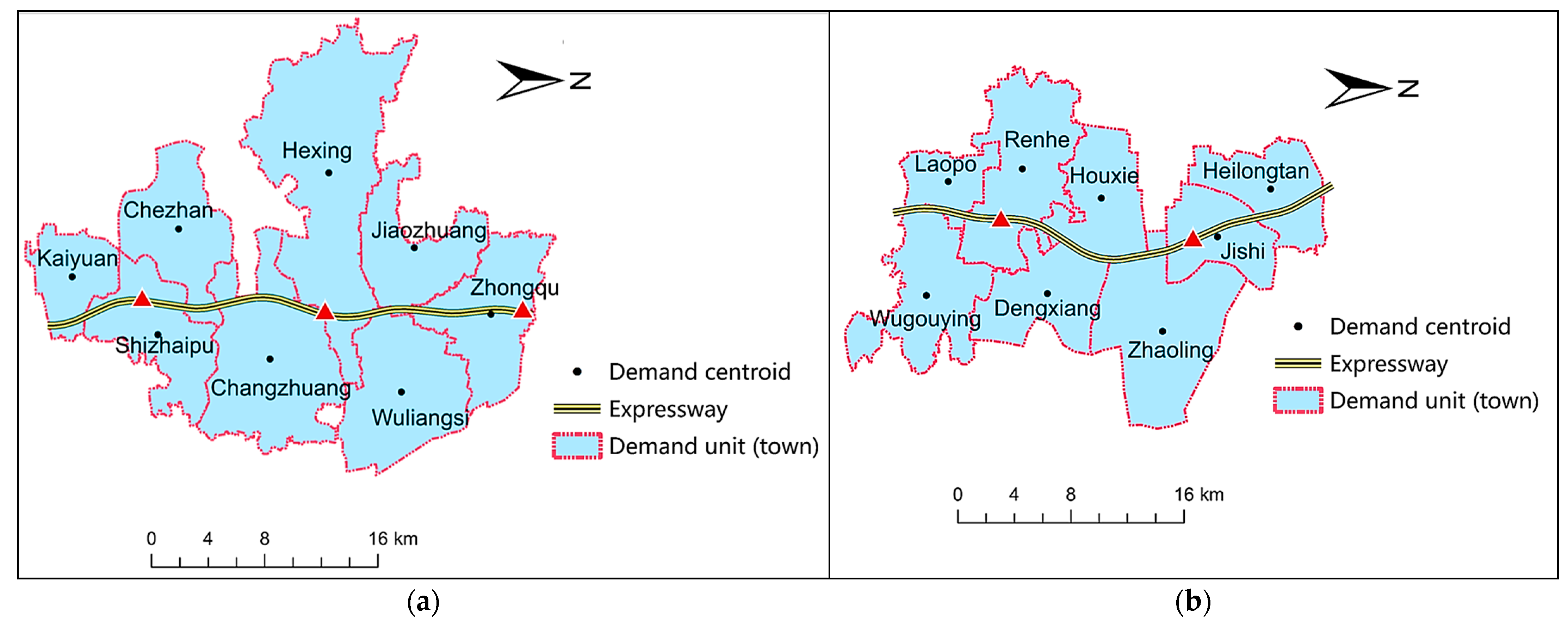
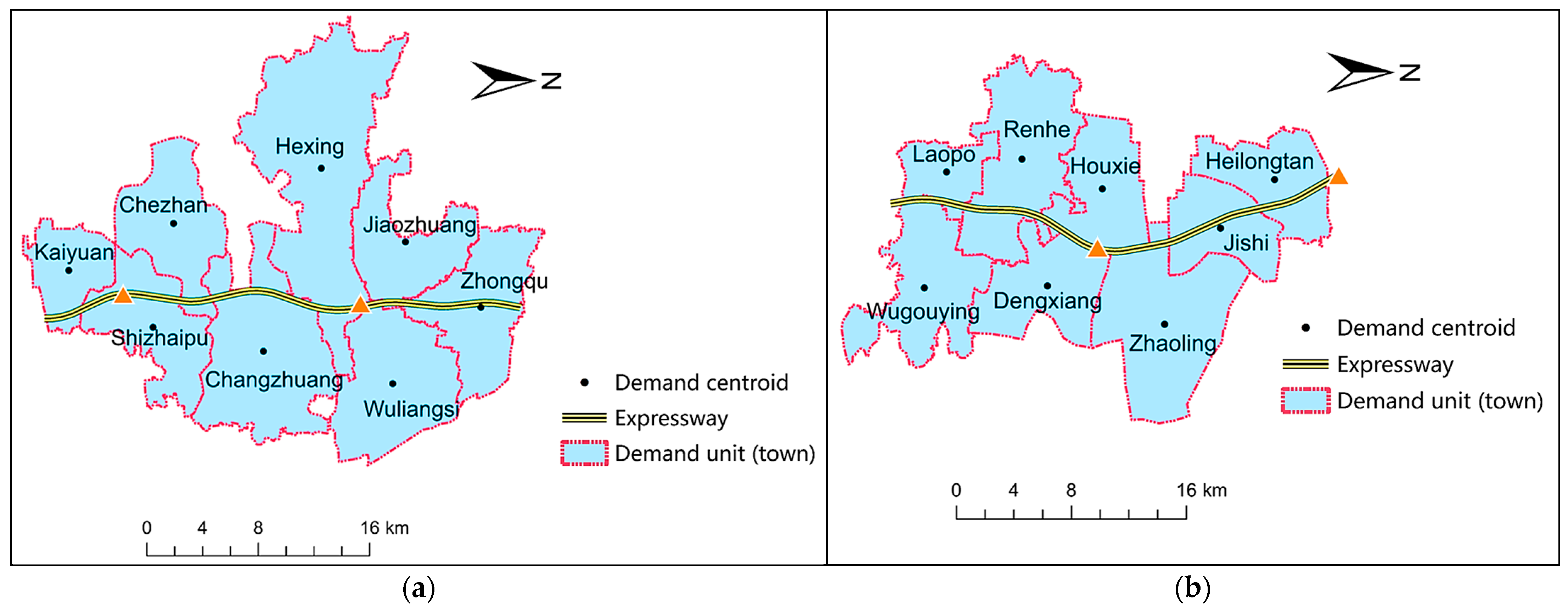
4.2.1. Comparison of Ramp Spacing Alternatives
4.2.2. Sensitivity Analysis of TDARs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | Notation |
|---|---|
| index of towns | |
| index of ramps | |
| the comprehensive level of service of roads within the town | |
| the distance from town to ramp | |
| the comprehensive aggregation scale of town | |
| the accessibility of town when considering distance factor | |
| the weight of the ramp attached to the toll station with location potential level | |
| the accessibility of town | |
| the accessibility of the standard town | |
| the location potential of town | |
| the location potential of the standard town | |
| the proportionality coefficient | |
| the elastic correction factor for the increase in location potential due to the traffic accessibility | |
| the elastic correction factor for the increase in location potential due to the comprehensive aggregation scale | |
| the location influence coefficient of town | |
| the traffic demand along the route allocated to town | |
| the cross-sectional flow of the toll station where ramp is located | |
| the cumulative probability of travel to ramp from a town which is kilometers away from ramp | |
| parameter of the function related to distance decay theory | |
| parameter of the function related to distance decay theory | |
| the transit traffic demand of expressway | |
| the traffic demand along the route of expressway | |
| the proportion of transit traffic demand | |
| Sets | |
| the set of towns | |
| the set of ramps set according to spacing alternative | |
| the set of ramps that can serve the town , | |
| the set of the original ramps on the expressway | |
| the set of ramps that can serve the town , | |
| the set of towns served by ramp |
References
- National Academies of Sciences, Engineering, and Medicine. An Expanded Functional Classification System for Highways and Streets; The National Academies Press: Washington, DC, USA, 2018; p. 84. [Google Scholar]
- Ma, J.; Li, D.; Tu, Q.; Du, M.; Jiang, J. Finding optimal reconstruction plans for separating trucks and passenger vehicles systems at urban intersections considering environmental impacts. Sustain. Cities Soc. 2021, 70, 102888. [Google Scholar] [CrossRef]
- Ma, J.; Wu, X.; Jiang, J. Lane restriction system to reduce the environmental cost of urban roads. Transp. Res. Part D: Transp. Environ. 2023, 115, 103575. [Google Scholar] [CrossRef]
- Liu, W.; Chen, X.; Hu, A. Study on Traffic Flow Parameters Model of Expressway Interchanges Opening Distance. Appl. Mech. Mater. 2012, 178, 2623–2628. [Google Scholar] [CrossRef]
- Chen, S.-K.; Mao, B.-H.; Liu, S.; Sun, Q.-X.; Wei, W.; Zhan, L.-X. Computer-aided analysis and evaluation on ramp spacing along urban expressways. Transp. Res. Part C Emerg. Technol. 2013, 36, 381–393. [Google Scholar] [CrossRef]
- Wang, R.; Hu, J.; Zhang, X. Analysis of the driver’s behavior characteristics in low volume freeway interchange. Math. Probl. Eng. 2016, 2016, 2679516. [Google Scholar] [CrossRef]
- Flintsch, A.M.; Guo, F.; Han, S.; Hancock, K.; Williams, B.; Li, Y.; Gibbons, R. Impact of Access Spacing Standards on Crash Risk after Controlling for Access Volumes; Virginia Transportation Research Council (VTRC): Charlottesville, VA, USA, 2020. [Google Scholar]
- Pilko, P.; Bared, J.G.; Edara, P.K.; Kim, T. Safety Assessment of Interchange Spacing on Urban Freeways: [Techbrief]; FHWA-HRT-07-031; United States. Federal Highway Administration. Office of Research, Development, and Technology: Washington, DC, USA, 2007.
- Guo, Y.Q. Effects of Ramp Spacing on Freeway Mainline Crashes. Appl. Mech. Mater. 2011, 97, 95–99. [Google Scholar] [CrossRef]
- Shea, M.S.; Le, T.Q.; Porter, R.J. Combined Crash Frequency–Crash Severity Evaluation of Geometric Design Decisions: Entrance–Exit Ramp Spacing and Auxiliary Lane Presence. Transp. Res. Rec. 2015, 2521, 54–63. [Google Scholar] [CrossRef]
- Le, T.Q.; Porter, R.J. Safety evaluation of geometric design criteria for spacing of entrance–exit ramp sequence and use of auxiliary lanes. Transp. Res. Rec. 2012, 2309, 12–20. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). A Policy on Geometric Design of Highways and Streets, 2011; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Guidelines for Design of Highway Grade-Separated Intersections (JTG/T D21-2014); People’s Communications Publishing House: Beijing, China, 2014. [Google Scholar]
- Board, T.R. HCM2010: Highway Capacity Manual, 5th ed.; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar]
- Chen, H.; Lu, L.; Lu, J.; Zhu, S.; Wei, D. Development and applications of models of average speed in the combination area of urban expressway ramps. Adv. Transp. Stud. 2015, 35, 19–42. [Google Scholar]
- Wang, F.; Li, Y.; Liu, J.; Li, Y.; Xia, L. Identification of extreme ramp spacing on Expressway Based on GPS Speed Data Driven Model. J. Highw. Transp. Dev. 2016, 33, 127–135. [Google Scholar]
- Jang, M.-S. Methodology for evaluating freeway interchange spacing for high design speed based on traffic safety: Focused on analysis of acceleration noise using microscopic traffic simulations. J. Korean Soc. Transp. 2009, 27, 145–153. [Google Scholar]
- Kim, H.R.; Kim, K.S.; Lee, G.H.; Shin, J.S.; Baek, J.G. Determining the Required Minimum Spacing between Freeway Interchange for High-speed Roadway. Int. J. Highw. Eng. 2017, 19, 45–55. [Google Scholar] [CrossRef]
- Torbic, D.J.; Harwood, D.W.; Gilmore, D.K.; Richard, K.R.; Bared, J.G. Safety analysis of interchanges. Transp. Res. Rec. 2009, 2092, 39–47. [Google Scholar] [CrossRef]
- Liu, Z.-P.; Zhou, X.-W. Research on Project Cost Calculation of Expressway. Constr. Econ. 2021, 42, 70–74. [Google Scholar] [CrossRef]
- Molan, A.M.; Hummer, J.E.; Ksaibati, K. Introducing the super DDI as a promising alternative service interchange. Transp. Res. Rec. 2019, 2673, 586–597. [Google Scholar] [CrossRef]
- Qiao, J.; Song, M. Study on Interchange Overpass Distance Based on Maximum Entropy Principle. In Proceedings of the ICTIS, Wuhan, China, 22–24 October 2011; pp. 481–487. [Google Scholar]
- Winkler, M.; Fan, W. Evaluating impacts on freeway capacity using VISSIM: Accounting for truck lane restrictions, driver behavior, and interchange density. Adv. Transp. Stud. 2011, 25, 15–28. [Google Scholar]
- Chen, D.; Mo, F.; Chen, Y.; Zhang, J.; You, X. Optimization of ramp locations along freeways: A dynamic programming approach. Sustainability 2022, 14, 9718. [Google Scholar] [CrossRef]
- Broniewicz, E.; Ogrodnik, K. A comparative evaluation of multi-criteria analysis methods for sustainable transport. Energies 2021, 14, 5100. [Google Scholar] [CrossRef]
- Roszkowska, E. Multi-criteria decision making models by applying the TOPSIS method to crisp and interval data. Mult. Criteria Decis. Mak. /Univ. Econ. Katow. 2011, 6, 200–230. [Google Scholar]
- Zhang, M.; Sun, Q.; Yang, X. Research on the assessment of the capacity of urban distribution networks to accept electric vehicles based on the improved TOPSIS method. IET Gener. Transm. Distrib. 2021, 15, 2804–2818. [Google Scholar] [CrossRef]
- Aljohani, K.; Thompson, R.G. A multi-criteria spatial evaluation framework to optimise the siting of freight consolidation facilities in inner-city areas. Transp. Res. Part A: Policy Pract. 2020, 138, 51–69. [Google Scholar] [CrossRef]
- Hamurcu, M.; Eren, T. Strategic planning based on sustainability for urban transportation: An application to decision-making. Sustainability 2020, 12, 3589. [Google Scholar] [CrossRef]
- Shishegaran, A.; Shishegaran, A.; Mazzulla, G.; Forciniti, C. A novel approach for a sustainability evaluation of developing system interchange: The case study of the Sheikhfazolah-Yadegar interchange, Tehran, Iran. Int. J. Environ. Res. Public Health 2020, 17, 435. [Google Scholar] [CrossRef] [PubMed]
- Vavrek, R.; Bečica, J. Capital city as a factor of multi-criteria decision analysis—Application on transport companies in the Czech Republic. Mathematics 2020, 8, 1765. [Google Scholar] [CrossRef]
- Li, Q.-l.; Wang, H.; Wu, Y.-l.; Wang, H.-t.; Zhu, S.-y. Expressway Interchange Minimum Clear Distance Model Based on Nonfree Lane Changing Behavior. J. Highw. Transp. Dev. 2022, 39, 165–173. [Google Scholar]
- Subiantoro, W.; Mudiyono, R. Evaluation of minimum ramp distance in efforts to improve performance on Jakarta-Cikampek toll road. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Semarang, Indonesia, 21–22 September 2021; p. 012015. [Google Scholar]
- Pei, Y.-L.; Cheng, G.-Z. Research on the relationship between discrete character of speed and traffic accident and speed management of freeway. Zhongguo Gonglu Xuebao 2004, 17, 74. [Google Scholar]
- Institute, B.G.M.E.D.R. Code for Design of Urban Road Engineering (CJJ 37-2012); China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Shuang, W.; Hao, J.; Ai, D.; Huang, X.; Zhang, L.; Meng, P.; Zhu, C. Zoning and Pattern of Rural Residential Land Consolidation Based on Locational Potential Theory. Trans. Chin. Soc. Agric. Eng. 2013, 29, 251–261+297. [Google Scholar]
- Chen, C.-H. A novel multi-criteria decision-making model for building material supplier selection based on entropy-AHP weighted TOPSIS. Entropy 2020, 22, 259. [Google Scholar] [CrossRef]
- Dong, X.; Lu, H.; Xia, Y.; Xiong, Z. Decision-making model under risk assessment based on entropy. Entropy 2016, 18, 404. [Google Scholar] [CrossRef]
- Zhao, H.; Yao, L.; Mei, G.; Liu, T.; Ning, Y. A fuzzy comprehensive evaluation method based on AHP and entropy for a landslide susceptibility map. Entropy 2017, 19, 396. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Consultants, C.F.H. Design Specification for Highway Alignment (JTG D20-2017); People’s Communications Publishing House: Beijing, China, 2017. [Google Scholar]
- Chen, Z.; Jin, F.; Yang, Y.; Wang, W. Distance-decay Pattern and Spatial Differentiation of Expressway Flow: An Empirical Study Using Data of Expressway Toll Station in Fujian Province. Prog. Geogr. 2018, 37, 1086–1095. [Google Scholar]
- Gao, S.; Wang, Y.; Gao, Y.; Liu, Y. Understanding urban traffic-flow characteristics: A rethinking of betweenness centrality. Environ. Plan. B Plan. Des. 2013, 40, 135–153. [Google Scholar] [CrossRef]
- Ma, J.; Xu, M.; Jiang, J. Mapping high-resolution urban road carbon and pollutant emissions using travel demand data. Energy 2023, 263, 126059. [Google Scholar] [CrossRef]

| Variable | Notation |
|---|---|
| Parameters | |
| the average speed | |
| the average delay | |
| the speed of vehicle | |
| the delay of vehicle | |
| the sample size of vehicles | |
| the accident rate of 100 million vehicle- kilometers | |
| the standard deviation of the speed of all vehicles | |
| the comprehensive level of service of roads within the town | |
| the grade of roads | |
| the length of the road with grade | |
| the evaluation value of the road with class | |
| the total length of the roads passing through the town | |
| the accessibility of town | |
| the distance from town to ramp | |
| the comprehensive aggregation scale of town | |
| the number of evaluation indicators for the comprehensive aggregation scale | |
| the weight of the evaluation indicator | |
| the value of the evaluation indicator of town | |
| the accessibility of the study district | |
| the project cost of constructing all ramps along the expressway section | |
| the density of ramps along the expressway section | |
| the relevant parameter of the project cost | |
| Sets | |
| the set of ramps set according to spacing alternative | |
| the set of ramps that can serve the town , | |
| the set of towns |
| Indicator (Criterion) | Dimension | Indicator Source |
|---|---|---|
| Average speed () | positive | VISSIM simulation |
| Average delay () | negative | VISSIM simulation |
| Accident rate () | negative | VISSIM simulation and calculation |
| Traffic accessibility () | positive | Calculation based on data |
| Project cost () | negative | Evaluation based on ramp data and terrain conditions |
| Indicator (Criterion) | Average Speed | Average Delay | Accident Rate | Traffic Accessibility | Project Cost |
|---|---|---|---|---|---|
| Weight () | 0.20211 | 0.25285 | 0.16918 | 0.13340 | 0.24246 |
| Spacing Alternative | Decision Matrix | ||||
|---|---|---|---|---|---|
| Average Speed | Average Delay | Accident Rate | Traffic Accessibility | Project Cost | |
| 0.47 | 0.66 | 0.54 | 1.00 | 0.00 | |
| 0.00 | 0.29 | 0.66 | 0.98 | 0.05 | |
| 0.65 | 0.72 | 0.92 | 0.99 | 0.10 | |
| 1.00 | 0.80 | 0.67 | 0.96 | 0.15 | |
| 0.43 | 0.60 | 0.87 | 0.94 | 0.20 | |
| 0.81 | 0.74 | 0.80 | 0.92 | 0.25 | |
| 0.55 | 0.70 | 1.00 | 0.91 | 0.30 | |
| 0.96 | 1.00 | 0.41 | 0.86 | 0.35 | |
| 0.58 | 0.92 | 0.67 | 0.83 | 0.40 | |
| 0.44 | 0.46 | 0.29 | 0.85 | 0.45 | |
| 0.89 | 0.68 | 0.64 | 0.71 | 0.50 | |
| 0.04 | 0.49 | 0.00 | 0.71 | 0.55 | |
| 0.70 | 0.64 | 0.42 | 0.60 | 0.60 | |
| 0.19 | 0.08 | 0.19 | 0.56 | 0.65 | |
| 0.79 | 0.35 | 0.59 | 0.55 | 0.70 | |
| 0.65 | 0.43 | 0.21 | 0.51 | 0.75 | |
| 0.35 | 0.00 | 0.42 | 0.44 | 0.80 | |
| 0.52 | 0.36 | 0.32 | 0.37 | 0.85 | |
| 0.13 | 0.12 | 0.24 | 0.24 | 0.90 | |
| 0.28 | 0.05 | 0.32 | 0.20 | 0.95 | |
| 0.45 | 0.07 | 0.34 | 0.00 | 1.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Zeng, Y.; Chen, D. Ramp Spacing Evaluation of Expressway Based on Entropy-Weighted TOPSIS Estimation Method. Systems 2023, 11, 139. https://doi.org/10.3390/systems11030139
Ma J, Zeng Y, Chen D. Ramp Spacing Evaluation of Expressway Based on Entropy-Weighted TOPSIS Estimation Method. Systems. 2023; 11(3):139. https://doi.org/10.3390/systems11030139
Chicago/Turabian StyleMa, Jie, Yilei Zeng, and Dawei Chen. 2023. "Ramp Spacing Evaluation of Expressway Based on Entropy-Weighted TOPSIS Estimation Method" Systems 11, no. 3: 139. https://doi.org/10.3390/systems11030139
APA StyleMa, J., Zeng, Y., & Chen, D. (2023). Ramp Spacing Evaluation of Expressway Based on Entropy-Weighted TOPSIS Estimation Method. Systems, 11(3), 139. https://doi.org/10.3390/systems11030139








