Abstract
Oilfields must increase their production due to the current price of oil barrels. The sale of these oilfields by big companies enabled new companies to enter the exploration and production segment of brownfields to increase oil and gas production through subsea intervention projects. However, these projects require specific product development that involves technical requirements that the engineering department must analyze. This research aims to apply the SWARA-MOORA-3NAG multicriteria decision analysis (MCDA) method in analyzing the technical proposals of subsea intervention equipment for ordering suppliers according to the engineering requirements defined at the initial stage of the projects of an oil and gas company. The research methodology was divided into five stages: (1) identification of the problem through observation of the current process and interviews with engineers; (2) data collection through bibliographic research in the Scopus database; (3) problem modeling; (4) proposition of the solution with the application of the SWARA-MOORA-3NAG method; and (5) analysis of the results found. The application of the SWARA-MOORA-3NAG method brought a new ordering of suppliers to the analyzed case, enabling comparison between the method previously used by the engineering department and the method proposed by this research, emphasizing that the MCDA methods can be inserted into the analysis processes of technical proposals in the engineering department of the company analyzed.
1. Introduction
The increase in the price of a barrel of oil since 2020 has attracted oil and gas companies to focus on brownfields despite the decline in the production of wells in these fields. Traditionally, when these wells begin to decline, oil and gas companies abandon them due to the risk of unwanted water or gas production that is difficult to remediate [1]. However, the subsea intervention in these wells became viable for production recovery due to the profit margin with the current oil and gas prices. This strategy was used by companies in Brazil, such as Trident, Perenco, and Karoon, to purchase brownfields from Petrobras.
In order to increase the production of brownfields, oil and gas companies seek companies capable of carrying out subsea interventions, to develop solutions that allow the growth of production safely. In this development scenario, these contracted companies develop products with the involvement of several suppliers who must follow the requirements defined by the engineering department. During this product development process, there is an initial stage in which suppliers prepare technical and commercial proposals, which are submitted to the company specializing in subsea intervention to evaluate whether they meet the requirements defined by the engineering department. However, when technical proposals from the suppliers have similar scopes of supply, each technical detail will be essential to identify the best recommendation.
The oil and gas extraction process is complex and involves many risks in terms of investment, environment, and human resources. The choice of a company with high technical capacity is of fundamental importance to the whole process. The decision-making group of an oil company needs to have precise and quality information to help in the decision-making process. A predominant factor, in this case, is the systematization of data, which is a critical factor for implementing artificial intelligence (A.I.) tools to support decision making. To avoid the analysis depending exclusively on human factors such as knowledge of the defined requirements, the possibility of using multicriteria decision analysis (MCDA) emerges to assist the decision-maker in choosing the most technically suitable supplier in the requested scope. In the last few years, we have observed a growth in the integration of machine learning methods with multicriteria methods to improve the elicitation of the weights attributed by decision-makers to the criteria used in decision support models: as an example, we cite the research developed by Souza Rodrigues et al. [2] that developed an algorithm called Ranking Trees, which merges some steps of machine learning with the random forest technique, to elicit all parameter combinations of the ELECTRE II, III, and IV methods. This process presents the decision-maker with an optimized ranking of solutions, increasing the quality of the decision. Another example of decision-maker interaction with artificial intelligence is the work of Floriano et al. [3], who developed the 3MO-AHP algorithm using the nondominated sorting genetic algorithm III (NSGA-III) to deal with the inconsistency problem of the AHP method. Another application can be observed in the research of Basilio et al. [4], where they integrated the latent Dirichlet allocation (LDA) method with the ELECTRE-I method to identify criminal demands, helping decision-makers of police organizations to choose the best strategies to fight crime.
Regarding the oil and gas industry, an integration of A.I. and MCDA can be observed in the research developed by Eke et al. [5] to identify and evaluate multiple options for decommissioning oil platforms. Furthermore, MCDA can be inserted into product development processes to predict software defects during development, as asserted by Özakıncı and Kolukısa Tarhan [6]. The integration of artificial intelligence with operations research methods allows the decision-maker to virtually test and economically evaluate the attractiveness of adopting evolving technologies in full-field offshore developments, as reported by Basilio et al. [7], using the method of “model-based systems metaheuristic engineering” (MBSME).
Basilio et al. [8,9,10] reported that decision making is endogenous to humans. Throughout the day, we make numerous decisions consciously and unconsciously. We make decisions from the color of the tie we will wear to whether or not we will acquire some asset, for example. We want to reinforce the idea that we daily make simple and complex decisions in several knowledge areas [8,9,10,11,12,13] and that making decisions is inherent to human life. Decision support methods have been and will continue to be developed and improved to support managers in company decision making. Numerous methods have been developed over the last 50 years, such as AHP, TOPSIS, VIKOR, PROMETHEE, and ANP. As recorded by Basilio et al. [8], these five methods are the most used in several areas of knowledge, the highlight being the AHP method. According to de Assis et al. [9], “the literature reports the growth of new techniques and the integration with fuzzy sets and associations to reduce the discretion of the decision-maker regarding weight elicitation” (p. 2). Thus, decision-makers have at their disposal a myriad of methods such as MAUT, ELECTRE-MOr, SMART, UTA, MACBETH, ELECTRE, NAIADE, ORESTE, REGIME, ARGUS, TACTIC, EA FAHP, MELCHIOR, PAMSSEM, EVAMIX, QUALIFLEX, PCCA, MAPPAC, PRAGMA, PAC-MAN, IDRA, G-COPRAS, DRSA, SPOTIS, SIMUS, COMET, DARIA-TOPSIS, MABAC, MAIRCA, SF-AHP, WASPAS, TODIM, and SAPEVO-M [14,15,16,17,18,19,20,21,22,23,24].
When a particular MCDM method is finally recommended for a specific application, it is observed that its solution accuracy and ranking performance are seriously influenced by the value of its control parameter, as stated by Kahraman et al. [25]. The general objective of this research is to apply the hybrid method SWARA-MOORA-3NAG in analyzing technical proposals of subsea intervention equipment for ordering suppliers according to the engineering requirements defined in the initial stage of the projects of an oil and gas company. The choice for this method is due to the report by Hermogens [26], which states that the new proposal works, considering the original ordering of the MOORA method. According to Hermogenes [26], the new approach simplified the process. The SWARA-MOORA-3NAG also uses two more normalizations in its model; thus, in addition to presenting the results considering a single ordination, without disregarding MOORA and Tchebycheff’s ordination, the three normalizations applied to the model guarantee more excellent safety in decision making. As a contribution, the method eliminates the need to perform sensitivity analysis on the results, as reported by Hermogens [26]. The engineering department of this company performs this technical analysis, and there is no inclusion of the cost and delivery time criteria in the ordering, limiting the investigation to the technical scope of the proposals received by the suppliers.
In order to achieve the general objective, the following specific objectives were defined: (1) to identify the problems encountered in the analysis of the technical proposals of the suppliers; (2) to propose a multicriteria decision analysis method to assist engineers in this analysis; and (3) to apply the SWARA-MOORA-3NAG method and analyze the results obtained with its implementation.
This article is structured as follows: Section 2 briefly describes the methods. Section 3 presents the description of the problem. Section 4 reports the main applications of multicriteria methods applied to the oil and gas sector. Section 5 describes the proposed solution with the application of the SWARA-MOORA-3NAG method. The main discussions are summarized in Section 6.
2. Literature Review
The bibliographic research carried out in the Scopus database was fundamental to the literature review since the MCDA methods can assist in ordering suppliers in the technical scope according to the established engineering requirements. The need to combine existing MCDA methods with the particularities of each project is important to achieve success, as performed by Janowska-Renkas et al. [27] in the combination of the methods EA FAHP (extent analysis fuzzy analytic hierarchy process) and FuzzyTOPSIS (fuzzy technique for order preference by similarity to an ideal solution) in the optimal selection of high-performance concrete for monolithic beam structures of bridges.
Numerous MCDA methods have been developed in recent decades and are currently applied in various domains, such as their use to prioritize the redesign of streets in Quebec City, Canada [28]. The benefits of implementing these methods can also be found at the national level in Pakistan, where its application in energy shortages to order renewable sources of green hydrogen can help the country find the solutions for this problem [29].
Different sectoral investments in energy must be made in more suitable areas of cities, and recent concepts such as smart cities are also using MCDA methods for selecting locations for electric vehicle charging stations [30]. In addition, it was observed that for energy-efficient home projects, a concept adopted by smart cities, there is an increase in environmental impact in the construction and demolition phases, and MCDA methods can order solutions so that this impact is as small as possible [31]. Complementing this discussion, we can report on the work of Wang et al. [32], who used a combination of DEA window analysis and the Malmquist index approach to assess the efficiency of the cybersecurity industry.
MCDA methods can also be associated with product development projects, such as prioritizing technical design and engineering requirements using the quality function deployment (QFD) tool to ensure quality during product and service development to meet customer needs [33]. The QFD tool transforms these customer requirements into technical requirements and evaluates the product parameters of the competitor’s product to meet customer requirements by increasing their satisfaction [34]. One of the possibilities of applying the QFD tool was proposed by Vongvit et al. [35], by using Fuzzy-QFD technique to insert design changes in a 3-axis CNC (computerized numerical control) machine to make it a 5-axis machine that meets customer requirements.
Among the options for using MCDA methods, we highlight the proposal of a model for evaluating business projects for admission to an incubator, in which there is the possibility of classification in order of selection priority through the combination of momentum methods to build prospective scenarios and the AHP-TOPSIS-2N method to classify alternatives [36]. In the case of startups, Simões et al. [37] use the combination of cognitive mapping and the decision expert (DEX) technique to evaluate the growth potential of startups, bringing together a panel of experienced entrepreneurs and business investors to identify and articulate the criteria to be considered in the evaluation and classification of these startups.
In several industries, MCDA has been widely applied, as we can report in sustainable supplier selection (SSS), where Dang et al. [38] integrated spherical fuzzy analytical hierarchical process (SF-AHP) and grey complex proportional assessment (G-COPRAS) to assess and choose a possible supplier based on their capability to adapt to the COVID-19 epidemic sustainably.
In the oil and gas industry, as presented by Barata et al. [39], MCDA methods can be used to classify the degree of organizational sustainability of supplier companies, highlighting the advanced level of maturity of these companies in the context of sustainability. Additionally, in this same industry, Miri Lavasani et al. [40] emphasize the importance of using the AHP method to estimate the weights needed to group the sources of nonpar proportional risks to identify acceptable risks in offshore wells. Among the various options of existing MCDA methods, this research addresses the application of the hybrid method SWARA-MOORA-3NAG in analyzing technical proposals for subsea intervention projects in the oil and gas industry.
3. Methodology
The methodology applied to this research was elaborated to identify the problem, present solutions to solve it, and finally, determine whether the proposed solution met the research objective. Figure 1 shows the structure of the methodology used.

Figure 1.
Research methodology.
The first step is identifying the problem by observing the company’s current process analyzed in this research. Through this observation, it was determined that the ordering of suppliers performed by the engineering department, in the analysis of technical proposals, presented criteria in which there were no weights to be associated with technical requirements, and that they could impact the decision of the best supplier for the projects of subsea intervention. This observation was confirmed in unstructured interviews with three engineers responsible for these technical analyses, who emphasized the need to apply improvements in this analysis. This interview was conducted on 8 November 2022, with the question, “What is your assessment of the methodology of analysis of technical proposals sent by suppliers used by the company currently?” Although they agree that the current methodology helps identify the requirements requested, these engineers commented that different weights should be inserted in the criteria adopted due to the degree of importance of each requirement.
Then, with the problem identified, it was necessary to conduct bibliographic research that associated MCDA methods with product development. This bibliographical research was carried out using the Scopus database in November 2022 with the search string “requirements” and “design” and “multi-criteria decision analysis (MCDA)”, in which the 15 most recent articles were chosen, including the five most cited articles in this database. The reading of these papers facilitated the literature review on the theme proposed by this research, to identify the applications of MCDA methods in the product development processes in several industries.
The third stage was modeling the problem identified, to describe it in detail with the help of tools such as rich picture and mind map. The fourth step was structuring the solution by applying the hybrid method SWARA-MOORA-3NAG. Finally, the results were analyzed in the last step so that the ordering proposed by the hybrid method chosen was adjusted for the process of the analyzed company.
4. Description of the Problem
Ordering suppliers in the public administration’s bidding processes or the quotation stages in remote administration is fundamental for choosing products or services that meet the customer’s expectations. However, in some processes, the criterion weight of the cost and lead time sent by these suppliers is greater than other technical criteria. In this scenario, the contracting company can opt for the lowest cost and shorter lead time without having a detailed technical analysis that ensures the reliability of what is being offered. Generally, the technical analysis is performed by a team with technical knowledge, who compares the requirements requested in the technical specification with the technical proposal of the supplier. The cost and lead time analysis depends on evaluating other teams, such as the supply chain and projects.
In order to analyze this scenario in the company chosen for this research, it was observed that the engineering department is responsible for elaborating a technical specification of the product to be developed with all the requirements of the project. This technical specification is sent to the supply chain department, which directs it to the suppliers to submit the commercial and technical proposals. While technical proposals are analyzed by engineering, the commercial proposals are verified by supply chain and project departments.
Based on the process of the company analyzed, it was found that the ordering of suppliers indicated by the engineering team had a technical characteristic in which fulfilling the requested requirements was fundamental to the project’s success. However, the proposed ordering was based on requirements that had the same weight, through a document generated in Microsoft Excel, as shown in Table 1. Additionally, the definitions of the requirements proposed in this research are based on the documentation already used by the company analyzed, following systems engineering principles. The evaluation of suppliers followed the requirements list included in the technical specification document sent to the vendors.

Table 1.
Technical analysis used by the company.
The score entered ranges from 0 to 100, according to the requirements requested by engineering in the technical specification sent to the supplier. For example, if there are 100 design requirements and the vendor has submitted a technical proposal with 87 requirements met, the score will be 87. In addition, the technical analysis of suppliers consists of the structuring of seven requirements that must be checked in the technical proposal received. The engineering department prepared the description of each condition according to Table 2.

Table 2.
Description of technical requirements.
If all the requirements proposed by the engineering team had the same weight, there would be no need to use the MCDA methods since the analysis methodology proposed by engineering would meet the ordering requirements. However, it was found that this method was problematic because the non-inclusion of all project documentation by the supplier, such as the design databook, could not have the same weight as meeting the design requirements. It was observed that some suppliers chose not to provide the design databook due to some information that was considered as the intellectual property of each supplier, and it differentiated them from its competitors. Therefore, the ordering proposed by engineering could be improved so that there was the inclusion of weights by requirements, and in this case, the MCDA methods become fundamental to assist the engineering department in choosing the best technical proposal.
To assist in this stage of the identification of problems, two structuring tools were used: rich picture and mind map. The rich picture was fundamental for the macro analysis of the problem, in which the interruption of an oil well’s production allows the implementation of several solutions for subsea intervention so that it returns to its maximum production, as shown in Figure 2.
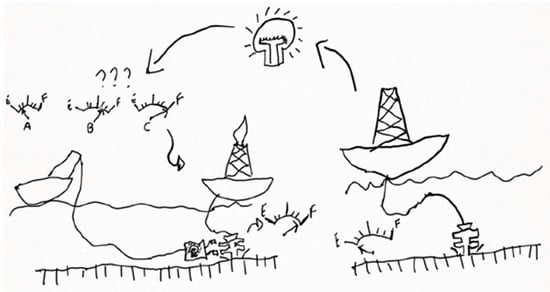
Figure 2.
Rich picture. Source: The authors. Note: This figure was produced by soft system methodology (SSM) [41].
Additionally, the mind map (e.g., Figure 3) was essential for the visualization of the requirements that are fundamental to the engineering department in the analysis of the technical proposal sent by suppliers, so that the best solution is chosen for the return to production of the oil well.
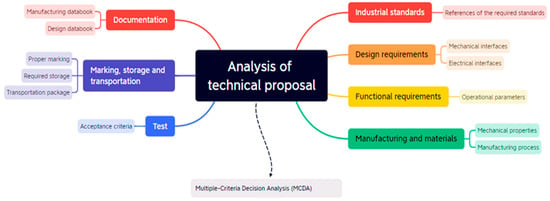
Figure 3.
Mind map.
5. Proposal of the Solution
5.1. Theoretical Foundation for the SWARA-MOORA-3NAG Method
According to Keršuliene et al. [42], the SWARA (step-wise weight assessment ratio analysis) method allows the inclusion of the expert’s opinion about the significant proportion of the attributes in the rational decision determination process. Regarding the MOORA (multiobjective optimization based on ratio analysis) method, the multiple objective optimization, which refers to a matrix of alternative responses to objectives, is essential for the alternatives to be classified according to the index obtained [43]. In addition to the SWARA and MOORA methods, Hermogenes et al. [44] add two normalizations to the existing normalization, and also present an overall absolute ordering represented by the 3NAG identification in the method.
Keršuliene et al. [42] define that the SWARA method begins with defining and ordering the criteria. The decision-maker determines the most relevant criterion according to their perception, then compares it with the other criteria by ranking priorities. The reported values in these views are called . Equation (1) presents the step in which it is necessary to calculate the coefficient from the value .
For example, if the most important criterion is the functional requirement and the second most important is manufacturing requirement and materials, which is 5% less important than the functional requirement, this means that of the functional requirement will be zero and the of manufacturing and materials requirements will be 0.05. Therefore, of the functional requirement will be 1, and the of manufacturing and materials requirements will be 1.05. Then, in Equation (2), are the attribute weight, and the weights are recalculated, in which will be equal to 1 for the first criterion, and for the other criteria, it is necessary to divide the result of the previous criterion by of the criterion that is being analyzed.
Finally, the final weight is calculated according to Equation (3).
The MOORA method proposed by Brauers and Zavadskas [43] is also known as the matrix of responses of the different alternatives for different objectives, where is the response of alternative to objective , and . Equation (4) represents the dimensionless number of the normalized response in the interval between zero and one, in which the alternative is better when closer to zero.
The answers are added in maximization and subtracted in minimization according to Equation (5).
where corresponds to the objectives of maximization and to the objectives of minimization. All the values of criteria are added to each alternative, and, in the end, the total subtraction of these criteria for each alternative is performed. After performing these steps for all alternatives, you can order them to define the best options. Equation (6), proposed by Brauers and Zavadskas [43], measures the distance between the alternatives and the reference point by the metric Tchebycheff Min-Max, where the coordinate from the reference point of the maximum objective.
After applying the SWARA, MOORA, and metric Tchebycheff Min-Max methods, Hermogenes et al. [44] propose subtracting the distances from the alternatives to verify the absolute ordering as a result of the first normalization from the MOORA method, according to Equation (7). This equation belongs to the 3NAG method, in which it adds two normalizations to the normalization performed by the MOORA method, as well as including three orders to propose the overall absolute ordering.
where is the cardinal value of each alternative in absolute ordering in the first normalization, is the cardinal value of the alternative observed in the MOORA method, and is the metric Tchebycheff Min-Max calculation of the cardinal value of the alternative. After this first absolute ordering, Hermogenes et al. [44] recommend applying the method a second time. However, in the second normalization stage, , which is the ratio of the element by the sum of the elements, should be used, as per Equation (8).
After normalization with this new equation, it is necessary to apply the method to the end, when new absolute orderings will be checked according to Equation (9), where is the cardinal value of each alternative in absolute ordering in the second normalization.
Next, it is necessary to apply the methods for the third and final time, using the same values of the decision matrix, in which the equation of the third normalization stage, , is the ratio of the element by the maximum value observed in the analyzed criterion, as presented in Equation (10).
After normalization with Equation (10), it is necessary to apply the method to the end to find the new absolute ordering as indicated in Equation (11), where is the cardinal value of each alternative in absolute ordering in the third normalization.
Finally, Hermogenes et al. [44] emphasize that during the analysis of the results of absolute orderings generated from each normalization, it is necessary to add the values observed for each alternative, as presented in Equation (12).
where represents the value of the overall absolute ordering of each alternative, in which and indicate that the sum begins in the first alternative and extends to the last analyzed alternative. Additionally, indicates the absolute orderings analyzed in the previous steps, represented by the sum of , , and for each alternative analyzed. Hermogenes et al. [44] mention that although the method uses three normalization processes, the simplicity in its execution still remains because only the normalization equations must be changed in each cycle to obtain a more robust result that helps the decision-maker.
5.2. Practical Application
In order to apply the SWARA-MOORA-3NAG method, the SM-3NAG software proposed by Hermogenes et al. [44] was used to sort the suppliers. Initially, the alternatives were inserted in the software as suppliers A, B, and C. Then, the criteria were included in order of preference, with the classification of monotonic cost or profit. The monotonic cost criterion (C) defines that the higher the value, the worse it will be for the alternative. In contrast, the monotonic criterion of profit (P) means that the higher the value, the better it will be for the alternative. Table 3 presents the information in the software for the monotonic criteria of cost and profit.

Table 3.
Definition of criteria.
After defining the alternatives and criteria, the weights of each criterion were inserted into the software according to Table 4.

Table 4.
Evaluation of criteria weights.
The choice of criteria weights was based on the importance of each requirement in the proposal submitted by the suppliers. The functional and design requirements are important to ensure that the product proposed by the supplier meets the project’s requirements. Despite its relevance, the definition of the manufacture method and raw material used has a lower weight than the functional requirements and design because the suppliers can offer different materials or change the manufacturing process but still meet the product’s design and functional characteristics. The tests are mandatory for product delivery. However, the suppliers do not always detail these tests at this design stage because the technical details will still be discussed in the project’s progress.
Additionally, the industrial standards have mandatory or recommended requirements, so suppliers would not need to include the recommended requirements by the standard in their proposal. Generally, the functional and design requirements defined by the engineering team already follow the mandatory requirements of the applied industrial standard. Despite its importance, the criterion of marking, storage, and transport was also not considered as critical as the other criteria mentioned. Finally, some suppliers choose not to submit all the design and manufacturing documentation of the project because it contains intellectual property that differs from competitors, so it obtained the lowest weight among the chosen criteria.
6. Discussion of the Results and Final Considerations
After the definition of the weights, the data in Table 1 were included in the software so that the ordering and normalization of the SWARA-MOORA-3NAG method could be performed. After the software was run, the criteria weights were obtained according to Table 5.

Table 5.
The final weight of criteria.
Table 6 shows the absolute orderings in each normalization and the overall absolute ordering, indicating that supplier C presented the best technical proposal to the engineering department.

Table 6.
Absolute ordering.
Note that the normalizations of the three absolute orderings did not change the overall absolute ordering, keeping vendor C as the first option, vendor B as the second, and vendor A as the last option. Comparing Table 3 with Table 1 presented in Section 4 of this paper, it is observed that prior to implementing the hybrid method, the ordering made by the engineering department would choose supplier A as the best option, since the criterion used had the same weight for all the requirements evaluated in the technical proposal. Therefore, the application of the hybrid method SWARA-MOORA-3NAG made it possible to insert the weights of the criteria to be ordered so that the decision-maker can use this information to differentiate supplier C from supplier B since, according to Table 1, suppliers B and C had the same score in the analysis previously made by the engineering department.
This research applied the concepts of the hybrid method SWARA-MOORA-3NAG in the analysis of technical proposals of subsea intervention equipment to meet the following specific objectives: (1) to identify the problems encountered in the analysis of the technical proposals of suppliers; (2) to propose a multicriteria decision analysis method to assist engineers in this analysis; and (3) to apply the SWARA-MOORA-3NAG method and analyze the results obtained with its implementation.
The identification of the problem showed that the analysis of technical proposals carried out by the engineering department of the analyzed company required improvements in the choice of the most technically suitable supplier according to the requirements requested. In addition, the proposition of the multicriteria decision analysis method SWARA-MOORA-3NAG, as well as the theoretical basis applied to this method, allowed a new analysis methodology to be carried out by the engineers. Finally, applying the SWARA-MOORA-3NAG method presented a new absolute ordering different from the previous ordering process used by the engineering department.
Additionally, the relationship between humans and A.I. (artificial intelligence), as MCDA methods, should exist in a social system in which humans will always actively participate in some decision-making loops that will influence the operations of A.I. [45]. Then, carefully questioning and evaluating whether A.I. deployment is beneficial from a team perspective is important when applying the MCDA methods in the current process [46,47,48,49,50,51,52]. Even if the SWARA-MOORA-3NAG aids in the decision making of the best supplier to attend the technical requirements, the definition of the weight for each requirement depends on the human factor with proper technical knowledge.
The contributions of this research to the organizational scope of the company can be verified in the analysis processes carried out after the insertion of SWARA-MOORA-3NAG, emphasizing the importance of defining the weights of the criteria to engineers to assist in decision making. In relation to the academic field, this research contributed to the approach of a new hybrid method of MCDA in the oil and gas industry, presenting results that can be analyzed by several researchers for new applications. Compared to other MCDA methods, SWARA-MOORA-3NAG contributes to eliminating the possibility of doubts because of the proposal to run three normalizations, bringing more confidence to decision-makers in the scope proposed in this research.
It is important to highlight that this study is limited to a process of the engineering department of the company analyzed, and the cost and delivery time criteria were not inserted as criteria of the hybrid method applied, because they were not part of the scope of technical analysis performed by the engineering department. Finally, the researcher interested in applying this methodology can evaluate scenarios in other departments, such as the project or supply chain, to apply SWARA-MOORA-3NAG with the inclusion of the cost and delivery time criteria and evaluate whether it will affect the overall absolute ordering presented in this article.
Author Contributions
Conceptualization, P.G.F.; data curation, O.L.G.Q. and E.L.P.J.; formal analysis, R.L.F.B.; investigation, P.G.F.; methodology, P.G.F.; project administration, M.d.S.; supervision, C.F.S.G. and M.d.S.; validation, C.d.S.R.J.; writing—original draft, P.G.F.; writing—review and editing, M.P.B. and R.C.A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
https://github.com/mcda-software/SWARA-MOORA-3NAG/blob/main/SM-3NAG.py (accessed on 20 January 2022).
Conflicts of Interest
The authors declare that they have no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AHP | Analytic hierarchy process |
| ANP | Analytical network process |
| COMET | Characteristic objects method |
| COPRAS | Complex proportional assessment |
| CRITIC | Criteria importance through intercriteria correlation |
| DARIA-TOPSIS | Data variability assessment technique for order of preference by similarity to ideal solution |
| DEX | Decision expert |
| DRSA | Dominance-based rough set approach |
| EA FAHP | Extent analysis fuzzy analytic hierarchy process |
| ELECTRE | Élimination et choix traduisant la realité (French) |
| ELECTRE-MOr | Élimination et choice traduisant la realité-multicriteria sorting method with ordinal weight input and multiple decision maker |
| FuzzyTOPSIS | Fuzzy technique for order preference by similarity to an ideal solution |
| G-COPRAS | Grey complex proportional assessment |
| MACBETH | Measuring attractiveness by a categorical-based evaluation technique |
| MABAC | Multi-attributive border approximation area comparison |
| MAIRCA | Multi-attributive ideal-real comparative analysis |
| MCDA | Multicriteria decision analysis |
| MCDM | Multicriteria decision making |
| MODM | Multiobjective decision making |
| MOORA | Multiobjective optimization by ratio analysis |
| MULTIMOORA | MOORA plus the full multiplicative form |
| NAIADE | Novel approach to imprecise assessment and decision environment |
| PCCA | Pairwise criterion comparison approach |
| PROMETHEE | Preference ranking organization method for enrichment of evaluation |
| QFD | Quality function deployment |
| SAPEVO-M | Simple aggregation of preferences expressed by ordinal vectors group decision making |
| SF-AHP | Spherical fuzzy analytical hierarchical process |
| SIMUS | Sequential interactive modelling for urban systems |
| SPOTIS | Stable preference ordering towards ideal solution |
| SWARA | Step-wise weight assessment ratio analysis |
| WASPAS | Weighted aggregated sum product assessment |
| WPM | Weighted product model |
| WSM | Weighted sum model |
| TODIM | Tomada de decisão interativa multicritério (Portuguese) |
| TOPSIS | Technique for order of preference by similarity to ideal solution |
| VIKOR | Visekriterijumska optimizacija i kompromisno resenje (Serbian) |
References
- Al Douseri, K.M.M.; Barnes, C.; Young, D.; Peter, E.S. Swellable packers provide a brownfield water management solution in open and cased hole—Case histories including straddles, plugs, slim hole sidetracks and testing in corroded casing. In Proceedings of the SPE Offshore Europe Oil and Gas Conference and Exhibition, Aberdeen, UK, 8–11 September 2009. [Google Scholar]
- Souza Rodrigues, B.; Martins Floriano, C.; Pereira, V.; Costa Roboredo, M. An algorithm to elicitate ELECTRE II, III and IV parameters. Data Technol. Appl. 2021, 55, 82–96. [Google Scholar] [CrossRef]
- Floriano, C.M.; Pereira, V.; Rodrigues, B.S. 3MO-AHP: An inconsistency reduction approach through mono-, multi- or many-objective quality measures. Data Technol. Appl. 2022, 56, 645–670. [Google Scholar] [CrossRef]
- Basilio, M.P.; Brum, G.S.; Pereira, V. A model of policing strategy choice: The integration of the Latent Dirichlet Allocation (LDA) method with ELECTRE I. J. Model. Manag. 2020, 15, 849–891. [Google Scholar] [CrossRef]
- Eke, E.; Iyalla, I.; Andrawus, J.; Prabhu, R. Optimising offshore structures decommissioning—A multi-criteria decision approach. In Proceedings of the Society of Petroleum Engineers—SPE Nigeria Annual International Conference and Exhibition, Online, 11–13 August 2020. [Google Scholar]
- Özakıncı, R.; Kolukısa Tarhan, A. A Decision Analysis Approach for Selecting Software Defect Prediction Method in the Early Phases; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Basilio, L.P.; Noronha, C.; Sousa, D.; Machado, P.; Andreotti, M.; Juliano, D.; Boeira, P. Economic evaluation of emerging technologies in the O&G industry: A model-based systems metaheuristic engineering method. In Proceeding of Rio Oil & Gas Expo and Conference, Rio de Janeiro, Brazil, 21–24 September 2020; Volume 20, p. 413. [Google Scholar]
- Basílio, M.P.; Pereira, V.; Costa, H.G.; Santos, M.; Ghosh, A. A systematic review of the applications of multi-criteria decision aid methods (1977–2022). Electronics 2022, 11, 1720. [Google Scholar] [CrossRef]
- de Assis, G.S.; dos Santos, M.; Basilio, M.P. Use of the WASPAS Method to Select Suitable Helicopters for Aerial Activity Carried Out by the Military Police of the State of Rio de Janeiro. Axioms 2023, 12, 77. [Google Scholar] [CrossRef]
- Costa, I.P.A.; Costa, A.P.A.; Sanseverino, A.M.; Gomes, C.F.S.; Santos, M. Bibliometric studies on multi-criteria decision analysis (mcda) methods applied in military problems. Pesqui. Oper. 2022, 42, 1–26. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Siksnelyte-Butkiene, I.; Zavadskas, E.K.; Streimikiene, D. Multi-criteria decision-making (MCDM) for the assessment of renewable energy technologies in a household: A review. Energies 2020, 13, 1164. [Google Scholar] [CrossRef]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are MCDA methods benchmarkable? a comparative study of TOPSIS., VIKOR., COPRAS, and PROMETHEE II methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of-the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Sałabun, W.; Piegat, A.; Wątróbski, J.; Karczmarczyk, A.; Jankowski, J. The Comet Method: In the First MCDA Method Completely Resistant to Rank Reversal Paradox; European Working Group “Multiple Criteria Decision Aiding”: Agios Nikolaos, Greece, 2019; Volume 39. [Google Scholar]
- Kizielewicz, B.; Sałabun, W. A new approach to identifying a multi-criteria decision model based on stochastic optimization techniques. Symmetry 2020, 12, 1551. [Google Scholar] [CrossRef]
- Ayan, B.; Abacıoğlu, S. Bibliometric analysis of the MCDM methods in the last decade: WASPAS, MABAC, EDAS, CODAS, COCOSO, and MARCOS. Int. J. Bus. Econ. Stud. 2022, 4, 65–85. [Google Scholar] [CrossRef]
- Stanković, M.; Stević, Ž.; Das, D.K.; Subotić, M.; Pamučar, D. A new fuzzy MARCOS method for road traffic risk analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Pythagorean fuzzy choquet integral based MABAC method for multiple attribute group decision making. Int. J. Intell. Syst. 2016, 31, 989–1020. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Więckowski, J.; Wątróbski, J. Toward reliability in the MCDA rankings: Comparison of distance-based methods. In Intelligent Decision Technologies; Czarnowski, I., Howlett, R.J., Jain, L.C., Eds.; Smart Innovation, Systems and Technologies Series; Springer: Singapore, 2021; pp. 321–329. [Google Scholar]
- Wątróbsk, J.; Bączkiewicz, A.; Ziemba, E.; Sałabun, W. Sustainable cities, and communities assessment using the DARIA-TOPSIS method. Sustain. Cities Soc. 2022, 83, 103926. [Google Scholar] [CrossRef]
- Stoilova, S.; Munier, N. A novel fuzzy SIMUS multi-criteria decision-making method: An application in railway passenger transport planning. Symmetry 2021, 13, 483. [Google Scholar] [CrossRef]
- De Paula, N.O.B.; Costa, I.P.A.; Drumond, P.; Moreira, M.A.L.; Gomes, C.F.S.; Santos, M.; Maêda, S.M.N. Strategic support for the distribution of vaccines against COVID-19 to Brazilian remote areas: A multi-criteria approach in the light of the ELECTRE-MOr method. Procedia Comput. Sci. 2022, 199, 40–47. [Google Scholar] [CrossRef]
- Tenório, F.M.; Moreira, M.A.L.; Costa, I.P.A.; Gomes, C.F.S.; Santos, M.; Silva, F.C.A.; Silva, R.F.; Basilio, M.P. SADEMON: The Computational Web Platform to the SAPEVO-M Method. Procedia Comput. Sci. 2022, 214, 125–132. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Oztaysi, B. Fuzzy multi-criteria decision-making: A literature review. Int. J. Comput. Intell. Syst. 2015, 8, 637–666. [Google Scholar] [CrossRef]
- Niteroi, R.J.; Hermogenes, L.R.S. Ordering Sales Channels for E-Commerce: Structuring from the Momentum Method and Modeling with the Proposed New SWARA-MOORA-3NAG Multi-Criteria Method. Master Thesis, Federal Fluminense University, Rio de Janeiro, Brazil, 2022. [Google Scholar]
- Janowska-Renkas, E.; Jakiel, P.; Fabianowski, D.; Matyjaszczyk, D. Optimal Selection of High-Performance Concrete for Post-Tensioned Girder Bridge Using Advanced Hybrid MCDA Method. Materials 2021, 14, 6553. [Google Scholar] [CrossRef]
- Marleau Donais, F.; Abi-Zeid, I.; Waygood, E.O.D.; Lavoie, R. A Framework for Post-Project Evaluation of Multi-criteria Decision Aiding Processes from the Stakeholders′ Perspective: Design and Application. Group Decis. Negot. 2021, 30, 1161–1191. [Google Scholar] [CrossRef]
- Zhao, J.; Patwary, A.K.; Qayyum, A.; Alharthi, M.; Bashir, F.; Mohsin, M.; Hanif, I.; Abbas, Q. The determinants of renewable energy sources for the fueling of green and sustainable economy. Energy 2022, 238, 122029. [Google Scholar] [CrossRef]
- Sisman, S.; Ergul, I.; Aydinoglu, A.C. Designing GIS-based site selection model for urban investiment planning in smart cities with the case of electric vehicle charging stations. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2021, 46, 515–522. [Google Scholar] [CrossRef]
- Motuziene, V.; Rogoža, A.; Lapinskiene, V.; Vilutiene, T. Construction solutions for energy efficient single-family house based on its life cycle multi-criteria analysis: A case study. J. Clean. Prod. 2016, 112, 532–541. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Vo, N.T.M.; Nguyen, V.T.T. Wireless Communications for Data Security: Efficiency Assessment of Cybersecurity Industry—A Promising Application for UAVs. Drones 2022, 6, 363. [Google Scholar] [CrossRef]
- Franceschini, F.; Rossetto, S. QFD: The problem of comparing technical/engineering design requirements. Res. Eng. Des. 1995, 7, 270–278. [Google Scholar] [CrossRef]
- Abraham, M.K.; Pandey, V.; Lal, R.R. Investigation of customer focussed steel plant product with quality function deployment. Int. J. Mech. Eng. Technol. 2017, 8, 19–25. [Google Scholar]
- Vongvit, R.; Kongprasert, N.; Fournaise, T.; Collange, T. Integration of Fuzzy-QFD and T.R.I.Z. methodology for product development. In Proceedings of the 3rd International Conference on Control, Automation and Robotics (ICCAR), Nagoya, Japan, 22–24 April 2017; pp. 326–329. [Google Scholar]
- Oliveira, A.S.; Gomes, C.F.S.; Clarkson, C.T.; Sanseverino, A.M.; Barcelos, M.R.S.; Costa, I.P.A.; Santos, M. Multiple Criteria Decision Making and Prospective Scenarios Model for Selection of Companies to Be Incubated. Algorithms 2021, 14, 111. [Google Scholar] [CrossRef]
- Simões, J.C.M.; Ferreira, F.A.F.; Peris-Ortiz, M.; Ferreira, J.J.M. A cognition-driven framework for the evaluation of startups in the digital economy: Adding value with cognitive mapping and rule-based expert systems. Manag. Decis. 2020, 58, 2327–2347. [Google Scholar] [CrossRef]
- Dang, T.-T.; Nguyen, N.-A.-T.; Nguyen, V.-T.-T.; Dang, L.-T.-H. A Two-Stage Multi-Criteria Supplier Selection Model for Sustainable Automotive Supply Chain under Uncertainty. Axioms 2022, 11, 228. [Google Scholar] [CrossRef]
- Barata, J.F.F.; Quelhas, O.L.G.; Costa, H.G.; Gutierrez, R.H.; Lameira, V.J.; Meiriño, M.J. Multi-criteria indicator for sustainability rating in suppliers of the oil and gas industries in Brazil. Sustainability 2014, 6, 1107–1128. [Google Scholar] [CrossRef]
- Miri Lavasani, S.M.; Yang, Z.; Finlay, J.; Wang, J. Fuzzy risk assessment of oil and gas offshore wells. Process Saf. Environ. Prot. 2011, 89, 277–294. [Google Scholar] [CrossRef]
- Checkland, P.B. Soft systems methodology. In Rational Analysis for a Problematic World Revisited; Rosenhead, J., Ed.; John Wiley & Sons: Chichester, UK, 1989; p. 386. [Google Scholar]
- Keršuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Zavadskas, E.K. The MOORA method and its application to privatization in a transition economy. Control Cybern. 2006, 35, 445–469. [Google Scholar]
- Hermogenes, L.; Almeida, I.; Gomes, C.; Santos, M. Proposta do método híbrido SWARA-MOORA-3NAG e desenvolvimento de uma ferramenta computacional em PYTHON. In Proceedings of the LIV Simposio Brasileiro De Pesquisa Operacional, Juiz de Fora, Brazil, 8–11 November 2022; p. 152417. [Google Scholar]
- Abbas, H.A. Social integration of artificial intelligence: Functions, automation, allocation logic and huma-autonomy trust. Cogn. Comput. 2019, 11, 159–171. [Google Scholar] [CrossRef]
- Bansal, G.; Nushi, B.; Kamar, E.; Horvitz, E.; Weld, D.S. Is the most accurate AI the best teammate? Optimizing A.I. for teamwork. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; pp. 11405–11414. [Google Scholar]
- Rocha Junior, C.S.; Moreira, M.A.L.; Costa, I.P.A.; Gomes, C.F.S.; Santos, M.; Silva, F.C.A.; Pereira, R.C.A.; Basilio, M.P.; Pereira, D.A.M. IoT technology proposal for multi-adaptative sensing integrated into data science and analytics scenarios. Procedia Comput. Sci. 2022, 214, 108–116. [Google Scholar] [CrossRef]
- Nassim Mellem, P.M.; de Araújo Costa, I.P.; de Araújo Costa, A.P.; Lellis Moreira, M.Â.; Simões Gomes, C.F.; dos Santos, M.; de Pina Corriça, J.V. Prospective Scenarios Applied in Course Portfolio Management: An Approach in Light of the Momentum and ELECTRE-MOr Methods. Procedia Comput. Sci. 2022, 199, 48–55. [Google Scholar] [CrossRef]
- Santos, N.; Rocha Junior, C.d.S.; Moreira, M.Â.L.; Santos, M.; Gomes, C.F.S.; Costa, I.P.d.A. Strategy Analysis for Project Portfolio Evaluation in a Technology Consulting Company by the Hybrid Method THOR. Procedia Comput. Sci. 2022, 199, 134–141. [Google Scholar] [CrossRef]
- Costa, I.P.d.A.; Moreira, M.Â.L.; Costa, A.P.d.A.; de Souza de Barros, L.F.H.; Gomes, C.F.S.; Santos, M.D. Strategic Study for Managing the Portfolio of IT Courses Offered by a Corporate Training Company: An Approach in the Light of the ELECTRE-MOr Multicriteria Hybrid Method. Int. J. Inf. Technol. Decis. Mak. 2022, 21, 351–379. [Google Scholar] [CrossRef]
- Costa, I.P.d.A.; Basílio, M.P.; Maêda, S.M.d.N.; Rodrigues, M.V.G.; Moreira, M.Â.L.; Gomes, C.F.S.; dos Santos, M. Algorithm Selection for Machine Learning Classification: An Application of the MELCHIOR Multicriteria Method. Front. Artif. Intell. Appl. 2021, 341, 154–161. [Google Scholar]
- de Almeida, I.D.P.; de Araújo Costa, I.P.; de Araújo Costa, A.P.; de Pina Corriça, J.V.; Lellis Moreira, M.Â.; Simões Gomes, C.F.; dos Santos, M. A Multicriteria Decision-Making Approach to Classify Military Bases for the Brazilian Navy. Procedia Comput. Sci. 2022, 199, 79–86. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).