A Multivariate Deep Learning Model with Coupled Human Intervention Factors for COVID-19 Forecasting
Abstract
:1. Introduction
2. Methods and Data
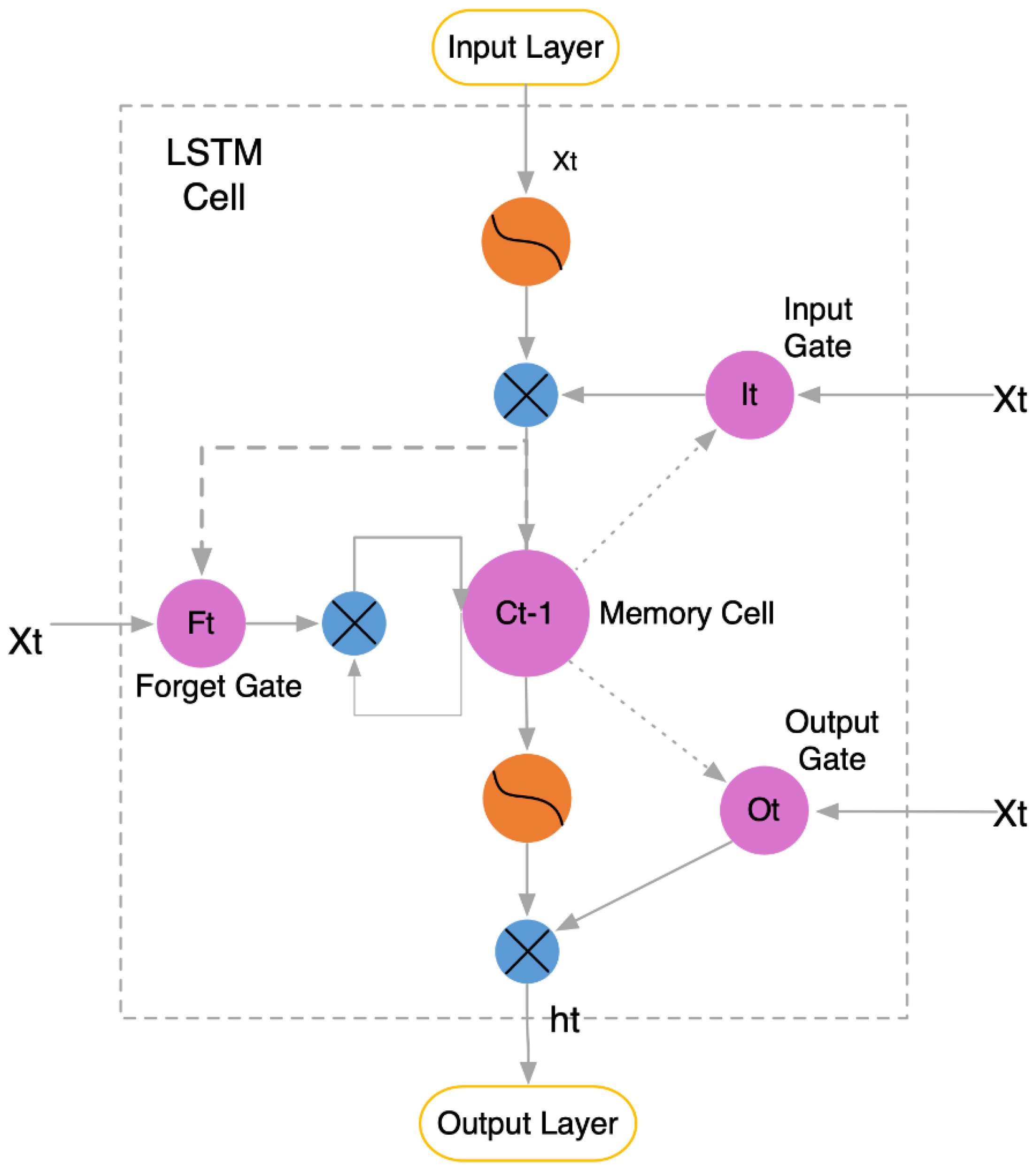
2.1. LSTM Model Principles
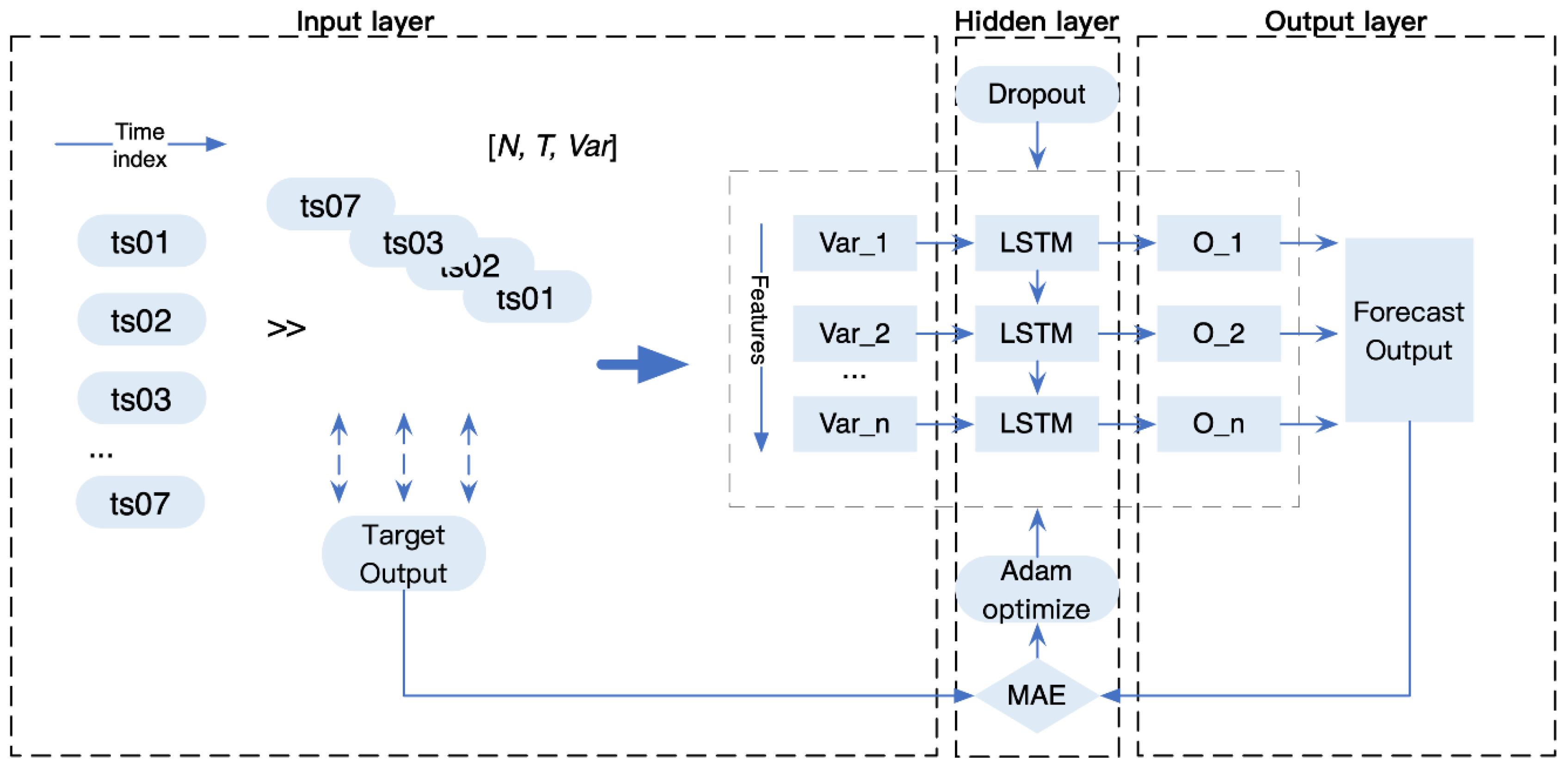
2.2. Multivariate Epidemic Prediction Model with Coupled Human Factors
2.3. Data Collection
2.3.1. COVID-19 Data Collection
2.3.2. Human Intervention Data Collection
3. Experiment
3.1. Evaluation Metrics
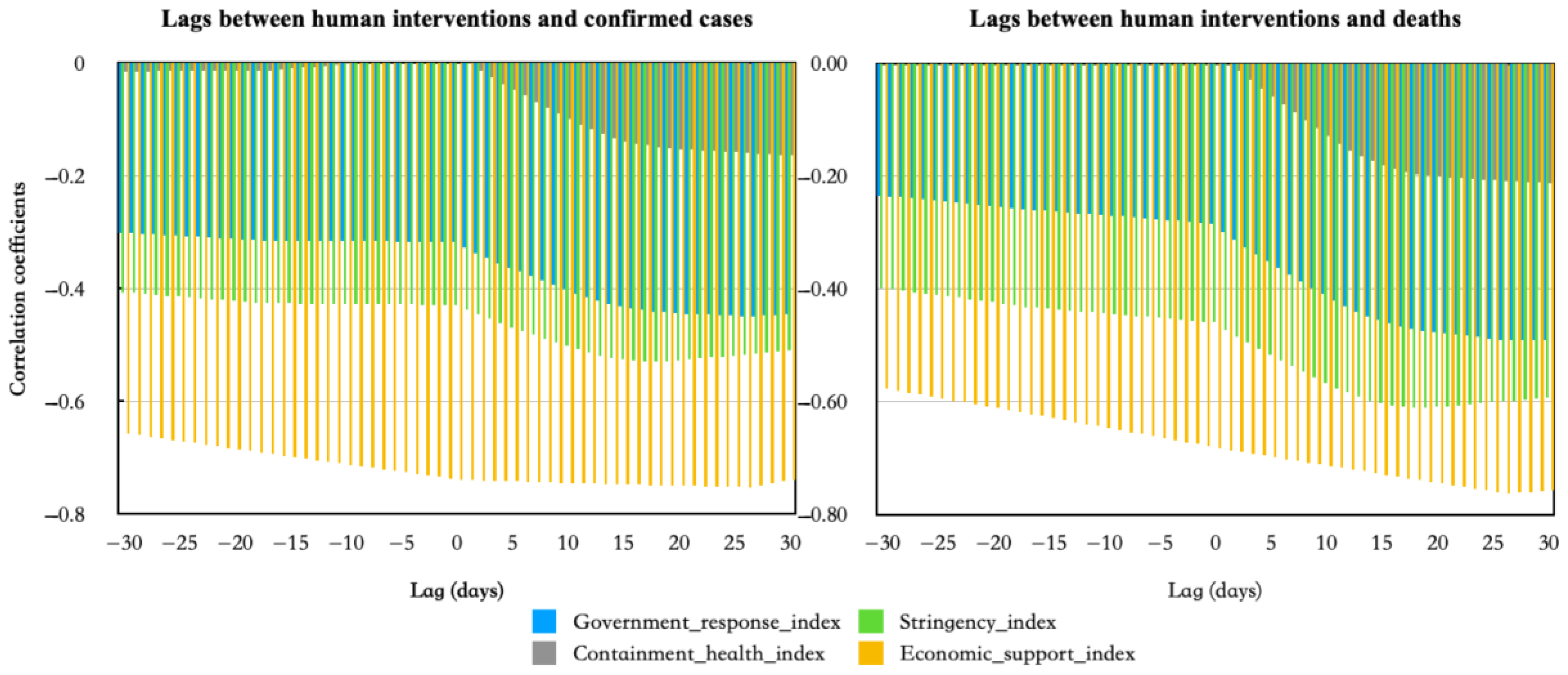
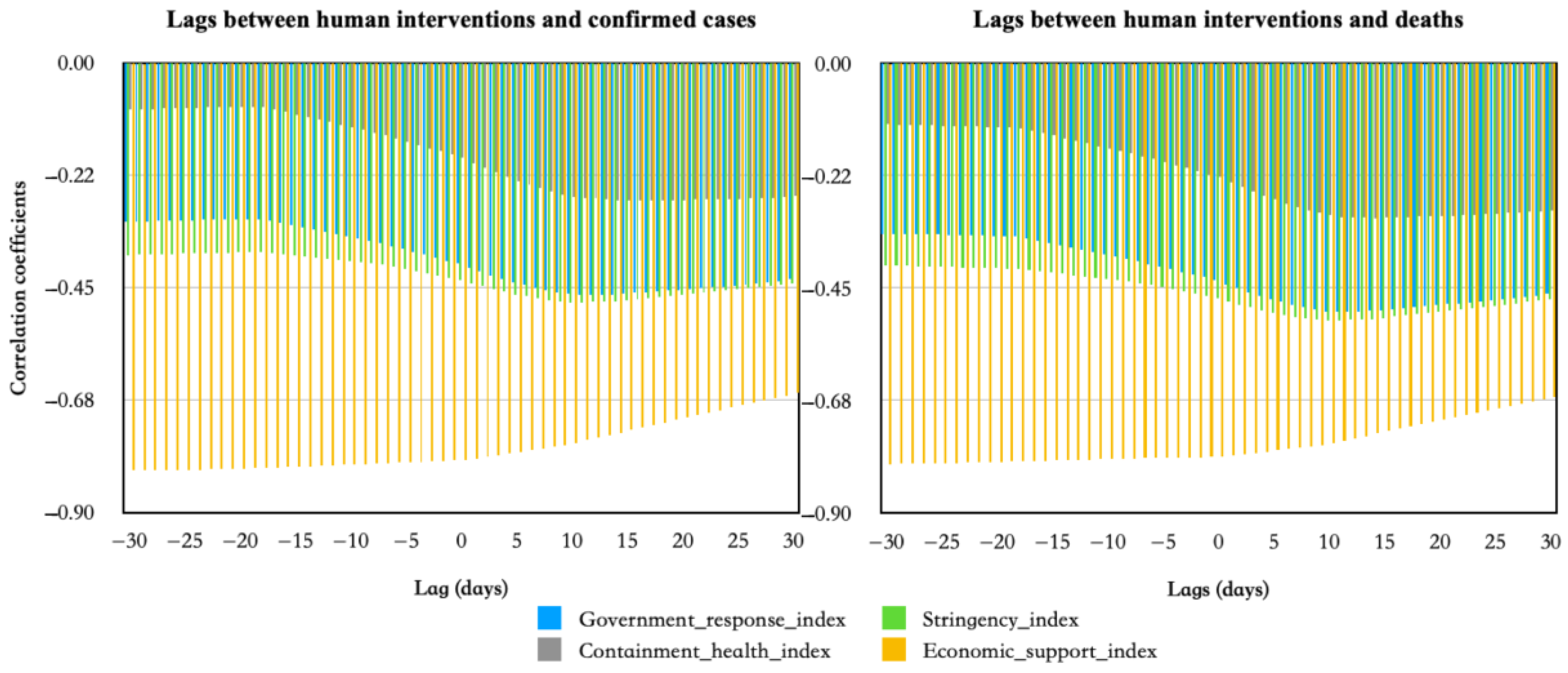
3.2. Results of Correlation and Lag between Human Influences and COVID-19 Epidemic
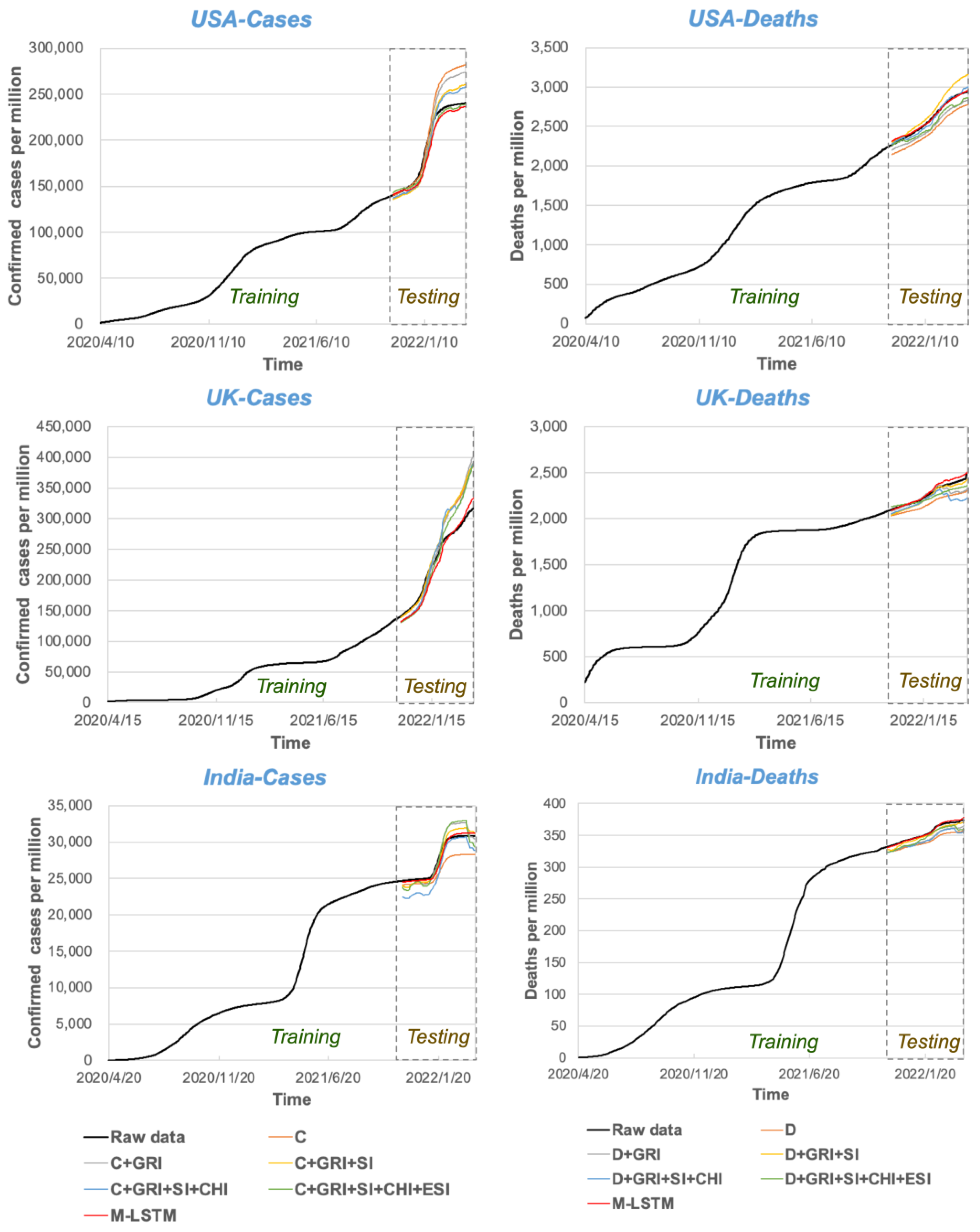
3.3. Evaluation Results of the Prediction Effectiveness of Multivariate LSTM Models Coupled with Human Influences
4. Conclusion and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baker, R.E.; Mahmud, A.S.; Miller, I.F.; Rajeev, M.; Rasambainarivo, F.; Rice, B.L.; Takahashi, S.; Tatem, A.J.; Wagner, C.E.; Wang, L.F.; et al. Infectious Disease in an Era of Global Change. Nat. Rev. Microbiol. 2022, 20, 193–205. [Google Scholar] [CrossRef] [PubMed]
- Yi, J.; Zhang, H.; Mao, J.; Chen, Y.; Zhong, H.; Wang, Y. Review on the COVID-19 Pandemic Prevention and Control System Based on AI. Eng. Appl. Artif. Intell. 2022, 114, 105184. [Google Scholar] [CrossRef] [PubMed]
- Kassania, S.H.; Kassanib, P.H.; Wesolowskic, M.J.; Schneidera, K.A.; Detersa, R. Automatic Detection of Coronavirus Disease (COVID-19) in X-Ray and CT Images: A Machine Learning Based Approach. Biocybern. Biomed. Eng. 2021, 41, 867–879. [Google Scholar] [CrossRef] [PubMed]
- Zgheib, R.; Kamalov, F.; Chahbandarian, G.; Labban, O.E. Diagnosing COVID-19 on Limited Data: A Comparative Study of Machine Learning Methods. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Shenzhen, China, 12–15 August 2021; Volume 12837 LNCS. [Google Scholar]
- Akinnuwesi, B.A.; Fashoto, S.G.; Mbunge, E.; Odumabo, A.; Metfula, A.S.; Mashwama, P.; Uzoka, F.M.; Owolabi, O.; Okpeku, M.; Amusa, O.O. Application of Intelligence-Based Computational Techniques for Classification and Early Differential Diagnosis of COVID-19 Disease. Data Sci. Manag. 2021, 4, 10–18. [Google Scholar] [CrossRef]
- Qu, Z.; Li, Y.; Jiang, X.; Niu, C. An Innovative Ensemble Model Based on Multiple Neural Networks and a Novel Heuristic Optimization Algorithm for COVID-19 Forecasting. Expert Syst. Appl. 2023, 212, 118746. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Liu, P.; Troeger, C.E.; Carter, A.; Reiner, R.C.; Barber, R.M.; Collins, J.; Lim, S.S.; Pigott, D.M.; Vos, T.; et al. Predictive Performance of International COVID-19 Mortality Forecasting Models. Nat. Commun. 2021, 12, 2609. [Google Scholar] [CrossRef]
- Guo, S.; Fang, F.; Zhou, T.; Zhang, W.; Guo, Q.; Zeng, R.; Chen, X.; Liu, J.; Lu, X. Improving Google Flu Trends for COVID-19 Estimates Using Weibo Posts. Data Sci. Manag. 2021, 3, 13–21. [Google Scholar] [CrossRef]
- Ng, P.C.; Spachos, P.; Plataniotis, K.N. COVID-19 and Your Smartphone: BLE-Based Smart Contact Tracing. IEEE Syst. J. 2021, 15, 5367–5378. [Google Scholar] [CrossRef] [PubMed]
- Esmail, S.; Danter, W. Viral Pandemic Preparedness: A Pluripotent Stem Cell-Based Machine-Learning Platform for Simulating SARS-CoV-2 Infection to Enable Drug Discovery and Repurposing. Stem. Cells Transl. Med. 2021, 10, 239–250. [Google Scholar] [CrossRef]
- Ly, K.T. A COVID-19 Forecasting System Using Adaptive Neuro-Fuzzy Inference. Financ. Res. Lett. 2020, 41, 101844. [Google Scholar] [CrossRef]
- Parbat, D.; Chakraborty, M. A Python Based Support Vector Regression Model for Prediction of COVID19 Cases in India. Chaos Solitons Fractals 2020, 138, 109942. [Google Scholar] [CrossRef] [PubMed]
- Chimmula, V.K.R.; Zhang, L. Time Series Forecasting of COVID-19 Transmission in Canada Using LSTM Networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef]
- Shastri, S.; Singh, K.; Kumar, S.; Kour, P.; Mansotra, V. Time Series Forecasting of Covid-19 Using Deep Learning Models: India-USA Comparative Case Study. Chaos Solitons Fractals 2020, 140, 110227. [Google Scholar] [CrossRef]
- Kırbaş, İ.; Sözen, A.; Tuncer, A.D.; Kazancıoğlu, F.Ş. Comparative Analysis and Forecasting of COVID-19 Cases in Various European Countries with ARIMA, NARNN and LSTM Approaches. Chaos Solitons Fractals 2020, 138, 110015. [Google Scholar] [CrossRef] [PubMed]
- Marzouk, M.; Elshaboury, N.; Abdel-Latif, A.; Azab, S. Deep Learning Model for Forecasting COVID-19 Outbreak in Egypt. Process Saf. Environ. Prot. 2021, 153, 363–375. [Google Scholar] [CrossRef]
- Devaraj, J.; Madurai Elavarasan, R.; Pugazhendhi, R.; Shafiullah, G.M.; Ganesan, S.; Jeysree, A.K.; Khan, I.A.; Hossain, E. Forecasting of COVID-19 Cases Using Deep Learning Models: Is It Reliable and Practically Significant? Results Phys. 2021, 21, 103817. [Google Scholar] [CrossRef]
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, V. Inferring Change Points in the Spread of COVID-19 Reveals the Effectiveness of Interventions. Science 2020, 369, eabb9789. [Google Scholar] [CrossRef] [PubMed]
- Haug, N.; Geyrhofer, L.; Londei, A.; Dervic, E.; Desvars-Larrive, A.; Loreto, V.; Pinior, B.; Thurner, S.; Klimek, P. Ranking the Effectiveness of Worldwide COVID-19 Government Interventions. Nat. Hum. Behav. 2020, 4, 1303–1312. [Google Scholar] [CrossRef] [PubMed]
- Hale, T.; Angrist, N.; Goldszmidt, R.; Kira, B.; Petherick, A.; Phillips, T.; Webster, S.; Cameron-Blake, E.; Hallas, L.; Majumdar, S.; et al. A Global Panel Database of Pandemic Policies (Oxford COVID-19 Government Response Tracker). Nat. Hum. Behav. 2021, 5, 529–538. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Coronavirus (COVID-19) Cases—Our World in Data. Available online: https://ourworldindata.org/covid-cases (accessed on 13 February 2022).

| Index Name | Government Response Index | Containment and Health Index | Stringency Index | Economic Support Index |
|---|---|---|---|---|
| C1 | x | x | x | |
| C2 | x | x | x | |
| C3 | x | x | x | |
| C4 | x | x | x | |
| C5 | x | x | x | |
| C6 | x | x | x | |
| C7 | x | x | x | |
| C8 | x | x | x | |
| E1 | x | x | ||
| E2 | x | x | ||
| E3 | ||||
| E4 | ||||
| H1 | x | x | x | |
| H2 | x | x | ||
| H3 | x | x | ||
| H4 | ||||
| H5 | ||||
| H6 | x | x | ||
| H7 | x | x | ||
| H8 | x | x |
| Country | Data Type | Government Response Index | Stringency Index | Containment Health Index | Economic Support Index |
|---|---|---|---|---|---|
| USA | Confirmed cases | −0.318 ** | −0.430 ** | 0.011 | −0.739 ** |
| Deaths | −0.284 ** | −0.460 ** | 0.022 | −0.683 ** | |
| UK | Confirmed cases | −0.642 ** | −0.720 ** | −0.531 ** | −0.766** |
| Deaths | −0.324 ** | −0.526 ** | −0.226 ** | −0.495 ** | |
| India | Confirmed cases | −0.402 ** | −0.434 ** | −0.190 ** | −0.795 ** |
| Deaths | −0.434 ** | −0.470 ** | −0.228 ** | −0.788 ** |
| Dataset | Input Variables | MAE | RMSE | R2 |
|---|---|---|---|---|
| Confirmed cases | C | 24,017.09 | 16,754.50 | 0.642 |
| C + GRI | 19,280.49 | 15,318.06 | 0.769 | |
| C + GRI + SI | 12,011.64 | 10,755.52 | 0.911 | |
| C + GRI + SI + CHI | 10,408.69 | 9229.33 | 0.933 | |
| C + GRI + SI + CHI + ESI | 6960.93 | 5311.93 | 0.970 | |
| M-LSTM (R_thred > 0.4) | 8370.55 | 6751.52 | 0.957 | |
| Deaths | D | 161.50 | 160.10 | 0.478 |
| D + GRI | 109.36 | 107.05 | 0.761 | |
| D + GRI + SI | 108.30 | 91.73 | 0.765 | |
| D + GRI + SI + CHI | 32.36 | 28.48 | 0.979 | |
| D + GRI + SI + CHI + ESI | 82.24 | 73.49 | 0.865 | |
| M-LSTM (R_thred > 0.4) | 20.87 | 15.08 | 0.991 |
| Dataset | Input Variables | MAE | RMSE | R2 |
|---|---|---|---|---|
| Confirmed cases | C | 31,945.93 | 23,168.87 | 0.696 |
| C + GRI | 35,955.69 | 27,135.31 | 0.615 | |
| C + GRI + SI | 34,315.57 | 24,584.63 | 0.650 | |
| C + GRI + SI + CHI | 31,845.91 | 25,464.80 | 0.698 | |
| C + GRI + SI + CHI + ESI | 28,594.80 | 23,038.30 | 0.757 | |
| M-LSTM (R_thred > 0.7) | 12,572.57 | 10,922.31 | 0.953 | |
| Deaths | D | 108.79 | 105.49 | 0.065 |
| D + GRI | 61.08 | 40.12 | 0.705 | |
| D + GRI + SI | 36.46 | 32.90 | 0.895 | |
| D + GRI + SI + CHI | 110.47 | 82.54 | 0.036 | |
| D + GRI + SI + CHI + ESI | 55.33 | 46.36 | 0.758 | |
| M-LSTM (R_thred > 0.5) | 28.62 | 22.13 | 0.935 |
| Dataset | Input Variables | MAE | RMSE | R2 |
|---|---|---|---|---|
| Confirmed cases | C | 1896.81 | 1658.97 | 0.514 |
| C + GRI | 1087.70 | 901.78 | 0.840 | |
| C + GRI + SI | 712.68 | 654.50 | 0.931 | |
| C + GRI + SI + CHI | 1686.22 | 1468.51 | 0.616 | |
| C + GRI + SI + CHI + ESI | 1277.73 | 1104.02 | 0.780 | |
| M-LSTM (R_thred > 0.4) | 426.37 | 343.09 | 0.975 | |
| Deaths | D | 13.65 | 13.38 | 0.005 |
| D + GRI | 9.46 | 9.41 | 0.522 | |
| D + GRI + SI | 4.35 | 4.09 | 0.899 | |
| D + GRI + SI + CHI | 11.51 | 11.18 | 0.293 | |
| D + GRI + SI + CHI + ESI | 7.85 | 7.31 | 0.671 | |
| M-LSTM (R_thred > 0.4) | 1.77 | 1.39 | 0.983 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Z.; Zhang, B.; Wang, H. A Multivariate Deep Learning Model with Coupled Human Intervention Factors for COVID-19 Forecasting. Systems 2023, 11, 201. https://doi.org/10.3390/systems11040201
Qu Z, Zhang B, Wang H. A Multivariate Deep Learning Model with Coupled Human Intervention Factors for COVID-19 Forecasting. Systems. 2023; 11(4):201. https://doi.org/10.3390/systems11040201
Chicago/Turabian StyleQu, Zongxi, Beidou Zhang, and Hongpeng Wang. 2023. "A Multivariate Deep Learning Model with Coupled Human Intervention Factors for COVID-19 Forecasting" Systems 11, no. 4: 201. https://doi.org/10.3390/systems11040201
APA StyleQu, Z., Zhang, B., & Wang, H. (2023). A Multivariate Deep Learning Model with Coupled Human Intervention Factors for COVID-19 Forecasting. Systems, 11(4), 201. https://doi.org/10.3390/systems11040201





