Carbon Reduction Subsidy, Remanufacturing Subsidy or Consumer Recycling Subsidy? A Low-Carbon Closed-Loop Supply Chain Network Operation Decision
Abstract
1. Introduction
- How do the CO2e reduction subsidy, remanufacturing subsidy and consumer recycling subsidy policies affect the production, recycling, CO2e reduction and profit distribution of the LC-CLSCN system?
- When the three policies exist separately, which policy is more conducive to promoting the system’s forward and reverse product circulation, reducing CO2e and promoting the benefits of members and the system?
- Under the coexistence of these three subsidy policies, which policy has a more significant impact on the LC-CLSCN system?
2. Literature Review
2.1. The Decision of CLSCN
2.2. LC-CLSC and Sustainable CLSC Operations Considering Government Policy
2.3. The Operation of LC-CLSCN Considering Government Policy
2.4. Research Gaps
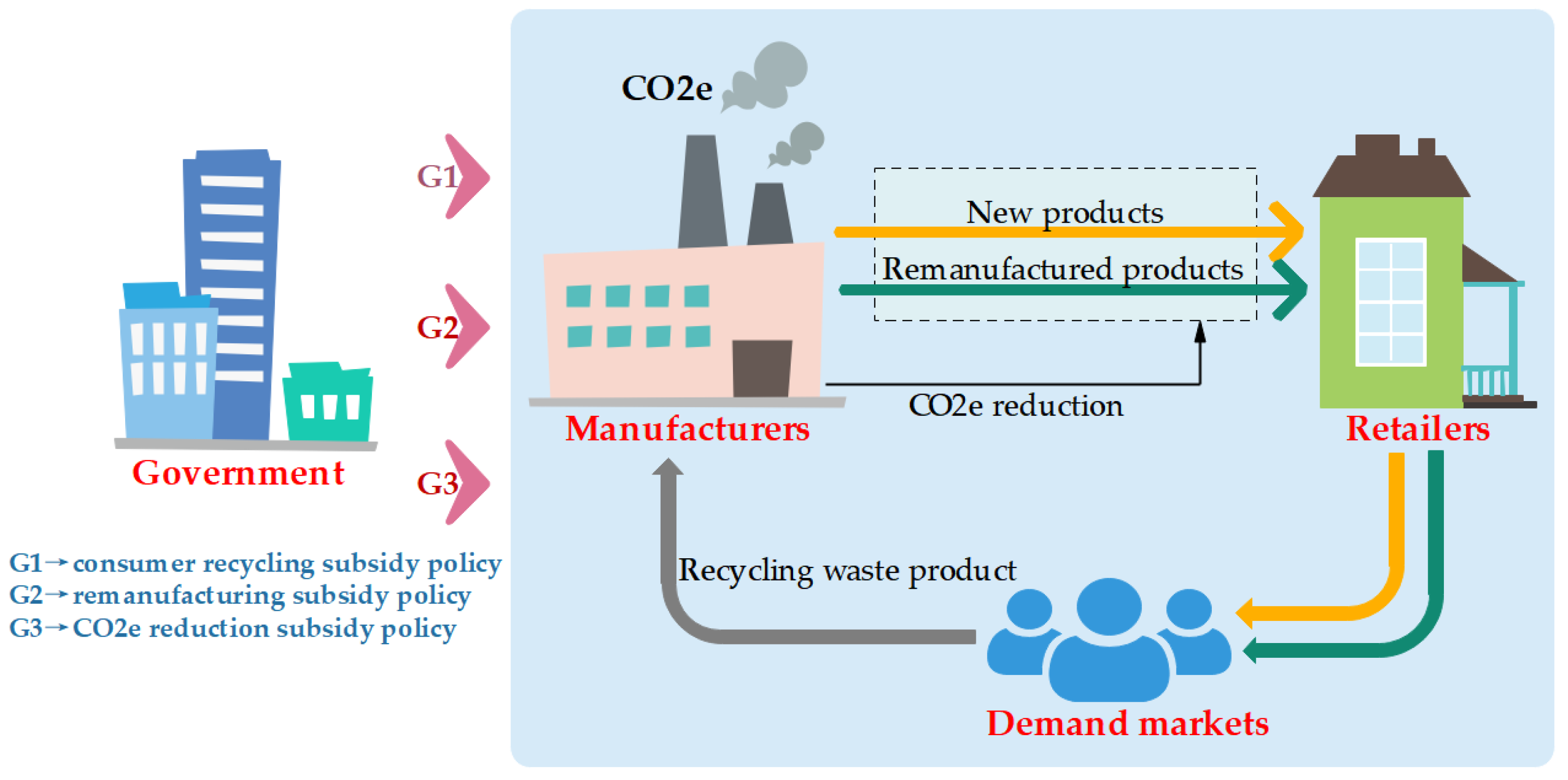
3. Problem Description and Assumptions
- According to the research objective, to ensure the rationality of the model, we assume that the baseline CO2e per unit of a new product is and the baseline CO2e per unit of a remanufactured product is , where is the CO2e reduction coefficient of remanufactured products. To reduce CO2e, we assume that manufacturers implement CO2e reduction. According to Wang and Wu [4], we assume that is the CO2e reduction cost of a manufacturer, where is the CO2e reduction cost coefficient and is the CO2e reduction per unit product (CO2e reduction level). After the manufacturer reduces CO2e, the CO2e per unit of new product is , and the CO2e per unit of remanufactured product is .
- Under the remanufacturing subsidy policy, consumer recycling subsidy policy and CO2e reduction subsidy policies, this paper provides a new assumption that there are different subsidy environments in the supply chain system, that is, the government can implement these three policies separately or simultaneously. In the remanufacturing subsidy policy, the government offers a unit of remanufactured product subsidy to manufacturers. Regarding the consumer recycling subsidy policy, the government provides a unit recycling subsidy to consumers. Under the CO2e reduction subsidy policy, the government provides a unit CO2e reduction subsidy to manufacturers.
- This study adopts a single-period model; that is, members are in a stable and mature period. During this period, prices, market demand and recycling rate are relatively stable. Therefore, it is assumed that all recycled waste products are used for remanufacturing, and consumers can distinguish between new products and remanufactured products. Many studies have made similar assumptions, such as Hammond and Beullens [22] and Chang et al. [57].
- To better analyze the impact of three subsidy policies on manufacturers’ CO2e reduction. This study only considers CO2e in the process of product production and remanufacturing and does not consider CO2e in the process of recycling and marketing. Many studies also made a similar model assumption, such as Zhang et al. [14], Luo et al. [34] and Tao et al. [52].
4. Research Method and Mathematical Model Formulation
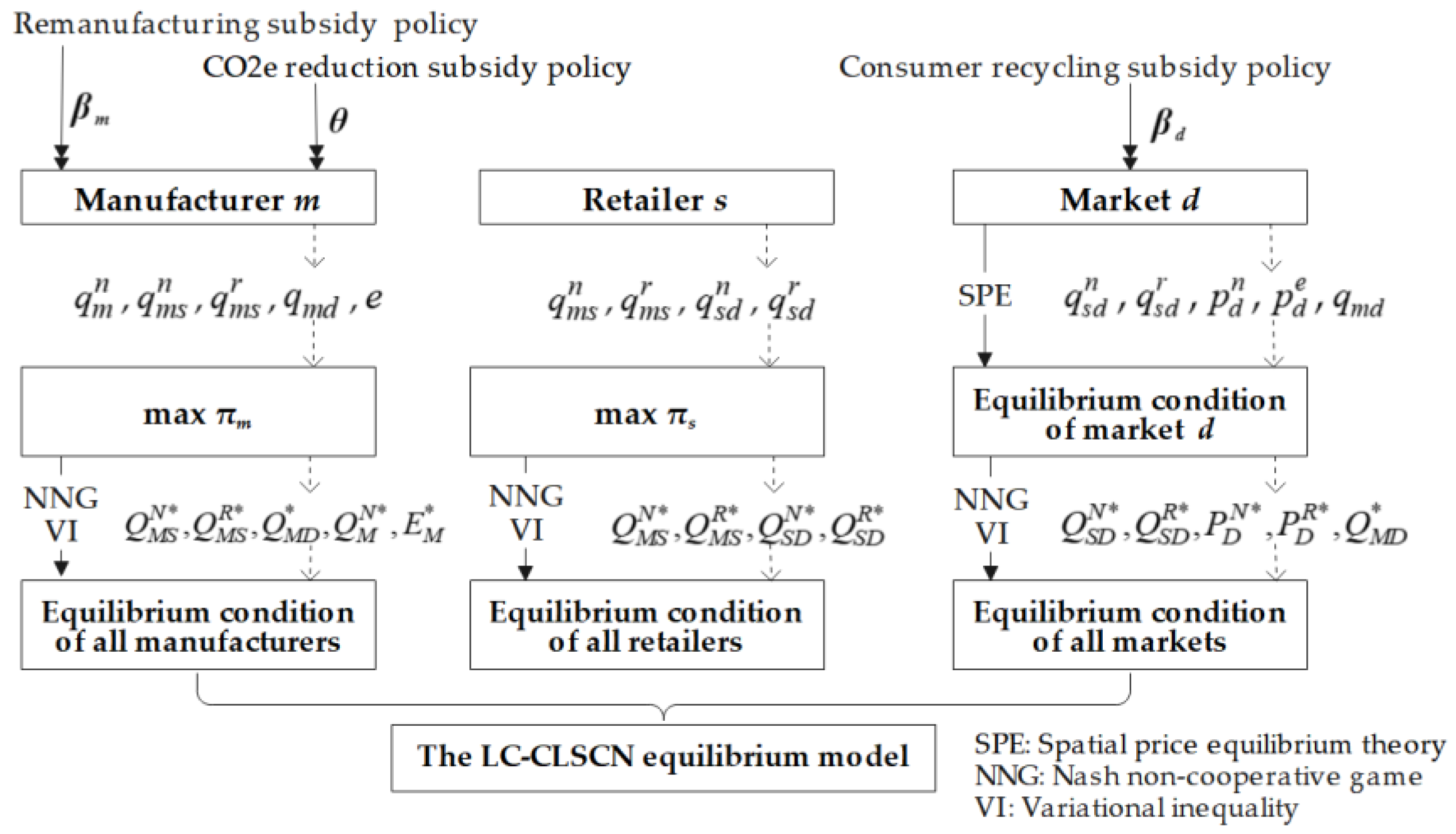
4.1. Research Method
4.2. Mathematical Model Formulation
4.2.1. Manufacturers
4.2.2. Retailers
4.2.3. Markets
4.2.4. The LC-CLSCN Equilibrium Model under Different Subsidy Policies
5. Numerical Examples
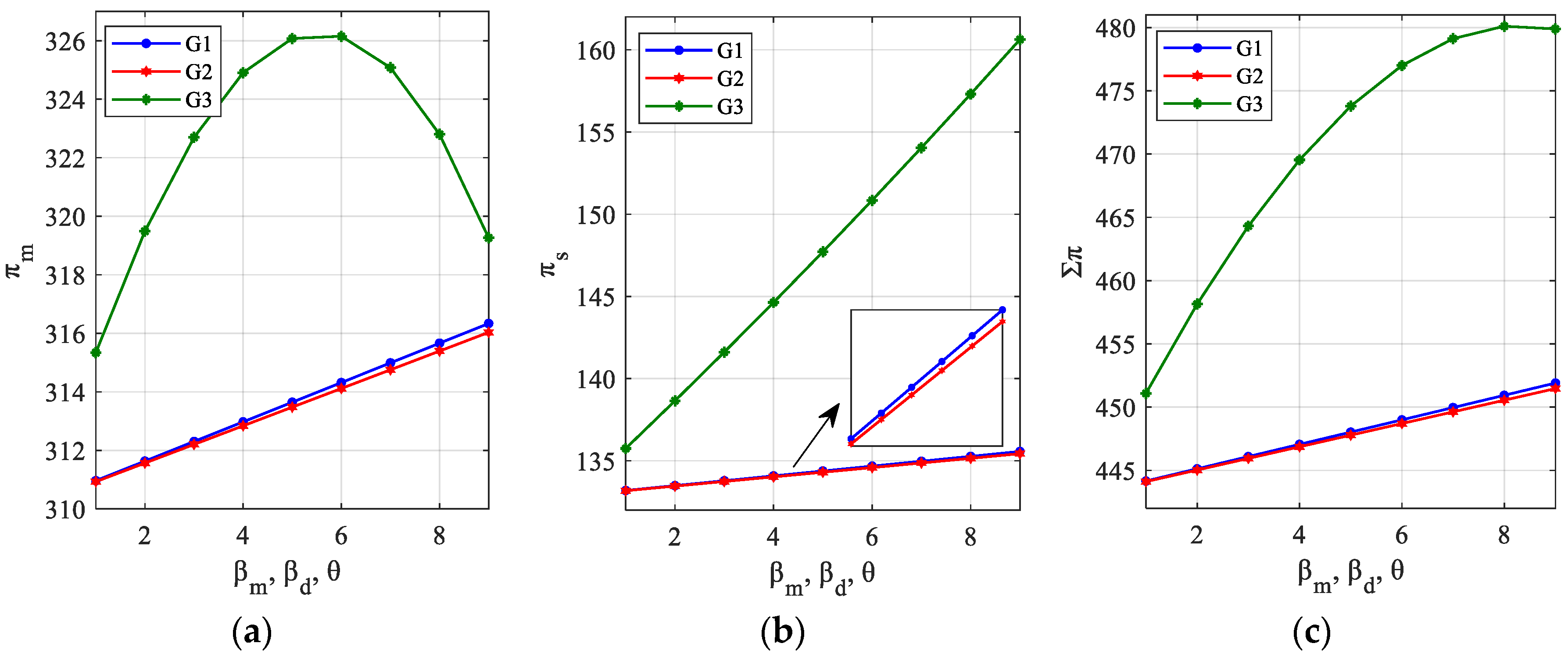
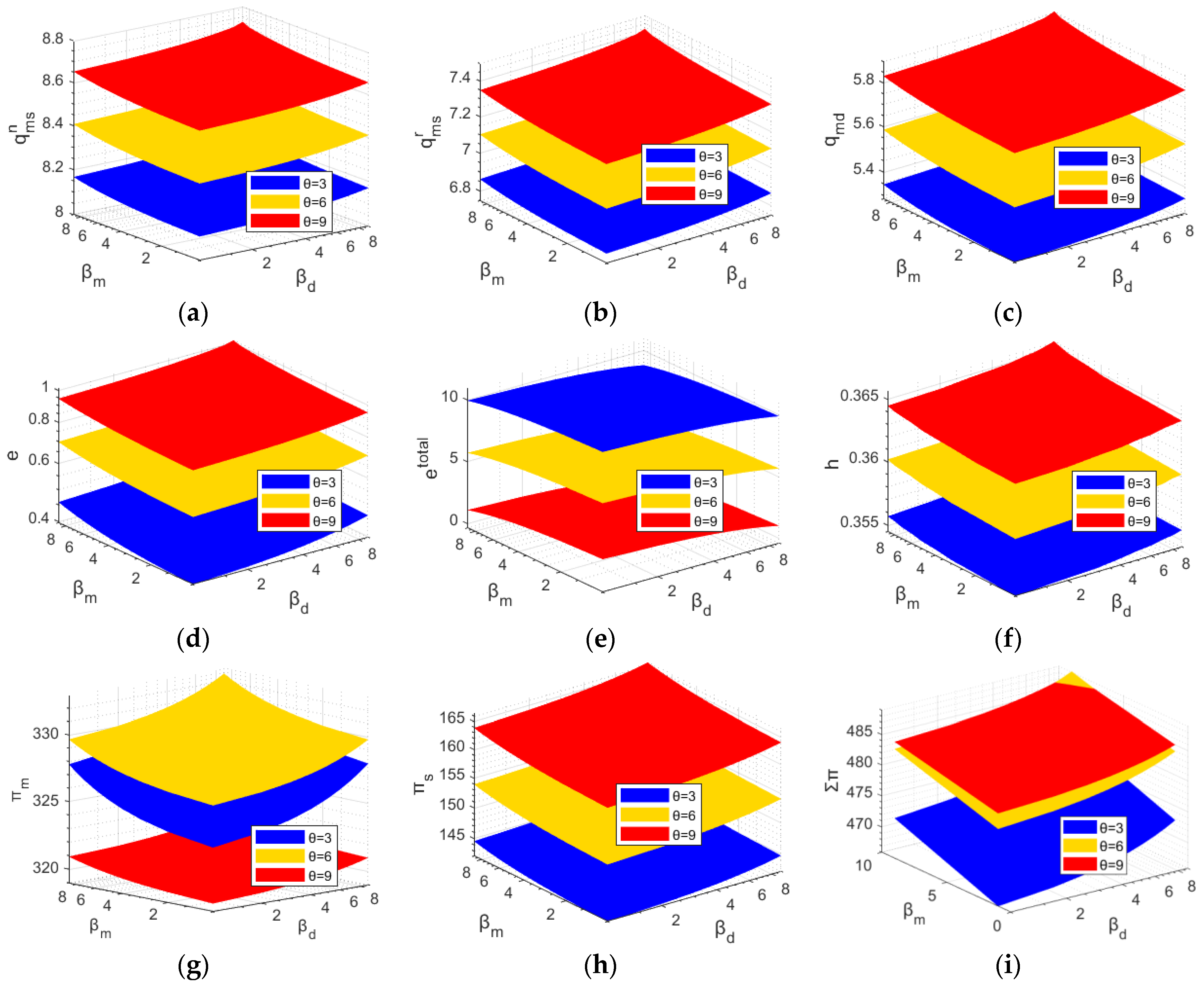
5.1. Numerical Example 1
5.2. Numerical Example 2
6. Discussion, Implications and Recommendations
6.1. Results and Discussion
6.2. Implications
6.3. Management Recommendations
6.3.1. Government
6.3.2. Enterprise Members
7. Conclusions, Limitations and Future Direction
7.1. Conclusions
7.2. Limitations and Future Direction
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Y. A Robust Possibilistic Programming Approach for a Road-Rail Intermodal Routing Problem with Multiple Time Windows and Truck Operations Optimization under Carbon Cap-and-Trade Policy and Uncertainty. Systems 2022, 10, 156. [Google Scholar] [CrossRef]
- Cao, K.; Xu, Y.; Wang, J. Should Firms Provide Online Return Service for Remanufactured Products? J. Clean. Prod. 2020, 272, 122641. [Google Scholar] [CrossRef]
- Soon, A.; Heidari, A.; Khalilzadeh, M.; Antucheviciene, J.; Zavadskas, E.K.; Zahedi, F. Multi-Objective Sustainable Closed-Loop Supply Chain Network Design Considering Multiple Products with Different Quality Levels. Systems 2022, 10, 94. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Q. Carbon Emission Reduction and Product Collection Decisions in the Closed-Loop Supply Chain with Cap-and-Trade Regulation. Int. J. Prod. Res. 2021, 59, 4359–4383. [Google Scholar] [CrossRef]
- Cheng, P.; Ji, G.; Zhang, G.; Shi, Y. A Closed-Loop Supply Chain Network Considering Consumer’s Low Carbon Preference and Carbon Tax under the Cap-and-Trade Regulation. Sustain. Prod. Consum. 2022, 29, 614–635. [Google Scholar] [CrossRef]
- Nagurney, A.; Dong, J.; Zhang, D. A Supply Chain Network Equilibrium Model. Transp. Res. Part E Logist. Transp. Rev. 2002, 38, 281–303. [Google Scholar] [CrossRef]
- Xu, L.; Wang, C.; Miao, Z.; Chen, J. Governmental Subsidy Policies and Supply Chain Decisions with Carbon Emission Limit and Consumer’s Environmental Awareness. RAIRO-Oper. Res. 2019, 53, 1675–1689. [Google Scholar] [CrossRef]
- Zhou, X.; Wei, X.; Lin, J.; Tian, X.; Lev, B.; Wang, S. Supply Chain Management under Carbon Taxes: A Review and Bibliometric Analysis. Omega 2021, 98, 102295. [Google Scholar] [CrossRef]
- Cao, K.; Xu, X.; Wu, Q.; Zhang, Q. Optimal Production and Carbon Emission Reduction Level under Cap-and-Trade and Low Carbon Subsidy Policies. J. Clean. Prod. 2017, 167, 505–513. [Google Scholar] [CrossRef]
- Cao, K.; He, P.; Liu, Z. Production and Pricing Decisions in a Dual-Channel Supply Chain under Remanufacturing Subsidy Policy and Carbon Tax Policy. J. Oper. Res. Soc. 2020, 71, 1199–1215. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, R.; Shen, L.; Miller, W. Recycling Decisions of Low-Carbon e-Commerce Closed-Loop Supply Chain under Government Subsidy Mechanism and Altruistic Preference. J. Clean. Prod. 2020, 259, 120883. [Google Scholar] [CrossRef]
- Nagurney, A.; Besik, D.; Li, D. Strict Quotas or Tariffs? Implications for Product Quality and Consumer Welfare in Differentiated Product Supply Chains. Transp. Res. Part E Logist. Transp. Rev. 2019, 129, 136–161. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, X.-T.; Fan, Z.-P.; Wong, K.-H. Remanufacturing Strategy Choice of a Closed-Loop Supply Chain Network Considering Carbon Emission Trading, Green Innovation, and Green Consumers. Int. J. Environ. Res. Public Health 2022, 19, 6782. [Google Scholar] [CrossRef]
- Zhang, G.; Cheng, P.; Sun, H.; Shi, Y.; Zhang, G.; Kadiane, A. Carbon Reduction Decisions under Progressive Carbon Tax Regulations: A New Dual-Channel Supply Chain Network Equilibrium Model. Sustain. Prod. Consum. 2021, 27, 1077–1092. [Google Scholar] [CrossRef]
- Jena, S.K.; Ghadge, A.; Sarmah, S.P. Managing Channel Profit and Total Surplus in a Closed-Loop Supply Chain Network. J. Oper. Res. Soc. 2018, 69, 1345–1356. [Google Scholar] [CrossRef]
- Fu, R.; Qiang, Q.; Ke, K.; Huang, Z. Closed-Loop Supply Chain Network with Interaction of Forward and Reverse Logistics. Sustain. Prod. Consum. 2021, 27, 737–752. [Google Scholar] [CrossRef]
- Wan, N. The Impacts of Low Carbon Subsidy, Collection Mode, and Power Structure on a Closed-Loop Supply Chain. J. Renew. Sustain. Energy 2018, 10, 065904. [Google Scholar] [CrossRef]
- Diabat, A.; Jebali, A. Multi-Product and Multi-Period Closed Loop Supply Chain Network Design under Take-Back Legislation. Int. J. Prod. Econ. 2021, 231, 107879. [Google Scholar] [CrossRef]
- Li, B.; Geng, Y.; Xia, X.; Qiao, D. The Impact of Government Subsidies on the Low-Carbon Supply Chain Based on Carbon Emission Reduction Level. Int. J. Environ. Res. Public Health 2021, 18, 7603. [Google Scholar] [CrossRef]
- Xu, J.; Wang, P.; Xu, Q. Impact of Information Asymmetry on the Operation of Green Closed-Loop Supply Chain under Government Regulation. Sustainability 2022, 14, 7999. [Google Scholar] [CrossRef]
- Salehi-Amiri, A.; Zahedi, A.; Gholian-Jouybari, F.; Rodríguez, E.Z.; Hajiaghaei-Keshteli, M. Designing a Closed-Loop Supply Chain Network Considering Social Factors; A Case Study on Avocado Industry. Appl. Math. Model. 2022, 101, 600–631. [Google Scholar] [CrossRef]
- Hammond, D.; Beullens, P. Closed-Loop Supply Chain Network Equilibrium under Legislation. Eur. J. Oper. Res. 2007, 183, 895–908. [Google Scholar] [CrossRef]
- Feng, P.; Zhou, X.; Zhang, D.; Chen, Z.; Wang, S. The Impact of Trade Policy on Global Supply Chain Network Equilibrium: A New Perspective of Product-Market Chain Competition. Omega 2022, 109, 102612. [Google Scholar] [CrossRef]
- Wu, H.; Xu, B.; Zhang, D. Closed-Loop Supply Chain Network Equilibrium Model with Subsidy on Green Supply Chain Technology Investment. Sustainability 2019, 11, 4403. [Google Scholar] [CrossRef]
- Jiang, G.; Wang, Q.; Wang, K.; Zhang, Q.; Zhou, J. A Novel Closed-Loop Supply Chain Network Design Considering Enterprise Profit and Service Level. Sustainability 2020, 12, 544. [Google Scholar] [CrossRef]
- Polat, L.O.; Gungor, A. WEEE Closed-Loop Supply Chain Network Management Considering the Damage Levels of Returned Products. Environ. Sci. Pollut. Res. 2020, 28, 7786–7804. [Google Scholar] [CrossRef]
- Chen, C.-K.; Ulya, M.A. Analyses of the Reward-Penalty Mechanism in Green Closed-Loop Supply Chains with Product Remanufacturing. Int. J. Prod. Econ. 2019, 210, 211–223. [Google Scholar] [CrossRef]
- Sriyanto, S.; Lodhi, M.S.; Salamun, H.; Sardin, S.; Pasani, C.F.; Muneer, G.; Zaman, K. The Role of Healthcare Supply Chain Management in the Wake of COVID-19 Pandemic: Hot off the Press. Foresight 2022, 24, 429–444. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, K.; Chen, S.; Fu, X.; Feng, S.; Zhuang, Z. A Sustainable Agricultural Supply Chain Considering Substituting Organic Manure for Chemical Fertilizer. Sustain. Prod. Consum. 2022, 29, 432–446. [Google Scholar] [CrossRef]
- Chauhan, C.; Singh, A. A Review of Industry 4.0 in Supply Chain Management Studies. J. Manuf. Technol. Manag. 2020, 31, 863–886. [Google Scholar] [CrossRef]
- Sun, L.; Cao, X.; Alharthi, M.; Zhang, J.; Taghizadeh-Hesary, F.; Mohsin, M. Carbon Emission Transfer Strategies in Supply Chain with Lag Time of Emission Reduction Technologies and Low-Carbon Preference of Consumers. J. Clean. Prod. 2020, 264, 121664. [Google Scholar] [CrossRef]
- Dey, B.K.; Park, J.; Seok, H. Carbon-Emission and Waste Reduction of a Manufacturing-Remanufacturing System Using Green Technology and Autonomated Inspection. RAIRO Oper. Res. 2022, 56, 2801–2831. [Google Scholar] [CrossRef]
- Li, N.; Deng, M.; Mou, H.; Tang, D.; Fang, Z.; Zhou, Q.; Cheng, C.; Wang, Y. Government Participation in Supply Chain Low-Carbon Technology R&D and Green Marketing Strategy Optimization. Sustainability 2022, 14, 8342. [Google Scholar] [CrossRef]
- Luo, R.; Zhou, L.; Song, Y.; Fan, T. Evaluating the Impact of Carbon Tax Policy on Manufacturing and Remanufacturing Decisions in a Closed-Loop Supply Chain. Int. J. Prod. Econ. 2022, 245, 108408. [Google Scholar] [CrossRef]
- Xia, L.; Guo, T.; Qin, J.; Yue, X.; Zhu, N. Carbon Emission Reduction and Pricing Policies of a Supply Chain Considering Reciprocal Preferences in Cap-and-Trade System. Ann. Oper. Res. 2017, 268, 149–175. [Google Scholar] [CrossRef]
- Shu, T.; Huang, C.; Chen, S.; Wang, S.; Lai, K.K. Trade-Old-for-Remanufactured Closed-Loop Supply Chains with Carbon Tax and Government Subsidies. Sustainability 2018, 10, 3935. [Google Scholar] [CrossRef]
- Fander, A.; Yaghoubi, S. Dynamic and Stochastic Modeling for a Closed-Loop Automotive Supply Chain under Fuel Issue and Government Intervention: A Case Study. Comput. Ind. Eng. 2022, 25, 108765. [Google Scholar] [CrossRef]
- Zhao, J.; Zeng, D.; Che, L.; Zhou, T.; Hu, J. Research on the Profit Change of New Energy Vehicle Closed-Loop Supply Chain Members Based on Government Subsidies. Environ. Technol. Innov. 2020, 19, 100937. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, L. Altruistic Mode Selection and Coordination in a Low-Carbon Closed-Loop Supply Chain under the Government’s Compound Subsidy: A Differential Game Analysis. J. Clean. Prod. 2022, 366, 132863. [Google Scholar] [CrossRef]
- Dey, B.K.; Yilmaz, I.; Seok, H. A Sustainable Supply Chain Integrated with Autonomated Inspection, Flexible Eco-Production, and Smart Transportation. Processes 2022, 10, 1775. [Google Scholar] [CrossRef]
- Awan, U.; Sroufe, R.; Bozan, K. Designing Value Chains for Industry 4.0 and a Circular Economy: A Review of the Literature. Sustainability 2022, 14, 7084. [Google Scholar] [CrossRef]
- Song, L.; Yan, Y.; Yao, F. Closed-Loop Supply Chain Models Considering Government Subsidy and Corporate Social Responsibility Investment. Sustainability 2020, 12, 2045. [Google Scholar] [CrossRef]
- Mondal, C.; Giri, B.C.; Biswas, S. Integrating Corporate Social Responsibility in a Closed-Loop Supply Chain under Government Subsidy and Used Products Collection Strategies. Flex. Serv. Manuf. J. 2022, 34, 65–100. [Google Scholar] [CrossRef]
- Mondal, C.; Giri, B.C. Tax-Subsidy or Reward-Penalty? Determining Optimal Strategy in Sustainable Closed-Loop Supply Chain under Quality-Dependent Return. Int. J. Syst. Sci. Oper. Logist. 2021, 1–26. [Google Scholar] [CrossRef]
- Johari, M.; Hosseini-Motlagh, S.-M. Coordination of Social Welfare, Collecting, Recycling and Pricing Decisions in a Competitive Sustainable Closed-Loop Supply Chain: A Case for Lead-Acid Battery. Ann. Oper. Res. 2019, 1–36. [Google Scholar] [CrossRef]
- Shu, T.; Liu, Q.; Chen, S.; Wang, S.; Lai, K.K. Pricing Decisions of CSR Closed-Loop Supply Chains with Carbon Emission Constraints. Sustainability 2018, 10, 4430. [Google Scholar] [CrossRef]
- Ali, H.; Ryan, S.M. Closed-Loop Supply Chain Network Design with Multiple Transportation Modes under Stochastic Demand and Uncertain Carbon Tax. Int. J. Prod. Econ. 2018, 195, 118–131. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Sun, H.; Zhao, X. Three-Echelon Closed-Loop Supply Chain Network Equilibrium under Cap-and-Trade Regulation. Sustainability 2021, 13, 6472. [Google Scholar] [CrossRef]
- Cheng, P.; Zhang, G.; Sun, H. The Sustainable Supply Chain Network Competition Based on Non-Cooperative Equilibrium under Carbon Emission Permits. Mathematics 2022, 10, 1364. [Google Scholar] [CrossRef]
- Wang, J.; Shao, W. Optimal Decisions in the Closed-Loop Supply Chain Considering Capacity Constraints and Stochastic Demand under the Cap-and-Trade Regulation. Complexity 2022, 2022, 2600196. [Google Scholar] [CrossRef]
- Allevi, E.; Gnudi, A.; Konnov, I.V.; Oggioni, G. Evaluating the Effects of Environmental Regulations on a Closed-Loop Supply Chain Network: A Variational Inequality Approach. Ann. Oper. Res. 2018, 261, 1–43. [Google Scholar] [CrossRef]
- Tao, Z.G.; Guang, Z.Y.; Hao, S.; Song, H.J.; Xin, D.G. Multi-Period Closed-Loop Supply Chain Network Equilibrium with Carbon Emission Constraints. Resour. Conserv. Recycl. 2015, 104, 354–365. [Google Scholar] [CrossRef]
- Bian, J.; Xuan, Z. Tax or Subsidy? An Analysis of Environmental Policies in Supply Chains with Retail Competition. Eur. J. Oper. Res. 2020, 283, 901–914. [Google Scholar] [CrossRef]
- Li, B.; Chen, W.; Xu, C.; Hou, P. Impacts of Government Subsidies for Environmental-Friendly Products in a Dual-Channel Supply Chain. J. Clean. Prod. 2018, 171, 1558–1576. [Google Scholar] [CrossRef]
- Chan, C.K.; Zhou, Y.; Wong, K.H. A Dynamic Equilibrium Model of the Oligopolistic Closed-Loop Supply Chain Network under Uncertain and Time-Dependent Demands. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 325–354. [Google Scholar] [CrossRef]
- Ding, J.; Chen, W.; Wang, W. Production and Carbon Emission Reduction Decisions for Remanufacturing Firms under Carbon Tax and Take-Back Legislation. Comput. Ind. Eng. 2020, 143, 106419. [Google Scholar] [CrossRef]
- Chang, X.; Xia, H.; Zhu, H.; Fan, T.; Zhao, H. Production Decisions in a Hybrid Manufacturing–Remanufacturing System with Carbon Cap and Trade Mechanism. Int. J. Prod. Econ. 2015, 162, 160–173. [Google Scholar] [CrossRef]
- Candogan, O.; Epitropou, M.; Vohra, R.V. Competitive Equilibrium and Trading Networks: A Network Flow Approach. Oper. Res. 2021, 69, 114–147. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, G.; Zhong, Y.; Da, L. The Equilibrium of Multi-Period Closed-Loop Supply Chain Network with Manufacturer-Collection Channel under Government Subsidies. Chin. J. Manag. Sci. 2015, 23, 56–64. [Google Scholar] [CrossRef]
- Zhu, Z.; Liao, H. Do Subsidies Improve the Financial Performance of Renewable Energy Companies? Evidence from China. Nat. Hazards 2019, 95, 241–256. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, Y.; Zhou, D.; Zhu, P. Which Subsidy Mode Improves the Financial Performance of Renewable Energy Firms? A Panel Data Analysis of Wind and Solar Energy Companies between 2009 and 2014. Sustainability 2015, 7, 16548–16560. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, X.; Lin, R. Government Incentive Mechanism of Closed-Loop Supply Chain Based on Information Asymmetry. RAIRO Oper. Res. 2021, 55, 3359–3378. [Google Scholar] [CrossRef]
- Panda, S.; Modak, N.M.; Cárdenas-Barrón, L.E. Coordinating a Socially Responsible Closed-Loop Supply Chain with Product Recycling. Int. J. Prod. Econ. 2017, 188, 11–21. [Google Scholar] [CrossRef]
- Yan, K.; Liu, S.; Zuo, M.; Zheng, J.; Xu, Y. Dual-Channel Supply Chain Pricing Decisions under Discounted Advertising Value. Systems 2022, 10, 76. [Google Scholar] [CrossRef]
- Fontoura, P.; Coelho, A. The Influence of Supply Chain Leadership and Followership on Organizational Performance: An Empirical Study on a Portuguese Energy Supplier. Balt. J. Manag. 2020, 15, 333–353. [Google Scholar] [CrossRef]
- Yang, T.; Li, C.; Yue, X.; Zhang, B. Decisions for Blockchain Adoption and Information Sharing in a Low Carbon Supply Chain. Mathematics 2022, 10, 2233. [Google Scholar] [CrossRef]
| Literature | SS-SC | SCN | Government Policy | Method | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RR | LC | RR | LC | CRP | CRSP | RSP | Other | GT | VI | |
| Wang and Wu [4] | √ | √ | √ | √ | ||||||
| Cheng et al. [5], Zhou et al. [13] | √ | √ | √ | √ | √ | |||||
| Wang et al. [11] | √ | √ | √ | √ | ||||||
| Cao et al. [9], Li et al. [19] | √ | √ | √ | |||||||
| Zhang et al. [14] | √ | √ | √ | √ | √ | |||||
| Jena et al. [15] | √ | √ | √ | √ | ||||||
| Wan [17] | √ | √ | √ | √ | √ | |||||
| Xu et al. [20], Mondal and Giri [44], Shu et al. [46] | √ | √ | √ | √ | ||||||
| Xia et al. [35] | √ | √ | √ | |||||||
| Shu et al. [36] | √ | √ | √ | √ | √ | |||||
| Zhao et al. [38] | √ | √ | √ | √ | ||||||
| Zhang and Yu [39] | √ | √ | √ | √ | √ | |||||
| Song et al. [42], | √ | √ | √ | |||||||
| Wu et al. [24], Zhang et al. [48], Cheng et al. [49], Allevi et al. [51], Tao et al. [52] | √ | √ | √ | √ | √ | |||||
| Bian and Xuan [53] | √ | √ | √ | √ | ||||||
| Li et al. [54] | √ | √ | √ | |||||||
| Chan et al. [55] | √ | √ | √ | |||||||
| This paper | √ | √ | √ | √ | √ | √ | √ | |||
| Symbols | Descriptions |
|---|---|
| , | The conversion rate of raw materials and waste products, , |
| , | The number of new products and remanufactured products produced by manufacturer m, , |
| , | The number of new products and remanufactured products wholesaled by manufacturer m to retailer s, , |
| , | The number of new products and remanufactured products retailed by retailer s to market d, , |
| , | The price of new products and remanufactured products wholesaled by manufacture m to retailer s |
| , | The price of new products and remanufactured retailed by retail s to market d |
| , | The number and price of waste products recycled by manufacturer m from market d, |
| , | The price of new products and remanufactured products purchased by consumers in market d, , |
| , | The new product and remanufactured product demand functions of market d, , |
| , | The production costs of new products and remanufactured products of manufacturer m, , |
| , | The transaction costs between manufacturer m and retailer s (retailer s and manufacturer m borne, respectively), , |
| The transaction costs between retailer s and market d (retailer s borne), | |
| , | The transaction costs borne by consumers buying new products and remanufactured products, respectively, , |
| Recycling negative utility function | |
| Waste product recycling rate | |
| The member’s profit, |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| G2 | 7.8650 | 7.8726 | 7.8802 | 7.8878 | 7.8954 | 7.9030 | 7.9105 | 7.9181 | 7.9257 | |
| G1 | 7.8654 | 7.8734 | 7.8814 | 7.8894 | 7.8974 | 7.9054 | 7.9133 | 7.9213 | 7.9293 | |
| G3 | 7.9342 | 8.0117 | 8.0898 | 8.1687 | 8.2482 | 8.3284 | 8.4094 | 8.4910 | 8.5734 | |
| G1 | 6.5606 | 6.5682 | 6.5758 | 6.5834 | 6.5910 | 6.5986 | 6.6061 | 6.6137 | 6.6213 | |
| G2 | 6.5610 | 6.5690 | 6.5770 | 6.5850 | 6.5930 | 6.6010 | 6.6089 | 6.6169 | 6.6249 | |
| G3 | 6.6298 | 6.7073 | 6.7854 | 6.8643 | 6.9438 | 7.0240 | 7.1050 | 7.1866 | 7.2690 | |
| G2 | 5.0443 | 5.0519 | 5.0595 | 5.0671 | 5.0747 | 5.0823 | 5.0898 | 5.0974 | 5.1050 | |
| G1 | 5.0447 | 5.0527 | 5.0607 | 5.0687 | 5.0767 | 5.0847 | 5.0926 | 5.1006 | 5.1086 | |
| G3 | 5.1135 | 5.1910 | 5.2691 | 5.3480 | 5.4275 | 5.5077 | 5.5887 | 5.6703 | 5.7527 | |
| G2 | 0.3497 | 0.3498 | 0.3500 | 0.3501 | 0.3503 | 0.3505 | 0.3506 | 0.3508 | 0.3509 | |
| G1 | 0.3497 | 0.3499 | 0.3500 | 0.3502 | 0.3503 | 0.3505 | 0.3507 | 0.3508 | 0.3510 | |
| G3 | 0.3511 | 0.3527 | 0.3542 | 0.3557 | 0.3573 | 0.3588 | 0.3602 | 0.3617 | 0.3631 | |
| G2 | 0.1565 | 0.1641 | 0.1717 | 0.1793 | 0.1869 | 0.1945 | 0.2020 | 0.2096 | 0.2172 | |
| G1 | 0.1569 | 0.1649 | 0.1729 | 0.1809 | 0.1889 | 0.1969 | 0.2048 | 0.2128 | 0.2208 | |
| G3 | 0.2257 | 0.3032 | 0.3813 | 0.4602 | 0.5397 | 0.6199 | 0.7009 | 0.7825 | 0.8649 | |
| G2 | 14.885 | 14.767 | 14.647 | 14.528 | 14.408 | 14.288 | 14.168 | 14.047 | 13.926 | |
| G1 | 14.879 | 14.754 | 14.629 | 14.503 | 14.377 | 14.250 | 14.123 | 13.996 | 13.869 | |
| G3 | 13.791 | 12.540 | 11.249 | 9.9167 | 8.5428 | 7.1264 | 5.6664 | 4.1619 | 2.6121 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, C.; Yao, F.; Zhang, Q.; Wang, J.; Wang, Y. Carbon Reduction Subsidy, Remanufacturing Subsidy or Consumer Recycling Subsidy? A Low-Carbon Closed-Loop Supply Chain Network Operation Decision. Systems 2023, 11, 126. https://doi.org/10.3390/systems11030126
Duan C, Yao F, Zhang Q, Wang J, Wang Y. Carbon Reduction Subsidy, Remanufacturing Subsidy or Consumer Recycling Subsidy? A Low-Carbon Closed-Loop Supply Chain Network Operation Decision. Systems. 2023; 11(3):126. https://doi.org/10.3390/systems11030126
Chicago/Turabian StyleDuan, Caiquan, Fengmin Yao, Qiwen Zhang, Jiali Wang, and Ying Wang. 2023. "Carbon Reduction Subsidy, Remanufacturing Subsidy or Consumer Recycling Subsidy? A Low-Carbon Closed-Loop Supply Chain Network Operation Decision" Systems 11, no. 3: 126. https://doi.org/10.3390/systems11030126
APA StyleDuan, C., Yao, F., Zhang, Q., Wang, J., & Wang, Y. (2023). Carbon Reduction Subsidy, Remanufacturing Subsidy or Consumer Recycling Subsidy? A Low-Carbon Closed-Loop Supply Chain Network Operation Decision. Systems, 11(3), 126. https://doi.org/10.3390/systems11030126






