1. Introduction
In a flexible job shop, a variety of sudden disturbances often occur, such as machine failure, urgent order insertion, part arrival time deviation, processing time delay, etc. These disturbances are characterized by random and discrete distributions [
1], and these disturbances cannot be predicted in advance. Therefore, the rescheduling procedure after the disturbance must be timely and accurate, so as not to delay the delivery term and bring losses to the enterprise.
Numerous academics have undertaken studies from the perspectives of optimization algorithms and intelligent scheduling in order to meet the needs of automation and intelligent production of modern enterprise shop scheduling. As an earlier intelligent optimization algorithm, the Genetic algorithm (GA) has been improved by many scholars, and has been proven to be quite effective at solving the shop scheduling problem. For example, Dai et al. [
2] established a multi-objective optimization model to minimize energy consumption and completion time for flexible job-shop scheduling problems with transportation constraints. Zhang et al. [
3] ameliorated the genetic programming super-heuristic algorithm for dynamic flexible job shop scheduling and proposed an individual adaptation strategy. Liu et al. [
4] proposed a genetic algorithm based on the multi-objective and multi-population framework for the multi-objective job-shop scheduling problem. Yan et al. [
5] discussed the influence of finite transportation conditions on flexible job-shop scheduling problems and improved the genetic algorithm. Kacem et al. [
6,
7] used the local heuristic method for initialization, and then used the genetic algorithm for multi-objective optimization of the initial solution. For solving multi-objective problems, Wu et al. [
8] and Yu et al. [
9] combined genetic algorithms with local search algorithms, such as the immune algorithm, to amplify the ability of local search in the algorithm. On the basis of certain research studies on shop scheduling and algorithms, many scholars seek more suitable algorithms. Afsar et al. [
10] proposed a multi-objective optimization model and a new enhanced mode gene algorithm for the green-scheduling problem of the job shop. Alkhateeb et al. [
11] integrated the optimization operator of the simulated annealing algorithm into the Cuckoo search algorithm and proposed a discrete simulated annealing algorithm to solve the job-shop problem. Caldeira et al. [
12] proposed a multi-objective discrete Jaya algorithm for solving scheduling problems based on the Pareto multi-objective algorithm. Ibrahim et al. [
13] proposed an efficient solution strategy with better performance for job-shop scheduling problems by combining the artificial algae algorithm with the differential evolution algorithm. Brandimarte et al. [
14], aiming to solve the multi-objective Flexible Job Shop Problem (FJSP), used the assignment rule to solve the machine selection problem, and then adopted tabu search to solve the shop scheduling problem. Baykasoglu et al. [
15] studied the dynamic flexible job-shop scheduling problem under new order arrival, delivery date change, machine failure, order cancellation, and urgent order arrival. Mohan et al. [
16] summarized the development of a dynamic job-shop scheduling problem, and pointed out that future research should be in-depth in the direction of integration, practicability, multi-targeting, and networking. Although the algorithm in the job-shop scheduling problem has been the subject of extensive research, it is rarely applied to actual or intelligent production in enterprises. As a result, the research focus of job-shop scheduling has changed to successful algorithm implementation, intelligent scheduling implementation in production, and intelligent scheduling achievement.
In order to keep high decision accuracy, make shop scheduling intelligent, and reduce the artificial experience judgment operation, research should be conducted from the viewpoints of machine learning and deep learning. Priore et al. [
17] summarized scheduling methods of machine learning to select the most appropriate scheduling rules for a flexible manufacturing system at any given time. Wang et al. [
18] proposed a dynamic scheduling method based on deep reinforcement learning and adopted Proximal Policy Optimization (PPO) to find the optimal scheduling strategy. Zhang et al. [
19] suggested a graph neural network-based approach to integrate the states encountered in the solving process through end-to-end deep reinforcement learning. Chen et al. [
20] proposed a self-learning genetic algorithm (SLGA) and made an intelligent adjustment of its key parameters using reinforcement learning. Cao et al. [
21] aimed at the problem of wireless network resource allocation, and proposed a machine learning method based on support vector machines and deep belief networks to directly calculate approximate solutions. Weckman et al. [
22] used the genetic algorithm to investigate a neural network scheduler for job shop scheduling. Based on a graph neural network, Hameed [
23] proposed a new method to solve job-shop scheduling problems by using deep reinforcement learning. Inspired by the idea of machine learning to job-shop scheduling, many scholars have further studied digital twinning and cloud computing. Fang et al. [
24] developed a new shop scheduling method based on digital twin (DT) to reduce scheduling deviation. Zhang et al. [
25] introduced digital twin technology to further integrate the physical space and virtual space of the workshop for realizing dynamic scheduling. From the standpoint of cloud computing, Tong et al. [
26] proposed a task scheduling algorithm combining Q learning and heterogeneous earliest completion time method. Morariu et al. [
27] proposed a machine learning method for reality perception and optimization in the cloud environment to reduce the cost of cloud computing implementation and deployment for manufacturing enterprises. Liu et al. [
28] suggested a user scheduling algorithm for data acquisition in edge learning, taking into account communication reliability and information volume of data samples. Ghasemi et al. [
29] introduced evolutionary learning to the simulation method of stochastic optimization. In addition to the above research, many scholars also study shop scheduling from other perspectives and technical means. Amiri et al. [
30] presented an algorithm iteration that can simulate stochastic gradient descent to significantly reduce the average completion time, aiming at the computational task scheduling problem of multiple workers in large-scale distributed learning problems. Faraji et al. [
31] proposed a new power management system based on weather and load forecasting for optimal day-ahead automatic scheduling and operation of the microgrid. Müller et al. [
32] studied five constraint programming solvers and developed a prediction method of the best solver according to the instance features or parameters for a given problem. Jun et al. [
33] suggested a method, which could be called Random Forest for Obtaining Rules for Scheduling (RANFORS), to extract scheduling rules from optimal scheduling. Li et al. [
34] proposed an elite non-dominated sorting hybrid algorithm to solve multi-objective flexible job shop scheduling problems with sequence-dependent setup time and cost.
Obviously, machine learning, which is an important means to realize precision and intelligence in modern intelligent manufacturing enterprises, can be applied to find rules and predict development from previous production experience and data.
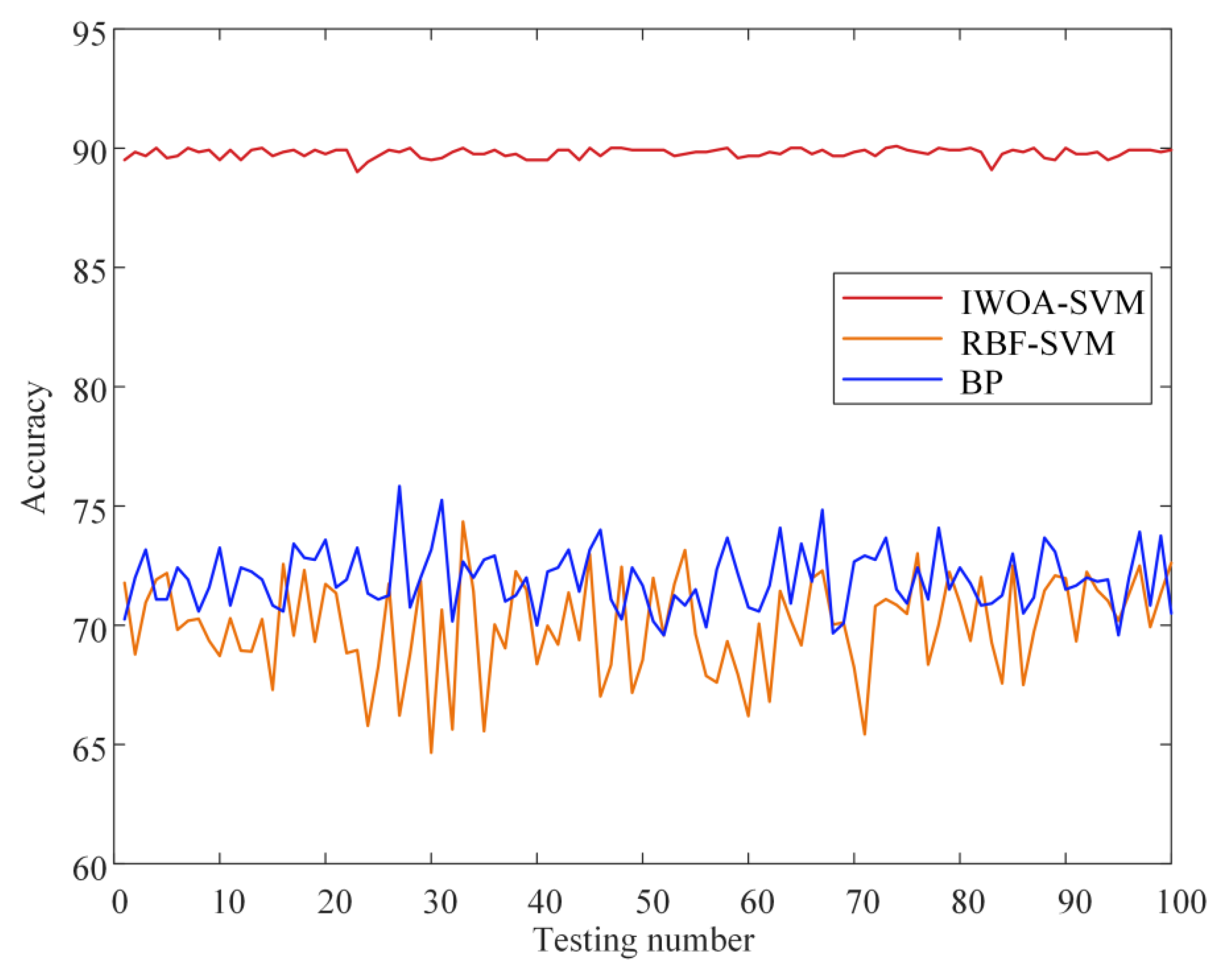
Therefore, this paper develops a prediction method based on an improved whale optimization algorithm and support vector machine (WOA-SVM) for rescheduling mode decisions in a flexible job shop. A big sample of data is produced when there is a random disturbance. A variety of machine learning methods are used to train and predict the data, and are compared with the method proposed in this paper. It is proved that the proposed method can respond to rescheduling decisions quickly.
3. Rescheduling Mode Selection Model Based on Machine Learning
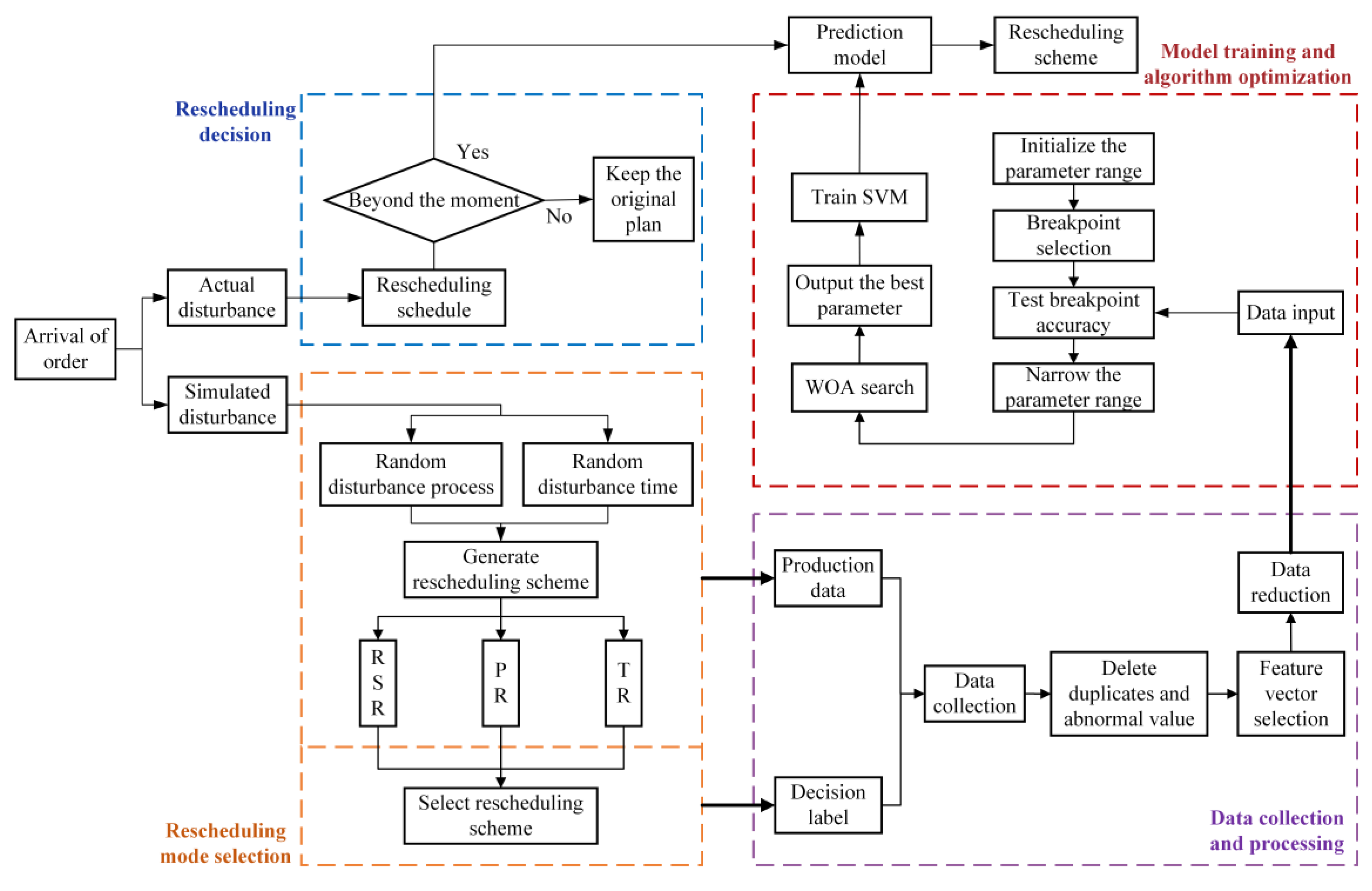
For realizing fast and accurate rescheduling mode decisions, the rescheduling mode selection model based on machine learning is adopted. Its framework is displayed in
Figure 2. Firstly, it is assumed that a disturbance occurs during processing. Rescheduling mode selection is carried out, and then the data collection and processing start. These steps are repeated several times. Next, model training and algorithm optimization are performed and output the prediction model. Lastly, the actual disturbance can be disposed of in the rescheduling decision module when it happens in the actual production process.
3.1. Rescheduling Decision
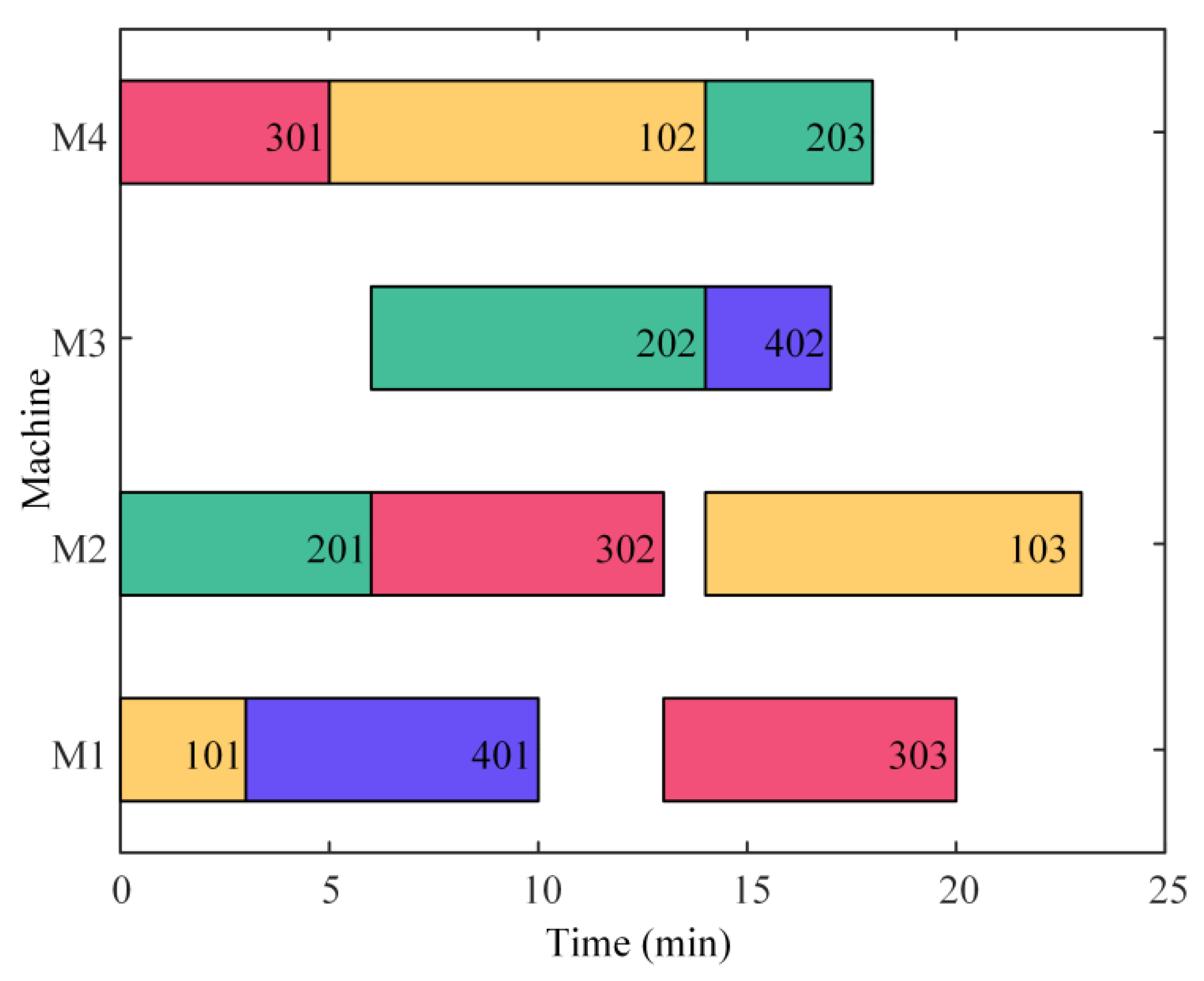
When a disturbance occurs in actual production, we need to estimate the effect of the disturbance and the necessity of rescheduling, first. Therefore, a rescheduling schedule is constructed to define the time limit for each process in which rescheduling is triggered.
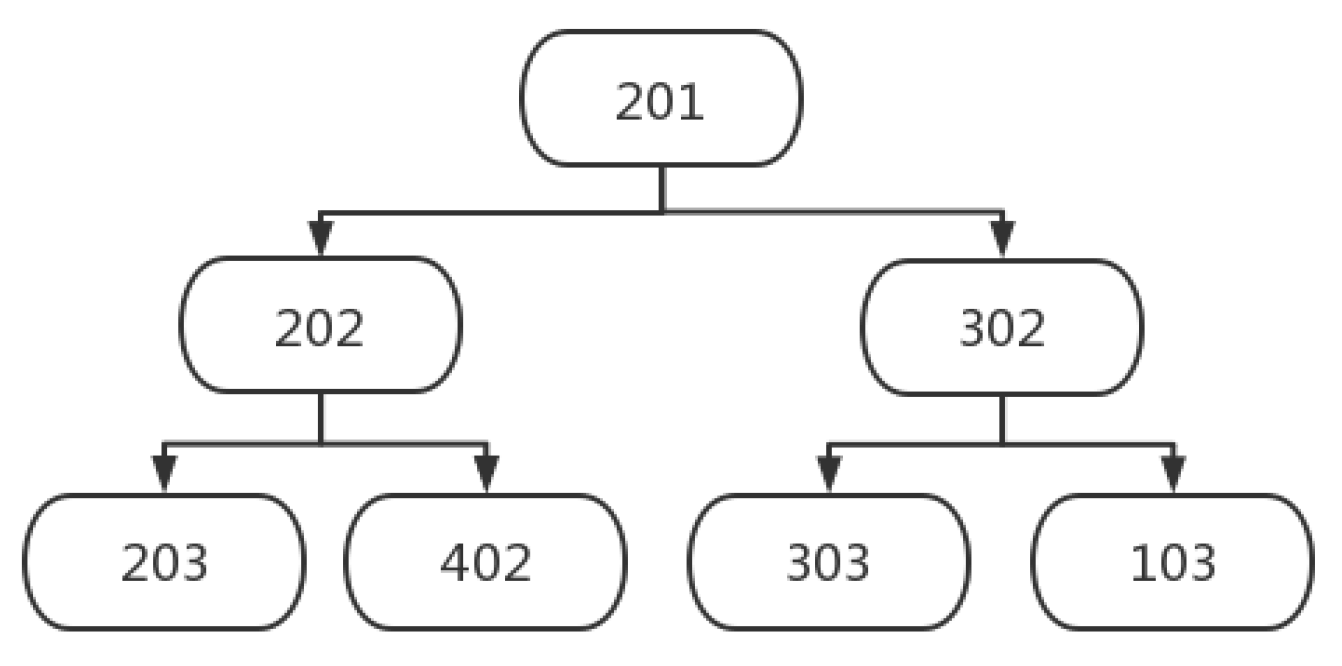
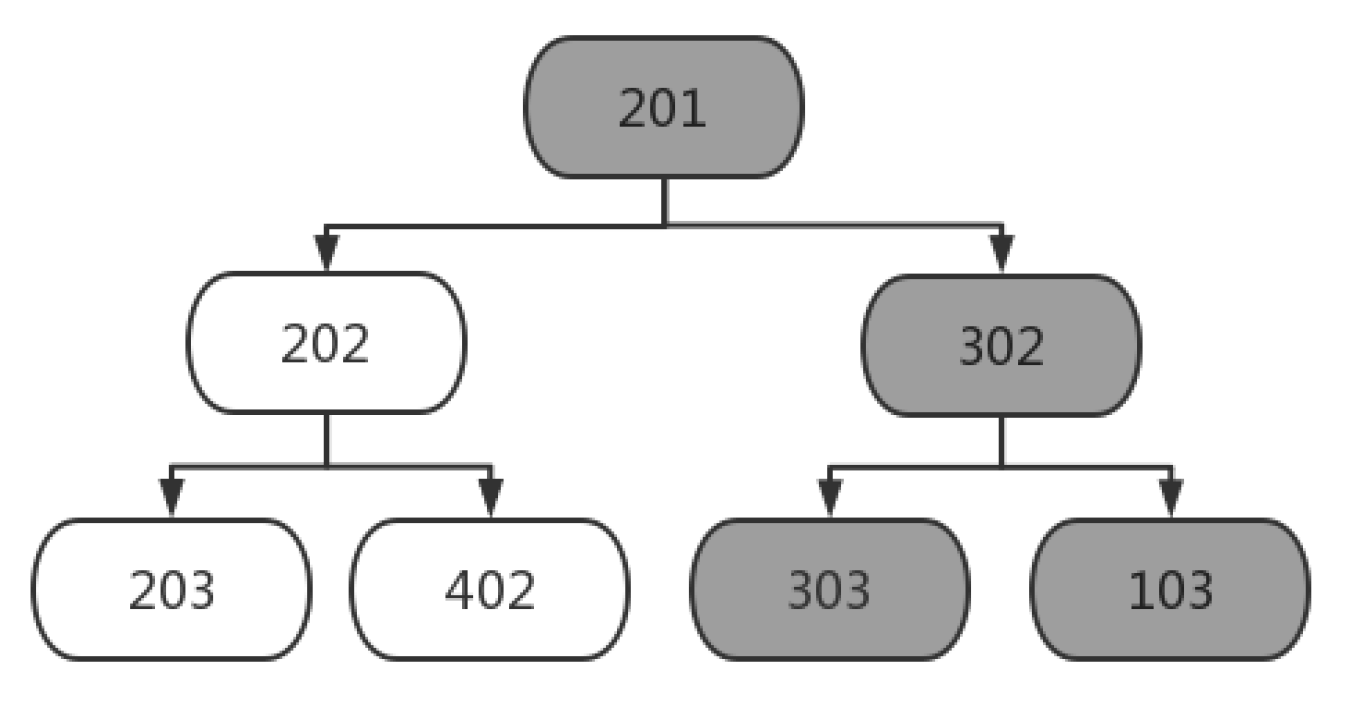
The dynamic correlation among processes in the scheduling scheme [
37] is constructed, and the linkage influence brought by the disturbance of a certain process has been described in
Figure 1.
Figure 3 displays the correlation among processes. When
is disturbed, the processes
and
will be influenced directly, and the processes
,
,
and
will be influenced indirectly. It is obvious that each process directly affects at most two processes, including the next adjacent process on the machine and the next adjacent process on the workpiece. Therefore, two dimensions are used to summarize the two different types of impacts (machine dimension and workpiece dimension).
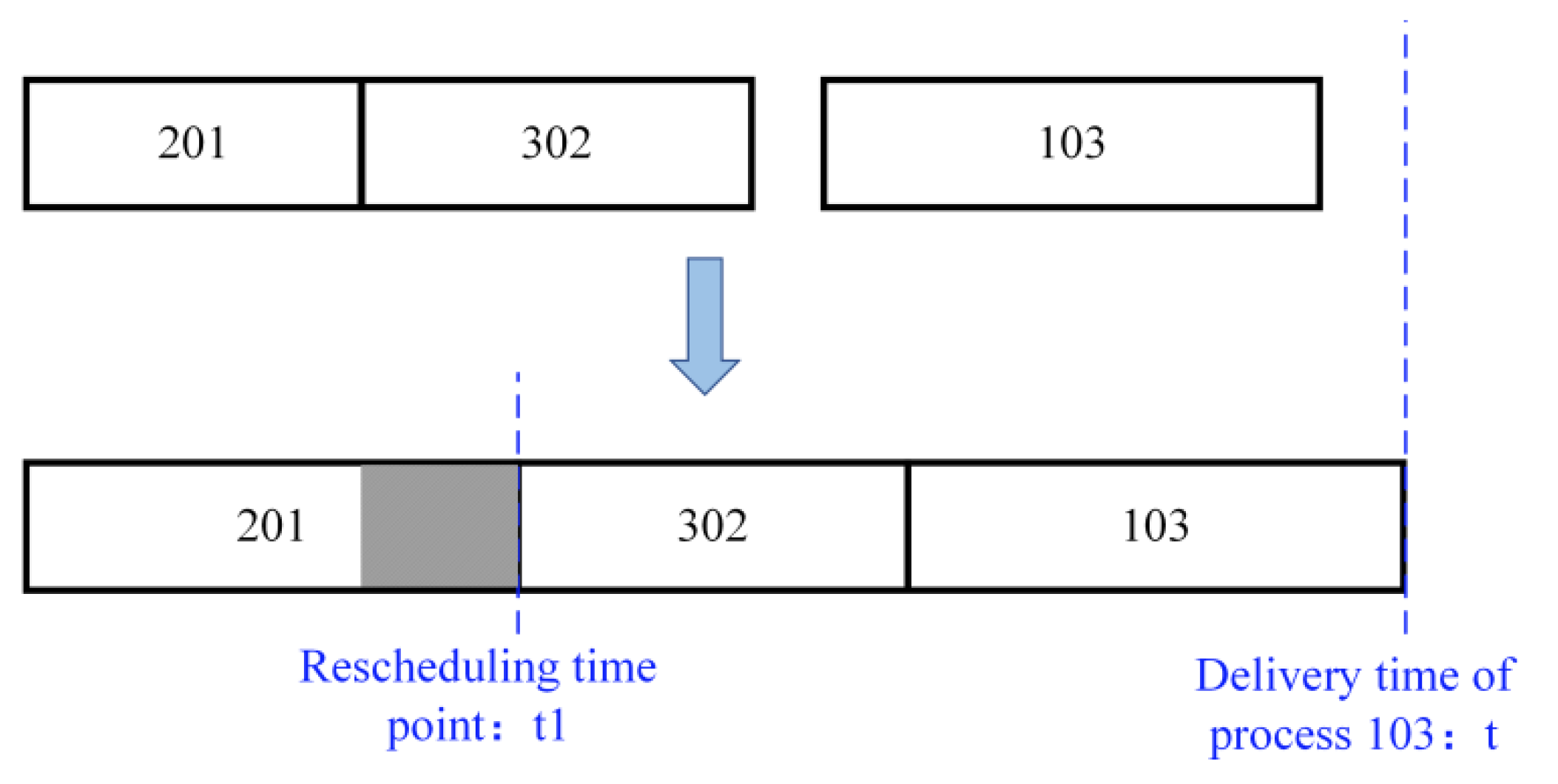
The latest tolerated completion time of each working procedure can be derived backwards from the connection between the two dimensions of the machine and the workpiece, if each workpiece’s delivery date or the latest acceptable completion time can be determined.
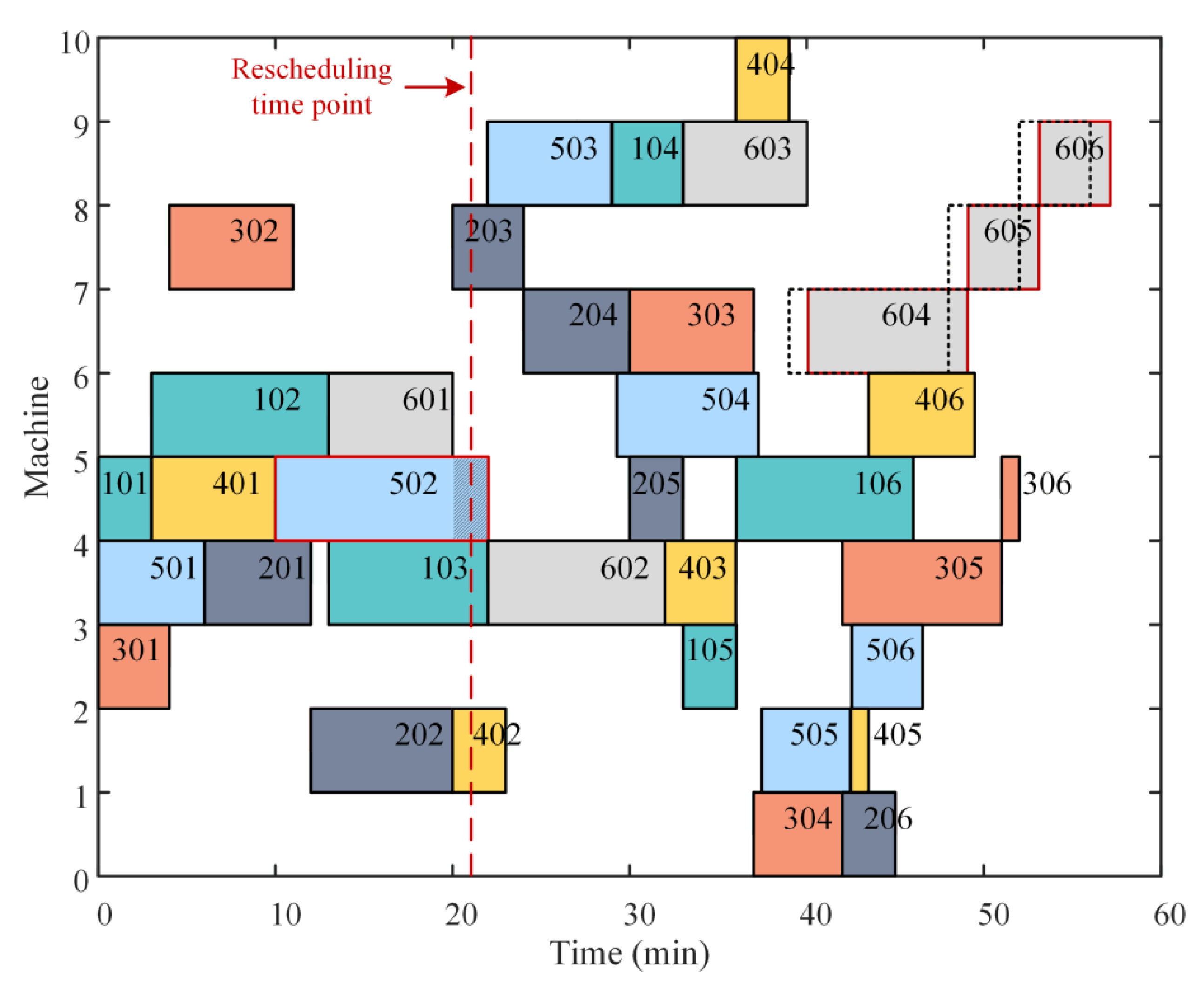
Figure 4 demonstrates the determination of the rescheduling time point. If the delivery time of process 103 is
, it can still be completed, although process 201 is delayed to time point
. Therefore,
can be defined as the rescheduling time point of process 201.
The above example simply illustrates that the calculation of the rescheduling time point of a certain process needs to take into account the delivery time of all the workpieces and the linkage effect of the two dimensions. Then, the rescheduling time points of all processes are calculated, and the rescheduling schedule is constructed. The initial scheduling scheme is maintained if the disruption in actual production does not last longer than the associated rescheduling time. If not, the production plan needs to be rescheduled.
3.2. Rescheduling Mode Selection
When the production order arrives, the rescheduling mode selection consists of the following steps. Firstly, the original scheduling scheme and rescheduling schedule are generated. Secondly, the disturbance process and the disturbance duration, which can trigger rescheduling, are randomly generated. Finally, based on the three scheduling modalities, the three rescheduling strategies are constructed.
There are three rescheduling modes: right shift rescheduling (RSR), partial rescheduling (PR), and total rescheduling (TR) [
1,
2]. RSR means that the sequence and machine among working procedures will not be changed, but the processing start time will be adjusted. PR can be used to rearrange the affected processes that have not started at the rescheduling time point, and maintain the original scheme for other unaffected processes. TR is a complete rescheduling of all processes that have not started at a rescheduling point in time. RSR has the least impact on the original scheduling scheme among the three rescheduling techniques, followed by PR, while TR has the greatest impact.
After the disturbance occurs, three rescheduling schemes are generated, and their corresponding maximum completion times
,
, and
are obtained to make rescheduling decisions:
In Formula (1), represents a minimal positive number. It can be used to choose an optimal rescheduling scheme when the of different rescheduling modes is equal. represents the minimum completion time of the three rescheduling schemes. The corresponding schemes are selected through the function defined in Formula (2). , , and , respectively, represent the three rescheduling schemes. They are decision labels in the data collection and processing module.
3.3. Data Collection and Processing
In the process of data collection, an important parameter (mean activity level of key branches) needs to be calculated based on the RSR scheme. As shown in
Figure 5, the key branch is defined as the branch from a disturbed process to an overdue process. If one overdue process happens several times, the branch with the most compact time between processes and the preferential machine dimension influence will be selected. If the disturbance in process 201 leads to the overdue completion of processes 103 and 303, two key branches (201→302→103; 201→302→303) will occur.
For obtaining the key branches, the average activity level of the key branches is defined as follows:
Formula (3) indicates some information in the key branch process set. is the average activity level of the key branch, is the activity level of the process, and is the number of the key branches. Formula (4) represents the activity level of , which is the process of the branch . represents the number of selectable machining machines in the process , and represents the maximum number of selectable machining machines in all the processes.
After data collection, duplicate samples and abnormal samples need to be deleted. For the abnormal samples, the data belonging to RSR will not appear for individuals whose average activity level of key branches is greater than 0. However, during the optimization process, the algorithm could find itself in a local optimal condition. Therefore, these samples should be deleted.
The next step is feature selection. Since most of the collected data have a nonlinear relationship with the decision label, the Spearman Correlation Coefficient [
38] is used to analyze the data correlation, and then the feature vector with a correlation coefficient less than 0.1 is deleted. The feature vector finally selected is shown in
Table 3:
The feature vectors from 1 to 10 are as follows: ① the value beyond the time point of the processing end time of the disturbed procedure; ② the number of unprocessed procedures; ③ the number of affected procedures; ④ whether the disturbed procedure and overdue procedure are the same as the workpiece; ⑤ the load rate; ⑥ the total remaining processing time; ⑦ the total remaining idle time; ⑧ the proportion of PR procedures; ⑨ the proportion of TR procedures; and ⑩ the average activity level of key branches.
It is important to explain the decision label in addition to the feature vectors mentioned previously. There are three kinds of prediction results: RSR, PR, and TR, which are represented by labels “a”, “b”, and “c”, respectively, just as shown in Formula (2).
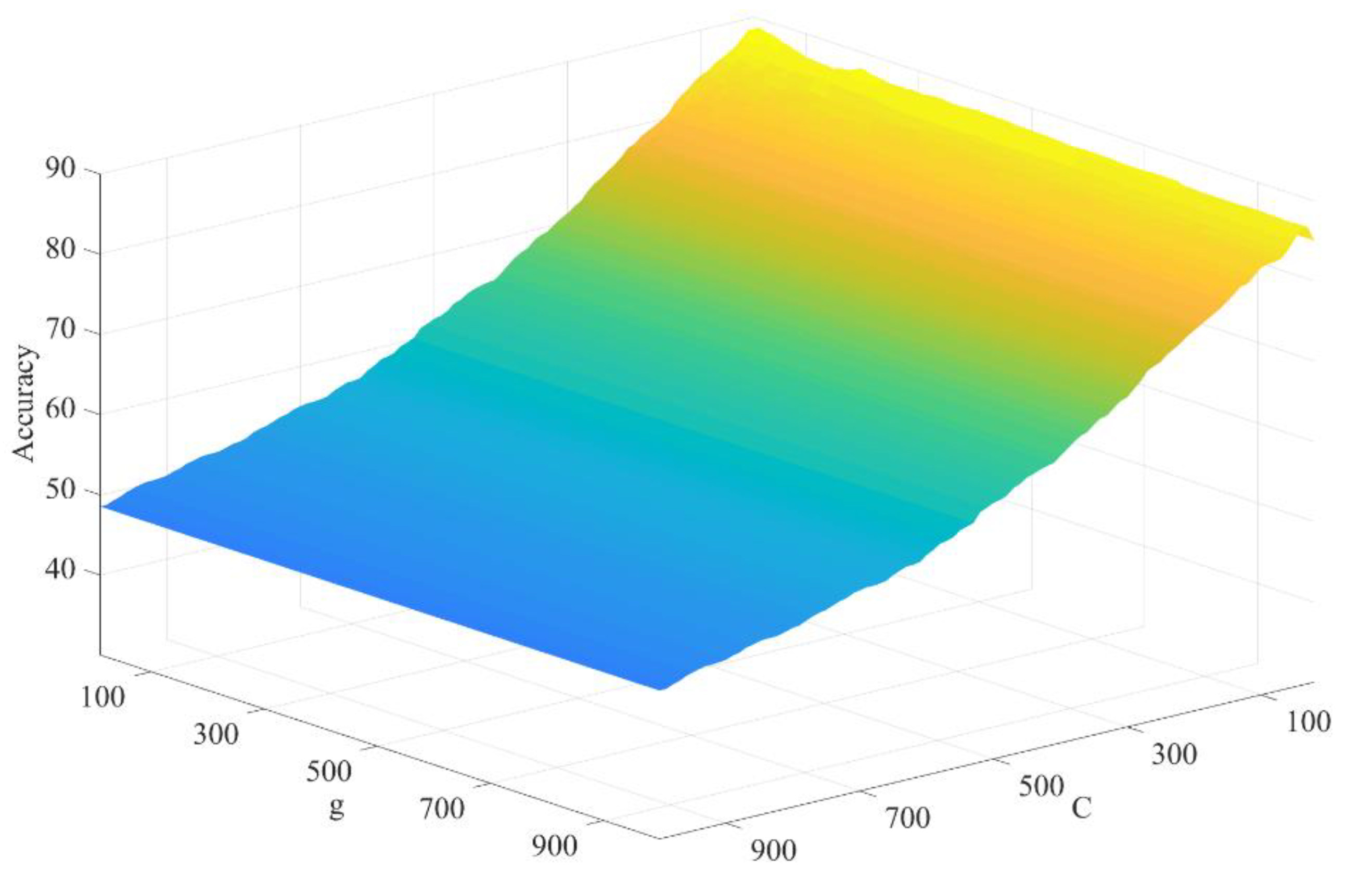
3.4. Model Training and Algorithm Optimization
Finally, the processed data are input into the model training and optimization module to train the machine learning model. When the rescheduling needs to be carried out in actual production, the disturbance data are input into the trained model, and the rescheduling selection decision is output. Model training and algorithm optimization are described in the next chapter.