Real-Time Scheduling of Pumps in Water Distribution Systems Based on Exploration-Enhanced Deep Reinforcement Learning
Abstract
1. Introduction
2. Methods
2.1. Reinforcement Learning (RL)
- S is the state space, which is a set of states;
- A is the action space, which is a set of executable actions for the agent;
- P is the transition distribution, which describes the probability distribution of the next time step state under different and ;
- R is the reward function, is the step reward after the agent takes an under state ; and
- is the discount factor used to calculate the cumulative reward (), which is defined as:
2.2. Design of Significant Factors for RL Application to Pump Scheduling
2.2.1. State Space
2.2.2. Action Space
2.2.3. Reward Function
- (1)
- Energy cost of pumps
- (2)
- Hydraulic constraint
- (3)
- Tank-level variation
| Algorithm 1 Reward function | |
| 1: | for do |
| 2: | Take action for state , collecting ,. |
| 3: | if hydraulic punishment = False then |
| 4: | if then |
| 5: | |
| 6: | else |
| 7: | if then |
| 8: | |
| 9: | else |
| 10: | |
| 11: | end if |
| 12: | end if |
| 13: | else |
| 14: | |
| 15: | break |
| 16: | end if |
| 17: | end for |
2.3. Reinforcement Learning Model
2.3.1. Proximal Policy Optimisation (PPO)
| Algorithm 2 PPO | |
| 1: | , |
| 2: | for k = 0, 1, 2, …, do |
| 3: | Collect set of trajectories by running policy in the environment. |
| 4: | Compute reward-to-go based on the collected trajectories. |
| 5: | . |
| 6: | Update the policy by maximising the PPO objective: |
| 7: | by regression on mean-squared error: |
| 8: | end for |
2.3.2. Exploration Enhancement
3. Case Study: EPANet Net3
- (1)
- All the control rules for the lake source, pipe 330 and pump 335, were removed. In addition, pipe 330 was kept closed. This means that these two raw sources only supply water through pumps 10 and 335, which are controlled by the agent, rather than supply water under specific control rules;
- (2)
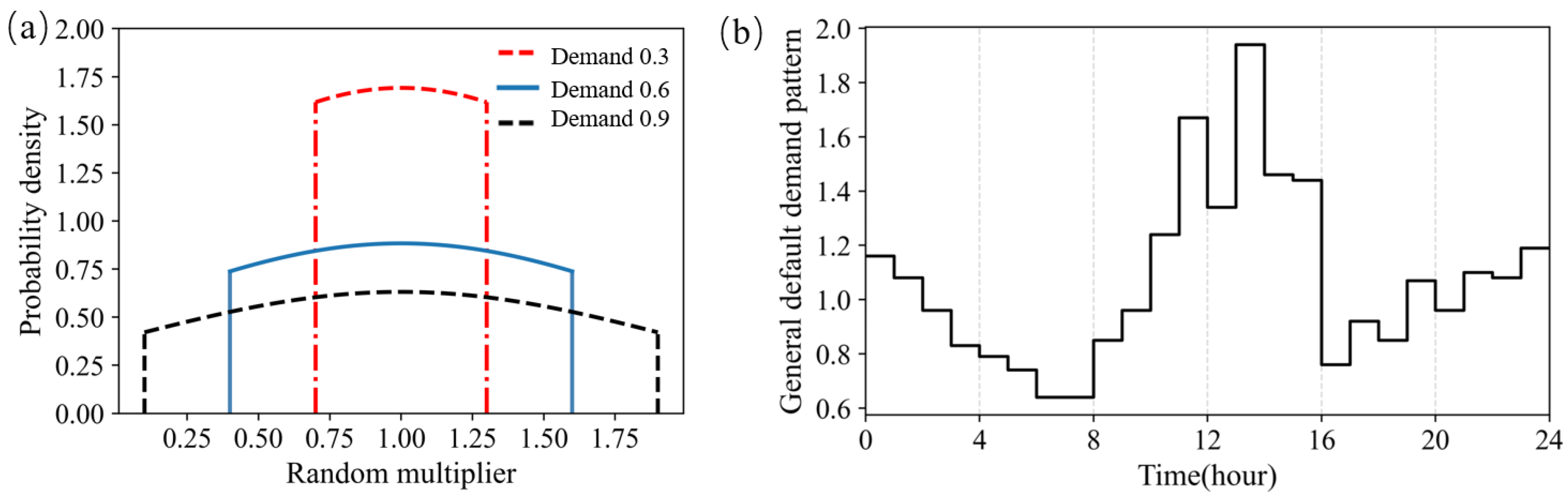
- To simulate the stochastic water demand in a real-world WDS, the randomisation method described above was used.
3.1. Effects of the Penalty Form of Tank-Level Variation
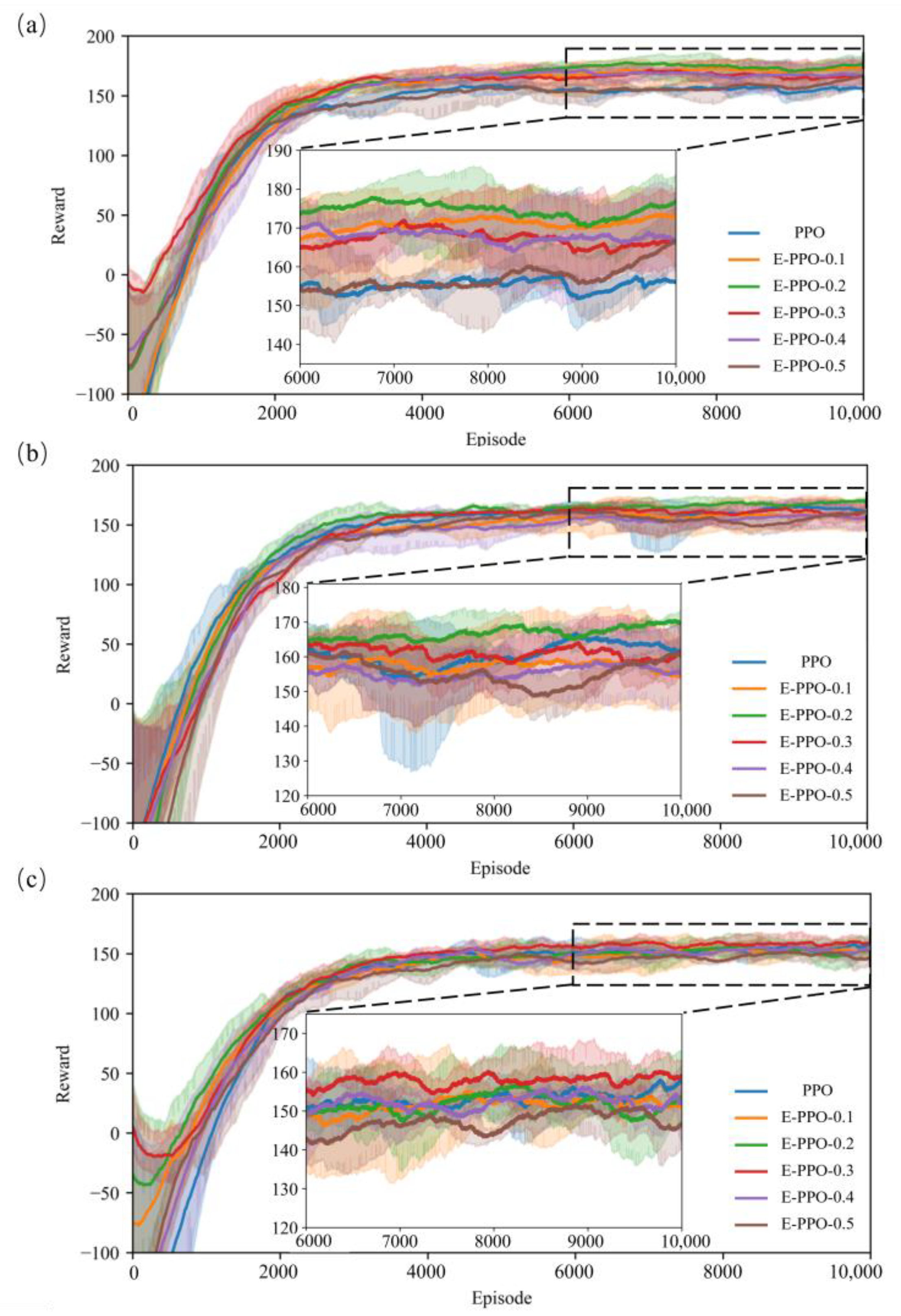
3.2. Effects of Cross Entropy
3.3. Comparison of Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Zyl, J.E.; Savic, D.A.; Walters, G.A. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Res. Plan. Man. 2004, 130, 160–170. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Modell. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef]
- Bohórquez, J.; Saldarriaga, J.; Vallejo, D. Pumping Pattern Optimization in Order to Reduce WDS Operation Costs. Procedia Eng. 2015, 119, 1069–1077. [Google Scholar] [CrossRef]
- Cimorelli, L.; Covelli, C.; Molino, B.; Pianese, D. Optimal Regulation of Pumping Station in Water Distribution Networks Using Constant and Variable Speed Pumps: A Technical and Economical Comparison. Energies 2020, 13, 2530. [Google Scholar] [CrossRef]
- Perera, A.; Nik, V.M.; Scartezzini, J. Impacts of extreme climate conditions due to climate change on the energy system design and operation. Energy Procedia 2019, 159, 358–363. [Google Scholar] [CrossRef]
- Xu, B.; Fu, R.; Lau, C.K.M. Energy market uncertainty and the impact on the crude oil prices. J. Environ. Manag. 2021, 298, 113403. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, G.; Xu, Z.; Yan, X.; Khu, S.; Yang, J.; Zhao, J. Influence of Russia-Ukraine War on the Global Energy and Food Security. Resour. Conserv. Recycl. 2023, 188, 106657. [Google Scholar] [CrossRef]
- Lin, B.; Su, T. Does COVID-19 open a Pandora’s box of changing the connectedness in energy commodities? Res. Int. Bus. Financ. 2021, 56, 101360. [Google Scholar] [CrossRef]
- Si, D.; Li, X.; Xu, X.; Fang, Y. The risk spillover effect of the COVID-19 pandemic on energy sector: Evidence from China. Energy Econ. 2021, 102, 105498. [Google Scholar] [CrossRef]
- Wakeel, M.; Chen, B.; Hayat, T.; Alsaedi, A.; Ahmad, B. Energy consumption for water use cycles in different countries: A review. Appl. Energy 2016, 178, 868–885. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Germanopoulos, G. Optimal Pump Scheduling in Water-Supply Networks. J. Water Res. Plan. Man. 1992, 118, 406–422. [Google Scholar] [CrossRef]
- Yu, G.; Powell, R.S.; Sterling, M.J.H. Optimized pump scheduling in water distribution systems. J. Optimiz. Theory Appl. 1994, 83, 463–488. [Google Scholar] [CrossRef]
- Brion, L.M.; Mays, L.W. Methodology for Optimal Operation of Pumping Stations in Water Distribution Systems. J. Hydraul. Eng. 1991, 117, 1551–1569. [Google Scholar] [CrossRef]
- Maskit, M.; Ostfeld, A. Multi-Objective Operation-Leakage Optimization and Calibration of Water Distribution Systems. Water 2021, 13, 1606. [Google Scholar] [CrossRef]
- Lansey, K.E.; Awumah, K. Optimal Pump Operations Considering Pump Switches. J. Water Res. Plan. Man. 1994, 120, 17–35. [Google Scholar] [CrossRef]
- Carpentier, P.; Cohen, G. Applied mathematics in water supply network management. Automatica 1993, 29, 1215–1250. [Google Scholar] [CrossRef]
- Brdys, M.A.; Puta, H.; Arnold, E.; Chen, K.; Hopfgarten, S. Operational Control of Integrated Quality and Quantity in Water Systems. IFAC Proc. Vol. 1995, 28, 663–669. [Google Scholar] [CrossRef]
- Biscos, C.; Mulholland, M.; Le Lann, M.; Brouckaert, C.; Bailey, R.; Roustan, M. Optimal operation of a potable water distribution network. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2002, 46, 155–162. [Google Scholar] [CrossRef]
- Giacomello, C.; Kapelan, Z.; Nicolini, M. Fast Hybrid Optimization Method for Effective Pump Scheduling. J. Water Res. Plan. Man. 2013, 139, 175–183. [Google Scholar] [CrossRef]
- Geem, Z.W. Harmony Search in Water Pump Switching Problem. In Proceedings of the International Conference on Natural Computation, Changsha, China, 27–29 August 2005; pp. 751–760, ISBN 978-3-540-28320-1. [Google Scholar]
- Wu, P.; Lai, Z.; Wu, D.; Wang, L. Optimization Research of Parallel Pump System for Improving Energy Efficiency. J. Water Res. Plan. Man. 2015, 141, 4014094. [Google Scholar] [CrossRef]
- Mackle, G.; Savic, G.A.; Walters, G.A. Application of genetic algorithms to pump scheduling for water supply. In Proceedings of the First International Conference on Genetic Algorithms in Engineering Systems: Innovations and Applications, Sheffield, UK, 12–14 September 1995; pp. 400–405. [Google Scholar]
- Zhu, J.; Wang, J.; Li, X. Optimal scheduling of water-supply pump stations based on improved adaptive genetic algorithm. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 2716–2721. [Google Scholar]
- Goldberg, D.E.; Kuo, C.H. Genetic Algorithms in Pipeline Optimization. J. Comput. Civ. Eng. 1987, 1, 128–141. [Google Scholar] [CrossRef]
- Wegley, C.; Eusuff, M.; Lansey, K. Determining Pump Operations using Particle Swarm Optimization. In Proceeding of the Joint Conference on Water Resource Engineering and Water Resources Planning and Management, Minneapolis, MN, USA, 30 July–2 August 2000. [Google Scholar]
- Al-Ani, D.; Habibi, S. Optimal pump operation for water distribution systems using a new multi-agent Particle Swarm Optimization technique with EPANET. In Proceedings of the 2012 25th IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Montreal, QC, Canada, 29 April–2 May 2012; pp. 1–6. [Google Scholar]
- Zhao, W.; Beach, T.H.; Rezgui, Y. A systematic mixed-integer differential evolution approach for water network operational optimization. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170879. [Google Scholar] [CrossRef]
- Li, D.; Chen, D.; Jin, B.; Shi, L.; Goh, J.; Ng, S. MAD-GAN: Multivariate Anomaly Detection for Time Series Data with Generative Adversarial Networks. In Artificial Neural Networks and Machine Learning—ICANN 2019: Text and Time Series; Springer: Cham, Switzerland, 2019; pp. 703–716. [Google Scholar]
- Jiao, Y.; Rayhana, R.; Bin, J.; Liu, Z.; Wu, A.; Kong, X. A steerable pyramid autoencoder based framework for anomaly frame detection of water pipeline CCTV inspection. Measurement 2021, 174, 109020. [Google Scholar] [CrossRef]
- Nasser, A.A.; Rashad, M.Z.; Hussein, S.E. A Two-Layer Water Demand Prediction System in Urban Areas Based on Micro-Services and LSTM Neural Networks. IEEE Access 2020, 8, 147647–147661. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A.; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Environ. Monit. Assess. 2017, 189, 313. [Google Scholar] [CrossRef]
- Joo, C.N.; Koo, J.Y.; Yu, M.J. Application of short-term water demand prediction model to Seoul. Water Sci. Technol. 2002, 46, 255–261. [Google Scholar] [CrossRef]
- Geem, Z.W.; Tseng, C.; Kim, J.; Bae, C. Trenchless Water Pipe Condition Assessment Using Artificial Neural Network. In Pipelines 2007; American Society of Civil Engineers: Reston, VA, USA, 2007; pp. 1–9. [Google Scholar]
- Xu, J.; Wang, H.; Rao, J.; Wang, J. Zone scheduling optimization of pumps in water distribution networks with deep reinforcement learning and knowledge-assisted learning. Soft Comput. 2021, 25, 14757–14767. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Lobbrecht, A.H.; Solomatine, D.P. Neural Networks and Reinforcement Learning in Control of Water Systems. J. Water Res. Plan. Man. 2003, 129, 458–465. [Google Scholar] [CrossRef]
- Fu, G.; Jin, Y.; Sun, S.; Yuan, Z.; Butler, D. The role of deep learning in urban water management: A critical review. Water Res. 2022, 223, 118973. [Google Scholar] [CrossRef]
- Broad, D.R.; Dandy, G.C.; Maier, H.R. Water Distribution System Optimization Using Metamodels. J. Water Res. Plan. Man. 2005, 131, 172–180. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Hajgató, G.; Paál, G.; Gyires-Tóth, B. Deep Reinforcement Learning for Real-Time Optimization of Pumps in Water Distribution Systems. J. Water Res. Plan. Man. 2020, 146, 4020079. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Jang, S.; Kim, H. Entropy-Aware Model Initialization for Effective Exploration in Deep Reinforcement Learning. Sensors 2022, 22, 5845. [Google Scholar] [CrossRef]
- Varno, F.; Soleimani, B.H.; Saghayi, M.; Di Jorio, L.; Matwin, S. Efficient Neural Task Adaptation by Maximum Entropy Initialization. arXiv 2019, arXiv:1905.10698. [Google Scholar]
- Ormsbee, L.; Hoagland, S.; Hernandez, E.; Hall, A.; Ostfeld, A. Hydraulic Model Database for Applied Water Distribution Systems Research. J. Water Res. Plan. Man. 2022, 148, 04022037. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Barton, A.F.; Mala-Jetmarova, H.; Al Nuaimat, A.; Ahmed, S.T.; Sultanova, N.; Yearwood, J. An algorithm for minimization of pumping costs in water distribution systems using a novel approach to pump scheduling. Math. Comput. Model. 2013, 57, 873–886. [Google Scholar] [CrossRef]



| Symbol | Hyperparameter | Value |
|---|---|---|
| Structure and number of neurons in layers of the actor network | [256, 128, 64] | |
| Structure and number of neurons in layers of the critic network | [256, 128, 1] | |
| Learning rate of the actor network | ||
| Learning rate of the critic network | ||
| Maximum episode length | 24 | |
| Discounter factor | 0.9 | |
| Clip range | 0.2 | |
| Epochs | 10 | |
| Benchmark reward of energy cost | 406.54 | |
| Negative reward for the hydraulic constraint | −200 |
| Uncertainty Parameter of Demand | Test Case | Energy Cost (USD/Day) | ||||
|---|---|---|---|---|---|---|
| GA | PSO | DE | PPO | E-PPO | ||
| 0.30 | Case 1 | 190.251 | 231.889 | 205.586 | 213.210 | 207.941 |
| Case 2 | 193.700 | 256.125 | 231.793 | 215.387 | 209.001 | |
| Case 3 | 206.623 | 283.127 | 239.610 | 218.477 | 215.993 | |
| Case 4 | 198.713 | 242.322 | 229.684 | 218.099 | 211.868 | |
| Case 5 | 190.328 | 223.991 | 212.200 | 237.575 | 215.848 | |
| 0.60 | Case 1 | 194.435 | 279.038 | 223.849 | 214.965 | 206.268 |
| Case 2 | 204.636 | 279.256 | 229.777 | 214.099 | 208.265 | |
| Case 3 | 194.163 | 255.669 | 226.321 | 229.907 | 204.839 | |
| Case 4 | 190.837 | 245.699 | 221.987 | 232.683 | 203.932 | |
| Case 5 | 200.929 | 268.320 | 224.463 | 216.151 | 209.488 | |
| 0.90 | Case 1 | 187.169 | 238.844 | 214.211 | 230.172 | 208.123 |
| Case 2 | 185.796 | 232.904 | 219.973 | 211.734 | 196.397 | |
| Case 3 | 201.102 | 259.644 | 216.285 | 209.971 | 186.099 | |
| Case 4 | 201.855 | 257.274 | 219.415 | 218.811 | 202.868 | |
| Case 5 | 217.869 | 253.887 | 238.714 | 227.810 | 220.299 | |
| Uncertainty Parameter of Demand | Time (s) | ||||||
|---|---|---|---|---|---|---|---|
| GA | PSO | DE | PPO Training | E-PPO Training | PPO Application | E-PPO Application | |
| 0.3 | 1699.32 | 1291.18 | 1448.63 | 5479.30 | 5573.58 | 0.42 | 0.41 |
| 0.6 | 1640.72 | 1214.62 | 1475.45 | 5333.92 | 5407.01 | 0.44 | 0.42 |
| 0.9 | 1586.19 | 1181.03 | 1408.05 | 5833.19 | 5506.07 | 0.42 | 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Gao, J.; Zhong, D.; Wu, R.; Liu, L. Real-Time Scheduling of Pumps in Water Distribution Systems Based on Exploration-Enhanced Deep Reinforcement Learning. Systems 2023, 11, 56. https://doi.org/10.3390/systems11020056
Hu S, Gao J, Zhong D, Wu R, Liu L. Real-Time Scheduling of Pumps in Water Distribution Systems Based on Exploration-Enhanced Deep Reinforcement Learning. Systems. 2023; 11(2):56. https://doi.org/10.3390/systems11020056
Chicago/Turabian StyleHu, Shiyuan, Jinliang Gao, Dan Zhong, Rui Wu, and Luming Liu. 2023. "Real-Time Scheduling of Pumps in Water Distribution Systems Based on Exploration-Enhanced Deep Reinforcement Learning" Systems 11, no. 2: 56. https://doi.org/10.3390/systems11020056
APA StyleHu, S., Gao, J., Zhong, D., Wu, R., & Liu, L. (2023). Real-Time Scheduling of Pumps in Water Distribution Systems Based on Exploration-Enhanced Deep Reinforcement Learning. Systems, 11(2), 56. https://doi.org/10.3390/systems11020056






