Hierarchical Coordinated Energy Management Strategy for Hybrid Energy Storage System in Electric Vehicles Considering the Battery’s SOC
Abstract
1. Introduction
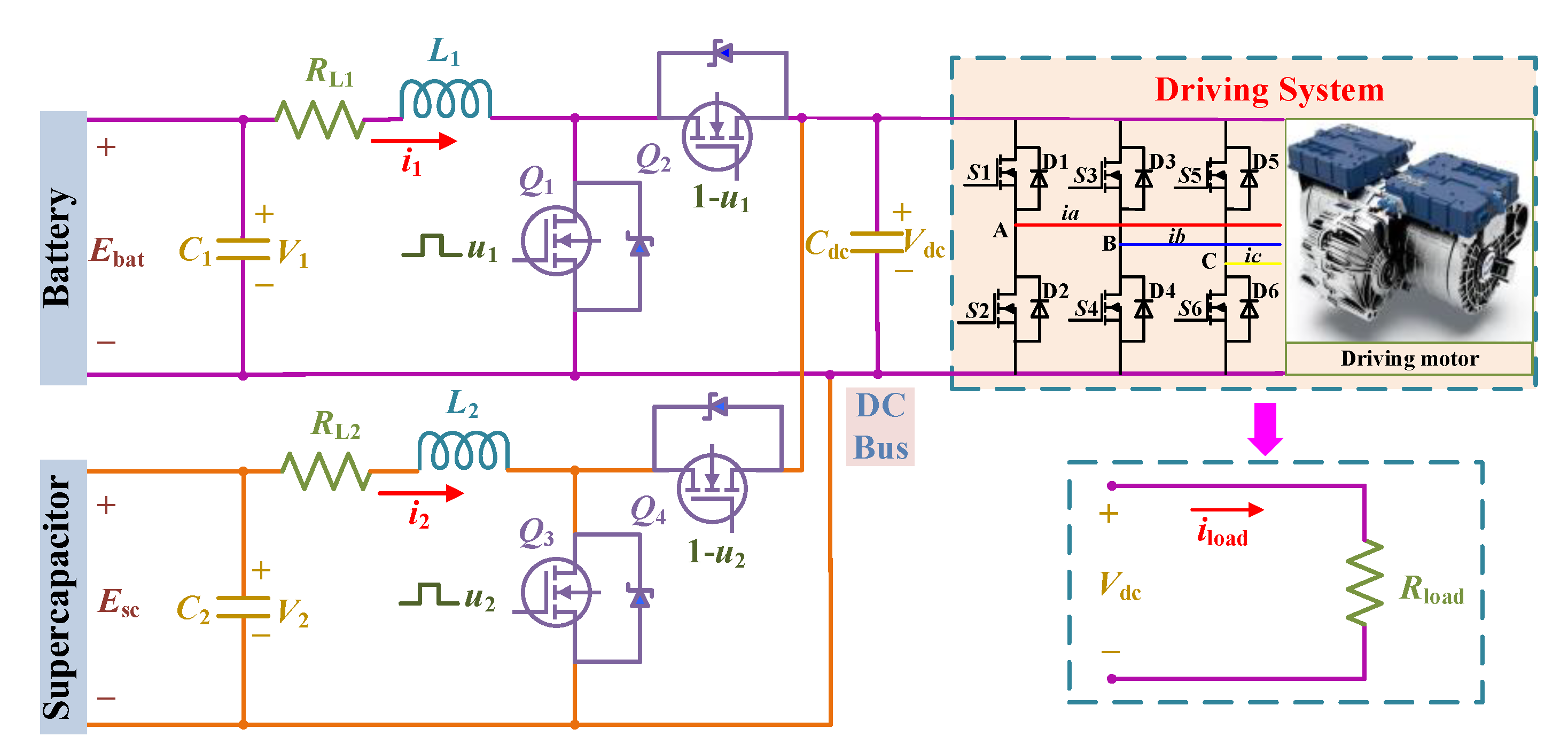
2. The Topology of Battery–SC HESS
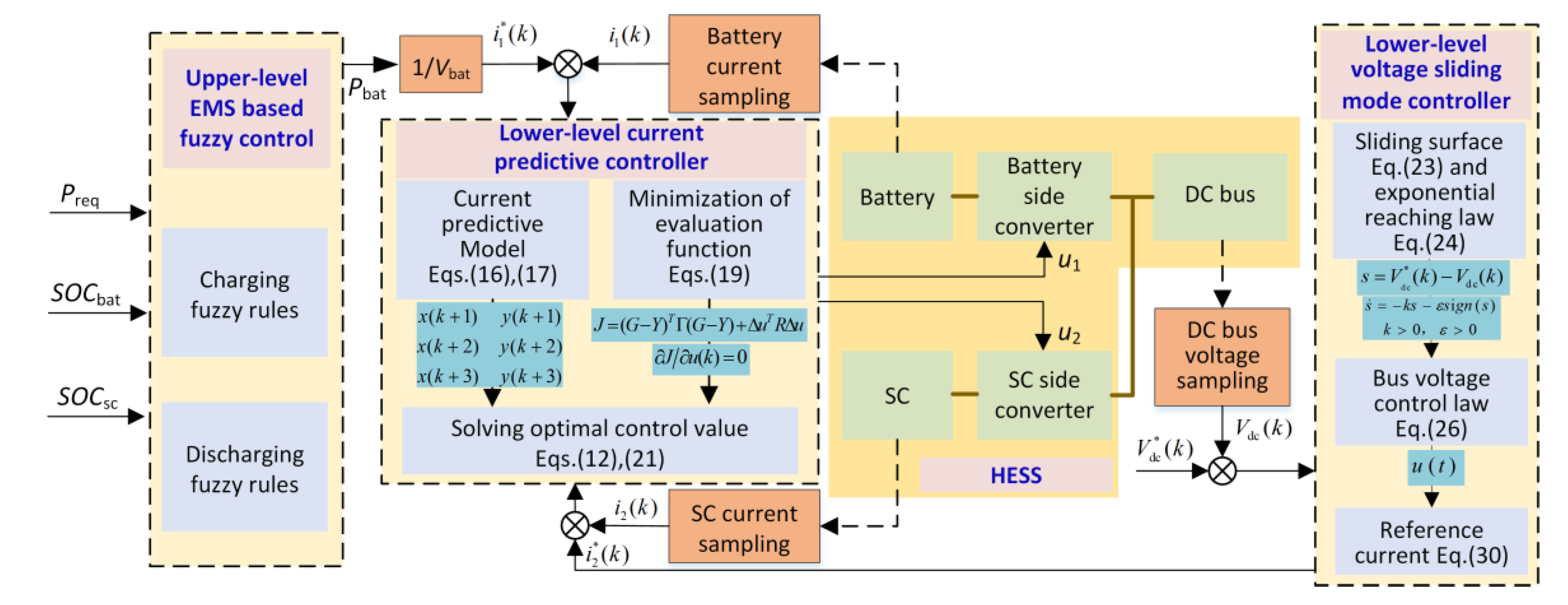
3. The HCEMS-MPC Strategy of HESS
3.1. Upper-Level Energy Management Based on Fuzzy Control
3.2. The Lower-Level Current Predictive Controller
- (1)
- The prediction time domain is p, the control time domain is m, and m ≤ p.
- (2)
- Outside of the control time domain, the control variable remains unchanged; that is, Δu(k + i) = 0, i = m, m + 1, …, p − 1.
3.3. The Lower-Level Voltage Sliding Mode Controller
4. Simulation and Results
4.1. Simulation Configuration
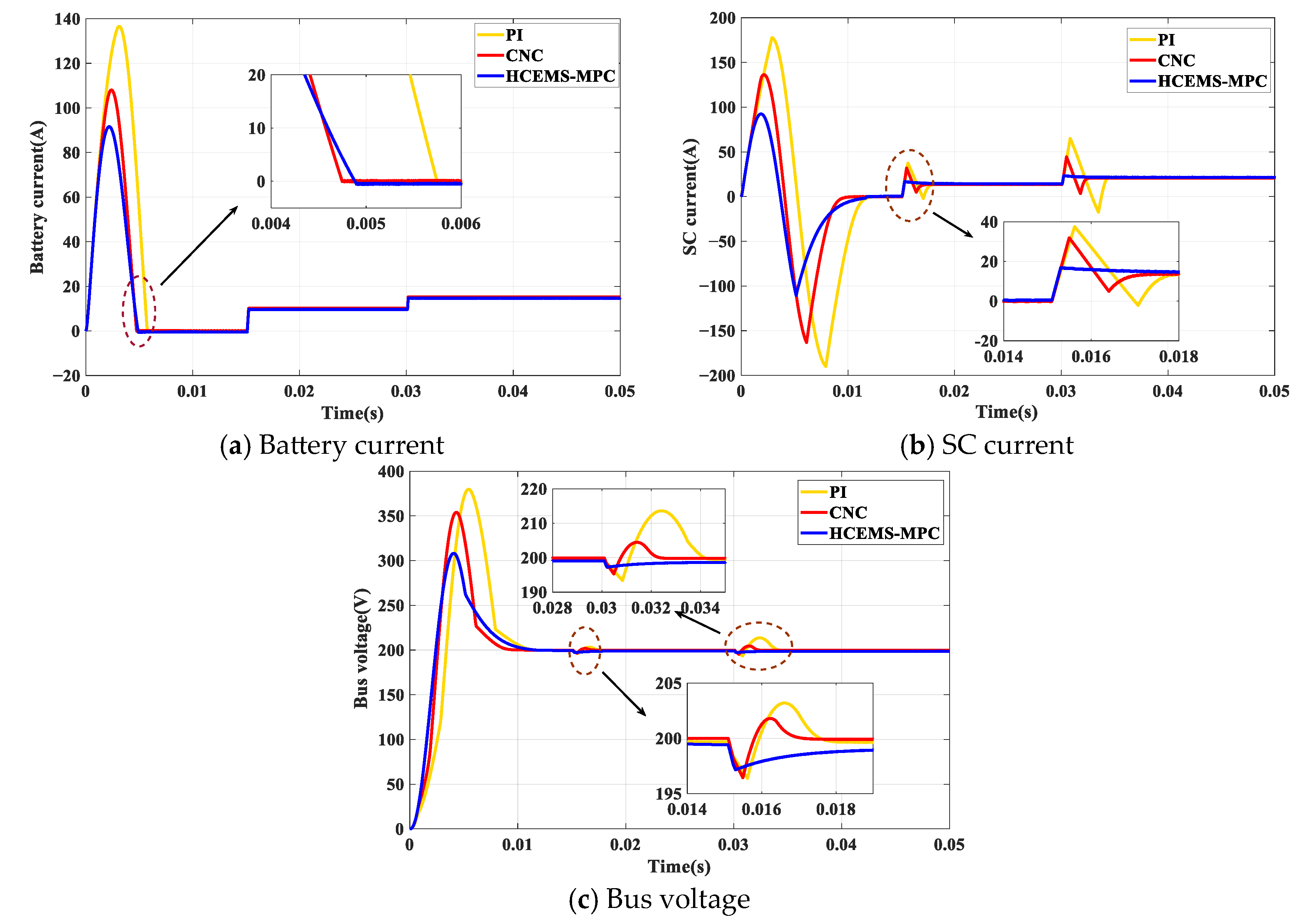
4.2. The Results under Power Step Change
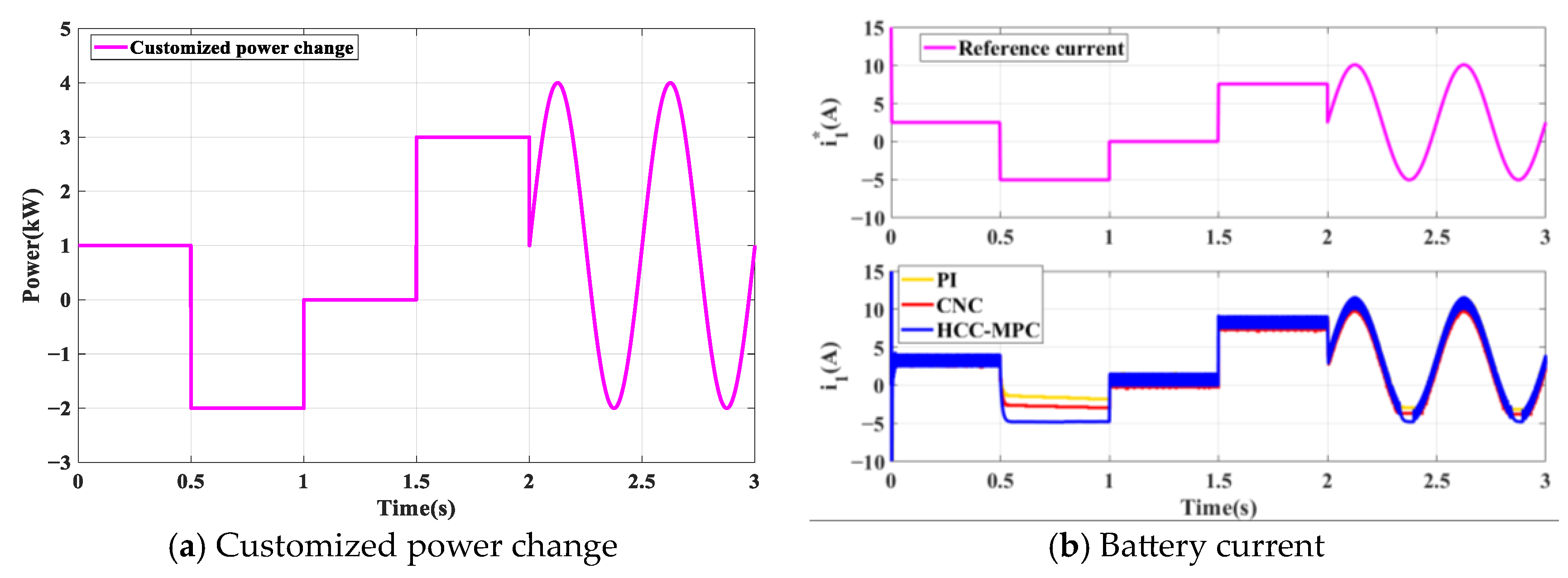
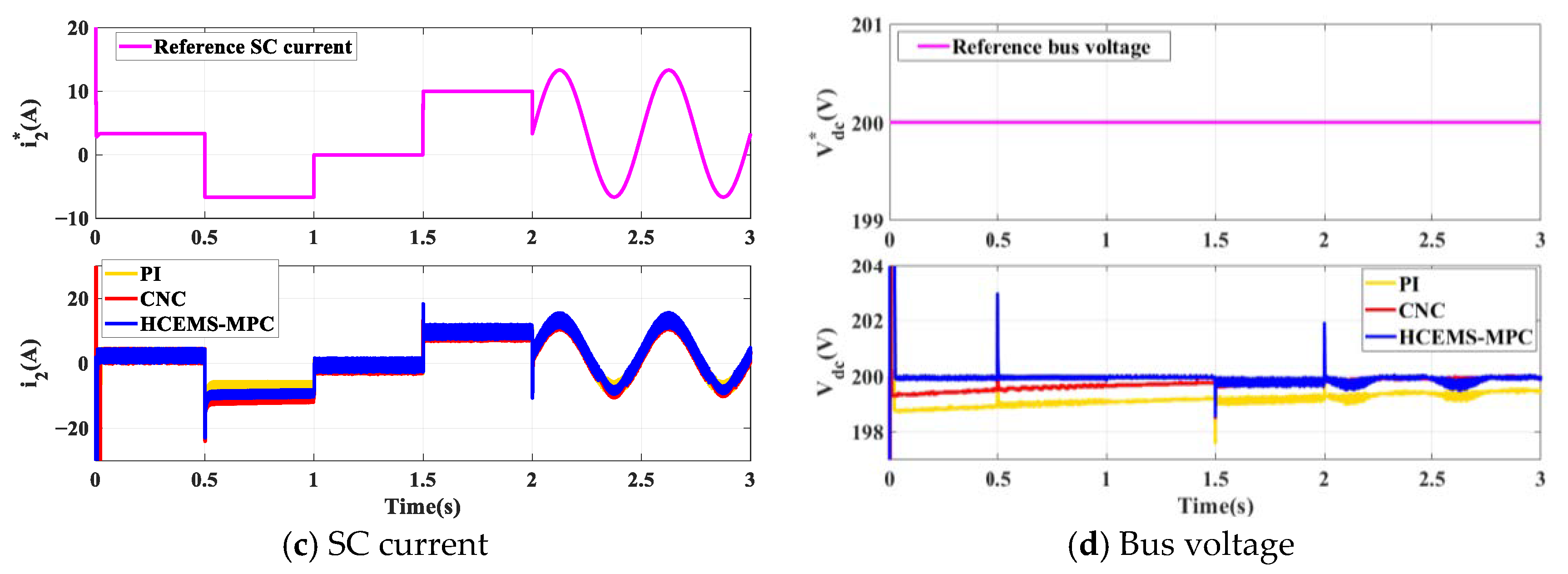
4.3. The Results under Customized Power Change
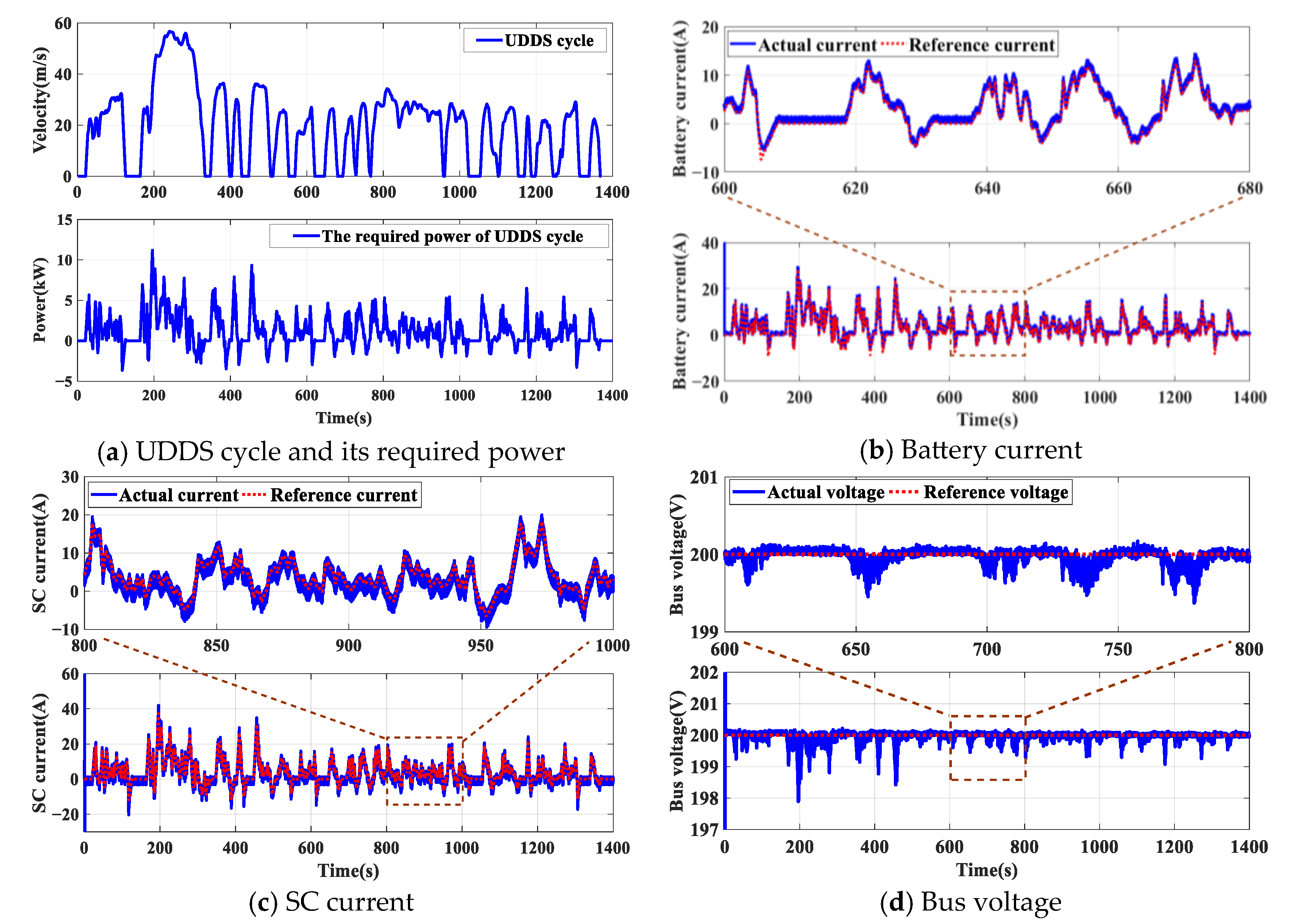
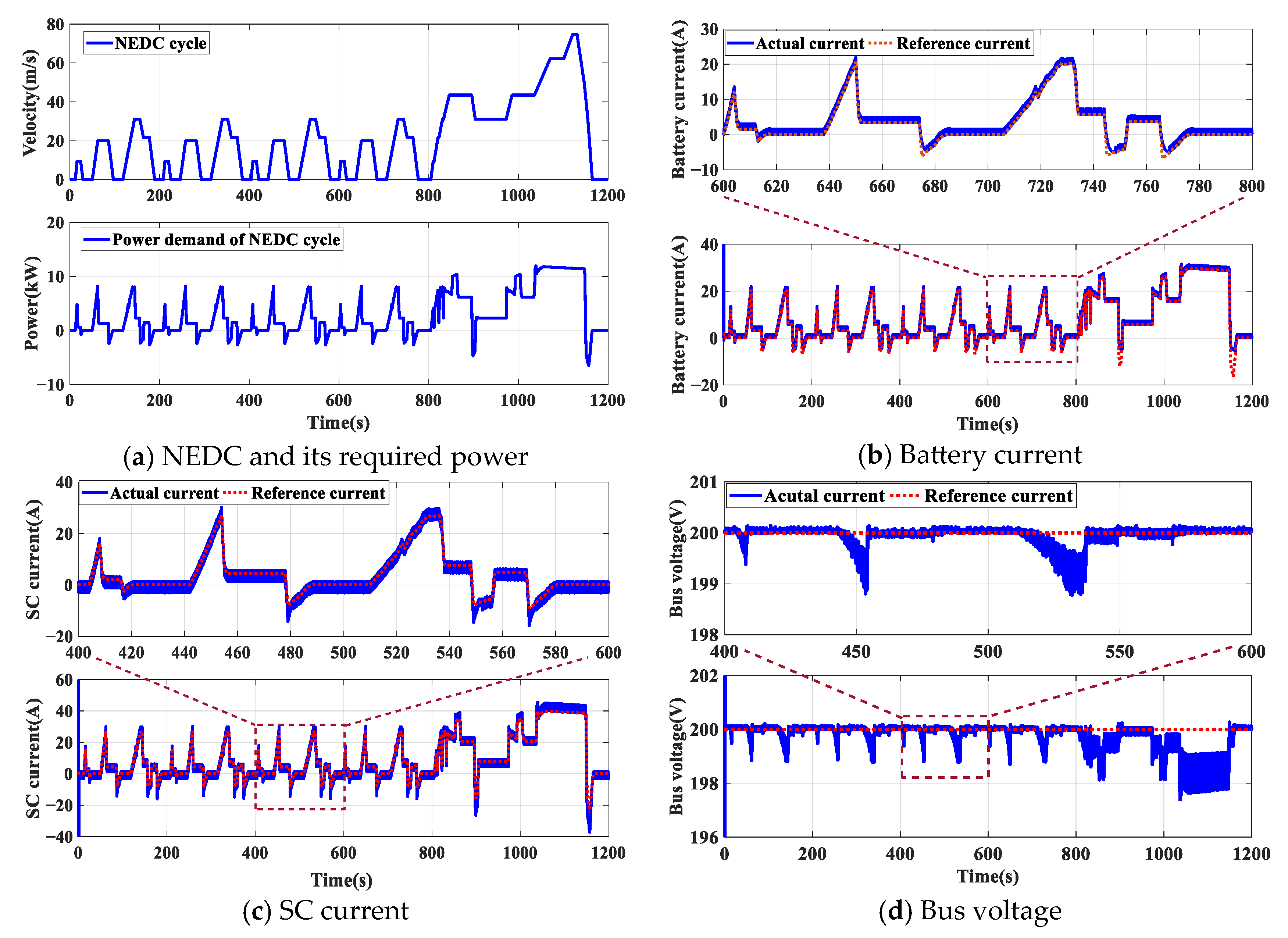
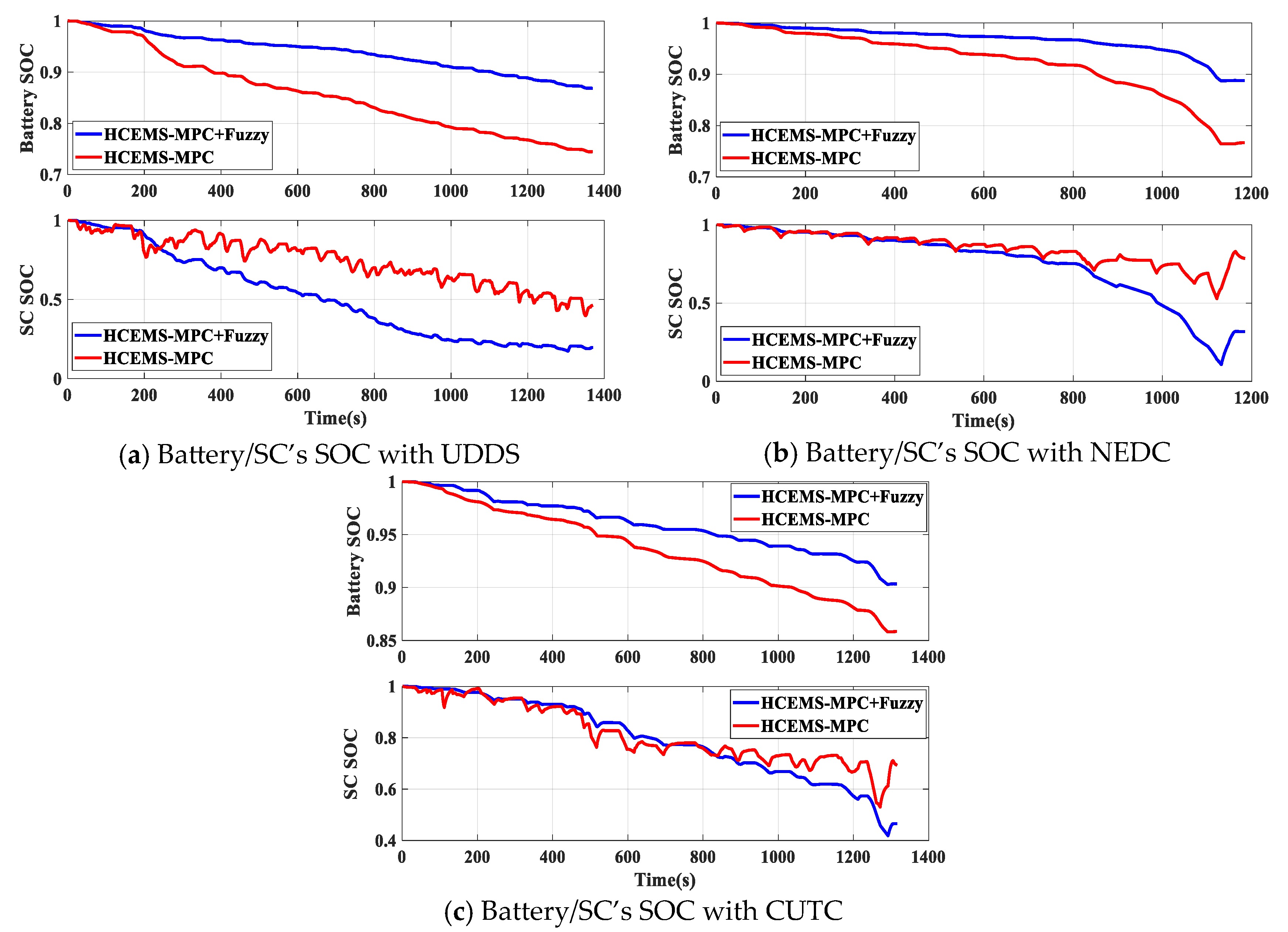
4.4. The Results under Standard Driving Cycles
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, W.; Li, M.; Chen, Z. An Energy Management Strategy for Hybrid Energy Storage Systems coordinate with state of thermal and power. Control. Eng. Pract. 2022, 122, 105122. [Google Scholar]
- Salari, O.; Zaad, K.H.; Bakhshai, A.; Jain, P. Reconfigurable Hybrid Energy Storage System for an Electric Vehicle DC–AC Inverter. IEEE Trans. Power Electron. 2020, 35, 12846–12860. [Google Scholar] [CrossRef]
- Akar, F.; Tavlasoglu, Y.; Vural, B. An Energy Management Strategy for a Concept Battery/Ultracapacitor Electric Vehicle With Improved Battery Life. IEEE Trans. Transp. Electrif. 2017, 3, 191–200. [Google Scholar] [CrossRef]
- Kouchachvili, L.; Yaici, W.; Entchev, E. Hybrid battery/supercpacitor energy storage system for the electric vehicles. J. Power Sources 2018, 374, 237–248. [Google Scholar] [CrossRef]
- Song, Z.; Hou, J.; Hofmann, H.; Li, J.; Ouyang, M. Sliding-mode and Lyapunov function-based control for battery/super- capacitor hybrid energy storage system used in electric vehicles. Energy 2017, 122, 601–612. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Wu, X.; Sha, D.; Lin, F.; Fang, X. An Adaptive Energy Management Strategy of Stationary Hybrid Energy Storage System. IEEE Trans. Transp. Electrif. 2022, 8, 2261–2272. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Han, X.; Ouyang, M. Optimization for a hybrid energy storage system in electric vehicles using dynamic programing approach. Appl. Energy 2015, 139, 151–162. [Google Scholar] [CrossRef]
- Zhang, Q.; Deng, W.; Li, G. Stochastic control of predictive power management for battery/ supercapacitor hybrid energy storage systems of electric vehicles. IEEE Trans. Ind. Inform. 2018, 14, 3023–3030. [Google Scholar] [CrossRef]
- Jia, C.; Cui, J.; Qiao, W.; Qu, L. Real-Time Model Predictive Control for Battery- Supercapacitor Hybrid Energy Storage Systems Using Linear Parameter Varying Models. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 11, 251–263. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Hou, J.; Han, X.; Ouyang, M. Energy management strategies comparison for electric vehicles with hybrid energy storage system. Appl. Energy 2014, 134, 321–331. [Google Scholar] [CrossRef]
- Nosrati, K.; Mansouri, H.R.; Saboori, H. Fractional-order PID controller design of frequency deviation in a hybrid renewable energy generation and storage system. CIRED Open Access Proc. J. 2017, 1, 1148–1152. [Google Scholar] [CrossRef][Green Version]
- Xu, D.; Liu, Q.; Yan, W.; Yang, W. Adaptive terminal sliding mode control for hybrid energy storage systems of fuel cell, battery and supercapacitor. IEEE Access 2019, 7, 29295–29303. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Z.; Yuan, X.; Wang, Y.; Shen, X. L2-gain adaptive robust control for hybrid energy storage system in electric vehicles. IEEE Trans. Power Electron. 2020, 36, 7319–7332. [Google Scholar] [CrossRef]
- Li, D.; De Schutter, B. Distributed model-free adaptive predictive control for urban traffic networks. IEEE Trans. Control. Syst. Technol. 2021, 30, 180–192. [Google Scholar] [CrossRef]
- Dong, H.; Xi, J. Model Predictive Longitudinal Motion Control for the Unmanned Ground Vehicle With a Trajectory Tracking Model. IEEE Trans. Veh. Technol. 2021, 71, 1397–1410. [Google Scholar] [CrossRef]
- Saeed, S.; Zhao, W.; Wang, H.; Tao, T.; Khan, F. Fault-tolerant deadbeat model predictive current control for a five-phase PMSM with improved SVPWM. Chin. J. Electr. Eng. 2021, 7, 111–123. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Divan, D. Robust predictive control for modular solid-state transformer with reduced dc link and parameter mismatch. IEEE Trans. Power Electron. 2021, 36, 14295–14311. [Google Scholar] [CrossRef]
- Chen, M.; Cheng, Z.; Liu, Y.; Cheng, Y.; Tian, Z. Multitime-scale optimal dispatch of railway FTPSS based on model predictive control. IEEE Trans. Transp. Electrif. 2020, 6, 808–820. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Manandhar, U.; Gooi, H.B.; Foo, G. A model predictive current-controlled bidirectional three-level DC/DC converter for hybrid energy storage system in DC microgrids. IEEE Trans. Power Electron. 2019, 34, 4025–4030. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Q.; Zhou, J.; Chen, X. A model predictive control method for hybrid energy storage systems. CSEE J. Power Energy Syst. 2020, 7, 329–338. [Google Scholar]
- Zhong, L.; Yin, B.; Liu, W.; Gao, Y.; Zheng, Z.; Li, C.; Ni, F. Research on Model Predictive Controlled HESS for Seamless Mode Switching of DC Microgrid. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Morato, M.M.; Normey-Rico, J.E.; Sename, O. Model predictive control design for linear parameter varying systems: A survey. Annu. Rev. Control. 2020, 49, 64–80. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, X. Composite Non-Linear Control of Hybrid Energy-Storage System in Electric Vehicle. Energies 2022, 15, 1567. [Google Scholar] [CrossRef]

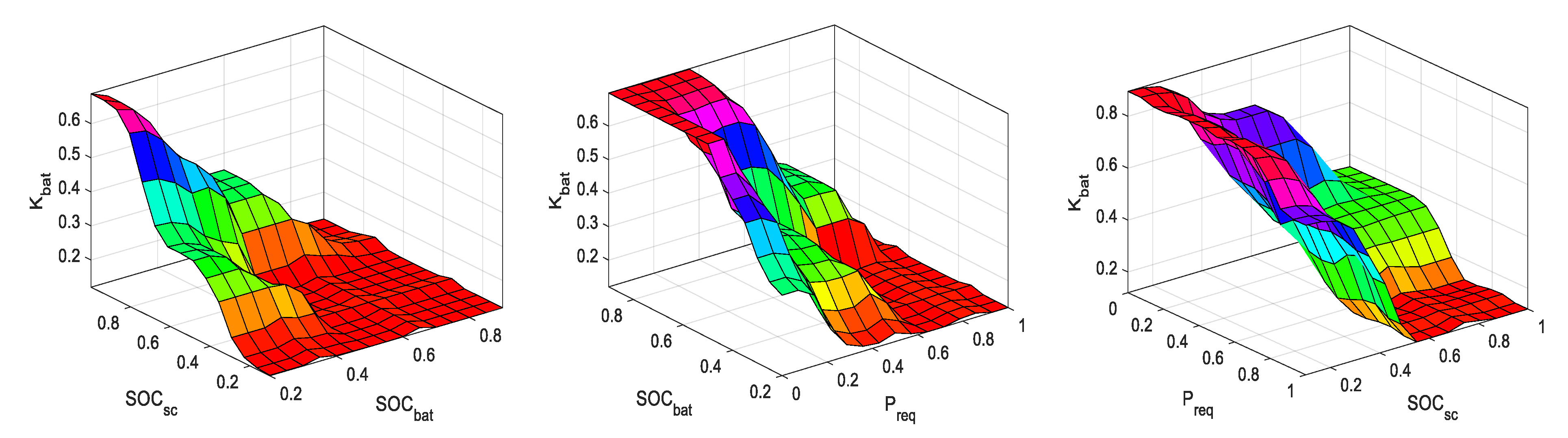


| Fuzzy variables | Preq | SOCbat | SOCsc | Kbat |
| Fuzzy domain | [0, 1] | [0.2, 1] | [0.1, 1] | [0, 1] |
| Fuzzy language values | S, M, L, TL | S, M, L | S, M, L | S, M, L, TL |
| Kbat | SOCsc | |||
| S | M | L | ||
| SOCbat | S | S | S | M |
| M | S | S | S | |
| L | S | S | S | |
| Kbat | Preq | ||||
| S | M | L | TL | ||
| SOCbat (SOCsc = S) | S | TL | L | M | M |
| M | TL | TL | L | L | |
| L | TL | TL | TL | L | |
| SOCbat (SOCsc = M) | S | M | S | S | S |
| M | L | M | S | S | |
| L | TL | L | S | S | |
| SOCbat (SOCsc = L) | S | M | S | S | S |
| M | M | S | S | S | |
| L | L | M | S | S | |
| Simulation Cases | Sections | |
|---|---|---|
| 1 | Power step change | 4.2 |
| 2 | Customized power change | 4.3 |
| 3 | Standard driving cycle (UDDS, NEDC, CUTC) | 4.4 |
| Parameter | Value |
|---|---|
| L1: Battery-side inductance (H) | 2.6 × 10−3 |
| L2: SC-side inductance (H) | 1.8 × 10−3 |
| R1: Inductor L1 series resistance(Ω) | 0.2 |
| R2: Inductor L2 series resistance(Ω) | 0.15 |
| Cdc: Load-side capacitor (F) | 1.5 × 10−3 |
| C1: Battery-side capacitor (F) | 0.7 × 10−2 |
| C2: SC-side capacitor (F) | 0.5 × 10−2 |
| UDDS | NEDC | CUTC | ||
|---|---|---|---|---|
| Before fuzzy control | Battery’s SOC | 0.744 | 0.766 | 0.858 |
| SC’s SOC | 0.463 | 0.784 | 0.692 | |
| After fuzzy control | Battery’s SOC | 0.869 | 0.887 | 0.903 |
| SC’s SOC | 0.212 | 0.317 | 0.465 | |
| Strategy | First Simulation | Second Simulation | Third Simulation | Fourth Simulation |
|---|---|---|---|---|
| PI | 31.59 | 31.57 | 31.61 | 31.56 |
| CNC | 33.67 | 33.71 | 33.64 | 33.66 |
| HCEMS-MPC | 32.15 | 32.11 | 32.09 | 32.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Lu, Z.; Cao, X.; Hou, Y. Hierarchical Coordinated Energy Management Strategy for Hybrid Energy Storage System in Electric Vehicles Considering the Battery’s SOC. Systems 2023, 11, 498. https://doi.org/10.3390/systems11100498
Huang W, Lu Z, Cao X, Hou Y. Hierarchical Coordinated Energy Management Strategy for Hybrid Energy Storage System in Electric Vehicles Considering the Battery’s SOC. Systems. 2023; 11(10):498. https://doi.org/10.3390/systems11100498
Chicago/Turabian StyleHuang, Wenya, Zhangyu Lu, Xu Cao, and Yingjun Hou. 2023. "Hierarchical Coordinated Energy Management Strategy for Hybrid Energy Storage System in Electric Vehicles Considering the Battery’s SOC" Systems 11, no. 10: 498. https://doi.org/10.3390/systems11100498
APA StyleHuang, W., Lu, Z., Cao, X., & Hou, Y. (2023). Hierarchical Coordinated Energy Management Strategy for Hybrid Energy Storage System in Electric Vehicles Considering the Battery’s SOC. Systems, 11(10), 498. https://doi.org/10.3390/systems11100498






