Effectiveness of AR Board Game on Computational Thinking and Programming Skills for Elementary School Students

Abstract

This study integrated the augmented reality (AR) technology into the “Coding Ocean” board game to provide players with real-time simulation of ship paths and learning scaffolds. Combined with Scratch block-based programming, an interactive learning environment is developed to assist elementary school students in learning coding skills from the unplugged board game to enhance their computational thinking concepts. The AR board game is focused on the programming concepts of sequential, and/or and loop. Through the process of treasure hunting, the basic concepts of computational thinking can be developed, i.e., abstraction, problem decomposition, pattern recognition and algorithmic thinking. In order to investigate the learning effectiveness of the AR board game on computational thinking and programming skills, a number of 51 third graders from an elementary school were recruited as research samples. The experimental group (n = 26) used the AR board game and the control group (n = 25) used the traditional board game for game-based learning. The experimental results indicate: (1) the learning effectiveness of computational thinking for the experimental group was significantly higher than that of the control group; (2) the learning achievement of the block-based programming skills for the experimental group was significantly higher than that of the control group; (3) the cognitive load of the experimental group was significantly lower than that of the control group. The AR technology can combine the unplugged board games with plugged learning modules to assist students in game-based learning, which is useful for enhancing computational thinking abilities while reducing the cognitive load.

1. Introduction

According to the 2017 report from Innovation and Science Australia (ISA), 92% of the world’s future jobs will require digital skills and the government must respond to the changing nature of work by equipping all Australians with skills relevant to the 2030 job market [1]. A Google search for the term “Education” makes it clear that parents and teachers expect students to rely on information literacy to develop problem-solving skills and prepare themselves for future jobs [2]. Human society is highly dependent on digital skills, and the importance of computing education is growing. Since Estonia released its ProgeTiger programme in 2012, programming and STEAM subjects have been included in the national curricula, with the goal of providing children and teenagers with the skills they need in the future [3].

The United Kingdom released its National Curriculum for 2014, which regulated the teaching of coding and computing education through a four-stage computation curriculum, hoping that students could become digitally literate and able to create programs [4]. Later, some scholars surveyed 21 European ministries of education, aiming to understand how computing education was integrated into the curricula of European countries [5]. It can be seen that computing education is highly valued by many countries and will become a major issue for future curricula in fundamental education.

Likewise, the Ministry of Education in Taiwan formulated its Curriculum Guidelines of 12-year Basic Education in 2018, in which the main goal of the technology domain is to develop students’ information literacy. Therefore, computational thinking is considered an important subject in the technology domain [6], one whose major purpose is to cultivate talents with future information technology (IT) for the country.

Computational thinking comprises the attitudes and skills for the application of general information. Starting from computer science, it uses fundamental concepts to design systems, solve problems, and understand human activities and behaviors. A series of thought processes have been used in various fields and have become an important thinking model that everyone must learn and apply, not just for computer scientists [7]. Computational thinking is not exactly the same as programming, but programming can stimulate computational thinking [8]. The demonstration of computational thinking abilities and the relative knowledge can also be achieved and practiced with the aid of programming skills [9]. Therefore, programming and computational thinking are closely related.

Most schools conduct plugged activities in computer courses to teach programming and information science. Visual block-based programming has been widely used in introductory courses for elementary school students [10]. Some of these, for example, use Scratch to teach programming, where the commands are stacked by dragging and dropping. Block-based programming helps to reduce the frustration of syntax errors for beginners when they are learning traditional programming languages [11]. It not only establishes the foundation for students to learn programming skills, but also fosters computational thinking concepts [12].

Computational thinking and programming skills can also be applied in various courses from K-12 to higher education, and the use of Computer Science Unplugged (CS Unplugged) teaching resources is suitable for beginners, especially elementary school students [13]. Unplugged teaching does not require a computer, and it can be performed with the use of papers, pens and simple teaching materials (including board games), which is beneficial to teachers and students that lack the computer equipment that is typically necessary for carrying out computing education. Learners must use logical thinking to decompose abstract problems into small components, solve problems step by step, and predict results after independent thinking or group discussion.

In recent years, the age groups that computer applications are aimed at have become younger, and children have been exposed to information technologies as early as preschool. The Asia International Children and Teens Coding Education Association (ACTC), established in 2016, is focused on programming education for children and teenagers. Through the promotion of unplugged games for children from Google, it is hoped that children aged 5–12 can develop computational thinking, programming logic and problem-solving skills [14]. Brackmann et al. [15] have found that, after participating in unplugged activities, the informational literacy of students was significantly improved, confirming that unplugged teaching activities can effectively improve computational thinking abilities.

Augmented reality (AR) has become more popular over the last number of years. Unlike virtual reality (VR), which creates a non-existent virtual world, AR focuses on a combination with the real world by integrating embedded information with the student’s learning experience. Enhancing sensory stimulation in a real environment can not only make the interactive experience more impressive, but also maintain the original context and sense of space, making learning easier and more effective. By strengthening the real situation, the use of traditional computer I/O devices such as the keyboard and mouse can be replaced by practical operations to increase contextual awareness and flexibility of learning situations. In addition to expanding contextual information, the learning venues also become more flexible. This has a great impact on instructional design for the enhancement of students’ interest and learning motivations. Therefore, AR will bring great changes to educational applications.

Situated learning is a learner-centered method to place learners in teaching or learning contexts and engage in action learning, reflective inquiry, and environmental feedback. The goal is to enable learners to interact in multiple contexts and develop appropriate constructions of individual knowledge. In recent years, a large number of educational applications used context-awareness technology to construct a ubiquitous learning environment and enhance learners’ willingness and learning effectiveness. In addition, AR integrates real situations and related information through pattern recognition and/or the Global Positioning System (GPS) to generate composite images to assist learning. Therefore, integrating the concept of contextual awareness and the attractive features of augmented reality to build an AR learning system with high interactivity and media richness can effectively improve learners’ willingness and learning efficiency. When students learn a new concept or skill, the AR technology can be used to provide better support or scaffolding for them to analogize new knowledge from known things to improve their learning ability.

In order to enhance students’ computational thinking and assist computing education in elementary schools, this study integrated the AR technology into the “Coding Ocean” board game [16] to provide players with real-time simulation of ship paths and scaffolds for learning programming skills. The AR board game can also serve as a referee to reduce the workload of on-site teachers, and Scratch block-based modules were designed to improve students’ programming skills. To investigate the learning effectiveness of the AR board game on computational thinking and programming skills as well as its impact on cognitive load, the research objectives of this study are listed as follows:

(1)

Design an AR board game for learning computational thinking concepts.

(2)

Explore the effectiveness of the AR board game on computational thinking abilities.

(3)

Explore the effectiveness of the AR board game on Scratch programming skills.

(4)

Investigate the cognitive load after learning with the AR board game.

2. Materials and Methods

This study mainly examined the learning effectiveness of elementary school students on computational thinking abilities, Scratch programming skills, and cognitive load after learning with the AR board game. The relevant studies on augmented reality, computational thinking, and cognitive load are summarized as follows.

2.1. Augmented Reality

Augmented reality is a technology that creates intended meanings through the interaction of virtual elements with real objects. AR must contain the following major features. Firstly, a combination of real and virtual objects, registered in 3D and interactive in real time [17], and secondly a combination of virtualization technologies and observation in the real world. AR has been widely used in education, engineering, industrial design, art and entertainment, etc. The real environment and the virtual environment are two ends of a continuum, and AR is closer to the real environment (Figure 1). Mixed reality (MR) is between the real environment and the virtual environment [18].

In addition to entertainment, AR has gradually been applied in education and has great potential for the future [19]. Compared with traditional teaching methods, the use of AR in teaching enables students to obtain higher satisfaction and improve learning outcomes [20]. The 2016 Horizon Report [21] points out that AR is considered to be an emerging technology and has a great potential for educational applications. The following are the relevant studies on the applications of AR in teaching activities.

Chang et al. [22] evaluated whether AR guidance for heritage places and educational activities could effectively enhance the sense of presence and learning performance. The results of this study show that students using the AR guidance system achieved significant learning outcomes. Participants effectively enhanced their sense of presence and learning motivation when interacting with the AR guidance system.

Tobar-Muñoz, Baldiris and Fabregat [23] adopted a design-based research (DBR) method to investigate the effectiveness of students’ reading comprehension and learning motivation. Their results show that, firstly, although the results of using traditional reading comprehension methods were the same as those of using AR games, learners showed greater learning motivation and interest in reading for the latter. Secondly, when reading the text in the game, students would connect text in the book to ponder answers, explore options, and find clues. Finally, they found that AR games could promote problem-solving and exploration abilities and enrich students’ learning experience in reading comprehension.

Radosavljevic, Radosavljevic, and Grgurovic [24] have mentioned that, in a postal service internship course, the relevant students were allowed to learn the procedures of postal parcel handling through practical methods for exploring the difference between traditional learning and AR learning. Their results show that students using the AR system could shorten the time required to complete tasks, and their efficiency was higher than that of traditional learning. In addition, AR also stimulated students’ learning interest and enthusiasm, and significantly improved learning motivation and creativity.

Kellems et al. [25] modeled the step-by-step solutions of four math problems with a video for students diagnosed with special learning difficulties (SLD) to examine the learning effectiveness of solving math problems through AR exercises. Their results show that, after using the AR course materials, the students made significant and immediate progress. In the four categories of math problems, they retained at least three problem-solving abilities acquired after learning with AR exercises.

Most studies have shown that AR has a significant impact on learning outcomes because it can enhance learning interest and learning motivation and has been effective in reducing cognitive load. In addition, learners developed problem-solving skills through AR learning and had a positive learning attitude and experience.

2.2. Computational Thinking

Computational thinking had been traced in the field of computing and computer science in the 1940s. In 1945, Polya [26], an American mathematician, devoted himself to exploring the disciplines and methods of psychology and how to solve problems related to mathematics. His book “How to Solve It” talked about the many ways to solve problems and caused him to be regarded as a pioneer of computational thinking. Newell et al. believed that computers would automate processes in all fields and that the concept of algorithmizing would become part of our culture and eventually appear in all fields [27]. Knuth stated that algorithms are a form of teaching (learning from dumb machines) that allows people to gain a deep understanding of problems. In addition, learning algorithmic methods helps people understand various concepts in many domains [28].

Papert [29] believed that computational thinking is a psychological skill that children develop from programming practice. Wilson [30] considered computation to be a new scientific paradigm that complemented traditional theory and experience. Meanwhile, others used the term “computational thinking” to refer to the design process in computer science: designing, testing, and using computational models to promote scientific development.

Wing [31] used “Computational Thinking” as an abbreviation for “thinking like a computer scientist” and believed that this is a basic ability in everyone’s life, not just a programming skillset possessed by computer scientists. It has been further defined as “a thinking process that involves clearly posing a problem and formulating a solution, which can be effectively executed by a computer (human or machine)”. First of all, humans perform calculations, which implies that people do not need machines to learn computational thinking. Finally, today’s “computers” combine human and machine intelligence. Therefore, computational thinking involves not only problem-solving but also formulating the problems in an understandable way. Since Wing elaborated the core concepts of computational thinking, scholars have gradually extended it to other perspectives.

The Taiwanese Ministry of Education [32] carried out a national project to promote computational thinking for students and society in general. The government believed that computational thinking was the foundation of “Information Technology Application”, “Information Science” and “Programming” (Figure 2), and further defined it as “the thinking ability to effectively apply computational methods and tools to solve problems”. The Computer Science Teachers Association (CSTA) [33] has defined computational thinking as “the thought process involved in expressing solutions as computational steps or algorithms that can be executed by a computer”.

In the Australian Digital Technologies Curriculum [34], computational thinking is defined as “a problem-solving method that is applied to create solutions that can be implemented using digital technologies, domain knowledge, algorithms and practices”. In the UK’s computing curriculum, it is defined as “a thinking model that can propose a computing architecture for digital systems and problems” [35]. Google [2] believes that “this is a course focusing on problem-solving, programming, and STEM subjects, which can help students face various challenges in the future”.

In 2010, Google proposed that the characteristics of computational thinking include: problem decomposition, pattern recognition, abstraction and algorithmic thinking [36]. The British Broadcasting Corporation (BBC) uses “key techniques (cornerstones)” to denote these abilities [37]. There is no specific order for the thought process of computational thinking and one can decide which ability to start with. Most people begin with problem decomposition, and the whole process is usually repeated back and forth. Figure 3 illustrates the flowchart of a thought process with computational thinking.

The International Society for Technology in Education (ISTE) further defined the standards of computational thinking in action [38]:

• Students gain insight into problems and apply technology-assisted methods such as data analysis and model formulation to explore and find solutions.
• Students collect data or identify relevant data and use technological tools to analyze and represent data to facilitate decision-making and problem-solving.
• Students break problems into small components, extract key information, and develop descriptive models to clearly understand complex information.
• Students understand how automatic systems work and use algorithms to formulate a series of steps to create and examine their performance.

To sum up, according to the definition and learning objectives of various scholars for computational thinking, this study designed an AR board game to help elementary school students enhance their computational thinking and programming skills.

2.3. Cognitive Load

In the early days, cognitive load was mostly discussed in the research areas of human factor and ergonomics, focusing on the level of psychological cognition, and exploring the suitability of tasks and jobs for the performers. Later, Sweller [39,40,41] applied its theory to the field of education. It was pointed out that traditional problem-solving strategies may result in the lack of cognitive ability to create a schema in learning because problem-solving skills would occupy most of the individual’s working memory and would therefore generate a cognitive load. Cognitive load is a multi-dimensional concept [42], which is the result of the interaction between “mental load” and “mental effort”.

Based on the limited capacity and short-term characteristics of working memory for processing and storing information, Sweller, van Merriënboer, and Paas [43] defined cognitive load as the load imposed on an individual cognitive system when a person is engaged in a specific job. When learners feel that the learning content is more difficult (mental load) in a task structure, sequence of information, etc., or that more mental effort is required, the cognitive load increases. The difficulty of teaching materials and the amount of mental effort needed to engage in learning activities were closely related to the generation of cognitive load. Through using different teaching strategies or presentation styles of teaching materials in the learning process, the impact on learners’ cognitive load was discussed. On the other hand, effective ways to control or reduce cognitive load have been proposed to improve learning effectiveness [44,45].

Cognitive load theory (CLT) includes three types of cognitive load [46]: intrinsic cognitive load, extraneous cognitive load, and germane cognitive load. These interact in the working memory and reflect the processing efficiency in learning outcomes. It is generally believed that the total cognitive load is composed of these three types of cognitive load. Cognitive overload occurs when the total cognitive load exceeds the learner’s working memory capacity [47]. The three types of cognitive load are briefly described below:

• Intrinsic cognitive load

Learners’ are often affected by the difficulty of the teaching materials, that is, the degree of correlation in the teaching materials. Another factor is related to their previous knowledge and specialized knowledge. If learners can combine information with existing schemas, the load of working memory can be reduced. Conversely, if new information must be processed in working memory alone, it will cause more cognitive load.

• Extraneous cognitive load

The generation of extraneous cognitive load is affected by the design of learning materials, presentation methods or teaching activities. Therefore, teachers can reduce cognitive load by presenting and reorganizing information in teaching activities. However, it has a decisive influence only when the teaching materials are difficult.

• Germane cognitive load

Instructional designers provide additional information or arrange learning activities to meet the needs of learners, which seems to increase cognitive load, but it is helpful for schema construction and automation. Therefore, learners can reduce extraneous cognitive load and increase germane cognitive load through a good instructional design.

2.4. AR Board Game Design

The “Coding Ocean” board game uses the unplugged approach to cultivate computational thinking abilities for solving coding problems. For young students, teachers or parents often need to assist in judging whether the movement and sequence on the game board are consistent with the played cards and game rules. In plugged board games such as the first-generation Dash Coding Robot, the programming concepts applied to the robot are difficult to acquire and transfer from the board game in a short period of time. The AR board game (Figure 4) developed in this study can serve the role of a referee, enabling students to clarify programming concepts. During a game round, the multiple-choice questions use Scratch block-based modules to connect the programming concepts of sequential, and/or and loop contained in the board game, which is helpful for students to understand computational thinking and programming skills.

The development environment of the AR board game is the Macintosh Operating System (MacOS), with Unity 3D and Vuforia as development tools, and the C# language was selected in Visual Studio 2017 for user interface design (Figure 5). Unity 3D is a cross platform 2D and 3D game engine that includes sound, graphics, and other functions. There is a visual editing interface and dynamic game preview, which greatly reduces the difficulty of game development. It can be used to design games for most platforms such as Windows, Android, Mac, iOS, and Linux, etc. After the 2017.2 version, Unity 3D integrated the Vuforia AR suite by Qualcomm, making the development of AR/VR games more convenient and also improving the performance of its applications.

2.4.1. Cards and Components

The “Coding Ocean” board game simulates a sea battle between the blue team and the green team. Each team has three small swirls (light-blue color) and two large swirls (dark-blue color). The swirls are used to block the opponent’s ship and have no effect on one’s own team. They cannot be “passed” but can be “removed” with one or two specific cards. In addition, the two teams are assigned two fake treasures with a bomb picture on the back and one real treasure with a picture of gold and jewels on the back. The front of the real and fake treasures is a picture of a treasure chest, which must be placed face up on the game board and can only be turned over when the ship moves to the grid of the opponent’s treasure chest. After flipping, the picture with a bomb means the game continues, and the picture of gold and jewels means the arriving team wins.

In this study, the blue and green ships were designed by 3D printing to mark the current positions of the two teams on the game board, with the gun muzzle pointing to the moving direction. The components initially allocated to the green and blue teams include ships, swirls, cards, and treasures as shown in Figure 6.

The AR board game uses a total of 75 “Coding Ocean” cards for moving the ship, removing a swirl, and performing loop operation (

Table 1. Coding Ocean cards for movement operations.

Cards	Forward	Backward	Left Turn	Right Turn
Frontside
Backside
Number	19	8	8	8
Function	Move forward a grid with the same direction	Move backward a grid with the same direction	Turn left 90 degrees and stay at the same grid	Turn right 90 degrees and stay at the same grid

). There are four movement operations: forward, backward, left turn and right turn. There are 19 forward cards and eight backward cards, which can make the ship move forward one grid and move back one grid respectively without changing its direction. There are eight left-turn cards and eight right-turn cards, which can turn the ship 90 degrees left and 90 degrees right respectively, adjusting its direction without movement. Through different combinations of cards, the player can move the ship on the game board according to the card commands, and finally achieve the destination grid for obtaining the real treasure.

There are eight Poseidon cards and eight Mazu cards (

Table 2. Coding Ocean cards for removing swirls and performing loop operations.

Cards	Poseidon	Mazu	Loop2	Loop3
Frontside
Backside
Number	8	8	8	8
Function	Use alone to remove a small swirl. Use both to remove a large swirl.		Loop two times	Loop three times

). These cards can remove a small swirl when used alone, but removing a large swirl requires the use of a Poseidon card and a Mazu card at the same time. After removing the opponent’s swirl and using a forward card, the ship can advance to the grid safely.

There are eight Loop2 cards and eight Loop3 cards, which can be used to repeat the card commands twice and three times, respectively. For example, a loop card and a movement card can be placed below another loop card to form a nested loop as shown in Figure 7a. At least a movement card can be placed below a loop card as shown in Figure 7b, and at most two movement cards can be placed below a loop card as shown in Figure 7c.

The loop card cannot repeat the commands of removing a small or large swirl. Therefore, the Poseidon or Mazu card should not be placed below the loop card as shown in Figure 8a, and the correct usage to remove the swirl is shown in Figure 8b.

2.4.2. AR Board Game’s Rules

At the beginning of the board game, only the ships of two teams can be placed at the START grid in the middle, with the gun muzzles facing the right side. The green team’s ship, swirls, treasures and other components are placed on the left side of the board, and those of the blue team are placed on the right side. When playing the game, the cards are placed on the 3 × 6 cardboard from top to bottom and from left to right to form the commands, and up to six cards can be played in each round. The player can press the “Start” button to scan the cards, which cannot be arbitrarily replaced at this moment because the commands will be written to the tablet for execution.

Figure 9 shows that both teams have decided to move forward one grid. When encountering a large swirl placed by the green team (as shown inside the red frame), the green team can use a forward card to pass it directly, but the blue team needs to use a Poseidon card and a Mazu card to remove the swirl. The grids of the game board are similar to a program that stores data in a matrix, where each component will be distinguished by its data structure (swirls and treasures are static and ships are dynamic). Because the storage capacity (grid size) is limited, each team can only place one component in the same grid.

Before playing the AR board game, the player must first set the positions of small and large swirls placed by the opponent on the tablet screen. Each grid on the map is indexed by a letter (the x-coordinate) and a number (the y-coordinate). In the middle is the START position (the grid D4) for both ships and no adjustments can be made (Figure 10). The white square inside a grid means that there is no swirl. The player can click on the white square once and then a small swirl (E4) in light-blue color will appear, and if they click twice and then a large swirl (C4) in dark-blue color will appear. After clicking three times, the grid will return to the original white square (without any swirl).

Coding Ocean is a turn-based board game, where two teams take turns in attack and defense actions until one of them finds the real treasure. At the beginning, each team holds four movement cards and two cards for removing swirls or performing a loop operation. In each round, the players can choose whether to play cards or not, and then select which cards to discard in their hands. After redrawing new cards, they must fill up four movement cards and two cards for removing swirls or performing a loop operation. The major steps for playing the AR board game is described below, and a flowchart representing an example playthrough of a round of the AR board game is shown in Figure 11.

(1)

Play cards

• Write commands: After observing the positions of components placed by two teams on the game board, the player may think about what commands the cards in his hand can give and then arrange them correctly for scanning.
• Execute commands: The player then presses the “Start” button to scan the cards and the tablet will execute the commands in the sequence from left to right. It is important to note that cards cannot be replaced at this moment.
• Discard cards: All used cards have to be placed in the discard area on the left side of the game board, and the unused cards can also be discarded.
• Draw enough cards: No matter how many cards are used or discarded, the player must refill a total of four movement cards and two cards, for removing swirls or performing a loop operation, from the area of new cards on the right side.

(2)

Abstain from playing

• Claim a waiver: The player can pass a round if there is no suitable cards to play, and he or she cannot change their mind after giving up the round.
• Discard one or more cards: Discard at least one and up to six cards in one’s hand.
• Draw enough cards: regardless of how many cards are discarded, the cards in hand must be filled up to four movement cards and two cards for removing swirls or performing loop operation.

2.4.3. Coding Board Game and Computational Thinking

According to different conditions and the cards in hand, a variety of ship paths are considered in order to reach the treasure. The ship path in each round can be arranged by logical thinking, which indirectly enables those students unfamiliar with syntax to develop computational thinking concepts. The connection between the board game and the essential computational thinking abilities of abstraction, problem decomposition, pattern recognition, and algorithmic thinking [32] are summarized as follows:

• Abstraction

One of the learning objectives of abstraction is understanding the relationship between words and images. When playing the coding board game, students must think about the meaning of each card, and then connect the commands executed in each round with the planned ship path. Figure 12 takes the “forward” card as an example to explain the connection between the function and meaning of a game card.

• Problem Decomposition

The learning objectives of problem decomposition are: (1) to break down a problem into smaller components and (2) to analyze the solution steps of problems. In the coding board game, “How to reach the grid with the real treasure as soon as possible” is the major problem faced by the students. “Which path will encounter the fewest swirls during the movement” is one of the small problems after decomposition. Therefore, they must analyze the possible paths to the treasure based on the current ship position and surrounding swirls and consider the pros and cons of each path (Figure 13).

• Pattern Recognition

There are seven learning objectives of pattern recognition and the coding board game involves five of them: (1) predicting problem patterns and finding patterns for testing, (2) summarizing the ways to solve a problem, (3) identifying patterns in problems, (4) generalizing the pattern of repeated commands in the loop, and (5) understanding the problem-solving patterns and characteristics of loops. After observing the positions of all components on the game board, students can choose the most suitable movement path for the current situation where the numbers in Figure 14 are the steps in the path. In order to reach the grid with treasure as soon as possible, the loop cards will be used under suitable conditions.

• Algorithmic Thinking

The learning objective of algorithmic thinking is to design a set of commands for solving similar problems such that it can be executed repeatedly. In order to practice the possible movement paths in mind, students need to arrange movement commands with cards while avoiding errors according to the game rules (Figure 15). If the commands can be successfully executed, students can apply them to similar situations in the future. When playing the coding board game, students are encouraged to continuously design more algorithms that can be successfully executed in response to various problems.

2.4.4. Operation of the AR Board Game

In the AR board game, the students play the cards in their hands to shorten their time spent treasure hunting. The step-by-step execution of the program in the computer is simulated by the sequence of playing cards, which allows students to understand the operation of the computer and cultivates an ability to imagine the execution according to their own predictions. They can use and/or logic and the loop function to judge how to play cards to pass through the obstacles in the game, which can be used not only in a program, but also in mathematics or logical judgments in their daily life.

The moving cards simplify the program variables into four types with each type meaning a different task. In addition, students can use the Poseidon cards and Mazu cards to obtain additional resources. The AR operation can guide them through the real-time simulation path and help them to gradually grasp the timing required to use a certain card or to combine several cards to understand the meaning of a card command and its execution result (Figure 16a). Therefore, AR is used as an aid to help students clarify the questions in the programming process, similar to the role of a game referee. The questions combine the computational thinking concepts in the board game with the building block modules to promote students’ understanding of Scratch programs as shown in Figure 16b.

A player is required to be familiar with the basic operations of the AR board game before they can focus on designing card commands. As shown in Figure 17a, the student must place cards correctly to be scanned by the tablet camera. When a white cube appears above each card, the player can click the “Write” button and the scanned cards will appear on the screen. If they are the same as the played cards, the student can click the “Check” button on the lower right corner, and the system will execute the commands from the played cards. If the movement exceeds the range of game board or a wrong card is placed below the loop card, a warning message of “Card Error” will appear, and the wrong card will be marked with a red frame as shown in Figure 17b.

If the scan result does not match the played cards or any card is placed incorrectly, the player can click on the wrong card and replace it directly. The cards for replacement in the board game and a blank card for removal will be displayed on the screen. The player can click on one of the nine cards to replace the wrong card (Figure 18).

After replacing the wrong card, the scan result will be updated and checked. As shown in Figure 19, the Poseidon card in the red box has been changed to a forward card. If the order of the cards is correct, the player can click the “Check” button on the lower right corner, and the AR system will evaluate the commands again.

The simulation of ship paths on the game board will be displayed if the commands given by the played cards are correct. After confirming that the path simulation is consistent with the planned movement, the player can click the “Execute” button on the lower right corner to move the ship accordingly (Figure 20).

When the ship encounters a large (or small) swirl, the player must answer the test question about block-based programming before removing the swirl (Figure 21). The player checks all answers to select the correct one, and then clicks the “OK” button on the lower right corner. If the answer is correct, the player can remove the swirl immediately. The AR board game will also record the answer in the learning portfolio.

The game stops when the opponent’s real treasure is found, and the player can click the “End” button; however, the game cannot be ended until all questions have been answered. Figure 22 shows an example of the questions about Scratch programming “Which set of building blocks can move the ship to the grid with treasure?” After the end of the game, the total score will be calculated and displayed on the screen. The player can click the “Record” button to view the correct answers and verify the concepts. The operating process of the AR board game is shown in Figure 23.

3. Results

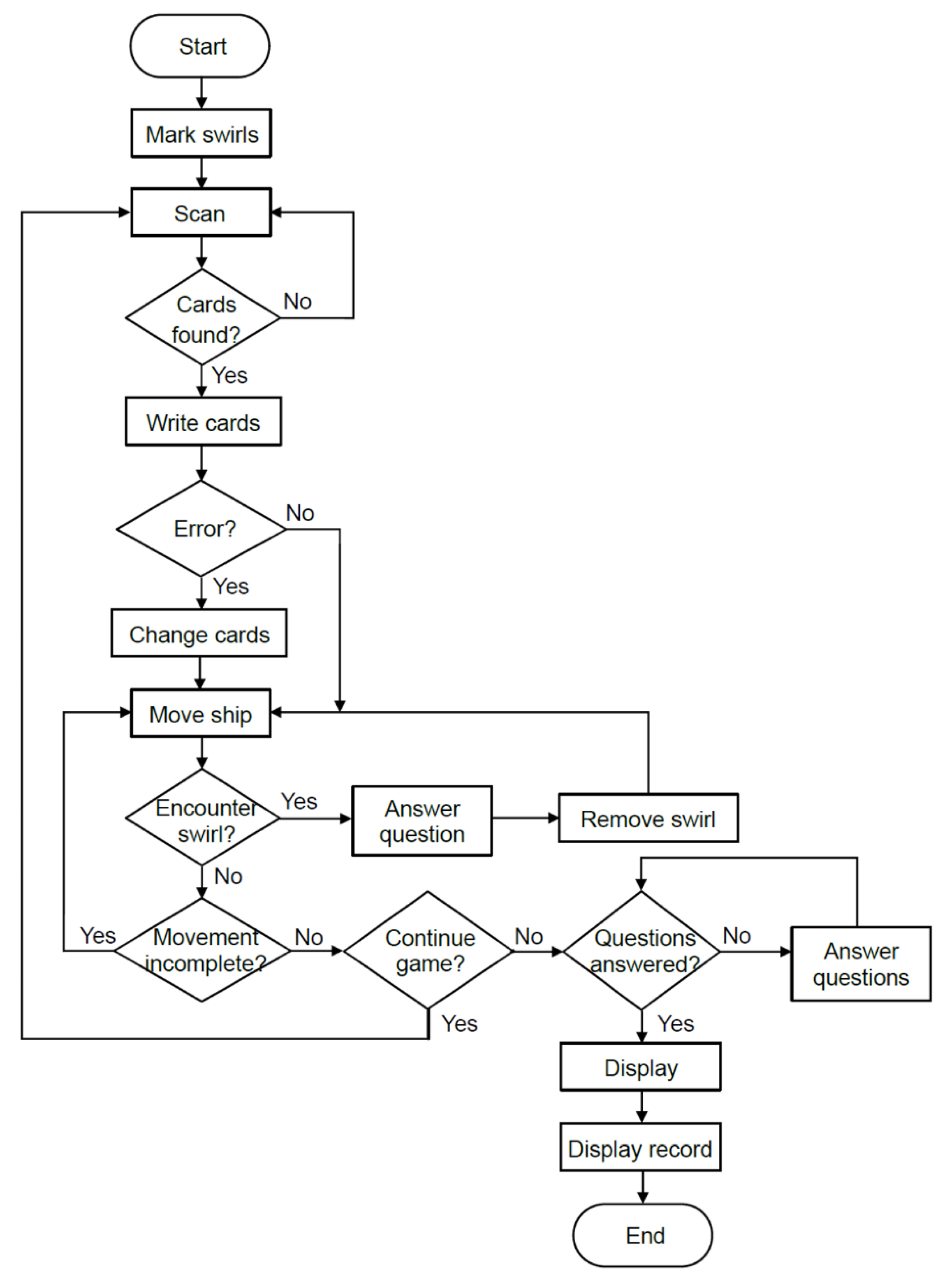
A teaching experiment was performed to evaluate students’ computational thinking concepts, Scratch programming skills, cognitive load, and system satisfaction after learning with coding board games. This study randomly selected two classes of third graders from an elementary school in Taipei as research samples. A quasi-experiment was conducted using the two-group pretest-posttest design. One class used the AR board game as the experimental group (n = 26, 14 males and 12 females) and the other used the traditional coding board game as the control group (n = 25, 14 males and 11 females). The former scanned cards to obtain the ship path, and the latter played cards and moved the ship by themselves, both under the supervision of teachers (Figure 24).

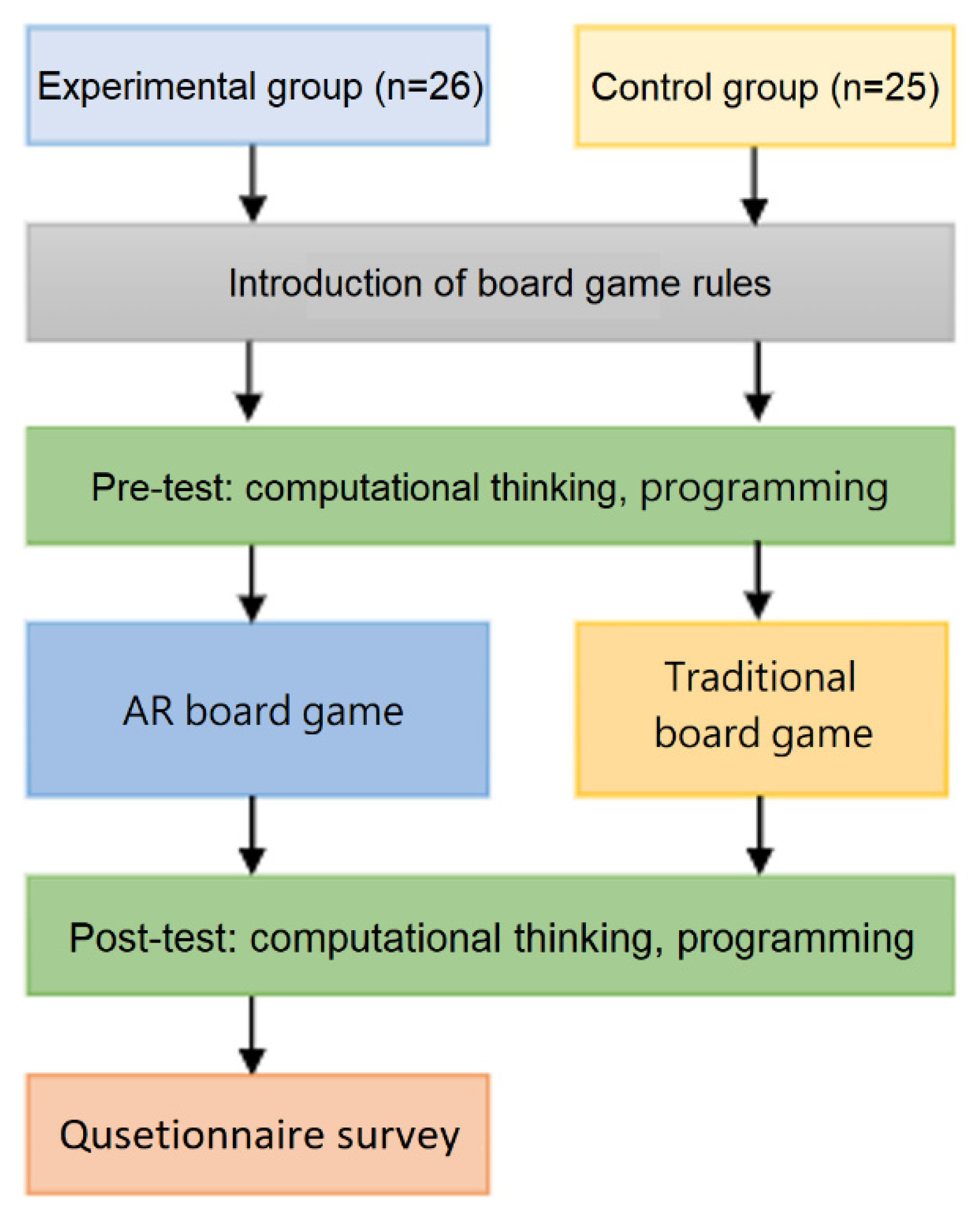
Before playing the board game, an introduction to the game rules was provided for both groups, and the achievement tests (pre-tests) of computational thinking concepts and Scratch programming skills were conducted. After the treatment, the post-tests of computational thinking concepts and Scratch programming skills as well as the questionnaires for measuring cognitive load and user satisfaction (experimental group only) were performed. A flowchart representing the teaching experiment is shown in Figure 25. The test questions were designed based on the International Contest on Informatics and Computers by Bebras [48], an international initiative aiming to promote informatics (computer science, or computing) and computational thinking among school students at all ages.

3.1. Computational Thinking

In the teaching experiment, the experimental group used the AR board game while the control group used the traditional board game for learning computational thinking concepts and Scratch programing skills. In the following, a one-way analysis of covariance (ANCOVA) was conducted to investigate whether there were significant differences in the learning effectiveness between the two groups. The test results were analyzed using IBM SPSS 24.0 software and the descriptive statistics of computational thinking scores and the results of paired-sample t-test for both groups are shown in

Table 3. Descriptive statistics of computational thinking test scores for both groups.

Group	Pre-Test	SD	Post-Test	SD	t	p
Experimental group (n = 26)	58.08	20.98	78.46	12.55	−7.14	<0.001 ***
Control group (n = 25)	50.00	16.33	60.00	18.26	−3.40	0.002 **

** p < 0.01, *** p < 0.001.

.

The post-test score of the experimental group (78.46) is higher than that of the control group (60.00), and the standard deviation of the experimental group (12.55) is lower than that of the control group (18.26), indicating that the distribution of post-test scores in the experimental group is relatively concentrated. From the results of the paired-sample t-test, both the experimental group (t = −7.14, p < 0.001) and the control group (t = −3.40, p = 0.002 < 0.01) made significant progress. The results suggest that the computational thinking abilities of both groups improved significantly after using the AR board game and the traditional coding board game.

To further compare the learning effectiveness between the two groups, the ANCOVA was conducted using the type of board games as the independent variable, the post-test score as the dependent variable, and the pre-test score as the covariate. Before that, the assumptions for the homogeneity of within-group regression coefficients and variance had to be satisfied. The test result for the homogeneity of within-group regression coefficients shows that there is no significant difference (F = 2.295, p = 0.137 > 0.05), conforming to the hypothesis of homogeneity. Levene’s test was used to verify if there was homogeneity of variance between the two groups. The test result shows that the variance did not reach the significance level (F = 2.405, p = 0.127 > 0.05), satisfying the assumption of the homogeneity of variance and confirming that the ANCOVA could be performed. The ANCOVA results in

Table 4. ANCOVA results on computational thinking between the two groups.

Source	Type III Sum of Squares	df	Mean Square	F	p	η2
Group	2414.342	1	2414.342	16.952	<0.001 ***	0.261
Deviation	6836.464	48	142.426
Sum	262,000.000	51

*** p < 0.001.

indicate a significant difference between the two groups (F = 16.952, p < 0.001).

In

Table 5. Post-test means of the two groups before and after adjustment.

Group	Mean	Adjusted Mean
Experimental group (n = 26)	78.46	76.32
Control group (n = 25)	60.00	62.23

, the average score of the experimental group is adjusted from 78.46 to 76.32, and the average score of the control group is adjusted from 60.00 to 62.23. After excluding the influence of the pre-test score, the adjusted mean of the post-test score for the experimental group is higher than that of the control group, indicating that the learning effectiveness of the AR board games is higher than that of the traditional coding board game.

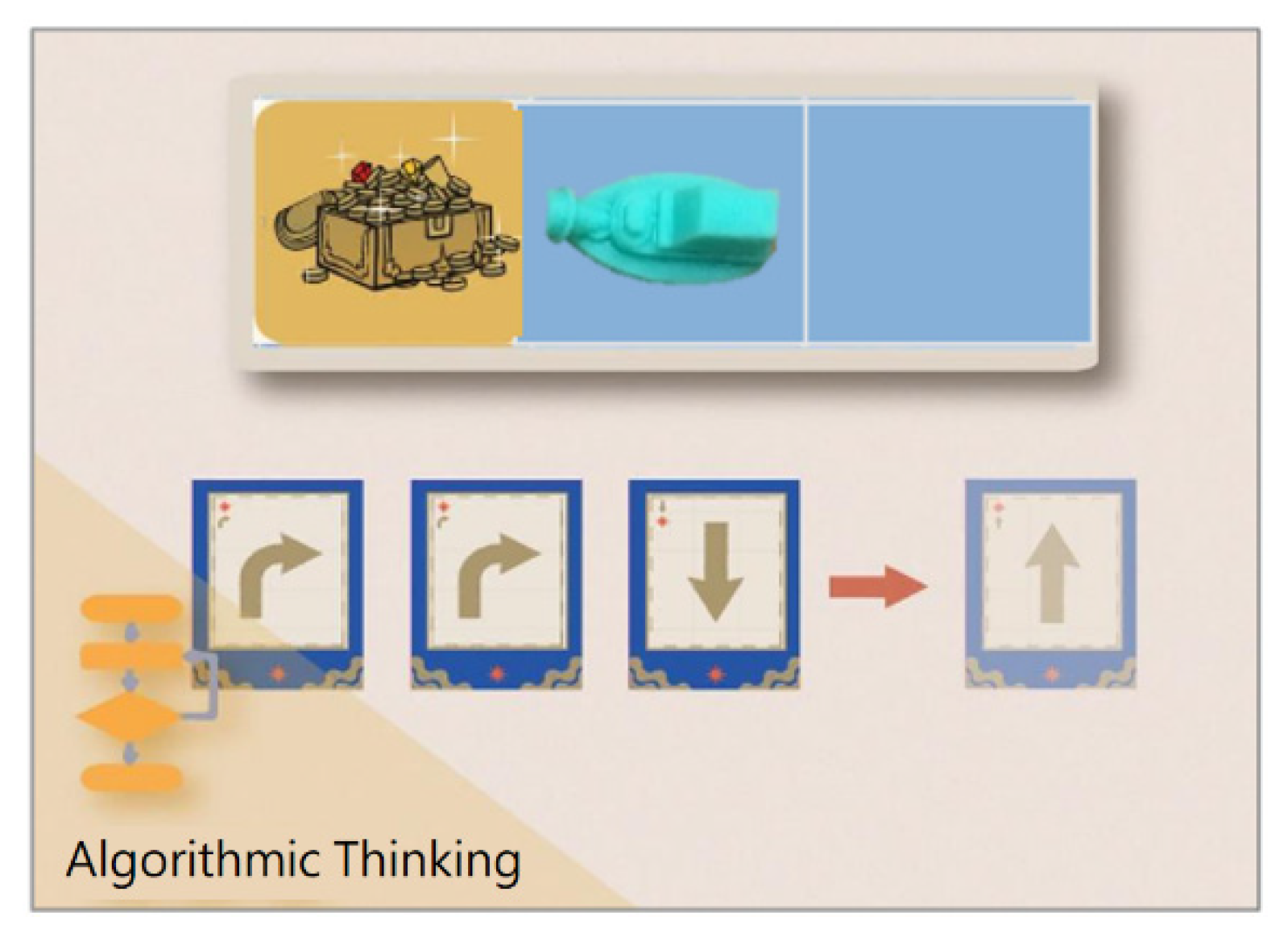
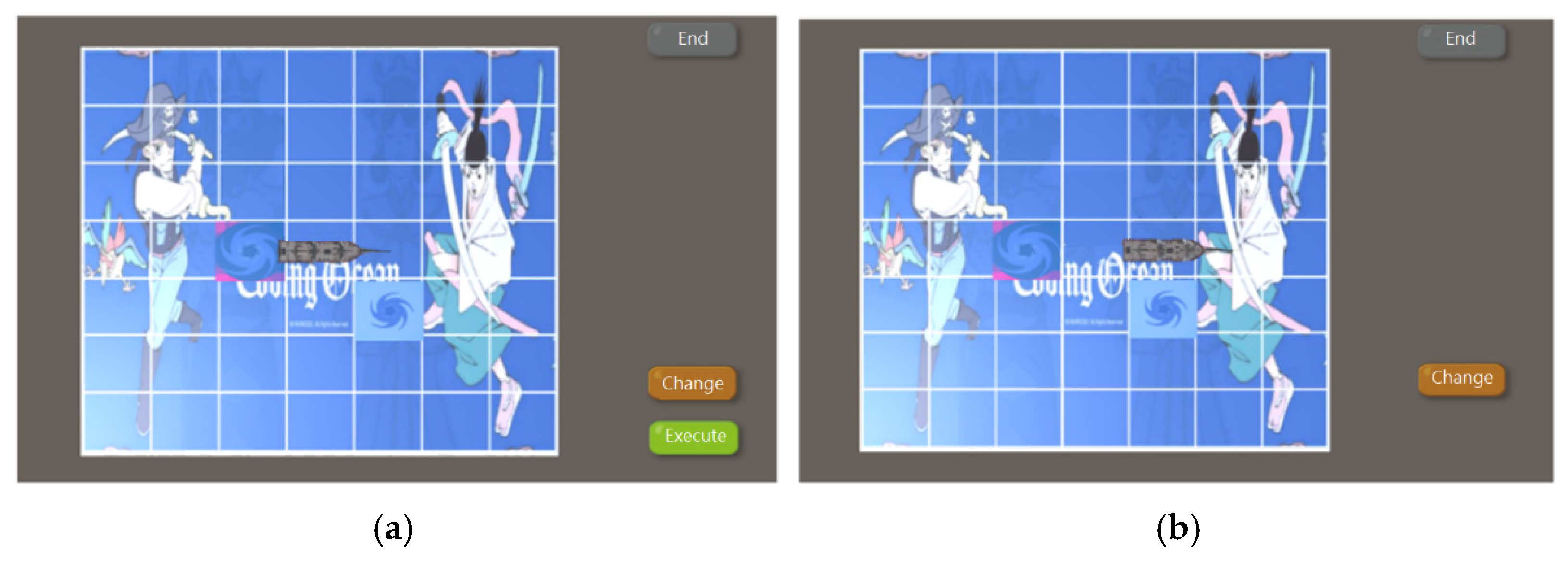
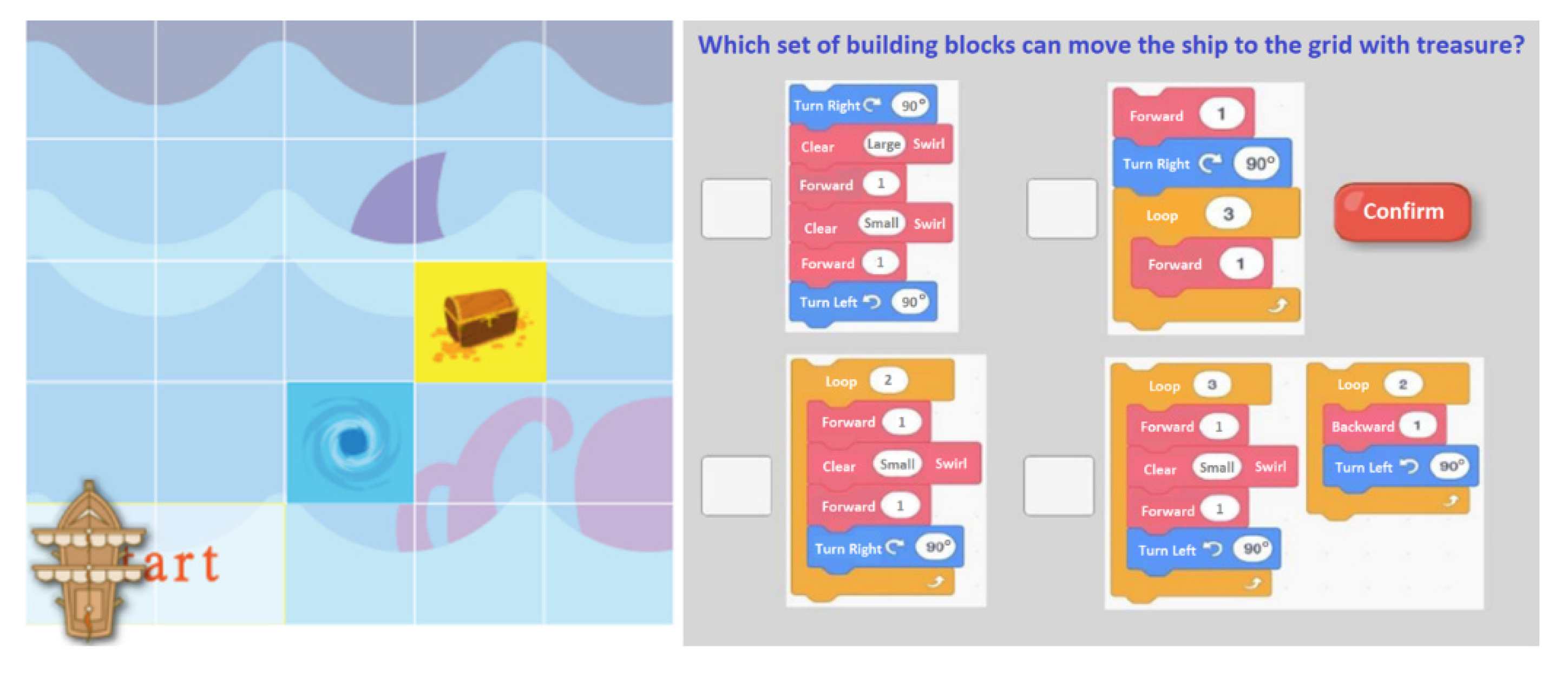
The above results show that using the AR board game was more effective for students in learning computational thinking concepts than using the traditional board game. It can be inferred from this that the research subjects were third graders without formal exposure to computing education. Playing the coding board game could improve their computational thinking abilities. The AR board game provided immediate assistance in clarifying students’ doubts, such as “whether the imagined path matches the actual movement” and “what is the best way to reach the grid with treasure”.

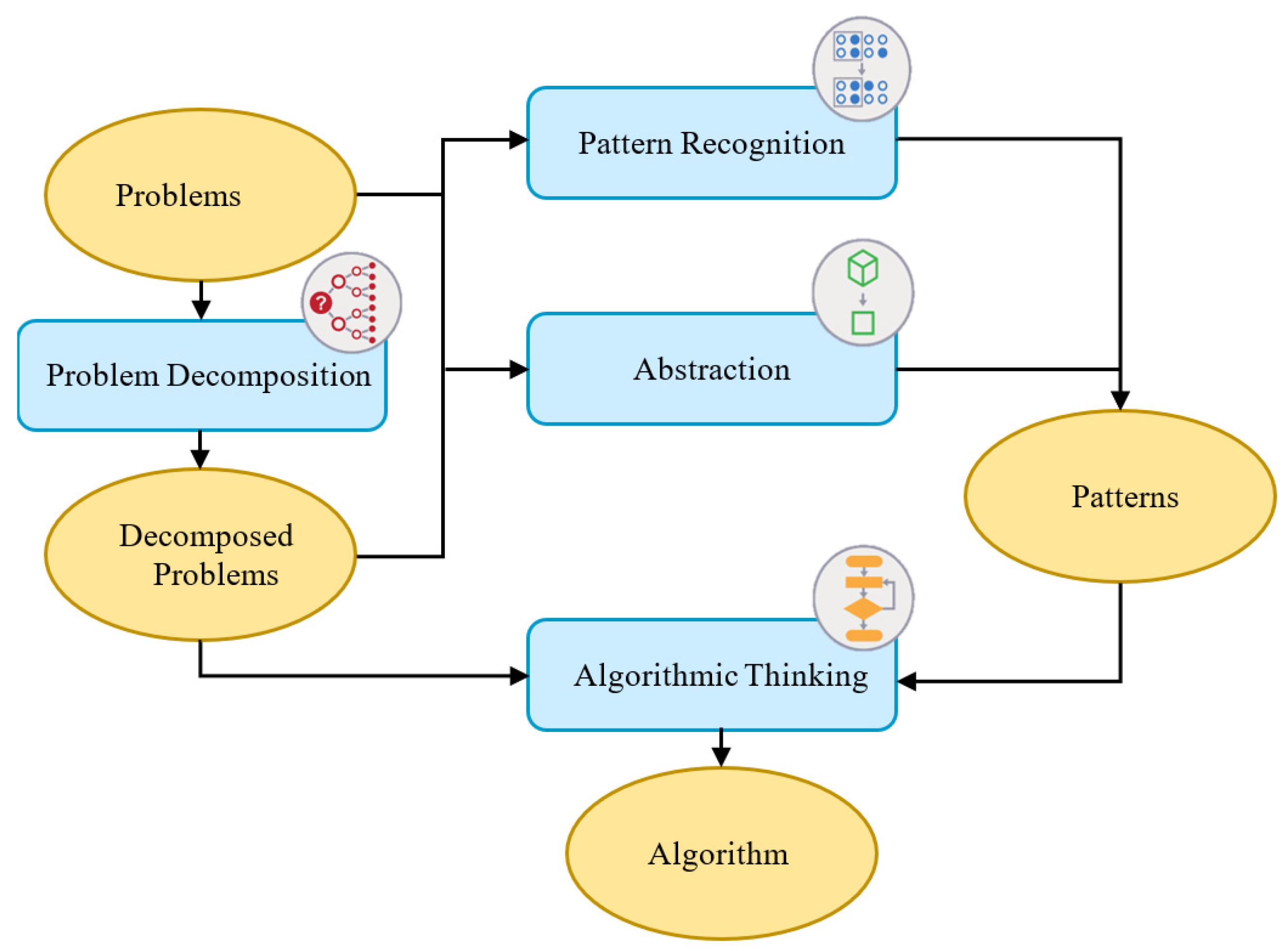
In order to further understand if there are significant differences in the performance of four computational thinking abilities between the two groups, the ANCOVA was conducted by using the type of board games as the independent variable, the post-test score for each computational thinking ability as the dependent variable, and the pre-test score for each computational thinking ability as the covariate.

Before performing the one-way ANCOVA, the homogeneity of the within-group regression coefficients had to be tested.

Table 6. Homogeneity of within-group regression coefficients.

Ability	Source	Type III Sum of Squares	df	Mean Square	F	p
Abstraction	Group*pre-test	46.573	1	46.573	0.885	0.352
	deviation	2472.668	47	52.610
Pattern recognition	Group*pre-test	6.479	1	6.479	0.182	0.672
	deviation	1673.399	47	35.604
Algorithmic thinking	Group*pre-test	243.885	1	243.885	2.755	0.104
	deviation	4160.041	47	88.512
Problem decomposition	Group*pre-test	620.820	1	620.820	8.004	0.007 **
	deviation	3645.282	47	77.559

** p < 0.01.

shows the results of the homogeneity of regression coefficients for the four computational thinking abilities between the two groups. Among the four computational thinking abilities, abstraction (F = 0.885, p = 0.352 > 0.05), pattern recognition (F = 0.182, p = 0.672 > 0.05) and algorithmic thinking (F = 2.755, p = 0.104 > 0.05) did not reach a significant level, confirming that that the ANCOVA could be conducted. However, problem decomposition (F = 8.004, p = 0.007 < 0.05) reached a significant level, indicating that the slopes of regression lines are not the same. That is, the relationship between the pre-test and post-test for problem decomposition varies due to the use of different types of board games. As a result, the assumption was not satisfied and the ANCOVA could not be conducted.

Before conducting the ANCOVA, the Levene’s test was used to verify the homogeneity of variance for the three abilities. According to the test results, the variance did not reach a significant level for abstraction (F = 0.164, p = 0.688 > 0.05), pattern recognition (F = 0.015, p = 0.902 > 0.05) or algorithmic thinking (F = 1.868, p = 0.178 > 0.05). Therefore, the assumption for the homogeneity of variance was satisfied and the ANCOVA could be conducted. According to the ANCOVA results in

Table 7. ANCOVA results of computational thinking abilities for the two groups.

Ability	Source of Variance	Type III Sum of Squares	df	Mean Square	F	p	η2
Abstraction	Group	75.794	1	75.794	1.444	0.235	0.029
	Deviation	2519.241	48	52.484
	Sum	40,000.000	51
Pattern recognition	Group	44.970	1	44.970	1.285	0.263	0.026
	Deviation	1679.878	48	34.997
	Sum	9600.000	51
Algorithmic thinking	Group	2013.812	1	2013.812	21.949	<0.001 ***	0.314
	Deviation	4403.927	48	91.748
	Sum	179,200.000	51

*** p < 0.001.

, only the difference in algorithmic thinking between the two groups was significant (F = 21.949, p < 0.001), indicating that using different types of board games had a significant impact on the algorithmic thinking ability.

In the three computational thinking abilities, the adjusted means of post-test scores for the experimental group are higher than those of the control group (

Table 8. The mean of post-test scores for the two groups before and after adjustment.

Ability	Group	Mean	Adjusted Mean
Abstraction	Experimental group (n = 26)	27.69	27.08
	Control group (n = 25)	24.00	24.64
Pattern recognition	Experimental group (n = 26)	13.08	12.69
	Control group (n = 25)	10.40	10.80
Algorithmic thinking	Experimental group (n = 26)	65.38	63.96
	Control group (n = 25)	49.60	51.08

), abstraction (27.082 > 24.635), pattern recognition (12.690 > 10.802), and algorithmic thinking (63.962 > 51.080). Additionally, algorithmic thinking has the most significant difference and the AR board game performed better than the traditional board game.

Based on the above results, the computational thinking abilities of students could be improved by both types of coding board games, but only the algorithmic thinking ability has a significant difference, with the AR board game performing better than the traditional coding board game. The possible reasons are as follows.

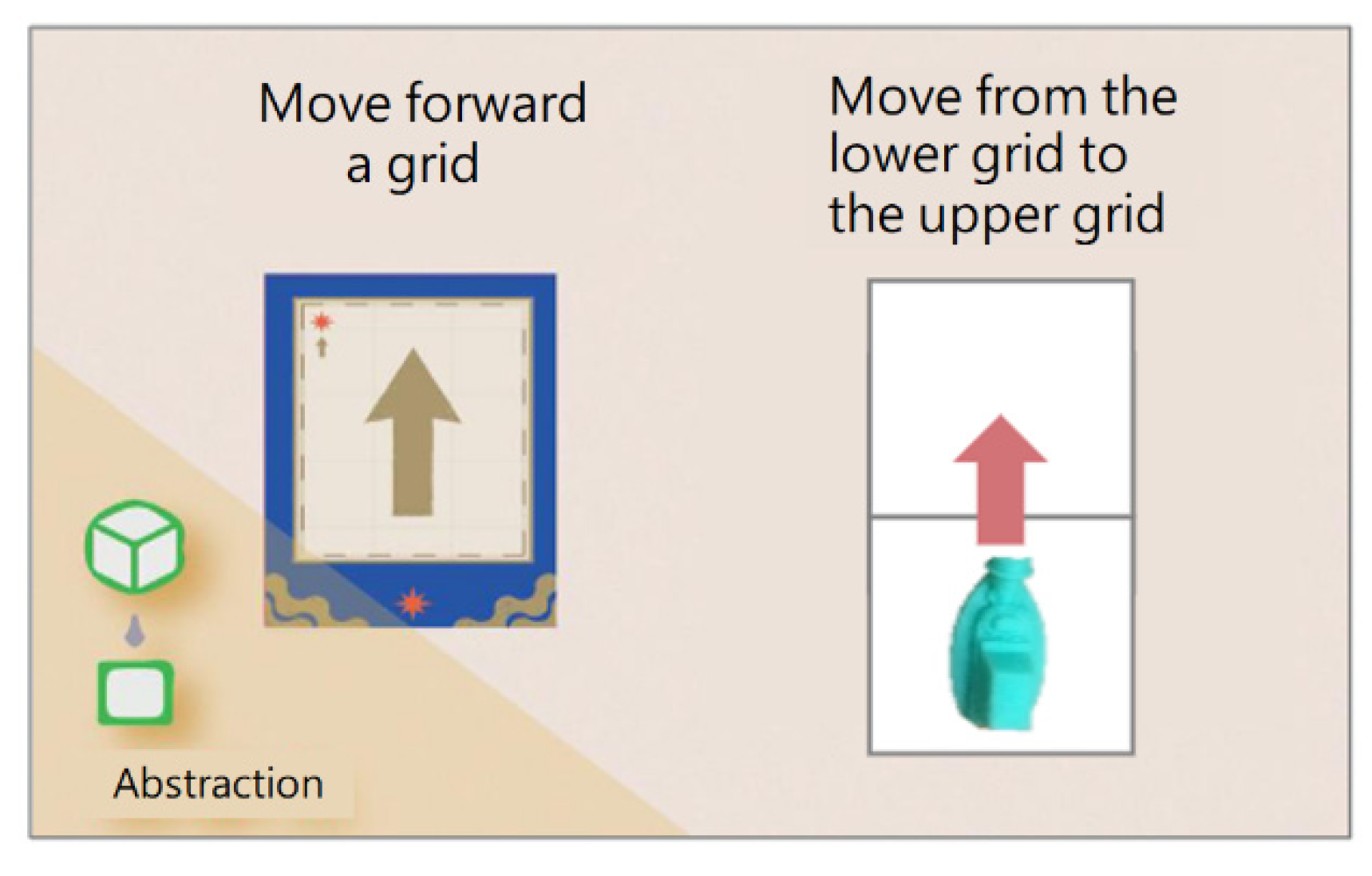
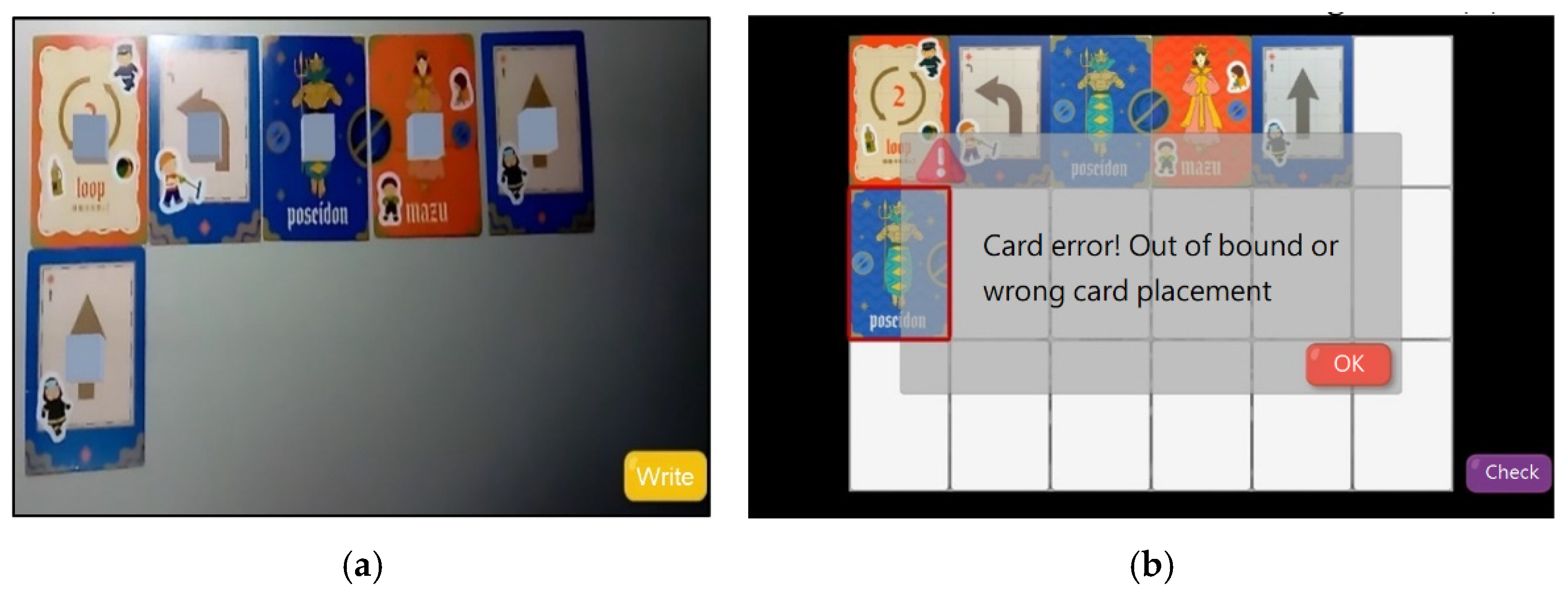
The improvement of algorithmic thinking ability is related to the question of whether the learning process can be applied for the effective assistance of students in solving problems. Using the AR board game, students could correct wrong cards immediately through real-time simulation. In each round, learning experiences from designing effective commands are continuously accumulated and applied in similar situations to find the best ship path. Therefore, it is helpful in terms of improving algorithmic thinking ability.

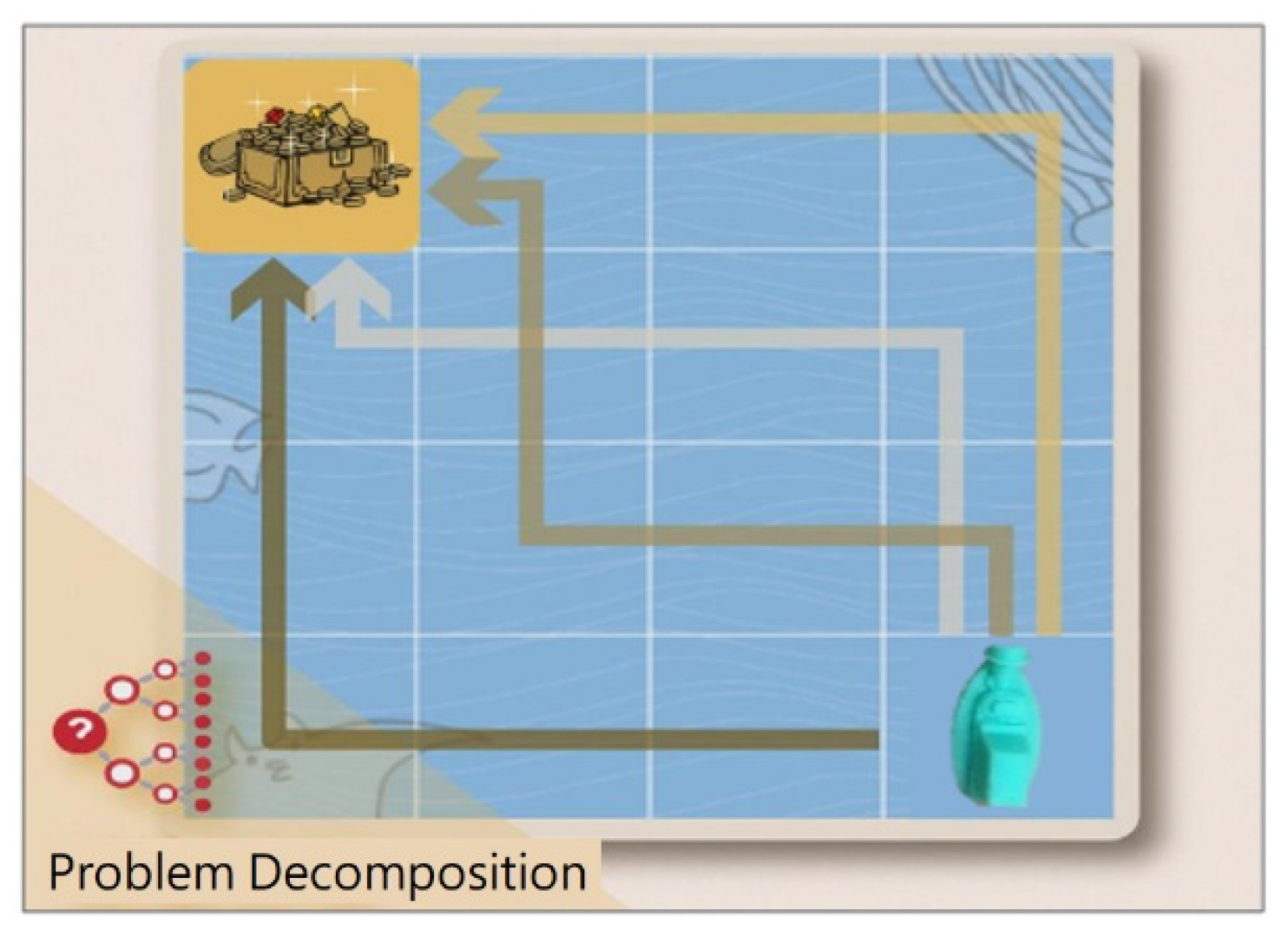
Problem decomposition involves the thought process of each possible ship path. Students needed more time to decompose the problem into different situations in order to determine the best path to reach the grid with treasure. Therefore, its learning effectiveness is not as significant as that of algorithmic thinking, which is why the assumption of the homogeneity of regression coefficients was not satisfied.

3.2. Scratch Programming Skills

In this study, descriptive statistics were used to compare the differences between the pre-test and post-test scores for the two groups. The effectiveness of the AR board game in learning Scratch programming skills was evaluated and compared with that of a traditional board game. According to the descriptive statistics in

Table 9. Descriptive statistics of Scratch programming skills and results of paired-sample t-test.

Group	Pre-Test	SD	Post-Test	SD	t	p
Experimental Group (n = 26)	40.31	21.61	65.38	19.59	−6.92	<0.001 ***
Control Group (n = 25)	38.40	19.39	46.56	22.39	−2.09	0.048 *

* p < 0.05, *** p < 0.001.

, the average post-test score of the experimental group is higher than that of the control group, and the standard deviation of the former is smaller than that of the latter, showing that the distribution of post-test scores in the experimental group is more concentrated. The results of a paired-sample t-test show a significant difference between the pre-test and post-test scores of the experimental group (t = −6.92, p < 0.001) and the control group (t = −2.09, p = 0.048 < 0.05), indicating students’ Scratch programming skills improved significantly through both the AR board game and the traditional coding board game.

To further consider if there is a significant difference in Scratch programming skills between the two groups, an ANCOVA was conducted using the type of board games as the independent variable, the post-test score of Scratch programming skills as the dependent variable, and the pre-test score of Scratch programming skills as the covariate. As shown in

Table 10. ANCOVA results on Scratch programming skills between the two groups.

Source	Type III Sum of Squares	df	Mean Square	F	p	η2
Group	3979.032	1	3979.032	13.358	0.001 **	0.218
Deviation	14,298.420	48	297.884
Sum	186,984.000	51

** p < 0.01.

, there is a significant difference between the two groups (F = 13.358, p = 0.001 < 0.05), indicating that there is a significant difference in the post-test scores of Scratch programming skills between the two groups due to the use of different types of board games.

The above results show that the students using the AR board game had a more significant learning effectiveness than those using the traditional board game. It can be inferred that the third graders had not learned the block-based programming at school, so playing the coding board game was a little difficult for them. The real-time simulation of ship path in the AR board game can serve as a referee and provide learning scaffolds, enabling students to clearly understand the timing associated with using a certain card and the correct way to organize cards for correct execution. After considering the feasibility of each path, students gradually became familiar with the game rules and became more focused in the process of converting cards into commands to quickly reach the grid with the treasure, which is helpful for improving Scratch programming skills.

3.3. Cognitive Load

A questionnaire survey was conducted to measure the cognitive load of students after using different types of board games for learning computational thinking concepts and Scratch programming skills. The questionnaire was designed using a 5-point Likert scale, and the score from “strongly disagree” to “strongly agree” ranged, respectively, from 1 to 5 points. The value of internal consistency for the questionnaire was Cronbach’s alpha = 0.762, which is within the acceptable range. The mean score and standard deviation for each question were analyzed by the independent samples t-test to investigate whether the difference of cognitive load between the two groups was significant due to the use of different types of coding board games.

According to the results of the independent sample t-test (

Table 11. Questionnaire and independent sample t-test results on cognitive load for both groups.

Dimension	Type	Questions	Experimental Group		Control Group		p
			Mean	SD	Mean	SD
Computational thinking	Intrinsic load	1. I think the board game makes the learning of computational thinking concepts clearer and easier to understand.	4.19	0.90	4.16	0.90	0.898
	Extraneous load	2. I think the board game is helpful for cultivating computational thinking.	4.00	0.80	3.84	0.85	0.492
	Germane load	3. The board game can arouse my motivation to learn computational thinking.	4.00	0.80	3.56	1.04	0.003 **
Programming skills	Intrinsic load	4. I think the board game makes the learning of programming skills clearer and easier to understand.	3.73	0.92	3.36	1.00	0.173
	Extraneous load	5. I think the board game is helpful for cultivating programming skills.	4.00	0.94	3.48	1.26	0.100
	Germane load	6. The board game can arouse my motivation to learn programming concepts.	4.19	0.80	3.80	1.08	0.007 **
Overall	Germane load	7. The board game helps me concentrate on learning computational thinking and programming concepts.	3.73	0.88	3.80	1.04	0.798
		8. The board game increases my intention to learn about the contents of computational thinking and programming.	4.15	0.83	3.36	1.22	<0.001 ***
		9. I think it is very meaningful to learn computational thinking concepts and programming skills.	4.12	0.82	3.80	1.32	0.314
		10. I am willing to put more effort into learning computational thinking concepts and programming skills.	4.12	0.82	3.28	1.17	0.005 **

** p < 0.01, *** p < 0.001.

), the scores of most questions are higher than 4 for the experimental group, and only Question 4 (3.73) and Question 7 (3.73) are lower than 4. For the control group, only the score of Question 1 (4.16) is higher than 4, and the remaining questions have scores less than 4. Furthermore, the average score of each question in the experimental group is higher than that in the control group except for Question 7 (3.73), which is slightly less than that of the control group (3.73 < 3.80). Question 7 belongs to the attitude towards germane cognitive load. The possible reasons why the two groups had scores less than 4 can be explained as follows. Firstly, it might be related to the age of the students, as third graders are in the stage of establishing and cultivating concentration. When the two groups used the coding board games for learning, they may have focused more on how to win the game by moving the ship according to intuition. Following the learning scaffolds of the AR board game, the experimental group was less distracted than the control group. Secondly, according to the analytical results, the two types of coding board games had a positive impact on the two groups. Therefore, students may have not realized they were concentrated on learning computational thinking concepts and programming skills while playing the board game, but in fact gained the related skills while finding the correct ship path in each game round.

According to the above results, there are significant differences in cognitive load between the two groups in Question 3 (p = 0.003 < 0.01), Question 6 (p = 0.007 < 0.01), Q8 (p < 0.001), and Question 10 (p = 0.005 < 0.01). These four questions belong to the type of germane cognitive load, indicating that students who used the AR board game had a lower germane cognitive load. Conversely, it could arouse their motivation to learn computational thinking concepts and programming skills. The results are the same as those reported in [22,23,24,25], showing that the experimental group had a higher motivation to learn computational thinking and programming skills and that they would like to expend more effort when playing the AR board game.

The results of independent samples t-test in

Table 12. Group means and results of independent sample t-test on cognitive load.

Group	Samples	Mean	SD	t	p
Experimental group	26	40.23	5.18	2.494	0.016 *
Control group	25	36.44	5.67

* p < 0.05.

show that the overall cognitive load of the experimental group (mean = 40.23; SD = 5.18) is lower than that of the control group (mean = 36.44; SD = 5.67), a higher score meaning a lower cognitive load. The t-test results (t = 2.494, p = 0.016 < 0.05) show that use of the AR board game incurred a cognitive load that was significantly lower than that associated with using the traditional coding board game.

3.4. System Satisfaction

The system satisfaction of the AR board game was measured through a questionnaire survey by the experimental group. The questionnaire contained 10 questions, including three questions in learning contents, three questions in interface design, and four questions in operating experience (

Table 13. Questionnaire results of user satisfaction for the experimental group.

Dimension	Questions	Mean	SD
Learning contents	1. The real-time simulation of the ship’s movement path is very clear.	4.35	0.94
	2. I could understand the programming concept of each card.	3.96	0.87
	3. The text descriptions of the test questions are simple and clear.	4.08	0.98
Dimensional satisfaction		4.13	0.93
Interface design	4. This AR board game is easy to operate.	3.58	0.95
	5. The icons and text descriptions are of appropriate size.	3.65	0.94
	6. This simulation of the ship’s movement is helpful for improving computational thinking abilities.	4.19	0.57
Dimensional satisfaction		3.81	0.63
Operating experience	7. Learning computational thinking concepts with this AR system is fun.	4.15	0.83
	8. Learning programming skills with this system is pleasant.	4.23	0.82
	9. It is appropriate to use the AR system as a referee.	4.12	0.86
	10. This AR system can enhance the learning effectiveness of computational thinking concepts and programming concepts.	3.85	0.78
Dimensional satisfaction		4.10	0.57
Overall satisfaction		4.01	0.71

). This study adopted a 5-point Likert scale (scoring: 5 = strongly agree; 4 = agree; 3 = neutral; 2 = disagree; 1 = strongly disagree). The value of Cronbach’s alpha was 0.853, indicating that the questionnaire had a high reliability. The mean scores of most questions are higher than 4, and the average score of overall satisfaction is 4.01, showing that the attitudes of the students in terms of their operating experience with the AR board game were mainly between “satisfied” and “highly satisfied”. The questionnaire results can be used as a reference for system design and improvement in the future.

According to the results of the user satisfaction survey, the dimensional average score is 3.81 for interface design, 4.13 for learning contents, and 4.10 for operating experience, with the overall average score higher than 4. Among all dimensions, Question 4 (“This system is easy to operate”) and Question 5 (“The icons and text descriptions were of appropriate size”) have lower average scores. The observation from the teaching experiment revealed that students used tablets as a tool for scanning AR cards, and that they might encounter some problems when playing the AR board game for the first time. Firstly, students were unfamiliar with the tablet camera because scanning all cards at the same time was a laborious task. Secondly, after watching the simulation of movement path on the screen, students accidentally pressed the wrong icon out of curiosity. This could be the reason why the average score of Question 4 is the lowest (3.58). Thirdly, limited by the tablet’ screen size, the images of ships and swirls in the path simulation were small, and the resolution of Q&A icons was also affected. This could be the reason for the lower average score (3.65) in Question 5.

4. Discussion

Computational thinking is an important subject for the development of information literacy, and it is an ability that can be used in daily life and in various professional fields. This study developed an AR coding game in order to cultivate students’ basic concepts of computational thinking through practice to enhance their problem-solving skills and innovative thinking skills. The instant feedback mechanism could guide students toward the correct path with correct card commands, helping them to improve their learning in computational thinking and programming abilities.

Based on the findings of the teaching experiment, the contribution of this study is discussed from the aspects of “integration of the AR technology”, “enhancement of programming skills “ and “ promotion of information education” as listed below.

(1)

Integrating computational thinking with the AR board game.

There is a clear connection between the coding board game and the important concepts of computational thinking, so it is possible for researchers to understand which computational thinking concept is involved in the learning process. The real-time simulation of the ship’s movement in the AR board game can effectively motivate players to continuously practice and develop computational thinking concepts, as well as programming skills, in the process of treasure hunting.

(2)

Transition from unplugged to plugged board games.

Traditional coding board games have the advantage of unplugged learning. They can cultivate computational thinking and programming skills without computer teaching activities and are thus suitable for beginners in learning the basic concepts. After using the coding board game for a period of time, they can decide whether to switch to the plugged board game, which is more powerful, to learn advanced programming skills based on the individual cognitive load and learning experience of the students.

The AR board game combines the unplugged and plugged learning activities by integrating the block-based programming modules with the card commands and uses situations related to the mission of treasure hunting to strengthen the connection between computational thinking concepts and programming skills. It is useful for elementary school students to understand the basic logic concepts in the form of unplugged and plugged learning activities by playing the AR board game, and they can easily switch to real programming environments in the future.

(3)

Providing on-site assistance and learning scaffolds.

Teachers may not have time to consider each student’s learning situation when teaching computing courses. Although traditional coding board games can be used as introductory learning materials for students who are new to programming, they may face various problems such as an unawareness of the game’s rules. The AR board game can direct students through the real-time simulation of the ship path such that they are able to gradually grasp the timing required for using a certain card, understand the meaning of card commands, and acquire programming skills. At the same time, the AR board game can serve as the game referee to reduce the workload of on-site teachers.

In this study, the rules of the AR board game were simplified to make it suitable for elementary school students. The programming skills were focused on sequential, and/or, and loop commands. In the future, the rules can be extended according to the student age, learning contents, and research objectives. There are some other programming concepts, such as conditional judgment (if/else), function, and flow control (for/while), etc., which can be linked with the block-based programming modules. Teachers can also require students to complete some tasks without using a certain card, with the objective of further improving computational thinking abilities under some constraints.

5. Conclusions

Coding board games can improve computational thinking concepts, so it is appropriate for students who are learning programming skills. After playing the coding board game for a period of time, they can decide whether to learn programming based on their previous experience and individual status. The AR board game developed in this study has the advantages of unplugged and plugged board games even as it integrates block-based programming with the commands of AR board game. This can help students to learn computational thinking concepts and programming skills with lower cognitive load, which is useful for computing education in elementary schools.

5.1. Research Findings

In this study, an AR board game was developed to assist elementary school students to learn computational thinking concepts and block-based coding skills. A teaching experiment was conducted with 51 third graders as participants. There were 26 students in the experimental group using the AR board game and 25 students in the control group using the traditional board game as the learning tools. The experimental results of the AR board game on students’ computational thinking concepts, Scratch programming skills, cognitive load and system satisfaction are described as follows:

(1)

Integrating AR into the coding board game is an effective way to improve computational thinking abilities and programming skills.

According to the ANCOVA results, students made progress after using the AR board game and the traditional board game, and the learning effectiveness of the former is significantly higher than that of the latter, especially for the algorithmic thinking concept.

(2)

Integrating AR into the coding board game helps enhance programming skills.

Using both the AR board game and the traditional board game could improve Scratch programming skills. The learning effectiveness of the experimental group was significantly higher than that of the control group, indicating that the AR board game is more effective for enhancing Scratch programming skills.

(3)

Integrating AR into the coding board game can reduce cognitive load.

Compared with traditional board games, the cognitive load of students was reduced after playing the AR board game, indicating that it could arouse their motivation in learning computational thinking concepts and thus incurred a lower cognitive load.

(4)

Students were satisfied with the learning experience of the AR board game.

The AR board game provided students with real-time simulation of the ship paths using the AR technology. Students could develop computational thinking concepts and practice the programming skills by playing cards to move the ship to in finding treasure. The average scores for the dimensions of learning contents, interface design, and operating experience are 4.13, 3.81, and 4.10, respectively, and the overall average score is higher than 4, showing that most students were satisfied with the AR board game.

The AR board game can also serve as a referee and provide learning scaffolds, enabling students to clearly understand the function of a certain card and the execution results of card commands, which is helpful for students who are learning computational thinking concepts and programming skills. Therefore, it is suitable for application in formal educational contexts for the promotion of information education.

5.2. Future Works

AR is a technology that allows a real-world view of computer-generated or situational information extracted through pattern recognition or GPS data elements. These elements are displayed on top of the real-world view using a mobile-device camera and provides scaffolding by simply viewing the site or a QR code through an AR device. This study combined the AR technology with a coding board game to improve the computational thinking concepts of elementary school students. The following suggestions regarding its applications are put forward as a reference for future works.

(1)

Self-directed learning of computational thinking and programming skills.

The COVID-19 pandemic has disrupted education around the world, and many countries have implemented distance learning in response. In addition, self-directed learning skills are highly valued. If the AR board game can be revised as an online game, it can help students cultivate computational thinking and programming concepts remotely, when they cannot actually play the board game face to face.

(2)

Learning effectiveness for adults’ computational thinking.

The applications of the AR board game can be extended to adults whose major is not within the area of information science. This could be undertaken to further investigate the AR board game’s effectiveness on the computational thinking of adults and the learning materials for integration.