Designing a MCDM Model for Selection of an Optimal ERP Software in Organization
Abstract
:1. Introduction
- ✓
- Improved management decision making.
- ✓
- Improved financial management.
- ✓
- Ease of expansion/growth and increased flexibility.
- ✓
- Improved customer service and retention.
- ✓
- Faster, more accurate transactions.
- ✓
- Improved inventory/asset management.
- ✓
- Headcount reduction.
- ✓
- Fewer physical resources/better logistics and Increased revenue.
2. Literature Review
3. Methodology
- 1.
- Identification of the Problem.
- 2.
- Application of FAHP.
- 3.
- Application of TOPSIS.
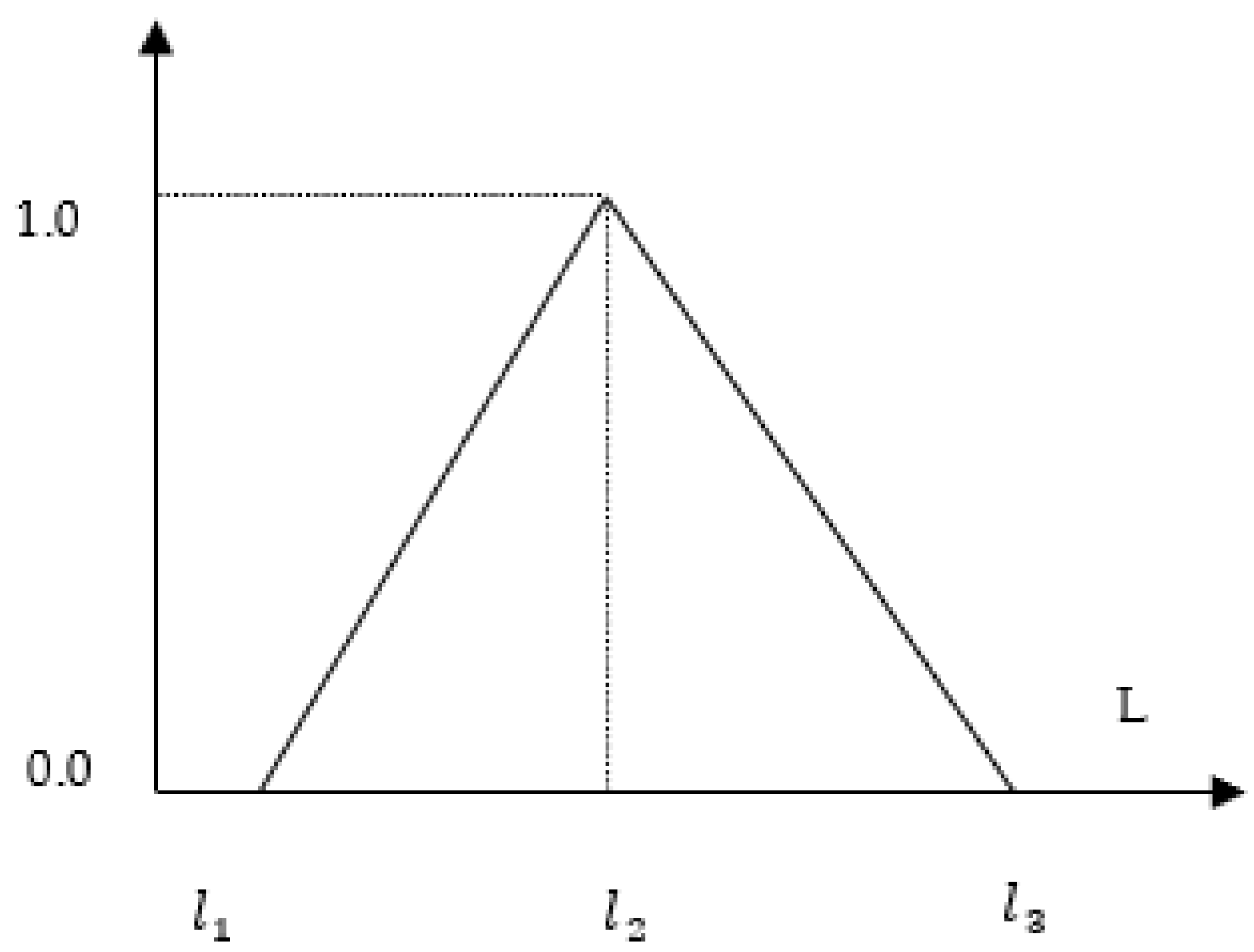
3.1. Fuzzy Set Theory
3.2. Fuzzy Analytical Hierarchy Process (FAHP) Model
3.3. The Order of Preference by Similarity to the Ideal Solution Model Technique (TOPSIS)
4. Results
5. Conclusions
- ✓
- The decision-making model is used to evaluate and decide on a suitable ERP software to be applied in any industry.
- ✓
- This is the first study to apply the method that includes a real-life case study where the industry demanded a suitable ERP implementation but was unclear due to a high variability of ERP providers in the market.
- ✓
- The study applied a suitable MCDM Model that could prove to be a suitable resource for decision-makers when choosing a suitable ERP system.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deloitte Consulting. ERPs Second Wave; Deloitte Consulting: London, UK, 1999. [Google Scholar]
- Davenport, T.; Harris, J.; Cantrell, S. The Return of Enterprise Solutions, Accenture. 2002. Available online: https://www.scirp.org/(S(i43dyn45teexjx455qlt3d2q))/reference/ReferencesPapers.aspx?ReferenceID=9926 (accessed on 18 February 2022).
- Hamdan, S.; Cheaitou, A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput. Oper. Res. 2017, 81, 282–304. [Google Scholar] [CrossRef]
- Wang, C.N.; Nguyen, V.T.; Thai, H.T.N.; Duong, D.H. Multi-criteria decision making (MCDM) approaches for solar power plant location selection in Vietnam. Energies 2018, 11, 1504. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.C.; Chang, C.T. Comparative analysis of MCDM methods for ranking renewable energy sources in Taiwan. Renew. Sustain. Energy Rev. 2018, 92, 883–896. [Google Scholar] [CrossRef]
- Pintelon, L.; Di Nardo, M.; Murino, T.; Pileggi, G.; Vander Poorten, E. A new hybrid MCDM approach for RPN evaluation for a medical device prototype. Qual. Reliab. Eng. Int. 2021, 37, 2189–2213. [Google Scholar] [CrossRef]
- Shyur, H.J.; Shih, H.S. A hybrid MCDM Model for strategic vendor selection. Math. Comput. Model. 2006, 44, 749–761. [Google Scholar] [CrossRef]
- Yang, Y.P.O.; Shieh, H.M.; Leu, J.D.; Tzeng, G.H. A novel hybrid MCDM Model combined with DEMATEL and ANP with applications. Int. J. Oper. Res. 2008, 5, 160–168. [Google Scholar]
- Oltra-Badenes, R.; Gil-Gomez, H.; Guerola-Navarro, V. Methodology for the selection of ERP systems for SMEs. 3C EMPRESA 2018, 7, 10–32. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Chiang, C.H.; Li, C.W. Evaluating intertwined effects in e-learning programs: A novel hybrid MCDM Model based on factor analysis and DEMATEL. Expert Syst. Appl. 2007, 32, 1028–1044. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lien, H.P.; Tzeng, G.H. Measures and evaluation for environment watershed plans using a novel hybrid MCDM Model. Expert Syst. Appl. 2010, 37, 926–938. [Google Scholar] [CrossRef]
- Wu, H.Y.; Chen, J.K.; Chen, I.S.; Zhuo, H.H. Ranking universities based on performance evaluation by a hybrid MCDM Model. Measurement 2012, 45, 856–880. [Google Scholar] [CrossRef]
- Hu, S.K.; Lu, M.T.; Tzeng, G.H. Exploring smart phone improvements based on a hybrid MCDM Model. Expert Syst. Appl. 2014, 41, 4401–4413. [Google Scholar] [CrossRef]
- Gürbüz, T.; Alptekin, S.E.; Alptekin, G.I. A hybrid MCDM methodology for ERP selection problem with interacting criteria. Decis. Support Syst. 2012, 54, 206–214. [Google Scholar] [CrossRef]
- Park, J.J.H.; Jeong, H.Y. The QoS-based MCDM system for SaaS ERP applications with Social Network. J. Supercomput. 2013, 66, 614–632. [Google Scholar] [CrossRef]
- Hinduja, A.; Pandey, M. An integrated intuitionistic fuzzy MCDM approach to select cloud-based ERP system for SMEs. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 1875–1908. [Google Scholar] [CrossRef]
- Kazancoglu, Y.; Burmaoglu, S. ERP software selection with MCDM: Application of TODIM method. Int. J. Bus. Inf. Syst. 2013, 13, 435–452. [Google Scholar] [CrossRef]
- Brzozowski, M.; Birfer, I. Applications of MCDM methods in the ERP system selection process in enterprises. Handel Wewnętrzny 2017, 3, 40–52. [Google Scholar]
- Temur, G.T.; Bolat, B. A robust MCDM approach for ERP system selection under uncertain environment based on worst case scenario. J. Enterp. Inf. Manag. 2018, 31, 405–425. [Google Scholar] [CrossRef]
- Jafarnejad, A.; Ansari, M.; Youshanlouei, H.R.; Mood, M. A hybrid MCDM approach for solving the ERP system selection problem with application to steel industry. Int. J. Enterp. Inf. Syst. IJEIS 2012, 8, 54–73. [Google Scholar] [CrossRef]
- Naveed, Q.N.; Islam, S.; Qureshi, M.R.N.M.; Aseere, A.M.; Rasheed, M.A.A.; Fatima, S. Evaluating and Ranking of Critical Success Factors of Cloud Enterprise Resource Planning Adoption Using MCDM Approach. IEEE Access 2021, 9, 156880–156893. [Google Scholar] [CrossRef]
- Amirkabiri, A.; Rostamiyan, M. Development of a hybrid methodology (MCDM) for ERP system selection (Case study: Mahan Airlines). Rev. Publicando 2018, 5, 1180–1196. [Google Scholar]
- Rouyendegh, B.D.; Erkan, T.E. ERP system selection by AHP method: Case study from Turkey. Int. J. Bus. Manag. Stud. 2011, 3, 39–48. [Google Scholar]
- Ayağ, Z.; Yücekaya, A. A fuzzy ANP-based GRA approach to evaluate ERP packages. Int. J. Enterp. Inf. Syst. IJEIS 2019, 15, 45–68. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.R.; Al Noman, A.; Tasnim, F.; Nafisa, N.; Hossain, S. A Hybrid MCDM Approach based on AHP, and TOPSIS to select an ERP system in Bangladesh. In Proceedings of the 2021 International Conference on Information and Communication Technology for Sustainable Development (ICICT4SD), Dhaka, Bangladesh, 27–28 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 161–165. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Chang, D. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Hwang, C.; Yoon, K. Multiple Attribute Decision Making; Springer: New York, NY, USA, 1981. [Google Scholar]
- Yoon, K. A reconciliation among discrete compromise solutions. J. Oper. Res. Soc. 1987, 38, 277–286. [Google Scholar] [CrossRef]
- Hwang, C.; Lai, Y.; Liu, T. A new approach for multiple objective decision making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Duong, T.T.T.; Thao, N.X. TOPSIS model based on entropy and similarity measure for market segment selection and evaluation. Asian J. Econ. Bank. 2021, 5, 194–203. [Google Scholar] [CrossRef]
| No | Main Criteria | Sub-Criteria | Criteria Definition | Literature Review | Expert Opinions | Symbol of the Criteria |
|---|---|---|---|---|---|---|
| 1 | Software related criteria | Compatibility | The suitability of the software compared to previous systems or the processes inside the business; whether the new software is comfortable for all users in the company. | Gürbüz et al. [14] | X | ERP01 |
| Technical aspects | The technology implementations applied to the system including the system requirements, assets requirement, and hardware requirements. | Kazancoglu et al. [17] | X | ERP02 | ||
| Cost | The amount of investment required for businesses to implement the software within the business model. Lower cost is generally considered. | Gürbüz et al. [14] Temur et al. [19] Kazancoglu et al. [17] | X | ERP03 | ||
| Implementation time | The time required for the software to be applied directly into the system. | Kazancoglu et al. [17] | X | ERP04 | ||
| Functionality | The different functions that each ERP system provides that allows businesses to utilize to the best potential. Some functions are implemented but sometimes are not applied completely. | Temur et al. [19] Kazancoglu et al. [17] | X | ERP05 | ||
| System reliability | How reliable the system is depending on the durability and accessibility over time. The system is also checked for its maintenance assessment and how frequent maintenance is required. | Gürbüz et al. [14] Temur et al. [19] | X | ERP06 | ||
| 2 | Vendor related criteria | Ease of customization | How accessible can the system be to change it according to the requirement of the vendor. | Kazancoglu et al. [17] | X | ERP07 |
| Better fit with organizational structure | Does the ERP assist in providing a clearer structure indicating how the business’s organization should be formed with a proper hierarchical system? | Gürbüz et al. [14] | X | ERP08 | ||
| Fit with parent/allied organizational system | The system can adapt to change and can assist with tasks with other ERP systems from the vendor. | Gürbüz et al. [14] Temur et al. [19] | X | ERP09 | ||
| Cross module integration | The system can easily be integrated with multiple modules from other ERP systems | Temur et al. [19] | X | ERP10 | ||
| Support and service | How accessible is it for vendors to ask for support and require service from the providing company | Temur et al. [19] | X | ERP11 | ||
| 3 | Customer related criteria | Methodology of software | How accessible is the ERP system to other users in the system | Gürbüz et al. [14] | X | ERP12 |
| Domain knowledge | Where is the main domain located, and is it suitable for the company’s needs? | Gürbüz et al. [14] | X | ERP13 | ||
| Market position | How strong is the ERP system in the market compared to other ERP systems? | Temur et al. [19] Kazancoglu et al. [17] | X | ERP14 | ||
| Reputation | How reputable is the ERP system compared to other ERP systems? | Gürbüz et al. [14] | X | ERP15 |
| Criteria | Fuzzy Sum of Each Row | Fuzzy Synthetic Extent | Degree of Possibility (Mi) | Normalization |
|---|---|---|---|---|
| ERP01 | (10.44, 14.38, 19.93) | (0.03, 0.06, 0.11) | 0.4536 | 0.0479 |
| ERP02 | (11.93, 16.13, 21.78) | (0.03, 0.06, 0.12) | 0.5132 | 0.0542 |
| ERP03 | (14.07, 20.59, 28.18) | (0.04, 0.08, 0.15) | 0.6731 | 0.0711 |
| ERP04 | (12.77, 18.39, 25.43) | (0.04, 0.07, 0.14) | 0.6046 | 0.0639 |
| ERP05 | (18.85, 25.70, 32.92) | (0.05, 0.10, 0.18) | 1.0000 | 0.1057 |
| ERP06 | (11.14, 15.40, 21.38) | (0.03, 0.06, 0.11) | 0.4958 | 0.0524 |
| ERP07 | (10.61, 14.90, 20.88) | (0.03, 0.06, 0.11) | 0.4797 | 0.0507 |
| ERP08 | (15.68, 22.71, 30.34) | (0.04, 0.09, 0.16) | 0.9055 | 0.0957 |
| ERP09 | (16.49, 23.77, 32.08) | (0.05, 0.09, 0.17) | 0.9416 | 0.0995 |
| ERP10 | (11.70, 16.89, 23.61) | (0.03, 0.06, 0.13) | 0.6861 | 0.0725 |
| ERP11 | (9.84, 13.70, 18.80) | (0.03, 0.05, 0.10) | 0.5108 | 0.0540 |
| ERP12 | (15.55, 20.10, 27.73) | (0.04, 0.08, 0.15) | 0.8408 | 0.0888 |
| ERP13 | (9.39, 13.30, 19.17) | (0.03, 0.05, 0.10) | 0.5127 | 0.0542 |
| ERP14 | (8.94, 12.35, 17.53) | (0.03, 0.05, 0.09) | 0.4462 | 0.0471 |
| ERP15 | (8.81, 11.59, 16.58) | (0.02, 0.04, 0.09) | 0.4005 | 0.0423 |
| Criteria | ERP System Alternatives | |||
|---|---|---|---|---|
| ERPsys1 | ERPsys2 | ERPsys3 | ERPsys4 | |
| ERP01 | 0.3763 | 0.4704 | 0.5644 | 0.5644 |
| ERP02 | 0.4704 | 0.5644 | 0.5644 | 0.3763 |
| ERP03 | 0.4549 | 0.3790 | 0.5307 | 0.6065 |
| ERP04 | 0.4241 | 0.4241 | 0.6786 | 0.4241 |
| ERP05 | 0.5111 | 0.3833 | 0.5111 | 0.5750 |
| ERP06 | 0.5147 | 0.4411 | 0.5882 | 0.4411 |
| ERP07 | 0.4842 | 0.4842 | 0.4842 | 0.5447 |
| ERP08 | 0.5482 | 0.5482 | 0.4796 | 0.4111 |
| ERP09 | 0.3790 | 0.4549 | 0.6065 | 0.5307 |
| ERP10 | 0.5267 | 0.5267 | 0.4096 | 0.5267 |
| ERP11 | 0.5132 | 0.4491 | 0.5774 | 0.4491 |
| ERP12 | 0.5132 | 0.5774 | 0.4491 | 0.4491 |
| ERP13 | 0.5774 | 0.5132 | 0.4491 | 0.4491 |
| ERP14 | 0.5603 | 0.4981 | 0.4981 | 0.4358 |
| ERP15 | 0.4824 | 0.5427 | 0.5427 | 0.4221 |
| Criteria | ERP System Alternatives | |||
|---|---|---|---|---|
| ERPsys1 | ERPsys2 | ERPsys3 | ERPsys4 | |
| ERP01 | 0.0180 | 0.0225 | 0.0270 | 0.0270 |
| ERP02 | 0.0255 | 0.0306 | 0.0306 | 0.0204 |
| ERP03 | 0.0324 | 0.0270 | 0.0377 | 0.0431 |
| ERP04 | 0.0271 | 0.0271 | 0.0433 | 0.0271 |
| ERP05 | 0.0540 | 0.0405 | 0.0540 | 0.0608 |
| ERP06 | 0.0270 | 0.0231 | 0.0308 | 0.0231 |
| ERP07 | 0.0245 | 0.0245 | 0.0245 | 0.0276 |
| ERP08 | 0.0524 | 0.0524 | 0.0459 | 0.0393 |
| ERP09 | 0.0377 | 0.0453 | 0.0603 | 0.0528 |
| ERP10 | 0.0382 | 0.0382 | 0.0297 | 0.0382 |
| ERP11 | 0.0277 | 0.0242 | 0.0312 | 0.0242 |
| ERP12 | 0.0456 | 0.0513 | 0.0399 | 0.0399 |
| ERP13 | 0.0313 | 0.0278 | 0.0243 | 0.0243 |
| ERP14 | 0.0264 | 0.0235 | 0.0235 | 0.0205 |
| ERP15 | 0.0204 | 0.0230 | 0.0230 | 0.0179 |
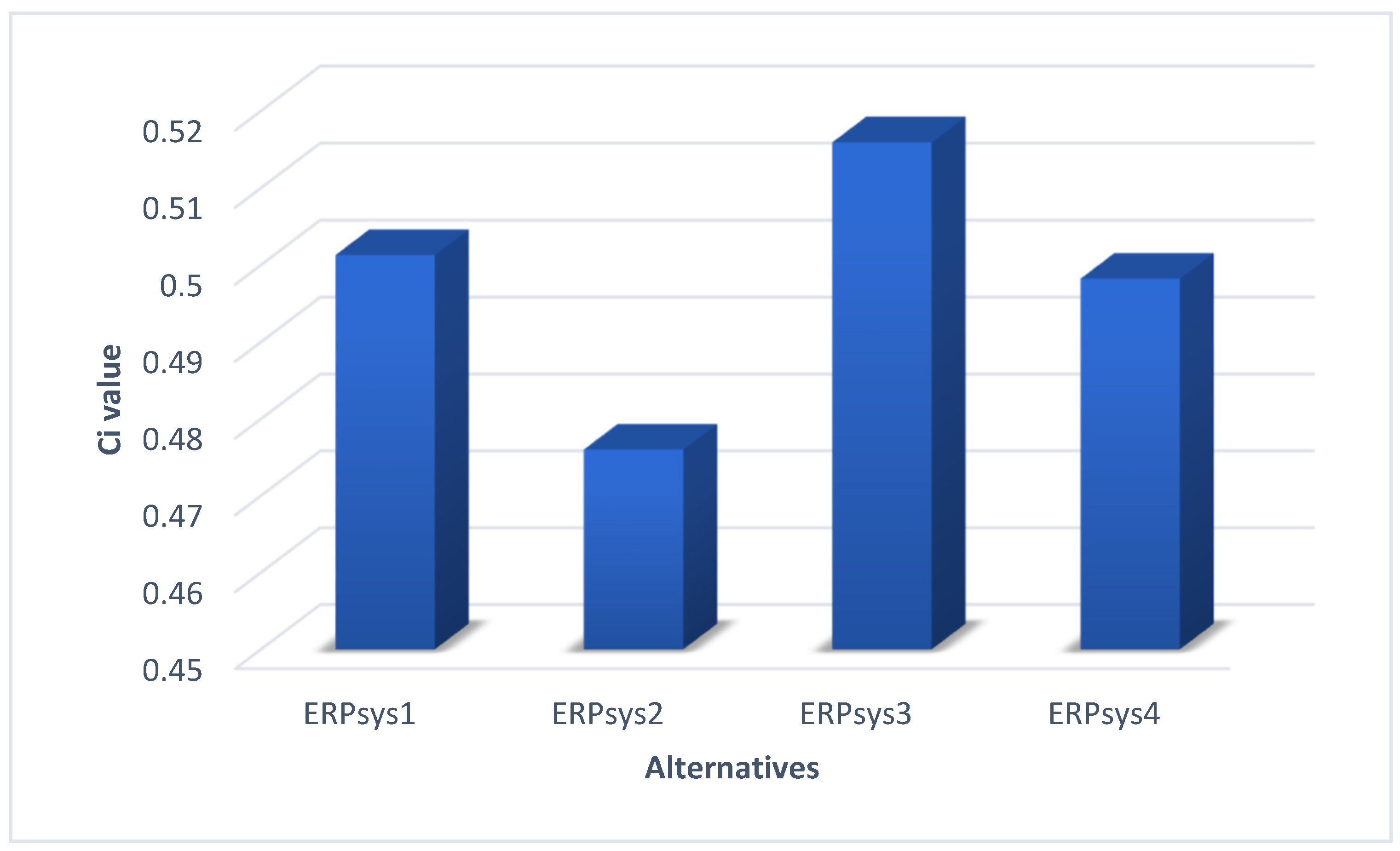
| ERP System Alternatives | Si+ Value | Si− Value | Ci Value |
|---|---|---|---|
| ERPsys1 | 0.0451 | 0.0453 | 0.5013 |
| ERPsys2 | 0.0560 | 0.0509 | 0.4760 |
| ERPsys3 | 0.0635 | 0.0676 | 0.5159 |
| ERPsys4 | 0.0606 | 0.0602 | 0.4982 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thanh, N.V. Designing a MCDM Model for Selection of an Optimal ERP Software in Organization. Systems 2022, 10, 95. https://doi.org/10.3390/systems10040095
Thanh NV. Designing a MCDM Model for Selection of an Optimal ERP Software in Organization. Systems. 2022; 10(4):95. https://doi.org/10.3390/systems10040095
Chicago/Turabian StyleThanh, Nguyen Van. 2022. "Designing a MCDM Model for Selection of an Optimal ERP Software in Organization" Systems 10, no. 4: 95. https://doi.org/10.3390/systems10040095
APA StyleThanh, N. V. (2022). Designing a MCDM Model for Selection of an Optimal ERP Software in Organization. Systems, 10(4), 95. https://doi.org/10.3390/systems10040095






