Abstract
To evaluate fuzzy information precisely, researchers and practitioners are apt to use linguistic variables to model vague or uncertain contexts in natural language. In this paper, some new operation laws for continuous linguistic terms using strict t-norms and t-conorms are defined. Significantly, these operation laws have some desirable properties and are closed on the restricted continuous linguistic term set. On the basis of these new linguistic operation laws, a series of triangular t-(co)norm-based linguistic generalized power geometric operators are developed. In order to consider the interactive influence and interrelationship of decision makers (DMs) and attributes, a decision-making trial and evaluation laboratory (DEMATEL)-based method for linguistic multiple attributes group decision making (MAGDM) is proposed. In the method, the weighting information for DMs and attributes are dependent on the initial direct-relation matrices among DMs and attributes, respectively. Finally, a numerical example is provided. In comparison with the existing methods, two aspects of the DEMATEL-based method for linguistic MAGDM in the work can be highlighted: the underlying operators for linguistic terms using strict t-norms and t-conorms that are closed on the set of the restricted continuous linguistic term set; and the techniques in determining the weighting information, with which the weighting information for DMs and attributes are determined by the interactive influence and interrelationship among DMs or attributes.
1. Introduction
Multiple attributes group decision making selects the best alternative(s) among a family of alternatives using the available information for each attribute given by a group of DMs. However, in the real world, there are vague or uncertain contexts that cannot be evaluated precisely in a numerical way [1]; then, researchers and practitioner are apt to use linguistic information to model uncertainty or evaluate fuzzy information in natural language, i.e., linguistic variables [2,3,4]. In contrast to the usual fuzzy set or intuitionistic fuzzy set in modeling quantitative aspects, linguistic variables can be reasonably used to represent one’s evaluation preference for the alternatives [5]. Linguistic decision making has became popular in solving complex selection problems. Until now, multiple attributes group decision making using linguistic variables have been applied to many fields, such as personnel evaluation, military-system performance evaluation, tenure evaluation for university faculty [6,7], and contractor selection [5].
In the literature, there are two typical linguistic models: one is on the basis of the extension principle [8,9,10,11,12], where the linguistic process is embedded to match a pre-defined fuzzy sets of linguistic terms; the other one is based on symbols and makes computations on the indices of linguistic labels [13], such as the two-tuple linguistic representation model [14,15,16,17], the virtual linguistic model [18], intervals of linguistic terms [19], the proportional two-tuple model [20], and four-tuple linguistic representation [21]. Recently, in order to accommodate DMs’ preferences in a more flexible way, some innovative linguistic settings have been proposed. For instance, hesitant fuzzy linguistic term sets [22] are proposed to consider several possible linguistic values; coupled with probabilistic information [23], the probabilistic linguistic term is innovated; linguistic Z-Numbers [24] and two-dimensional linguistic variables [5] are linguistic information with both cognitive information and the reliability of information.
As is known, the usual resolution scheme for linguistic MAGDM is composed of the aggregation phase and the exploitation phase. In first phase, individual decision matrices are aggregated to an overall one by reasonable linguistic aggregation operators, such as those in [4,7,11,18,19,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. Among these linguistic aggregation operators, the power ones, developed by the classical power average and geometric operators [39,40] and featuring their discounted weighting on the outer input arguments, are of great importance from the perspective of the consensus degree in aggregation. In [25], the partitioned Bonferroni mean in the linguistic two-tuple environment is used to capture the expressed interrelationship among the attributes. In the exploitation phase, the alternatives must be ranked by a structured criterion to obtain the most desirable one. Many known techniques can be employed to formulate a reasonable criterion by aggregating the preference values of different attributes, such as the projection method [41], the extended VIKOR method [42], and the DEMATEL method [43].
In particular, the linguistic term set is considered in this work. The points of departure for the work lie in two aspects: the underlying operations for the linguistic terms and the aggregations of the linguistic terms. For the former, the underlying linguistic operations are fundamental in the methodologies for the linguistic decision making. Up to now, there are some known operations on the linguistic term set [4,18,44]. By these operations, some unreasonable linguistic terms that are larger than the maximum linguistic term can be obtained. In other words, the closeness of these operations cannot be guaranteed (see Example 1). Thus, it is necessary to provide more reasonable operations for the linguistic terms. Specifically, in this paper, to overcome some defects of the classical operation laws for linguistic terms, some new operation laws for continuous linguistic terms using strict t-norm and t-conorm are defined and a series of triangular t-(co)norm-based (T-based) linguistic generalized power geometric operators, i.e., a T-based linguistic generalized power geometric (T-LGPG) operator, T-based linguistic weighted generalized power geometric (T-LWGPG) operator, T-based linguistic ordered weighted generalized power geometric (T-LOWGPG) operator and T-based linguistic hybrid generalized power geometric (T-LHGPG) operator, are developled. The decision-making trial and evaluation laboratory (DEMATEL) method [45,46] is a useful tool for analyzing correlations among factors and solutions of the correlated factor analysis problems. Thereby, the DEMATEL method is employed in determining weighting information for DMs and attributes by initial direct-relation matrices for DMs and attributes, respectively. By this means, the weighting vector for DMs and attributes can be determined objectively by the interactive influence and interrelationship among DMs and attributes.
This paper is organized as follows. In Section 2, some basic concepts on t-norms and t-conorms, and linguistic term sets, are reviewed; then, some new operations in a linguistic environment using strict t-norms and t-conorms are defined; based on these new operations, the linguistic generalized power operations are developed and their properties are investigated; in the end of this part, the linguistic approaches to MAGDM are presented. In order to show the feasibility of the operators and the method, an illustrative example and some discussions are given in Section 3. Finally, some concluding remarks are summarized.
2. Methods and Methodology
2.1. Preliminaries
2.1.1. Some Concepts and Results on t-Conorms
In this part, a short review on t-norms and t-conorms is presented; the details can also be found in the monographs [47,48].
A triangular norm (t-norm for short) is a binary function which is commutative, nondecreasing, and associative with neutral element 1; a triangular conorm (t-conorm for short) is a binary function which is commutative, nondecreasing, and associative with neutral element 0. T-norms and t-conorms, with different neutral elements (1 and 0, respectively), are widely used in fuzzy logical operations and information aggregation. T-norm and t-conorm are said to be dual to each other if it holds that , which is a t-conorm if T is a t-norm; and is a t-norm if R is a t-conorm. The most referred to t-norms in applications are the product t-norm and the ukasiewicz t-norm , which are, respectively, defined by
Dually, the most referred t-conorms are the product t-conorm and the ukasiewicz t-conorm , which are, respectively, given by , and .
The idempotents of a t-norm T are those x satisfying . The bounds 0 and 1 are trivial idempotents. A continuous t-norm T is called Archimedean if it has no non-trivial idempotents. An Archimedean t-norm T is called strict if for all . An Archimedean t-norm, which is not strict, is called nilpotent. The typical strict and nilpotent t-norm and t-conorm are the product t-norm and the ukasiewicz t-norm , respectively. Archimedean t-conorms can be represented by one-place functions, i.e., the so-called generators.
Theorem 1
([48]). Let T and R be t-norm and t-conorm, respectively. Then, the following statements hold.
- 1.
- T is Archimedean if and only if there is a continuous strictly decreasing unary function with , such thatfor all , where t is called additive generator of T.
- 2.
- R is Archimedean if and only if there is a continuous strictly increasing unary function with , such thatfor all , where s is called additive generator of R.
In fact, if ), then R is nilpotent (strict). Moreover, if T and R are strict, then Equations (1) and (2) reduce to and , respectively. Note that there are families of parameterized strict t-conorms, such as the Hamacher family, the Frank family, the Schweizer–Sklar family, and the Aczl–Alsina family, which are widely employed in many fields of research. Without loss of generality, the Hamacher t-norms and t-conorms shown in Table 1 will be used.

Table 1.
Hamacher t-norm and t-conorm .
In particular, (the Einstein t-norm), and ; (the Einstein t-conorm); .
2.1.2. Linguistic Term Sets and the Related Notations
In practical decision making, there exists many uncertain or vague contexts, which can be modelled by linguistic information. Computing with words (CW) is one of the prominent methodologies in processing linguistic information.
In this part, some linguistic notations are recalled.
Definition 1
([4]). For an even and positive integral n, a linguistic term set (also be called the linguistic evaluation scales) is a finite and totally ordered discrete linguistic term set with , where is a possible value of linguistic terms and is the granularity in the linguistic term set.
Usually, . In general, the following requirements on the linguistic term set S are necessary.
- There exists the negation operator: such that ;
- The set is ordered: if and only if if and only if ;
- Max operator: if ;
- Min operator: if .
In the literature [4], there are many classical forms of linguistic term sets having some particular characteristic of information representation. Here, the notation will be used throughout of the paper. The continuous linguistic term set is given by , where the maximum element is consistent with and the minimum element is consistent with . If , then is called an original linguistic term; otherwise, is called a virtual linguistic term.
2.2. New Operations in Linguistic Environment Using Strict t-Conorms
Definition 2.
Let and , then the operations on are, respectively, defined as:
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- ,
where R is a strict t-conorm whose generator is and T is a strict t-norm, the generator of which is .
Trivially, the above operations are closed in . Further, the following properties of the above operations can be easily checked.
Theorem 2.
Let and , then
- 1.
- ;
- 2.
- ;
- 3.
- if ;
- 4.
- ;
- 5.
- ;
- 6.
- ;
- 7.
- ;
- 8.
- ;
- 9.
- if ;
- 10.
- ;
- 11.
- ;
- 12.
- ;
Up to now, there exist some known operations on the linguistic term set [4]. Based on the continuous linguistic evaluation scale , where q is a sufficiently large positive integer, Dai et al. [44] defined ⊕ and as, respectively,
- ;
- ;
- ;
- ;
By these operations, some unreasonable linguistic terms that exceed the maximum linguistic term can be obtained. For illustration, an example is presented in the following.
Example 1.
Let , thus ; then, by the operations in [4,18,44], some of the obtained results , , and are bigger than (perfect), which seems to be unrealistic and meaningless. Nevertheless, by Definition 2, it can be obtained that, if , then , , and , all of which are between two original linguistic terms. Therefore, the newly proposed operations in Definition 2 can fix the referred defect by their closeness in .
Note that, here, only strict t-norms and t-conorms are employed in the operations, to guarantee the reasonability of the obtained results. If some nilpotent t-norms and t-conorms are employed, some obtained results may be unreasonable. For instance, put in Example 1; then, it can be obtained that . In other words, two `medium’ results in `perfect’, which are uninterpretable in practical information aggregating.
Definition 3.
The relative deviation of two linguistic terms and in S is defined by
2.3. Generalized Power Geometric of Linguistic Terms Using Strict t-Norms and t-Conorms
In this part, based on the new operators on the restricted continuous linguistic term set, the triangular (co)norms-based (T-based) linguistic generalized power geometric (T-LGPG) operator, the T-based linguistic weighted generalized power geometric (T-LWGPG) operator, the T-based linguistic ordered weighted generalized power geometric (T-LOWGPG) operator and the T-based linguistic hybrid generalized power geometric (T-LHGPG) operator are defined.
2.3.1. Reviews on Generalized Power Geometric Operator
Definition 4
([49,50]). Let be a set of real numbers. The generalized power geometric (GPG) operator is defined as
where and with being the support for from satisfying the following properties.
- 1.
- ;
- 2.
- ;
- 3.
- If , then , where is the distance between a and b. In other words, the closer two numbers, the more they support each other.
If is chosen suitably, the GPG operator reduces to power geometric (PG) operator [39], i.e.,
In what follows, the T-LGPG operator, T-LWGPG operator, T-LOWGPG operator and the T-LHGPG operator, are, respectively, defined.
2.3.2. T-LGPG Operator
Definition 5.
Assume , let R be a strict t-conorm whose additive generator is and T be a strict t-norm, the additive generator of which is . Then, T-LGPG operator is defined as
where and with being the support for from satisfying the following properties.
- 1.
- ;
- 2.
- ;
- 3.
- If , then , where is the relative deviation of and . In other words, the closer two linguistic terms, the more they support each other.
Theorem 3.
Assume ; let R be a strict t-conorm whose additive generator is and T be a strict t-norm, the additive generator of which is . Then
where
Proof.
It can be obtained by direct calculation in virtue of Definitions 2 and 5. □
In particular, if , then
which can be seen as the T-based linguistic power geometric (T-LPG) operator.
Corollary 1.
If for all , then
Proof.
In this case, it can be obtained that . □
Trivially, the following properties of T-LGPG operator hold:
- Commutativity: for any permutation of ;
- Idempotency: ;
- Boundedness: , where and .
Nevertheless, the T-LGPG operator is not monotonic, which can be shown by a counterexample.
Example 2.
2.3.3. T-LWGPG Operator
In fact, in the T-LGPG operator, all the input arguments in consideration are of equal importance. Sometimes, different weightings of the input arguments are necessary in practice. Hereby, the T-LWGPG operator is presented in the following, where different weights can be assigned to each input argument according to the differences in their importance.
Definition 6.
Let , then T-LWGPG operator is defined as
where is the associated weighting vector such that and ,
By direct calculation, the following result can be derived.
Theorem 4.
Assume , let R be a strict t-conorm whose additive generator is and T be a strict t-norm, the additive generator of which is , then
where
In particular, if there is no support between the input arguments, i.e., for then , which can be seen as the T-based linguistic generalized weighted geometric (T-LGWG) operation of . Note that the properties of idempotency and boundedness of the T−LWGPG operator can be easily checked. However, commutativity of the T−LWGPG operator does not hold. Actually, in Example 2, if we further assume , then and
2.3.4. T-LOWGPG Operator
The ordered weighted average operator by Yager [51] is featured by its reordering steps. Furthur, Yager provided a generalization of the OWA operator, i.e., GOWA operator [52]. By incorporating these elements into the linguistic operator, the T-LOWGPG operator can be defined.
Definition 7.
Let , then T-LOWGPG operator is defined as
where , , , , , , is a basic unit-interval monotonic(BUIM) function satisfying and if , and is the i-th largest argument of
Theorem 5.
If , then .
Proof.
Since , then ; thus,
By commutativity of the T−LGPG operator, it follows that . □
Combining the above theorem and Corollary 1, the following result can be derived.
Corollary 2.
If and for all , then
Corollary 3.
If then ; If then ;
Proof.
For the former case, ; then,
;
For the latter case, the result can be checked similarly. □
2.3.5. T-LHGPG Operator
In order to systhesize the charcteristics of the ordered weighted averaging operators and the weighted arithmetic averaging operators, Xu and Da [53] defined the hybrid weighted averaging (HWA) operator. Recently, Liao and Xu [54] established a family of intuitionistic fuzzy hybrid weighted aggregation operators. In line with the two operators, the T-LHGPG operator for linguistic terms is defined.
Definition 8.
Let , then T-LHGPG operator is defined as
where is an associated vector with and ; is the i-th largest argument of the weighted linguistic terms , is the weighting vector satisfying that and , m is the balancing coefficient.
Remark 1.
The associated vector can be determined as that in Definition 7. Particularly, if the weighting vector , then
if , then , i.e., the T-based arithmetic generalized geometric operator of the weighted linguistic terms .
The four generalized power operations of linguistic terms in the above consider both the underlying linguistic terms and the interactions among them. The importance of all the underlying inputs is emphasized in the T-LWGPG operator, and the T-LOWGPG operator highlights the importance of each argument in their ordering, and, further, the T-LHGPG operator underlines both the underlying linguistic terms and their ordering position. Moreover, the weight for the linguistic term , presented in aforementioned definitions, relies on all the underlying inputs and considers the mutual supportive information of the inputs in the aggregating process, which can relieve the effect of outliers among the inputs on the aggregated results by setting fewer weights for them. In practical MAGDM, it is unavoidable that some DMs may present unexpectedly lower (or higher) uncertain preference values to the dissatisfying (or preferred) alternatives. The dramatic emphasis of these linguistic operators lies in that the underlying weights are settled by the measurement for the mutual supportive information among all the inputs. If the evaluation by a DM is more similar (or closer) to those by the other DMs, then more weight would be assigned to the corresponding input in these operators. Therefore, using these operators in the settlement of linguistic MAGDM problems can result in more reasonable and significantly balanced conclusions.
2.3.6. Determination of for the Operators
In order to quantify , the following steps are recommended.
- For a set of linguistic terms , a consensus degree matrix can be constructed in virtue of the relative deviation of linguistic terms. That is,where and is the relative deviation of and given in Definition 3.
- Compute the average support of from all the other linguistic terms by
- Normalize the average support to obtain the relative support of from all the other linguistic terms, which is viewed as . Namely,
2.4. Framework of the Linguistic MAGDM Using T-Based Linguistic Generalized Power Geometric Operators
As is illustrated in the above-mentioned section, T-based linguistic generalized power average operators take account of the interactive supports of the input arguments in the aggregation process, which can lessen the influence of outer data on the aggregated results by discounting the weights to those unfair ones. Therefore, power operators show their superiority in aggregating information by different DMs from the angle of consensus. Following that, the T-based linguistic generalized power average operators will be used in the method for linguistic MAGDM. Furthermore, in existing literature, MAGDM research mainly focuses on the decision matrices by DMs to obtain the desirable alternative and ignore the correlations among the related attributes. In what follows, the linguistic MAGDM considering both the decision matrices and correlation information among the attributes are investigated.
2.4.1. Presentation of Linguistic MAGDM
Linguistic MAGDM is to select the best alternatives from a set of alternatives on the basis of linguistic preference values on different attributes by a group of decision makers (DMs). The related symbols and notations in the linguistic MAGDM are stipulated as follows.
- is a set of m attributes and is the ith attribute;
- is a set of n alternatives and is the jth alternative;
- is a set of l decision makers(DMs) or experts and is the kth DM;
- The individual linguistic decision matrix given by is , where is a linguistic individual preference value for alternative on the attribute . In detail,
- The overall linguistic decision matrix is , where is a comprehensive preference value for alternative on the attribute , by a synthesized consideration of the individual preference values . In detail,
- The overall rating value of the j-th alternative is , which is a full and complete evaluation from each attribute and on the basis of which the alternatives can be ranked.
2.4.2. DEMATEL-Based Method for Determining the Individual Attribute Weights and DMs’ Weights
In this part, the principal procedure of the DEMATEL-based method for determining weights for attributes and DMs is presented.
Suppose that the set of attributes is and the correlations among attributes can be depicted as in Figure 1. In detail, the arrowed line linking two attributes means that there exists a correlation between them. The value of the line represents the intensity degree of the correlation. The larger the value, the higher the intensity degree. Further, the direction of the arrowed line shows the influence relationship.
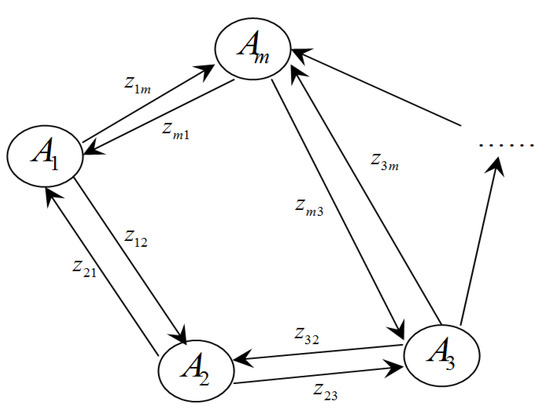
Figure 1.
The correlations among attributes.
In virtue of the DEMATEL method [45,46], the procedure of the DEMATEL-based method for determining the individual attribute weight by each DM is summarized as follows:
- (i)
- Construct the initial direct relation matrix by DM , where represents the existence and intensity of the correlation between attributes and . Usually, . For DM , , there is the most intensity of correlation between attributes and , while means there is no correlation between attributes and . In particular, there is no correlation between and itself, i.e., .
- (ii)
- Obtain the normalized the direct-relation matrix , where . Generally, the normalized matrix is characterized as a sub-stochastic matrix obtained from an absorbing Markov chain matrix by deleting all rows and columns associated with the absorbing states. For each normalized matrix , the following properties hold.(1) (the null matrix).(2) , where is the identity matrix.
- (iii)
- Obtain the individual overall relation matrix for DM , where represents the overall intensity of correlation between attributes and . Specifically, .
- (iv)
- Calculate the individual overall intensity that attribute influences others by ; calculate the individual overall intensity that attribute is influenced by others by .
- (v)
- Calculate the individual prominence of each attribute. The individual prominence of the attribute is calculated by , which characterizes the importance of the attribute by DM . The larger the individual prominence , the more important the attribute is by DM .
- (vi)
- Obtain the individual attribute weighting vector , where .
Similarly, an initial direct relation matrix for DMs can be used to illustrate the correlations and interactive influences among DMs. Therefore, by similar steps as above, a weighting vector for DMs can also be obtained.
2.4.3. Individual Attribute Weight and Overall Attribute Weight
According to the DEMATEL-based method in the above, different initial direct relation matrices by different DMs may result in different attribute weights, which are called individual attribute weights by DMs. Following that, to obtain an overall attribute weight, a method to aggregate individual attribute weights by minimizing relative entropy is presented.
Definition 9
([55]). Let and be two weighting vectors such that , and . Then is called the relative entropy of to .
The relative entropy is used to model the dissimilarity of and . The relative entropy reaches its minimum, i.e., , if .
Assume the initial direct relation matrix by DM is and the individual attribute weighting vector can be obtained by the DEMATEL-based method. In order to obtain the overall attribute weighting vector , the following mathematical programming model can be structured.
where is the weighting vector for DMs and it can be assigned beforehand or objectively determined by some known methods. Here, the weighting vector for DMs is determined by the DEMATEL-based method in the above subsection. To obtain the solution of the programming problem, a Lagrange function is defined as
where is the Lagrange multiplier. Thus, the following equations can be obtained:
By calculation with the above series of equations, it follows that
Thus, the overall attribute weighting vector can be obtained.
2.4.4. Algorithm for the Approach to Linguistic MAGDM
The linguistic approach to decision making, based on T-based generalized power geometric operators, can be summarized as follows:
- Through full negotiation and investigation, a group of DMs and the initial direct relation matrix for DMs are determined by the advisory committee for decision making. By the initial direct relation matrix for DMs and the similar steps in Section 2.4.2, the weighting vector for DMs can be determined.
- On the basis of their experience and knowledge about referred alternatives, each DM provides his/her individual linguistic decision matrix and initial direct relation matrices .
- Obtain the overall decision matrix by T-LWGPG operator. In detail, is calculated bywhere is the weighting vector for DMs obtained in the first step.
- By the initial direct relation matrices for attributes, the individual attribute weighting vectors can be obtained. Obtain the attribute weighting vector by Equation (18).
- Obtain the overall rating values for each alternative by T-LHGPG operator, i.e.,where the associated weighting vector is the attribute weighting vector .
- Rank all the alternatives by overall rating values .
3. Illustrative Example and Discussion
In this section, the aforementioned approach is employed in evaluating university faculty for tenure and promotion, which is adapted from [6,7]. Then, some remarks on the selection of the parameters are provided. Finally, some comparison analysis with existing methods are performed.
3.1. On the Evaluation for Tenure and Promotion
Academic tenure was introduced to guarantee the right of the teachers and researchers to academic freedom. However, since the 1970s, colleges and universities in the US have seen a steady decline in the percentage of tenured or tenure-track teaching positions. For those that are tenure track, in general, it takes years to earn tenure while working as an assistant professor. However, the statistics from the United States Department of Education shows that the combined tenured/tenure-track rate was 56% for 1975, 46.8% for 1989, and 31.9% for 2005. In other words, 68.1% of US college scholars were neither tenured nor eligible for tenure in 2005. In Columbia University, only 10–20% of assistant professors can ultimately obtain tenure. Therefore, tenure has gradually become a type of job security for scholars. The scholars in universities are apt to fiercely pursue and compete for limited resources. In order to consider all the necessary elements fully and comprehensively, tenure is usually determined by a combinational consideration of research, teaching, and service, with each factor weighted according to the principles of a particular university.
In the following, let be the set of five faculty candidates (alternatives) to be evaluated using linguistic terms. Assume that three attributes, including : teaching, : research, and : service, are taken into account for evaluating the university faculty for tenure and promotion. Four DMs are requested by the advisory committee for evaluation to assess the five faculty candidates in linguistic terms, where the set of linguistic terms . The decision matrices are listed in Table 2, Table 3, Table 4 and Table 5, respectively.

Table 2.
Decision matrix given by DM .

Table 3.
Decision matrix given by DM .

Table 4.
Decision matrix given by DM .

Table 5.
Decision matrix given by DM .
In addition, the DMs should provide their initial direct-relation matrices for attributes based on their knowledge background (see Table 6, Table 7, Table 8 and Table 9).

Table 6.
Initial direct-relation matrix for attributes by DM .

Table 7.
Initial direct-relation matrix for attributes by DM .

Table 8.
Initial direct-relation matrix for attributes by DM .

Table 9.
Initial direct-relation matrix for attributes by DM .
The advisory committee for evaluation should give the initial direct-relation matrix for DMs (See Table 10). In what follows, it is assumed that for both the Hamacher t-norm and t-conorm and .

Table 10.
Initial direct-relation matrix for DMs given by the advisory committee.
Firstly, by the initial direct relation matrix for DMs given by the advisory committee for evaluation, with the similar steps as those in Section 2.4.2, the weighting vector for DMs can be obtained. Namely, . Consequently, by Equation (19), the overall decision matrix can be obtained
Secondly, by the initial direct-relation matrices for attributes and the steps in Section 2.4.2, the individual attribute weighting vectors can be obtained, respectively, and listed as follows: ; ; ; . By Equation (18) and the weighting vector for DMs, the overall attribute weighting vector can be obtained. By Equation (20), the overall rating values for each candidate can be obtained. Namely, Here, the BUIM function is used.
Finally, the five faculty candidates can ranked as
3.2. Notes for the Parameters
Practically, too many parameters may lead to some confusions in applications and distortions in the results in some sense. However, the following facts must be highlighted. Using 900 different combinations of the parameters (from 1 to 30) of Hamacher t-norms and t-conorms and assuming , it can be found that the ranking orders are sensitive to the different combinations of the parameters of Hamacher t-norms and t-conorms. Therefore, in order to guarantee the stability of the ranking results, the parameters for the related Hamacher t-norm and t-conorm should be consisitent. In other words, the duality of the Hamacher t-norm and t-conorm should be maintained in the approach. From the aspect of simplicity of calculation, and are recommended in the approach.
For illustration, the interactions of the overall rating values to the parameter are shown in Figure 2, where and are used and the parameter ranges from 0.01 to 5. Clearly, the ranking results are stable with respect to the parameters in the range. However, from the angle of the simplicity of calculation, the parameter should not be too large.
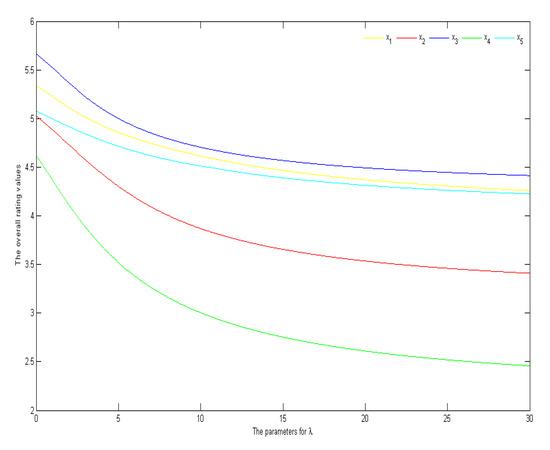
Figure 2.
The interactions of the overall rating values to the parameter .
3.3. Comparison Analysis with Existing Works
For convenience, some results of the tenure evaluation in the literature are listed in Table 11. It is demonstrated that the best candidate by the method in the paper is , which is consistent with those by the existing methods.

Table 11.
Ranking results of the related works.
Compared with the methods in [6,7], the method in this paper can be illuminated considering the following two aspects.
(i) The employed operations for linguistic terms. In this paper, the newly proposed linguistic operations are based on strict t-norms and t-conorms and closed on the set of the restricted continuous linguistic term set . In the methods in [6,7], the classical linguistic operations [4], which are not closed on , are used. As demonstrated in Example 1, the classical linguistic operations may result in some unrealistic and meaningless results. Therefore, the underlying operations for linguistic terms are more reasonable than those employed in [6,7].
(ii) The techniques to determine the weighting information. In the method by Merig et al. [6], the weights for DMs and attributes are given by subjective knowledge and experience. Consequently, the inevitably excessive preference of some DM or attribute may lead to some biased results. In the method by Zhou et al. [7], the weights for both DMs and attributes are all determined by the mutual supports of input arguments from the angle of the consistency of the preference values; thus, they ignored the fact that the attribute values of an alternative may be quite different on different attributes. In the approach of this paper, the DMs’ weights and attribute weights are objectively determined by the initial direct-relation matrices using the DEMATEL-based method. In other words, weighting information for DMs and attributes are dependent on the interactive influence and interrelationship among DMs or attributes. Hence, objectivity and reasonability can be guaranteed.
4. Conclusions
In this paper, to overcome some defects of the classical operation laws for linguistic terms, some new operation laws for continuous linguistic terms using strict t-norms and t-conorms were defined and a series of T-based linguistic generalized power geometric operators, i.e., T-LGPG operator, T-LWGPG operator, T-LOWGPG operator and T-LHGPG operator, were developed. In addition, then, the DEMATEL method was employed in determining weighting information for DMs and attributes by initial direct-relation matrices for DMs and attributes, respectively. By these means, the weighting vector for DMs and attributes can be determined objectively by the interactive influence and interrelationship among DMs and attributes. An illustrative example on faculty evaluation for tenure was presented. Comparison analysis with existing methods was performed. In contrast with the existing methods, the method in the work can be highlighted in two aspects: the newly proposed linguistic operations, which are based on strict t-norms and t-conorms and closed on the set of the restricted continuous linguistic term set ; and the techniques in determining the weighting information, with which the DMs’ weights and attribute weights were objectively determined by the initial direct relation matrices using the DEMATEL-based method.
Notably, in the method, the original linguistic term sets are used and the underlying operations are based only on the pertaining indices. Thus, the method in this work may not applicable in more practical and more complex situations where hesitancy may exist, i.e., people may use more than one linguistic term to express her/his evaluations or preferences. In order to facilitate linguistic decision making in more complex environments, there are some innovative extensions for the linguistic terms, such as the hesitant fuzzy linguistic term sets [22], the linguistic Z-Numbers [24], the 2-dimension linguistic variables [5], the probabilistic linguistic terms [56] and the reformulated probabilistic linguistic terms [43], which provide some insightful directions for the further research on the topic. In the future, these innovative derivatives could be appealingly engaged in the methodologies for linguistic decision making.
Author Contributions
Conceptualization, Z.Y.; methodology, Z.Y.; validation, Z.Y.; formal analysis, Z.Y.; writing—original draft preparation, L.Y.; writing—review and editing, L.Y.; supervision, L.Y.; funding acquisition, L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Science and Technology Project of Jiangxi Provincial Educational Department of China under GJJ212609 and is partially supported by the PhD Research Startup Foundation of Nanchang Normal University under Grant NSBSJJ2020015.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are very grateful to Shuping Wan in Jiangxi University of Finance and Economics for his valuable suggestions on the preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Romero, Á.L.; Rodríguez, R.M.; Martínez, L. Computing with comparative linguistic expressions and symbolic translation for decision making: ELICIT information. IEEE Trans. Fuzzy Syst. 2020, 28, 2510–2522. [Google Scholar] [CrossRef]
- Dong, Y.C.; Xu, Y.F.; Li, H.Y. On consistency measures of linguistic preference relations. Eur. J. Oper. Res. 2008, 189, 430–444. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E. Choice functions and mechanisms for linguistic preference relations. Eur. J. Oper. Res. 2000, 120, 144–161. [Google Scholar] [CrossRef]
- Xu, Z.S. Linguistic Decision Making, Theory and Methods; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Verma, R.; Merigo, J.M. Multiple attribute group decision making based on 2-dimension linguistic intuitionistic fuzzy aggregation operators. Soft Comput. 2020, 24, 17377–17400. [Google Scholar] [CrossRef]
- Merigó, J.M.; Gil-Lafuente, A.M.; Zhou, L.G.; Chen, H.Y. Induced and linguistic generalized aggregation operators and their application in linguistic group decision making. Group Decis. Negot. 2012, 21, 531–549. [Google Scholar] [CrossRef]
- Zhou, L.G.; Chen, H.Y. A generalization of the power aggregation operators for linguistic environment and its application in group decision making. Knowl. Based Syst. 2012, 26, 216–224. [Google Scholar] [CrossRef]
- Bordogna, G.; Fedrizzi, M.; Pasi, G. A linguistic modeling of consensus in group decision making based on OWA operators. IEEE Trans. Syst. Man Cybern. Part Syst. Hum. 1997, 27, 126–133. [Google Scholar] [CrossRef]
- Cabrerizo, F.J.; Herrera-Viedma, E.; Pedrycz, W. A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts. Eur. J. Oper. Res. 2013, 230, 624–633. [Google Scholar] [CrossRef]
- Degani, R.; Bortolan, G. The problem of linguistic approximation in clinical decision making. Int. J. Approx. Reason. 1988, 2, 143–162. [Google Scholar] [CrossRef] [Green Version]
- Herrera, F.; Herrera-Viedma, E. Aggregation operators for linguistic weighted information. IEEE Trans. Syst. Man Cybern. Part Syst. Hum. 1997, 27, 646–656. [Google Scholar] [CrossRef] [Green Version]
- Torra, V. The weighted OWA operator. Int. J. Intell. Syst. 1997, 12, 153–166. [Google Scholar] [CrossRef]
- Delgado, M.; Verdegay, J.L.; Vila, M. On aggregation operations of linguistic labels. Int. J. Intell. Syst. 1993, 8, 351–370. [Google Scholar] [CrossRef]
- Dong, Y.C.; Xu, Y.F.; Li, H.Y.; Feng, B. The OWA-based consensus operator under linguistic representation models using position indexes. Eur. J. Oper. Res. 2010, 203, 455–463. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Wan, S.P. 2-tuple linguistic hybrid arithmetic aggregation operators and application to multi-attribute group decision making. Knowl. Based Syst. 2013, 45, 31–40. [Google Scholar] [CrossRef]
- Wan, S.P. Some hybrid geometric aggregation operators with 2-tuple linguistic information and their applications to multi-attribute group decision making. Int. J. Comput. Intell. Syst. 2013, 6, 750–763. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.S. A method based on linguistic aggregation operators for group decision making with linguistic preference relations. Inf. Sci. 2004, 166, 19–30. [Google Scholar] [CrossRef]
- Xu, Z.S. Induced uncertain linguistic OWA operators applied to group decision making. Inf. Fusion 2006, 7, 231–238. [Google Scholar] [CrossRef]
- Wang, J.H.; Hao, J.Y. A new version of 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2006, 14, 435–445. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Pedrycz, W. A construction of sound semantic linguistic scales using 4-tuple representation of term semantics. Int. J. Approx. Reason. 2014, 55, 763–786. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S. Novel basic operational laws for linguistic terms, hesitant fuzzy linguistic term sets and probabilistic linguistic term sets. Inf. Sci. 2016, 372, 407–427. [Google Scholar] [CrossRef]
- Wang, J.Q.; Cao, Y.X.; Zhang, H.Y. Multi-criteria decision-making method based on distance measure and Choquet integral for linguistic Z-numbers. Cogn. Comput. 2017, 9, 827–842. [Google Scholar] [CrossRef]
- Dutta, B.; Guha, D. Partitioned Bonferroni mean based on linguistic 2-tuple for dealing with multi-attribute group decision making. Appl. Soft Comput. 2015, 37, 166–179. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.M.; Liu, P.D. Multiple attribute group decision-making methods based on trapezoidal fuzzy two-dimension linguistic power generalized aggregation operators. Soft Comput. 2016, 20, 2689–2704. [Google Scholar] [CrossRef]
- Merigó, J.M.; Palacios-Marqueé, D.; Zeng, S.Z. Subjective and objective information in linguistic multi-criteria group decision making. Eur. J. Oper. Res. 2016, 248, 522–531. [Google Scholar] [CrossRef]
- Merigó, J.M.; Casanovas, M.; Martínez, L. Linguistic aggregation operators for linguistic decision making based on the Dempster-Shafer theory of evidence. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2010, 18, 287–304. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wu, J.T.; Wang, J.; Zhang, H.Y.; Chen, X.H. Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inf. Sci. 2014, 288, 55–72. [Google Scholar] [CrossRef]
- Wu, D.R.; Mendel, J.M. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Trans. Fuzzy Syst. 2007, 15, 1145–1161. [Google Scholar] [CrossRef]
- Wu, Z.B.; Chen, Y.H. The maximizing deviation method for group multiple attribute decision making under linguistic environment. Fuzzy Sets Syst. 2007, 158, 1608–1617. [Google Scholar] [CrossRef]
- Xu, Y.J.; Da, Q.L. Standard and mean deviation methods for linguistic group decision making and their applications. Expert Syst. Appl. 2010, 37, 5905–5912. [Google Scholar] [CrossRef]
- Xu, Y.J.; Merigó, J.M.; Wang, H.M. Linguistic power aggregation operators and their application to multiple attribute group decision making. Appl. Math. Model. 2012, 36, 5427–5444. [Google Scholar] [CrossRef]
- Xu, Z.S. Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment. Inf. Sci. 2004, 168, 171–184. [Google Scholar] [CrossRef]
- Xu, Z.S. An approach based on the uncertain LOWG and induced uncertain LOWG operators to group decision making with uncertain multiplicative linguistic preference relations. Decis. Support Syst. 2006, 41, 488–499. [Google Scholar] [CrossRef]
- Xu, Z.S. On generalized induced linguistic aggregation operators. Int. J. Gen. Syst. 2006, 35, 17–28. [Google Scholar] [CrossRef]
- Xu, Z.S. EOWA and EOWG operators for aggregating linguistic labels based on linguistic preference relations. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2004, 12, 791–810. [Google Scholar] [CrossRef]
- Zhou, L.G.; Chen, H.Y. The induced linguistic continuous ordered weighted geometric operator and its application to group decision making. Comput. Ind. Eng. 2013, 66, 222–232. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Power-geometric operators and their use in group decision making. IEEE Trans. Fuzzy Syst. 2010, 18, 94–105. [Google Scholar]
- Yager, R.R. The power average operator. IEEE Trans. Syst. Man Cybern. Part Syst. Humans 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Ju, Y.B.; Wang, A.H. Projection method for multiple criteria group decision making with incomplete weight information in linguistic setting. Appl. Math. Model. 2013, 37, 9031–9040. [Google Scholar] [CrossRef]
- Ju, Y.B.; Wang, A.H. Extension of VIKOR method for multi-criteria group decision making problem with linguistic information. Appl. Math. Model. 2013, 37, 3112–3125. [Google Scholar] [CrossRef]
- Yi, Z.H. Decision-making based on probabilistic linguistic term sets without loss of information. Complex Intell. Syst. 2022, 8, 2435–2449. [Google Scholar] [CrossRef]
- Dai, Y.Q.; Da, Q.L.; Xu, Z.S. New evaluation scale of linguistic information and its application. Chin. J. Manag. Sci. 2008, 16, 145–149. [Google Scholar]
- Fontela, E.; Gabus, A. World Problems, an Invitation to Further Thought within the Framework of DEMATEL; Battelle Memorial Institute Geneva Research Centre: Geneva, Switzerland, 1972. [Google Scholar]
- Suo, W.L.; Feng, B.; Fan, Z.P. Extension of the DEMATEL method in an uncertain linguistic environment. Soft Comput. 2012, 16, 471–483. [Google Scholar] [CrossRef]
- Alsina, C.; Frank, M.J.; Schweizer, B. Associative Functions: Triangular Norms and Copulas; World Scientific Publishing Co.: Singapore, 2006. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Norms; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Dyckhoff, H.; Pedrycz, W. Generalized means as model of compensative connectives. Fuzzy Sets Syst. 1984, 14, 143–154. [Google Scholar] [CrossRef]
- Zhang, Z.M. Generalized Atanassov’s intuitionistic fuzzy power geometric operators and their application to multiple attribute group decision making. Inf. Fusion 2013, 14, 460–486. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized OWA aggregation operators. Fuzzy Optim. Decis. Mak. 2004, 3, 93–107. [Google Scholar] [CrossRef]
- Xu, Z.S.; Da, Q.L. An overview of operators for aggregating information. Int. J. Intell. Syst. 2003, 18, 953–969. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S. Intuitionistic fuzzy hybrid weighted aggregation operators. Int. J. Intell. Syst. 2014, 29, 971–993. [Google Scholar] [CrossRef]
- Qian, M.P.; Gong, G.L.; Clark, J.W. Relative entropy and learning rules. Phys. Rev. A 1991, 43, 1061–1070. [Google Scholar] [CrossRef] [PubMed]
- Liao, H.C.; Mi, X.; Xu, Z.S. A survey of decision-making methods with probabilistic linguistic information: Bibliometrics, preliminaries, methodologies, applications and future directions. Fuzzy Optim. Decis. Mak. 2020, 19, 81–134. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).