Combining the MDM and BWM Algorithm to Determine the Optimal Crowdfunding Tokenization Solution for Digital Assets Market Startups
Abstract
:1. Introduction
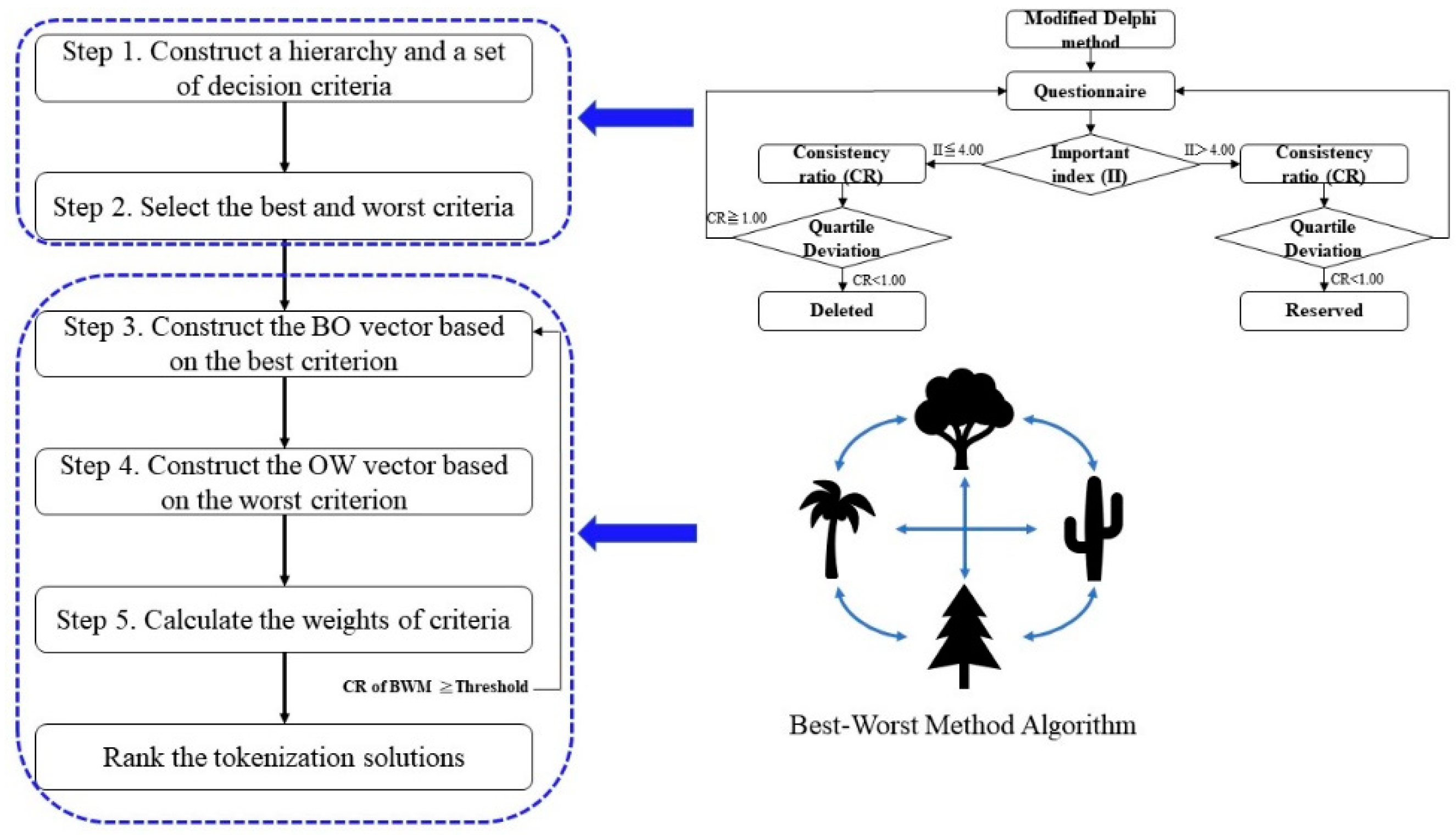
2. Determination Model
2.1. Modified Delphi Method
- Anonymity: All experts express their opinions individually and strictly comply with the principle of anonymity.
- Iterations: A facilitator gathers the expert opinions and distributes them among the other experts. This process is repeated.
- Controlled feedback: In each round, experts answer a pre-designed questionnaire. The results are used as a reference for the next assessment.
- Statistical group response: The number of opinions gathered must be calculated before a comprehensive judgment is made.
- Expert consensus: The final goal is the integration of all expert opinions to reach a consensus.
- A.
- Select anonymous experts;
- B.
- Conduct the first round of the survey;
- C.
- Conduct the second round of the survey;
- D.
- Conduct the third round of the survey;
- E.
- Integrate expert opinions and reach a consensus.
2.2. Best Worst Method
3. Case Study
- Finance: Including issuance, platform, and transaction costs.
- ◆
- Issuance costs: The costs of token issuance vary depending on the types of token-financing solutions; for example, MINT coin exchanges.
- ◆
- Platform fees: Fees for token-financing solutions differ across platforms; for example: the platform fee that Binance charges.
- ◆
- Transaction costs: There are various transaction costs involved in token-financing schemes, for example, handling fees.
- Laws and regulations: Including place of issuance, government policy, token security regulations, and information disclosure transparency.
- ◆
- Place of issuance: The laws, regulations, and restrictions on issuing tokens in different countries.
- ◆
- Government policy: The amount of government support for token financing.
- ◆
- Token security regulations: The laws and regulations for token security.
- ◆
- Information disclosure transparency: The laws and regulations for the level of information disclosures when companies issue tokens.
- Risk: Including financing schedules, token price fluctuations, reputation, share-holding proportions, and financing success rates.
- ◆
- Financing schedule: The duration of the financing schedule; for example, ICO has shorter financing schedule relative to STO.
- ◆
- Token price fluctuation: Significant fluctuations in token transaction price affect financing efficiency.
- ◆
- Reputation: The degree of corporate reputation required by the token-financing solution; for example, ICO has fewer corporate reputation requirements.
- ◆
- Shareholding proportion: The proportion of equity holding corresponding to the tokens held by investors.
- ◆
- Financing success rate: The company’s success rate in token financing for different financing solutions.
- Investors: Including financing object and financing threshold.
- ◆
- Financing object: The types of investors that companies deal with when issuing tokens for financing; for example, ICO and IEO focus on retail investors, whereas STO targets professional investors.
- ◆
- Financing threshold: The entry threshold for companies to issue tokens; for example, STO has a higher threshold.
- Online community: Including online share of voice, online public sentiment, and online trend.
- ◆
- Online share of voice: The influence of investors on the preference for online share of voice on different financing platforms.
- ◆
- Online public sentiment: The influence of investors on public sentiments on social media on different financing platforms.
- ◆
- Online trend: The influence of investors on the development of the overall environment and trends of token financing.
- Token-financing solutions: Including ICO, IEO, and STO.
- ◆
- ICO: It combines blockchain technology and the concept of virtual tokens to develop, maintain, and exchange for financing.
- ◆
- IEO: Tokens are endorsed, issued, and sold on exchanges, which are responsible for Know Your Customer (KYC) and Anti-Money Laundering (AML) systems.
- ◆
- STO: Through the securitization of corporate assets, the government-regulated ICO ties the corporate assets to tokens and sells them.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FinTech | financial technology |
| JOBS | Jumpstart Our Business Startups |
| ICO | initial coin offerings |
| IEO | initial exchange offerings |
| STO | security token offerings |
| AHP | analytic hierarchy process |
| BWM | best worst method |
| MDM | modified Delphi method |
| BO | Best-to-Others |
| OW | Others-to-Worst |
| LP | linear programming |
| CR | consistency ratio |
References
- Gai, K.; Qiu, M.; Sun, X. A survey on FinTech. J. Netw. Comput. Appl. 2018, 103, 262–273. [Google Scholar] [CrossRef]
- Lee, I.; Shin, Y.J. Fintech: Ecosystem, business models, investment decisions, and challenges. Bus. Horiz. 2018, 61, 35–46. [Google Scholar] [CrossRef]
- Mackenzie, A. The fintech revolution. Lond. Bus. Sch. Rev. 2015, 26, 50–53. [Google Scholar] [CrossRef]
- Ivanov, V.; Knyazeva, A. US Securities-Based Crowdfunding under Title III of the JOBS Act; DERA White Paper; Securities Exchange Commission: Washington, DC, USA, 2017.
- Rossi, M. The new ways to raise capital: An exploratory study of crowdfunding. Int. J. Financ. Res. 2014, 5, 8–18. [Google Scholar] [CrossRef]
- Walthoff-Borm, X.; Schwienbacher, A.; Vanacker, T. Equity crowdfunding: First resort or last resort? J. Bus. Ventur. 2018, 33, 513–533. [Google Scholar] [CrossRef]
- Massolution. 2015CF: The Crowdfunding Industry Report. Massolution. 2015. Available online: https://www.smv.gob.pe/Biblioteca/temp/catalogacion/C8789.pdf (accessed on 20 January 2022).
- Statista Inc. Alternative Financing Report 2021. 2021. Available online: https://www.statista.com/study/47352/fintech-report-alternative-financing/ (accessed on 10 January 2022).
- Bagheri, A.; Chitsazan, H.; Ebrahimi, A. Crowdfunding motivations: A focus on donors’ perspectives. Technol. Forecast. Soc. Chang. 2019, 146, 218–232. [Google Scholar] [CrossRef]
- Lu, Y.; Chang, R.; Lim, S. Crowdfunding for solar photovoltaics development: A review and forecast. Renew. Sustain. Energy Rev. 2018, 93, 439–450. [Google Scholar] [CrossRef]
- Petruzzelli, A.M.; Natalicchio, A.; Panniello, U.; Roma, P. Understanding the crowdfunding phenomenon and its implications for sustainability. Technol. Forecast. Soc. Chang. 2019, 141, 138–148. [Google Scholar] [CrossRef]
- Estrin, S.; Gozman, D.; Khavul, S. Case Study of the Equity Crowdfunding Landscape in London: An Entrepreneurial and Regulatory Perspective; FIRES Case Study; Utrecht University: Utrecht, The Netherlands, 2016; pp. 1–62. [Google Scholar]
- Agrawal, A.; Catalini, C.; Goldfarb, A. Some simple economics of crowdfunding. Innov. Policy Econ. 2014, 14, 63–97. [Google Scholar] [CrossRef] [Green Version]
- Kuti, M.; Madarász, G. Crowdfunding. Public Financ. Q. 2014, 59, 355–366. [Google Scholar]
- Zhu, H.; Zhou, Z.Z. Analysis and outlook of applications of blockchain technology to equity crowdfunding in China. Financ. Innov. 2016, 2, 29. [Google Scholar] [CrossRef] [Green Version]
- Baber, H. Blockchain-Based Crowdfunding. In Blockchain Technology for Industry 4.0; Springer: Singapore, 2020; pp. 117–130. [Google Scholar]
- Chod, J.; Lyandres, E. A theory of icos: Diversification, agency, and information asymmetry. Manag. Sci. 2021, 67, 5969–5989. [Google Scholar] [CrossRef]
- Chod, J.; Trichakis, N.; Yang, S.A. Platform tokenization: Financing, governance, and moral hazard. Manag. Sci. 2022. forthcoming. [Google Scholar] [CrossRef]
- Howell, S.T.; Niessner, M.; Yermack, D. Initial coin offerings: Financing growth with cryptocurrency token sales. Rev. Financ. Stud. 2020, 33, 3925–3974. [Google Scholar] [CrossRef] [Green Version]
- Ante, L.; Fiedler, I. Cheap Signals in Security Token Offerings (STOs). Quant. Financ. Econ. 2020, 4, 608–639. [Google Scholar] [CrossRef]
- Amsden, R.; Schweizer, D. Are Blockchain Crowdsales the New ‘Gold Rush’? Success Determinants of Initial Coin Offerings. Success Determinants of Initial Coin Offerings. 16 April 2018. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3163849 (accessed on 24 March 2021).
- Miglo, A. Choice between IEO and ICO: Speed vs. Liquidity vs. Risk. Risk. 26 March 2020. Available online: https://mpra.ub.uni-muenchen.de/99600/1/MPRA_paper_99600.pdf (accessed on 5 April 2021).
- Kondova, G.; Simonella, G. Blockchain in Startup Financing: ICOs and STOs in Switzerland. J. Strateg. Innov. Sustain. 2019, 14, 43–48. [Google Scholar]
- Gryglewicz, S.; Mayer, S.; Morellec, E. Optimal financing with tokens. J. Financ. Econ. 2021, 142, 1038–1067. [Google Scholar] [CrossRef]
- Borri, N. Conditional tail-risk in cryptocurrency markets. J. Empir. Financ. 2019, 50, 1–19. [Google Scholar] [CrossRef]
- Canh, N.P.; Wongchoti, U.; Thanh, S.D.; Thong, N.T. Systematic risk in cryptocurrency market: Evidence from DCC-MGARCH model. Financ. Res. Lett. 2019, 29, 90–100. [Google Scholar] [CrossRef]
- Liu, Y.; Tsyvinski, A. Risks and returns of cryptocurrency. Rev. Financ. Stud. 2021, 34, 2689–2727. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Xiong, X.; Wang, P. Downside risk and the cross-section of cryptocurrency returns. J. Bank. Financ. 2021, 133, 106246. [Google Scholar] [CrossRef]
- Borri, N.; Shakhnov, K. Regulation spillovers across cryptocurrency markets. Financ. Res. Lett. 2020, 36, 101333. [Google Scholar] [CrossRef]
- Chokor, A.; Alfieri, E. Long and short-term impacts of regulation in the cryptocurrency market. Q. Rev. Econ. Financ. 2021, 81, 157–173. [Google Scholar] [CrossRef]
- Feinstein, B.D.; Werbach, K. The impact of cryptocurrency regulation on trading markets. J. Financ. Regul. 2021, 7, 48–99. [Google Scholar] [CrossRef]
- Beneki, C.; Koulis, A.; Kyriazis, N.A.; Papadamou, S. Investigating volatility transmission and hedging properties between Bitcoin and Ethereum. Res. Int. Bus. Financ. 2019, 48, 219–227. [Google Scholar] [CrossRef]
- Okorie, D.I.; Lin, B. Crude oil price and cryptocurrencies: Evidence of volatility connectedness and hedging strategy. Energy Econ. 2020, 87, 104703. [Google Scholar] [CrossRef]
- Sebastião, H.; Godinho, P. Bitcoin futures: An effective tool for hedging cryptocurrencies. Financ. Res. Lett. 2020, 33, 101230. [Google Scholar] [CrossRef]
- Thampanya, N.; Nasir, M.A.; Huynh, T.L.D. Asymmetric correlation and hedging effectiveness of gold & cryptocurrencies: From pre-industrial to the 4th industrial revolution. Technol. Forecast. Soc. Chang. 2020, 159, 120195. [Google Scholar]
- Köchling, G.; Schmidtke, P.; Posch, P.N. Volatility forecasting accuracy for Bitcoin. Econ. Lett. 2020, 191, 108836. [Google Scholar] [CrossRef]
- Ma, F.; Liang, C.; Ma, Y.; Wahab, M.I.M. Cryptocurrency volatility forecasting: A Markov regime-switching MIDAS approach. J. Forecast. 2020, 39, 1277–1290. [Google Scholar] [CrossRef]
- Walther, T.; Klein, T.; Bouri, E. Exogenous drivers of Bitcoin and Cryptocurrency volatility—A mixed data sampling approach to forecasting. J. Int. Financ. Mark. Inst. Money 2019, 63, 101133. [Google Scholar] [CrossRef]
- Yen, K.C.; Cheng, H.P. Economic policy uncertainty and cryptocurrency volatility. Financ. Res. Lett. 2021, 38, 101428. [Google Scholar] [CrossRef]
- Al Rahahleh, N.; Bhatti, M.I. Co-movement measure of information transmission on international equity markets. Phys. A Stat. Mech. Appl. 2017, 470, 119–131. [Google Scholar] [CrossRef]
- Do, H.Q.; Bhatti, M.I.; Shahbaz, M. Is ‘oil and gas’ industry of ASEAN5 countries integrated with the US counterpart? Appl. Econ. 2020, 52, 4112–4134. [Google Scholar] [CrossRef]
- Li, Y.; Guo, J. The asymmetric impacts of oil price and shocks on inflation in BRICS: A multiple threshold nonlinear ARDL model. Appl. Econ. 2022, 54, 1377–1395. [Google Scholar] [CrossRef]
- Hamdan, S.; Cheaitou, A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput. Oper. Res. 2017, 81, 282–304. [Google Scholar] [CrossRef]
- Lin, S.W. Identifying the critical success factors and an optimal solution for mobile technology adoption in travel agencies. Int. J. Tour. Res. 2017, 19, 127–144. [Google Scholar] [CrossRef]
- Lin, C.Y. Optimal Core Operation in Supply Chain Finance Ecosystem by Integrating the Fuzzy Algorithm and Hierarchical Framework. Int. J. Comput. Intell. Syst. 2020, 13, 259–274. [Google Scholar] [CrossRef]
- Yang, Y.; Song, X. Research on Face Intelligent Perception Technology Integrating Deep Learning under Different Illumination Intensities. J. Comput. Cogn. Eng. 2022, 1, 32–36. [Google Scholar]
- Awad, J.; Jung, C. Extracting the Planning Elements for Sustainable Urban Regeneration in Dubai with AHP (Analytic Hierarchy Process). Sustain. Cities Soc. 2022, 76, 103496. [Google Scholar] [CrossRef]
- Achu, A.L.; Thomas, J.; Reghunath, R. Multi-criteria decision analysis for delineation of groundwater potential zones in a tropical river basin using remote sensing, GIS and analytical hierarchy process (AHP). Groundw. Sustain. Dev. 2020, 10, 100365. [Google Scholar] [CrossRef]
- Gündoğdu, F.K.; Duleba, S.; Moslem, S.; Aydın, S. Evaluating public transport service quality using picture fuzzy analytic hierarchy process and linear assignment model. Appl. Soft Comput. 2021, 100, 106920. [Google Scholar] [CrossRef]
- Kilic, B.; Ucler, C. Stress among ab-initio pilots: A model of contributing factors by AHP. J. Air Transp. Manag. 2019, 80, 101706. [Google Scholar] [CrossRef]
- Kumar, S.; Raut, R.D.; Nayal, K.; Kraus, S.; Yadav, V.S.; Narkhede, B.E. To identify industry 4.0 and circular economy adoption barriers in the agriculture supply chain by using ISM-ANP. J. Clean. Prod. 2021, 293, 126023. [Google Scholar] [CrossRef]
- Bathrinath, S.; Bhalaji, R.K.A.; Saravanasankar, S. Risk analysis in textile industries using AHP-TOPSIS. Mater. Today Proc. 2021, 45, 1257–1263. [Google Scholar] [CrossRef]
- Emamat, M.S.M.M.; de Miranda Mota, C.M.; Mehregan, M.R.; Sadeghi Moghadam, M.R.; Nemery, P. Using ELECTRE-TRI and FlowSort methods in a stock portfolio selection context. Financ. Innov. 2022, 8, 1–35. [Google Scholar] [CrossRef]
- Lam, K.; Zhao, X. An application of quality function deployment to improve the quality of teaching. Int. J. Qual. Reliab. Manag. 1998, 15, 389–413. [Google Scholar] [CrossRef]
- Cheng, E.W.; Li, H. Construction partnering process and associated critical success factors: Quantitative investigation. J. Manag. Eng. 2002, 18, 194–202. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega 2016, 64, 126–130. [Google Scholar] [CrossRef]
- Mi, X.; Tang, M.; Liao, H.; Shen, W.; Lev, B. The state-of-the-art survey on integrations and applications of the best worst method in decision making: Why, what, what for and what’s next? Omega 2019, 87, 205–225. [Google Scholar] [CrossRef]
- Kheybari, S.; Kazemi, M.; Rezaei, J. Bioethanol facility location selection using best-worst method. Appl. Energy 2019, 242, 612–623. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, B.; Wang, P. A weighting model based on best–worst method and its application for environmental performance evaluation. Appl. Soft Comput. 2021, 103, 107168. [Google Scholar] [CrossRef]
- Liang, F.; Brunelli, M.; Rezaei, J. Consistency issues in the best worst method: Measurements and thresholds. Omega 2020, 96, 102175. [Google Scholar] [CrossRef]
- Rezaei, J.; van Roekel, W.S.; Tavasszy, L. Measuring the relative importance of the logistics performance index indicators using Best Worst Method. Transp. Policy 2018, 68, 158–169. [Google Scholar] [CrossRef]
- Linstone, H.A.; Turoff, M. (Eds.) The Delphi Method; Addison-Wesley: Reading, MA, USA, 1975; pp. 3–12. [Google Scholar]
- Murry, J.W., Jr.; Hammons, J.O. Delphi: A versatile methodology for conducting qualitative research. Rev. High. Educ. 1995, 18, 423–436. [Google Scholar] [CrossRef]
- Okoli, C.; Pawlowski, S.D. The Delphi method as a research tool: An example, design considerations and applications. Inf. Manag. 2004, 42, 15–29. [Google Scholar] [CrossRef] [Green Version]
- Skulmoski, G.J.; Hartman, F.T.; Krahn, J. The Delphi method for graduate research. J. Inf. Technol. Educ. Res. 2007, 6, 1–21. [Google Scholar] [CrossRef]
- Wu, C.R.; Lin, C.T.; Chen, H.C. Evaluating competitive advantage of the location for Taiwanese hospitals. J. Inf. Optim. Sci. 2007, 28, 841–868. [Google Scholar] [CrossRef]
- Hasson, F.; Keeney, S. Enhancing rigour in the Delphi technique research. Technol. Forecast. Soc. Chang. 2011, 78, 1695–1704. [Google Scholar] [CrossRef]
- Sung, W.C. Application of Delphi method, a qualitative and quantitative analysis, to the healthcare management. J. Healthc. Manag. 2001, 2, 11–19. [Google Scholar]
- Ali-Yrkkö, J.; Rouvinen, P.; Seppälä, T.; Ylä-Anttila, P. Who captures value in global supply chains? Case Nokia N95 Smartphone. J. Ind. Compet. Trade 2011, 11, 263–278. [Google Scholar] [CrossRef] [Green Version]
- Linden, G.; Kraemer, K.L.; Dedrick, J. Who captures value in a global innovation network? The case of Apple’s iPod. Commun. ACM 2009, 52, 140–144. [Google Scholar] [CrossRef]
- Ketokivi, M.; Turkulainen, V.; Seppälä, T.; Rouvinen, P.; Ali-Yrkkö, J. Why locate manufacturing in a high-cost country? A case study of 35 production location decisions. J. Oper. Manag. 2017, 49, 20–30. [Google Scholar] [CrossRef]
- Cong, L.W.; Li, Y.; Wang, N. Tokenomics: Dynamic adoption and valuation. Rev. Financ. Stud. 2021, 34, 1105–1155. [Google Scholar] [CrossRef]
- Myalo, A.S. Comparative analysis of ICO, DAOICO, IEO and STO. Case study. Financ. Theory Pract. 2019, 23, 6–25. [Google Scholar] [CrossRef]
- Momtaz, P.P. Entrepreneurial finance and moral hazard: Evidence from token offerings. J. Bus. Ventur. 2021, 36, 106001. [Google Scholar] [CrossRef]
- Giudici, G.; Adhami, S. The impact of governance signals on ICO fundraising success. J. Ind. Bus. Econ. 2019, 46, 283–312. [Google Scholar] [CrossRef]
- Fisch, C.; Masiak, C.; Vismara, S.; Block, J. Motives and profiles of ICO investors. J. Bus. Res. 2021, 125, 564–576. [Google Scholar] [CrossRef]

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Consistency Index | 0.00 | 0.44 | 1.00 | 1.63 | 2.30 | 3.00 | 3.71 | 4.47 | 5.23 |
| Constructs | Criteria | Sources |
|---|---|---|
| Finance | Issuance costs | [73,74] |
| Platform fees | [73] | |
| Transaction costs | [73] | |
| Laws and regulations | Place of issuance | |
| Government policy | ||
| Token security regulations | [74] | |
| Information disclosure transparency | [17] | |
| Risk | Financing schedule | |
| Token price fluctuation | [73] | |
| Reputation | [75] | |
| Shareholding proportion | ||
| Financing success rate | [76] | |
| Investors | Financing object | |
| Financing threshold | ||
| Online community | Online share of voice | [77] |
| Online public sentiment | ||
| Online trend |
| Experts | Dimension | |
|---|---|---|
| The Best Criterion | The Worst Criterion | |
| A | Risk | Investor |
| B | Risk | Online community |
| C | Finance | Online community |
| D | Risk | Investor |
| E | Risk | Online community |
| F | Finance | Online community |
| Expert | Finance | Laws and Regulations | Risk | Investor | Online Community |
|---|---|---|---|---|---|
| A | 4 | 2 | 1 | 7 | 6 |
| B | 2 | 2 | 1 | 4 | 5 |
| C | 1 | 3 | 2 | 4 | 7 |
| D | 3 | 2 | 1 | 6 | 5 |
| E | 2 | 2 | 1 | 3 | 4 |
| F | 1 | 2 | 2 | 3 | 6 |
| Exp. | Finance | Laws and Regulations | Risk | Investor | Online Community | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Issuance Costs | Platform Fees | Transaction Costs | Place of Issuance | Govern-ment Policy | Token Security Regulations | Information Disclosure Transparency | Financing Schedule | Token Price Fluctuation | Reputation | Shareholding Proportion | Financing Success Rate | Financing Object | Financing Threshold | Online Share of Voice | Online Public Sentiment | Online Trend | ||
| A | Best | Platform fees | Government policy | Financing success rate | Financing threshold | Online share of voice | ||||||||||||
| BO | 2 | 1 | 3 | 7 | 1 | 4 | 3 | 2 | 7 | 6 | 3 | 1 | 4 | 1 | 1 | 3 | 6 | |
| B | Best | Issuance costs | Government policy | Financing success rate | Financing threshold | Online share of voice | ||||||||||||
| BO | 1 | 2 | 3 | 6 | 1 | 3 | 2 | 2 | 3 | 5 | 3 | 1 | 6 | 1 | 1 | 3 | 5 | |
| C | Best | Issuance costs | Information disclosure transparency | Financing schedule | Financing threshold | Online share of voice | ||||||||||||
| BO | 1 | 2 | 4 | 5 | 2 | 4 | 1 | 1 | 5 | 7 | 4 | 2 | 5 | 1 | 1 | 3 | 5 | |
| D | Best | Platform fees | Government policy | Financing success rate | Financing threshold | Online share of voice | ||||||||||||
| BO | 2 | 1 | 4 | 6 | 1 | 4 | 2 | 2 | 6 | 5 | 3 | 1 | 3 | 1 | 1 | 2 | 5 | |
| E | Best | Issuance costs | Government policy | Financing success rate | Financing threshold | Online share of voice | ||||||||||||
| BO | 1 | 2 | 3 | 5 | 1 | 3 | 2 | 2 | 3 | 4 | 3 | 1 | 5 | 1 | 1 | 2 | 3 | |
| F | Best | Issuance costs | Information disclosure transparency | Financing schedule | Financing threshold | Online share of voice | ||||||||||||
| BO | 1 | 2 | 3 | 4 | 2 | 3 | 1 | 1 | 4 | 5 | 3 | 2 | 3 | 1 | 1 | 3 | 4 | |
| Expert | Finance | Laws and Regulations | Risk | Investor | Online Community |
|---|---|---|---|---|---|
| A | 5 | 6 | 7 | 1 | 3 |
| B | 3 | 3 | 5 | 2 | 1 |
| C | 7 | 5 | 3 | 4 | 1 |
| D | 4 | 5 | 6 | 1 | 2 |
| E | 2 | 2 | 3 | 2 | 1 |
| F | 6 | 4 | 2 | 3 | 1 |
| Exp. | Finance | Laws and Regulations | Risk | Investor | Online Community | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Issuance Costs | Platform Fees | Transaction Costs | Place of Issuance | Government Policy | Token Security Regulations | Information Disclosure Transparency | Financing Schedule | Token Price Fluctuation | Reputation | Shareholding Proportion | Financing Success Rate | Financing Object | Financing Threshold | Online Share of Voice | Online Public Sentiment | Online Trend | ||
| A | Worst | Transaction costs | Place of issuance | Token price fluctuation | Financing object | Online trend | ||||||||||||
| OW | 2 | 3 | 1 | 1 | 7 | 4 | 3 | 6 | 1 | 2 | 5 | 7 | 1 | 4 | 6 | 3 | 1 | |
| B | Worst | Transaction costs | Place of issuance | Reputation | Financing object | Online trend | ||||||||||||
| OW | 3 | 2 | 1 | 1 | 6 | 4 | 3 | 5 | 3 | 1 | 3 | 5 | 1 | 6 | 5 | 3 | 1 | |
| C | Worst | Transaction costs | Place of issuance | Reputation | Financing object | Online trend | ||||||||||||
| OW | 4 | 3 | 1 | 1 | 5 | 3 | 5 | 7 | 5 | 1 | 4 | 2 | 1 | 5 | 6 | 3 | 1 | |
| D | Worst | Transaction costs | Place of issuance | Token price fluctuation | Financing object | Online trend | ||||||||||||
| OW | 2 | 4 | 1 | 1 | 6 | 3 | 3 | 5 | 1 | 2 | 4 | 6 | 1 | 3 | 5 | 3 | 1 | |
| E | Worst | Transaction costs | Place of issuance | Reputation | Financing object | Online trend | ||||||||||||
| OW | 3 | 2 | 1 | 1 | 5 | 3 | 2 | 4 | 3 | 1 | 3 | 4 | 1 | 5 | 3 | 2 | 1 | |
| F | Worst | Transaction costs | Place of issuance | Reputation | Financing object | Online trend | ||||||||||||
| OW | 4 | 3 | 1 | 1 | 4 | 2 | 4 | 5 | 4 | 1 | 3 | 2 | 1 | 3 | 4 | 2 | 1 | |
| Objective | Construct | Weight | CR | CR Threshold | Criterion | Weight | CR | CR Threshold |
|---|---|---|---|---|---|---|---|---|
| Optimal token-financing solution | Finance | 0.301 | 0.018 | 0.373 | Issuance costs | 0.136 | 0.034 | 0.158 |
| Platform fees | 0.119 | |||||||
| Transaction costs | 0.046 | |||||||
| Laws and regulations | 0.209 | Place of issuance | 0.015 | 0.023 | 0.331 | |||
| Government policy | 0.090 | |||||||
| Token security regulations | 0.033 | |||||||
| Information disclosure transparency | 0.071 | |||||||
| Risk | 0.304 | Financing schedule | 0.092 | 0.025 | 0.373 | |||
| Token price fluctuations | 0.032 | |||||||
| Reputation | 0.019 | |||||||
| share-holding proportion | 0.048 | |||||||
| Financing success rate | 0.112 | |||||||
| Investor | 0.115 | Financing object | 0.020 | 0.000 | 0.000 | |||
| Financing threshold | 0.096 | |||||||
| Online community | 0.071 | Online share of voice | 0.044 | 0.020 | 0.216 | |||
| Online public sentiment | 0.018 | |||||||
| Online Trend | 0.008 |
| Criterion | Solution | Weight of Solution | CR | CR Threshold |
|---|---|---|---|---|
| Issuance costs | ICO | 0.069 | 0.045 | 0.211 |
| IEO | 0.040 | |||
| STO | 0.027 | |||
| Platform fees | ICO | 0.084 | 0.021 | 0.209 |
| IEO | 0.012 | |||
| STO | 0.023 | |||
| Transaction costs | ICO | 0.031 | 0.024 | 0.216 |
| IEO | 0.005 | |||
| STO | 0.010 | |||
| Place of issuance | ICO | 0.002 | 0.02 | 0.209 |
| IEO | 0.010 | |||
| STO | 0.003 | |||
| Government policy | ICO | 0.025 | 0.018 | 0.209 |
| IEO | 0.050 | |||
| STO | 0.014 | |||
| Token security regulations | ICO | 0.003 | 0.021 | 0.209 |
| IEO | 0.023 | |||
| STO | 0.007 | |||
| Information disclosure transparency | ICO | 0.035 | 0.016 | 0.209 |
| IEO | 0.025 | |||
| STO | 0.011 | |||
| Financing schedule | ICO | 0.016 | 0.015 | 0.216 |
| IEO | 0.062 | |||
| STO | 0.013 | |||
| Token price fluctuation | ICO | 0.002 | 0.019 | 0.216 |
| IEO | 0.013 | |||
| STO | 0.004 | |||
| Reputation | ICO | 0.016 | 0.018 | 0.209 |
| IEO | 0.006 | |||
| STO | 0.010 | |||
| Share-holding proportion | ICO | 0.005 | 0.015 | 0.216 |
| IEO | 0.033 | |||
| STO | 0.010 | |||
| Financing success rate | ICO | 0.057 | 0.017 | 0.209 |
| IEO | 0.042 | |||
| STO | 0.013 | |||
| Financing object | ICO | 0.010 | 0.018 | 0.209 |
| IEO | 0.007 | |||
| STO | 0.002 | |||
| Financing threshold | ICO | 0.066 | 0.019 | 0.227 |
| IEO | 0.021 | |||
| STO | 0.009 | |||
| Online share of voice | ICO | 0.008 | 0.018 | 0.227 |
| IEO | 0.032 | |||
| STO | 0.004 | |||
| Online public sentiment | ICO | 0.007 | 0.016 | 0.209 |
| IEO | 0.010 | |||
| STO | 0.002 | |||
| Online trend | ICO | 0.001 | 0.014 | 0.227 |
| IEO | 0.006 | |||
| STO | 0.002 |
| Solution | Weight | Rank |
|---|---|---|
| ICO | 0.439 | 1 |
| IEO | 0.397 | 2 |
| STO | 0.164 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou, C.-H.; Lin, C.-Y. Combining the MDM and BWM Algorithm to Determine the Optimal Crowdfunding Tokenization Solution for Digital Assets Market Startups. Systems 2022, 10, 87. https://doi.org/10.3390/systems10040087
Chou C-H, Lin C-Y. Combining the MDM and BWM Algorithm to Determine the Optimal Crowdfunding Tokenization Solution for Digital Assets Market Startups. Systems. 2022; 10(4):87. https://doi.org/10.3390/systems10040087
Chicago/Turabian StyleChou, Chien-Heng, and Chun-Yueh Lin. 2022. "Combining the MDM and BWM Algorithm to Determine the Optimal Crowdfunding Tokenization Solution for Digital Assets Market Startups" Systems 10, no. 4: 87. https://doi.org/10.3390/systems10040087
APA StyleChou, C.-H., & Lin, C.-Y. (2022). Combining the MDM and BWM Algorithm to Determine the Optimal Crowdfunding Tokenization Solution for Digital Assets Market Startups. Systems, 10(4), 87. https://doi.org/10.3390/systems10040087





