A Heterogeneous Information-Based Multi-Attribute Decision Making Framework for Teaching Model Evaluation in Economic Statistics

Abstract

A teaching model is a stable teaching procedure established under the guidance of certain teaching ideas or theories. As a methodological major in higher education, economic statistics cross various fields of natural science and social science, showing the characteristics of intersection, integration, and marginality. Therefore, this paper proposes a multi-attribute decision-making (MADM) framework for teaching model evaluation based on heterogeneous information. First, the attribute system of competition–academic research–master of knowledge–practical operation (CAMP) is constructed. Second, heterogeneous information is introduced in the process of teaching model evaluation; Third, a weight determination method based on a trust relationship of the fuzzy–social network is proposed, which provides a better solution to the problem of decision makers’ (DMs’) weight allocation in teaching model evaluation. Furthermore, a combined attribute weights determination method under an intuitionistic fuzzy number is constructed, which improves the shortcomings of the weight method in teaching model evaluation. Finally, through empirical research and stability analysis, the proposed evaluation framework has good effectiveness and feasibility, and policy suggestions for improvements to the economic statistical teaching model are then proposed.

1. Introduction

As a bridge between teaching theory and teaching practice, teaching models have always been an important research topic in educational circles. A teaching model is a plan that can be used to set up courses, design teaching materials, guide classes, or improve teaching in other situations. A teaching model has the dual function of practice and theory. In practice, teaching models can guide teaching activities, estimate teaching results and improve teaching methods. In theory, it can not only encourage the educator to accept the theoretical knowledge but also further promote the development of teaching theory [1,2]. A teaching model plays an important role in the educational process. Therefore, universities and scholars around the world have never interrupted the exploration of this theme [3]. As early as the 1970s, scholars carried out research on teaching models, producing the teaching model of Gagne, the teaching model of Taba, and other achievements. The teaching model of Gagne, as a representative result of this period, combines scientific psychology with education and has been adopted and recognized by educators in many countries around the world. However, this model ignores the organization of teaching content. In addition, this model focuses on the learning process but ignores the teaching process. Since then, the improvement and development of teaching models have been continuously considered [4,5]. Especially since the 21st century, with the further improvement of higher education, many representative achievements have emerged, such as the conceived design implement operate (CDIO) engineering teaching model [6], outcomes-based education (OBE) teaching model [7], and flipped classroom (FC) teaching model. For a long time, many of the above teaching models have made important contributions to the development of higher education and talent training [8].

Corresponding to the rapid development of various teaching models, the evaluation of teaching models is gradually attracting the attention of scholars [9,10]. It is of great significance to carry out the evaluation of teaching models to explore the teaching effects, study their problems and deficiencies, and even promote the development of teaching [11,12]. As far as economic statistics is concerned, there are no systematic research results for teaching model evaluation. The details will be covered in the next section. This is the main motivation for us to carry out this study.

The purpose of this paper is to propose a MADM framework for statistical teaching model evaluation. First, the relationship between statistical capacity and teaching activities is analyzed. The CAMP multi-attribute system is constructed from the four aspects of competition, academic research, mastery of knowledge, and practical operation to provide more representative attributes for the teaching model evaluation of economic statistics. Second, heterogeneous information, including real numbers, linguistic numbers, interval numbers, and intuitionistic fuzzy numbers, is introduced to solve the multidimensional, systematic, and complex characteristics of the evaluation of the statistical teaching model as well as the problem of the diversification of evaluation information [13]. When there are multiple types or properties of attributes in the evaluation attribute system, heterogeneous information can be more targeted to select the appropriate collection form, which has been widely used in multi-attribute problems and group decision-making to solve practical problems such as supplier selection and personnel assessment [14], and then, the fuzzy–social network is used to determine the weights of DMs in this paper [15,16]. As a method to measure the trust relationship between DMs, the fuzzy–social network can indirectly reflect the importance of members [17], so it is widely used in multi-attribute evaluation, MADM problems, and other issues [18]. Finally, in the aspect of determining attribute weights, the entropy weight method and the AHP weight method are combined to construct subjective and objective combined weight methods. To avoid the teaching model, the evaluation results of persuasion are not high or unstable in this way.

The contribution of this paper can be concluded as follows: (1) On the basis of analyzing the relationship between statistical capacity and teaching activities, a CAMP multi-attribute system is constructed to provide more representative criteria for teaching model evaluation of economic statistics. (2) Heterogeneous information is introduced into the evaluation of the teaching model to solve the problem of diversified evaluation information by combining the multidimensional, systematic, and complex characteristics in the evaluation of the teaching model of economic statistics. (3) This paper proposes a method to determine DMs’ weights based on the trust relationship strength of the fuzzy–social network. This method fully considers the trust relationship between DMs and can better solve the problem of peer evaluation to determine the weight of DMs. (4) Combining the objective weight method of the intuitionistic fuzzy entropy weight method with the subjective weight method of the analytic hierarchy process, a combined weight method is constructed to determine the attribute weights to further provide a more reliable tool for teaching model evaluation.

The rest of this paper is organized as follows: In Section 2, we summarize the existing teaching model evaluation methods and further point out the shortcomings of existing research. In Section 3, we construct the CAMP multi-attribute system and introduce the basic concept of heterogeneous information and fuzzy–social network. The entropy–AHP method is proposed in Section 4. The MADM framework of the teaching model evaluation based on heterogeneous information is also proposed in this section. Section 5 carries out the actual teaching model evaluation according to the framework of this paper. Furthermore, the stability is analyzed in this section, which proves the stability of the proposed MADM framework. In Section 6, policy recommendations based on the results are put forth. Finally, Section 7 summarizes this paper and discusses the focus of future research.

2. Literature Review

In this section, we summarize the existing teaching model evaluation methods. Furthermore, we point out the shortcomings of existing methods in the evaluation of the economic statistics teaching model. Related research can be traced back to the end of the 19th century; after long-term development and multiple stages of evolution, numerous studies have emerged. The representative models include the Tyler model [9], Context–Input–Process–Product (CIPP) evaluation model [10,11], Objective Dissociation evaluation model, Response evaluation model [12,19] and the student’s evaluations of university teaching (SETs) [20,21].

As shown in

Table 1. Comparison of some evaluation methods.

Model	Merits	Demerits	Reference
Tyler model	Integrate social needs into evaluation Strong reference value	The link between teaching process and results is ingroed Overly result-oriented	[9]
CIPP	Highly systematic	Lack of value judgment in the results Process are complicated	[10,11]
Response evaluation	Strong operability Simple process	Difficult to collect quantitative data	[12,19]
SETs	Emphasis on student evaluation	Unstable evaluation information	[20,21]

, the Tyler model highlights the importance of social needs in the evaluation process and creates a precedent for teaching model evaluation research. However, the Taylor model ignores the intermediate link because it pays too much attention to the evaluation of results [9]. CIPP model emphasizes the improvement of the teaching model through evaluation and evaluates the teaching model from the four aspects of context, input, process, and product to achieve a multilevel and systematic evaluation [10]. However, the CIPP model pays too much attention to descriptive evaluation, which makes the evaluation result lack value judgment, and the evaluation process and steps are complicated [11]. The response evaluation model is based on actual problems of participants in educational activities and carries out evaluation around the educational practitioners. This model mainly adopts the natural observation method and discussion method, so it is difficult to collect quantitative data directly [12,19]. SETs are used to evaluate the teaching effect of teachers. Its remarkable feature is that students participate in the evaluation of teaching quality as the main evaluators [20]. However, the evaluation information of students is easily affected by subjective factors, so it lacks certain stability and reliability [21]. Their characteristics are shown in Table 1.

However, the existing methods are difficult to be directly applied to the evaluation of the statistics teaching model. As a methodology, economic statistics is the profession of collecting, analyzing, presenting, and interpreting data. It is widely used in economics, business, and finance [22,23]. In the teaching process, students are required not only to have a solid theoretical foundation in mathematics and econometrics but also to have enough practical ability in data processing and analysis [24]. The teaching process involves both the transmission of theoretical knowledge and the cultivation of practical skills. Because of this characteristic, in recent years, the teaching model of economic statistics in North America, Britain, Japan, and other countries has paid more attention to the cultivation of data collection, processing, and analysis and has strengthened the statistical practice in the teaching process [25]. Under such a trend, statistical educators in China have actively discussed the research and innovation of teaching models, and numerous achievements of statistical teaching models have emerged [26].

Existing methods have shortcomings when applied to the evaluation of the teaching model of economic statistics:

(1)

As an interdisciplinary and borderline major, statistical teaching has its own uniqueness [23,24]. On the one hand, it should not only be based on the teaching of knowledge theory but also pay attention to the training of practical skills. On the other hand, we should pay attention not only to the progress of the teaching process but also to the acquisition of teaching results. Therefore, the evaluation of the teaching model of economic statistics should not be solely guided by the classroom teaching effect or practical operation ability but should also be fully integrated into the evaluation process. However, the existing methods generally lack thinking about the nature and characteristics of different majors. In particular, the understanding and embodiment of the characteristics of the statistics specialty are insufficient, so it is difficult to directly evaluate the teaching model of economic statistics.

(2)

The teaching model of economic statistics presents the characteristics of multidimensiond, systematicness, and complexity [25,26]. In regard to the content, it involves the whole process of teaching, from theoretical knowledge to practical skills. With regard to form, it involves all-round cultivation from classroom teaching to post guidance. On the subject, it involves the diverse roles of teachers, students, and employers. Therefore, in the evaluation, the above multiple dimensions should be considered comprehensively to construct the indicator system. At the same time, the system includes objective facts, subjective feelings, and expected conditions with different properties, different sources, and even different forms of diversified attributes. In addition, especially in the face of subjective feelings, expected conditions, and other types of attributes, evaluators often have difficulty directly providing accurate evaluation information and even appear in the special situation of hesitation between several options or scores. The evaluation information in existing methods appears mainly in the single form of qualitative data or real numbers, which cannot meet the needs of diversified information collection in the evaluation of statistical teaching models and can adversely affect the effectiveness of the evaluation results.

(3)

As a kind of peer evaluation, the educators usually participate in the process of teaching model evaluation. Due to differences in professional background, knowledge level, qualifications, and work experience among different DMs, different members should not be treated equally in the evaluation process. Especially when there are opinion leaders or industry authorities among the DMs, the opinions of other members will be influenced to some extent by such members. At this point, if the method of equal authority is adopted, part of the authoritative information will be covered up, while the method of empowerment by the organizer is difficult to objectively grasp the relative relationship between DMs. Therefore, how determining the weight of DMs is important for the peer evaluation of teaching model evaluation.

(4)

The weight determination method of attributes is single, and the persuasiveness and stability of the evaluation results need to be improved. The weight structure has different effects on the evaluation results of the teaching model. In the existing methods, the weight of evaluation attributes is simply determined by the subjective weight method (such as the analytic hierarchy process and Delphi method) or objective weight methods (such as the entropy weight method and data envelopment analysis method) [11,27]. However, these two methods have shortcomings in the evaluation of teaching models: the subjective weighting method mainly relies on experts to judge the importance of attributes, but experts do not consider their actual value in this process, so it is difficult to reflect the real information of evaluation attribute [28]. At the same time, the teaching model evaluation results in too many subjective factors and lacks convincing results. The objective weighting method judges the importance of attributes according to their actual value, and the weight structure changes with the values of an attribute, so it is not stable enough when evaluating the teaching model.

3. Materials and Methods

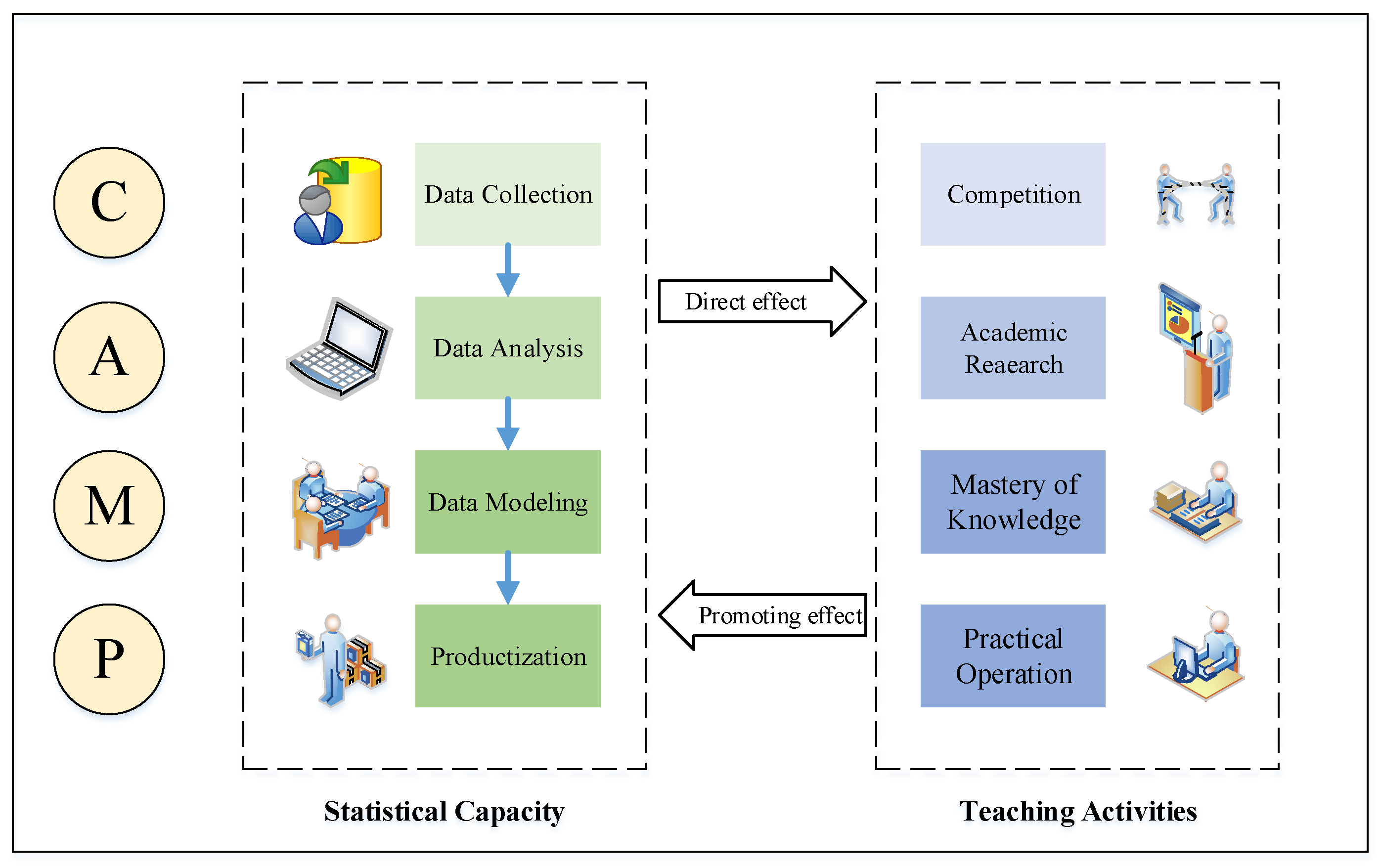
3.1. Multi-Attribute System of CAMP

With the rapid development of the era of big data and increasingly mature information technology, the status and role of data are also increasingly emerging. Combined with the current background and the demand for talent, students majoring in economic statistics should master statistical abilities ranging from data collection, analysis, and modeling to productization. A good statistical teaching model should integrate the training of the above statistical ability into the teaching process. Therefore, the above statistical ability has a direct effect on teaching activities.

At present, combined with discipline competition, academic research can further improve students’ mastery of knowledge and practical operation abilities. This is one of the important characteristics of the teaching practice of economic statistics in China. Teachers carry out teaching activities around the above four aspects and combine theoretical teaching with practical training. This can further promote the cultivation of students’ statistical ability, that is, produce a ‘promoting effect’.

Based on this actual background, this paper further puts forward the teaching model evaluation attribute system, including four aspects of CAMP. In the evaluation process, emphasis is placed on integrating the cultivation of statistical capacity into this system, teaching effect is taken as the evaluation basis, and the cultivation of statistical capacity is taken as the evaluation scale. The relationship between the statistical capacity and teaching activities is shown in Figure 1.

The specific connotations of the four aspects of CAMP are as follows:

C: Competition. This refers to discipline competitions related to economic statistics. Through participating in competitions, students can practice their data collection, statistical analysis, and modeling abilities. A good teaching model should pay attention to the cultivation of students’ statistical ability and thinking. The cultivation effect will also be reflected in the competition.

A: Academic Research. This refers to students’ participation in the reading, research, and creation of academic papers on economic statistics. Through academic research, students can gain a deeper grasp of statistical methods and understand the development frontier. This is an important embodiment of students’ ability.

M: Mastery of knowledge. That is, students’ mastery of teaching content and professional knowledge. It is the direct expression of the teaching effect.

P: Practical operation. Students participate in statistical practice and further operation, which is the most critical reflection standard of the teaching effect.

According to the above four aspects, we evaluate the training effect of statistical capacity under different teaching models and build an evaluation attribute system. Since the system is composed of attributes with different properties, we select heterogeneous information to collect corresponding evaluation information. The results are listed in

Table 2. CAMP multi-attribute system.

Aspect	Attribute	Form of Data	Reference
Competition	Cultivation of competitive atmosphere	Linguistic number	[23,24]
	Skills of competition	Real number	[26]
Academic Research	Creation of academic atmosphere	Linguistic number	[24,26]
	Academic level	Real number	[25,29]
Mastery of knowledge	Understanding of knowledge	Interval number	[26,30]
	Innovation ability	Interval number	[24,25]
Practical Operation	Ability of practical operation	Intuitionistic fuzzy number	[25]
	Professional skills	Intuitionistic fuzzy number	[26,29]

.

(1)

Competition

Cultivation of competitive atmosphere (C₁). This attribute is used to measure and reflect the cultivation status of students’ competitive atmosphere [23,24]. Due to the subjectivity of the content of this attribute, we adopt the form of linguistic numbers to collect its evaluation information.

Skills of competition (C₂). It refers to students’ core professional qualities or skills. For students majoring in economic statistics, competitive ability includes data collection ability, the ability to analyze data with models, and the ability to use relevant statistical software [26]. This attribute uses the form of real numbers.

(2)

Academic Research

Creation of academic atmosphere (C₃). This attribute reflects the ability to create an academic atmosphere [24,26]. C₃ makes it difficult to give quantitative information directly, so it adopts the form of linguistic numbers to collect the information of the evaluator.

Academic level (C₄). It is the direct embodiment of training quality, which used to measure the academic level of students [25,29]. It is objectively reflected by real numbers.

(3)

Master of Knowledge

Understanding of knowledge (C₅). It refers to students’ understanding and mastery and reflects students’ knowledge understanding and mastery of economic statistics [26,30]. It also has the characteristics of subjectivity, and it is often difficult for evaluators to give accurate evaluation information. Thus, C₅ adopts the form of interval numbers.

Innovation ability (C₆). Education involves spreading and developing knowledge. This attribute is used to reflect students’ innovation ability after receiving knowledge [24,25]. C₆ also has the characteristics of subjectivity in the evaluation information, so the form of interval numbers is used to collect the evaluation information of evaluator.

(4)

Practical operation

Ability of practical operation (C₇). It refers to the level of students’ practical ability in statistical technology and method application [25]. It is often difficult for evaluator to give accurate evaluation information. The information of C₇ is collected in the form of intuitionistic fuzzy numbers.

Professional skills (C₈). The attribute measures students’ professional skills [26,29]. Considering that it is difficult to give quantitative information, the evaluation information is collected in the form of intuitionistic fuzzy numbers.

3.2. Related Concepts of Heterogeneous Information

(1)

Interval Number

Definition 1.

Let$x^L$be the lower bound of the interval, and let$x^U$be the upper bound of the interval. Then, the interval number I is of the form

$$I=[x^L,x^U]$$

(1)

where$x^L<x^U$. When the interval number is used to collect evaluation information, the evaluation information of an evaluation object i and indicator j is in the form of$I_{ij}=[x_{ij}^L,x_{ij}^U]$, indicating that the performance of the evaluation object in indicator j is between the lower$x_{ij}^L$and upper$x_{ij}^U$.

The interval number applies to subjective evaluation information that is difficult to directly quantify. The form of the interval can provide relatively sufficient evaluation choices for evaluators, and to a certain extent, it can avoid the indecision of evaluators in the evaluation process.

(2)

Real Number

Definition 2.

By definition 1, the real numbers can be thought of as special interval numbers. When $x^L=x^U$, the interval number I is a real number.

When real number $R_{ij}$ is used to represent evaluation information, a truthful number represents the performance of an evaluation object i under indicator j. The data form of real number are suitable for quantitative indicators and can realize the efficient collection of evaluation information through accurate numbers.

(3)

Linguistic Number

Definition 3.

Set $S=\left\{S_{\alpha }\right|\alpha =0,1,2,\cdots ,k-1\}$ as an ordered collection of linguistic numbers.

where k is odd and represents the $\alpha$th language variable of set S. The representative variable is k = 6. At this point, we can obtain the set S = {S₀, S₁, S₂, S₃, S₄, S₅, S₆} = {very poor, relatively poor, poor, medium, good, fairly good, very good} [31]. Linguistic numbers are also suitable for indicators that are difficult to directly quantify, but linguistic numbers are more in line with the characteristics of language and allow the evaluator to give evaluation information more intuitively [32].

(4)

Intuitionistic Fuzzy Number

Definition 4.

Let$X=\left\{x_1,x_2,\cdots ,x_n\right\}$be a fixed set. Then, an intuitionistic fuzzy set (IFS) A on set X is [33]

$$A=\left\{〈x,{\mu }_A\left(x\right),v_A\left(x\right)〉\left|x\in X\right.\right\}$$

(2)

where${\mu }_A(x)$and$v_A(x)$are the membership degree and nonmembership degree of element x in X belonging to A, respectively, and${\mu }_A\in [0,1]$,$v_A\in [0,1]$.$\forall x\in X$,$0\le {\mu }_A(x)+{\nu }_A(x)\le 1$.

${\pi }_A(x)=1-{\mu }_A(x)-{\nu }_A(x)$ is called the hesitation that element x of set X belongs to A. Obviously, for, $\forall x\in X$, ${\pi }_A(x)\in [0,1]$. The intuitionistic fuzzy set A on X can be regarded as the set of all intuitionistic fuzzy numbers, denoted as IFS(X). For convenience, intuitionistic fuzzy numbers (IFNs) are usually expressed as $\alpha =\left({\mu }_{\alpha },{\nu }_{\alpha }\right)$, ${\mu }_{\alpha }\in [0,1]$, $v_{\alpha }\in [0,1]$, ${\mu }_{\alpha }+v_{\alpha }\in [0,1]$, ${\mu }_{\alpha }(x)+{\nu }_{\alpha }(x)+{\pi }_{\alpha }(x)=1$.

In this paper, the three data forms of interval numbers, real numbers, and linguistic numbers are finally converted into intuitionistic fuzzy numbers. An important reason for this is that intuitionistic fuzzy numbers have been widely studied by scholars in the field of evaluation and decision-making since they were put forward [34,35]. At present, relatively mature research results and effective method systems have been obtained on the distance measure, integration operator, and sorting method of intuitionistic fuzzy numbers, and the maturity of this method is relatively high [36,37]. Using this data form will further ensure the effectiveness of the follow-up work in the evaluation of teaching models.

3.3. Conversion Methods of Heterogeneous Information

(1)

Conversion between interval number and intuitionistic fuzzy number

In the process of transforming the interval number to an intuitionistic fuzzy number, the original value of the interval number should be normalized first. Any interval number $I_{ij}$ is treated as follows:

$$\begin{array}{l}{I}_{ij}^{*}=[{\overline{x}}_{ij}^L,{\overline{x}}_{ij}^U]\\ {\overline{x}}_{ij}^L=\frac{x_{ij}^L}{\sqrt{{\displaystyle \sum _{i=1}^m[{(x_{ij}^L)}^2+{(x_{ij}^U)}^2]}}}\\ {\overline{x}}_{ij}^U=\frac{x_{ij}^U}{\sqrt{{\displaystyle \sum _{i=1}^m[{(x_{ij}^L)}^2+{(x_{ij}^U)}^2]}}}\end{array}$$

(3)

After obtaining the interval number after normalization, we can construct the corresponding intuitionistic fuzzy number. According to the method of [38], we can obtain the corresponding intuitionistic fuzzy number according to the following formula:

$$\begin{array}{l}{a}_{ij}=\left({\mu }_{ij},{\upsilon }_{ij},{\pi }_{ij}\right),i=1,2,\cdots ,m,j=1,2,\cdots ,n,\\ {\mu }_{ij}={\overline{x}}_{ij}^L,\\ {\upsilon }_{ij}=1-{\overline{x}}_{ij}^U,\\ {\pi }_{ij}={\overline{x}}_{ij}^U-{\overline{x}}_{ij}^L,\end{array}$$

(4)

(2)

Conversion between real numbers and intuitionistic fuzzy numbers

Normalization is also needed before the real number is converted to an intuitionistic fuzzy number. For any real number $R_{ij}^{*}$, the normalization formula is as follows:

$$R_{ij}^{*}=\frac{R_{ij}}{\sqrt{{\displaystyle \sum _{i=1}^m{R}_{ij}^2}}}$$

(5)

where $R_{ij}$ is the original evaluation indicator value. Furthermore, the real numbers can be converted into intuitionistic fuzzy numbers according to the following formula, and the hesitation of the intuitionistic fuzzy numbers obtained after the conversion is 0:

$$\begin{array}{l}{a}_{ij}=\left({\mu }_{ij},{\upsilon }_{ij},{\pi }_{ij}\right),i=1,2,\cdots ,m,j=1,2,\cdots ,n,\\ {\mu }_{ij}=R_{ij}^{*},\\ {\upsilon }_{ij}=1-R_{ij}^{*},\\ {\pi }_{ij}=0,\end{array}$$

(6)

(3)

Conversion between linguistic numbers and intuitionistic fuzzy numbers

This paper adopts the research results of [38] on the conversion method between linguistic numbers and intuitionistic fuzzy numbers.

Table 3. Conversion between linguistic numbers and intuitionistic fuzzy numbers.

Linguistic Number	Intuitionistic Fuzzy Number
very good	(0.90, 0.10, 0.00)
good	(0.75, 0.20, 0.05)
medium	(0.50, 0.45, 0.05)
bad	(0.35, 0.60, 0.05)
very bad	(0.10, 0.90, 0.00)

lists a set of linguistic numbers that can be converted to intuitionistic fuzzy numbers. This paper will use the process in the table to transform the linguistic number.

3.4. Fuzzy–Social Network

Social network refers to a stable network system composed of social relationships between individuals [15,16]. As shown in Figure 2, the nodes (A,B,C,D,E) represent individuals in the network (Individuals can be experts, DMs, organizations, or countries), and edges represent trust relationships between individuals. Directed edges between nodes indicate the direction of the trust relationship between individuals. Fuzzy–social network uses fuzzy numbers to express the degree of the trust relationship.

Hesitant probabilistic fuzzy trust–social network (HPFT–SN) proposed by [18] is mainly used in this paper. Some basic concepts are shown below.

Definition. Let $h(p_{AB})=\cup \{({\gamma }^{\lambda }|p^{\lambda }),\lambda =1,2,\cdots l\}$ be a hesitant probabilistic fuzzy trust (HPFT) function. The function indicates the trust relationship from A to B.

Where, $({\gamma }^{\lambda }|P^{\lambda })$ represents a set of trust relationship strengths (TRSs). l refers to the number of TRSs in $h(P_{AB})$. ${\gamma }^{\lambda }$ represents the strength of the trust relationship from A to B, ${\gamma }^{\lambda }\in [0,1]$. The larger ${\gamma }^{\lambda }$ is, the stronger strength. Any ${\gamma }^{\lambda }$ in $h(P_{AB})$ must satisfy ${\gamma }^{\lambda }<{\gamma }^{\lambda +1}$: that is, the TRSs are arranged in ascending order. $P^{\lambda }$ is the probability value corresponding to ${\gamma }^{\lambda }$, and $P^{\lambda }\in [0,1]$, ${\displaystyle \sum P^{\lambda }=1}$.

Definition. Let $h(p_i)=\cup \left\{\left({\gamma }_i{}^{{\lambda }_i}|P_i{}^{{\lambda }_i}\right),{\lambda }_i=1,2,\cdots ,l_i\right\},i=1,2,\cdots ,n$ be a set of HPFT functions, ${\theta }_i$ be the corresponding weights, The definition of the HPFT geometric weighted average integration (HPFT-GWA) operator is as follows:

$$HPFT-GWA\left\{h\left(p_i\right)\right\}=\cup \left\{{\displaystyle \prod _{i=1}^n{\left({\gamma }_i{}^{{\lambda }_i}\right)}^{{\theta }_i}}{|}^{\raisebox{1ex}{${\displaystyle \sum _{i=1}^n{p}_i{}^{{\lambda }_i}}$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}\right\}$$

(7)

where, $l_i$ refers to the number of TRSs in different HPFT functions $h(p_i)$, ${\lambda }_i=1,2,\cdots ,l_i$. n is the number of $h(p_i)$.

4. A Heterogeneous Information-Based MADM Framework

4.1. Fuzzy–Social Network for Determining DMs’ Weights

In the fuzzy–social network, due to the different degrees of direct and indirect connection between DMs, the centrality of each DM is usually used to determine the weights. The method proposed in [18] is difficult to achieve the differential allocation of DMs’ weights; that is, it is difficult to reflect the status difference of DMs in the social network. In order to better solve the problem, this paper further proposes a method to determine the DMs’ weights based on the degree of centrality.

(1)

Compute the degree centrality $C\left(e_j\right)$ of DM_j.

The HPFT-GWA aggregation operator introduced in Section 2 is used to calculate the degree of centrality of each DM. Let $h\left(p_{ij}\right)$ represent the trust function of i to j, then the degree centrality of j is:

$$C\left(e_j\right)={\displaystyle \prod _{i=1,i\ne j}^{n}h\left(p_{ij}\right)}=\cup \left\{{\displaystyle \prod _{i=1,i\ne j}^n{\left({\gamma }_i{}^{{\lambda }_i}\right)}^{\frac{1}{n}}}{|}^{\raisebox{1ex}{${\displaystyle \sum _{i=1,i\ne j}^n{p}_i{}^{{\lambda }_i}}$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}\right\}$$

(8)

where, n refers to the number of DMs that have a trust relationship to DM_j throughout the social network.

(2)

Obtain the degree of trust $TD(e_j)$.

$$TD(e_j)={\displaystyle \sum _{{\lambda }_i}^{l_i}\left[\left({\displaystyle \prod _{i=1,i\ne j}^n{\left({\gamma }_i{}^{{\lambda }_i}\right)}^{\frac{1}{n}}}\right)\ast \left(\raisebox{1ex}{${\displaystyle \sum _{i=1,i\ne j}^n{p}_i{}^{{\lambda }_i}}$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\right)\right]}$$

(9)

(3)

Compute the total degree of trust $TD$.

$$TD={\displaystyle \sum _{j=1}^{m}TD(e_j)}$$

(10)

where, m refers to the number of DMs in the social network.

(4)

Determining the weights of DMs.

The weight of DM j can be obtained by the equation:

$$w_j=\frac{TD(e_j)}{TD}$$

(11)

It can be seen from the above formula that in social networks, DMs with higher trust (such as senior scholars and industry authorities, etc.) have a higher corresponding weight. In the field of higher education, such people tend to have more work experience, a deeper understanding of different teaching models, and more accurate evaluation, so their corresponding weight should be larger. Conversely, the less qualified members of the expert group are less trusted and ultimately less weighted. This is closely related to our practical problems, which is conducive to solving the weight problem in the peer evaluation of teaching model evaluation, avoiding the loss of important evaluation information caused by an equal weight of each expert, and the problem that the important relationship between DMs cannot be objectively reflected due to artificial weight assignment.

4.2. Entropy–AHP Method for Determining Attribute Weights

In the field of intuitionistic fuzzy entropy weight methods, there are many construction methods and research achievements. This solved the problem in which a group of intuitionistic fuzzy sets could not be distinguished when the membership and nonmembership degrees were the same, and the hesitation degrees were the same [37,39].

Furthermore, this paper proposes a combined weight determination method based on intuitionistic fuzzy entropy and the AHP method. The specific steps are as follows:

(1)

Determine the objective weight $w^o$ of attribute

In the first step, according to the expert’s intuitionistic fuzzy integrated evaluation information, the intuitionistic fuzzy entropy of each attribute is calculated. For any $A=\{[x_i,u_A(x_i),v_A(x_i)|x_i\in X]\}$, intuitionistic fuzzy entropy $E(A)$ is calculated as follows:

$$E(A)=\frac{1}{2m}{\displaystyle \sum _{i=1}^n\left[\frac{1-\max (u_A(x_i),v_A(x_i))}{1-\min (u_A(x_i),v_A(x_i))}+{\pi }_A(x_i)\right]}$$

(12)

In this formula, m refers to the number of fuzzy numbers in A.

The second step is to further calculate the objective weight of each attribute according to the intuitionistic fuzzy entropy. The method is as follows.

$$w_j^o=\frac{1-E^2(a_j)}{{\displaystyle \sum _{j=1}^m[1-E^2(a_j)]}}$$

(13)

(2)

Determine the subjective weight $w^s$ of attribute

The analytic hierarchy process (AHP) is a commonly used method to determine the attribute weights, which can flexibly compare the importance of different attributes through stratification and comparison of important relationships. This paper uses a one-to-five scale to compare the importance. As this method is widely used, the specific steps are not shown in this paper.

(3)

Determine the combined weights $w^c$ of attribute

By combining the objective weight $w^o$ and the subjective weight $w^s$, we can finally obtain the combined weight $w_j^c$ of each attribute.

$$w_j^c=\alpha w_j^o+(1-\alpha )w_j^s$$

(14)

where $\alpha$ is the weight adjustment coefficient, $0\le \alpha \le 1$, $0\le w_j^c\le 1$, and ${\displaystyle \sum _{j=1}^m{w}_j^c=1}$.

4.3. Aggregation Operator and Score Function of Heterogeneous Information

In the MADM process, it is necessary to aggregate the evaluation information of each evaluator to realize the overall understanding of teaching models. There are many kinds of aggregation operators in intuitionistic fuzzy sets [40]. This includes the intuitionistic fuzzy weighted arithmetic average (IFWAA) operator, intuitionistic fuzzy generalized ordered weighted average (IFGOWA) operator, intuitionistic fuzzy set weighted arithmetic average (FIFWAA) operator, and corresponding operators [41,42]. Based on the existing research on aggregation operators, it is not difficult to find that there are various types in the intuitionistic fuzzy sets environment, so different operators have their own emphases and characteristics.

As the evaluation information in this study has the characteristics of diversity in form, although it is uniformly transformed into an intuitionistic fuzzy number, the evaluation information is given subjectively by the evaluators. Therefore, to ensure the original level of each attribute as far as possible and reduce the interference of aggregation operators to the results, the intuitionistic fuzzy weighted arithmetic average (IFWAA) operator is selected as the aggregation operator in this study, and the specific definition is as follows:

Definition 5.

Suppose${\alpha }_j=<{\mu }_j,{\nu }_j>(j=1,2,\cdots ,n)$is the set of intuitionistic fuzzy numbers. The intuitionistic fuzzy arithmetic weighted average (IFAWA) operator is defined as follows:

$$\mathrm{IFAWA}({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)=\underset{j=1}{\overset{n}{\Sigma }}{\omega }_j{\alpha }_j=〈1-{\displaystyle \prod _{j=1}^n{(1-{\mu }_j)}^{w_j},}{\displaystyle \prod _{j=1}^n{({\nu }_j)}^{w_j}}〉$$

(15)

where ${\omega }_j$ refers to the corresponding weights of each ${\alpha }_j$ in the set.

To numerically calculate or compare the evaluation information of intuitionistic fuzzy numbers, distance measures or score functions are two important tools. In this paper, the score function of an intuitionistic fuzzy number is used to calculate the attribute values.

Definition 6.

Suppose$\alpha =(\mu ,\nu )$is an intuitionistic fuzzy number. Then, the scoring function$\mathrm{S}(\alpha )$can be calculated as follows:

$$\mathrm{S}(\alpha )=\mu -\nu$$

(16)

According to the value of the intuitionistic fuzzy number $\alpha =(\mu ,\nu )$, we can obtain $\mathrm{S}(\alpha )\in [-1,1]$.

For any two intuitionistic fuzzy numbers ${\alpha }_1=({\mu }_1,{\nu }_1)$ and ${\alpha }_2=({\mu }_2,{\nu }_2)$, the order relation can be defined according to the score function:

$$\left\{\begin{array}{c}\mathrm{S}({\alpha }_1)>\mathrm{S}({\alpha }_2),\\ \mathrm{S}({\alpha }_1)=\mathrm{S}({\alpha }_2)\cap h({\alpha }_1)>h({\alpha }_2),\\ \mathrm{S}({\alpha }_1)=\mathrm{S}({\alpha }_2)\cap h({\alpha }_1)=h\left({\alpha }_2\right),\end{array}\begin{array}{c}\\ \\ \end{array}\right.\begin{array}{c}{\alpha }_1>{\alpha }_2\\ {\alpha }_1>{\alpha }_2\\ {\alpha }_1={\alpha }_2\end{array}$$

(17)

where $h\left(\alpha \right)$ is the exact function of any intuitionistic fuzzy number $\alpha =(\mu ,\nu )$, and its calculation method is

$$h(\alpha )=\mu +\nu$$

(18)

4.4. MADM Framework for Statistical Teaching Model Evaluation

This paper evaluates teaching models based on heterogeneous information and constructs the corresponding MADM framework according to the following steps, as shown in Figure 3.

Step 1: Information collection. According to the CAMP multi-attribute system constructed in Table 1, the evaluation information of each evaluator is collected in accordance with the corresponding data form.

Step 2: Information conversion. According to the conversion methods in Equations (3)–(6) and Table 2, different forms of heterogeneous information are transformed into the intuitionistic fuzzy number form.

Step 3: Determine the weights of DMs and attribute. According to the social network relationship between DMs, we can calculate their weight by using Equations (8)–(11), and then, Equations (12)–(14) are used to determine the combined weights, and the subjective weight and objective weight of attribute are determined. Finally, the combination of subjective weight and objective weight is used as the attribute weights.

Step 4: Information aggregation. On the premise of obtaining the evaluators and evaluation information, the IFWAA aggregation operator shown in Equation (15) can be used to summarize the evaluation information of each evaluator into a group evaluation information matrix.

Step 5: Determine the MADM results. According to the aggregated data of Step 4, the MADM results are determined by Equations (16)–(18). According to the evaluation results, the effects, advantages, and disadvantages of different teaching models are further analyzed.

Step 6: Analysis and conclusion. According to the evaluation results, the advantages and disadvantages of different teaching models are analyzed, and suggestions are provided for improvement and perfection.

5. Case Study: Evaluation of Teaching Models in Economic Statistics

5.1. Backgrounds of Teaching Models

In this Section, four teaching models that are popular and common in the economic statistics field in China are introduced as alternatives: CDIO, OBE, flipped classroom, and blended. Information about these four models follows.

(1)

CDIO teaching model

The CDIO teaching model was proposed by the MIT faculty of Aeronautics and Astronautics. This model takes the life cycle of products as the carrier and further systematically cultivates students’ comprehensive qualities such as professional knowledge, personal ability, and professional ability based on the design of products. It aims to combine the imparting of theoretical knowledge with the cultivation of practical ability and integrate it into the teaching process [43]. However, the CDIO model is regarded as a type of elite education that has relatively high requirements on the professional ability of teachers and the basic level of students.

(2)

OBE teaching model

Spady defined the OBE teaching model as ‘clearly, focusing and organizing the education system around ensuring that students receive the experience to achieve substantial success in future life’ [44]. That is, the OBE teaching model focuses on the expected learning output and plans students’ training programs and teaching contents according to the ability and level that students should achieve upon graduation. Therefore, it changes the orientation of education from content-based to student-oriented, enabling students to grasp their own learning objectives more clearly, and attaches great importance to the evaluation of students’ output in this model.

(3)

Flipped Classroom teaching model

The flipped classroom teaching model reverses the stage of knowledge imparting and knowledge internalization in the learning process. Students complete the stage of knowledge imparting with the assistance of information technology before class and internalize knowledge through group discussion and teacher guidance in class, allowing students to participate more in the learning process [45]. Students can realize personalized learning and master the content and amount of learning independently. This is more conducive to stimulating students’ autonomy, creativity, and enthusiasm. However, the model has high requirements for the preparation of teaching videos, support of information technology, and requirements for students’ quality [46].

(4)

Blended teaching model

The blended teaching model combines traditional teaching with online teaching. This model can not only play the leading role in traditional teachings, such as the guidance, inspiration, and supervision of students, but can also expand the flexibility of online learning and the richness of learning resources. Based on MOOCs, SPOCs, and other online learning approaches, there are many explorations and developments of blended teaching [47].

5.2. The Processes of Evaluation

To better evaluate a teaching model of economic statistics, we selected six DMs. Among them are four professional teachers of economic statistics who have rich teaching experience and teaching achievements. The other two are well-known scholars in the field of economic statistics in China who have long been engaged in research work related to economic statistics education.

According to the CAMP multi-attribute system constructed in this paper, six DMs took the training effect of different teaching models on the comprehensive statistical ability of CAMP as the standard to evaluate the four teaching models. Finally, we obtained the evaluation information from

Table 4. Evaluation information of CDIO Teaching Model (A).

	1	2	3	4	5	6
C1	very good	good	good	medium	good	very good
C2	5	3	4	3	5	4
C3	good	very good	very good	good	good	very good
C4	3	4	3	2	3	4
C5	[9,10]	[7,8]	[8,9]	[5,6]	[9,10]	[8,9]
C6	[9,10]	[8,9]	[9,10]	[6,7]	[9,10]	[9,10]
C7	(0.6,0.2)	(0.9,0.1)	(0.7,0.3)	(0.8,0.9)	(0.9,0.2)	(0.8,0.1)
C8	(0.8,0.3)	(0.9,0.05)	(0.4,0.5)	(0.5,0.6)	(0.8,0.3)	(0.8,0.2)

,

Table 5. Evaluation information of OBE Teaching Model (B).

	1	2	3	4	5	6
C1	medium	medium	good	medium	medium	good
C2	2	3	2	3	2	2
C3	good	medium	very good	medium	medium	good
C4	2	3	4	2	3	2
C5	[7,8]	[6,7]	[5,6]	[8,9]	[7,8]	[8,9]
C6	[7,8]	[5,6]	[7,8]	[6,7]	[8,9]	[7,8]
C7	(0.7,0.2)	(0.8,0.2)	(0.5,0.4)	(0.6,0.3)	(0.8,0.1)	(0.8,0.2)
C8	(0.6,0.3)	(0.7,0.1)	(0.5,0.3)	(0.4,0.5)	(0.6,0.4)	(0.6,0.3)

,

Table 6. Evaluation information of Flipped Classroom Teaching Model (C).

	1	2	3	4	5	6
C1	good	medium	medium	bad	medium	medium
C2	3	2	2	1	2	2
C3	medium	good	very good	medium	good	good
C4	3	3	4	2	3	4
C5	[6,7]	[7,8]	[6,7]	[7,8]	[8,9]	[7,8]
C6	[5,6]	[6,7]	[7,8]	[7,8]	[7,8]	[7,8]
C7	(0.6,0.4)	(0.7,0.3)	(0.7,0.2)	(0.7,0.3)	(0.9,0.1)	(0.9,0.2)
C8	(0.6,0.3)	(0.7,0.2)	(0.6,0.4)	(0.5,0.4)	(0.8,0.2)	(0.7,0.3)

and

Table 7. Evaluation information of Blending Teaching Model (D).

	1	2	3	4	5	6
C1	medium	medium	medium	medium	medium	medium
C2	1	2	2	1	1	2
C3	good	medium	medium	medium	medium	good
C4	3	2	1	1	2	3
C5	[4,5]	[5,6]	[4,5]	[6,7]	[6,7]	[6,7]
C6	[5,6]	[6,7]	[4,5]	[5,6]	[7,8]	[6,7]
C7	(0.6,0.4)	(0.6,0.2)	(0.4,0.5)	(0.6,0.3)	(0.7,0.3)	(0.7,0.2)
C8	(0.5,0.4)	(0.5,0.3)	(0.5,0.5)	(0.4,0.3)	(0.6,0.4)	(0.5,0.3)

.

After obtaining the above evaluation information, we transform the real number, interval number, and linguistic number into intuitionistic fuzzy numbers through the previous transformation method. We do not show the specific conversion process here. The final conversion results are shown in

Table A1. Converted evaluation information of CDIO teaching model.

	1	2	3	4	5	6
C1	(0.9000, 0.1000)	(0.7500, 0.2000)	(0.7500, 0.2000)	(0.5000, 0.4500)	(0.7500, 0.2000)	(0.9000, 0.1000)
C2	(0.5000, 0.5000)	(0.3000, 0.7000)	(0.4000, 0.6000)	(0.3000, 0.7000)	(0.5000, 0.5000)	(0.4000, 0.6000)
C3	(0.7500, 0.2000)	(0.9000, 0.1000)	(0.9000, 0.1000)	(0.7500, 0.2000)	(0.7500, 0.2000)	(0.9000, 0.1000)
C4	(0.3779, 0.6220)	(0.5039, 0.4960)	(0.3779, 0.6220)	(0.2519, 0.7480)	(0.3779, 0.6220)	(0.5039, 0.4960)
C5	(0.3131, 0.3479)	(0.2435, 0.2784)	(0.2784, 0.3131)	(0.1740, 0.2088)	(0.3131, 0.3479)	(0.2784, 0.3131)
C6	(0.2914, 0.3238)	(0.2590, 0.2914)	(0.2914, 0.3238)	(0.1943, 0.2266)	(0.2914, 0.3238)	(0.2914, 0.3238)
C7	(0.6000, 0.2000)	(0.9000, 0.1000)	(0.7000, 0.3000)	(0.8000, 0.9000)	(0.9000, 0.2000)	(0.8000, 0.1000)
C8	(0.8000, 0.3000)	(0.9000, 0.0500)	(0.4000, 0.5000)	(0.5000, 0.6000)	(0.8000, 0.3000)	(0.8000, 0.2000)

,

Table A2. Converted evaluation information of OBE teaching model.

	1	2	3	4	5	6
C1	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.7500, 0.2000)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.7500, 0.2000)
C2	(0.3430, 0.6570)	(0.5145, 0.4855)	(0.3430, 0.6570)	(0.5145, 0.4855)	(0.3430, 0.6570)	(0.3430, 0.6570)
C3	(0.7500, 0.2000)	(0.5000, 0.4500)	(0.9000, 0.1000)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.7500, 0.2000)
C4	(0.2949, 0.7051)	(0.4423, 0.5577)	(0.5898, 0.4102)	(0.2949, 0.7051)	(0.4423, 0.5577)	(0.2949, 0.7051)
C5	(0.2721, 0.3109)	(0.2332, 0.2721)	(0.1943, 0.2332)	(0.3109, 0.3498)	(0.2721, 0.3109)	(0.3109, 0.3498)
C6	(0.2789, 0.3187)	(0.1992, 0.2391)	(0.2789, 0.3187)	(0.2391, 0.2789)	(0.3187, 0.3586)	(0.2789, 0.3187)
C7	(0.7000, 0.2000)	(0.8000, 0.2000)	(0.5000, 0.4000)	(0.6000, 0.3000)	(0.8000, 0.1000)	(0.8000, 0.2000)
C8	(0.6000, 0.3000)	(0.7000, 0.1000)	(0.5000, 0.3000)	(0.4000, 0.5000)	(0.6000, 0.4000)	(0.6000, 0.3000)

,

Table A3. Converted evaluation information of FC teaching model.

	1	2	3	4	5	6
C1	(0.7500, 0.2000)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.3500, 0.6000)	(0.5000, 0.4500)	(0.5000, 0.4500)
C2	(0.5883, 0.4117)	(0.3922, 0.6078)	(0.3922, 0.6078)	(0.1961, 0.8039)	(0.3922, 0.6078)	(0.3922, 0.6078)
C3	(0.5000, 0.4500)	(0.7500, 0.2000)	(0.9000, 0.1000)	(0.5000, 0.4500)	(0.7500, 0.2000)	(0.7500, 0.2000)
C4	(0.3779, 0.6220)	(0.3779, 0.6220)	(0.5039, 0.4960)	(0.2520, 0.7480)	(0.3779, 0.6220)	(0.5039, 0.4960)
C5	(0.2346, 0.2737)	(0.2737, 0.3128)	(0.2346, 0.2737)	(0.2737, 0.3128)	(0.3128, 0.3519)	(0.2737, 0.3128)
C6	(0.2045, 0.2454)	(0.2454, 0.2863)	(0.2863, 0.3271)	(0.2863, 0.3271)	(0.2863, 0.3271)	(0.2863, 0.3271)
C7	(0.6000, 0.4000)	(0.7000, 0.3000)	(0.7000, 0.2000)	(0.7000, 0.3000)	(0.9000, 0.1000)	(0.9000, 0.2000)
C8	(0.6000, 0.3000)	(0.7000, 0.2000)	(0.6000, 0.4000)	(0.5000, 0.4000)	(0.8000, 0.2000)	(0.7000, 0.3000)

and

Table A4. Converted evaluation information of blended teaching model.

	1	2	3	4	5	6
C1	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.5000, 0.4500)
C2	(0.2582, 0.7418)	(0.5164, 0.4836)	(0.5164, 0.4836)	(0.2582, 0.7418)	(0.2582, 0.7418)	(0.5164, 0.4836)
C3	(0.7500, 0.2000)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.5000, 0.4500)	(0.7500, 0.2000)
C4	(0.5669, 0.4331)	(0.3779, 0.6220)	(0.1889, 0.8110)	(0.1889, 0.8110)	(0.3779, 0.6220)	(0.5669, 0.4331)
C5	(0.2005, 0.2506)	(0.2506, 0.3008)	(0.2005, 0.2506)	(0.3008, 0.3509)	(0.3008, 0.3509)	(0.3008, 0.3509)
C6	(0.2368, 0.2841)	(0.2841, 0.3315)	(0.1894, 0.2368)	(0.2368, 0.2841)	(0.3315, 0.3788)	(0.2841, 0.3315)
C7	(0.6000, 0.4000)	(0.6000, 0.2000)	(0.4000, 0.5000)	(0.6000, 0.3000)	(0.7000, 0.3000)	(0.7000, 0.2000)
C8	(0.5000, 0.4000)	(0.5000, 0.3000)	(0.5000, 0.5000)	(0.4000, 0.3000)	(0.6000, 0.4000)	(0.5000, 0.3000)

.

The social network relationship among the six DMs is shown in Figure 4. Intuitively, there are three directed edges pointing to DM 2 and DM 5, so they have a high status in this social network. However, both DM 3 and DM 4 have only one directed edge pointing to themselves, so their position should be relatively low. DM 1 and DM 6 should fall somewhere in between. In fact, DM 2 and DM 5 are well-known scholars in the field of economic statistics in China. This shows that the method in this paper can more accurately reflect the relationship between DMs.

After investigation, the HPFT relationship between them is shown in

Table 8. HPFT relationship of DMs.

	DM 1	DM 2	DM 3	DM 4	DM 5	DM 6
DM 1	/	{0.8|0.8, 0.9|0.2}	/	{0.4|0.5, 0.5|0.5}	/	/
DM 2	/	/	{0.5|0.7, 0.6|0.3}	/	/	/
DM 3	/	{0.9|0.6, 1|0.4}	/	/	{0.8|0.3, 0.9|0.7}	{0.6|0.8, 0.7|0.2}
DM 4	{0.6|0.8, 0.7|0.2}	/	/	/	{0.7|0.6, 0.8|0.4}	{0.8|0.7, 0.9|0.3}
DM 5	/	{0.7|0.4, 0.8|0.6}	/	/	/	/
DM 6	{0.7|0.6, 0.8|0.4}	/	/	/	{0.8|0.4, 0.9|0.6}	/

. For the convenience of calculation, ${\lambda }_i=2$ is uniformly selected here. “/” in Table 8 means that there is no direct trust relationship between DMs. That is, there are no directed edge joins in Figure 4.

According to the trust relationship between DMs, degree centrality $C\left(e_j\right)$, degree of trust $TD\left(e_j\right)$, and the total degree of trust $TD$ can be calculated in sequence using Equation (8)–(10). The specific calculation process is not shown here. Finally, we can obtain DMs’ weights, as shown in

Table 9. Weights of DMs.

DM	1	2	3	4	5	6
Weight	0.1681	0.2072	0.1314	0.1115	0.2037	0.1780

.

Then, we aggregate the evaluation information of each DM according to the IFWAA operator and obtain the group evaluation information of the above four teaching models. The results are shown in

Table 10. Aggregated evaluation information.

	(A)	(B)	(C)	(D)
C1	(0.8033,0.1723)	(0.5965,0.3502)	(0.5417,0.4055)	(0.5000,0.4500)
C2	(0.4111,0.5889)	(0.4034,0.5966)	(0.4127,0.5873)	(0.4053,0.5947)
C3	(0.8443,0.1398)	(0.6816,0.2789)	(0.7309,0.2291)	(0.6066,0.3399)
C4	(0.4179,0.5819)	(0.4043,0.5957)	(0.4079,0.5920)	(0.4146,0.5853)
C5	(0.2736,0.3038)	(0.2660,0.3014)	(0.2705,0.3079)	(0.2616,0.3073)
C6	(0.2745,0.3045)	(0.2671,0.3031)	(0.2647,0.3032)	(0.2694,0.3122)
C7	(0.8217,0.1910)	(0.7391,0.1991)	(0.7929,0.2221)	(0.6219,0.2881)
C8	(0.7783,0.3585)	(0.5939,0.2534)	(0.6812,0.2724)	(0.5124,0.354)

.

After obtaining the above evaluation information matrix, the attribute weights are determined.

First, the objective weight of each attribute is calculated. According to the aggregated evaluation information, the entropy value of each attribute can be obtained by using Equation (12), as shown in

Table 11. Entropy value of each attribute.

C1	C2	C3	C4
0.3424	0.3383	0.2123	0.3378
C5	C6	C7	C8
0.6911	0.6904	0.1986	0.3045

.

Furthermore, according to the entropy value of each attribute, the weight can be calculated according to Equation (13), and the results are shown in

Table 12. Objective weight of each attribute.

C1	C2	C3	C4
0.1353	0.1358	0.1464	0.1358
C5	C6	C7	C8
0.0801	0.0802	0.1473	0.1391

.

Then, the AHP method is used to calculate the subjective weight of each attribute. After the consultation of six decision makers and evaluation organizers, the judgment matrix is obtained as follows.

$$\mathrm{A}=\left[\begin{array}{cc}\begin{array}{cccc}1.00& 0.33& 0.50& 0.50\\ 3.00& 1.00& 2.00& 2.00\\ 2.00& 0.50& 1.00& 2.00\\ 2.00& 0.50& 0.50& 1.00\end{array}& \begin{array}{cccc}0.25& 0.50& 0.20& 0.25\\ 0.50& 2.00& 0.50& 0.33\\ 0.50& 1.00& 0.50& 0.50\\ 1.00& 1.00& 0.33& 0.20\end{array}\\ \begin{array}{cccc}4.00& 2.00& 2.00& 2.00\\ 2.00& 0.50& 1.00& 1.00\\ 5.00& 2.00& 2.00& 3.00\\ 4.00& 3.00& 2.00& 5.00\end{array}& \begin{array}{cccc}1.00& 2.00& 0.50& 0.50\\ 0.50& 1.00& 0.25& 0.33\\ 2.00& 4.00& 1.00& 1.00\\ 2.00& 3.00& 1.00& 1.00\end{array}\end{array}\right]$$

According to matrix A, the consistency ratio is further calculated and $CR=0.0342<0.10$ is obtained. Therefore, it can be considered that the consistency of the judgment matrix is acceptable without modification. Thus, we can obtain the results of subjective weight, as shown in

Table 13. Subjective weight of each attribute.

C1	C2	C3	C4
0.0409	0.1169	0.0902	0.0710
C5	C6	C7	C8
0.1482	0.0703	0.2243	0.2381

.

Finally, according to Equation (14), letting α = 0.6, we can obtain the combined weight of each attribute. The results are shown in

Table 14. Combined weight of each attribute.

C1	C2	C3	C4
0.0976	0.1282	0.1239	0.1099
C5	C6	C7	C8
0.1073	0.0763	0.1781	0.1787

.

5.3. Results

According to Definition 6, the score function is calculated. The calculation results and ranking are shown in

Table 15. Score function of each teaching model.

	(A)	(B)	(C)	(D)
C1	0.6310 (1)	0.2463 (2)	0.1362 (3)	0.0500 (4)
C2	−0.1778 (2)	−0.1932 (4)	−0.1746 (1)	−0.1894 (3)
C3	0.7045 (1)	0.4027 (3)	0.5018 (2)	0.2667 (4)
C4	−0.1640 (1)	−0.1914 (4)	−0.1841 (3)	−0.1707 (2)
C5	−0.0302 (1)	−0.1841 (4)	−0.0374 (2)	−0.0457 (3)
C6	−0.0300 (1)	−0.0374 (2)	−0.0385 (3)	−0.0428 (4)
C7	0.6307 (1)	0.5400 (3)	0.5708 (2)	0.3338 (4)
C8	0.4198 (1)	0.3405 (3)	0.4088 (2)	0.1584 (4)
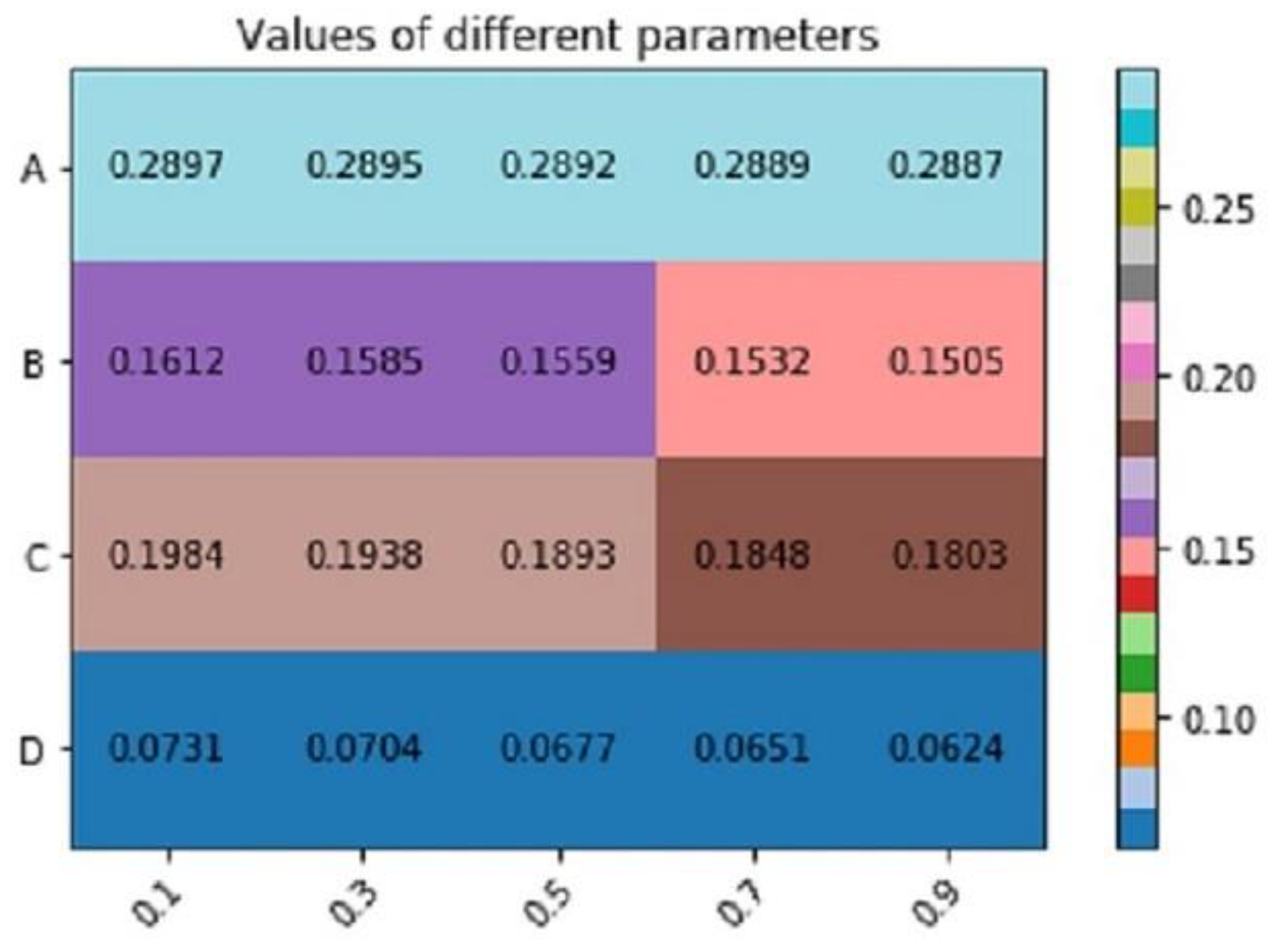
Total value	0.2891 (1)	0.1545 (3)	0.1871 (2)	0.0664 (4)

.

According to the results in Table 15, we can obtain the ranking result of four teaching models: $\mathrm{A}\succ \mathrm{C}\succ \mathrm{B}\succ \mathrm{D}$. Therefore, A is the optimal choice of the teaching model.

5.4. Comparison and Analysis

To prove the effectiveness, we compare the MADM framework (denoted as method one and let α = 0.6) proposed in this paper with other multi-attribute evaluation methods in teaching model evaluation. According to the methods proposed in [26,48,49] (denoted as method two, method three, and method four, respectively), we can obtain the different evaluation results listed in

Table 16. Results obtained by different methods.

Method	A	B	C	D	Sorting Result
method 1	0.2891	0.1545	0.1871	0.0664	$\mathrm{A}\succ \mathrm{C}\succ \mathrm{B}\succ \mathrm{D}$
method 2	0.2918	0.1825	0.2345	0.0946	$\mathrm{A}\succ \mathrm{C}\succ \mathrm{B}\succ \mathrm{D}$
method 3	0.2886	0.1492	0.1780	0.0610	$\mathrm{A}\succ \mathrm{C}\succ \mathrm{B}\succ \mathrm{D}$
method 4	0.3799	0.2090	0.2077	0.0834	$\mathrm{A}\succ \mathrm{B}\succ \mathrm{C}\succ \mathrm{D}$

.

It can be seen from Table 16 that the optimal alternative achieved by all methods is the same, i.e., A. Thus, the method proposed in this paper has excellent effectiveness. Noted that the sorting results of all alternatives tend to be consistent except for method four, the main reason for the difference of results mainly comes from information from attribute weight and the aggregation method. Moreover, compared with others, the MADM framework proposed in this paper has the following significant characteristics. First, there are various forms of evaluation information. Different forms of information differ in the accuracy and effectiveness of collection. Compared with Fermatean fuzzy number [26], real number, and other single data forms [48,49], the heterogeneous information forms (including real number, interval number, intuitionistic fuzzy number, and linguistic number) of the framework, which can collect evaluation information more accurately. Second, the weighting method in this paper can avoid the deficiency of subjective weight and objective weight to a certain extent. For one thing, it not only relies on subjective judgment (for example, it was entirely decided by DMs in [26]), making the results more convincing. At the same time, this method does not rely on data structure completely, such as an objective weighting method (for example, the entropy weight method in [48]), which can enhance the stability of weight results. This also makes the results in this paper more stable compared with the results of subjective and objective weighting, as shown in Table 16. In addition, the IFAWA integration operator used in this paper, compared with other methods, can more intuitively reflect the characteristics of evaluation objects and reduce the loss of evaluation information in the integration process.

To further verify the stability of the MADM framework proposed in this paper, the following sensitivity analysis was conducted: for the parameters $\alpha$ in Equation (14), we successively take $\alpha =0.1$, $\alpha =0.3$, $\alpha =0.5$ and $\alpha =0.7$ and $\alpha =0.9$ to calculate the values of each teaching model, as shown in Figure 5.

Figure 5 shows that when the parameters in Equation (14) are given different values, the ranking results of all teaching models do not change. Therefore, the MADM framework based on heterogeneous information and combined weight proposed in this paper has high stability.

6. Policy Implications

Breaking down the barriers between knowledge and practice and strengthening the training of statistical skills in combination with practice is important [12]. Economic statistics, as a highly applicable subject, requires students majoring in statistics to have solid professional knowledge, especially flexible knowledge application and practical operation ability. The results of combined weights in this paper can also be verified: the weights of practical operation ability (w₇ = 0.1781) and professional skill level (w₈ = 0.1787) are particularly prominent in the attribute system. Therefore, the teaching model of economic statistics should break the barrier between classroom teaching and practical operation, integrate the cultivation of statistical skills in classroom teaching, and help students master the application of classroom knowledge into practice through the introduction of practical cases, description of application scenarios and demonstration of classroom operation. Second, students should be actively guided to participate in discipline competitions, academic innovation, and practice to exercise their knowledge transfer, expand their application ability and cultivate their systematic thinking. At the same time, attention should be given to the supervision of students’ practice processes, regular exchanges and symposia should be organized, students’ problems should be solved in a timely manner, and behavior norms should be ensured.

Integration of different teaching models to avoid the pursuit of unity and homogeneity should be attempted [49]. Different teaching models of economic statistics have their own characteristics. According to the MADM results in 4.3, we conclude that although CDIO has excellent overall performance, FC is superior to the former in terms of ‘competition skills’. In addition, FC, with its flexible learning form and full communication, also has outstanding performance in promoting students’ knowledge mastery and creating an academic atmosphere. Therefore, statistical educators should fully recognize the advantages of different teaching models, actively try to break through the boundaries between different teaching models, and explore the depth of integration between different teaching models. For example, on the basis of the CDIO, the FC teaching model can be integrated into classroom teaching. In this way, students can not only strengthen their autonomy and enthusiasm through classroom communication but also cultivate students’ systematic thinking of statistics. In addition, the administrative departments of universities should pay attention to the differences between different disciplines, increase the autonomy of universities in the choice of teaching model, guide universities to select and improve the personalized teaching model based on the characteristics of disciplines, and avoid the pursuit of unification and homogeneity [50].

Regular evaluation of the teaching model should be carried out to ensure continuous improvement of teaching quality [51]. The administration of universities can set up an evaluation group composed of senior teachers to evaluate different teaching models on a regular basis and force the improvement of teaching models according to the evaluation results. The MADM framework proposed in this paper can also be used as a reference. Meanwhile, the process supervision and overall supervision of teaching quality should be strengthened. With regard to the process of teaching activities, from the perspective of students and teachers: the student’s knowledge, understanding, mastering, practical operation ability, and so on should be measured. Furthermore, to be examined are the teacher’s teaching process, content, and ways to be measured. In this way, managers can grasp the situation of teaching quality in time, find problems and deficiencies, and ensure that the teaching model can maintain the optimal effect. In addition, a teaching feedback mechanism between students, teachers, and educational managers should be set up, such as teachers and students’ forums, opinion consultation meetings, and other forms, to strengthen the communication between teachers and students on teaching activities. On this basis, management departments urge teachers to make dynamic adjustments to teaching activities according to students’ feedback and suggestions.

7. Conclusions

The evaluation of teaching models is of great significance in exploring the current development situation, discovering problems, and guaranteeing the quality of teaching. Economic statistics have the outstanding characteristics of intersections, integration, and marginality. Its teaching activities also show the outstanding characteristics of multiple dimensions and complexity. Therefore, the above characteristics should be fully considered in the evaluation of a teaching model. Based on an analysis of the relationship between statistical capacity and teaching activities, this paper constructed the CAMP teaching model evaluation attribute system in line with the characteristics of economic statistics. We further introduced heterogeneous information and fuzzy–social network into the evaluation process. Furthermore, a MADM framework of statistical teaching models based on heterogeneous information is proposed. The methods of DMs and attribute weights are both innovated in this MADM framework. Through empirical research, it was concluded that the CDIO engineering teaching model has important reference value and significance for training the statistical capacity of students who are economic statistics majors. It also verifies the effectiveness and stability of the method in this paper. Therefore, the MADM framework has certain extensibility. After adjusting the multi-attribute system, the framework can be used in other subjects’ teaching model evaluation, curriculum evaluation, and even personnel evaluation.

However, this paper mainly refers to the existing mature methods for the conversion of heterogeneous information. This approach will inevitably make part of the information conversion results not conform to the logic and rules of teaching model evaluation. Therefore, in the next step, we will further improve and perfect the conversion method of heterogeneous information based on the information characteristics in this field. In addition, in the MADM framework, the evaluators are mainly teaching workers, and students’ participation in the process is not considered. Therefore, important information in the evaluation of the teaching model is easy to be omitted, which still needs to be improved.