Abstract
Evaluating pharmaceutical enterprises with sustainable and high-quality development ability (SHQDA) can not only provide strategies for the pharmaceutical management department in formulating enterprise development plans, but also provide suggestions and guidance for enterprises to enhance their core competitiveness. Nevertheless, the prior research possesses several deficiencies in coping with the assessment of enterprises with SHQDA under uncertain environments to predict the psychological behavior of the evaluator and the correlation among the evaluation criteria. To conquer the aforementioned defects, we propose an integrated framework for rating pharmaceutical enterprises that incorporates regret theory, measurement alternatives and ranking based on the compromise solution (MARCOS) and Heronian mean operating within a single-value neutrosophic set (SVNS) environment. First, the single-valued neutrosophic number (SVNN) is employed to portray the assessment information of experts. Then, a novel single-valued neutrosophic score function is presented to enhance the rationality of the SVNN comparison. Next, a combined criteria weight model is constructed by synthesizing the best and worst method (BWM) and criteria importance through intercriteria correlation (CRITIC) approach to attain more reasonable and credible weight information. Furthermore, the integrated assessment framework combining regret theory-MARCOS method and Heronian mean operator is put forward to assess and select the enterprises with SHQDA under a single-valued neutrosophic setting. Ultimately, an empirical concerning the pharmaceutical enterprises assessment is presented within SVNS to illustrate the usefulness and effectiveness of the presented SVNS regret theory-MARCOS method. Thereafter, the sensitivity analysis and comparison analysis are implemented to provide evidence for the rationality and superiority of the proposed method.
1. Introduction
With the deepening and development of global economic integration, the world economy has developed rapidly. However, rapid economic development has also brought a series of challenges to environmental protection, ecological governance and social stability. At the same time of rapid economic development, maintaining a beautiful environment and ecological balance is an important guarantee for the development of the green economy. Therefore, it is of great significance to evaluate enterprises from the perspective of SHQDA to improve the quality of economic development [1]. Because the evaluation process involves evaluation criteria of different dimensions and experts and scholars in different fields, the evaluation of enterprises with SHQDA can be regarded as a multi criteria group decision-making (MCGDM) problem. Although scholars put forward some models to solve such problems, the above results rarely consider the factors such as expert preference and the uncertainty and incompleteness of decision environment. Therefore, it is necessary to establish an evaluation model under fuzzy uncertainty environment to provide scientific and reasonable decision support for evaluation experts.
In the analysis of practical decision problems, it is difficult for experts to meet the requirements of experts in dealing with complex and uncertain decision-making problems by expressing the preferences of experts through accurate values. Limited by the objective complexity of decision-making problems and the limitations of decision makers’ subjective understanding, a new mathematical tool called fuzzy set [2] is propounded to utilize membership degree to represent uncertain information. Because of the limitation that fuzzy set only uses membership function to describe fuzzy information, the intuitionistic fuzzy set (IFS) [3] theory is developed to more reasonably represent uncertain information by adding non membership and hesitation functions on the basis of fuzzy set. At present, the research on intuitionistic fuzziness has achieved fruitful results and has been widely used in the fields [4,5,6,7,8]. Although IFSs have been deeply studied and solved many uncertain decision and evaluation problems, they cannot represent indeterminate and inconsistent information. In order to conquer this defect, Smarandache [9] originated a novel uncertain model called neutrosophic set (NS) from the perspective of philosophy to describe people’s judgment of actual information. NS is made up of the truth-membership, indeterminacy-membership and falsity-membership functions and their ranges are all . Although NS further popularizes fuzzy set and IFS, it is difficult to be directly applied to realistic problems because of the rang of the membership-functions. Therefore, Wang et al. [10] firstly developed the single-valued neutrosophic (SVN) set to further enrich the applications of neutrosophic theory in practical issues. Owing to its superiority for depicting uncertain information, the investigations on SVNS receive an increasing attention in basic theory construction and practical application extension. Those research achievements can be mainly divided into the following three aspects: theories exploration [11,12,13], decision methodology establishment [14,15,16] and actual applications [17,18,19,20]. In addition, Ye [21] introduced some SVN cross-entropy to build the MCDM decision approach. Smarandache [22] and Nafei et al. [23] presented the constructed innovative MCDM decision algorithm on the basis of the novel SVN score functions. Rong et al. [24] proposed a novel MCDM approach based on some new generalized SVN archimedean copula power aggregation operators. Mishra et al. [25] propounded a SVN-WASPAS decision model based on some novel similarity measures to select the optimal sustainable biomass crop. Afterwards, Rani et al. [26] suggested the SVN-CRITIC-MULTIMOORA decision framework to choose the best food waste treatment method. Tan et al. [27] brought an integrated assessment framework through combining the game theory and grey relational analysis within SVN setting to assess the typhoon disaster. Furthermore, Pamucar et al. [28] settled the sustainable road transportation alternative fuel vehicles assessment problem by a hybrid FUCOM and neutrosophic fuzzy MARCOS approach using the Dombi operators. From the mentioned works on SVNS, research on combined weight determination and behavioral decision theory are not integrated to provide decision support for actual applications.
The most important process of MCGDM is to develop decision analysis by utilizing different decision methodologies. To date, lots of decision techniques, such as TOPSIS [29], VIKOR [30], MACONT [31] and so on, are propounded to provide decision support for coping with the realistic complex decision and evaluation problems. Recently, Stević et al. [32] originated a novel decision algorithm called the MARCOS method to select the most desirable supplier. The MARCOS method takes into consideration the ideal and anti-ideal solution and the utility function of alternatives and can obtain a more robust and credible decision utility value of alternative than other methods. In light of its superiority in handling decision issues, lots of research based on MARCOS method and uncertain tools has been completed. Fan et al. [33] suggested an innovative risk assessment model by combining the BWM method and MARCOS method under D numbers environment for enhancing the application of Failure modes and effects analysis, where the D-BWM method is introduced to figure out the subjective weight of the risk parameters. Pamucar et al. [34] constructed a comprehensive airport service quality evaluation framework based on the presented grey Step-wise Weight Assessment Ratio Analysis grey MARCOS method. Gong et al. [35] introduced an evaluation model through synthesizing the MARCOS method and BWM approach under interval type-2 fuzzy seeting to evaluate the renewable energy accommodation potential. Torkayesh et al. [36] propounded an integrated uncertain decision model to select the optimal landfill location for the healthcare waste system with the aid of Geographic Information System (GIS), the MARCOS method and BWM approach within grey interval information. Furthermore, considering that the uncertain and vagueness of the realistics decision problems, Ecer and Pamucar [37] offered the intuitionistic fuzzy group MARCOS algorithm to evaluate the performance of insurance companies in terms of healthcare services in the COVID-19 pandemic. Kundu et al. [38] proffered a fuzzy MCGDM model to select a appropriate magnetic resonance imaging on the basis of the MARCOS method, wherein the preference selection index is utilized to determine the importance of the assessment index. Ali [39] brought forward a q-rung orthopair fuzzy MARCOS MCGDM methodology based on a novel score function and CRITIC method to solid waste management problems. Vesković et al. [40] presented a large-scale MCGDM approach by integrating fuzzy FUCOM (full consistency method) and fuzzy MARCOS approach to choose the optimal reach stacker in a container terminal when the criteria weight is unknown for experts. Darko and Liang [41] put forward an innovative decision support model with the aid of probabilistic linguistic MARCOS and LINMAP methods to recommend satisfactory restaurants by the online reviews. The existing works enrich decision support models for experts to develop decision analysis in different fields. The more investigations under uncertain settings for solving decision problems can be studied in [42,43,44,45]. Nevertheless, those extensions of the MARCOS method ignore the psychological behavioral of decision experts in the process of practical decision analysis, which will lead to unreasonable decision outcomes. On the other hand, there is no research to combine the MARCOS method and SVNNs to build a decision model. Accordingly, it is necessary for experts to take into account this defect and further strengthen the feasibility of the MARCOS technique in dealing with decision and assessment problems.
In view of the mentioned literature analysis and discussion, we can find that the SVNS has a powerful capability to portray the uncertainty and vagueness of practical assessment information. The MARCOS decision technique can exhibit a more efficient performance in the course of the actual decision analysis. Accordingly, the motivations of this research can be listed as below:
- ♠
- The prior score functions of SVNS possess several deficiencies in the aspect of ranking SVNNs and can produce ambiguous and inconsistent ranking results.
- ♠
- Considering the complexity and conflict of actual decision and assessment problems, it is necessary for decision makers to predict the combination of the subjective and objective weight of criteria for analyzing the decision issues. In order to enhance the practicability of the designed method in this paper, the combined weight of criteria is employed to acquire a more exact rank of pharmaceutical enterprises.
- ♠
- The extant extensions of MARCOS decision technique fail to consider the psychology factor of decision makers during the decision analysis procedure. Hence, it is essential to fuse the behavioral decision theory to the MARCOS algorithm to achieve more robust results.
- ♠
- There is no research on pharmaceutical enterprises assessment with SHQDA by considering the uncertainty and ambiguity of the assessment procedure.
Based on the motivations of this research, the goals and contributions of this investigation are epitomized as below:
- ✓
- A novel score function is brought forward and the corresponding elegant properties are taken over;
- ✓
- A synthesize criteria weight determination method is developed based on the BWM approach and improved CRITIC method using the novel score function to ascertain a more rational weight information of criterion;
- ✓
- An integrated assessment framework combining the regret theory-MARCOS method and Heronian mean operator is put forward on the basis of the presented score function;
- ✓
- A pharmaceutical enterprises assessment problem is utilized to elucidate the practicability and robustness of the advanced approach;
- ✓
- An analysis of the contrast and an examination of the parameter discussion demonstrate, respectively, the validity and stability of the suggested method.
The following is an overview of the organization of this paper. Section 2 succinctly retrospects some essential preliminaries of this research. Section 3 propounds a novel SVNS score function and explores some valuable properties of it. Section 4 builds up a hybrid SVNS regret theory-MARCOS group decision framework for the evaluating pharmaceutical enterprise with SHQDA. Section 4 employs the constructed approach to resolve the pharmaceutical enterprises evaluation problem and the sensitivity analysis and contrast analysis are implemented with the previous decision approaches. Some conclusion remarks are given in the end. A diagram of this research is displayed in Figure 1 to improve the readability of the paper.
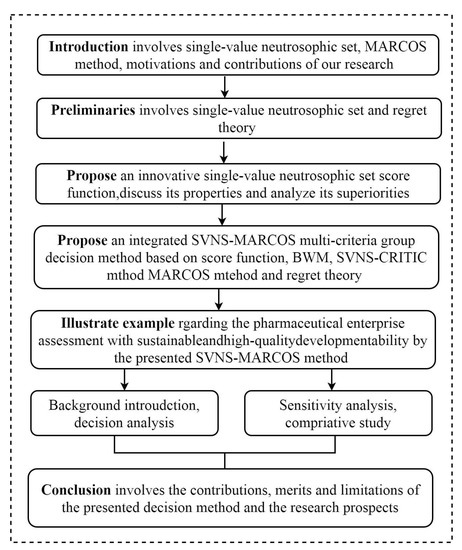
Figure 1.
The diagram of this research.
2. Preliminaries
In this section, we briefly review several background knowledge of this research, including the related theories of the SVNS and regret theory.
2.1. Single Valued Neutrosophic
Definition 1
([10]). Let Y be a finite universe of discourse. A SVNS H in Y is stipulated by a truth-membership, an indeterminacy-membershipand a falsity-membership function, wherein the functionsandare the real subset of. Formally, the SVNS is defined as follows:
where, and. Besides, the sum ofandis specified as. For simplicity, the tripletis called a SVNN and signified as.
In addition, several fundamental logical operations of SVNN are defined by [10,22], which are described as below.
Definition 2.
Consider thatandare two SVNNs and. Then, the basic operations for two SVNNs are stated as below:
Definition 3
([12]). Consider thatandare two SVNNs and. Then, the Einstein operations for two SVNNs are depicted as below:
Based on the Einstein operations of two SVNNs, the correspondingly aggregation operators are introduced as follows.
Definition 4
([12]). Assume thatis a family of SVNNs. Then:
whereis the weight ofwithwith. SVNEWA and SVNEWG are the SVN Einstein weighted averaging operator and SVN Einstein weighted geometric operator, respectively.
In order to measure the difference of two SVNNs, the single-valued neutrosophic distance measure is defined as below.
Definition 5
([20]).Given two SVNNsandthere are two SVNNs and. Then, the Euclidean distance on two SVNNandis defined as:
2.2. Regret Theory
As an important behavioral decision theory, the core of regret theory [46] is to compare the outcomes of the selected scheme with the possible results of other schemes, so as to measure the degree of rejoice and regret of the decision maker, and choose the outcome that the decision maker will not regret. In short, decision makers will feel regretful when the selected scheme is worse than the others, and decision makers will feel rejoice when the selected scheme is better than the others.
Definition 6
([46]).Assume the a is the outcome of choosing scheme, then the utility value deduced fromcan be ascertained by the following formulation:
whereis a monotonically increasing concave utility function meetingand. ϑ signifies the risk aversion of decision maker. The higher the degree of risk aversion of decision maker, the smaller the value of ϑ.
Definition 7
([46]).Suppose thatandare the outcomes of schemeand, respectively. Then, the regret-rejoice value of choosing schemerather than schemeis stated as follows:
whereand, respectively, indicate the utility values of schemeand. signifies the risk aversion of decision maker; the greater the value of γ, the higher the degree of regret avoidance. is a monotonically increasing concave utility regret-rejoice function meeting, and. When, then the decision maker will feel rejoice to choose schemeand abandon scheme scheme; on the contrary, they will feel regret.
It is worth noting that the risk aversion parameter and are, respectively, taken as and based on the experiments analysis [47].
Definition 8
([48]).Suppose thatare the outcomes of choosing scheme, then the decision maker’s perceived utility value of schemecan be computed by:
whereand. denotes the regret value when the decision maker chooses the schemeand abandons the ideal scheme. Accordingly, the decision maker’s perceived utility value of the scheme includes two parts: the utility value of the current scheme and the regret value of the current scheme compared to the ideal scheme.
3. An Innovative Single-Valued Neutrosophic Score Function
In this part, considering that the extant score function possesses some deficiencies in distinguishing two SVNNs, we propound a novel SVN score function and further probe several momentous properties of it. Then, we further validate the effectiveness and reasonability and analyze the merits of the presented score function.
3.1. Several Prior Single-Valued Neutrosophic Score Functions
The score function is a momentous conception to transform SVNN into a real number, which has been widely applied to the decision analysis field. Based on the definition of SVNS, some SVN score functions are presented for a SVNN and displayed in Table 1.

Table 1.
The prior score functions and accuracy functions.
3.2. A New SVN Score Function
Definition 9.
Imagine a SVNN, a novel score function is defined as follows:
Theorem 1.
For a SVNN, monotonically increases with the increase of, and monotonically decreases with the increase ofor.
Proof.
Based on the propounded score function, we compute the first partial derivative of to as below:
By the same manner, we can attain the the first partial derivative of to and as follows:
Thus, the proof is achieved. □
Theorem 2.
For a SVNN, then one has:
T1:;
T2:iff;
T3:iff.
Proof.
In view of the monotonicity of the presented score function, we can find that possesses maximum value when , and possesses minimum value when , namely, , . Thus, the proof is achieved. □
In order to validate the rationality and superiority of the developed SVN score function, several numerical cases are employed to expound the reasonability of the proffered score function by means of the rank outcomes. The comparison results are displayed in Table 2.

Table 2.
Comparison outcomes obtain the extant SVN score functions and the advance score function.
With the aid of Table 2, we can observe that the existing SVN score functions Smarandache [22], Sahin [11], Garg [14] and Nafei et al. [23] have some deficiencies and disadvantages in comparing the SVNNs. Nevertheless, we can easily discover that the proposed SVN score function not only validly avoid the unreasonable results obtained by by the prior SVN score functions but also attain more efficacious and credible ranking outcomes. Furthermore, some conclusions based on Table 2 can be attained as follow:
- ¶
- For the Case 1 and Case 2, the score functions proposed by Smarandache [22] and Sahin [11] is invalid to compare the SVNNs and ; thus, we further compute the corresponding accuracy function and find that the accuracy values of and are still equal, namely, for Case 1 and for Case 1. That means the comparison rules proposed by Smarandache [22] and Sahin [11] cannot rank Case 1 and Case 2. However, the presented score function can rapidly acquire the rank result of Case 1 and Case 2 by a step. Accordingly, the propose score function is more universal and a shortcut to rank SVNNs.
- ¶
- For the Case 3, we can find that the extant score function presented by Smarandache [22], Sahin [11], Garg [14] and Nafei et al. [23] are all invalid to rank and . It is obvious that the presented score function can effectively deal with this situation.
- ¶
- For the Case 4, the presented extant score functions in Sahin [11], Garg [14] and Nafei et al. [23] are unable to settle this case. It is can be found that the rank outcome obtain by is the same as the score function advanced by Smarandache [22], which further tests the validity and feasible of .
In view of the mentioned discussion and analysis, the propounded score function is universal, reasonable and fast in ranking SVNNs compared to some extant works.
4. SVN-MARCOS Method Based on the Regret Theory
4.1. Problem Statement
We consider a pharmaceutical enterprise assessment problem with SVNNs-based assessment information, which can be viewed as a MCGDM problem. In such a situation, we specify several necessary notions of the MCGDM problem to help experts to construct the decision model mathematically. The set are a group of m pharmaceutical enterprises. The set are a group of n criteria, and the importance degree of criteria is denoted as and and . The expert group is made up of Q experts with corresponding weight and and . Suppose that the matrices are the assessment matrices provided by expert group, where signifies the assessment opinion given by experts for pharmaceutical enterprises with the respect criteria . It should be pointed out that the assessment opinion is expressed by experts utilizing linguistic terms according to their cognition capability, after which the linguistic assessment opinions are shifted to SVNNs. As a consequence, the SVNNs based assessment matrices from experts can be constructed as follows:
4.2. Obtaining SVN Assessment Information
In order to attain the most satisfactory scheme from the group of schemes, we first construct the expert assessment committee by inviting experts and scholars from the related fields. A mapping relation listed in Table 3, from linguistic terms to SVNN, is provided for an expert assessment committee to give their preference for the identified scheme under diverse criteria. After that, the linguistic evaluation information of pharmaceutical enterprises is achieved through the cognition preference ability and knowledge background of the experts.

Table 3.
Preference ratings of pharmaceutical enterprises in view of linguistic terms.
After obtain the linguistic assessment information of pharmaceutical enterprises, we further get the SVN evaluation matrices through transforming the preference provided from the expert committee.
4.3. Obtaining the Fused SVN Assessment Information
In this subsection, the similarity measure-based expert weight determination algorithm and SVN Einstein weighted averaging operator are employed to acquire the aggregated SVN assessment matrix. First, the expert weight stands for the importance degree and familiarity of the expert with the decision issues, so the expert weight in the proposed method is determined by similarity-based approach objectively. The core of this weight identification technique is consider the consistency between the expert assessment matrix and the ideal matrix, namely, the higher the consistency with the ideal matrix, the expert should be given a higher weight. In such a situation, motivated by the thought of the TOPSIS method, the SVN distance measure and SVN Einstein weighted averaging operator are utilized to ascertain the importance of expert. Then, based on the weight information of the expert, the SVN Einstein weighted averaging operator is used to attain the fused SVN group assessment matrix. Lastly, the normalized SVN group assessment matrix is identified through transforming the cost criteria to benefit criteria.
First, based on the SVNS assessment matrices from the expert , we can compute the mean of experts assessment value for pharmaceutical enterprises under the criteria as below:
In light of the similarity measure determination method based on the distance measure, the similarity measure between and is worked out as follows:
where is the distance measure between and , which can be calculated by:
Then, inspired by the TOPSIS approach, the positive and negative ideal similarity measure are, respectively, calculated by the following formulation:
The importance degree of each expert could be ascertained as follows:
Furthermore, based on the weight of experts and the expert assessment matrices , the aggregated assessment matrix can be obtained by the following formulation:
Ultimately, considering that different kinds of criteria will lead the irrational consequence in the same decision problem, e should normalize the decision data to a unified form. In this research, we achieve the normalized assessment matrix through shifting the cost criteria into benefit criteria. It can be conducted by the following formulation:
4.4. The Determination of Assessment Criteria Weight
In order to ascertain the importance of criteria during in the course of decision analysis, this subsection suggests a combinative weight determination model through taking the BWM approach and CRITIC method into account, which considers the influence of subjective preference and objective information simultaneously. The detailed computation process of combinative weight is expounded as below.
Subjective weight calculation by BWM. The BWM algorithm proposed by Rezaei [49] is a famous technique to pairwise determine the subjective weight of the criteria. This subsection will utilize the BWM to ascertain the subjective weight of criteria to fully show experts’ subjective preference.
Firstly, we identify the best criterion (the most important criterion) and worst criterion (the last important criterion) after the discussion of the expert committee.
Then, we further ascertain the preference including the the best criterion to other criteria and other criteria to the worst criterion based on the scale 1 to 9. The Best-to-others comparative vector is signified as , where stands for the preference of the best criteria compared to other criteria. In the same manner, other-to-Worst comparative vector is signified as , where stands for the preference of other criteria compared to the worst criteria. Note that .
Furthermore, the subjective weight of criteria obtained by BWM method will meet the condition that and hold for every pair of and , respectively. Hence, we shall minimize the maximum absolute differences and for all t, and the model can be attained as below:
Next, we shift the model in Equation (17) into a linear programming model as follows:
Finally, we can attain the subjective weight vector of criteria with the help of LINGO software and the consistency coefficient of the comparison. It is known that the comparison system exhibit a high level of consistency if the consistency coefficient closer to zero.
Objective weight calculation by the CRITIC method. The objective weight computed based on the provided practical decision data is important for the decision analysis process. In this part, we extend the CRITIC [50] method to SVN environment on the basis of the presented score function for determining the objective weight of the criteria.
First, we identify the correlation coefficient matrix of criteria based on the score function and the normalized group assessment matrix . Assume that denote the correlation coefficient matrix, where stands for the correlation coefficient between the tth criteria and th criteria:
Then, we calculate the standard deviations of criteria with the following equation:
Next, we estimate the quantity of information of every criteria via the following equation
Finally, we compute the objective weight of each criterion with the following equation:
Ascertain the combined weight of the criteria. Based on the BWM approach and SVN-CRITIC method, the synthesize weight of criterion can be identified with the following formula:
in which and are the preference parameter of the subjective weight and objective weight, respectively, and satisfy . From the formulation, we can easily obtain that if , is degenerated as objective weight , and if , is degenerated as objective weight . Decision experts can freely adjust the parameter according to their knowledge experience and actual application condition.
4.5. Ranking by Utilizing the Proposed SVN Regret Theory-MARCOS Approach
This subsection will put forward a novel extension of the MARCOS approach based on the regret theory under an SVN environment to consider the psychological behavioral of expert during the process of decision analysis. In addition, considering that the influence between the perceived utility values of pharmaceutical enterprises under different criteria, the Heronian mean operator is utilized to characterize the interrelationship between perceived utility values under two different criteria of the same pharmaceutical enterprise.
(1) Deduce the utility matrix of the pharmaceutical enterprise. The utility matrix of pharmaceutical enterprise can be calculated based on the presented SVN score function:
where is the score value of group assessment information and can be computed by , is the utility value of pharmaceutical enterprise under diverse criteria, and signifies the risk aversion of expert and is determined by the risk preference of expert.
(2) Determine the positive ideal point vector. Considering the principle of determining the ideal pharmaceutical enterprise, the positive ideal point vector denoted as and positive ideal point under the criteria is computed by the following formula:
(3) Attain the regret matrix of the pharmaceutical enterprise. By comparing it with the positive ideal point of the criteria, the regret matrix of a pharmaceutical enterprise can be identified by:
where is the regret value of pharmaceutical enterprise with respect to criteria . is the utility value of ideal point and signifies the risk aversion of the decision maker.
(4) Compute the perceived utility matrix of pharmaceutical enterprise. In light of Definition 8, we construct the perceived utility valued matrix based on the original utility value and regret value of the pharmaceutical enterprise:
where is the perceived utility value of the pharmaceutical enterprise under the criteria .
(5) Construct the extended perceived utility matrix. Considering that the classical MARCOS method ignores the psychological feature of expert in selecting the optimal pharmaceutical enterprise, we build the MARCOS-based on regret theory to enhance the practicability of the MARCOS algorithm. For every criterion, we first determine the anti-ideal (AID) and the ideal (ID), where AID and ID denote the negative and oppositive solution, respectively:
Then, we add the outcomes of AID and ID to the perceived utility matrix to form an extended perceived utility matrix , displayed as below:
(6) During the procedure of the decision analysis, the interrelationship among the assessment criteria is momentous for acquiring more reasonable decision outcomes. Hence, the comprehensive perceived utility value of pharmaceutical enterprise under all criteria is determined by using the weighted Heronian mean operator:
where is the weight of the criterion j and and are the preference parameters.
(7) After obtaining the comprehensive perceived utility value of the pharmaceutical enterprise, the utility degrees of the pharmaceutical enterprise are worked out with the following formula:
(8) We further calculate the utility functions of pharmaceutical enterprise on the basis of the following equation:
where and indicate the utility function of anti-ideal and ideal point, respectively, which can be computed by , .
(9) Pharmaceutical enterprise ranking. The most satisfactory pharmaceutical enterprise can be determined by the utility functions of the pharmaceutical enterprise. The larger the utility function of the pharmaceutical enterprise, the better the pharmaceutical enterprise.
4.6. The Decision Procedures of the Propounded Approach
As discussed above, the proposed SVN regret theory-MARCOS method including four phases can be summed into thirteen steps and exhibited as follows.
Suppose that a MCGDM problem involves m pharmaceutical enterprises denoted as and n criteria denoted as whose goal is to select the best scheme under the criteria by the group of expert . We will use the proposed regret theory-based SVN-MARCOS method to deal with the MCGDM problem and obtain the optimal pharmaceutical enterprise.
Step 1: Achieving the SVN assessment information. The experts are invited to take part in the assessment and provide their viewpoints with the linguistic terms displayed in Table 3. Then, the SVN assessment matrices can be attained through transforming the linguistic assessments into SVNNs.
Step 2: Determining the expert weight information. The weight of expert is computed by the aid of Equations (9)–(14).
Step 3: Obtaining the normalized SVN group assessment matrix. First, the SVN group assessment matrix is determined by SVNEWA operators displayed in Equation (15). Then, the normalized SVN group assessment matrix is ascertained through Equation (16).
Step 4: Identifying the criteria weight information. The subjective weight of the criteria can be computed by the BWM method according to Equations (17) and (18). Next, the objective weight of the criteria can be worked out by the SVN-CRITIC method by means of Equations (19)–(22). Ultimately, the synthesize weight of the criteria is acquired, drawing support from Equation (23).
Step 5: Deducing the utility matrix of pharmaceutical enterprise. The utility matrix of the pharmaceutical enterprise is obtained using Equation (24).
Step 6: Determining positive ideal point vector. The positive ideal point under the criteria is computed with the aid of Equation (25).
Step 7: Attaining the regret matrix of the pharmaceutical enterprise. The regret matrix of the pharmaceutical enterprise can be identified with Equation (26).
Step 8: Achieving the perceived utility matrix of pharmaceutical enterprise. We construct the perceived utility valued matrix with Equation (27).
Step 9: Construct the extended perceived utility matrix. The extended perceived utility matrix is formed with Equations (28)–(30).
Step 10: Obtaining the comprehensive perceived utility value pharmaceutical enterprise. The comprehensive perceived utility value of the pharmaceutical enterprise is obtained with the help of Equation (31).
Step 11: Computing the utility degrees of the pharmaceutical enterprise. The utility degrees of the pharmaceutical enterprise are worked out using Equations (32) and (33).
Step 12: Computing the utility function of the pharmaceutical enterprise. The utility function of the pharmaceutical enterprise can be figured out with the aid of Equation (34).
Step 13: Ranking pharmaceutical enterprises. The order of pharmaceutical enterprises can be determined by the values of the utility function in descending order. That is, the best pharmaceutical enterprise is the one with the biggest utility function value.
In light of the mentioned decision procedures, a visual flowchart of the developed SVN regret theory-MARCOS group decision methodology is displayed in Figure 2.
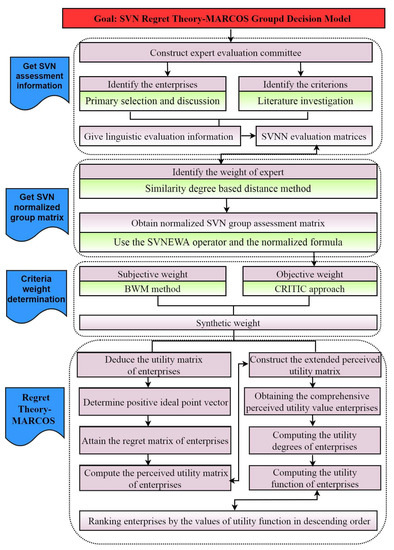
Figure 2.
The SVN regret theory-MARCOS group decision framework.
5. Illustrate Example
This section utilizes the introduced SVN regret theory-MARCOS group decision method for assessing and selecting a satisfactory pharmaceutical enterprises who have a SHQDA to confirm the feasibility and practicability of the proposed group decision framework. Furthermore, the sensitivity analysis and contrast study are also implemented to exhibit the stability and superiority separately.
5.1. Background Introduction
The sudden spread of COVID-19 has brought numerous challenges to human production life, economic development and public health defense. At present, scientists domestically and abroad are devoted to the research and development of new crown pneumonia drugs and have achieved some significant results. In order to further mitigate the epidemic, it is of great importance to choose pharmaceutical enterprises with sustainable and high-quality development capability for drug production and environmental protection. The pharmaceutical management department of a city will choose pharmaceutical enterprises to produce drugs from the perspective of sustainable and high-quality development. After preliminary qualification examination and screening, six enterprises denoted as in the region are selected as candidate enterprises for the evaluation committee to select the best pharmaceutical enterprises under different evaluation criteria. First, the The Pharmaceutical Administration Department invited four experts from the fields of drug research and development, production management and sustainable economic development to form an evaluation committee. Secondly, seven evaluation criteria are determined as the comprehensive evaluation criteria after the collective discussion of the evaluation committee and the investigation of existing literature [1]. The corresponding illustration of the evaluation criteria are shown in Table 4.

Table 4.
Depictions of the criteria for pharmaceutical enterprises ranking.
5.2. Decision Analysis
Due to the uncertainty and complexity of the assessment environment, the expert weight and criterion weight in the assessment process are completely unknown, and experts need to provide comparative preferences between the criteria to determine the subjective weight of the criteria. Based on the evaluation information provided by experts, this section applies the proposed group decision-making method to rank the six pharmaceutical enterprises in the region and select the best pharmaceutical enterprises. The specific decision-making steps and results are as follows.
Step 1: By mean of the linguistic terms listed in Table 3, four experts give their judgements and viewpoint of the pharmaceutical enterprises under the criteria listed in Table 5. Then, SVN assessment matrices can be attained and displayed in Appendix A (Table A1).

Table 5.
SVN assessment matrices provided by experts.
Step 3: Based on the SVNEWA operators displayed in Equation (15), the SVN group assessment matrix is determined and listed in Appendix A (Table A2). Furthermore, we omit the normalization process in this problem because all considered criteria are benefit type, namely, .
Step 4: In this step, we use the BWM and CRITIC method to determine the subjective and objective weight of the criteria, respectively. After a discussion by the evaluation committee, the criteria and are ascertained as the best criteria and worst criteria, respectively. Furthermore, the assessment committee provides the preference of criteria compared to other criteria and other criteria compared to the worst criteria , which are displayed in Table 6.

Table 6.
Pairwise comparison of the best criteria and worst criteria with other criteria.
By means of the following model, the subjective weight of the criteria can be ascertained:
By means of Equations (17) and (18), the subjective weights of the criteria are identified as: Furthermore, , . The objective weights of the criteria are computed through Equations (19)–(22) and listed as: Furthermore, the synthesize weight based on Equation (23) is figured out as
Step 5: The utility matrix of the pharmaceutical enterprise is calculated by Equation (24) and placed in Table 7. Here, is assigned as 0.88.

Table 7.
The utility matrix of the pharmaceutical enterprise.
Step 6: The ideal point under the criteria computed based on Equation (25) is determined as:
Here, is assigned as 0.88.
Step 7: Using Equation (26), the regret matrix of pharmaceutical enterprise can be identified, and placed in Table 8, is fitted as 0.3.

Table 8.
The regret matrix of pharmaceutical enterprises.
Step 8: Utilizing Equation (27), the perceived utility valued matrix can be attained, as exhibited in Table 9.

Table 9.
The perceived utility valued matrix of pharmaceutical enterprises.
Step 9: The extended perceived utility matrix is formed by using Equations (28)–(30), as shown in Table 10.

Table 10.
The extended perceived utility matrix of pharmaceutical enterprises.
Step 10: Utilizing Equation (31), the comprehensive perceived utility values of pharmaceutical enterprise are calculated as ; and are set as .
Step 11: Using Equations (32) and (33), the utility degrees of pharmaceutical enterprises are as below:
Step 12: The utility function of pharmaceutical enterprise can be worked out by Equation (34), displayed as:
Step 13: Based on the value of utility function of pharmaceutical enterprise, we can obtain the order relation of pharmaceutical enterprise as ; thus, the best pharmaceutical enterprise is .
5.3. Sensitivity Analysis
This section will conduct a sensitivity discussion to analyze the impact of different variables on the ranking of pharmaceutical enterprises. In the calculation process of the evaluation model of pharmaceutical enterprises from the perspective of sustainable and high-quality development, different prioritization results of pharmaceutical enterprises will be attained by setting diverse variables or parameters, which will affect the decision making of pharmaceutical management departments under different criteria. As a consequence, it is necessary to analyze the impact of different variables and parameters on the final ranking results. In this paper, the presented SVNS regret theory-MARCOS method involves the following three variables, different types of criteria weight, the preference parameters in the comprehensive weight and the parameters in Heronian mean operator. Based on the determination of those parameters, the sensitivity analysis is carried out by taking different parameter values. A detailed analysis will be implemented as follows.
Different types of weight analyses. In the proposed SVNS regret-MARCOS method, in order to enhance the feasibility of the advanced method in this paper, the combined weight of criteria is employed to acquire a more accurate rank of pharmaceutical enterprises. Considering the influence produced by different types of criteria weights, we apply different kinds of weights to recompute the mentioned empirical results; the corresponding results are displayed in Table 11 and Figure 3 (). From Table 11, it can be found that the ranks of pharmaceutical enterprises obtained by different kinds of weight is basically consistent, and the most satisfactory pharmaceutical enterprise is , which further illustrates the stability of the propounded approach in this paper. Next, we further discuss the decision results derived by the different comprehensive weight based on setting diverse parameters and .

Table 11.
The impact of different weight types for the ultimate decision results.
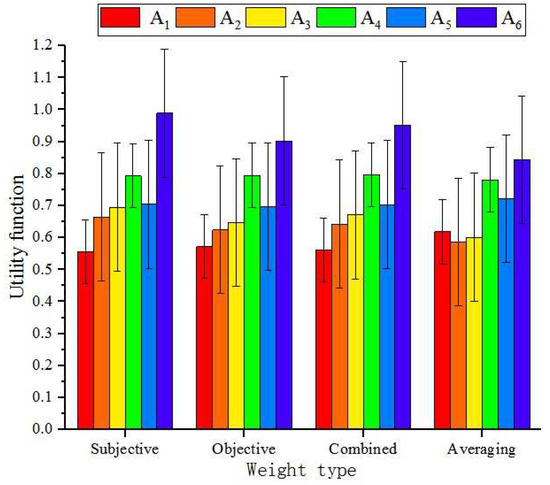
Figure 3.
Decision results obtained by different types of weight.
Combined weight analysis based on different preference parameters. In the proposed SVNS regret-MARCOS method, an adjustable combined weight model using two preference parameters and is employed for experts to select appropriate criteria weights. The parameters and can be regarded as the importance of subjective weight and objective weight. In the process of dealing with different practical decision problems, experts determine the criteria weight according to the subjectivity of the experts and the objectivity of the decision data; hence, selecting a suitable preference to determine the final weight is important for experts to acquire a more reasonable decision result. Based on the range of and , we take the values of from 0 to 1 and obtain the homologous utility functions and ranks of pharmaceutical enterprise, which are shown in Table 12 and Figure 4. Based on Table 12, we can observe that no matter how the value changes, the sorting of the rank of pharmaceutical enterprises is always . Accordingly, the proposed SVNS regret-MARCOS method is stable under different weights combination. Therefore, the presented SVNS regret-MARCOS method can provide a more stable decision outcome for selecting the optimal pharmaceutical enterprise.

Table 12.
The ultimate decision results obtained by different parameters and .
Figure 4.
The ultimate decision results obtained with different parameters and .
Comprehensive perceived utility value analysis based on different parameters in Heronian mean. In the suggested SVNS regret-MARCOS approach, we determine the comprehensive perceived utility value of pharmaceutical enterprises by utilizing the Heronian mean operator to consider the interrelationship of the perceived utility values under the criteria. The preference parameters and can flexibly control the information fusion procedure and attain a more rational comprehensive perceived utility value of the pharmaceutical enterprise. We set diverse values of and and obtain the corresponding comprehensive perceived utility values listed in Table 13. As seen in Table 13, the final ranks of the pharmaceutical enterprise is relatively stable for different parameter values of and , the best option is always the sixth pharmaceutical enterprise.

Table 13.
The ultimate decision results obtained by different parameters and .
5.4. Comparison Study
This subsection will implement a comparison study by utilizing the extant SVNS decision approaches to cope with the mentioned pharmaceutical enterprise assessment problem to further verify the efficiency and rationality of the advanced SVNS regret-MARCOS approach. By means of a literature overview, we can find that the existing decision approaches for SVN main include aggregation-based methods and the improvement of classical decision methods. Hence, the comparison utilizes the following methods to finish the comparison analysis, involving SVN weighted averaging and geometric operator [12], SVN Einstein averaging and geometric operator [12], SVN-WSM [25], SVN-WPM [25], SVN-WASPAS [25] and SVN-TOPSIS [17]. In order to guarantee the rationality of the comparison process, we utilize the combined weight determined to solve the numerical by the mentioned SVN approaches in this paper; the ranking value and rank are displayed in Table 14.

Table 14.
The impact of different weight types for the ultimate decision results.
Efficiency analysis. It can be seen from Table 15 that the results of ranking pharmaceutical enterprise by the proffered SVN regret theory-MARCOS approach are basically consistent with the previous SVN decision method [12,17,25]. The most satisfactory pharmaceutical enterprise determined by the SVNWA and SVNWG operator, SVNEWA and SVNEWG operator, SVN-WSM method, SVN-WPM method, SVN-WASPAS method, SVN-TOPSIS method and the method suggested in this paper is the sixth pharmaceutical enterprise. Hence, the validity and applicability of the designed SVN regret theory-MARCOS approach are verified. Furthermore, we provide a detailed discussion of the existing SVN approach and highlight the merits of the presented approach.

Table 15.
Characteristic comparison between the propounded methods and other SVN decision approaches.
Further analysis. For the extant SVNS decision approaches mentioned in this paper, the SVNWA operator, SVNWG operator, SVNEWA operator and SVNEWG operator are all aggregation-based decision methods, which obtain the ranks of pharmaceutical enterprise by aggregating the preference value of each pharmaceutical enterprise under different criteria. However, although those methods can obtain the rank values of pharmaceutical enterprises rapidly, those methods fail to consider the objective weight determination and the psychological behavioral of decision makers. Furthermore, the SVN-WSM method, SVN-WPM method, SVN-WASPAS method and SVN-TOPSIS method are determined by the final rank values of pharmaceutical enterprises on the basis of the utility theory, which states that experts are completely rational in the decision-making process. Obviously, this assumption will lead to unreasonable decision outcomes, owing to the complicated of realistic decision settings. Nevertheless, the propounded not only considers the combined weight of criteria by BWM and CRITIC methods but also takes the psychological preference of experts into consideration in assessment of the pharmaceutical enterprise, which effectively conquer the defect derived from the previous SVN decision methodology.
By the aid of the aforementioned comparison analysis, we further derive the conspicuous characteristics of these compared approaches according to the main characteristics of the MCGDM process, which are exhibited in Table 15. As seen in Table 15, we analyze the important feature of every method to further highlight the unique superiority of the developed method in this paper. In light of the above discussion, several advantages of the introduced SVNS regret theory-MARCOS approach are outlined as below:
- ✠
- The proposed SVNS regret theory-MARCOS approach can effectively cope with the practical uncertain assessment problems when the criteria weight and expert weight are all complete unknown.
- ✠
- The suggested method is built by an innovative SVNS score function, which further provides more credible outcome than other existing score functions.
- ✠
- The weight information of the assessment criteria takes the subjective preference and actual decision information simultaneously into account, which further enhances the reliability and credibility of the ranks in dealing with complex assessment problems.
- ✠
- The propounded SVNS regret theory-MARCOS method takes both the advantages of regret theory and MARCOS method, which comprehensively considers the psychological preference of experts and the utility function theory of decision information to attain a more credible and robust decision outcomes.
6. Conclusions
The ability of sustainable and high-quality development is one of the important indicators for pharmaceutical enterprises to win the core competitiveness under the background of green economic development. Evaluating pharmaceutical enterprises from the perspective of sustainable and high-quality development can provide valuable guidance strategies for pharmaceutical management departments in formulating development plans and rectification of pharmaceutical enterprises. In this paper, a hybrid assessment framework integrating regret theory, MARCOS method and Heronian mean operator under SVNS environment is constructed to cope with the pharmaceutical enterprises assessment problem with uncertainty. The proposed assessment framework can attain more reasonable and credible decision outcomes for experts by comprehensive considering the uncertainty, psychological impact of experts and intrinsic relevance in the course of assessment. First, we present a new SVNS score function to strengthen the validity and rationality of the SVNN comparison. Then, we determine the criteria weight by aggregating the BWM and improved SVN-CRITIC method using the proposed score function. Afterwards, we propound a hybrid assessment framework through aggregating the regret theory, MARCOS method and Heronian mean operator under a single-valued neutrosophic context. Furthermore, the case illustrates the applicability and feasibility of the presented assessment framework. Finally, the comparison and sensitivity study demonstrate the stability, superiority and rationality of the developed method. The proposed uncertain assessment framework possesses the following merits in dealing with the pharmaceutical enterprises’ assessment problem: (1) it can fully express the cognition preference of expert by considering three angles, including truth-membership, indeterminacy-membership and falsity-membership; (2) it can take into account the psychological behavioral factors of evaluators in the process of assessment; (3) it can validly settle the uncertain assessment issues when the weight information is completely unknown because of the ambiguity and indeterminacy of assessment environment; (4) it also considers the interrelation of diverse criteria and the comparison with anti-ideal and ideal solutions in the course of the assessment.
The investigation possesses several limitations when implementing the decision analysis. The criteria in this study are attained with the help of expert consultation and a literature research, which cannot guarantee that all criteria are considered. Thus, a comprehensive assessment index systems should be established by means of various aspects. Moreover, owing to the conflict and inconsistency of criteria, the interrelationship among the considered criteria should be considered in the course of expert information aggregation. Furthermore, we also had to take into account the consensus-reaching process of experts to achieve more robust and rational decision outcomes.
In the future, we will go on to develop the construction of uncertain assessment framework for addressing complex uncertain assessment issues. First, some novel decision models, namely the Simple Weighted Sum-Product method and MULTIMOOSRAL approach, can be constructed on the basis of the proposed score function. Additionally, we can introduce more decision models by combining the behavioral decision theories and decision algorithms to analyze the psychological cognition behavioral of expert. Moreover, we also employ the introduced assessment framework to address other realistic decision problems, such as renewable energy project management [51], food waste treatment technology selection [52] and a selection of desalination technology [53].
Author Contributions
Conceptualization, Y.R. and W.N.; Formal analysis, Y.R. and W.N.; Funding acquisition, L.Y.; Methodology, Y.R., W.N., H.G. and Y.L.; Project administration, L.Y.; Resources, Y.L.; Visualization, H.G. and Y.L.; Writing—original draft, Y.R.; Writing—review and editing, Y.R., W.N., H.G., Y.L. and L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Research Fund Program of Data Recovery Key Laboratory of Sichuan Province (No. DRN19014); the Scientific Research Project of Neijiang Normal University (No. 2018TD08); and the Application basic research project of Sichuan Province (No. 2021JY0108).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Samples of the compounds are available from the authors.
Abbreviations
The following abbreviations displayed as below:
| Full Name | Abbreviation | |
| Sustainable and High-Quality Development Ability | SHQDA | |
| Measurement Alternatives and Ranking based on the COmpromise Solution | MARCOS | |
| Multi Criteria Group Decision-Making | MCGDM | |
| Single-Valued Neutrosophic Set | SVNS | |
| Single-Valued Neutrosophic Number | SVNN | |
| CRiteria Importance Through Intercriteria Correlation | CRITIC | |
| Best and Worst Method | BWM | |
| Intuitionistic Fuzzy Set | IFS | |
| Single-Valued Neutrosophic | SVN | |
| Multi objective optimization based on the ratio analysis with the full multiplicative form | MULTIMOORA | |
| Technique for Order Preference by Similarity to an Ideal Solution | TOPSIS | |
| VIse KriterijumsaOptimiz acija I Kompromisno Resenje | VIKOR | |
| Mixed Aggregation by COmprehensive Normalization Technique | MACONT | |
| Weighted Aggregated Sum Product ASsessment | WASPAS | |
| LINear programming technique for Multidimensional Analysis of Preference | LINMAP | |
| Single-Valued Neutrosophic weighted averaging operator | SVNWA | |
| Single-Valued Neutrosophic geometric operator | SVNWG | |
| Single-Valued Neutrosophic Einstein weighted averaging operator | SVNEWA | |
| Single-Valued Neutrosophic Einstein geometric operator | SVNEWG |
Appendix A

Table A1.
SVN assessment matrices provided by experts.
Table A1.
SVN assessment matrices provided by experts.
| Expert | Pharmaceutical Enterprises | |||||||
|---|---|---|---|---|---|---|---|---|
| (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.90, 0.10, 0.10) | (0.80, 0.15, 0.20) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | (0.70, 0.25, 0.30) | ||
| (0.60, 0.35, 0.40) | (0.10, 0.90, 0.90) | (0.80, 0.15, 0.20) | (0.60, 0.35, 0.40) | (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.60, 0.35, 0.40) | ||
| (0.70, 0.25, 0.30) | (0.40, 0.65, 0.60) | (0.70, 0.25, 0.30) | (0.40, 0.65, 0.60) | (0.90, 0.10, 0.10) | (0.70, 0.25, 0.30) | (0.40, 0.65, 0.60) | ||
| (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | (0.60, 0.35, 0.40) | ||
| (0.50, 0.50, 0.50) | (0.60, 0.35, 0.40) | (0.40, 0.65, 0.60) | (0.90, 0.10, 0.10) | (0.60, 0.35, 0.40) | (0.90, 0.10, 0.10) | (0.50, 0.50, 0.50) | ||
| (0.60, 0.35, 0.40) | (0.50, 0.50, 0.50) | (0.60, 0.35, 0.40) | (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.40, 0.65, 0.60) | ||
| (0.60, 0.35, 0.40) | (0.60, 0.35, 0.40) | (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.60, 0.35, 0.40) | (0.60, 0.35, 0.40) | ||
| (0.60, 0.35, 0.40) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.60, 0.35, 0.40) | (0.60, 0.35, 0.40) | (0.70, 0.25, 0.30) | (0.40, 0.65, 0.60) | ||
| (0.50, 0.50, 0.50) | (0.30, 0.75, 0.70) | (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.60, 0.35, 0.40) | (0.60, 0.35, 0.40) | (0.50, 0.50, 0.50) | ||
| (0.80, 0.15, 0.20) | (0.10, 0.90, 0.90) | (0.60, 0.35, 0.40) | (0.90, 0.10, 0.10) | (0.50, 0.50, 0.50) | (0.90, 0.10, 0.10) | (0.40, 0.65, 0.60) | ||
| (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.60, 0.35, 0.40) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | ||
| (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | (0.80, 0.15, 0.20) | (0.90, 0.10, 0.10) | (0.80, 0.15, 0.20) | (0.60, 0.35, 0.40) | ||
| (0.50, 0.50, 0.50) | (0.50, 0.50, 0.50) | (0.60, 0.35, 0.40) | (0.40, 0.65, 0.60) | (0.30, 0.75, 0.70) | (0.50, 0.50, 0.50) | (0.10, 0.90, 0.90) | ||
| (0.60, 0.35, 0.40) | (0.70, 0.25, 0.30) | (0.50, 0.50, 0.50) | (0.50, 0.50, 0.50) | (0.80, 0.15, 0.20) | (0.40, 0.65, 0.60) | (0.10, 0.90, 0.90) | ||
| (0.50, 0.50, 0.50) | (0.80, 0.15, 0.20) | (0.40, 0.65, 0.60) | (0.70, 0.25, 0.30) | (0.70, 0.25, 0.30) | (0.60, 0.35, 0.40) | (0.60, 0.35, 0.40) | ||
| (0.90, 0.10, 0.10) | (0.70, 0.25, 0.30) | (0.50, 0.50, 0.50) | (0.80, 0.15, 0.20) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | (0.40, 0.65, 0.60) | ||
| (0.10, 0.90, 0.90) | (0.80, 0.15, 0.20) | (0.40, 0.65, 0.60) | (0.60, 0.35, 0.40) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.60, 0.35, 0.40) | ||
| (0.60, 0.35, 0.40) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.50, 0.50, 0.50) | (0.70, 0.25, 0.30) | (0.10, 0.90, 0.90) | ||
| (0.60, 0.35, 0.40) | (0.50, 0.50, 0.50) | (0.30, 0.75, 0.70) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | (0.70, 0.25, 0.30) | (0.80, 0.15, 0.20) | ||
| (0.70, 0.25, 0.30) | (0.40, 0.65, 0.60) | (0.40, 0.65, 0.60) | (0.60, 0.35, 0.40) | (0.60, 0.35, 0.40) | (0.80, 0.15, 0.20) | (0.60, 0.35, 0.40) | ||
| (0.80, 0.15, 0.20) | (0.30, 0.75, 0.70) | (0.50, 0.50, 0.50) | (0.70, 0.25, 0.30) | (0.60, 0.35, 0.40) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | ||
| (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | (0.40, 0.65, 0.60) | (0.60, 0.35, 0.40) | (0.90, 0.10, 0.10) | (0.60, 0.35, 0.40) | (0.50, 0.50, 0.50) | ||
| (0.60, 0.35, 0.40) | (0.40, 0.65, 0.60) | (0.60, 0.35, 0.40) | (0.90, 0.10, 0.10) | (0.80, 0.15, 0.20) | (0.50, 0.50, 0.50) | (0.80, 0.15, 0.20) | ||
| (0.60, 0.35, 0.40) | (0.50, 0.50, 0.50) | (0.50, 0.50, 0.50) | (0.80, 0.15, 0.20) | (0.80, 0.15, 0.20) | (0.80, 0.15, 0.20) | (0.90, 0.10, 0.10) |

Table A2.
SVN group assessment matrix.
Table A2.
SVN group assessment matrix.
| Pharmaceutical Enterprises | |||||||
|---|---|---|---|---|---|---|---|
| (0.6461, 0.3074, 0.3539) | (0.5850, 0.3836, 0.4150) | (0.6328, 0.3350, 0.3672) | (0.6821, 0.2754,0.3179) | (0.7008, 0.2524, 0.2992) | (0.6241, 0.3390, 0.3759) | (0.5871, 0.3603, 0.4129) | |
| (0.6286, 0.3209, 0.3714) | (0.5001, 0.4743, 0.4999) | (0.6658, 0.2986, 0.3342) | (0.5799, 0.3788,0.4201) | (0.7094, 0.2367, 0.2906) | (0.6823, 0.2752, 0.3177) | (0.5315, 0.4487, 0.4685) | |
| (0.6512, 0.3107, 0.3488) | (0.4685, 0.5392, 0.5315) | (0.6344, 0.3331, 0.3656) | (0.6358, 0.3283,0.3642) | (0.7327, 0.2384, 0.2673) | (0.6888, 0.2585, 0.3112) | (0.4984, 0.4999, 0.5016) | |
| (0.8069, 0.1579, 0.1931) | (0.5678, 0.3905, 0.4322) | (0.5032, 0.4923, 0.4968) | (0.7733, 0.1954,0.2267) | (0.7834, 0.1893, 0.2166) | (0.6990, 0.2796, 0.3010) | (0.4834, 0.5213, 0.5166) | |
| (0.6233, 0.3399, 0.3767) | (0.6376, 0.3241, 0.3624) | (0.5853, 0.3921, 0.4147) | (0.8171, 0.1685,0.1829) | (0.6844, 0.2628, 0.3156) | (0.6695, 0.2913, 0.3305) | (0.6200, 0.3450, 0.3800) | |
| (0.6282, 0.3213, 0.3718) | (0.6413, 0.3227, 0.3587) | (0.6072, 0.3591, 0.3928) | (0.8168, 0.1511,0.1832) | (0.7690, 0.2042, 0.2310) | (0.7815, 0.1677, 0.2185) | (0.6625, 0.3341, 0.3375) |
References
- Dong, J.; Ju, Y.; Dong, P.; Giannakis, M.; Wang, A.; Liang, Y.; Wang, H. Evaluate and select state-owned enterprises with sustainable high-quality development capacity by integrating FAHP-LDA and bidirectional projection methods. J. Clean. Prod. 2021, 329, 129771. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Haiyun, C.; Zhixiong, H.; Yüksel, S.; Dinçer, H. Analysis of the innovation strategies for green supply chain management in the energy industry using the QFD-based hybrid interval valued intuitionistic fuzzy decision approach. Renew. Sust. Energ. Rev. 2021, 143, 110844. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. An efficient intuitionistic fuzzy MULTIMOORA approach based on novel aggregation operators for the assessment of solid waste management techniques. Appl. Intell. 2021, 52, 4330–4363. [Google Scholar] [CrossRef]
- Xie, D.; Xiao, F.; Pedrycz, W. Information quality for intuitionistic fuzzy values with its application in decision making. Eng. Appl. Artif. Intell. 2022, 109, 104568. [Google Scholar] [CrossRef]
- Zeng, S.; Zhou, J.; Zhang, C.; Merigó, J.M. Intuitionistic fuzzy social network hybrid MCDM model for an assessment of digital reforms of manufacturing industry in China. Technol. Forecast. Soc. Chang. 2022, 176, 121435. [Google Scholar] [CrossRef]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Risk assessment of renewable energy investments: A modified failure mode and effect analysis based on prospect theory and intuitionistic fuzzy AHP. Energy 2022, 239, 121907. [Google Scholar] [CrossRef]
- Smarandache, F. A unifying field in Logics: Neutrosophic Logic. In Philosophy; American Research Press: Santa Fe, NM, USA, 1999; pp. 1–141. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single Valued Neutrosophic Sets. Multispace Multistruct. 2010, Volume 4, pp. 410–413. Available online: http://fs.unm.edu/SingleValuedNeutrosophicSets.pdf (accessed on 1 July 2022).
- Şahin, R. Multi-criteria neutrosophic decision making method based on score and accuracy functions under neutrosophic environment. arXiv 2014, arXiv:1412.5202. [Google Scholar]
- Liu, P. The aggregation operators based on archimedean t-conorm and t-norm for single-valued neutrosophic numbers and their application to decision making. Int. J. Fuzzy Syst. 2016, 18, 849–863. [Google Scholar] [CrossRef]
- Huang, H.L. New distance measure of single-valued neutrosophic sets and its application. Int. J. Intell. Syst. 2016, 31, 1021–1032. [Google Scholar] [CrossRef]
- Garg, H. An improved score function for ranking neutrosophic sets and its application to decision-making process. Int. J. Uncertain Quantif. 2016, 6, 377–385. [Google Scholar]
- Özlü, Ş. Generalized Dice measures of single valued neutrosophic type-2 hesitant fuzzy sets and their application to multi-criteria decision making problems. Int. J. Mach. Learn. Cybern. 2022, 1–30. [Google Scholar] [CrossRef]
- Garg, H. SVNMPR: A new single-valued neutrosophic multiplicative preference relation and their application to decision-making process. Int. J. Intell. Syst. 2022, 37, 2089–2130. [Google Scholar] [CrossRef]
- Garg, H. A novel divergence measure and its based TOPSIS method for multi criteria decision-making under single-valued neutrosophic environment. J. Intell. Fuzzy Syst. 2019, 36, 101–115. [Google Scholar]
- Mishra, A.R.; Rani, P.; Mardani, A.; Pardasani, K.R.; Govindan, K.; Alrasheedi, M. Healthcare evaluation in hazardous waste recycling using novel interval-valued intuitionistic fuzzy information based on complex proportional assessment method. Comput. Ind. Eng. 2020, 139, 106140. [Google Scholar] [CrossRef]
- Pamucar, D.; Deveci, M.; Schitea, D.; Erişkin, L.; Iordache, M.; Iordache, I. Developing a novel fuzzy neutrosophic numbers based decision making analysis for prioritizing the energy storage technologies. Int. J. Hydrogen Energy 2020, 45, 23027–23047. [Google Scholar] [CrossRef]
- Sun, Y.; Cai, Y. A Flexible Decision-Making Method for Green Supplier Selection Integrating TOPSIS and GRA Under the Single-Valued Neutrosophic Environment. IEEE Access 2021, 9, 83025–83040. [Google Scholar] [CrossRef]
- Ye, J. Single valued neutrosophic cross-entropy for multicriteria decision making problems. Appl. Math. Modell. 2014, 38, 1170–1175. [Google Scholar] [CrossRef]
- Smarandache, F. The Score, Accuracy, and Certainty Functions determine a Total Order on the Set of Neutrosophic Triplets (T, I, F). Neutrosophic Sets Syst. 2020, 38, 1–14. [Google Scholar] [CrossRef]
- Nafei, A.; Javadpour, A.; Nasseri, H.; Yuan, W. Optimized score function and its application in group multiattribute decision making based on fuzzy neutrosophic sets. Int. J. Intell. Syst. 2021, 36, 7522–7543. [Google Scholar] [CrossRef]
- Rong, Y.; Liu, Y.; Pei, Z. Generalized single-valued neutrosophic power aggregation operators based on Archimedean copula and co-copula and their application to multi-attribute decision-making. IEEE Access 2020, 8, 35496–35519. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Prajapati, R.S. Multi-criteria weighted aggregated sum product assessment method for sustainable biomass crop selection problem using single-valued neutrosophic sets. Appl. Soft Comput. 2021, 113, 108038. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Krishankumar, R.; Ravichandran, K.S.; Kar, S. Multi-criteria food waste treatment method selection using single-valued neutrosophic-CRITIC-MULTIMOORA framework. Appl. Soft Comput. 2021, 111, 107657. [Google Scholar] [CrossRef]
- Tan, R.; Yang, L.; Chen, S.; Zhang, W. Decision-making method based on game theory and grey theory in a single-value neutrosophic environment and its application to typhoon disaster assessment. Grey Syst. Theory Appl. 2021. [Google Scholar] [CrossRef]
- Pamucar, D.; Ecer, F.; Deveci, M. Assessment of alternative fuel vehicles for sustainable road transportation of United States using integrated fuzzy FUCOM and neutrosophic fuzzy MARCOS methodology. Sci. Total Environ. 2021, 788, 147763. [Google Scholar] [CrossRef] [PubMed]
- Solangi, Y.A.; Longsheng, C.; Shah, S.A.A. Assessing and overcoming the renewable energy barriers for sustainable development in Pakistan: An integrated AHP and fuzzy TOPSIS approach. Renew. Energy 2021, 173, 209–222. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Z.; Xu, Z.; Gou, X.; Herrera, F. Score function based on concentration degree for probabilistic linguistic term sets: An application to TOPSIS and VIKOR. Inf. Sci. 2021, 551, 270–290. [Google Scholar] [CrossRef]
- Wen, Z.; Liao, H. Pension service institution selection by a personalized quantifier-based MACONT method. Int. J. Strateg. Prop. Manag. 2021, 25, 446–458. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Fan, J.; Wang, S.; Wu, M. An integrated FMEA approach using Best-Worst and MARCOS methods based on D numbers for prioritization of failures. J. Intell. Fuzzy Syst. 2021, 41, 2833–2846. [Google Scholar] [CrossRef]
- Pamucar, D.; Yazdani, M.; Montero-Simo, M.J.; Araque-Padilla, R.A.; Mohammed, A. Multi-criteria decision analysis towards robust service quality measurement. Expert Syst. Appl. 2021, 170, 114508. [Google Scholar] [CrossRef]
- Gong, X.; Yang, M.; Du, P. Renewable energy accommodation potential evaluation of distribution network: A hybrid decision-making framework under interval type-2 fuzzy environment. J. Clean. Prod. 2021, 286, 124918. [Google Scholar] [CrossRef]
- Torkayesh, A.E.; Zolfani, S.H.; Kahvand, M.; Khazaelpour, P. Landfill location selection for healthcare waste of urban areas using hybrid BWM-grey MARCOS model based on GIS. Sustain. Cities Soc. 2021, 67, 102712. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. MARCOS technique under intuitionistic fuzzy environment for determining the COVID-19 pandemic performance of insurance companies in terms of healthcare services. Appl. Soft Comput. 2021, 104, 107199. [Google Scholar] [CrossRef] [PubMed]
- Kundu, P.; Görçün, Ö.F.; Küçükönder, H. Medical device selection in private hospitals by integrated fuzzy MCGDM methods: A case study in choosing MRI (Magnetic Resonance Imaging) system. J. Oper. Res. Soc. 2021, 1–21. [Google Scholar] [CrossRef]
- Ali, J. A q-rung orthopair fuzzy MARCOS method using novel score function and its application to solid waste management. Appl. Intell. 2021, 1–23. [Google Scholar] [CrossRef]
- Vesković, S.; Stević, Ž.; Nunić, Z.; Milinković, S.; Mladenović, D. A novel integrated large-scale group MCDM model under fuzzy environment for selection of reach stacker in a container terminal. Appl. Intell. 2022, 1–25. [Google Scholar] [CrossRef]
- Darko, A.P.; Liang, D. A heterogeneous opinion-driven decision-support model for tourists’ selection with different travel needs in online reviews. J. Oper. Res. Soc. 2022, 1–18. [Google Scholar] [CrossRef]
- Boral, S.; Chaturvedi, S.K.; Howard, I.M.; McKee, K.; Naikan, V.A. An integrated approach for fuzzy failure mode and effect analysis using fuzzy AHP and fuzzy MARCOS. In Proceedings of the 2020 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 14–17 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 395–400. [Google Scholar]
- Yazdani, M.; Torkayesh, A.E.; Stević, Ž.; Chatterjee, P.; Ahari, S.A.; Hernandez, V.D. An interval valued neutrosophic decision-making structure for sustainable supplier selection. Expert Syst. Appl. 2021, 183, 115354. [Google Scholar] [CrossRef]
- Boral, S.; Chaturvedi, S.K.; Howard, I.; Naikan, V.N.A.; McKee, K. An integrated interval type-2 fuzzy sets and multiplicative half quadratic programming-based MCDM framework for calculating aggregated risk ranking results of failure modes in FMECA. Process Saf. Environ. Prot. 2021, 150, 194–222. [Google Scholar] [CrossRef]
- Mešić, A.; Miškić, S.; Stević, Ž.; Mastilo, Z. Hybrid MCDM solutions for evaluation of the logistics performance index of the western balkan countries. Econ. Innov. Res. J. 2022, 10, 13–34. [Google Scholar]
- Loomes, G.; Sugden, R. Regret theory: An alternative theory of rational choice under uncertainty. Econ. J. 1982, 92, 805–824. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Quiggin, J. Regret theory with general choice sets. J. Risk Uncertain. 1994, 8, 153–165. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Gong, C.; Dinçer, H.; Yüksel, S. An integrated hesitant 2-tuple Pythagorean fuzzy analysis of QFD-based innovation cost and duration for renewable energy projects. Energy 2022, 248, 123561. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Saha, A.; Hezam, I.M.; Pamucar, D. Fermatean fuzzy Heronian mean operators and MEREC-based additive ratio assessment method: An application to food waste treatment technology selection. Int. J. Intell. Syst. 2022, 37, 2612–2647. [Google Scholar] [CrossRef]
- Mishra, A.R.; Liu, P.; Rani, P. COPRAS method based on interval-valued hesitant Fermatean fuzzy sets and its application in selecting desalination technology. Appl. Soft Comput. 2022, 119, 108570. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).