Stock Price Crash Warning in the Chinese Security Market Using a Machine Learning-Based Method and Financial Indicators
Abstract
1. Introduction
2. Background
2.1. XGBoost
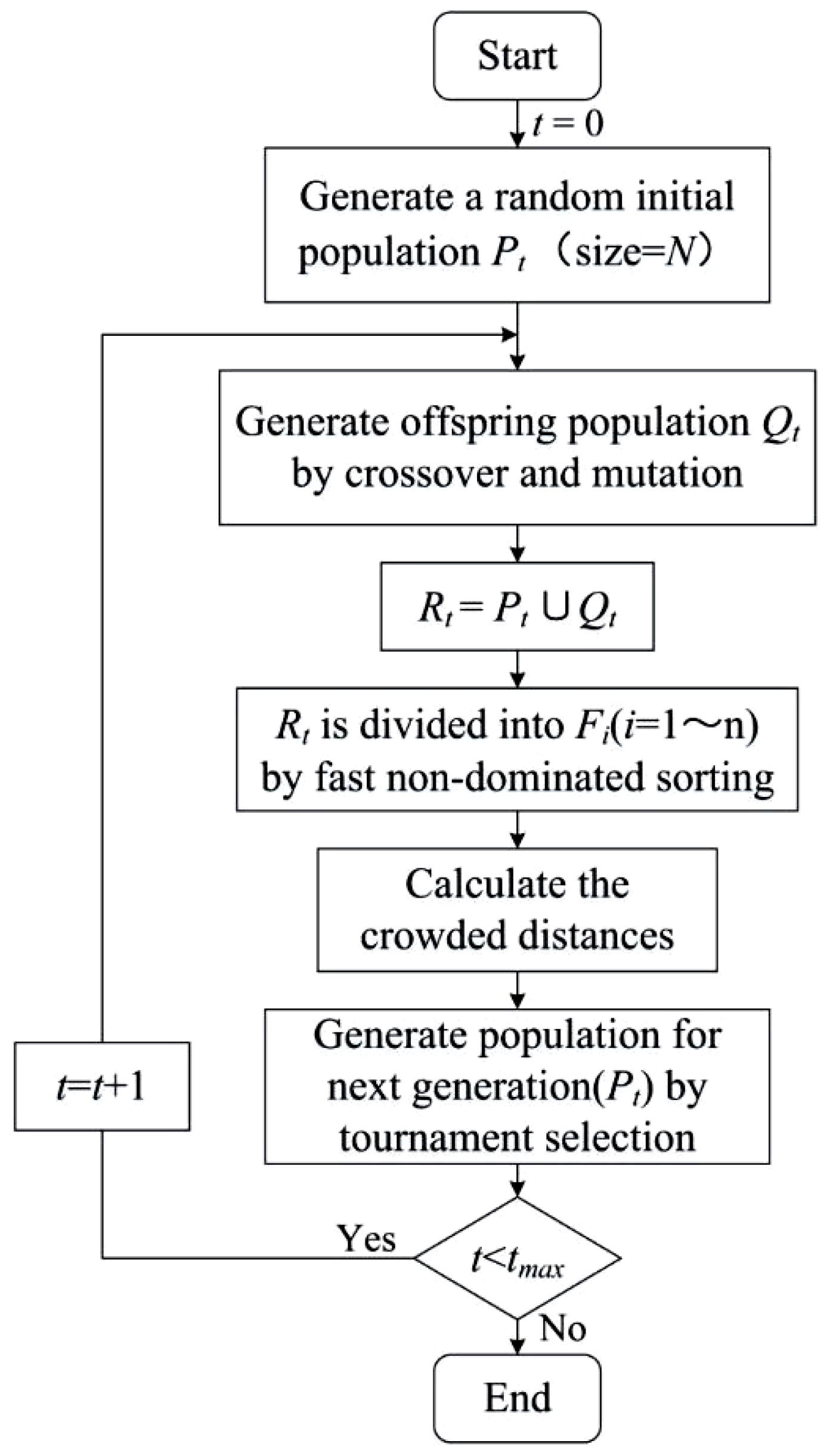
2.2. NSGA-II
- (1)
- Firstly, an initial population of N individuals is randomly generated.
- (2)
- They are then selected, crossed, and mutated to obtain the first-generation offspring population.
- (3)
- Next, from the second generation, the parent populations are merged with the offspring populations for the fast non-dominated sorting. In the meanwhile, the crowding distance is calculated for the individuals in each non-dominance layer, and the appropriate individuals are selected to form a new parent population based on the non-dominance relationship and the crowding distance of the individuals.
- (4)
- Finally, new offspring populations are generated by the basic operations of the genetic algorithm, and the above steps are repeated until the maximum number of iterations is reached. At that time, the operation is stopped, and the Pareto-optimal solution for multi-objective optimization is generated.
2.3. SHAP
- (1)
- Local accuracy
- (2)
- Missingness
- (3)
- Consistency
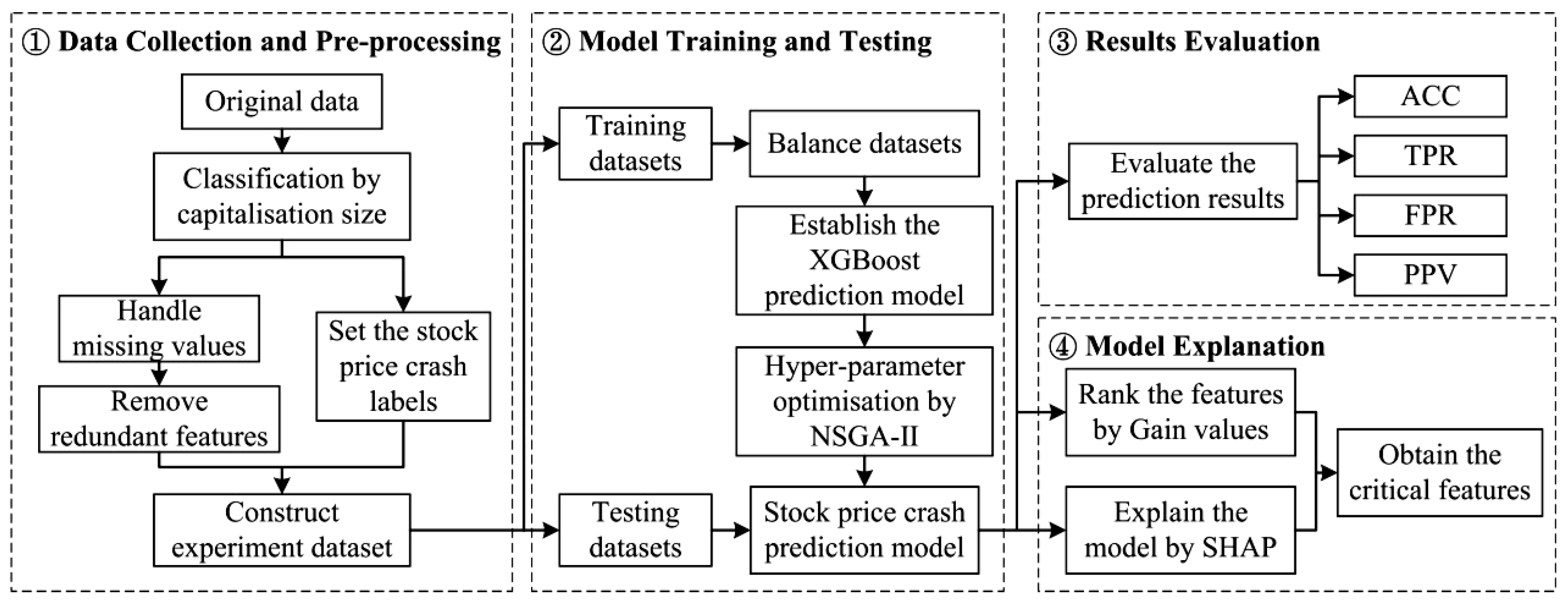
3. Proposed Method
- (1)
- Data Collection and Pre-processing component
- (2)
- Model Training and Testing component
- (3)
- Results Evaluation component
- (4)
- Model Explanation component
4. Experimental Design
4.1. Experiment Data
- (1)
- Weekly returns of individual stocks and weekly value-weighted market returns of the Chinese stock market ranging from 2015 to 2020 are derived from the CSMAR and RESSET databases.
- (2)
- The firm-specific weekly returns from the expanded market model regression are calculated by:where is the return of stock j in the week T; denotes the value-weighted market returns in the week T. The firm-specific weekly return is measured using the equation , where is the firm-specific weekly return for the stock j in the week T. is the residual return in Equation (12). Therefore, the occurrence of crashes is measured based on the number of firm-specific weekly returns exceeding 3.09 standard deviations below or above their average value in the given quarter, with 3.09 standard deviations chosen to generate profitability of 0.1% in the normal distribution. In other words, if a company satisfies the equation at least once within a season, it could suggest that the company experienced a stock price crash during that period, and therefore its stock crash label is set to 1 (CRASH = 1).
- (1)
- Samples of individual stocks in the same industry that did not experience a stock crash in the same period are selected as non-crash samples, with their labels set to 0 (CRASH = 0), and the ratio of stock-crash samples to non-crash samples in the dataset is 1:1. For the experiment samples, we selected a total of 37 financial indicators from six perspectives, which are debt-paying ability, operating capacity, growth ability, profitability, capital structure, and cash flow. Those variables are used as the features of the stock price crash prediction model (see Table 1).
- (2)
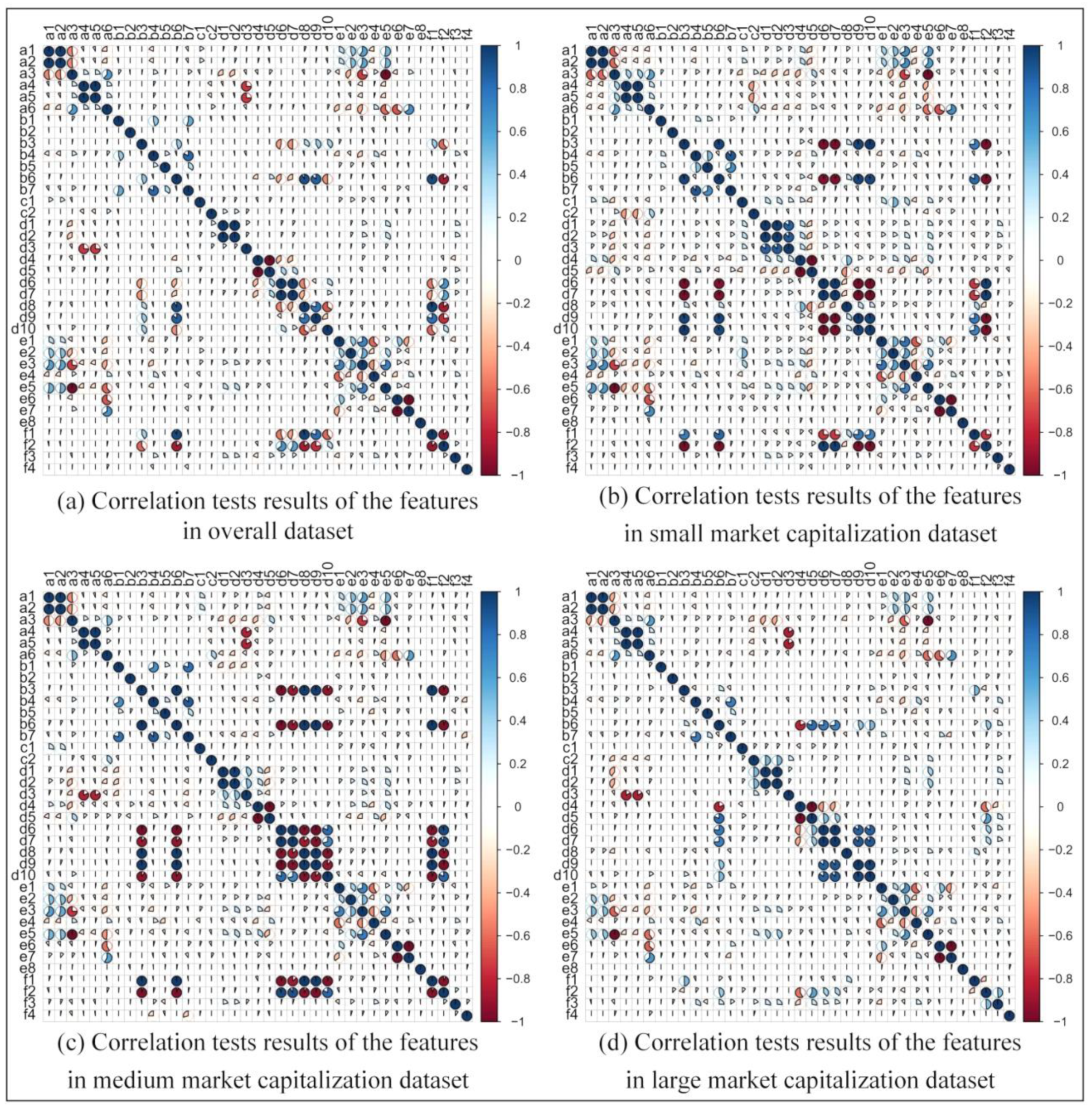
- Next, the abnormal sample in the acquired initial dataset is handled using multiple imputations to fill in the missing values of the dataset variables. The Pearson correlation coefficients are then calculated for all the selected features to test the correlation between them [68]. Based on this, the redundant features with Pearson correlation coefficients greater than 0.8 are removed to improve the training speed and predictive efficiency of the model [69]. Finally, the whole dataset is divided into a training set and a testing set at a ratio of 2:1 for each experiment.
4.2. NSGA-II Design
4.3. Result-Evaluation Measures
- (1)
- ACC is the accuracy of the prediction model for predicting stock-price-crash samples and non-stock-crash samples:
- (2)
- TPR is the proportion of stock-price-crash samples that are correctly predicted:
- (3)
- FPR is the proportion of non-crash samples incorrectly predicted to be crash samples:
- (4)
- PPV is the proportion of the actual stock-crash samples out of the samples that the model predicts to be stock-price-crash samples:
4.4. Model Explanation
4.5. Benchmark Methods
5. Experimental Results
5.1. Feature Correlation Test Results
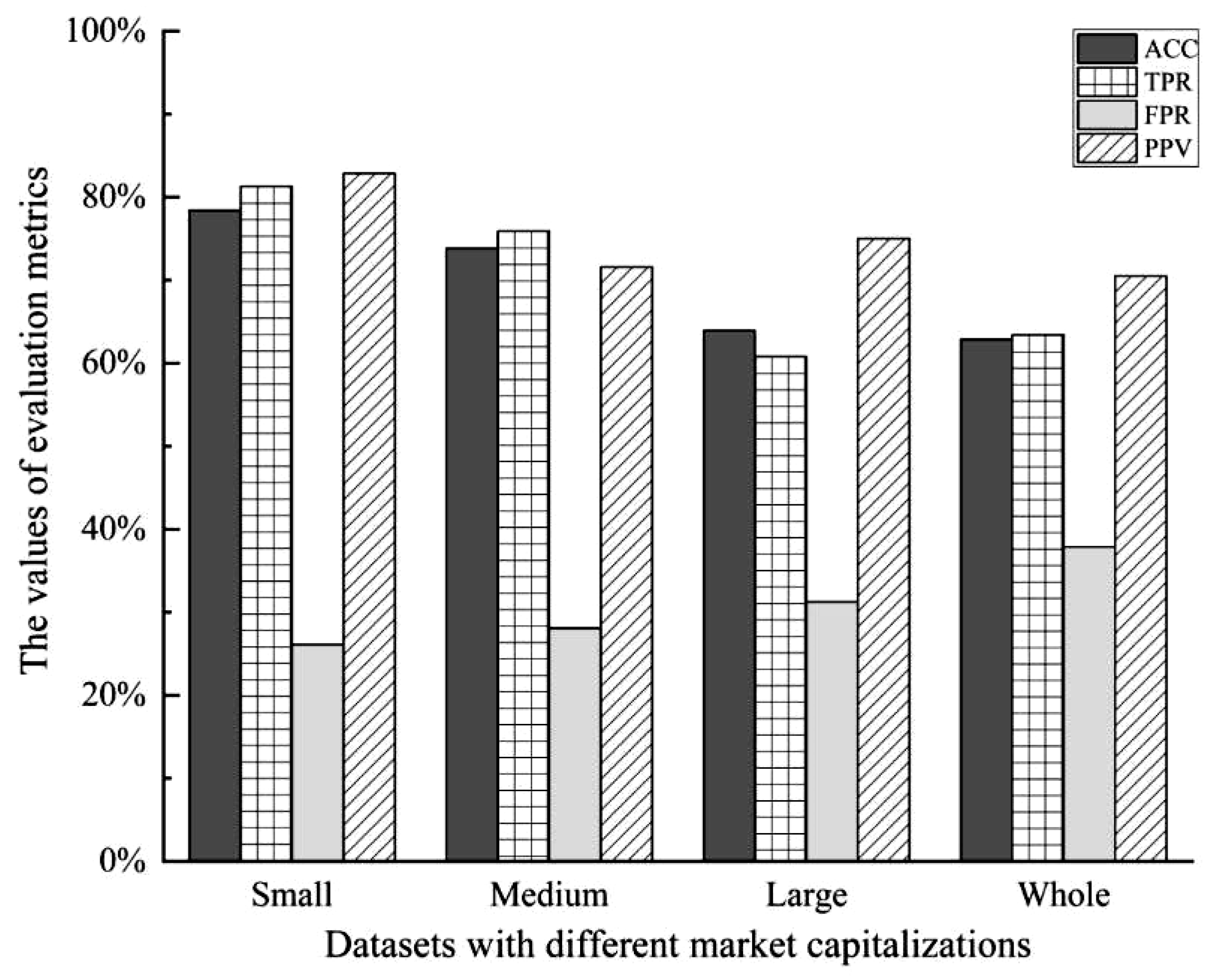
5.2. Stock Price Crash Prediction Results
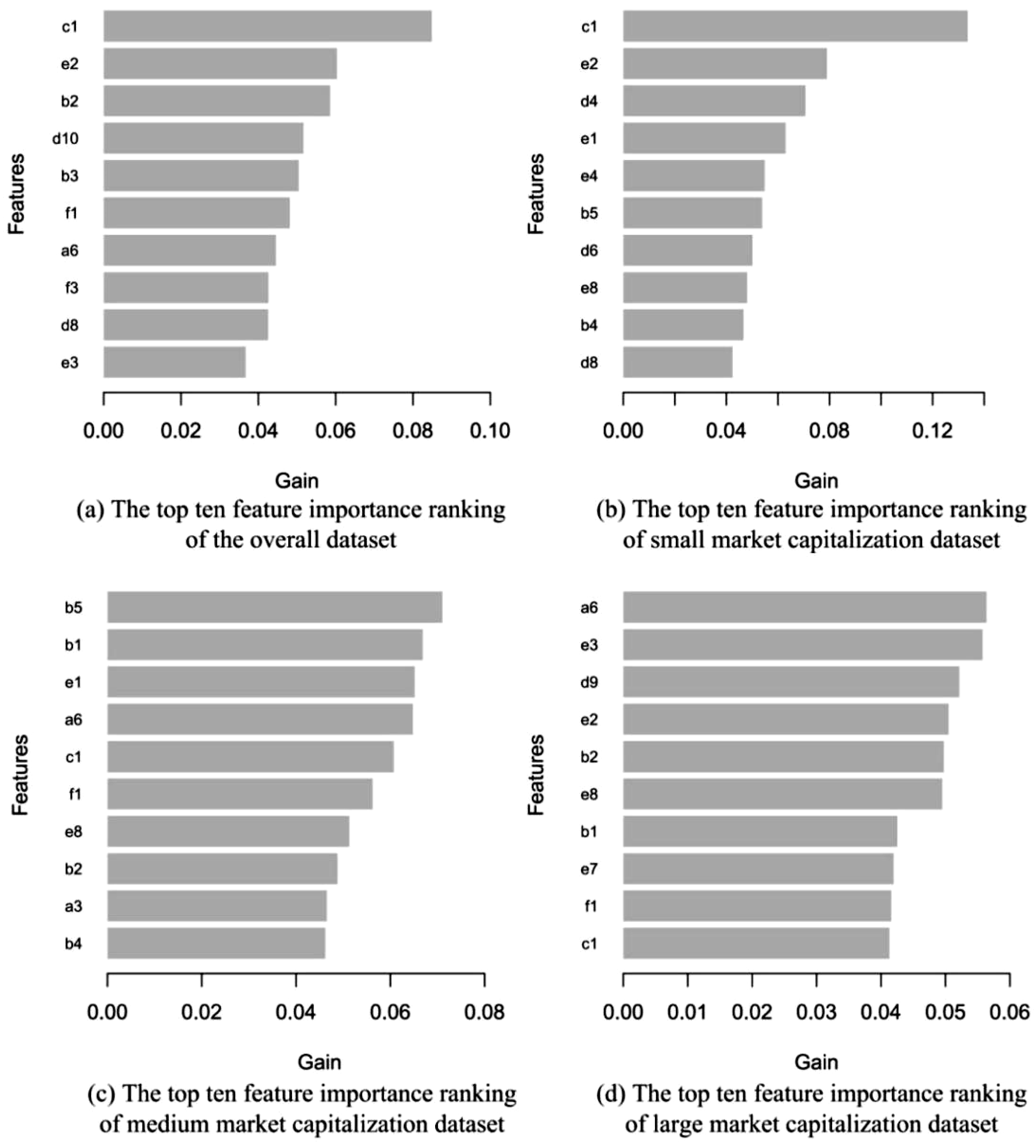
5.3. Feature Importance Analysis
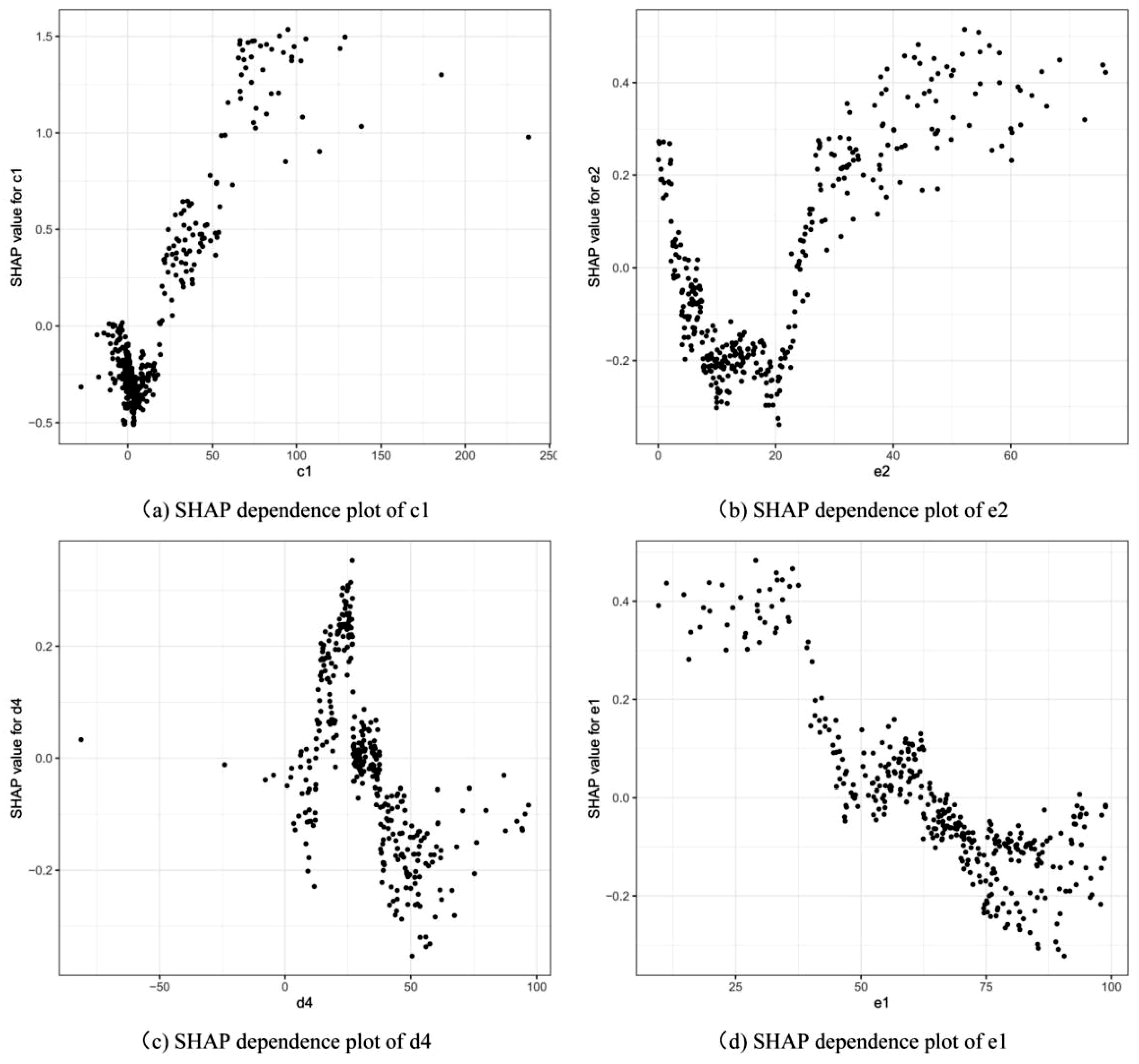
5.4. Results of the SHAP Approach
5.5. Managerial Insight
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, L.; Myers, S.C. R2 around the world: New theory and new tests. J. Financ. Econ. 2006, 79, 257–292. [Google Scholar] [CrossRef]
- Farmer, R.E.A. The stock market crash of 2008 caused the Great Recession: Theory and evidence. J. Econ. Dyn. Control 2012, 36, 693–707. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, J. Investor trading behaviour and stock price crash risk. Int. J. Financ. Econ. 2019, 24, 227–240. [Google Scholar] [CrossRef]
- Bond, S.; Devereux, M. Financial volatility, the stock market crash and corporate investment. Fisc. Stud. 1988, 9, 72–80. [Google Scholar] [CrossRef]
- Bleck, A.; Liu, X. Market transparency and the accounting regime. J. Account. Res. 2007, 45, 229–256. [Google Scholar] [CrossRef]
- Hutton, A.P.; Marcus, A.J.; Tehranian, H. Opaque financial reports, R2, and crash risk. J. Financ. Econ. 2009, 94, 67–86. [Google Scholar] [CrossRef]
- Kim, J.B.; Li, Y.; Zhang, L. Corporate tax avoidance and stock price crash risk: Firm-level analysis. J. Financ. Econ. 2011, 100, 639–662. [Google Scholar] [CrossRef]
- Xu, N.; Li, X.; Yuan, Q.; Chan, K.C. Excess perks and stock price crash risk: Evidence from China. J. Corp. Financ. 2014, 25, 419–434. [Google Scholar] [CrossRef]
- Li, E.Z.J.; Yu, H.; Lin, H.; Chen, G. Correlation analysis between stock prices and four financial indexes for some listed companies of mainland China. In Proceedings of the 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI 2017), Shanghai, China, 14–16 October 2017; 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Kaizoji, T.; Miyano, M. Stock market crash of 2008: An empirical study of the deviation of share prices from company fundamentals. Appl. Econ. Lett. 2019, 26, 362–369. [Google Scholar] [CrossRef]
- Wang, B.; Ho, K.C.; Liu, X.; Gu, Y. Industry cash flow volatility and stock price crash risk. Manag. Decis. Econ. 2022, 43, 356–371. [Google Scholar] [CrossRef]
- Feltham, G.A.; Ohlson, J.A. Valuation and clean surplus accounting for operating and financial activities. Contemp. Account. Res. 1995, 11, 689–731. [Google Scholar] [CrossRef]
- Jiang, J.; Chang, R. Relationship between key financial statements and stock price of GEM listed companies. Sci. Tec. Ind. 2013, 13, 69–73. [Google Scholar] [CrossRef]
- Xu, M.; Liu, X. The correlation between financial indexes and stock prices in ChiNext—Based on manufacturing and IT industry. Stat. Appl. 2018, 7, 281–290. [Google Scholar] [CrossRef]
- Sornette, D. Critical market crashes. Phys. Rep. 2003, 378, 1–98. [Google Scholar] [CrossRef]
- Herrera, R.; Schipp, B. Self-exciting extreme value models for stock market crashes. In Statistical Inference, Econometric Analysis and Matrix Algebra; Schipp, B., Kräer, W., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2009; pp. 209–231. [Google Scholar] [CrossRef]
- Lleo, S.; Ziemba, W.T. Stock market crashes in 2007-2009: Were we able to predict them? Quant. Financ. 2012, 12, 1161–1187. [Google Scholar] [CrossRef]
- Dai, B.; Zhang, F.; Tarzia, D.; Ahn, K. Forecasting financial crashes: Revisit to log-periodic power law. Complexity 2018, 2018, 4237471. [Google Scholar] [CrossRef]
- Kurz-Kim, J.R. Early warning indicator for financial crashes using the log periodic power law. Appl. Econ. Lett. 2012, 19, 1456–1469. [Google Scholar] [CrossRef]
- Pele, D.T.; Mazurencu-Marinescu, M. An econophysics approach for modeling the behavior of stock market bubbles: Case study for the bucharest stock exchange. In Emerging Macroeconomics: Case Studies–Central and Eastern Europe; Nova Science Publishers: London, UK, 2013; pp. 81–90. [Google Scholar]
- Zhang, Y.J.; Yao, T. Interpreting the movement of oil prices: Driven by fundamentals or bubbles? Econ. Model. 2016, 55, 226–240. [Google Scholar] [CrossRef]
- Tsuji, C. Is volatility the best predictor of market crashes? Asia-Pac. Financ. Mark. 2003, 10, 163–185. [Google Scholar] [CrossRef]
- Jones, J.S.; Kincaid, B. Can the correlation among Dow 30 stocks predict market declines? Evidence from 1950 to 2008. Manag. Financ. 2014, 40, 33–50. [Google Scholar] [CrossRef]
- Reza Razavi Araghi, S.M.; Lashgari, Z. The effect of internal control material weaknesses on future stock price crash risk: Evidence from Tehran Stock Exchange (TSE). Int. J. Account. Res. 2017, 5, 1–5. [Google Scholar] [CrossRef]
- Ouyang, H.B.; Huang, K.; Yan, H. Prediction of financial time series based on LSTM Neural Network. Chinese J. Manag. Sci. 2020, 28, 27–35. [Google Scholar] [CrossRef]
- Inthachot, M.; Boonjing, V.; Intakosum, S. Predicting SET50 index trend using artificial neural network and support vector machine. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Durham, UK, 2015; pp. 404–414. [Google Scholar] [CrossRef]
- Jaiwang, G.; Jeatrakul, P. A forecast model for stock trading using support vector machine. In Proceedings of the 20th International Computer Science and Engineering Conference: Smart Ubiquitos Computing and Knowledge, ICSEC 2016, Chiang Mai, Thailand, 14–17 December 2016. [Google Scholar] [CrossRef]
- Chatzis, S.P.; Siakoulis, V.A.; Petropoulos, E.; Stavroulakis, N. Vlachogiannakis, Forecasting stock market crisis events using deep and statistical machine learning techniques. Expert Syst. Appl. 2018, 112, 353–371. [Google Scholar] [CrossRef]
- Ning, T.; Miao, D.; Dong, Q.; Lu, X. Wide and deep learning for default risk prediction. Comput. Sci. 2021, 48, 197–201. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Guang, P.; Huang, W.; Guo, L.; Yang, X.; Huang, F.; Yang, M.; Wen, W.; Li, L. Blood-based FTIR-ATR spectroscopy coupled with extreme gradient boosting for the diagnosis of type 2 diabetes: A STARD compliant diagnosis research. Medicine 2020, 99, e19657. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, C.; Hu, X.; Zhang, C.; Kelley, S.P.; Atwood, J.L.; Lin, J. Machine learning sssisted synthesis of metal-organic nanocapsules. J. Am. Chem. Soc. 2020, 142, 1475–1481. [Google Scholar] [CrossRef]
- Huang, Q.; Xie, H. Research on the application of machine learning in stock index futures forecast—comparison and analysis based on BP neural network, SVM and XGBoost. Math. Pract. Th. 2018, 48, 297–307. [Google Scholar]
- Deng, S.; Huang, X.; Qin, Z.; Fu, Z.; Yang, T. A novel hybrid method for direction forecasting and trading of apple futures. Appl. Soft Comput. 2021, 110, 107734. [Google Scholar] [CrossRef]
- Deng, S.; Wang, X.H.J.; Qin, Z.; Fu, Z.; Wang, A.; Yang, T. A decision support system for trading in apple futures market using predictions fusion. IEEE Access 2021, 9, 1271–1285. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, D.; Bao, Z. A new data-driven predictor, PSO-XGBoost, used for permeability of tight sandstone reservoirs: A case study of member of chang 4+5, western Jiyuan Oilfield, Ordos Basin. J. Pet. Sci. Eng. 2021, 199, 108350. [Google Scholar] [CrossRef]
- Piehowski, P.D.; Sandoval, V.A.P.J.D.; Burnum, K.E.; Kiebel, G.R.; Monroe, M.E.; Anderson, G.A.; Camp, D.G.; Smith, R.D. STEPS: A grid search methodology for optimized peptide identification filtering of MS/MS database search results. Proteomics 2013, 13, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Mandal, P.; Dey, D.; Roy, B. Indoor lighting optimization: A comparative study between grid search optimization and particle swarm optimization. J. Opt. 2019, 48, 429–441. [Google Scholar] [CrossRef]
- Adnan, M.N.; Islam, M.Z. Optimizing the number of trees in a decision forest to discover a subforest with high ensemble accuracy using a genetic algorithm. Knowl.-Based Syst. 2016, 110, 86–97. [Google Scholar] [CrossRef]
- Islam, M.Z.; Estivill-Castro, V.; Rahman, M.A.; Bossomaier, T. Combining K-MEANS and a genetic algorithm through a novel arrangement of genetic operators for high quality clustering. Expert Syst. Appl. 2018, 91, 402–417. [Google Scholar] [CrossRef]
- Raman, M.R.G.; Somu, N.; Kirthivasan, K.; Liscano, R.; Shankar Sriram, V.S. An efficient intrusion detection system based on hypergraph-Genetic algorithm for parameter optimization and feature selection in support vector machine. Knowl.-Based Syst. 2017, 134, 1–12. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y. Application of improved XGBoost model in stock forecasting. Comput. Engine. Appl. 2019, 55, 202–207. [Google Scholar] [CrossRef]
- Ma, Y.; Yun, W. Research progress of genetic algorithm. Appl. Res. Comput. 2012, 29, 1201–1206. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M. Adaptive directed evolved NSGA2 based node placement optimization for wireless sensor networks. Wirel. Networks 2020, 26, 3539–3552. [Google Scholar] [CrossRef]
- Parizad, A.; Hatziadoniu, K. Security/stability-based Pareto optimal solution for distribution networks planning implementing NSGAII/FDMT. Energy 2020, 192, 116644. [Google Scholar] [CrossRef]
- Ji, B.; Yuan, X.; Yuan, Y. Modified NSGA-II for solving continuous berth allocation problem: Using multiobjective constraint-handling strategy. IEEE Trans. Cybern. 2017, 47, 2885–2895. [Google Scholar] [CrossRef]
- González-Álvarez, D.L.; Vega-Rodríguez, M.A. Analysing the scalability of multiobjective evolutionary algorithms when solving the motif discovery problem. J. Glob. Optim. 2013, 57, 467–497. [Google Scholar] [CrossRef]
- Cao, R.; Liao, B.; Li, M.; Sun, R. Predicting prices and analyzing features of online short-term rentals based on XGBoost. Data Anal. Knowl. Disc. 2021, 5, 51–65. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. Consistent feature attribution for tree ensembles. In Proceedings of the 2017 ICML Workshop on Human Interpretability in Machine Learning, Sydney, Australia, 10 August 2017; pp. 31–38. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Processing Syst. 2017, 30, 4766–4775. [Google Scholar]
- Heuillet, A.; Couthouis, F.; Díaz-Rodríguez, N. Explainability in deep reinforcement learning. Knowl.-Based Syst. 2021, 214, 106685. [Google Scholar] [CrossRef]
- Li, J.; Shi, H.; Hwang, K.S. An explainable ensemble feedforward method with Gaussian convolutional filter. Knowl.-Based Syst. 2021, 225, 107103. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Chen, Z.; Yang, X. Economic policy uncertainty and stock price crash risk. Account. Financ. 2019, 58, 1291–1318. [Google Scholar] [CrossRef]
- Yu, J.; Mai, D. Political turnover and stock crash risk: Evidence from China. Pac. Basin Financ. J. 2020, 61, 101324. [Google Scholar] [CrossRef]
- Schneider, G.; Troeger, V.E. War and the world economy: Stock market reactions to international conflicts. J. Confl. Resolut. 2006, 50, 623–645. [Google Scholar] [CrossRef]
- Baek, S.; Mohanty, S.K.; Glambosky, M. COVID-19 and stock market volatility: An industry level analysis. Financ. Res. Lett. 2020, 37, 101748. [Google Scholar] [CrossRef]
- Pourmansouri, R.; Mehdiabadi, A.; Shahabi, V.; Spulbar, C.; Birau, R. An investigation of the link between major shareholders’ behavior and corporate governance performance before and after the COVID-19 pandemic: A case study of the companies listed on the Iranian stock market. J. Risk Financ. Manag. 2022, 15, 208. [Google Scholar] [CrossRef]
- Aslam, F.; Mohmand, Y.T.; Ferreira, P.; Memon, B.A.; Khan, M.; Khan, M. Network analysis of global stock markets at the beginning of the coronavirus disease (COVID-19) outbreak. Borsa Istanb. Rev. 2020, 20, S49–S61. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Shapley, L.S. 17. A Value for n-Person Games. In Contributions to the Theory of Games (AM-28); Princeton University Press: Princeton, NJ, USA, 2016; Volume II, pp. 307–318. [Google Scholar] [CrossRef]
- Bogetoft, P.; Hougaard, J.L.; Smilgins, A. Applied cost allocation: The DEA-Aumann-Shapley approach. Eur. J. Oper. Res. 2016, 254, 667–678. [Google Scholar] [CrossRef][Green Version]
- Duan, X.; Zhan, J. Opposite Effects of intra-group and inter-group rivalries: A study based on the partitioning effects of mobility barriers. Chin. J. Manag. Sci. 2015, 23, 125–133. [Google Scholar] [CrossRef]
- Chen, J.; Hong, H.; Stein, J.C. Forecasting crashes: Trading volume, past returns, and conditional skewness in stock prices. J. Financ. Econ. 2001, 61, 345–381. [Google Scholar] [CrossRef]
- Kim, J.B.; Li, Y.; Zhang, L. CFOs versus CEOs: Equity incentives and crashes. J. Financ. Econ. 2011, 101, 713–730. [Google Scholar] [CrossRef]
- Wang, K.; Feng, X.; Liu, C. Wave filed separation of fast-slow shear waves by Pearson correlation coefficient method. Glob. Geol. 2012, 31, 371–376. [Google Scholar] [CrossRef]
- Xu, J.; Tang, B.; He, H.; Man, H. Semisupervised feature selection based on relevance and redundancy criteria. IEEE Trans. Neural Networks Learn. Syst. 2017, 28, 1974–7984. [Google Scholar] [CrossRef] [PubMed]
- Budholiya, K.; Shrivastava, S.K.; Sharma, V. An optimized XGBoost based diagnostic system for effective prediction of heart disease. J. King Saud Univ.-Comput. Inf. Sci. 2020, 34, 4514–4523. [Google Scholar] [CrossRef]
- Ryu, S.E.; Shin, D.H.; Chung, K. Prediction model of dementia risk based on XGBoost using derived variable extraction and hyper parameter optimization. IEEE Access 2020, 8, 177708–177720. [Google Scholar] [CrossRef]
- Deng, S.; Wang, C.; Fu, Z.; Wang, M. An intelligent system for insider trading identification in Chinese security market. Comput. Econ. 2021, 57, 593–616. [Google Scholar] [CrossRef]
- Salisu, A.A.; Swaray, R.; Oloko, T.F. US stocks in the presence of oil price risk: Large cap vs. small cap. Econ. Bus. Lett. 2017, 6, 116–124. [Google Scholar] [CrossRef]
- Chen, Z.; Ru, J. Herding and capitalization size in the Chinese stock market: A micro-foundation evidence. Empir. Econ. 2021, 60, 1895–1911. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, R.; Bajorath, J. Interpretation of compound activity predictions from complex machine learning models using local approximations and shapley values. J. Med. Chem. 2020, 63, 8761–8777. [Google Scholar] [CrossRef] [PubMed]


| Category | Codename | Features (Financial Indicator) |
|---|---|---|
| Debt-Paying Ability | a1 | Current Ratio |
| a2 | Quick Ratio | |
| a3 | Debt to Asset Ratio | |
| a4 | Equity Multiplier | |
| a5 | Debt to Equity Ratio | |
| a6 | Long-Term Debt to Asset Ratio | |
| Operating Capacity | b1 | Receivables Turnover Ratio |
| b2 | Inventory Turnover Ratio | |
| b3 | Operating Cycle | |
| b4 | Current Assets Turnover Ratio | |
| b5 | Fixed Assets Turnover Ratio | |
| b6 | Capital Intensity Rate | |
| b7 | Total Assets Turnover Ratio | |
| Growth Ability | c1 | Total Assets Growth Rate |
| c2 | Sustainable Growth Rate | |
| Profitability | d1 | Return on Assets Ratio |
| d2 | Return on Total Assets Ratio | |
| d3 | Return on Equity Ratio | |
| d4 | Gross Profit Margin Ratio | |
| d5 | Operating Expense Ratio | |
| d6 | Operating Profit Margin Ratio | |
| d7 | Net Profit Margin Ratio | |
| d8 | Expense to Sales Ratio | |
| d9 | Administration Expense Ratio | |
| d10 | Financial Expense Ratio | |
| Capital Structure | e1 | Current Assets to Total Assets Ratio |
| e2 | Cash to Assets Ratio | |
| e3 | Working Capital Over Total Assets Ratio | |
| e4 | Fixed Assets Ratio | |
| e5 | Shareholder Equity Ratio | |
| e6 | Current Liability Ratio | |
| e7 | Non-Current Liability Ratio | |
| e8 | Operating Profit Percentage | |
| Cash Flow | f1 | Operating Cash Flow to Sales Ratio |
| f2 | Net Operating Cash Flow to Sales Ratio | |
| f3 | Cash Return on Total Assets Ratio | |
| f4 | Cash Operating Index |
| Hyperparameters | Brief Description | Value Search Range |
|---|---|---|
| eta | It controls the learning rate, and it can be used to prevent overfitting by making the boosting process more conservative. | 0.01~0.3 |
| max_depth | The maximum depth of a tree. | 3~10 |
| min_child_weight | The minimum sum of instance weight (Hessian) needed in a child. If the tree partition step results in a leaf node with a sum of instance weight less than it, the building process will give up further partitioning. | 0.5~6 |
| colsample_bytree | The subsample ratio of columns when constructing each tree. | 0.4~1 |
| gamma | The minimum loss reduction required to make a further partition on a leaf node of the tree. The larger the gamma, the more conservative the algorithm will be. | 0~5 |
| nrounds | The maximum number of boosting iterations. | 75~100 |
| Positive Sample | Negative Sample | |
|---|---|---|
| Positive prediction | TP (True positive) | FP (False positive) |
| Negative prediction | FN (False negative) | TN (True negative) |
| No | Methods | Description |
|---|---|---|
| 1 | XGBoost–NSGA-II–SHAP (proposed method) | It combines XGBoost, NSGA-II, and SHAP. XGBoost is used to predict stock price crashes; NSGA-II is used to optimize the hyperparameters of the XGBoost prediction method; SHAP is adopted to explain the prediction model. |
| 2 | XGBoost–GS | It integrates XGBoost and grid search (GS). XGBoost is used to predict the stock price crash, and GS is used to optimize the hyperparameters of the prediction model. |
| 3 | RF | A stock price crash prediction model based on a random forest (RF)-based method. |
| 4 | DT | A stock price crash prediction model based on a decision tree (DT)-based method. |
| 5 | SVM | A stock price crash prediction model based on the support vector machine (SVM)-based method. |
| 6 | ANN | A stock price crash prediction model based on the artificial neural network (ANN)-based method. |
| Category | Filtered Features Codes | Filtered Features |
|---|---|---|
| Whole dataset | a2, a4, b6, b7, d1, d5, d7, d9, e5, e7, f2 | Quick Ratio, Equity Multiplier, Capital Intensity Rate, Total Assets Turnover Ratio, Return on Assets Ratio, Operating Expense Ratio, Net Profit Margin Ratio, Administration Expense Ratio, Shareholder Equity Ratio, Non-Current Liability Ratio, Net Operating Cash Flow to Sales Ratio. |
| Small-Capitalization dataset | a2, a4, b3, b6, b7, d1, d5, d7, d9, d10, e3, e5, e7, f2 | Quick Ratio, Equity Multiplier, Operating Cycle, Capital Intensity Rate, Total Assets Turnover Ratio, Return on Assets Ratio, Operating Expense Ratio, Net Profit Margin Ratio, Administration Expense Ratio, Financial Expense Ratio, Working Capital Over Total Assets Ratio, Shareholder Equity Ratio, Non-Current Liability Ratio, Net Operating Cash Flow to Sales Ratio. |
| Medium- Capitalization dataset | a2, a4, b3, b6, b7, d1, d3, d5, d6, d7, d10, e5, e7, f2 | Quick Ratio, Equity Multiplier, Operating Cycle, Capital Intensity Rate, Total Assets Turnover Ratio, Return on Assets Ratio, Return on Equity Ratio, Operating Expense Ratio, Operating Profit Margin Ratio, Net Profit Margin Ratio, Financial Expense Ratio, Shareholder Equity Ratio, Non-Current Liability Ratio, Net Operating Cash Flow to Sales Ratio. |
| Large- Capitalization dataset | a2, a4, b6, d1, d3, d5, d6, d7, d10, e5, e6 | Quick Ratio, Equity Multiplier, Capital Intensity Rate, Return on Assets Ratio, Return on Equity Ratio, Operating Expense Ratio, Operating Profit Margin Ratio, Net Profit Margin Ratio, Financial Expense Ratio, Shareholder Equity Ratio, Current Liability Ratio. |
| Method | SVM | RF | ANN | DT | XGBoost–GS | XGBoost–NSGA-II |
|---|---|---|---|---|---|---|
| Panel A. Stock samples of small market capitalization | ||||||
| ACC | 63.31% | 64.24% | 55.90% | 62.25% | 59.60% | 78.41% |
| TPR | 85.88% | 82.35% | 58.43% | 69.12% | 54.12% | 81.31% |
| FPR | 59.52% | 50.60% | 47.22% | 43.37% | 33.33% | 26.09% |
| PPV | 59.35% | 57.14% | 60.47% | 56.62% | 67.65% | 82.86% |
| Panel B. Stock samples of medium market capitalization | ||||||
| ACC | 50.67% | 57.04% | 50.33% | 61.96% | 62.67% | 73.83% |
| TPR | 47.59% | 55.71% | 69.01% | 59.74% | 61.33% | 75.90% |
| FPR | 46.34% | 41.67% | 66.67% | 36.05% | 35.82% | 28.09% |
| PPV | 45.71% | 56.52% | 48.51% | 59.74% | 65.71% | 71.59% |
| Panel C. Stock samples of large market capitalization | ||||||
| ACC | 52.84% | 54.03% | 49.54% | 58.82% | 48.63% | 63.93% |
| TPR | 35.54% | 39.60% | 45.54% | 50.47% | 48.15% | 60.81% |
| FPR | 31.97% | 32.73% | 46.96% | 34.35% | 50.00% | 31.25% |
| PPV | 49.35% | 52.63% | 46.00% | 54.55% | 73.39% | 75.00% |
| Panel D. Whole stock samples | ||||||
| ACC | 55.30% | 57.17% | 55.13% | 58.08% | 57.34% | 62.88% |
| TPR | 53.61% | 59.86% | 49.26% | 62.33% | 58.92% | 63.40% |
| FPR | 43.20% | 45.45% | 38.58% | 46.49% | 44.29% | 37.86% |
| PPV | 52.61% | 56.17% | 57.76% | 59.09% | 57.76% | 70.51% |
| Category | ACC | TPR | FPR | PPV |
|---|---|---|---|---|
| Small-capitalization dataset | 78.41% | 81.31% | 26.09% | 82.86% |
| Medium-capitalization dataset | 73.83% | 75.90% | 28.09% | 71.59% |
| Large-capitalization dataset | 63.93% | 60.81% | 31.25% | 75.00% |
| Whole dataset | 62.88% | 63.40% | 37.86% | 70.51% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, S.; Zhu, Y.; Duan, S.; Fu, Z.; Liu, Z. Stock Price Crash Warning in the Chinese Security Market Using a Machine Learning-Based Method and Financial Indicators. Systems 2022, 10, 108. https://doi.org/10.3390/systems10040108
Deng S, Zhu Y, Duan S, Fu Z, Liu Z. Stock Price Crash Warning in the Chinese Security Market Using a Machine Learning-Based Method and Financial Indicators. Systems. 2022; 10(4):108. https://doi.org/10.3390/systems10040108
Chicago/Turabian StyleDeng, Shangkun, Yingke Zhu, Shuangyang Duan, Zhe Fu, and Zonghua Liu. 2022. "Stock Price Crash Warning in the Chinese Security Market Using a Machine Learning-Based Method and Financial Indicators" Systems 10, no. 4: 108. https://doi.org/10.3390/systems10040108
APA StyleDeng, S., Zhu, Y., Duan, S., Fu, Z., & Liu, Z. (2022). Stock Price Crash Warning in the Chinese Security Market Using a Machine Learning-Based Method and Financial Indicators. Systems, 10(4), 108. https://doi.org/10.3390/systems10040108






