Online Teaching Quality Evaluation of Business Statistics Course Utilizing Fermatean Fuzzy Analytical Hierarchy Process with Aggregation Operator

Abstract

Due to the full-scale outbreak of COVID-19, many universities have adopted the way of online teaching to ensure the orderly development of teaching plans and teaching contents. However, whether online and offline teaching can develop homogeneously and how to ensure the teaching effect is a major challenge for colleges and universities. Therefore, it is urgent to construct a reasonable index system and evaluation approach for the quality of network teaching. Combined with the influencing factors and characteristics of online teaching, this study first puts forward a multi-index evaluation index system and then proposes a novel evaluation method for online teaching based on the analytical hierarchy process (AHP) and Dombi weighted partitioned Muirhead Mean (PMM) operator under Fermatean fuzzy (FF) environment. This presented method not only adapts to changeable evaluation information but also handles the elusive interrelationships among indexes, realizing the flexibility and comprehensiveness both in form and in the polyaddition process. The applicability and feasibility of this presented method are then discussed through the practical online teaching quality evaluation of a business statistics course case, and a group of tentative about the sensitivity analysis and comparative analysis further demonstrates the effectiveness and flexibility of the proposed method.

1. Introduction

With the continuous improvement in the integration of network information technology and higher education, online teaching, a new business type in the Internet era, is constantly embedded into the school system in the process of market-oriented operation. In order to hedge the influence of COVID-19 and ensure that colleges and universities are “closed without suspension”, online teaching is quickly implanted in colleges and universities due to its time-space flexibility, synchronicity and repeatability. However, in this way, teachers cannot readily perceive the learning condition of their student, and have aroused doubts about the quality of online teaching. To relieve this situation, Qu et al. [1] presented a method for forecasting students’ representation and grasp of learning contents in MOOCs according to online operation data related to assignments. Meanwhile, Qiu et al. [2] discovered that the method proposed by [1] neglected the intrinsic relationship among online operation behaviors and creatively put forward a novel behavior prediction approach, which mainly fused the behavior category characteristics and behavior data to obtain the category eigenvalues of each kind of behavior, and finally constructed a learning representation predictor. To carry out the online classroom smoothly, Toan et al. [3] proposed an integration model to choose an online platform with most effective performance and minimized the influence of the platform factor on the quality of online teaching. Utilizing performance evaluation matrix, Lee et al. [4] proposed the framework for assessment and analysis to strengthen learning satisfaction and teaching effectiveness.

In order to ensure the homogeneity and equivalence of online and offline teaching quality, online teaching quality evaluation is crucial. Most of the current research on online education quality evaluation focuses on student performance, including student engagement [1,2,5] and student achievement [5,6,7], to measure the effectiveness of online teaching. The reality is that the quality of online teaching is often affected by multi-dimensional factors, such as students’ participation, teachers’ adaptability, network environment collocation and so on. Therefore, the problem of the online teaching quality evaluation can be regarded as a multi-attribute decision making (MADM) problem, which requires the exploitation and adherence of a methodology for quality evaluation.

There are two essential questions in handling MADM problem: 1. How do decision makers deliver their assessment preference using an appropriate expression? 2. How is the alternative with the best performance determined? There exist lots of different sorts of effective tools to denote decision makers’ preference information, where fuzzy set is one of the most concerned [8,9,10,11,12,13,14,15,16,17]. The Fermatean fuzzy set (FFS) proposed by Senapati and Yager [18] is one of the most well-known and practical tools among them, which mainly restricts the summation of the cubes of the membership degree and the non-membership degree shall not exceed one. Due to this feature, FFS possesses a wider scope of application than intuitionistic fuzzy set (IFS) [19] and Pythagorean fuzzy set (PFS) [20]. Numerous research in relation to FFS for the MADM problem, such as Fermatean fuzzy (FF) function [21,22], aggregation operators of FFS [23,24], distance measure for FFS [25] and similarity measure for FFS [26], are becoming increasingly significant and popular in academia.

As the most effective and practical MADM method, the aggregation operator is applied by many scholars, allowing them to obtain the compressed information from disparate data headstreams to facilitate in profiting significant reasoning in the process of making the decision. Arithmetic mean (AM) and geometric mean (GM) operators [27] are the simplest aggregation operators, not taking into account the interrelationship among data parameters and failing to capture the main decision-making focus. The comprehensive values obtained through these operators are not affected by the combination of individual opinions. In the realistic decision-making environment, human opinion is irregular and unfathomable, and aggregation operators are supposed to possess the function to seize the correlation between data parameters. Many aggregation operators blending the interrelationship among arguments have been explored, such as the Choquet integral [28], the Bonferroni mean (BM) operator [29], the Maclaurin symmetric mean (MSM) operator [30] and the Muirhead mean (MM) [31] operator. Considering that the Dombi operation [32] has the preponderance in good flexibility with a general parameter, Liu et al. [33] extended the BM operator and presented a series of aggregation operators combining Dombi operation and BM operator in intuitionistic fuzzy (IF) environment. References [34,35] combined the BM operator with Dombi operation under a two-tuple linguistic neutrosophic and a probabilistic linguistic q-rung orthopair fuzzy environment, respectively. In addition, the MSM operator has been extended frequently in a hesitant fuzzy environment [36], a Pythagorean fuzzy (PF) environment [37] and a complex q-rung orthopair fuzzy environment [38]. Xu et al. [39] proposed a novel aggregation method under interval-valued q-rung dual hesitant fuzzy environment merging the MM operator. Du and Liu [40] combined MM operator with VlseKriterijuska Optimizacija I Komoromisno Resenje (VIKOR) method and introduced a novel approach to handle the MADM problem.

However, in a practical situation, the interrelationship between all attributes may not always hold but may only appear in some attributes [41,42,43,44]. Taking excellent manager selection as an instance, we find the following four attributes: $s{x}_1$: Interpersonal relationship; $s{x}_2$: Management ability; $s{x}_3$: Working skill; $s{x}_4$: Awards. Obviously, the four attributes can be divided into two partitions: $p_1=\left\{s{x}_1,s{x}_2\right\}$ and $p_2=\left\{s{x}_3,s{x}_4\right\}$. Easy to observe, $s{x}_1$ and $s{x}_2$ belong to the partition $p_1$, having no correlation with $s{x}_3$ and $s{x}_4$, independent of this partition $p_2$. Hence, it is necessary to divide attributes into multiple partitions when the inter-relationships between whole attributes do not exist, but some attributes do share inter-relationships. Based on the above considerations, Yin et al. [45] made an analysis about partition BM (PBM) operator and then proposed the trapezoidal fuzzy two-dimensional linguistic PBM and trapezoidal fuzzy two-dimensional linguistic weighted PBM aggregation operators. Liu et al. [44] introduced a novel MADM approach fusing the weighted partitioned MSM (PMSM) operators for IF numbers (IFNs). Qin et al. [46] put forward a novel framework based on (weighted) Archimedean power partitioned MM (PMM) operator of q-rung orthopair fuzzy numbers. In the existing research of the aggregation operator, many scholars have paid attention to the intercorrelation between parameters, but most of the research contents fail to solve the problem of the segmentation structure between parameters based on association pattern. In addition, there is not yet an operator simultaneously meeting the following requirements:

(1)

Utilize the Dombi operation and present satisfactory flexibility in the aggregation of FFS;

(2)

Manage the condition in which the whole attributes are partitioned into several segments and a correlation exists between attributes in every segment and attributes in different segment have no inter-relationship with each other;

(3)

Flexibly handle various situations related to attributes: where there is no correlation between attributes, where there is correlation between two attributes and where there is correlation between three or more attributes.

When evaluating the quality of online teaching, it often needs to assess standing in multiple dimensions, such as the teacher dimension, the student dimension, the curriculum dimension and the technical dimension, each of which is often affected by multiple factors. Therefore, it is a very typical evaluation attribute group that needs to be divided into several partitions, and the assessment information is given by the decision makers’ subjective opinions, so the flexibility of the integrated method is highly required in the evaluation process. Hence, a qualified aggregation operator is supposed to be highly flexible, not only in form but also in dealing with the complex correlation between attributes. Based on the above-mentioned viewpoints, the intentions of this manuscript are stated in the following:

(1)

To develop an ideal aggregation operator of FFS which can precisely seize the complicated correlation between attributes, an MM operator and partitioned average (PA) operator are employed. As a general form of AM, GM, BM and MSM operators, the MM operator is a typical versatile aggregation operator possessing the ability to capture the complex correlation among attributes. Only by adjusting the value of the corresponding parameter can the MM operator address different situations, where the whole attributes fail to be related, where inter-relations exist between any two attributes and where there exists a relationship among any three or more attributes [47,48,49,50,51]. The PA operator possesses the capability to integrate the attribute evaluation value from diverse segments by the identical aggregation method and to aggregate the diverse segments’ integration results by the arithmetic average operator [52,53,54];

(2)

Referring the superiority of Dombi operation in great flexibility with a general parameter, the operational laws of FFS combined the Dombi operation are implemented to form the operations. The Dombi operation possess the superiority in two points: in applications, a special logic can be constructed just by adjusting an argument; the proper parameter and the proper operator can be discovered just by an algorithm [55,56];

(3)

According to the influence factors of the offline teaching and the characteristics of online teaching, an evaluation index system is innovatively established to objectively evaluate the quality of online teaching.

From the above considerations, the purpose of this study is to construct a reasonable evaluation index system for the online teaching quality evaluation and to propose a novel comprehensive evaluation model based on analytical hierarchy process approach for online teaching quality of business statistics course, wherein the FF Dombi weighted PMM operator is proposed by unifying the advantages of the Dombi operation, PA operator and MM operator. The structure of this manuscript is described as follows. In Section 2, a fundamental introduction of some basic knowledge is reviewed. Section 3 introduces the details about the proposed aggregation operator. An integral evaluation index system about online teaching is constructed in Section 4. Section 5 introduces a novel MADM model based on Fermatean fuzzy analytical hierarchy process (FF-AHP) and FF Dombi weighted PMM operator. A practical online teaching quality evaluation case of business statistics course is introduced to further verify the feasibility and applicability of the proposed approach in Section 6. The sensitivity analysis and comparative analysis are described in Section 7 to illustrate the superiority and effectiveness of the proposed method. Section 8 ends this manuscript with the conclusion.

2. Preliminaries

Essential definitions and relevant theorems regarding this study are briefly given in this section.

2.1. FFSs and Their Operational Rules

Definition 1 ([18]) .

Assume that the universe of discourse is denoted by M. An FFS $\mathsf{\Upsilon }$ belonging to M is mathematically expressed by:

$$\mathsf{\Upsilon }=\left\{〈m_i,{\alpha }_{\mathsf{\Upsilon }}\left(m_i\right),{\beta }_{\mathsf{\Upsilon }}\left(m_i\right)〉\left|m_i\in M\right.\right\}$$

(1)

where ${\alpha }_{\mathsf{\Upsilon }}\left(m_i\right):M\to \left[0,1\right]$ and ${\beta }_{\mathsf{\Upsilon }}\left(m_i\right):M\to \left[0,1\right]$. ${\alpha }_{\mathsf{\Upsilon }}\left(m_i\right)$ and ${\beta }_{\mathsf{\Upsilon }}\left(m_i\right)$ represent the membership and non-membership degrees of each element $m_i\in M$ in the set $\mathsf{\Upsilon }$, respectively, assuring the clause $0\le {\left[{\alpha }_{\mathsf{\Upsilon }}\left(m_i\right)\right]}^3+{\left[{\beta }_{\mathsf{\Upsilon }}\left(m_i\right)\right]}^3\le 1$. For an FFS $\mathsf{\Upsilon }$, $\tau =\sqrt[3]{1-{\left[{\alpha }_{\mathsf{\Upsilon }}\left(m_i\right)\right]}^3-{\left[{\beta }_{\mathsf{\Upsilon }}\left(m_i\right)\right]}^3}$ means the indeterminacy of $m_i\in M$ over $\mathsf{\Upsilon }$.

For ease of expression, instead of $\mathsf{\Upsilon }=\left\{〈m_i,{\alpha }_{\mathsf{\Upsilon }}\left(m_i\right),{\beta }_{\mathsf{\Upsilon }}\left(m_i\right)〉\left|m_i\in M\right.\right\}$, $\mathsf{\Upsilon }=〈{\alpha }_{\mathsf{\Upsilon }},{\beta }_{\mathsf{\Upsilon }}〉$ is applied to this study.

Definition 2 ([18]) .

For three FF numbers (FFNs) $\mathsf{\Upsilon }=〈{\alpha }_{\mathsf{\Upsilon }},{\beta }_{\mathsf{\Upsilon }}〉$, ${\mathsf{\Upsilon }}_1=〈{\alpha }_{{\mathsf{\Upsilon }}_1},{\beta }_{{\mathsf{\Upsilon }}_1}〉$ and ${\mathsf{\Upsilon }}_2=〈{\alpha }_{{\mathsf{\Upsilon }}_2},{\beta }_{{\mathsf{\Upsilon }}_2}〉$, $\epsilon$ is a positive real number, and the consequent laws hold validly:

(1) 

${\mathsf{\Upsilon }}_1\oplus {\mathsf{\Upsilon }}_2=〈\sqrt[3]{{\alpha }_{{\mathsf{\Upsilon }}_1}^3+{\alpha }_{{\mathsf{\Upsilon }}_2}^3-{\alpha }_{{\mathsf{\Upsilon }}_1}^3{\alpha }_{{\mathsf{\Upsilon }}_2}^3},{\beta }_{{\mathsf{\Upsilon }}_1}{\beta }_{{\mathsf{\Upsilon }}_2}〉$;

(2) 

${\mathsf{\Upsilon }}_1\otimes {\mathsf{\Upsilon }}_2=〈{\alpha }_{{\mathsf{\Upsilon }}_1}{\alpha }_{{\mathsf{\Upsilon }}_2},\sqrt[3]{{\beta }_{{\mathsf{\Upsilon }}_1}^3+{\beta }_{{\mathsf{\Upsilon }}_2}^3-{\beta }_{{\mathsf{\Upsilon }}_1}^3{\beta }_{{\mathsf{\Upsilon }}_2}^3}〉$;

(3) 

$\epsilon \mathsf{\Upsilon }=〈\sqrt[3]{1-{\left(1-{\alpha }_{\mathsf{\Upsilon }}^3\right)}^{\epsilon }},{\beta }_{\mathsf{\Upsilon }}^{\epsilon }〉$;

(4) 

${\mathsf{\Upsilon }}^{\epsilon }=〈{\alpha }_{\mathsf{\Upsilon }}^{\epsilon },\sqrt[3]{1-{\left(1-{\beta }_{\mathsf{\Upsilon }}^3\right)}^{\epsilon }}〉$;

(5) 

${\mathsf{\Upsilon }}^c=〈{\beta }_{\mathsf{\Upsilon }},{\alpha }_{\mathsf{\Upsilon }}〉$.

Definition 3 ([18]) .

For any FFN $\mathsf{\Upsilon }=〈{\alpha }_{\mathsf{\Upsilon }},{\beta }_{\mathsf{\Upsilon }}〉$, the score and accuracy functions are respectively described as follows:

$$sco(\mathsf{\Upsilon })={\alpha }_{\mathsf{\Upsilon }}^3-{\beta }_{\mathsf{\Upsilon }}^3$$

(2)

$$acc(\mathsf{\Upsilon })={\alpha }_{\mathsf{\Upsilon }}^3+{\beta }_{\mathsf{\Upsilon }}^3$$

(3)

Definition 4 ([18]) .

Let ${\mathsf{\Upsilon }}_1=〈{\alpha }_{{\mathsf{\Upsilon }}_1},{\beta }_{{\mathsf{\Upsilon }}_1}〉$, ${\mathsf{\Upsilon }}_2=〈{\alpha }_{{\mathsf{\Upsilon }}_2},{\beta }_{{\mathsf{\Upsilon }}_2}〉$ be two FFNs and $sco({\mathsf{\Upsilon }}_1)$, $sco({\mathsf{\Upsilon }}_2)$, $acc({\mathsf{\Upsilon }}_1)$ and $acc({\mathsf{\Upsilon }}_2)$ be the score and accuracy values of ${\mathsf{\Upsilon }}_1$ and ${\mathsf{\Upsilon }}_2$, respectively. Then:

(1) 

If$sco({\mathsf{\Upsilon }}_1)<sco({\mathsf{\Upsilon }}_2)$, then${\mathsf{\Upsilon }}_1<{\mathsf{\Upsilon }}_2$;

(2) 

If$sco({\mathsf{\Upsilon }}_1)>sco({\mathsf{\Upsilon }}_2)$, then${\mathsf{\Upsilon }}_1>{\mathsf{\Upsilon }}_2$;

(3) 

If $sco({\mathsf{\Upsilon }}_1)=sco({\mathsf{\Upsilon }}_2)$, then:

1. 

If $acc({\mathsf{\Upsilon }}_1)<acc({\mathsf{\Upsilon }}_2)$, then${\mathsf{\Upsilon }}_1<{\mathsf{\Upsilon }}_2$;

2. 

If$acc({\mathsf{\Upsilon }}_1)>acc({\mathsf{\Upsilon }}_2)$, then${\mathsf{\Upsilon }}_1>{\mathsf{\Upsilon }}_2$;

3. 

If $acc({\mathsf{\Upsilon }}_1)=acc({\mathsf{\Upsilon }}_2)$, then ${\mathsf{\Upsilon }}_1={\mathsf{\Upsilon }}_2$.

2.2. The Dombi Operation

The Dombi sum and Dombi product operations [57], special forms of t-norms and t-conorms, are given detailed definitions below.

Definition 5 ([57]) .

Let $\left(r,f\right)\in \left(0,1\right)\times \left(0,1\right)$ and $g\ge 0$. The definitions of the Dombi t-norm and Dombi t-conrom are described in following way:

$$D-tn\left(r,f\right)=\frac{1}{1+{\left[{\left(\frac{1-r}{r}\right)}^g+{\left(\frac{1-f}{f}\right)}^g\right]}^{\frac{1}{g}}}$$

(4)

$$D-tcn\left(r,f\right)=\frac{1}{1+{\left[{\left(\frac{r}{1-r}\right)}^g+{\left(\frac{f}{1-f}\right)}^g\right]}^{\frac{1}{g}}}$$

(5)

2.3. PA Operator

The PA operator possesses the ability to polymerize the parameters in diverse subregions utilizing the identical aggregation operator and aggregate the polymerization results of diverse subregions using the arithmetic average operator [53]. Its detailed expression is given as follows.

Definition 6 ([53]) .

Assume that $\left(r_1,r_2,r_3,\cdots ,r_n\right)$ is a collection of n real numbers, $S=\left\{r_1,r_2,r_3,\cdots ,r_n\right\}$ is the set of $r_1,r_2,r_3,\cdots ,r_n$, $S_h=\left\{r_1,r_2,r_3,\cdots ,r_{\left|S_h\right|}\right\}\left(h=1,2,3\cdots N\right)$ is N subregions of S satisfying the condition $S_1\cup S_2\cup S_3\cup \cdots \cup S_N=S$ and $S_1\cap S_2\cap S_3\cap \cdots \cap S_N=\varnothing$. The formal function is denoted by:

$$PtA\left(r_1,r_2,r_3,\cdots ,r_n\right)=\frac{1}{N}{\displaystyle \sum _{h=1}^N\left(\underset{i_h}{\overset{\left|S_h\right|}{AO\left(r_{i_h}\right)}}\right)}$$

(6)

where AO is an aggregation operator, and $PtA\left(r_1,r_2,r_3,\cdots ,r_n\right)$ is expressed as the PA operator.

2.4. MM Operator

Muirhead [58] initiatively recommended the MM operator to integrate real numbers. The MM operator possesses remarkable feature in seizing the interrelationships among several polymerized parameters and showcasing a general form of multiple other operators. The specific expression of the MM operator is shown below.

Definition 7 ([58]) .

Suppose that $\left(r_1,r_2,r_3,\cdots ,r_n\right)$ means n crisp numbers and $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$ indicates a collection of n real numbers, satisfying the condition $v_1,v_2,v_3,\cdots ,v_n\ge 0$ but not concurrently $v_1=v_2=v_3=\cdots =v_n=0$. $b\left(i\right)$ denotes any permutation of $\left(1,2,3,\cdots ,n\right)$, and $B_n$ is the convergence of all permutations of $\left(1,2,3,\cdots ,n\right)$. Then, the consequent function of MM operator is defined as follows:

$$M{M}^V\left(r_1,r_2,r_3,\cdots ,r_n\right)={\left(\frac{1}{n!}{\displaystyle \sum _{b\in B_n}{\displaystyle \prod _{i=1}^n{r}_{b\left(i\right)}^{v_i}}}\right)}^{\frac{1}{{\displaystyle \sum _{i=1}^n{v}_i}}}$$

(7)

There exist several distinctive forms of the MM operator with regard to diverse values of argument vector $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$:

(1)

When $V=\left(v,v,v,\cdots ,v\right)\left(v_i=v,i=1,2,3,\cdots ,n\right)$, the MM operator is turned into a GM operator [27]:

$$M{M}^{\left(v,v,v,\cdots ,v\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)={\left({\displaystyle \prod _{i=1}^n{r}_i}\right)}^{\frac{1}{n}}$$

(8)

(2)

When $V=\left(1,0,0,\cdots ,0\right)\left(v_1=1,v_i=0,i=2,3,\cdots ,n\right)$, then the MM operator is degenerated into the AM operator [27]:

$$M{M}^{\left(1,0,0,\cdots 0\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{r}_i}$$

(9)

(3)

When $V=\left(v_1,v_2,0,\cdots ,0\right)\left(v_1,v_2\ne 0,v_i=0,i=3,\cdots ,n\right)$, the MM operator is degenerated into the BM operator [29]:

$$M{M}^{\left(v_1,v_2,0,\cdots ,0\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)={\left(\frac{1}{n\left(n-1\right)}{\displaystyle \sum _{\begin{array}{l}i,j=1\\ i\ne j\end{array}}^n{r}_i^{v_1}{r}_j^{v_2}}\right)}^{\frac{1}{v_1+v_2}}$$

(10)

(4)

When $V=\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)\left(v_1=v_2=\cdots =v_k=1,v_{k+1}=v_{k+2}=\cdots =v_n=0\right)$, the MM operator is changed into the MSM operator [30]:

$$M{M}^{\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)={\left(\frac{{\displaystyle {\sum }_{1\le i_1<\cdots <i_k\le n}{\displaystyle \prod _{j=1}^k{r}_{i_j}}}}{C_n^k}\right)}^{\frac{1}{k}}$$

(11)

3. Fermatean Fuzzy Dombi (Weighted) Partitioned Muirhead Mean Operators

3.1. Fermatean Fuzzy Dombi Operation

Definition 8 ([23]) .

Assume that there exist three FFNs, namely, $\mathsf{\Upsilon }=〈{\alpha }_{\mathsf{\Upsilon }},{\beta }_{\mathsf{\Upsilon }}〉$, ${\mathsf{\Upsilon }}_1=〈{\alpha }_{{\mathsf{\Upsilon }}_1},{\beta }_{{\mathsf{\Upsilon }}_1}〉$ and ${\mathsf{\Upsilon }}_2=〈{\alpha }_{{\mathsf{\Upsilon }}_2},{\beta }_{{\mathsf{\Upsilon }}_2}〉$, and $\epsilon$ is a positive value. Then, the elementary operations of FFNs with respect to Dombi operation are shown in the following forms:

(1) 

${\mathsf{\Upsilon }}_1{\oplus }_{Dom}{\mathsf{\Upsilon }}_2=\left(\sqrt[3]{1-\frac{1}{1+{\left[{\left(\frac{{\alpha }_{{\mathsf{\Upsilon }}_1}^3}{1-{\alpha }_{{\mathsf{\Upsilon }}_1}^3}\right)}^g+{\left(\frac{{\alpha }_{{\mathsf{\Upsilon }}_2}^3}{1-{\alpha }_{{\mathsf{\Upsilon }}_2}^3}\right)}^g\right]}^{\frac{1}{g}}}},\sqrt[3]{\frac{1}{1+{\left[{\left(\frac{1-{\beta }_{{\mathsf{\Upsilon }}_1}^3}{{\beta }_{{\mathsf{\Upsilon }}_1}^3}\right)}^g+{\left(\frac{1-{\beta }_{{\mathsf{\Upsilon }}_2}^3}{{\beta }_{{\mathsf{\Upsilon }}_2}^3}\right)}^g\right]}^{\frac{1}{g}}}}\right);$

(2) 

${\mathsf{\Upsilon }}_1{\otimes }_{Dom}{\mathsf{\Upsilon }}_2=\left(\sqrt[3]{\frac{1}{1+{\left[{\left(\frac{1-{\alpha }_{{\mathsf{\Upsilon }}_1}^3}{{\alpha }_{{\mathsf{\Upsilon }}_1}^3}\right)}^g+{\left(\frac{1-{\alpha }_{{\mathsf{\Upsilon }}_2}^3}{{\alpha }_{{\mathsf{\Upsilon }}_2}^3}\right)}^g\right]}^{\frac{1}{g}}}},\sqrt[3]{1-\frac{1}{1+{\left[{\left(\frac{{\beta }_{{\mathsf{\Upsilon }}_1}^3}{1-{\beta }_{{\mathsf{\Upsilon }}_1}^3}\right)}^g+{\left(\frac{{\beta }_{{\mathsf{\Upsilon }}_2}^3}{1-{\beta }_{{\mathsf{\Upsilon }}_2}^3}\right)}^g\right]}^{\frac{1}{g}}}}\right);$

(3) 

${\left(\epsilon \mathsf{\Upsilon }\right)}_{Dom}=\left(\sqrt[3]{1-\frac{1}{1+{\left[\epsilon {\left(\frac{{\alpha }_{\mathsf{\Upsilon }}^3}{1-{\alpha }_{\mathsf{\Upsilon }}^3}\right)}^g\right]}^{\frac{1}{g}}}},\sqrt[3]{\frac{1}{1+{\left[\epsilon {\left(\frac{1-{\beta }_{\mathsf{\Upsilon }}^3}{{\beta }_{\mathsf{\Upsilon }}^3}\right)}^g\right]}^{\frac{1}{g}}}}\right);$

(4) 

${\left({\mathsf{\Upsilon }}^{\epsilon }\right)}_{Dom}=\left(\sqrt[3]{\frac{1}{1+{\left[\epsilon {\left(\frac{1-{\alpha }_{\mathsf{\Upsilon }}^3}{{\alpha }_{\mathsf{\Upsilon }}^3}\right)}^g\right]}^{\frac{1}{g}}}},\sqrt[3]{1-\frac{1}{1+{\left[\epsilon {\left(\frac{{\beta }_{\mathsf{\Upsilon }}^3}{1-{\beta }_{\mathsf{\Upsilon }}^3}\right)}^g\right]}^{\frac{1}{g}}}}\right).$

3.2. PMM Operator

The MM operator expresses the interrelationships among several polymerized parameters in the internal structure. However, in some practical conditions, the attributes will be divided into several subregions, where the attributes express the interrelationships between diverse arguments in the homogeneous subfield but stand alone in distinct subfields. The PBM operator can capture the association of any two attributes in the homogeneous subfield, while the PMSM operator can describe the relationship among multiple attributes in the homogeneous subfield. Motivated by this situation, this manuscript utilizes partitioned Muirhead Mean (PMM) operator, a general form of the above two operators, to describe the practical correlation among criteria. The mathematical definition is denoted below.

Definition 9 ([46]) .

Let $\left(r_1,r_2,r_3,\cdots ,r_n\right)$ be a group of non-negative numbers, $S=\left\{r_1,r_2,r_3,\cdots ,r_n\right\}$ is the set of $r_1,r_2,r_3,\cdots ,r_n$, $S_h=\left\{r_1,r_2,\cdots ,r_{\left|S_h\right|}\right\}\left(h=1,2,3\cdots N\right)$ is N subregions of S, in accord with the condition $S_1\cup S_2\cup S_3\cup \cdots \cup S_N=S$, and $S_1\cap S_2\cap S_3\cap \cdots \cap S_N=\varnothing$. Then, the PMM operator is given the following definition:

$$PM{M}^V\left(r_1,r_2,r_3,\cdots ,r_n\right)=\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left(\frac{1}{\left|S_h\right|!}{\displaystyle \sum _{b\in B_{\left|S_h\right|}}{\displaystyle \prod _{i_h=1}^{\left|S_h\right|}{r}_{b\left(i_h\right)}^{v_i{}_{{}_h}}}}\right)}^{\frac{1}{{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{v}_{i_h}}}}}$$

(12)

where $\left|S_h\right|$ means the number of arguments in the partition $S_h=\left\{r_1,r_2,\cdots ,r_{\left|S_h\right|}\right\}\left(h=1,2,3\cdots N\right)$, $b\left(i_h\right)$ denotes any permutation of $\left(1,2,\cdots ,\left|S_h\right|\right)$ and $B_{\left|S_h\right|}$ is the convergence of all permutations of $\left(1,2,\cdots ,\left|S_h\right|\right)$. $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$ indicates a collection of n real numbers, satisfying the condition $v_1,v_2,v_3,\cdots ,v_n\ge 0$ but not concurrently $v_1=v_2=v_3=\cdots =v_n=0$.

In the same light, the PMM operator can be transformed into some distinctive operators with respect to the diverse values of argument vector $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$:

(1)

When $V=\left(v,v,v,\cdots ,v\right)\left(v_i=v,i=1,2,3,\cdots ,n\right)$, the PMM operator is turned into partitioned GM (PGM) operator:

$$PM{M}^{\left(v,v,v,\cdots ,v\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)=\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left({\displaystyle \prod _{i_h=1}^{\left|S_h\right|}{r}_{i_h}}\right)}^{\frac{1}{\left|S_h\right|}}}$$

(13)

(2)

When $V=\left(1,0,0,\cdots ,0\right)\left(v_1=1,v_i=0,i=2,3,\cdots ,n\right)$, the PMM operator is degenerated into partitioned AM (PAM) operator:

$$PM{M}^{\left(1,0,0,\cdots ,0\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)=\frac{1}{N}{\displaystyle \sum _{h=1}^N\left(\frac{1}{\left|S_h\right|}{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{r}_{i_h}}\right)}$$

(14)

(3)

When $V=\left(v_1,v_2,0,\cdots ,0\right)\left(v_1,v_2\ne 0,v_i=0,i=3,\cdots ,n\right)$, the PMM operator is degenerated into PBM operator [45]:

$$PM{M}^{\left(v_1,v_2,0,\cdots ,0\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)=\frac{1}{N}{\displaystyle \sum _{h=1}^N\left({\left(\frac{1}{\left|S_h\right|\left(\left|S_h\right|-1\right)}{\displaystyle \sum _{\begin{array}{l}{i}_h,j_h=1\\ i_h\ne j_h\end{array}}^{\left|S_h\right|}{r}_{i_h}^{v_1}{r}_{j_h}^{v_2}}\right)}^{\frac{1}{v_1+v_2}}\right)}$$

(15)

(4)

When $V=\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)\left(v_1=v_2=\cdots =v_k=1,v_{k+1}=v_{k+2}=\cdots =v_n=0\right)$, the PMM operator is changed into PMSM operator [44]:

$$PM{M}^{\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)}\left(r_1,r_2,r_3,\cdots ,r_n\right)=\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left(\frac{{\displaystyle {\sum }_{1\le i_1<\cdots <i_k\le \left|S_h\right|}{\displaystyle \prod _{j=1}^k{r}_{i_j}}}}{C_{\left|S_h\right|}^k}\right)}^{\frac{1}{k}}}$$

(16)

Consequently, it is easy to conclude that the proposed PMM operator possesses mathematical properties such as Idempotency, Monotonicity and Boundedness. The detailed proof process is omitted here.

3.3. Fermatean Fuzzy Dombi (Weighted) Partitioned Muirhead Mean Operators

On the basis of above theoretical analysis, we can easily infer the mathematical definition of Fermatean fuzzy Dombi partitioned Muirhead mean (FFDPMM) operator, which accomplishes the effective fusion of the advantage information of the Dombi method with the PMM operator, not only realizing the generality and flexibility both in form and in the process of aggregation but handling various related situations within attributes flexibly, including the independence of all attributes or multiple attributes are interrelated.

Definition 10.

Let $\mathsf{\Upsilon }=\left\{〈m_i,{\alpha }_{\mathsf{\Upsilon }}\left(m_i\right),{\beta }_{\mathsf{\Upsilon }}\left(m_i\right)〉\left|m_i\in M\right.\right\}(i=1,2,\dots ,n)$ be a class of FFNs, abbreviated as${\mathsf{\Upsilon }}_i=〈{\alpha }_{{\mathsf{\Upsilon }}_i},{\beta }_{{\mathsf{\Upsilon }}_i}〉$, and $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$ indicates a collection of n real numbers, satisfying the condition $v_1,v_2,v_3,\cdots ,v_n\ge 0$ but not concurrently $v_1=v_2=v_3=\cdots =v_n=0$. Then, the FFDPMM operator is described in the following:

$$FFDPM{M}^V\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left(\frac{1}{\left|S_h\right|!}{\displaystyle \sum _{b\in B_{\left|S_h\right|}}{\displaystyle \prod _{i_h=1}^{\left|S_h\right|}{\mathsf{\Upsilon }}_{b\left(i_h\right)}^{v_i{}_{{}_h}}}}\right)}^{\frac{1}{{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{v}_{i_h}}}}}\right\}}_{Dom}$$

(17)

where $S=\left\{r_1,r_2,r_3,\cdots ,r_n\right\}$ is the set of $r_1,r_2,r_3,\cdots ,r_n$, $S_h=\left\{r_1,r_2,\cdots ,r_{\left|S_h\right|}\right\}\left(h=1,2,3\cdots N\right)$ is N subregions of S, satisfying the condition $S_1\cup S_2\cup S_3\cup \cdots \cup S_N=S$ and $S_1\cap S_2\cap S_3\cap \cdots \cap S_N=\varnothing$. $\left|S_h\right|$ denotes the number of arguments in the partition $S_h=\left\{r_1,r_2,\cdots ,r_{\left|S_h\right|}\right\}\left(h=1,2,3\cdots N\right)$, $b\left(i_h\right)$ denotes any permutation of $\left(1,2,\cdots ,\left|S_h\right|\right)$ and $B_{\left|S_h\right|}$ is the convergence of all permutations of $\left(1,2,\cdots ,\left|S_h\right|\right)$.

Theorem 1.

Suppose ${\mathsf{\Upsilon }}_i=〈{\alpha }_{{\mathsf{\Upsilon }}_i},{\beta }_{{\mathsf{\Upsilon }}_i}〉(i=1,2,\dots ,n)$ is a collection of FFNs, the final aggregation consequences by utilizing FFDPMM operator is a FFN and is equal to the full expansion formula:

$$FFDPM{M}^V\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)=〈ℝ,\mathbb{Z}〉$$

(18)

where:

$$ℝ={\{1-{\left[1+{\left[\frac{1}{N}\stackrel{N}{\sum _{h=1}}(\frac{{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{v}_{i_h}}}{\left|S_h\right|!}\sum _{b\in B_{\left|S_h\right|}}{\left(\stackrel{\left|S_h\right|}{\sum _{i_h=1}}\left(v_{i_h}{\left(\frac{1-{\alpha }_{{\sum }_{b\left(h_h\right)}}^3}{{\alpha }_{{\sum }_{b\left(i_h\right)}}^3}\right)}^g\right)\right)}^{-1}\right)}^{\frac{1}{g}}\right]}^{-1}\}}^{\frac{1}{3}}$$

(19)

$$\mathbb{Z}={\left\{{\left[1+{\left[\frac{1}{N}{\displaystyle \sum _{h=1}^N\left(\frac{{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{v}_{i_h}}}{\left|S_h\right|!}{\displaystyle \sum _{b\in B_{\left|S_h\right|}}{\left({\displaystyle \sum _{i_h=1}^{\left|S_h\right|}\left(v_i{}_{{}_h}{\left(\frac{{\beta }_{{\mathsf{\Upsilon }}_{b\left(i_h\right)}}^3}{1-{\beta }_{{\mathsf{\Upsilon }}_{b\left(i_h\right)}}^3}\right)}^g\right)}\right)}^{-1}}\right)}\right]}^{\frac{1}{g}}\right]}^{-1}\right\}}^{\frac{1}{3}}$$

(20)

The following Theorems discuss three mathematical properties of the FFDPMM operator:

Theorem 2. (Idempotency)

Assume $\mathsf{\Upsilon }=\left\{〈m_i,{\alpha }_{\mathsf{\Upsilon }}\left(m_i\right),{\beta }_{\mathsf{\Upsilon }}\left(m_i\right)〉\left|m_i\in M\right.\right\}i=1,2,\dots ,n$ is a group of FFNs, abbreviated as${\mathsf{\Upsilon }}_i=〈{\alpha }_{{\mathsf{\Upsilon }}_i},{\beta }_{{\mathsf{\Upsilon }}_i}〉$. If all IFFNS are equal, that is, ${\mathsf{\Upsilon }}_1={\mathsf{\Upsilon }}_2=\cdots ={\mathsf{\Upsilon }}_n=\mathsf{\Upsilon }$, then:

$$FFDPM{M}^V\left(\mathsf{\Upsilon },\mathsf{\Upsilon },\mathsf{\Upsilon },\cdots ,\mathsf{\Upsilon }\right)=\mathsf{\Upsilon }$$

(21)

Theorem 3. (Monotonicity)

Assume ${\mathsf{\Upsilon }}_i=〈{\alpha }_{{\mathsf{\Upsilon }}_i},{\beta }_{{\mathsf{\Upsilon }}_i}〉i=1,2,\cdots ,n$ and ${\mathsf{\Psi }}_i=〈{\alpha }_{{\psi }_i},{\beta }_{{\psi }_i}〉i=1,2,\cdots ,n$ are two groups of FFNs such that ${\alpha }_{{\mathsf{\Upsilon }}_i}\le {\alpha }_{{\psi }_i},{\beta }_{{\mathsf{\Upsilon }}_i}\ge {\beta }_{{\psi }_i}$ for$i=1,2,\cdots ,n$, then:

$$FFDPM{M}^V\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)\le FFDPM{M}^V\left({\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3,\cdots ,{\mathsf{\Psi }}_n\right)$$

(22)

Theorem 4. (Boundedness)

Assume ${\mathsf{\Upsilon }}_i=〈{\alpha }_{{\mathsf{\Upsilon }}_i},{\beta }_{{\mathsf{\Upsilon }}_i}〉i=1,2,\cdots ,n$ is a class of FFNs, ${\mathsf{\Upsilon }}^{\max }=\underset{1\le i\le n}{\max }\left\{{\mathsf{\Upsilon }}_i\right\},{\mathsf{\Upsilon }}^{\min }=\underset{1\le i\le n}{\min }\left\{{\mathsf{\Upsilon }}_i\right\}$, and then:

$${\mathsf{\Upsilon }}^{\min }\le FFDPM{M}^V\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)\le {\mathsf{\Upsilon }}^{\max }$$

(23)

It is easy to verify the above properties, so the proof process is omitted here. Obviously, if argument vector $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$ takes distinct special values, the FFDPMM would be degenerated into different operators:

(1)

When $V=\left(v,v,v,\cdots ,v\right)\left(v_i=v,i=1,2,3,\cdots ,n\right)$, the FFDPMM operator is turned into the FFDPGM operator:

$$FFDPM{M}^{\left(v,v,v,\cdots ,v\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left({\displaystyle \prod _{i_h=1}^{\left|S_h\right|}{r}_{i_h}}\right)}^{\frac{1}{\left|S_h\right|}}}\right\}}_{Dom}$$

(24)

(2)

When $V=\left(1,0,0,\cdots ,0\right)\left(v_1=1,v_i=0,i=2,3,\cdots ,n\right)$, the FFDPMM operator is degenerated into the FFDPAM operator:

$$FFDPM{M}^{\left(1,0,0,\cdots ,0\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N\left(\frac{1}{\left|S_h\right|}{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{r}_{i_h}}\right)}\right\}}_{Dom}$$

(25)

(3)

When $V=\left(v_1,v_2,0,\cdots ,0\right)\left(v_1,v_2\ne 0,v_i=0,i=3,\cdots ,n\right)$, the FFDPMM operator is degenerated into the FFDPBM operator:

$$FFDPM{M}^{\left(v_1,v_2,0,\cdots ,0\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N\left({\left(\frac{1}{\left|S_h\right|\left(\left|S_h\right|-1\right)}{\displaystyle \sum _{\begin{array}{l}{i}_h,j_h=1\\ i_h\ne j_h\end{array}}^{\left|S_h\right|}{r}_{i_h}^{v_1}{r}_{j_h}^{v_2}}\right)}^{\frac{1}{v_1+v_2}}\right)}\right\}}_{Dom}$$

(26)

(4)

When $V=\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)\left(v_1=v_2=\cdots =v_k=1,v_{k+1}=v_{k+2}=\cdots =v_n=0\right)$, the FFDPMM operator is changed into the FFDPMSM operator:

$$FFDPM{M}^{\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left(\frac{{\displaystyle {\sum }_{1\le i_1<\cdots <i_k\le \left|S_h\right|}{\displaystyle \prod _{j=1}^k{r}_{i_j}}}}{C_{\left|S_h\right|}^k}\right)}^{\frac{1}{k}}}\right\}}_{Dom}$$

(27)

Next, we mainly introduce the FFDPMM operator of the weighted form.

Definition 11.

Let $\mathsf{\Upsilon }=\left\{〈m_i,{\alpha }_{\mathsf{\Upsilon }}\left(m_i\right),{\beta }_{\mathsf{\Upsilon }}\left(m_i\right)〉\left|m_i\in M\right.\right\}i=1,2,\dots ,n$ be a class of FFNs, abbreviated as${\mathsf{\Upsilon }}_i=〈{\alpha }_{{\mathsf{\Upsilon }}_i},{\beta }_{{\mathsf{\Upsilon }}_i}〉$, and $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$ indicates a collection of n real numbers, satisfying the condition $v_1,v_2,v_3,\cdots ,v_n\ge 0$ but not concurrently $v_1=v_2=v_3=\cdots =v_n=0$. $\omega ={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)}^T$ is the weight vector relative to${\mathsf{\Upsilon }}_i,i=1,2,\cdots ,n$, in accord with ${\omega }_i\ge 0$ and ${\displaystyle \sum _{i=1}^n{\omega }_i}=1$. Then, the Fermatean fuzzy Dombi weighted partitioned Muirhead mean (FFDWPMM) operator is described in the following:

$$FFDWPM{M}^V\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left(\frac{1}{\left|S_h\right|!}{\displaystyle \sum _{b\in B_{\left|S_h\right|}}{\displaystyle \prod _{i_h=1}^{\left|S_h\right|}{\omega }_{b\left(i_h\right)}{\mathsf{\Upsilon }}_{b\left(i_h\right)}^{v_i{}_{{}_h}}}}\right)}^{\frac{1}{{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{v}_{i_h}}}}}\right\}}_{Dom}$$

(28)

where $S=\left\{r_1,r_2,r_3,\cdots ,r_n\right\}$ is the set of $r_1,r_2,r_3,\cdots ,r_n$, $S_h=\left\{r_1,r_2,\cdots ,r_{\left|S_h\right|}\right\}\left(h=1,2,3\cdots N\right)$ is N subregions of S, satisfying the condition $S_1\cup S_2\cup S_3\cup \cdots \cup S_N=S$, and $S_1\cap S_2\cap S_3\cap \cdots \cap S_N=\varnothing$. $\left|S_h\right|$ denotes the number of arguments in the partition $S_h=\left\{r_1,r_2,\cdots ,r_{\left|S_h\right|}\right\}\left(h=1,2,3\cdots N\right)$, $b\left(i_h\right)$ denotes any permutation of $\left(1,2,\cdots ,\left|S_h\right|\right)$, and $B_{\left|S_h\right|}$ is the convergence of all permutations of $\left(1,2,\cdots ,\left|S_h\right|\right)$.

Theorem 5.

Assume that ${\mathsf{\Upsilon }}_i=〈{\alpha }_{{\mathsf{\Upsilon }}_i},{\beta }_{{\mathsf{\Upsilon }}_i}〉(i=1,2,\dots ,n)$ is a family of FFNs, the final aggregated consequences by utilizing FFDWPMM operator is a FFN and is equal to the following mathematical form:

$$FFDWPM{M}^V\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)=〈\mathbb{Q},\mathbb{N}〉$$

(29)

where:

$$\mathbb{Q}={\left\{1-{\left[1+{\left[\frac{1}{N}{\displaystyle \sum _{h=1}^N\left(\frac{{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{v}_{i_h}}}{\left|S_h\right|!}{\displaystyle \sum _{b\in B_{\left|S_h\right|}}{\left({\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{\left({\omega }_{b\left(i_h\right)}{\left(v_i{}_{{}_h}{\left(\frac{1-{\alpha }_{{\Upsilon }_{b\left(i_h\right)}}^3}{{\alpha }_{{\Upsilon }_{b\left(i_h\right)}}^3}\right)}^g\right)}^{-1}\right)}^{-1}}\right)}^{-1}}\right)}\right]}^{\frac{1}{g}}\right]}^{-1}\right\}}^{\frac{1}{3}}$$

(30)

$$\mathbb{N}={\left\{{\left[1+{\left[\frac{1}{N}{\displaystyle \sum _{h=1}^N\left(\frac{{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{v}_{i_h}}}{\left|S_h\right|!}{\displaystyle \sum _{b\in B_{\left|S_h\right|}}{\left({\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{\left({\omega }_{b\left(i_h\right)}{\left(v_i{}_{{}_h}{\left(\frac{{\beta }_{{\Upsilon }_{b\left(i_h\right)}}^3}{1-{\beta }_{{\Upsilon }_{b\left(i_h\right)}}^3}\right)}^g\right)}^{-1}\right)}^{-1}}\right)}^{-1}}\right)}\right]}^{\frac{1}{g}}\right]}^{-1}\right\}}^{\frac{1}{3}}$$

(31)

Similar to the FFDPMM operator, the FFDWPMM operator possesses three mathematical characteristics: Idempotency, Monotonicity and Boundedness. In order to save space, it will not be described in detail here.

Apparently, if argument vector $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$ takes distinct special values, the FFDWPMM would be changed into several operators.

(1)

When $V=\left(v,v,v,\cdots ,v\right)\left(v_i=v,i=1,2,3,\cdots ,n\right)$, the FFDWPMM operator is turned into FFDWPGM operator:

$$FFDWPM{M}^{\left(v,v,v,\cdots ,v\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left({\displaystyle \prod _{i_h=1}^{\left|S_h\right|}{\omega }_{i_h}{r}_{i_h}}\right)}^{\frac{1}{\left|S_h\right|}}}\right\}}_{Dom}$$

(32)

(2)

When $V=\left(1,0,0,\cdots ,0\right)\left(v_1=1,v_i=0,i=2,3,\cdots ,n\right)$, the FFDWPMM operator is degenerated into FFDWPAM operator:

$$FFDWPM{M}^{\left(1,0,0,\cdots ,0\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N\left(\frac{1}{\left|S_h\right|}{\displaystyle \sum _{i_h=1}^{\left|S_h\right|}{\omega }_{i_h}{r}_{i_h}}\right)}\right\}}_{Dom}$$

(33)

(3)

When $V=\left(v_1,v_2,0,\cdots ,0\right)\left(v_1,v_2\ne 0,v_i=0,i=3,\cdots ,n\right)$, the FFDWPMM operator is degenerated into the FFDWPBM operator:

$$FFDWPM{M}^{\left(v_1,v_2,0,\cdots ,0\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N\left({\left(\frac{1}{\left|S_h\right|\left(\left|S_h\right|-1\right)}{\displaystyle \sum _{\begin{array}{l}{i}_h,j_h=1\\ i_h\ne j_h\end{array}}^{\left|S_h\right|}{\omega }_{i_h}{r}_{i_h}^{v_1}\otimes {\omega }_{j_h}{r}_{j_h}^{v_2}}\right)}^{\frac{1}{v_1+v_2}}\right)}\right\}}_{Dom}$$

(34)

(4)

When $V=\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)\left(v_1=v_2=\cdots =v_k=1,v_{k+1}=v_{k+2}=\cdots =v_n=0\right)$, the FFDWPMM operator is changed into FFDWPMSM operator:

$$FFDWPM{M}^{\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)}\left({\mathsf{\Upsilon }}_1,{\mathsf{\Upsilon }}_2,{\mathsf{\Upsilon }}_3,\cdots ,{\mathsf{\Upsilon }}_n\right)={\left\{\frac{1}{N}{\displaystyle \sum _{h=1}^N{\left(\frac{{\displaystyle {\sum }_{1\le i_1<\cdots <i_k\le \left|S_h\right|}{\displaystyle \prod _{j=1}^k{\omega }_{i_j}{r}_{i_j}}}}{C_{\left|S_h\right|}^k}\right)}^{\frac{1}{k}}}\right\}}_{Dom}$$

(35)

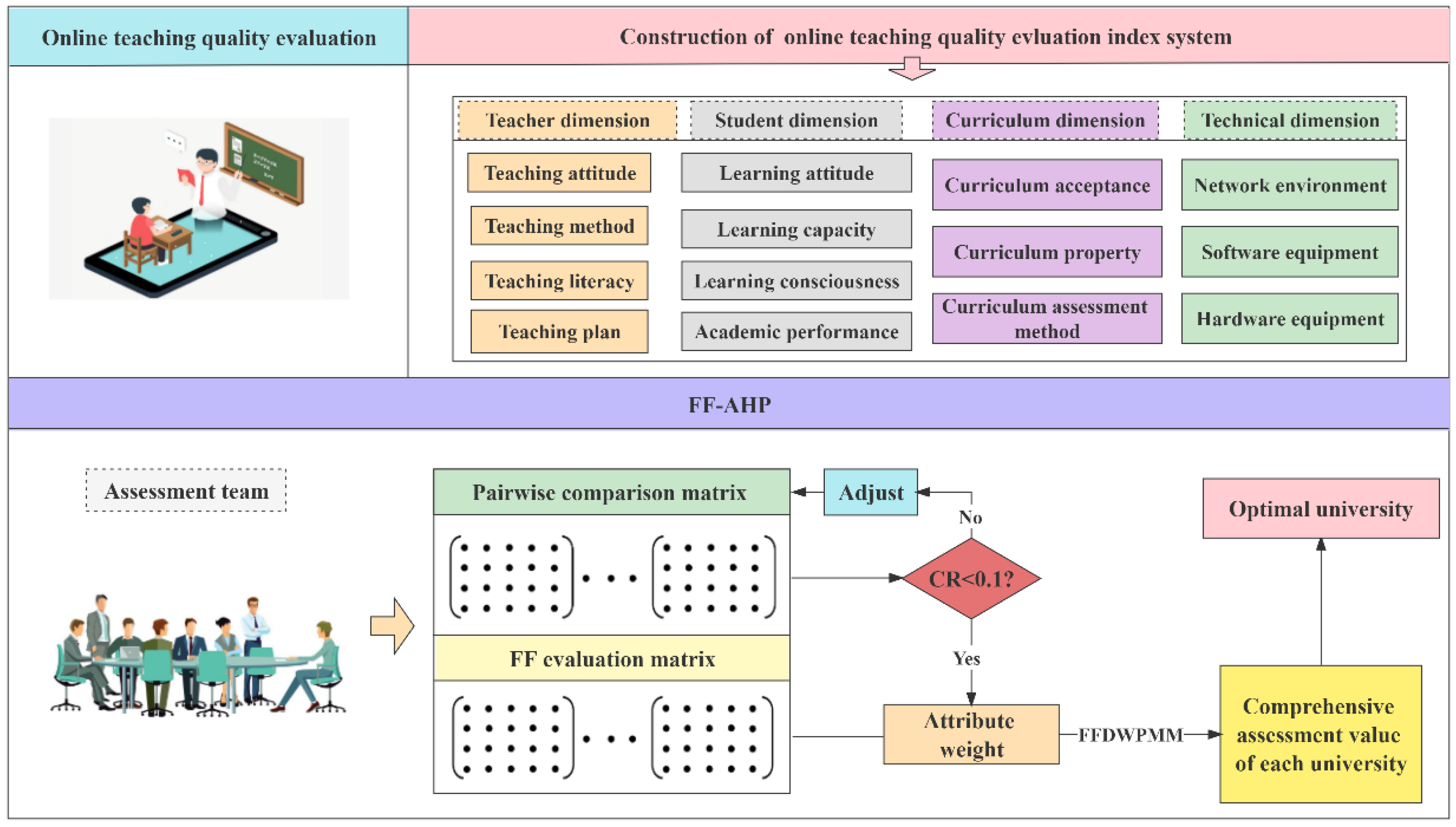
4. Construction of the Online Teaching Quality Evaluation Index System

The online teaching model is increasingly applied for college classrooms due to the dominant positions it creates, such as geographical location, unrestricted time and access, synchronization of involvement and creative teaching patterns [59,60,61]. Online teaching and offline teaching are two kinds of teaching activities with the same nature but different categories. Online teaching, a new teaching form based on modern communication technology, has many idiographic characteristics, such as environment networking, media data and resource sharing. Under the influence of COVID-19, online teaching has been integrated into college teaching, so the quality of online teaching will closely affect the process of students’ quality training. Therefore, the quality evaluation of online teaching in colleges and universities can not only supervise the professional construction of colleges and universities in the special period but can also provide references and suggestions for the development of online teaching pattern. On the basis of combing the literature related to classroom teaching [62,63,64] and teaching satisfaction [6,65,66], combined with the features of online teaching, 4 criteria levels and 14 attribute levels that affect the quality of online teaching, such as teacher factors, student factors, classroom factors and technical factors, are extracted to form an online teaching quality evaluation index system. The details are shown in the following

Table 1. The online teaching quality evaluation index system.

Target Level	Criterion Level	Attribute Level
Online teaching quality	$\mathrm{Teacher}\mathrm{dimension}(S_1$)	$\mathrm{Teaching}\mathrm{attitude}(c_1$)
		$\mathrm{Teaching}\mathrm{method}(c_2$)
		$\mathrm{Teaching}\mathrm{literacy}(c_3$)
		$\mathrm{Teaching}\mathrm{plan}(c_4$)
	$\mathrm{Student}\mathrm{dimension}(S_2$)	$\mathrm{Learning}\mathrm{attitude}(c_5$)
		$\mathrm{Learning}\mathrm{capacity}(c_6$)
		$\mathrm{Learning}\mathrm{consciousness}(c_7$)
		$\mathrm{Academic}\mathrm{performance}(c_8$)
	$\mathrm{Curriculum}\mathrm{dimension}(S_3$)	$\mathrm{Curriculum}\mathrm{acceptance}(c_9$)
		$\mathrm{Curriculum}\mathrm{property}(c_{10}$)
		$\mathrm{Curriculum}\mathrm{assessment}\mathrm{method}(c_{11}$)
	$\mathrm{Technical}\mathrm{dimension}(S_4$)	$\mathrm{Network}\mathrm{environment}(c_{12}$)
		$\mathrm{Software}\mathrm{equipment}(c_{13}$)
		$\mathrm{Hardware}\mathrm{equipment}(c_{14}$)

.

The teacher dimension ($S_1$) consists of four aspects: teachers’ teaching attitude ($c_1$), teaching method ($c_2$), teaching literacy ($c_3$) and teaching plan ($c_4$). Among them, teaching attitude ($c_1$) refers to the acquired psychological tendency of teachers to show their working attitude and react to it in online teaching. The positive work attitude is mainly manifested as taking the initiative to prepare lessons before class, teaching vividly in class and assessing and revising homework fairly after class.

Teaching method ($c_2$) refers to a series of teaching methods adopted by teachers to teach professional knowledge and learning experience to students, so that students can master subject knowledge and subject education ideas.

Teaching literacy ($c_3$) mainly includes three aspects: teachers’ own quality, knowledge level and professional skills. Teachers’ own knowledge reserve is the premise of excellent teaching literacy, teachers’ own quality determines the level of imparting knowledge and teachers’ professional skills are the external embodiment of excellent teaching literacy.

Teaching plan ($c_4$) is the overall planning of the teaching process. According to the teaching tasks and the total class hours, teachers design and arrange the proportion of different chapters in terms of time organization, assessment form and learning requirements.

The Student dimension ($S_2$) is embodied in four levels of students’ learning attitude ($c_5$), learning capacity ($c_6$), learning consciousness ($c_7$) and academic performance ($c_8$). Students’ learning attitude ($c_5$) means that students possess a positive or negative behavior tendency towards their long-term learning tasks. It can be judged from the emotional state of learning, the degree of seriousness of learning and so on. Learning attitude is one of the most important non-cognitive factors that affect students’ learning efficiency. Cultivating students’ positive learning attitude is an effective way to improve teachers’ teaching quality. In addition, the quality of learning attitude can reflect students’ satisfaction with online learning.

Learning capacity ($c_6$) is the inherent embodiment of students’ learning efficiency of curriculum content. Learning capacity will not only affect students’ interest and motivation, but also imply the attribution of their learning quality. Learning capacity determines students’ acceptance and acquisition of fresh knowledge, which is closely related to the quality of teaching.

Learning consciousness ($c_7$) refers to the subjective consciousness action produced by students in completing their schoolwork. It is reflected in that students preview knowledge before class, listen carefully in class, review actively after class and so on. Equipped with a good learning consciousness will enable students to actively make learning plans and goals, and then complete learning tasks in an efficient and planned manner.

Academic performance ($c_8$) measures the extent to which learners can master and apply knowledge and improve their skills and abilities through online teaching. Academic performance not only reflects the results of online teaching, but also related to the level of online education quality, which is the comprehensive level of teachers’ teaching output, learners’ learning input and online classroom implementation.

The curriculum dimension ($S_3$) includes curriculum acceptance ($c_9$), curriculum property ($c_{10}$) and curriculum assessment method ($c_{11}$). Among them, curriculum acceptance ($c_9$) refers to the psychological acceptance of the courses taught by teachers and students, including the judgment of the difficulty of the course content and the familiarity of the curriculum knowledge. Possessing a good acceptance degree of the courses will exert a certain promotion effect on the students’ mastery of knowledge and understanding of the content, which will make the teaching process smoother and will ensure the quality of teaching.

Curriculum property ($c_{10}$) refers to whether the category of the course subordinates to a compulsory course or an elective course, which mainly embodies its judgment on the importance of curriculum content and the measurement of the practical application of the course. The curriculum property will affect learners’ attention to the curriculum. Learners usually have a higher interest and motivation in learning compulsory courses with high credits and strong practicability.

Curriculum assessment method ($c_{11}$) refers to the method by which teachers test the learning situation of learners, including process assessment and horizontal assessment. Process assessment indicates the performance of learners in class, such as actively answering questions, high completion of homework and high enthusiasm for class. Horizontal assessment is to give the scores according to the degree of completion of the final paper handed in by the learners, embodying the familiarity with the knowledge and its application.

The technical dimension ($S_4$) includes network environment ($c_{12}$), software equipment ($c_{13}$) and hardware equipment ($c_{14}$). The network environment ($c_{12}$), related to space and scope, which not only refers to the place where network resources and network tools act but also includes learning atmosphere, learning experience and other states, is a combination of the macro- and micro-scales. Different from offline classroom teaching, online teaching runs in the network environment. Network stutter leads to poor knowledge teaching and learners’ lack of knowledge acquisition that will exert a negative impact on the overall teaching quality.

Software equipment ($c_{13}$) refers to all kinds of software facilities, which belong to internal factors, including online platform, school teaching organization ability, the teaching atmosphere and so on. In the process of online teaching, this software equipment is easily ignored. Teaching management ideas and teaching techniques adapted to the online teaching should be adopted to ensure the subjective experience of teachers and learners, so as to promote the high-quality development of online teaching.

Hardware equipment ($c_{14}$), belonging to external factors, mainly includes solid-state facilities for auxiliary teaching tasks such as computer equipment, seat equipment, mobile phones and other facilities. The hardware equipment is the basis of online teaching, and the quality of the basic equipment will affect the online teaching process to a great extent. In addition, mobile phones are widely used as an online learning tool because of its strong portability. However, mobile phones and other smart devices also have drawbacks such as unsmooth network connections, unstable networks and temporary failure, which have poor effects on the comprehensive teaching quality.

5. A Novel MADM Model Based on FF-AHP and FFDWPMM Operator

Analytical hierarchy process (AHP) is a quantitative decision analysis method for qualitative problems, which was first put forward by Satty [67], belonging to the research category of multi-objective decision optimization problems in operational research. This method decomposes the research objective into the component attributes of the problem from a systematic point of view. By comparing the influence of each attribute on the entire research objective, the influence of each attribute at each level on the final judgment result can be clearly and accurately quantified. The attributes of the online teaching quality evaluation index system are relatively complex and cannot be carried out standard quantitative processing, causing the evaluation of various attributes depends on decision maker’s subjective consciousness. Based on the above considerations, this manuscript utilizes the AHP to calculate the weight of attribute under FF situation, thus forming the FF-AHP method.

Considering a MADM case, which is made up of m alternatives, $FA=\left\{F{A}_1,F{A}_2,\cdots ,F{A}_m\right\}$ and n criteria $c=\left\{c_1,c_2,\cdots ,c_n\right\}$. Meanwhile, the n criteria are divided into N subregions, $s_h=\left\{c_1,c_2,\cdots ,c_{\left|s_h\right|}\right\}\left(h=1,2,\cdots ,N\right)$, satisfying the conditions: $s_1\cup s_2\cup \cdots \cup s_N=c$ and $s_1\cap s_2\cap \cdots \cap s_N=\varnothing$. $\left|s_h\right|$ indicates the number of arguments in the partition $s_h=\left\{c_1,c_2,\cdots ,c_{\left|s_h\right|}\right\}\left(h=1,2,\cdots ,N\right)$. The FF-AHP method’s main steps are listed as follows:

Step 1.

Build a hierarchical structure model. According to the influencing factors and internal logical relationships of the evaluation object, the corresponding hierarchical structure model is constructed.

Step 2.

Construct the pairwise comparison matrix $P={\left[{\varphi }_{ij}\right]}_{n\times n}$, where ${\varphi }_{ij}\left(i,j=1,2,3,\cdots ,n\right)$ denotes the relative importance scale of criteria $c_i$ to criteria $c_j$, utilizing practiced experts’ judgement information based on linguistic terms shown in

Table 2. Relative importance scale of AHP.

Scale Value	Scale Implication
1	Equal importance (EI)
3	Slight importance (SI)
5	High importance (HI)
7	Very high importance (VHI)
9	Certainly high importance (CHI)
2, 4, 6, 8	Intermediate states corresponding to the above judgments.

.

Step 3.

Compute the maximum eigenvalue of judgment ${\lambda }_{\max }$ referring to the mathematical formulas:

$${\Im }_i={\displaystyle \prod _{j=1}^n{\varphi }_{ij}}\left(i,j=1,2,3,\cdots ,n\right)$$

(36)

$${\omega }_i=\frac{{\aleph }_i}{{\displaystyle \sum _i^n{\aleph }_i}},{\aleph }_i=\sqrt[n]{{\Im }_i}$$

(37)

$${\lambda }_{\max }=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\left(P\omega \right)}_i}{{\omega }_i}}$$

(38)

where ${\Im }_i$ is obtained by multiplying the element ${\varphi }_{ij}$ in the comparison matrix P by row, and $\omega ={\left({\omega }_1,{\omega }_2,{\omega }_3,\cdots ,{\omega }_n\right)}^T$ represents the normalized weight vector.

Step 4.

Examine the consistency of each pairwise comparison matrix. The smaller the value of the consistency index (CI), the greater the consistency level. Considering that the consistency deviation may also be caused by random causes, it is necessary to compare CI with the random consistency index (RI) to obtain the consistency ratio (CR) to test whether the judgment matrix meets the requirement:

$$CI=\frac{{\lambda }_{\max }-n}{n-1},$$

(39)

$$CR=\frac{CI}{RI},$$

(40)

where the value of CR is delimited by the order of the comparison matrix (n) as given in

Table 3. The random consistency index.

n	1	2	3	4	5	6	7	8	9
RI	0.00	0.00	0.58	0.9	1.12	1.24	1.32	1.41	1.45

.

If $CR<0.1$, then the consistency of the comparison matrix is satisfactory and meets the requirements; if $CR\ge 0.1$, then the comparison matrix cannot be qualified for further computation. Thus, decision makers are required to modify the initial values in the comparison matrix for subsequent calculation process [68].

Step 5.

Construct the FF evaluation matrix $R={\left[{\mathsf{\Upsilon }}_{xy}\right]}_{m\times n}$ referring to the experts’ scoring value, where ${\mathsf{\Upsilon }}_{xy}=〈{\alpha }_{{\mathsf{\Upsilon }}_{xy}},{\beta }_{{\mathsf{\Upsilon }}_{xy}}〉\left(x=1,2,\cdots ,m;y=1,2,\cdots n\right)$ means FFNs on the evaluation information of alternative $F{A}_x\left(x=1,2,\cdots ,m\right)$ with regard to criteria $c_y\left(y=1,2,\cdots n\right)$.

Step 6.

Normalize the FF evaluation matrix $R={\left[{\mathsf{\Upsilon }}_{xy}\right]}_{m\times n}$. In general, two types of criteria may be contained in MADM case, namely, benefit criteria and cost criteria, exerting positive and negative impact on evaluation results. To eliminate the adverse effects, FF evaluation matrix $R={\left[{\mathsf{\Upsilon }}_{xy}\right]}_{m\times n}={\left[〈{\alpha }_{{\mathsf{\Upsilon }}_{xy}},{\beta }_{{\mathsf{\Upsilon }}_{xy}}〉\right]}_{m\times n}$ is normalized in this way: If $c_y$ belongs to benefit criteria, then $R={\left[{\mathsf{\Upsilon }}_{xy}\right]}_{m\times n}={\left[〈{\alpha }_{{\mathsf{\Upsilon }}_{xy}},{\beta }_{{\mathsf{\Upsilon }}_{xy}}〉\right]}_{m\times n}$; if $c_y$ belongs to cost criteria, then $R={\left[{\mathsf{\Upsilon }}_{xy}\right]}_{m\times n}={\left[〈{\beta }_{{\mathsf{\Upsilon }}_{xy}},{\alpha }_{{\mathsf{\Upsilon }}_{xy}}〉\right]}_{m\times n}$.

Step 7.

Compute the comprehensive assessment value ${\Gamma }_{A_x}\left(x=1,2,\cdots ,m\right)$ of each alternative. Utilizing the criteria weight vector $\omega ={\left({\omega }_1,{\omega }_2,{\omega }_3,\cdots ,{\omega }_n\right)}^T$ obtained by Step 3, and matrix $FF={\left[{\mathsf{\Upsilon }}_{xy}\right]}_{m\times n}$, calculating the comprehensive assessment value of alternative $F{A}_x\left(x=1,2,\cdots ,m\right)$ by utilizing the FFDWPMM operator defined in Equation (28).

Step 8.

Sort the alternatives by score value of comprehensive assessment value and choose one with optimal performance.

6. Practical Example

As China has made extraordinary achievements in the field of information technology, which has greatly promoted the development of economy, the value of information and data processing technology is increasing day by day. Especially in today’s era of data transformation, how to deal with data quickly and accurately and make correct decisions has become the focus of both the government and enterprises. Sole and Weinberg [69], professors of the School of Data at New York University, believe that “this is the most exciting era for statistics, because the availability of all kinds of data has never been improved, and we can analyze larger amounts of data to reach more accurate conclusions.” As a methodological discipline based on data collection, processing and analysis, business statistics has become an essential course for cultivating students with mathematical statistics knowledge, statistical literacy and awareness in the business school in colleges and universities, and exerts a significant role in supplying statistics talents to the country. Especially under the influence of COVID-19, when colleges and universities cannot teach offline normally, it is worthy to research whether the effectiveness of online teaching of business statistics courses is guaranteed.

6.1. The Subject Background of Business Statistics

Statistics is not only a significant foundation of big data, artificial intelligence and data economy but also a vital implement for modern industrial and commercial enterprise superintendents to make scientific decisions in the face of indeterminacy. Actually, the indeterminacy confronted by superintendents in decision making is increasing day by day, which requires superintendents to collect objective and practical data and extract serviceable information on the basis of processing and analyzing these data, so as to make appropriate decisions with quantitative basis. This raises the question of how to collect data, analyze data and interpret the consequences of the analysis, and statistics is an effective tool and means to solve these problems. Applying the concepts and methods of statistics to the business field and solving all kinds of problems constitute business statistics, which utilizes data and statistical methods to explore the quantitative characteristics and performance of business phenomena, explain related business phenomena and explore economic laws and apply them to empirical research and decision-making analysis.

6.2. Research Design

This research is divided into three stages as a whole. The first stage is the construction of the online teaching quality evaluation index system introduced in detail in Section 4. The second stage is the construction of a novel MADM model described in detail in Section 5. The third stage is to combine the evaluation index system with MADM model to assess and analyze the online teaching quality of the business statistics course. An illustrative diagram for online teaching quality evaluation is shown in Figure 1.

This research adopts the comprehensive sampling method of stratified sampling and random sampling and randomly selects four universities with rankings between 50 and 80 from different disciplines of universities offering business statistics courses (i.e., $F{A}_1$ is a comprehensive university; $F{A}_2$ is a university of science and technology; $F{A}_3$ is a normal university; and $F{A}_4$ is a university of finance and economics) to evaluate and analyze the online teaching quality of business statistics courses.

6.3. Evaluation Process

Several well-known domestic teaching experts are invited to form a review team to score the online teaching situation of the business statistics courses of 4 universities in multiple dimensions according to the 14 attributes from the online teaching evaluation index system constructed in this paper. The 14 attributes explained in Section 4 are as follows: $c_1$: Teaching attitude; $c_2$: Teaching method; $c_3$: Teaching literacy; $c_4$: Teaching plan; $c_5$: Learning attitude; $c_6$: Learning capacity; $c_7$: Learning consciousness; $c_8$: Academic performance; $c_9$: Curriculum acceptance; $c_{10}$: Curriculum property; $c_{11}$: Curriculum assessment method; $c_{12}$: Network environment; $c_{13}$: Software equipment; and $c_{14}$: Hardware equipment. Based on their interrelationship, the 14 attributes have been segmented into 4 partitions: $S_1$: Teacher dimension, $S_1=\left\{c_1,c_2,c_3,c_4\right\}$; $S_2$: Student dimension, $S_2=\left\{c_5,c_6,c_7,c_8\right\}$; $S_3$: Curriculum dimension, $S_3=\left\{c_9,c_{10},c_{11}\right\}$; and $S_4$: Technical dimension, $S_4=\left\{c_{12},c_{13},c_{14}\right\}$.

The presented FF-AHP method is confirmed in depth through a contradistinctive analysis of the online teaching quality of business statistics course in four universities. The specific assessment information for each attribute from research experts with extensive experience is presented in

Table 4. Assessment information denoted by FFNs.

Criterion	Attribute	University
		FA1	FA2	FA3	FA4
$S_1$	$c_1$	$〈0.78,0.45〉$	$〈0.68,0.34〉$	$〈0.77,0.82〉$	$〈0.93,0.63〉$
	$c_2$	$〈0.84,0.73〉$	$〈0.89,0.35〉$	$〈0.45,0.29〉$	$〈0.56,0.77〉$
	$c_3$	$〈0.83,0.26〉$	$〈0.67,0.56〉$	$〈0.64,0.44〉$	$〈0.83,0.64〉$
	$c_4$	$〈0.68,0.45〉$	$〈0.82,0.45〉$	$〈0.85,0.38〉$	$〈0.84,0.44〉$
$S_2$	$c_5$	$〈0.57,0.48〉$	$〈0.88,0.56〉$	$〈0.33,0.33〉$	$〈0.75,0.75〉$
	$c_6$	$〈0.88,0.46〉$	$〈0.90,0.43〉$	$〈0.67,0.38〉$	$〈0.83,0.45〉$
	$c_7$	$〈0.83,0.46〉$	$〈0.68,0.31〉$	$〈0.93,0.32〉$	$〈0.84,0.36〉$
	$c_8$	$〈0.62,0.67〉$	$〈0.66,0.46〉$	$〈0.75,0.46〉$	$〈0.78,0.34〉$
$S_3$	$c_9$	$〈0.83,0.45〉$	$〈0.73,0.23〉$	$〈0.92,0.34〉$	$〈0.77,0.46〉$
	$c_{10}$	$〈0.71,0.34〉$	$〈0.64,0.56〉$	$〈0.88,0.34〉$	$〈0.57,0.66〉$
	$c_{11}$	$〈0.84,0.67〉$	$〈0.77,0.81〉$	$〈0.68,0.56〉$	$〈0.82,0.24〉$
$S_4$	$c_{12}$	$〈0.69,0.49〉$	$〈0.86,0.47〉$	$〈0.78,0.54〉$	$〈0.72,0.33〉$
	$c_{13}$	$〈0.76,0.54〉$	$〈0.85,0.55〉$	$〈0.94,0.35〉$	$〈0.64,0.77〉$
	$c_{14}$	$〈0.58,0.34〉$	$〈0.63,0.26〉$	$〈0.68,0.53〉$	$〈0.46,0.82〉$

.

Step 1.

Build a hierarchical structure model. According to the influencing factors and internal logical relationships of the evaluation object, the corresponding hierarchical structure model is constructed. We have accomplished this task in Section 4.

Step 2.

Construct the pairwise comparison matrix $P={\left[{\varphi }_{ij}\right]}_{n\times n}$. According the review team’s preference language information, we have built up five pairwise comparison matrices, and the specific details are given in

Table 5. Pairwise comparison matrix of attributes with respect to the teacher dimension.

	$c_1$	$c_2$	$c_3$	$c_4$
$c_1$	1	4	1/3	2
$c_2$	1/4	1	7	3
$c_3$	3	1/7	1	4
$c_4$	1/2	1/3	1/4	1

,

Table 6. Pairwise comparison matrix of attributes with respect to the student dimension.

	$c_5$	$c_6$	$c_7$	$c_8$
$c_5$	1	1/4	1/3	3
$c_6$	4	1	2	6
$c_7$	3	1/2	1	5
$c_8$	1/3	1/6	1/5	1

,

Table 7. Pairwise comparison matrix of attributes with respect to the curriculum dimension.

	$c_9$	$c_{10}$	$c_{11}$
$c_9$	1	1/3	4
$c_{10}$	3	1	5
$c_{11}$	1/4	1/5	1

,

Table 8. Pairwise comparison matrix of attributes with respect to the technical dimension.

	$c_{12}$	$c_{13}$	$c_{14}$
$c_{12}$	1	3	6
$c_{13}$	1/3	1	4
$c_{14}$	1/6	1/4	1

and

Table 9. Pairwise comparison matrix of criteria.

	$S_1$	$S_2$	$S_3$	$S_4$
$S_1$	1	1/3	2	1/2
$S_2$	3	1	4	2
$S_3$	1/2	1/4	1	1/3
$S_4$	2	1/2	3	1

.

Step 3.

Compute the maximum eigenvalues of five pairwise comparison matrices. Utilizing the Equations (36)–(38), the maximum eigenvalues of five pairwise comparison matrices are ${\lambda }_{\max }^{S_1}=4.0571$, ${\lambda }_{\max }^{S_2}=4.0899$, ${\lambda }_{\max }^{S_3}=3.0858$, ${\lambda }_{\max }^{S_4}=3.0536$ and ${\lambda }_{\max }=4.0310$.

Step 4.

Examine the consistency of each pairwise comparison matrix. Referring to the Equations (39) and (40) and to Table 3, we have obtained $C{I}_{S_1}=0.0190$, $C{I}_{S_2}=0.0300$, $C{I}_{S_3}=0.0429$, $C{I}_{S_4}=0.0268$, $CI=0.0103$, $C{R}_{S_1}=0.0212$, $C{R}_{S_2}=0.0333$, $C{R}_{S_3}=0.0739$, $C{R}_{S_4}=0.0462$ and $CR=0.0115$. Due to the values of 5 CRs being less than 0.1, then the consistency of the 5 pairwise comparison matrices is satisfactory and meets the requirements. Then, the details about the weight coefficients of 14 attributes are denoted in the following

Table 10. Weight coefficients of 14 attributes.

Criterion	Criterion Weight	Attribute	Related Weight	Final Weight	CR
$S_1$	$0.1603$	$c_1$	$0.2359$	$0.0378$	$0.0212$
		$c_2$	$0.0610$	$0.0098$
		$c_3$	$0.5588$	$0.0895$
		$c_4$	$0.1444$	$0.0231$
$S_2$	$0.4668$	$c_5$	$0.1300$	$0.0607$	$0.0333$
		$c_6$	$0.4840$	$0.2260$
		$c_7$	$0.3310$	$0.1545$
		$c_8$	$0.0549$	$0.0256$
$S_3$	$0.0953$	$c_9$	$0.2797$	$0.0267$	$0.0739$
		$c_{10}$	$0.6267$	$0.0597$
		$c_{11}$	$0.0936$	$0.0089$
$S_4$	$0.2776$	$c_{12}$	$0.6442$	$0.1788$	$0.0462$
		$c_{13}$	$0.2706$	$0.0751$
		$c_{14}$	$0.0852$	$0.0237$

.

Step 5.

Construct the FF evaluation matrix referring to the experts’ scoring value. The specific assessment information is shown in Table 4.

Step 6.

Normalize the FF evaluation matrix. All the attributes from the evaluation index system are beneficial, so we have nothing to do.

Step 7.

Compute the comprehensive assessment value ${\Gamma }_{A_i}\left(i=1,2,3,4\right)$ of each university ($g=1$). Referring to the Definition 11, we can acquire the consequence: ${\Gamma }_{A_1}=〈0.2656,0.9335〉$, ${\Gamma }_{A_2}=〈0.2825,0.8957〉$, ${\Gamma }_{A_3}=〈0.2350,0.9101〉$ and ${\Gamma }_{A_4}=〈0.2731,0.9540〉$. Considering that this paper divides the 14 attributes into 4 partitions, the correlation coefficient of the attributes between the sections is set according to the number of each partition, that is, $V=\left(\stackrel{4}{\overbrace{\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}}},\stackrel{4}{\overbrace{\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}}},\stackrel{3}{\overbrace{\frac{1}{3},\frac{1}{3},\frac{1}{3}}},\stackrel{3}{\overbrace{\frac{1}{3},\frac{1}{3},\frac{1}{3}}}\right)$.

Step 8.

Rank the online teaching quality of business statistics course in four universities according to their comprehensive assessment values, and we have found that university $F{A}_2$ has the optimal performance in online teaching quality of business statistics course in four universities; the detailed results are given in

Table 11. The ranking order of four universities.

University	Score Value	Ranking Result
$F{A}_1$	$sc{o}_1=-0.7948$	${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$
$F{A}_2$	$sc{o}_2=-0.6960$
$F{A}_3$	$sc{o}_3=-0.7410$
$F{A}_4$	$sc{o}_4=-0.8479$

.

7. The Result Analysis

7.1. Sensitivity Analysis

We show that the proposed FFDWPMM operator introduced in Definition 11 is obviously related to the parameter g. This partition is a group of tentative conducted to observe the impact of the value of the parameter g on the final ranking results of the teaching quality evaluation of the four universities. The specific details are given tabularly in

Table 12. Effect of parameter g on ranking results.

Parameter Value	Ranking of Score Values	Ranking Result
$g=1$	$sc{o}_{F{A}_2}>sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}$	${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$
$g=2$	$sc{o}_{F{A}_2}>sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}$	${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$
$g=3$	$sc{o}_{F{A}_2}>sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}$	${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$
$g=4$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_2}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_2\succ {FA}_1\succ {FA}_4$
$g=5$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=6$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=7$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=8$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=9$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=10$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=11$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=12$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=13$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=14$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$
$g=15$	$sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_2}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$

and graphically in Figure 2. According to Table 12, it is clear that there exists a divergent ranking order under different values of parameter g, that is, when $1\le g\le 3$, the arrangement of the four universities is ${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$; when $g=4$, the arrangement of the four universities is ${FA}_3\succ {FA}_2\succ {FA}_1\succ {FA}_4$; and when $g\ge 5$, the arrangement of the four universities is ${FA}_3\succ {FA}_1\succ {FA}_2\succ {FA}_4$. However, under all the experiments, the university with the lowest comprehensive evaluation remains consistent with $F{A}_4$.

In addition, from Figure 2, we observe that the value of parameter g increases while the score values of the four universities increase, the overall dynamic changes are presented in an upward trend but the increasing speed of the score value of $F{A}_2$ is less than that of $F{A}_1$ and $F{A}_3$. Consequently, the phenomenon in Figure 2 shows that the overall ranking of $F{A}_2$ decreases gradually with the continuous increase in the value of parameter g. In detail, when $1\le g\le 3$, the ranking of $F{A}_2$ remains in the first place; when $g=4$, the score value of $F{A}_3$ is higher than that of $F{A}_2$, $F{A}_3$ changes into the first ranking order and $F{A}_2$ degenerates into the second ranking order; and, finally, when $g\ge 5$, the score value of $F{A}_1$ also exceeds that of $F{A}_2$, and the ranking order of $F{A}_2$ turns into the third. At this point, the arrangement of four universities tends to be stable, and the variation in their score values also remain flat. In general, we can infer that the divergent value of parameter g in the FFDWPMM operator can alter the corresponding arrangement orders of the four universities.

It is observed that the existing studies [29,30,31,36,38,47,49,50] possess the ability to express fuzzy information and capture the interrelationship among attributes, but they rarely take into consideration both the utilization of parameters to make the information aggregation process more flexible and the idea of blocking to deal with the complex relationships between attributes. Since the presented novel MADM model fusing the FF-AHP method and the FFDWPMM operator in this manuscript inclines to describe the fuzzy information, it not only ingeniously utilizes the Dombi operation to make the information aggregation process flexible, but also the PMM operator is introduced to deal with complex attribute association relationships. Consequently, the method shows the amelioration of its elasticity in practical applications.

7.2. Comparative Analysis

The above online teaching quality assessment example and sensitivity analysis of the parameter g can illustrate the applicability and flexibility of our proposed method, but to further demonstrate the effectiveness and superiority of our presented method, we select four aggregation methods for comparative analysis, namely, the FFDWA and FFDWG operators [23] and the FFDWPBM and FFDWPMSM operators introduced in Section 3. Consistent with this paper, the value of the parameter g of the four aggregation operators is supposed to be one. The ranking consequences are given in

Table 13. Ranking results of five aggregation methods.

Aggregation Method	Ranking of Score Values	Ranking Result
FFDWA [23]	$sc{o}_{F{A}_3}>sc{o}_{F{A}_2}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}$	${FA}_3\succ {FA}_2\succ {FA}_1\succ {FA}_4$
FFDWG [23]	$sc{o}_{F{A}_2}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}>sc{o}_{F{A}_3}$	${FA}_2\succ {FA}_1\succ {FA}_4\succ {FA}_3$
FFDWPBM	$sc{o}_{F{A}_2}>sc{o}_{F{A}_1}>sc{o}_{F{A}_3}>sc{o}_{F{A}_4}$	${FA}_2\succ {FA}_1\succ {FA}_3\succ {FA}_4$
FFDWPMSM	$sc{o}_{F{A}_2}>sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}$	${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$
FFDWPMM	$sc{o}_{F{A}_2}>sc{o}_{F{A}_3}>sc{o}_{F{A}_1}>sc{o}_{F{A}_4}$	${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$

.

Next, we provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn. Compared with the decision results of Table 13, it can be found that except for the FFDWA operator, the optimal university obtained by the other four aggregation methods is $F{A}_2$, and except for FFDWG operator, the other four aggregation methods all regard $F{A}_4$ as the lowest comprehensive quality on online teaching of business statistics course. The final ranking result acquired by this presented method is exactly consistent with FFDWPMSM operator introduced by Section 3, both of which are ${FA}_2\succ {FA}_3\succ {FA}_1\succ {FA}_4$, which are slightly different from the other three aggregation methods, but most of them exert the same judgment on the optimal university and the worst university in terms of comprehensive teaching quality. These results further verify the validity and effectiveness of the judgment in this paper. Through the results of the above comparison, the reasons for the differences in ranking order are summarized.

(1)

Firstly, the reason why FFDWA and FFDWG operators are different from the other four methods in the judgment of the optimal university and the worst university is that these two operators do not take into account the correlation among attributes. The FFDWPMM operator proposed in this paper, not only using the information between different attributes but also fully considering the correlation among different attributes, can effectively capture the correlation among attributes to reduce the distortion in the process of information aggregation. Therefore, the method proposed in this paper has more flexibility, stronger practicability and a wider application range.

(2)

Compared with the FFDWPBM operator introduced in Section 3, there mainly exists the divergence in the ranking order of $F{A}_1$ and $F{A}_3$, but obviously, the judgment of this proposed method is consistent with that of most of the above aggregation methods, which shows that the result obtained by this proposed method is more reliable. The FFDWPBM operator only considers the relationship between pairwise attributes. Specifically, when $V=\left(v_1,v_2,0,\cdots ,0\right)\left(v_1,v_2\ne 0,v_i=0,i=3,\cdots ,n\right)$, the FFDWPMM operator is simplified to the FFDWPBM operator. Thus, when there is a more complex correlation between various attributes, the method presented in this paper will be more flexible, universal and applicable to a wider range.

(3)

It is completely consistent with the results of the FFDWPMSM operator introduced in Section 3, which shows the effectiveness of the proposed method to a certain extent. The aggregation method proposed in this paper can meet the different demands of decision makers by adjusting $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$. When $V=\left(\stackrel{k}{\overbrace{1,1,\cdots 1}},\stackrel{n-k}{\overbrace{0,0,\cdots ,0}}\right)\left(v_1=v_2=\cdots =v_k=1,v_{k+1}=v_{k+2}=\cdots =v_n=0\right)$, the FFDWPMM operator degenerates to the FFDWPMSM operator, from which we can observe that the proposed method is more universal.

8. Conclusions

There exist differences in teaching media among online teaching models and traditional offline teaching models, so online teaching quality evaluation is supposed to explore new index evaluation systems and evaluation methods. The first purpose of the research is to construct a novel online teaching quality evaluation index system for the quality evaluation of business statistics course from the four dimensions of teacher, student, curriculum and technology. Another main purpose is to put forward a scientific and effective comprehensive evaluation model for online teaching quality of business statistics course, which utilizes the AHP method to determine the importance of index, as well proposes the FFDWPMM operator to aggregate the comprehensive score of all schemes.

The empirical research and comparative analysis through a practical case verify the superiority and effectiveness of this presented method. From the theoretical point of view, it not only enriches the theories and methods of online teaching quality evaluation of business statistics in colleges and universities, providing a reference for online teaching quality evaluation and construction, but also plays a foreshadowing role in ensuring the stable development of higher education quality.

In addition, through the comparative analysis of cases, it can be seen that students’ learning attitude, learning ability, learning consciousness and learning achievement all have an important impact on the quality of online teaching. Therefore, colleges and universities should pay attention to cultivating students’ habit of active learning and continuous learning from the perspective of practical significance. On the other hand, teachers should timely update their teaching concepts, reform teaching methods and teaching models and ensure the homogeneous development of online and offline teaching ability. The competent authorities should also strengthen technological innovation, improve the convenience of “teaching” and “learning” and stimulate the enthusiasm of teachers and students to use online teaching.

However, there exist room for improvement in this research. The setting of the correlation coefficient $V=\left(v_1,v_2,v_3,\cdots ,v_n\right)$ of the attributes in the FFDPMM and FFDWPMM operators, like most studies, either refers to the number of attributes or is convenient to calculate. In addition, there is a lack of the standardized theory for fitting the correlation coefficient of attributes, that is, how to reasonably set the correlation coefficient in different partitions according to the degree of correlation among attributes. Thus, the future work can start from the setting method of the correlation coefficient among attributes and put forward a more practical partitioned aggregation theory.