Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations
Abstract
1. Introduction
2. Materials and Methods
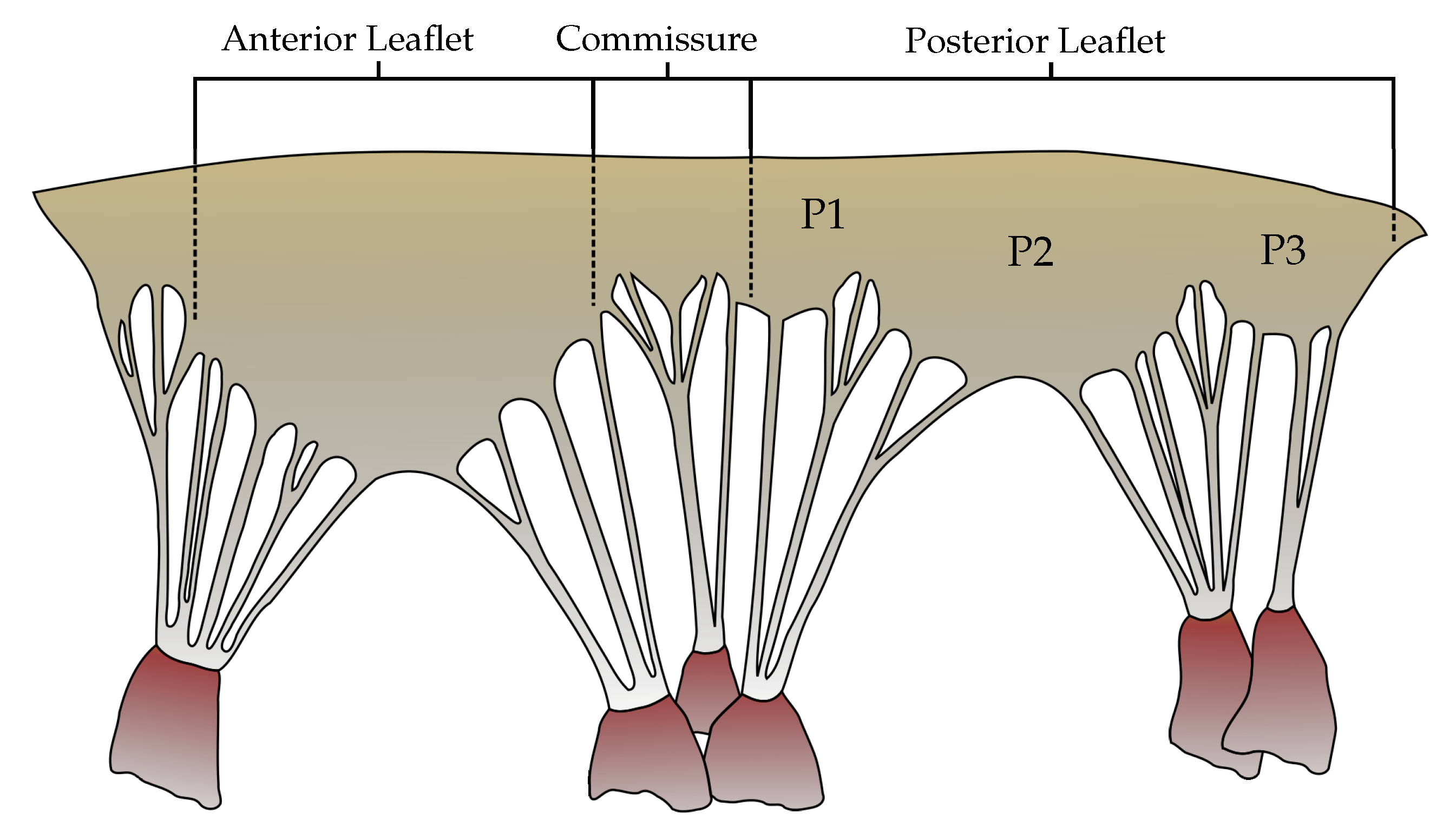
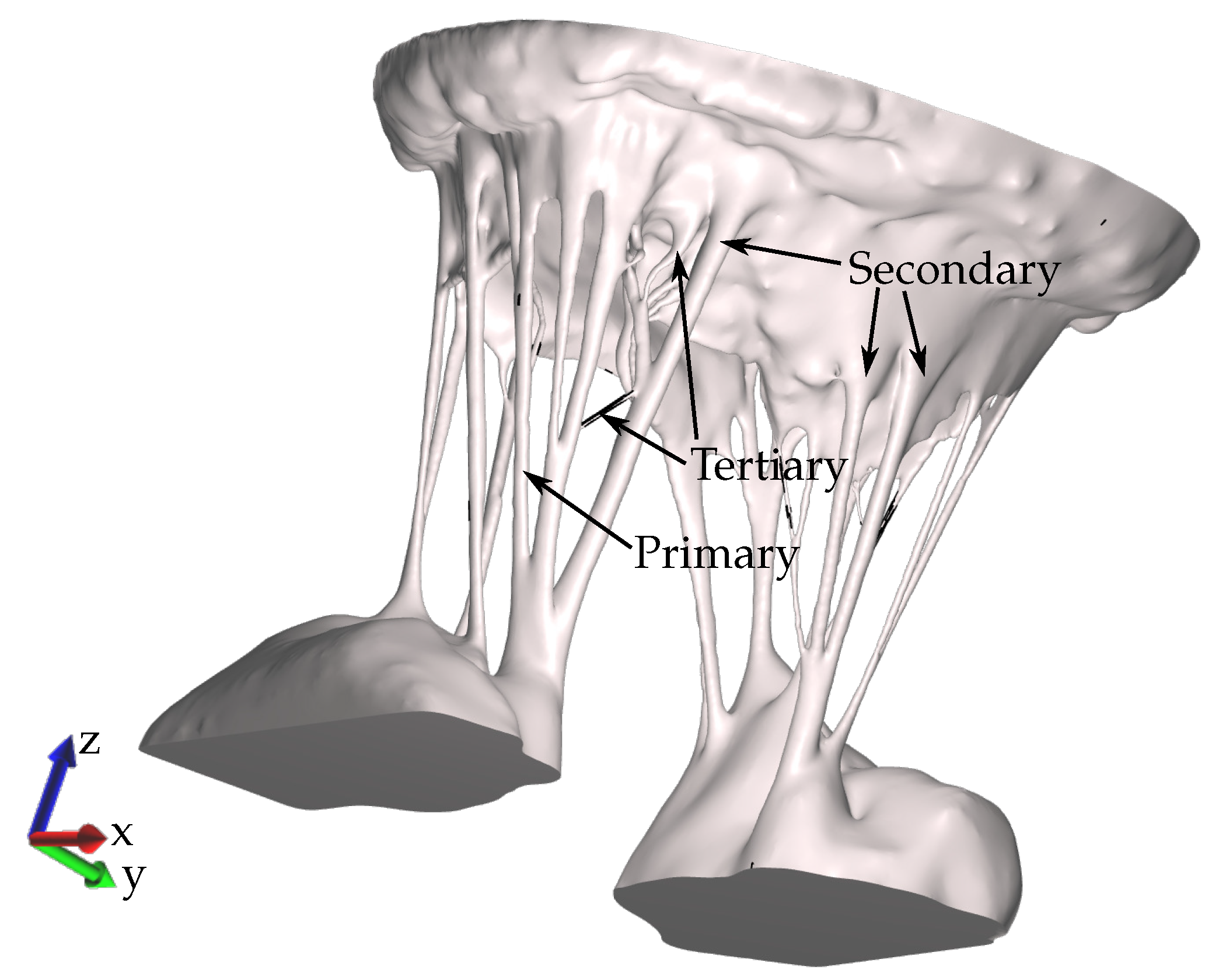
2.1. Model Acquisition
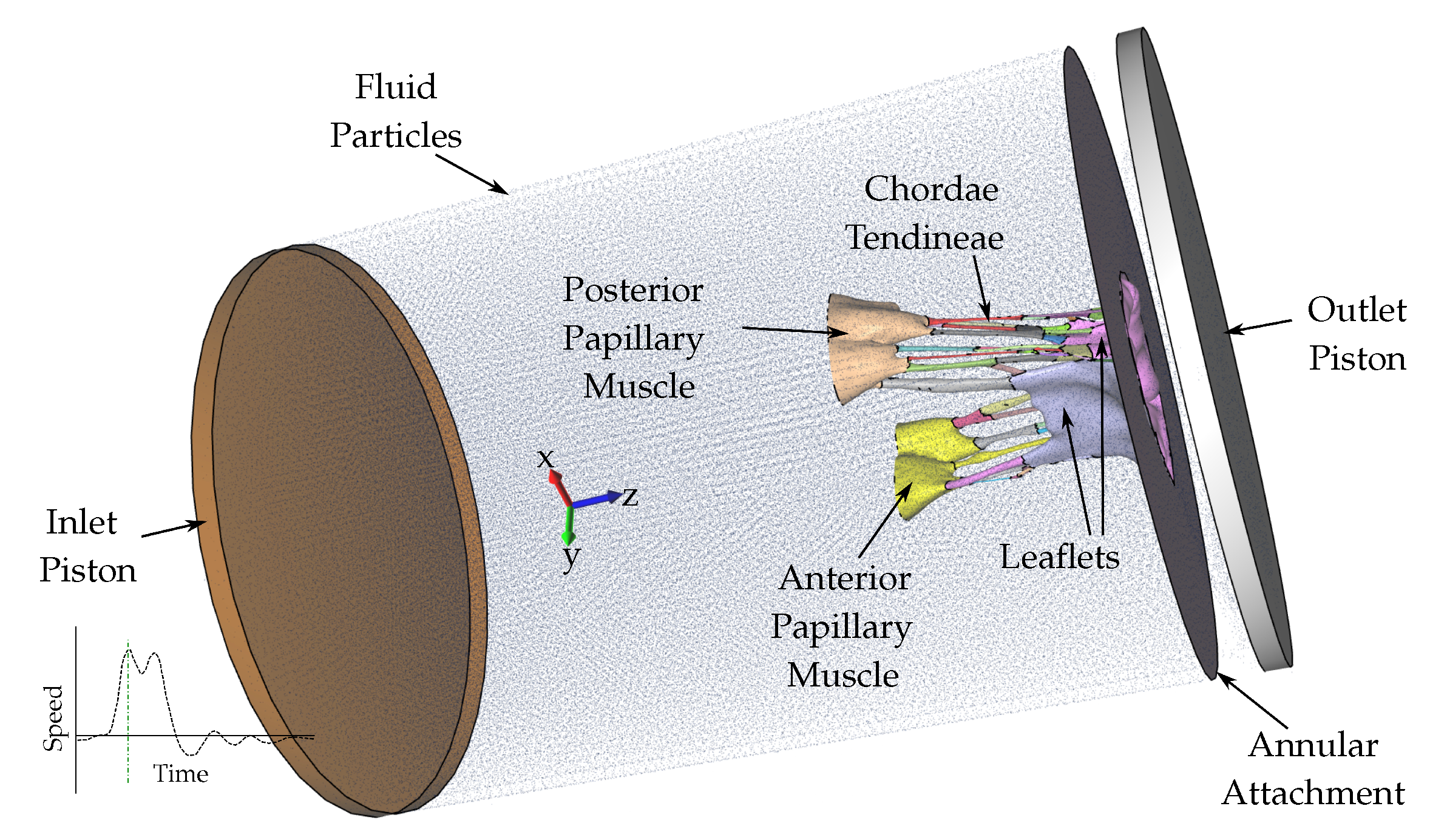
2.2. Fluid-Structure Interaction Analysis
2.3. Validation
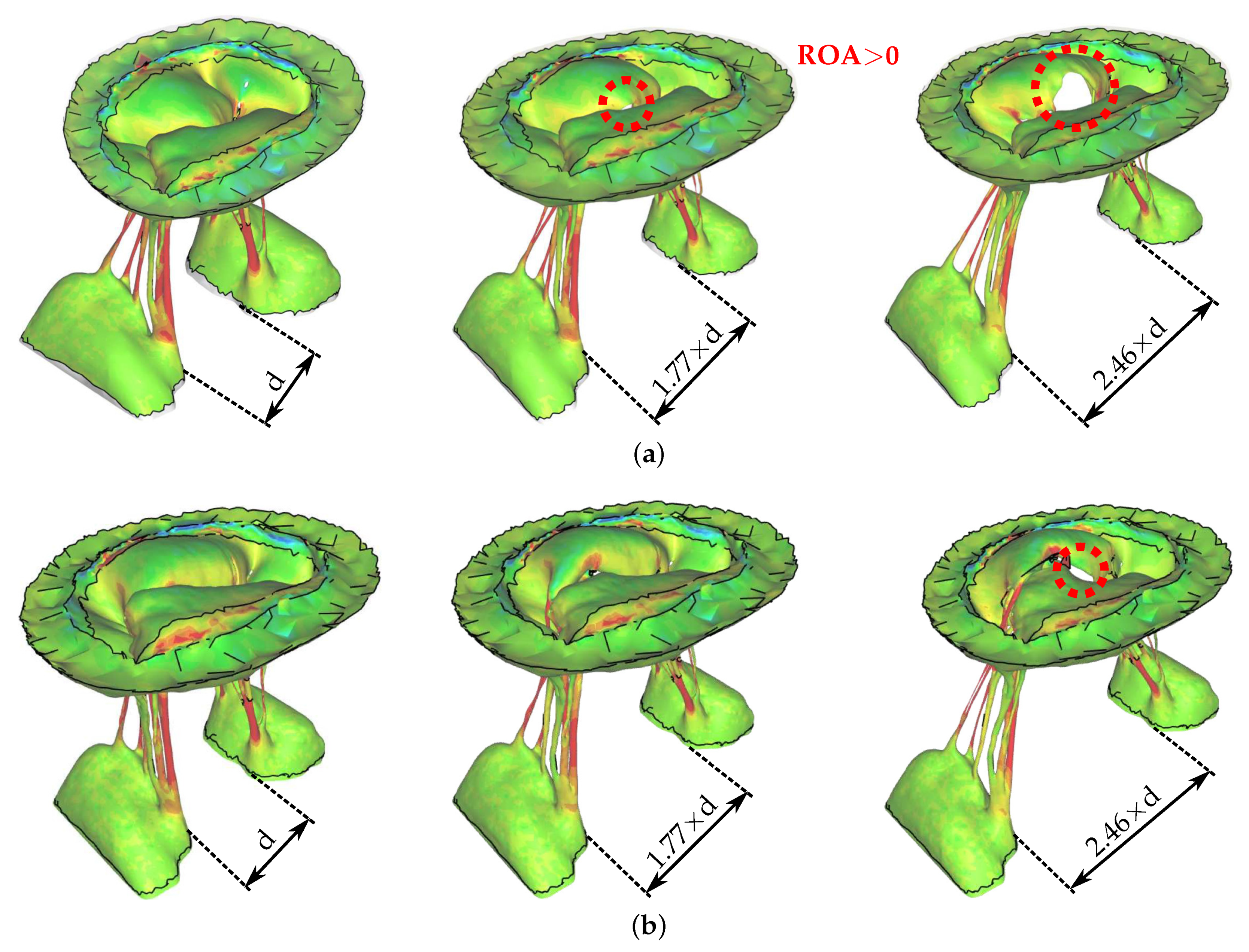
2.4. Papillary Muscles Displacements and Edge-to-Edge Repair
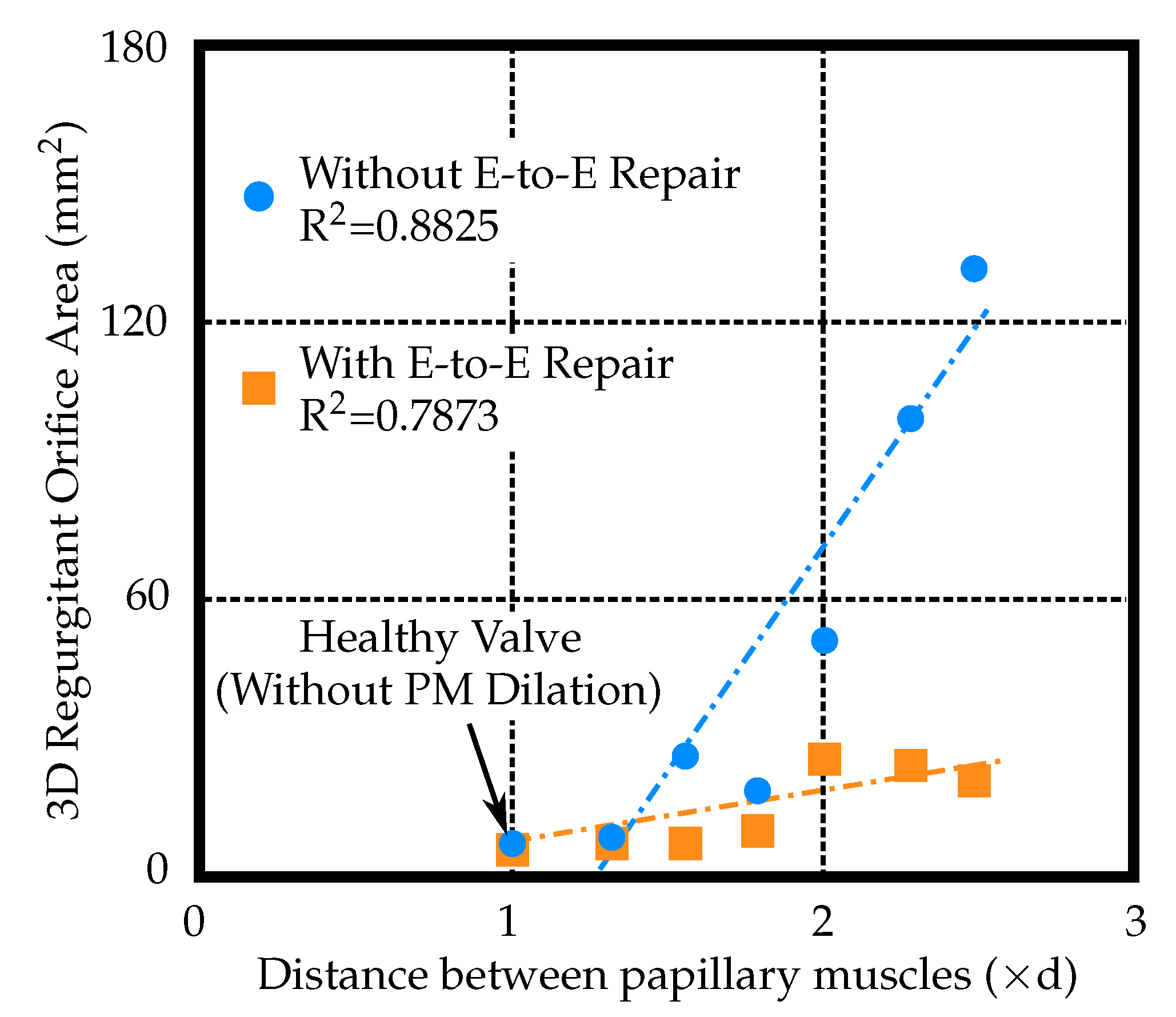
2.5. Regurgitant Orifice Area Measurements
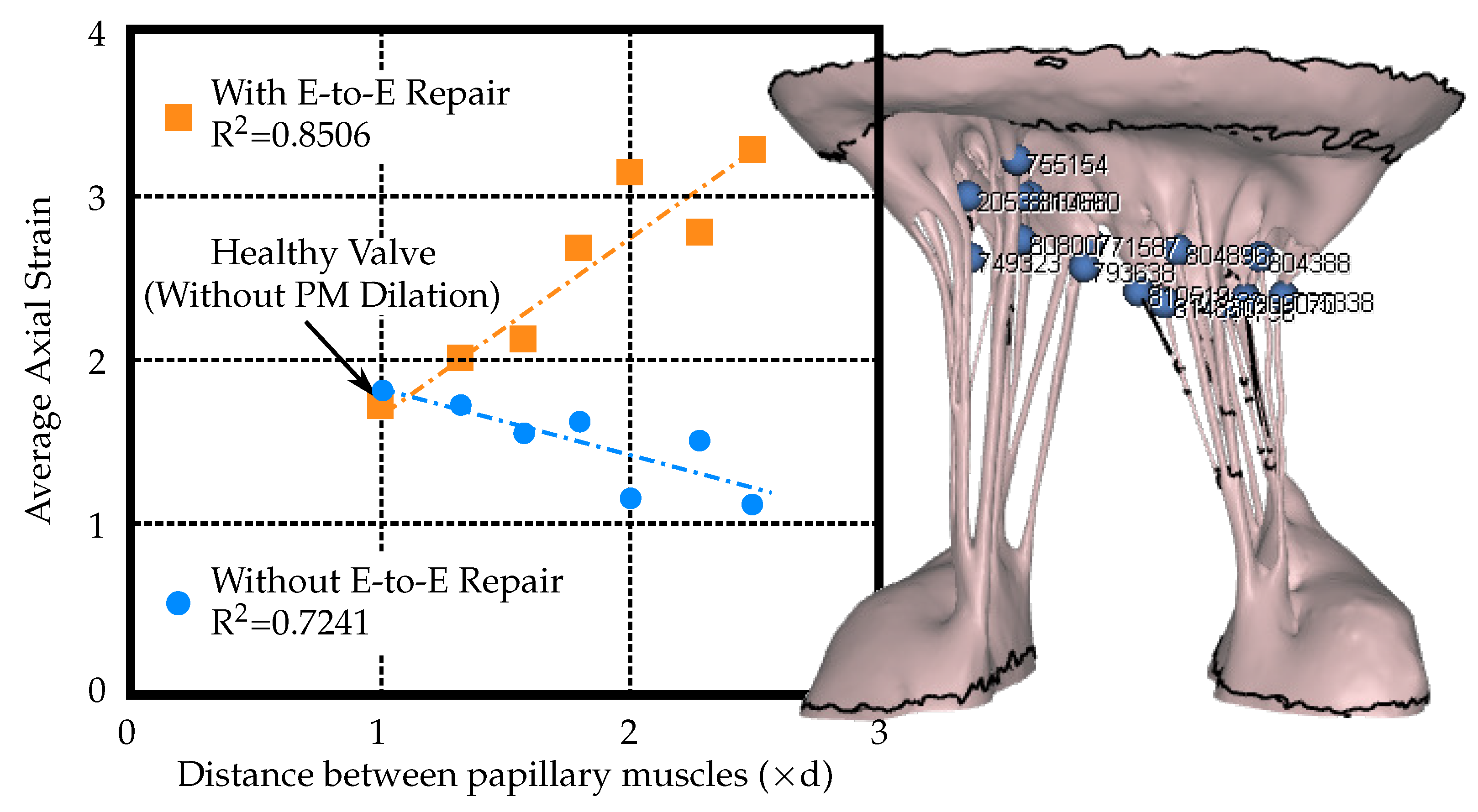
2.6. Strain Assessment
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FMR | Functional Mitral Regurgitation |
| MR | Mitral Regurgitation |
| MV | Mitral Valve |
| PMs | Pupillary Muscles |
| LV | Left Ventricle |
| DMR | Degenerative Mitral Regurgitation |
| FMR | Functional Mitral Regurgitation |
| E-to-E | Edge-to-Edge |
| FDA | Food & Drug Administration |
| FSI | Fluid-Structure Interaction |
| ROA | Regurgitant Orifice Area |
| CT | Micro Computed Tomography |
| DICOM | Digital Imaging and Communications in Medicine |
| SPH | Smoothed Particle Hydrodynamics |
References
- Mirabel, M.; Iung, B.; Baron, G.; Messika-Zeitoun, D.; Detaint, D.; Venoverschelde, J.; Butchart, E.; Vahanian, A. What are the characteristics of patients with severe, symptomatic, mitral regurgitation who are denied surgery? Eur. Heart J. 2007, 28, 1358–1365. [Google Scholar] [CrossRef]
- Carpentier, A.; Adams, D.; Filsoufi, F. Carperntier’s Reconstructive Valve Surgery, 1st ed.; Saunders: Welwyn Garden City, UK, 2010. [Google Scholar]
- Zoghbi, W.; Adams, D.; Bonow, R.; Sarano, M.; Foster, E.; Grayburn, P.; Hahn, R.; Han, Y.; Hung, J.; Lang, R.; et al. Recommendations for Noninvasive Evaluation of Native Valvular Regurgitation. J. Am. Soc. Echocardiogr. 2017, 30, 303–371. [Google Scholar] [CrossRef]
- Bonow, R.; Nishimura, R.; Otto, C. 2014 AHA/ACC guideline for the management of patients with valvular heart disease. JACC 2014, 63, e157–e185. [Google Scholar]
- Lefebvre, X.; Levine, R.; Vlahakes, G. Papillary muscle displacement causes systolic anterio motion of the mitral valve. Circulation 1992, 91, 1189–1195. [Google Scholar]
- Ress, S.; Rickards, A.; McDonald, L.; Ballester, M.; Jajoo, J. The mechanism of mitral valve regurgitation in dilated left ventricle. Clin. Cardiol. 1983, 6, 333–338. [Google Scholar]
- Alfieri, O.; Maisano, F.; Bonis, M.; Stefano, P.; Torracca, L.; Oppizzi, M.; Canna, G. The double-orifice technique in mitral valve repair: A simple solution for complex problems. J. Thorac. Cardiovasc. Surg. 2001, 122, 674–681. [Google Scholar] [CrossRef]
- Panaich, S.; Eleid, M. Current status is MitraClip for patients with mitral and tricuspid regurgitation. Trends Cardiovasc. Med. 2018, 28, 200–2009. [Google Scholar] [CrossRef]
- Praz, F.; Spargias, K.; Chrissoheris, M.; Bullesfeld, L.; Nickenig, G.; Deuschl, F.; Shueler, R.; Fam, N.; Moss, R.; Makar, M.; et al. Compassionate use of the PASCAL transcatheter mitral valve repair system for patients with severe mitral regurgitation: A multicentre, prospective, observational, first-in-man study. Lancet 2017, 390, 773–780. [Google Scholar] [CrossRef]
- Geis, N.; Puls, M.; Lubos, E.; Zuern, C.; Franke, J.; Shueler, R.; von Bardeleben, R.; Boekstegers, P.; Quarrak, T.; Zahn, R.; et al. Safety and efficacy of MitraClipTM therapy in patients with severely impaired left ventricular ejection fraction: Results from the German transcatheter mitral valve interventions TRAMI registry. Eur. J. Heart Fail. 2018, 20, 598–608. [Google Scholar] [CrossRef]
- Rahhab, Z.; Kortlandt, F.; Velu, J.; Schurer, R.; Delgado, V.; Tonino, P.; Boven, A.; den Branden, B.V.; Kraaijeveld, A.; Voskuil, M.; et al. Current MitraClip experience, safety and feasibility in the Netherlands. Neth. Heart J. 2017, 25, 394–400. [Google Scholar] [CrossRef]
- Robb, J.; Minakawa, M.; Koomalsingh, K.; Shuto, T.; Jassaar, A.; Ratcliffe, S.; Gorman, R.; Gorman, J. Posterior leaflet augmentation improves leaflet tethering in repair of ischemic mitral regurgitation. Eur. J. Cardiothorac. Surg. 2001, 40, 1501–1507. [Google Scholar] [CrossRef]
- Kunzelman, K.; Cochran, R.; Chuong, C.; Ring, W.; Verier, E.; Eberhart, R. Finite element analysis of the mitral valve. J. Heart Valve Dis. 1993, 2, 326–340. [Google Scholar] [PubMed]
- Kunzelman, K.; Cochran, R.; Chuong, C.; Ring, W.; Verier, E.; Eberhart, R. Finite element analysis of mitral valve pathology. J. Long Term Eff. Med. Implants 1993, 3. [Google Scholar] [CrossRef]
- Kunzelman, K.; Reimink, M.; Cochran, R. Annular dilatation increases stress in the mitral valve and delays coaptation: A finite element computer model. Cardiovasc. Surg. 1997, 5, 427–434. [Google Scholar] [CrossRef]
- Kunzelman, K.; Reimink, M.; Cochran, R. Flexible versus rigid ring annuloplasty for mitral valve annular dilation: A finite element model. J. Heart Valve Dis. 1998, 7, 108–116. [Google Scholar]
- Cochran, R.; Kunzelman, K. Effect of papillary muscle position on mitral valve function: Relationship to mitral homografts. Ann. Thorac. Surg. 1998, 66, S155–S161. [Google Scholar] [CrossRef]
- Reimink, M.; Kunzelman, K.; Verier, E.; Cochran, R. The effect of anterior chordal replacement on mitral valve function and stresses. ASAIO Trans. 1995, 41, M754–M762. [Google Scholar] [CrossRef]
- Kunzelman, K.; Reimink, M.; Verier, E.; Cochran, R. Replacement of mitral valve posterior chordae tendineae with expanded polytetrafluoroethylene suture: A finite element study. J. Card. Surg. 1996, 11. [Google Scholar] [CrossRef]
- Reimink, M.; Kunzelman, K.; Cochran, R. The effect of chordal replacement suture length on function and stresses in repaired mitral valves: A finite element study. J. Heart Valve Dis. 1996, 5, 365–375. [Google Scholar]
- Einstein, D.; Reinhall, P.; Kunzelman, K.; Cochran, R. Nonlinear finite element analysis of the mitral valve. J. Heart Valve Dis. 2005, 3, 376–385. [Google Scholar]
- Einstein, D.; Kunzelman, K.; Reinhall, P.; Nicosia, M.; Cochran, R. The Relationship of Normal and Abnormal Microstructural Proliferation to the Mitral Valve Closure Sound. Trans. ASME 2005, 127, 134–147. [Google Scholar] [CrossRef] [PubMed]
- Kunzelman, K.; Einstein, D.; Cochran, R. Fluid–structure interaction models of the mitral valve: Function in normal and pathological states. Philos. Trans. R. Soc. B 2007, 362, 1393–1406. [Google Scholar] [CrossRef]
- Einstein, D.; DelPin, F.; Jiao, X.; Kuprat, A.; Carson, J.; Kunzelman, K.; Cochran, R.; Guccione, J.; Ratclifee, M. Fluid-structure interactions of the mitral valve and left heart: Comprehensive strategies, past, present, and future. Int. J. Numer. Methods Biomed. Eng. 2010, 26, 348–380. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Jensen, M.; Einstein, D.; Yoganathan, A.; Cochran, R.; Kunzelman, K. Fluid-Structure Interaction Analysis of Papillary Muscle Forces Using a Comprehensive Mitral Valve Model with 3D Chordal Structure. Ann. Biomed. Eng. 2016, 44, 942–953. [Google Scholar] [CrossRef] [PubMed]
- Chandran, K.; Kim, H. Computational Mitral Valve Evaluation and Potential Clinical Applications. Ann. Biomed. Eng. 2015, 43, 1348–1362. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pouch, A.; Yushkevich, P.; Jackson, B.; Jassaar, A.; Vergnat, M.; Gorman, J.; Gorman, R.; Sehgal, C. Development of a semi-automated method for mitral valve modeling with medial axis representation using 3D ultrasound. Med. Phys. 2012, 39, 933–950. [Google Scholar] [CrossRef] [PubMed]
- Votta, E.; Caiani, E.; Veronesi, F.; Soncini, M.; Motevecchi, F.; Redaelli, A. Mitral valve finite-element modelling from ultrasound data: A pilot study for a new approach to understand mitral function and clinical scenarios. Philos. Trans. Ser. 2008, 366, 3411–3434. [Google Scholar] [CrossRef]
- Votta, E.; Le, T.; Stevanella, M.; Fusini, L.; Caiani, E.; Redaelli, A.; Sotiropoulos, F. Toward patient-specific simulations of cardiac valves: State-of-the-art and future directions. J. Biomech. 2013, 46, 217–228. [Google Scholar] [CrossRef]
- Rim, Y.; Laing, S.; McPherson, D.; Kim, H. Mitral Valve Repair Using ePTFE Sutures for Ruptured Mitral Chordae Tendineae: A Computational Simulation Study. Ann. Biomed. Eng. 2014, 42, 139–148. [Google Scholar] [CrossRef]
- Mansi, T.; Voigt, I.; Georgescu, B.; Zheng, X.; Mengue, E.; Hackl, M.; Ionasec, R.; Noack, T.; Seeburger, J.; Comaniciu, D. An integrated framework for finite-element modeling of mitral valve biomechanics from medical images: Application to MitralClip intervention planning. Med Image Anal. 2012, 16, 1330–1346. [Google Scholar] [CrossRef]
- Schievano, S.; Kunzelman, K.; Nicosia, M.; Cochran, R.; Einstein, D.; Khambadkone, S.; Bonhoeffer, P. Percutaneous Mitral Valve Dilatation: Single Balloon versus Double Balloon. A Finite Element Study. J. Heart Valve Dis. 2009, 18, 28–34. [Google Scholar] [PubMed]
- Wenk, J.; Zhang, Z.; Cheng, G.; Malhotra, D.; Bolton, G.A.; Burger, M.; Suzuki, T.; Saloner, D.; Wallace, A.; Guccione, J.; et al. First Finite Element Model of the Left Ventricle With Mitral Valve: Insights Into Ischemic Mitral Regurgitation. Ann. Thorac. Surg. 2010, 89, 1546–1554. [Google Scholar] [CrossRef] [PubMed]
- Maisano, F.; Redaelli, A.; Soncini, M.; Votta, E.; Arcobasso, L.; Alfieri, O. An Annular Prosthesis for the Treatment of Functional Mitral Regurgitation: Finite Element Model Analysis of a Dog Bone–Shaped Ring Prosthesis. Ann. Thorac. Surg. 2005, 79, 1268–1275. [Google Scholar] [CrossRef]
- Stevanella, M.; Maffessanti, F.; Conti, C.; Votta, E.; Arnoldi, A.; Lombardi, M.; Parodi, O.; Caiani, E.; Redaelli, A. Mitral Valve Patient-Specific Finite Element Modeling from Cardiac MRI: Application to an Annuloplasty Procedure. Cardiovasc. Eng. Technol. 2011, 2, 66–76. [Google Scholar] [CrossRef]
- Lau, K.; Diaz, V.; Scambler, P.; Burriesci, G. Mitral valve dynamics in structural and fluid–structure interaction models. Med Eng. Phys. 2010, 32, 1057–1064. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Einstein, D.; Bloodworth, C.; Cochran, R.; Yoganathan, A.; Kunzelman, K. Fluid–structure interaction and structural analyses using a comprehensive mitral valve model with 3D chordal structure. Int. J. Numer. Meth. Biomed. Eng. 2017, 33. [Google Scholar] [CrossRef]
- Toma, M.; Bloodworth, C.; Pierce, E.; Einstein, D.; Cochran, R.; Yoganathan, A.; Kunzelman, K. Fluid-Structure Interaction Analysis of Ruptured Mitral Chordae Tendineae. Ann. Biomed. Eng. 2017, 45, 619–631. [Google Scholar] [CrossRef]
- Toma, M.; Einstein, D.; Bloodworth, C.; Kohli, K.; Cochran, R.; Kunzelman, K.; Yoganathan, A. Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-valvular Spacer. Prosthesis 2020, 2, 65–75. [Google Scholar] [CrossRef]
- Toma, M.; Bloodworth, C.; Einstein, D.; Pierce, E.; Cochran, R.; Yoganathan, A.; Kunzelman, K. High-resolution subject specific mitral valve imaging and modeling: Experimental and computational methods. Biomech. Model. Mechanobiol. 2016, 15, 1619–1630. [Google Scholar] [CrossRef]
- Votta, E.; Maisano, F.; Soncini, M.; Redaelli, A.; Motevecchi, F.; Alfieri, O. 3-D Computational analysis of the stress distribution on the leaflets after edge-to-edge repair of mitral regurgitation. J. Heart Valve Dis. 2002, 11, 810–822. [Google Scholar]
- Avanzini, A. A computational procedure for prediction of structural effects of edge-to-edge repair on mitral valve. J. Biomech. Eng. 2008, 130. [Google Scholar] [CrossRef] [PubMed]
- Fucci, C.; Schreiber, M.; DalPan, F.; Donzella, G. Structural effects of an innovative surgical technique to repair heart valve defects. J. Biomech. 2005, 38, 2460–2471. [Google Scholar]
- Khalighi, A.; Drach, A.; Bloodworth, C.; Pierce, E.; Yoganathan, A.; Gorman, R.; Gorman, J.; Sacks, M. Mitral valve chordae tendineae: Topological and geometrical characterization. Ann. Biomed. Eng. 2017, 45, 378–393. [Google Scholar] [CrossRef] [PubMed]
- Bloodworth, C.; Pierce, E.; Easley, T.; Drach, A.; Khalighi, A.; Toma, M.; Jensen, M.; Sacks, M.; Yoganathan, A. Ex Vivo methods for informinig computational models of the mitral valve. Ann. Biomed. Eng. 2017, 45, 496–507. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Oshima, M.; Takagi, S. Decomposition and parallelization of strongly coupled fluid-structure interaction linear subsystems based on the Q1/P0 discretization. Comput. Struct. 2016, 173, 84–94. [Google Scholar] [CrossRef]
- Freed, A.; Einstein, D.; Vesely, I. Invariant formulation for dispersed transverse isotropy in aortic heart valves: An efficient means for modeling fiber splay. Biomech. Model. Mechanobiol. 2005, 4, 100–117. [Google Scholar] [CrossRef]
Sample Availability: The data are available from the authors upon reasonable request. |

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toma, M.; Einstein, D.R.; Kohli, K.; Caroll, S.L.; Bloodworth, C.H., IV; Cochran, R.P.; Kunzelman, K.S.; Yoganathan, A.P. Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations. Biology 2020, 9, 173. https://doi.org/10.3390/biology9070173
Toma M, Einstein DR, Kohli K, Caroll SL, Bloodworth CH IV, Cochran RP, Kunzelman KS, Yoganathan AP. Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations. Biology. 2020; 9(7):173. https://doi.org/10.3390/biology9070173
Chicago/Turabian StyleToma, Milan, Daniel R. Einstein, Keshav Kohli, Sheridan L. Caroll, Charles H. Bloodworth, IV, Richard P. Cochran, Karyn S. Kunzelman, and Ajit P. Yoganathan. 2020. "Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations" Biology 9, no. 7: 173. https://doi.org/10.3390/biology9070173
APA StyleToma, M., Einstein, D. R., Kohli, K., Caroll, S. L., Bloodworth, C. H., IV, Cochran, R. P., Kunzelman, K. S., & Yoganathan, A. P. (2020). Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations. Biology, 9(7), 173. https://doi.org/10.3390/biology9070173





