SynSigGAN: Generative Adversarial Networks for Synthetic Biomedical Signal Generation
Abstract
Simple Summary
Abstract
1. Introduction
- We propose a preprocessing stage to refine the biomedical signals while using a combination of discrete wavelet transform (DWT), thresholding, and Inverse discrete wavelet transform (IDWT). This model can be modified according to the signal requirement and it can be used for denoising and refining any kind of signals.
- Our proposed generative adversarial networks model can be applied in order to generate any kind of biomedical signals.
- We have an evaluation stage to ensure the authenticity and similarity of synthetic data as compared to the original data.
- As the data enhance, the approach can be reused in order to generate more synthetic data.
2. Related Works
3. Data
3.1. MIT-BIH Arrhythmia Database
- Normal Beat (NB)
- Rhythm Change (RC)
- Right Bundle Branch Block Beat (RBBB)
- Left Bundle Branch Block Beat (LBBB)
- Ventricular Escape Beat (VEB)
- Atrial Premature Beat (APB)
- Premature Ventricular Contraction (PVC)
- Nodal (Junctional) Escape Beat (NEB)
- Aberrated Atrial Premature Beat (AAPB)
- Fusion of Ventricular and Normal Beat (FVNB)
- Fusion of Paced and Normal Beat (FPNB)
- Ventricular Flutter Wave (VFW)
- Comment Annotations (CA)
- Paced Beat (PB)
- Non Conducted P Wave (Blocked APC) (NCPW)
- Change in Signal Quality (CSQ)
- Unclassifiable Beat (UB)
3.2. Siena Scalp EEG Database
3.3. Sleep-EDF Database
3.4. BIDMC PPG and Respiration Dataset
- Physiological signals sampled at 125 Hz.
- Parameters such as respiratory rate, heart rate and blood oxygen saturation level which are sampled at 1 Hz.
- Fixed parameters such as age and gender.
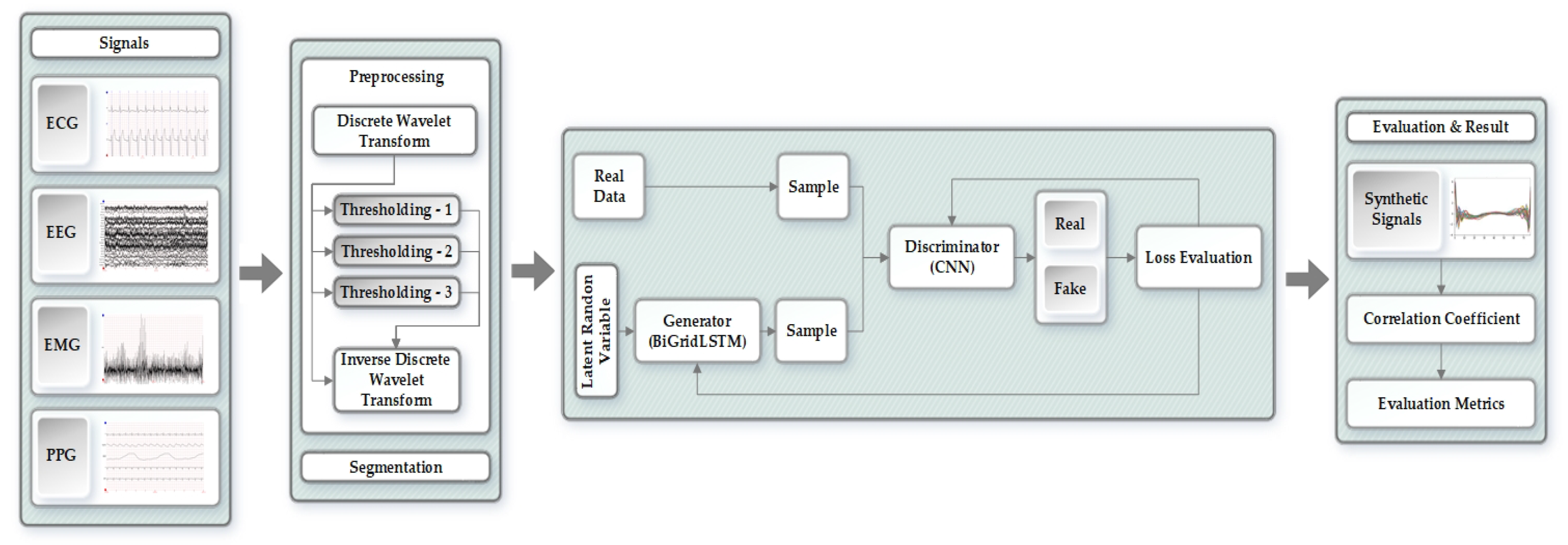
4. Proposed Methodology for Generating Synthetic Biomedical Signals
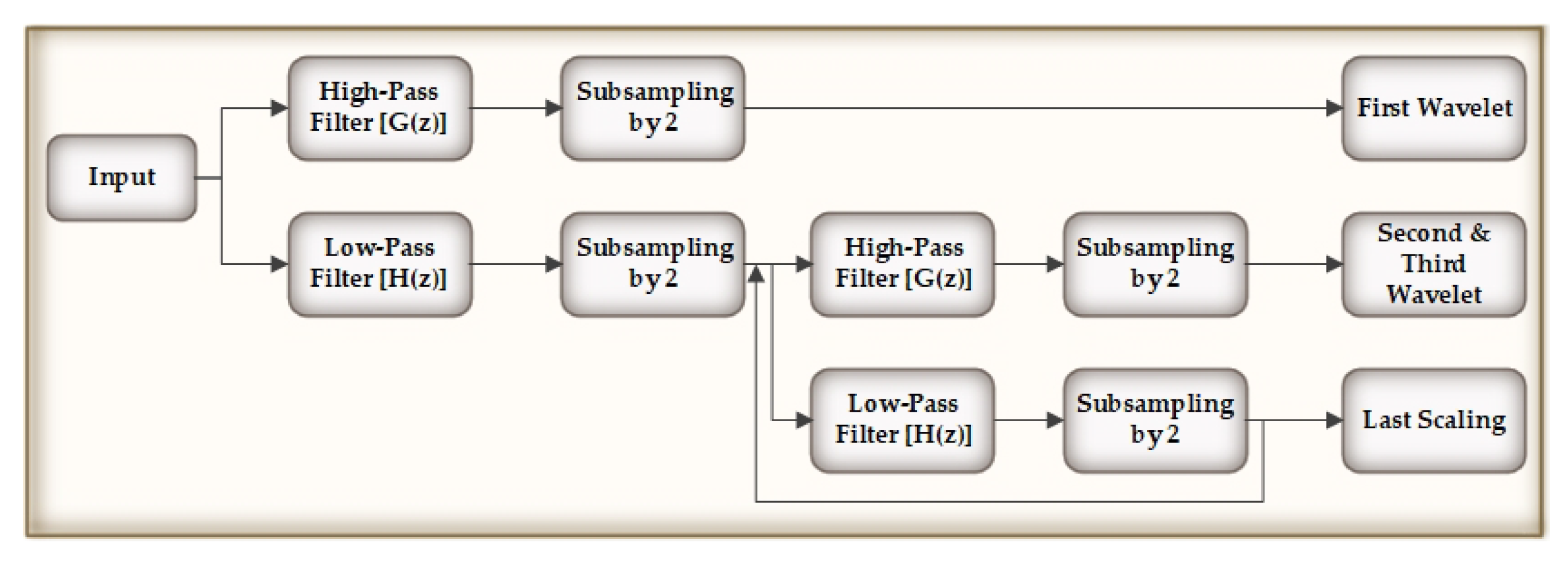
4.1. Preprocessing of the Original Signals
4.2. Segmentation
| Algorithm 1 Changing the size of vectors |
| Initialize M as new matrix for i = 1 to n do if then Append class to M else rational fraction approximation of and l end if end for Append to M |
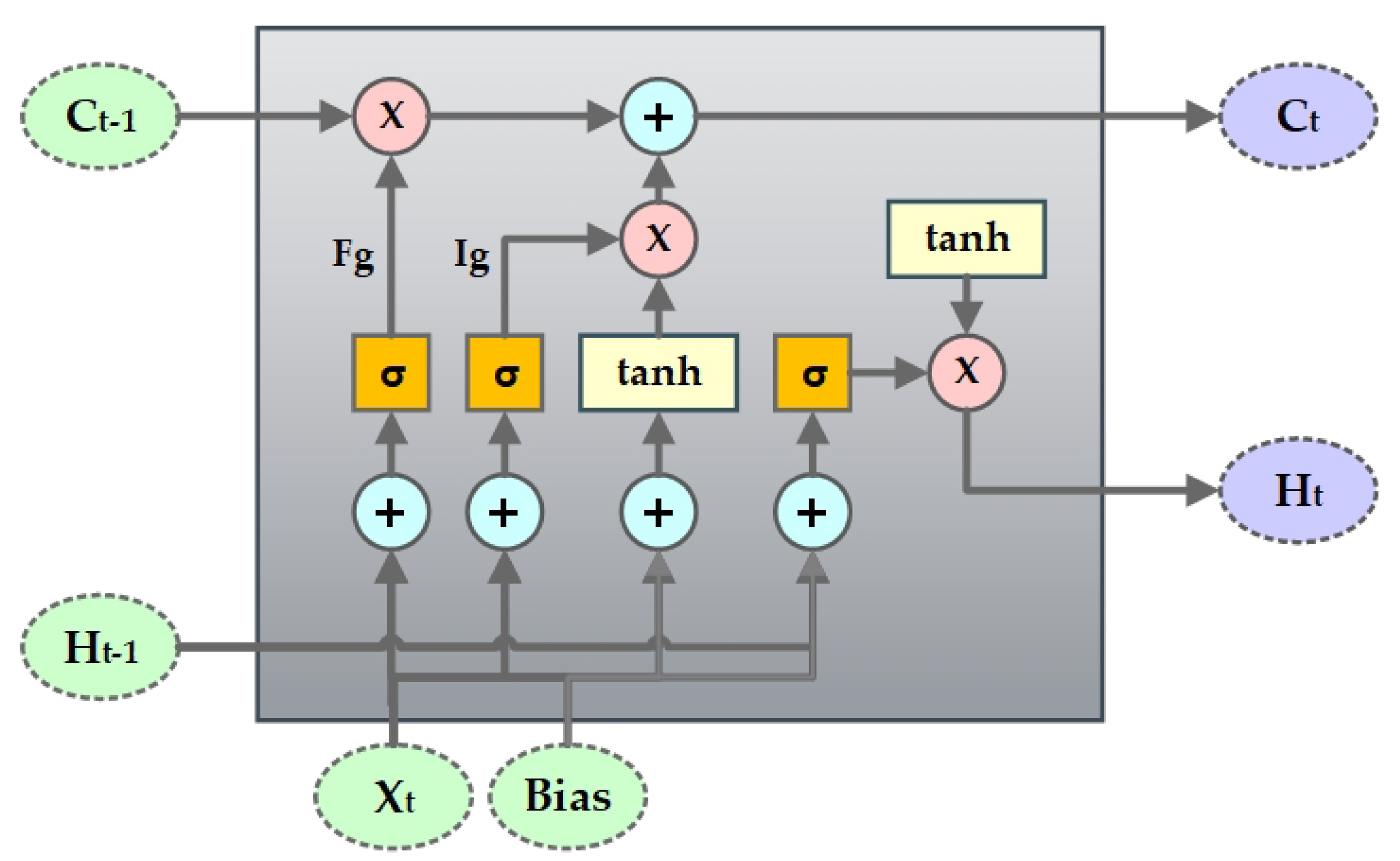
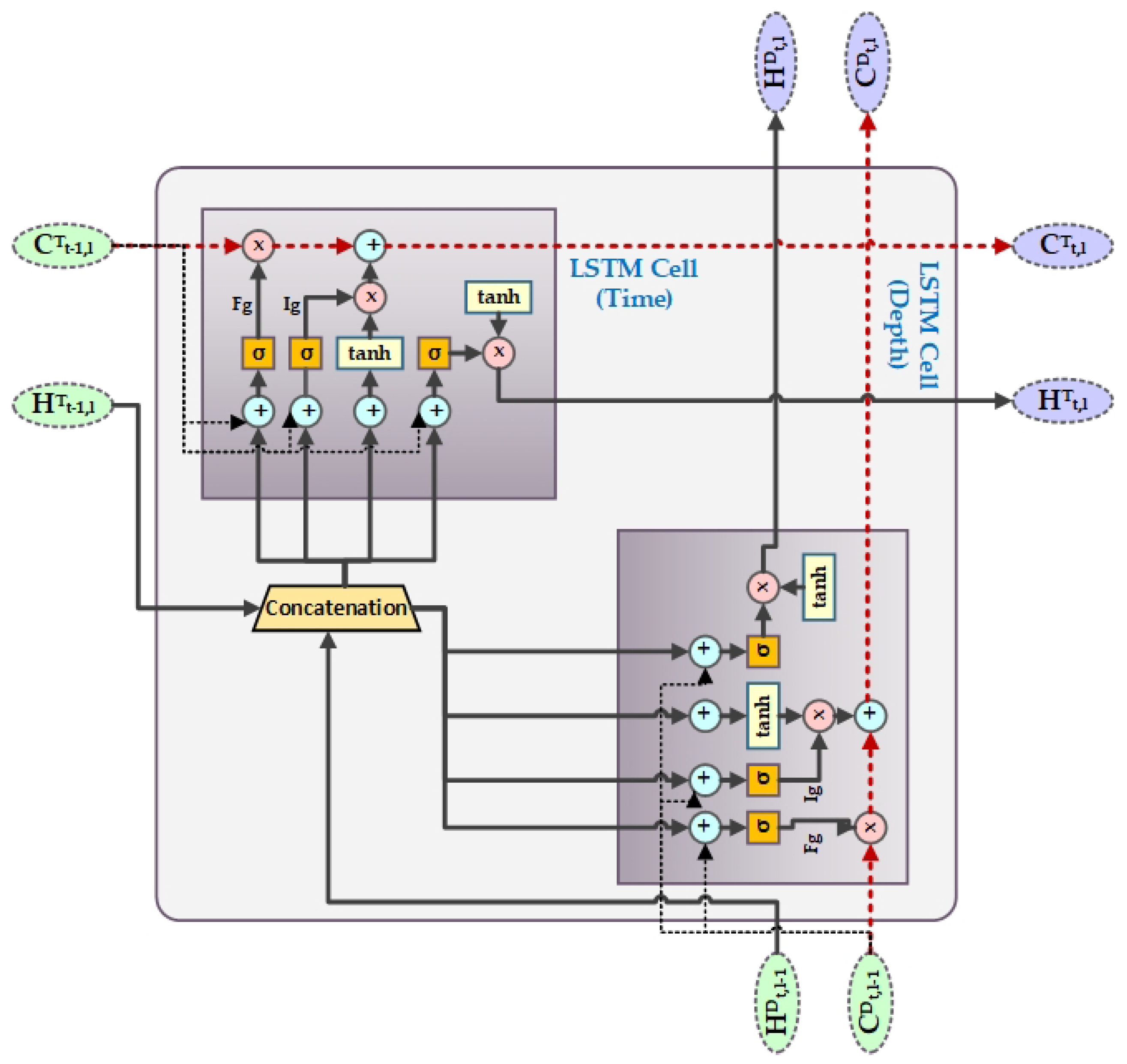
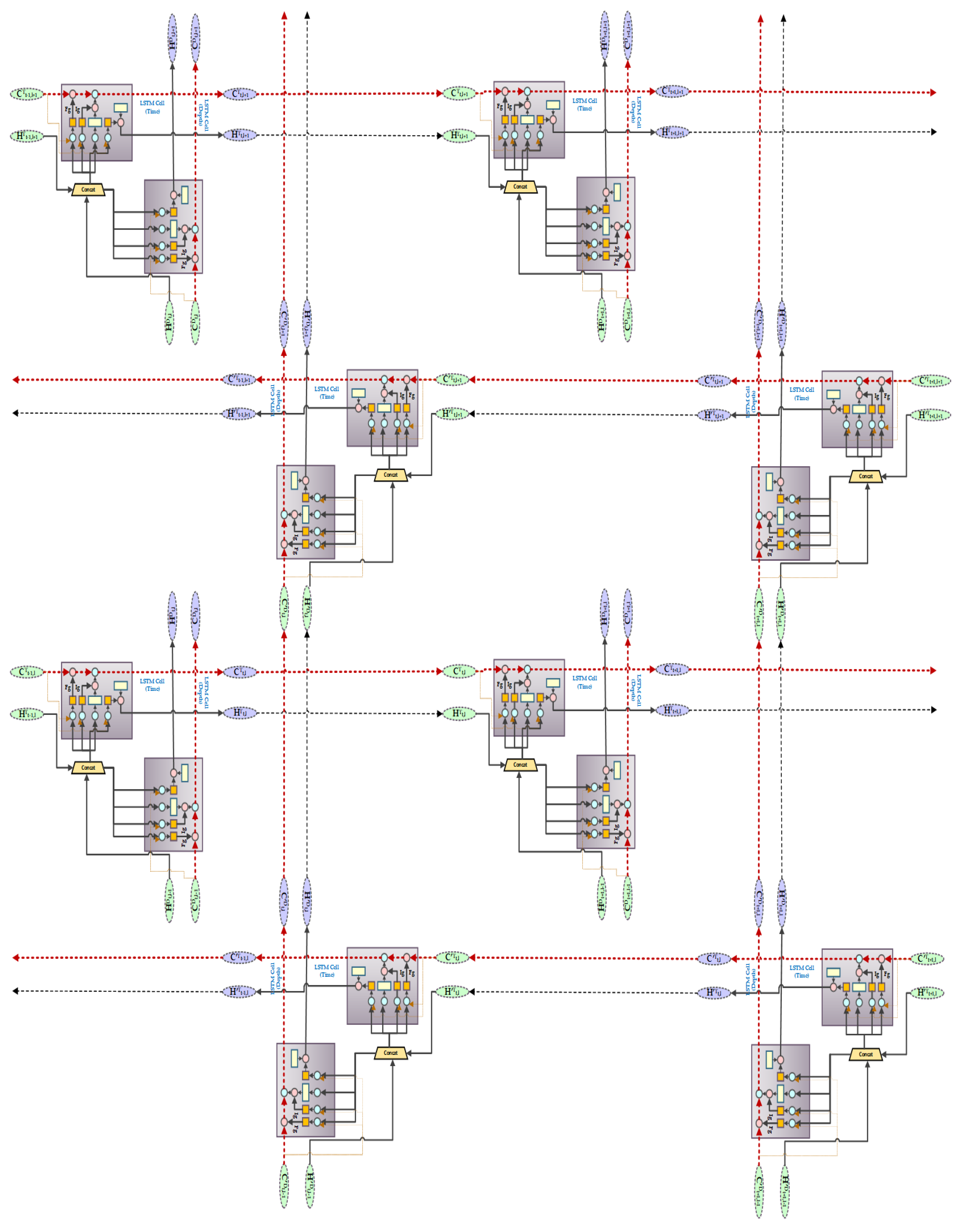
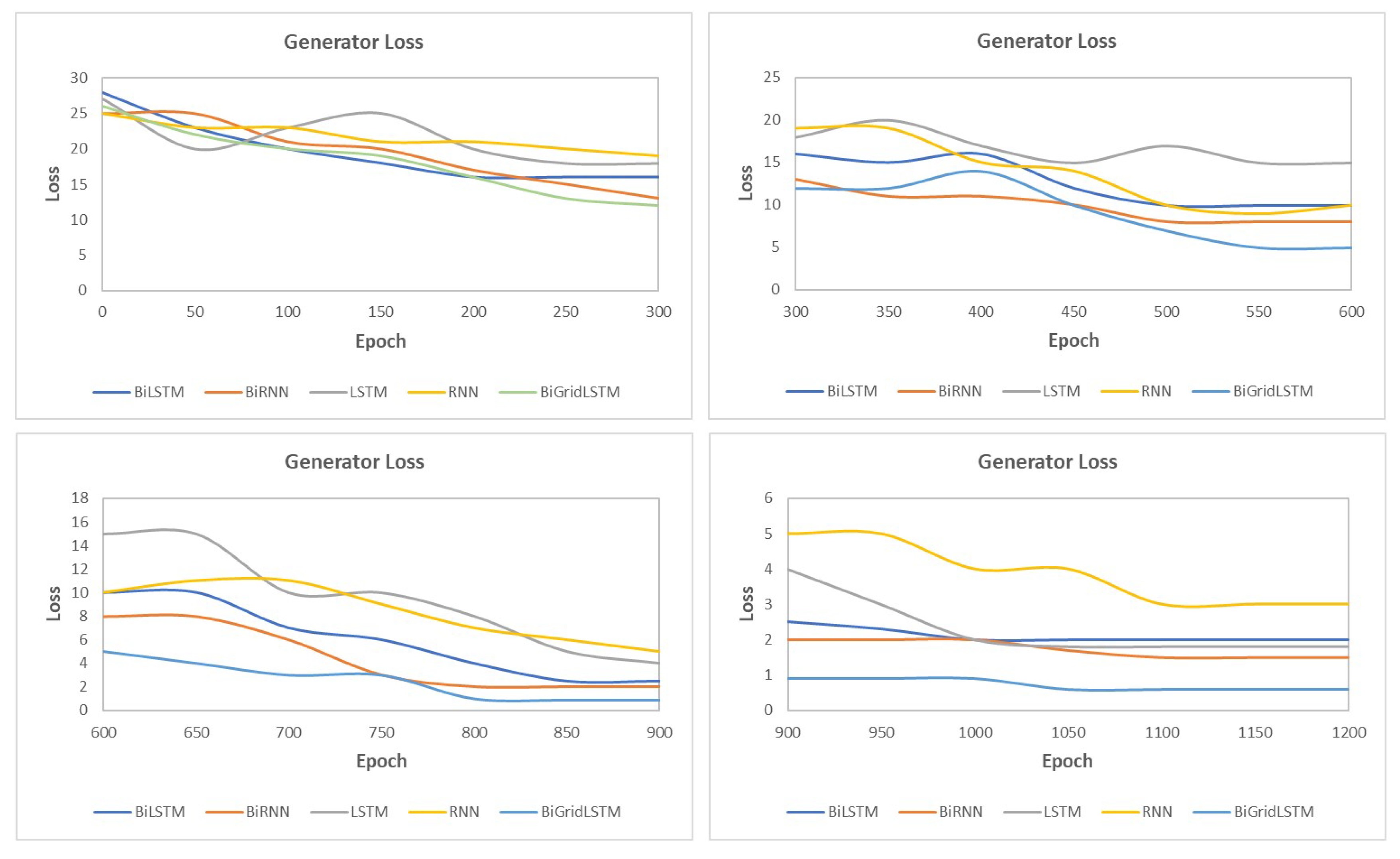
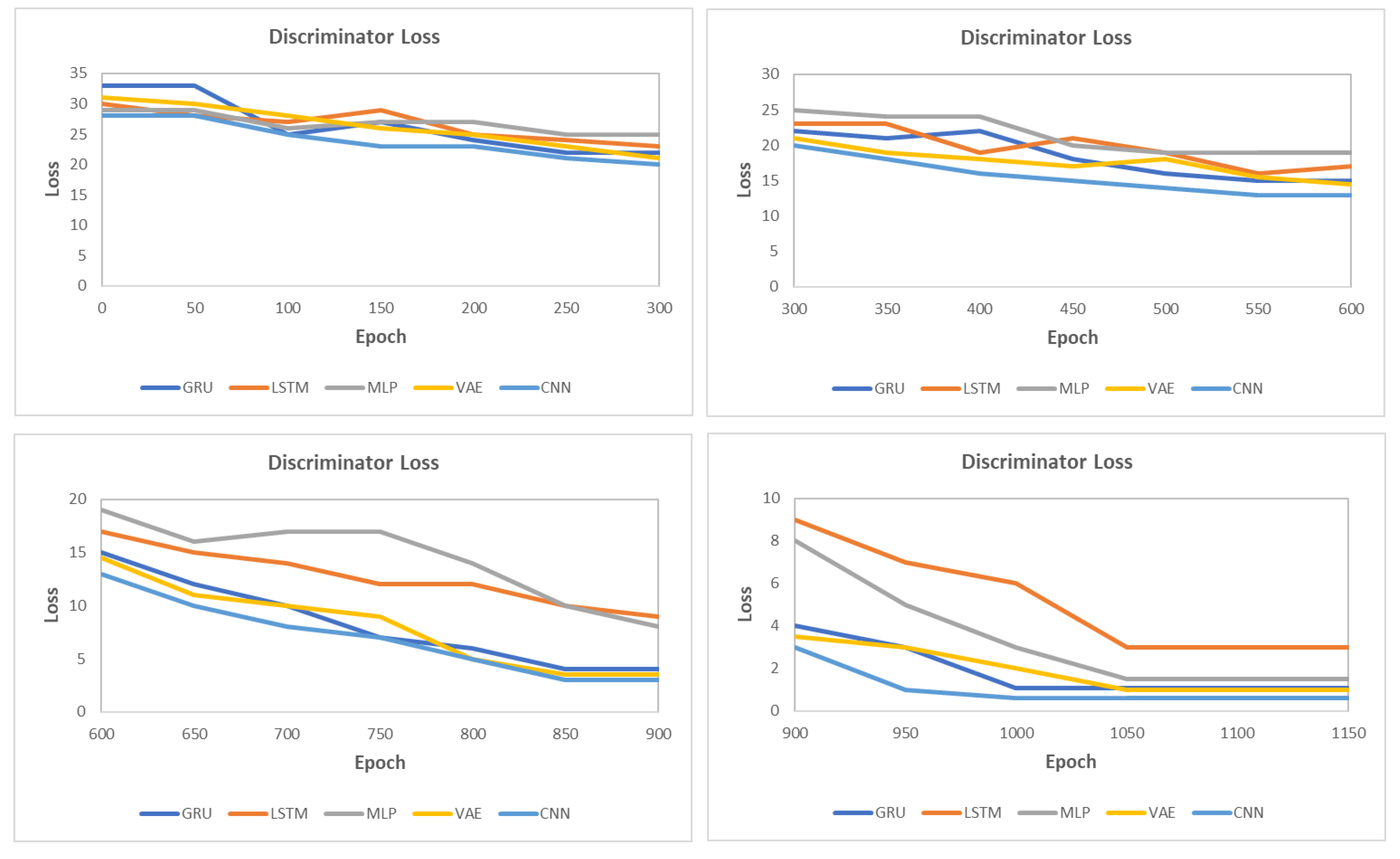
4.3. SynSigGAN: Generative Adversarial Networks
5. Evaluation and Results of the Proposed Approach
5.1. Root Mean Square Error
5.2. Percent Root Mean Square Difference
5.3. Mean Absolute Error
5.4. Fréchet Distance
5.5. Pearson’s Correlation Coefficient
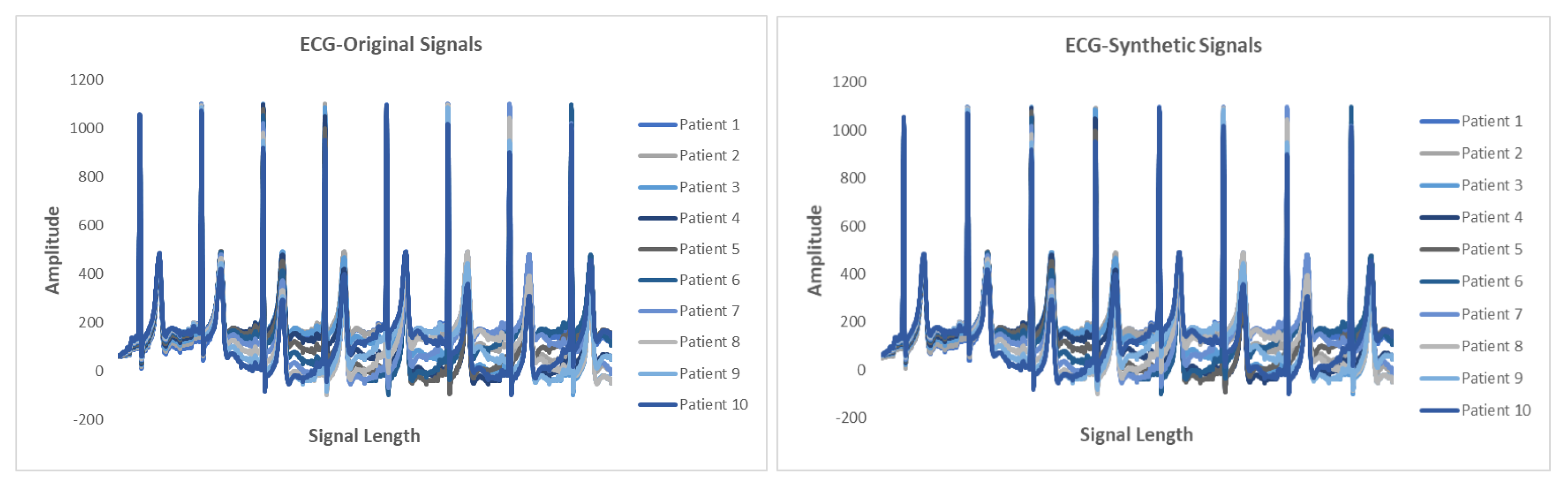
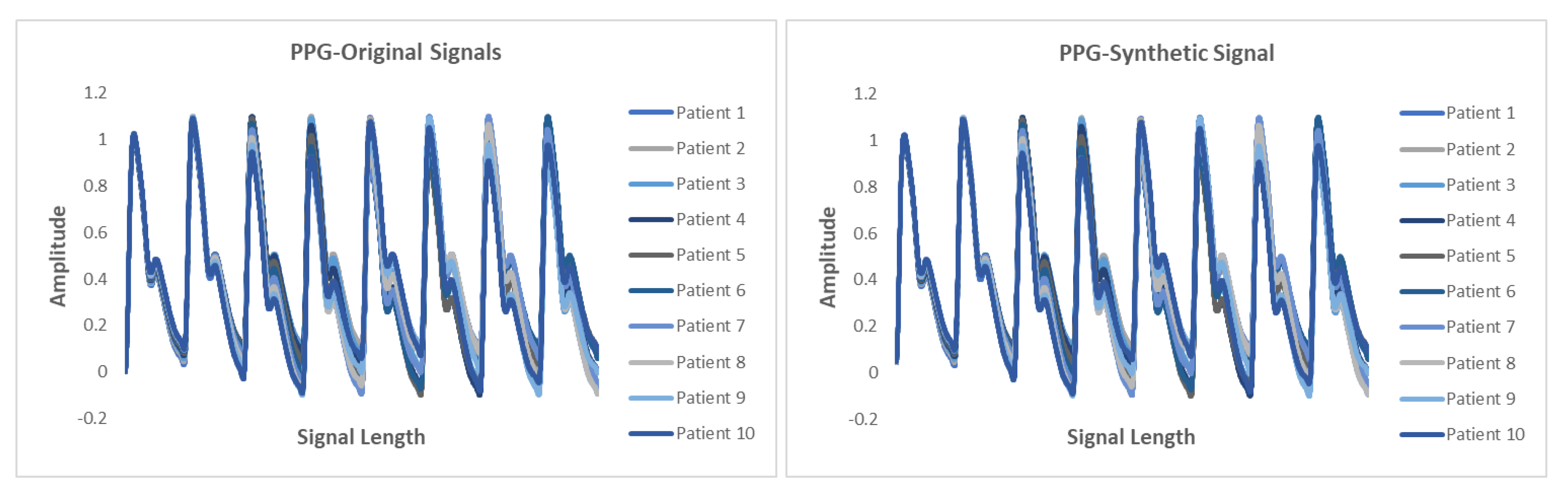
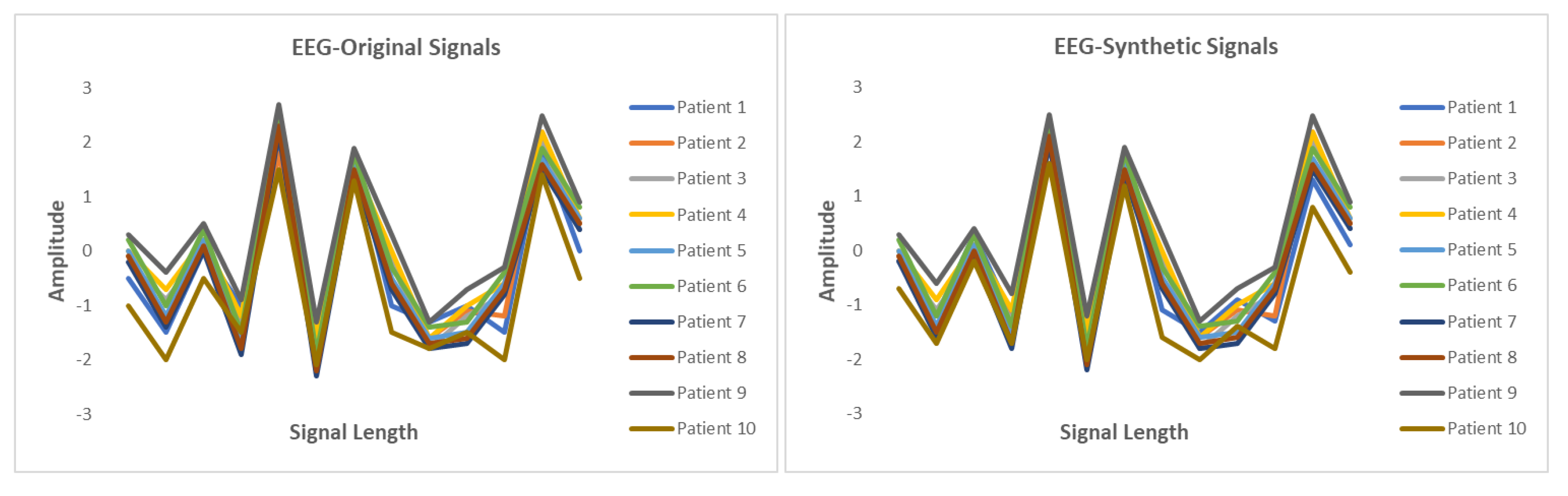
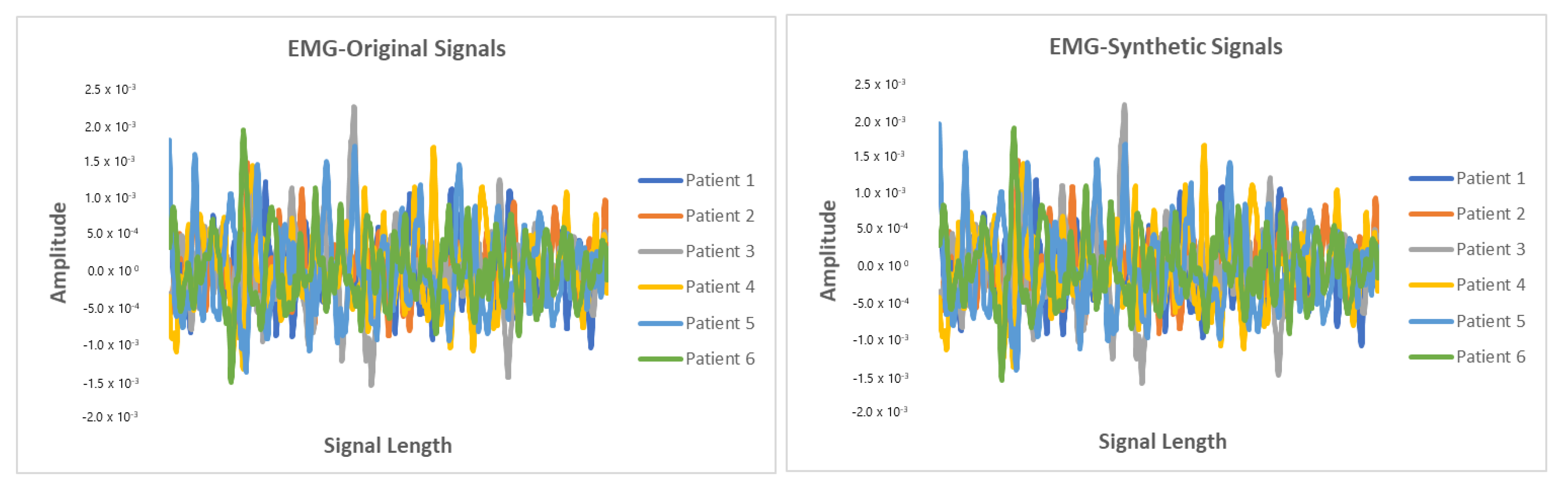
5.6. Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Deep Learning in Healthcare. Available online: https://missinglink.ai/guides/deep-learning-healthcare/deep-learning-healthcare/ (accessed on 1 November 2020).
- Ursin, G.; Sen, S.; Mottu, J.M.; Nygård, M. Protecting privacy in large datasets—First we assess the risk; then we fuzzy the data. Cancer Epidemiol. Prev. Biomarkers 2017, 26, 1219–1224. [Google Scholar] [CrossRef] [PubMed]
- McSharry, P.E.; Clifford, G.D.; Tarassenko, L.; Smith, L.A. A dynamical model for generating synthetic electrocardiogram signals. IEEE Trans. Biomed. Eng. 2003, 50, 289–294. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, S.; Dube, K.; Gallagher, T. Using the caremap with health incidents statistics for generating the realistic synthetic electronic healthcare record. In Proceedings of the 2016 IEEE International Conference on Healthcare Informatics (ICHI), Chicago, IL, USA, 4–7 October 2016; pp. 439–448. [Google Scholar]
- Moore, A.D. Synthesized EMG Waves and Their Implications. Am. J. Phys. Med. Rehabil. 1966, 46, 1302–1316. [Google Scholar]
- Murthy, I.; Reddy, M. ECG synthesis via discrete cosine transform. In Proceedings of the Images of the Twenty-First Century. Proceedings of the Annual International Engineering in Medicine and Biology Society, Seattle, WA, USA, 9–12 November 1989; pp. 773–774. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Zhu, F.; Ye, F.; Fu, Y.; Liu, Q.; Shen, B. Electrocardiogram generation with a bidirectional LSTM-CNN generative adversarial network. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-Valued (Medical) Time Series Generation with Recurrent Conditional Gans. arXiv 2017, arXiv:1706.02633. [Google Scholar]
- Delaney, A.M.; Brophy, E.; Ward, T.E. Synthesis of Realistic ECG using Generative Adversarial Networks. arXiv 2019, arXiv:1909.09150. [Google Scholar]
- Patki, N.; Wedge, R.; Veeramachaneni, K. The synthetic data vault. In Proceedings of the 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Montreal, QC, Canada, 17–19 October 2016; pp. 399–410. [Google Scholar]
- Campbell, M. Synthetic Data: How AI Is Transitioning From Data Consumer to Data Producer …and Why That’s Important. Computer 2019, 52, 89–91. [Google Scholar] [CrossRef]
- Ayala-Rivera, V.; Portillo-Dominguez, A.O.; Murphy, L.; Thorpe, C. COCOA: A synthetic data generator for testing anonymization techniques. In Proceedings of the International Conference on Privacy in Statistical Databases, Dubrovnik, Croatia, 14–16 September 2016; pp. 163–177. [Google Scholar]
- Choi, E.; Biswal, S.; Malin, B.; Duke, J.; Stewart, W.F.; Sun, J. Generating Multi-Label Discrete Patient Records Using Generative Adversarial Networks. arXiv 2017, arXiv:1703.06490. [Google Scholar]
- Torfi, A.; Beyki, M. Generating Synthetic Healthcare Records Using Convolutional Generative Adversarial Networks. 2019. Available online: http://hdl.handle.net/10919/96186 (accessed on 2 December 2020).
- Jordon, J.; Yoon, J.; van der Schaar, M. PATE-GAN: Generating synthetic data with differential privacy guarantees. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Narváez, P.; Percybrooks, W.S. Synthesis of Normal Heart Sounds Using Generative Adversarial Networks and Empirical Wavelet Transform. Appl. Sci. 2020, 10, 7003. [Google Scholar] [CrossRef]
- Aznan, N.K.N.; Atapour-Abarghouei, A.; Bonner, S.; Connolly, J.D.; Al Moubayed, N.; Breckon, T.P. Simulating brain signals: Creating synthetic eeg data via neural-based generative models for improved ssvep classification. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Hernandez-Matamoros, A.; Fujita, H.; Perez-Meana, H. A novel approach to create synthetic biomedical signals using BiRNN. Inf. Sci. 2020, 541, 218–241. [Google Scholar] [CrossRef]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.C.; Mark, R.; Mietus, J.; Moody, G.; Peng, C.; Stanley, H. Components of a new research resource for complex physiologic signals. PhysioBank PhysioToolkit PhysioNet 2000, 101, E215–E220. [Google Scholar]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Detti, P.; Vatti, G.; Zabalo Manrique de Lara, G. EEG Synchronization Analysis for Seizure Prediction: A Study on Data of Noninvasive Recordings. Processes 2020, 8, 846. [Google Scholar] [CrossRef]
- Detti, P. Siena Scalp EEG Database (Version 1.0.0), PhysioNet 2020. Available online: https://doi.org/10.13026/5d4a-j060 (accessed on 1 November 2020).
- Kemp, B.; Zwinderman, A.H.; Tuk, B.; Kamphuisen, H.A.; Oberye, J.J. Analysis of a sleep-dependent neuronal feedback loop: The slow-wave microcontinuity of the EEG. IEEE Trans. Biomed. Eng. 2000, 47, 1185–1194. [Google Scholar] [CrossRef] [PubMed]
- Pimentel, M.A.; Johnson, A.E.; Charlton, P.H.; Birrenkott, D.; Watkinson, P.J.; Tarassenko, L.; Clifton, D.A. Toward a robust estimation of respiratory rate from pulse oximeters. IEEE Trans. Biomed. Eng. 2016, 64, 1914–1923. [Google Scholar] [CrossRef]
- Chen, S.W.; Chen, Y.H. Hardware design and implementation of a wavelet de-noising procedure for medical signal preprocessing. Sensors 2015, 15, 26396–26414. [Google Scholar] [CrossRef]
- Ali, M.N.; El-Dahshan, E.S.A.; Yahia, A.H. Denoising of heart sound signals using discrete wavelet transform. Circuits Syst. Signal Process. 2017, 36, 4482–4497. [Google Scholar] [CrossRef]
- Hernandez-Matamoros, A.; Fujita, H.; Escamilla-Hernandez, E.; Perez-Meana, H.; Nakano-Miyatake, M. Recognition of ECG signals using wavelet based on atomic functions. Biocybern. Biomed. Eng. 2020, 40, 803–814. [Google Scholar] [CrossRef]
- Kachuee, M.; Fazeli, S.; Sarrafzadeh, M. Ecg heartbeat classification: A deep transferable representation. In Proceedings of the 2018 IEEE International Conference on Healthcare Informatics (ICHI), New York, NY, USA, 4–7 June 2018; pp. 443–444. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Fei, H.; Tan, F. Bidirectional grid long short-term memory (bigridlstm): A method to address context-sensitivity and vanishing gradient. Algorithms 2018, 11, 172. [Google Scholar] [CrossRef]
- Kalchbrenner, N.; Danihelka, I.; Graves, A. Grid long short-term memory. arXiv 2015, arXiv:1507.01526. [Google Scholar]
- Swinscow, T.D.V.; Campbell, M.J. Statistics at Scholar One; BMJ: London, UK, 2002. [Google Scholar]

| Methodology | SNR | RMSE | PRD |
|---|---|---|---|
| Low Pass Filtering | 16.34 | 6.01 | 17.89 |
| Short-Time Fourier Transform | 17.21 | 6.56 | 18.90 |
| Fast Fourier Transform | 15.99 | 7.10 | 17.34 |
| Wigner-Ville Distribution | 14.60 | 7.82 | 16.51 |
| Least Mean Squares | 16.91 | 6.11 | 16.01 |
| Frequency-Domain Adaptive Filtering | 17.83 | 8.25 | 17.88 |
| Wavelet Transformation | 19.82 | 4.56 | 14.34 |
| Correlation Values | Representation |
|---|---|
| 0 to 0.3 or 0 to −0.3 | Negligibly correlated |
| 0.3 to 0.5 or −0.3 to −0.5 | Low correlation |
| 0.5 to 0.7 or −0.5 to −0.7 | Moderately correlated |
| 0.7 to 0.9 or −0.7 to −0.9 | Highly correlated |
| 0.9 to 1 or −0.9 to 1 | Extensively correlated |
| Signal | Mean Correlation Coeficient | MAE | RMSE | PRD | FD |
|---|---|---|---|---|---|
| ECG | 0.9991 | 0.218 | 0.126 | 6.343 | 0.936 |
| EEG | 0.997 | 0.0475 | 0.0314 | 5.985 | 0.982 |
| EMG | 0.9125 | 0.0538 | 0.0529 | 2.971 | 0.921 |
| PPG | 0.9793 | 0.0635 | 0.0596 | 5.167 | 0.783 |
| Model | MAE | RMSE | PRD | FD |
|---|---|---|---|---|
| BiLSTM-GRU | 0.59 | 0.57 | 74.46 | 0.95 |
| BiLSTM-CNN GAN | 0.5 | 0.51 | 68.83 | 0.89 |
| RNN-AE GAN | 0.79 | 0.76 | 119.34 | 0.97 |
| BiRNN | 0.6 | 0.62 | 89.97 | 0.96 |
| LSTM-AE | 0.77 | 0.79 | 148.67 | 0.99 |
| BiLSTM-MLP | 0.75 | 0.78 | 146.35 | 0.99 |
| LSTM-VAE GAN | 0.71 | 0.72 | 144.74 | 0.98 |
| RNN-VAE GAN | 0.71 | 0.72 | 145.22 | 0.98 |
| BiGridLSTM-CNN | 0.36 | 0.25 | 66.21 | 0.79 |
| Patient | Length of Signal | Original Signal Data | Synthetic Signal Data Generated |
|---|---|---|---|
| Patient 1 | 125 | 20 | 20 |
| Patient 2 | 63 | 500 | 500 |
| Patient 3 | 71 | 17 | 17 |
| Patient 4 | 141 | 92 | 92 |
| Patient 5 | 139 | 72 | 72 |
| Patient 6 | 40 | 11 | 11 |
| Patient 7 | 93 | 101 | 101 |
| Patient 8 | 68 | 162 | 162 |
| Patient 9 | 117 | 14 | 14 |
| Patient 10 | 62 | 700 | 700 |
| Length of Signal | Original Signal Data | Synthetic Signal Data Generated | |
|---|---|---|---|
| Open-Eye | 19 | 8100 | 8100 |
| Closed-Eye | 18 | 6173 | 6173 |
| Patient | Length of Signal | Original Signal Data | Synthetic Signal Data Generated |
|---|---|---|---|
| Patient 1 | 78 | 70 | 70 |
| Patient 2 | 16 | 11 | 11 |
| Patient 3 | 43 | 191 | 191 |
| Patient 4 | 21 | 55 | 55 |
| Patient 5 | 90 | 41 | 41 |
| Patient 6 | 112 | 17 | 17 |
| Patient 7 | 143 | 54 | 54 |
| Patient 8 | 66 | 71 | 71 |
| Patient 9 | 156 | 15 | 15 |
| Patient 10 | 191 | 19 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hazra, D.; Byun, Y.-C. SynSigGAN: Generative Adversarial Networks for Synthetic Biomedical Signal Generation. Biology 2020, 9, 441. https://doi.org/10.3390/biology9120441
Hazra D, Byun Y-C. SynSigGAN: Generative Adversarial Networks for Synthetic Biomedical Signal Generation. Biology. 2020; 9(12):441. https://doi.org/10.3390/biology9120441
Chicago/Turabian StyleHazra, Debapriya, and Yung-Cheol Byun. 2020. "SynSigGAN: Generative Adversarial Networks for Synthetic Biomedical Signal Generation" Biology 9, no. 12: 441. https://doi.org/10.3390/biology9120441
APA StyleHazra, D., & Byun, Y.-C. (2020). SynSigGAN: Generative Adversarial Networks for Synthetic Biomedical Signal Generation. Biology, 9(12), 441. https://doi.org/10.3390/biology9120441






