Fluid-Structure Interaction Simulation of an Intra-Atrial Fontan Connection
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
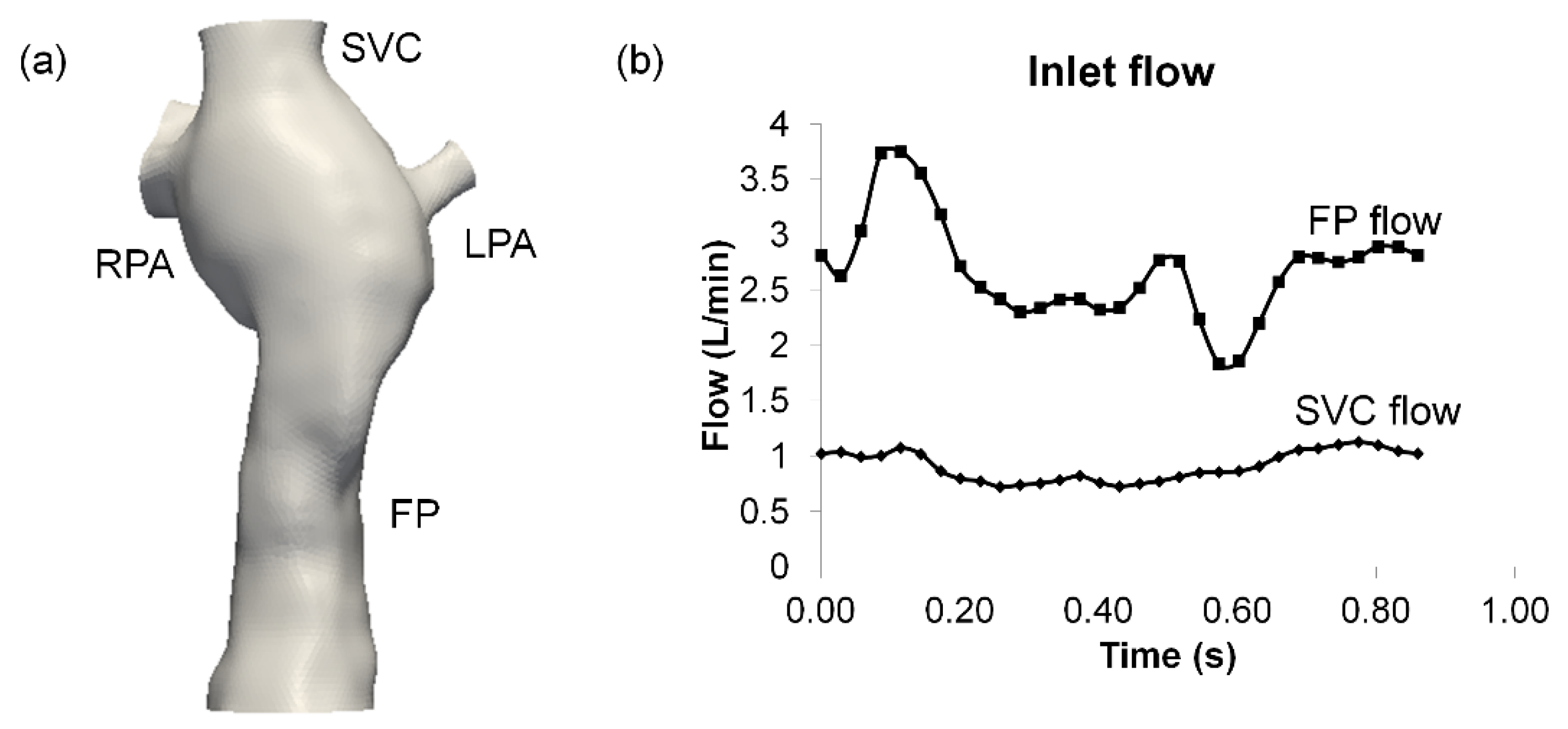
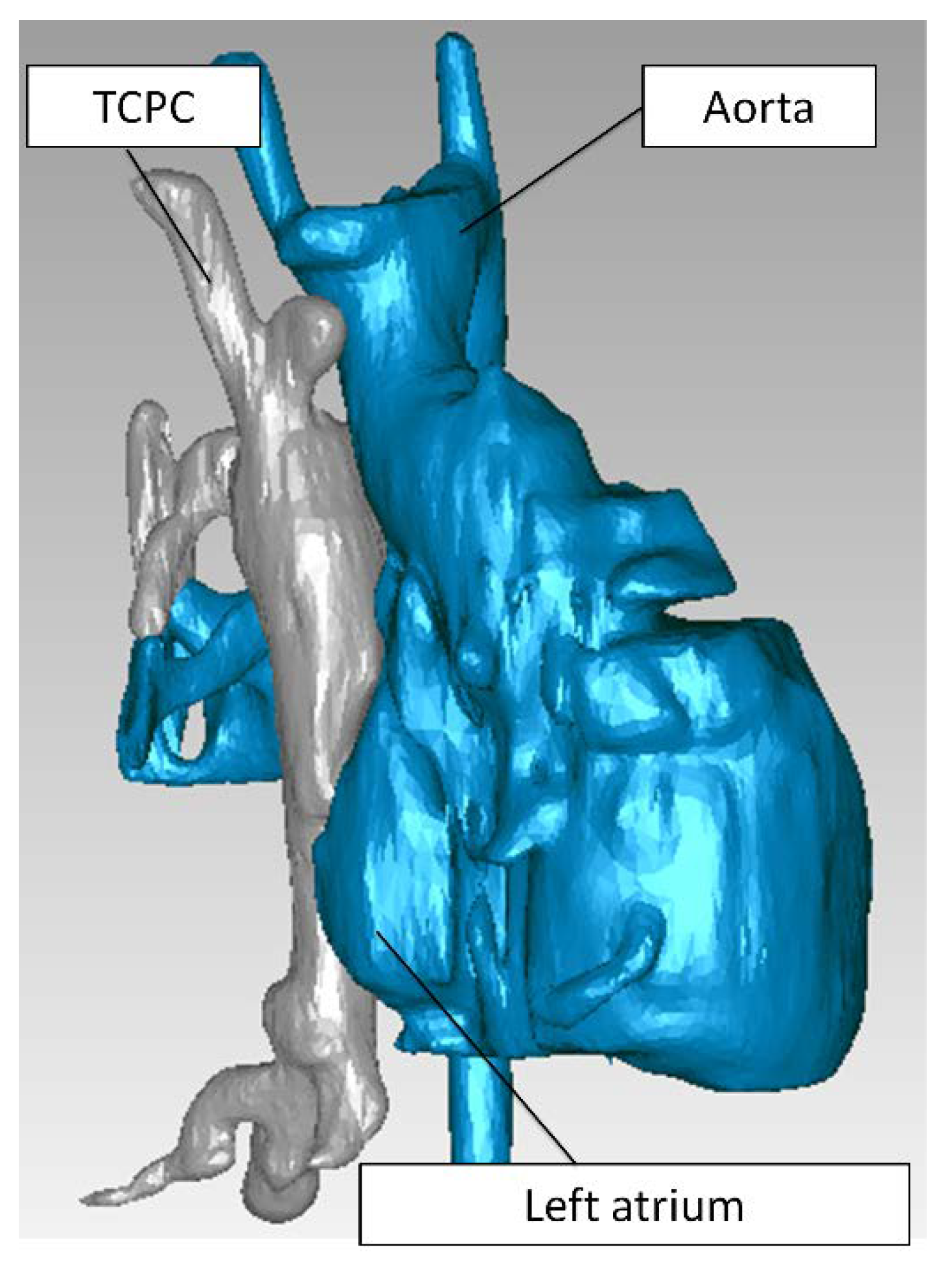
2.1. Patient Image Acquisition and Reconstruction
2.2. Hemodynamic Assessment
3. Results
3.1. Mesh Sensitivity
- (a)
- Very fine mesh—1 mm mesh edge length
- Fluid: 193,974 elements
- Structure:164,178 elements
- (b)
- Fine mesh—1.5 mm mesh edge length
- Fluid: 97,793 elements
- Structure: 82,206 elements
- (c)
- Coarse mesh—2 mm mesh edge length
- Fluid: 27,640 elements
- Structure: 44,406 elements
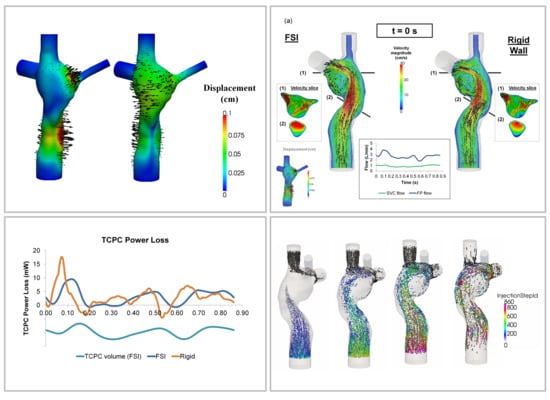
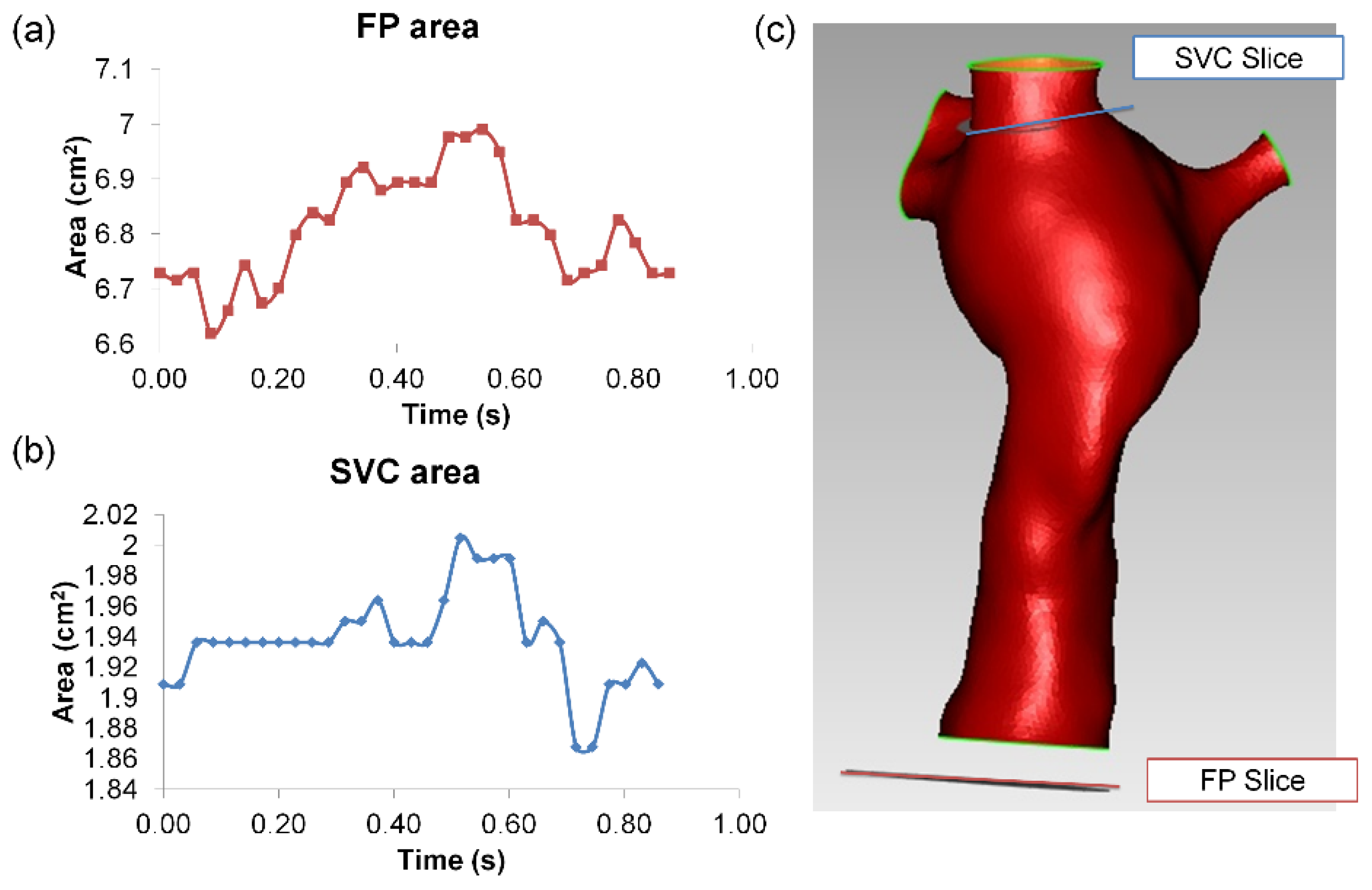
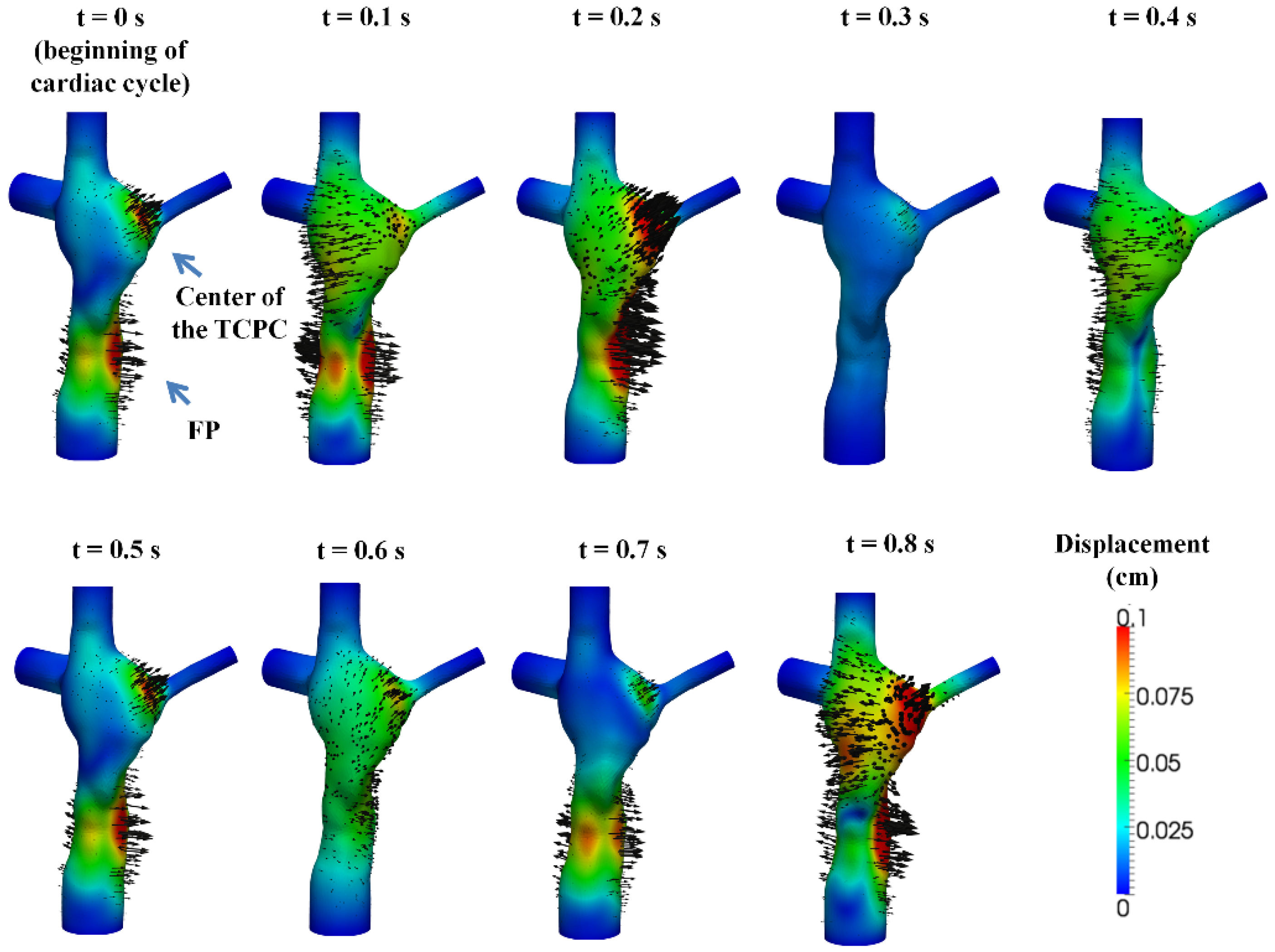
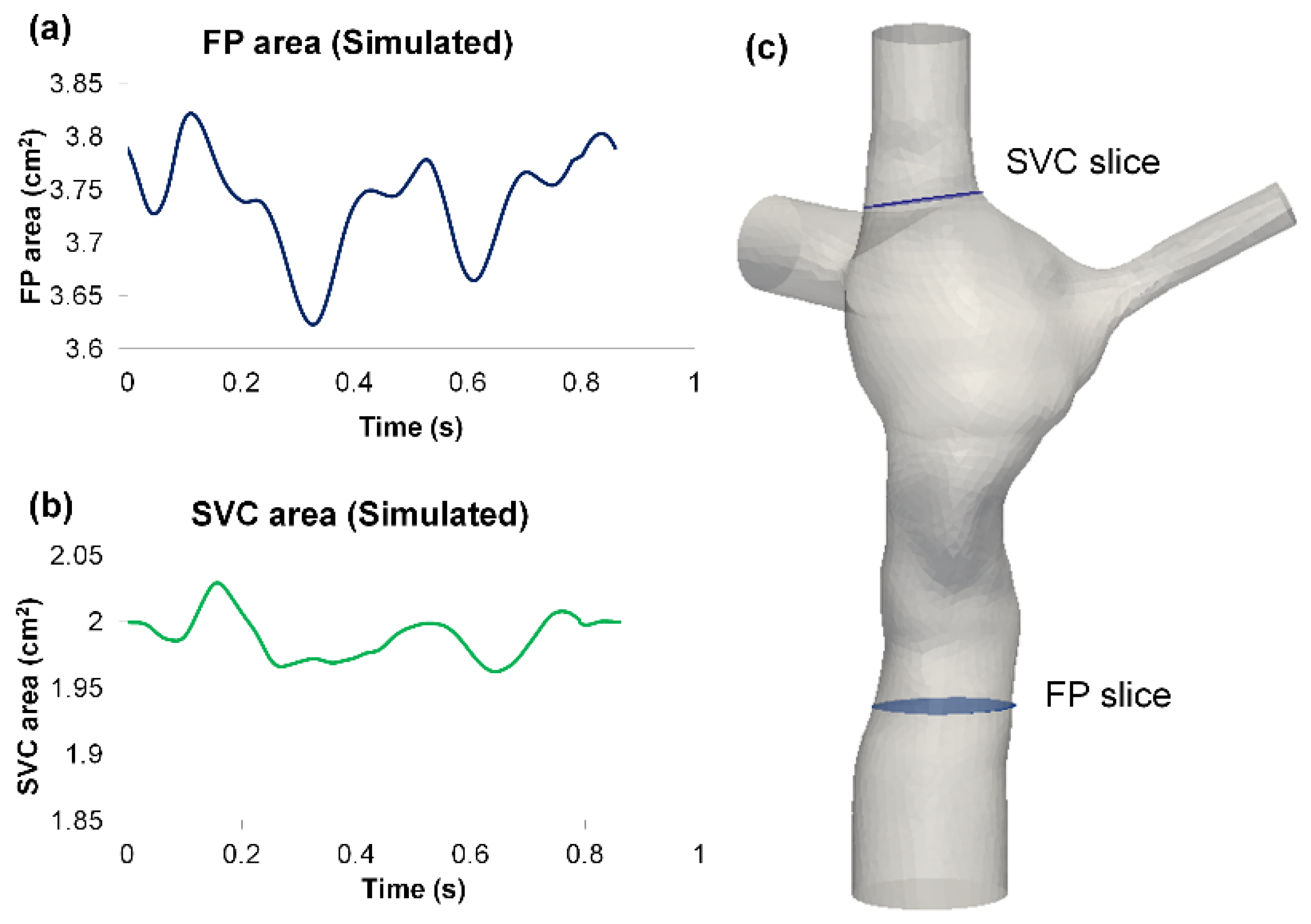
3.2. Simulated TCPC Wall Deformation
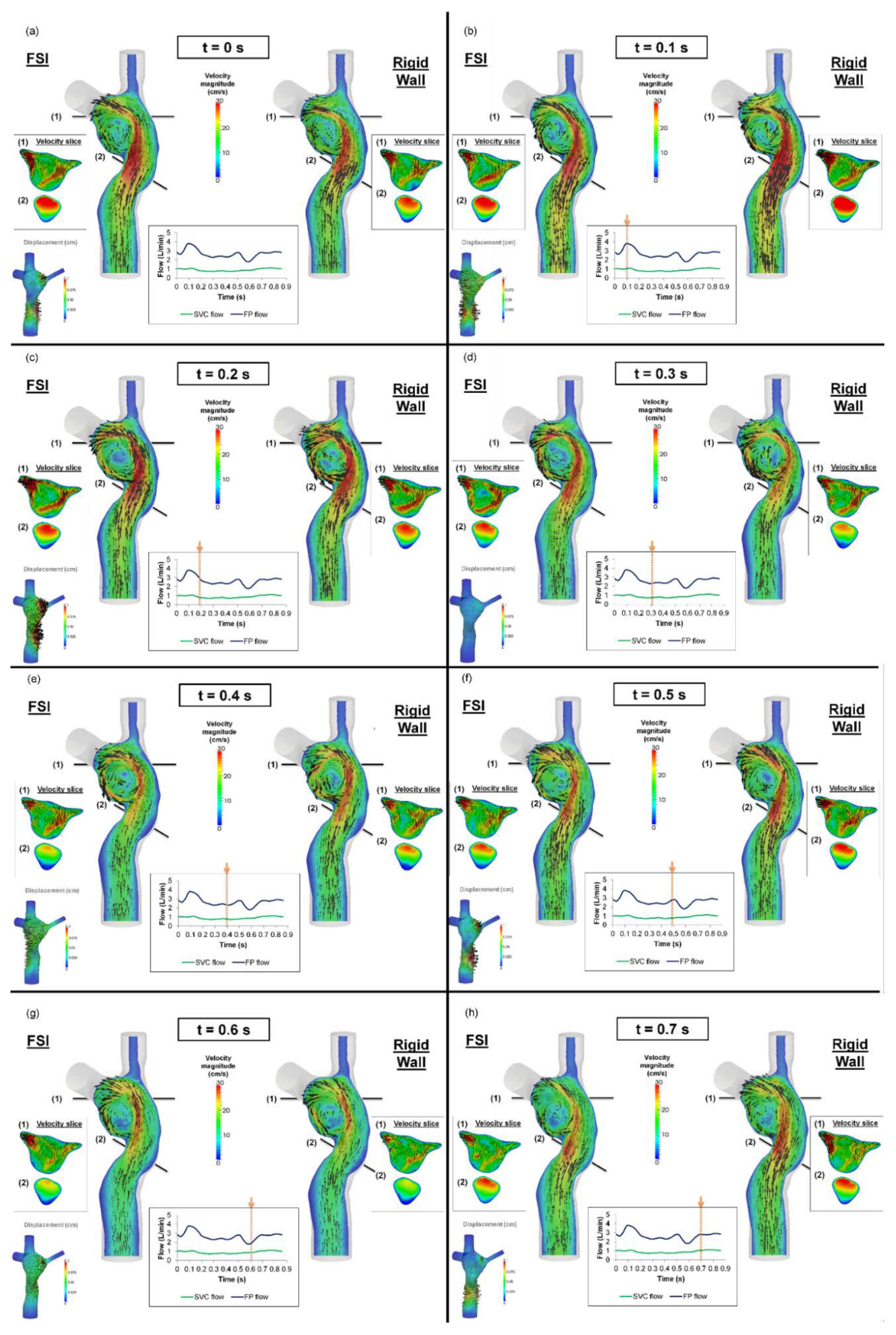
3.3. TCPC Flow Field
3.4. Pressure Drop and TCPC Power Loss
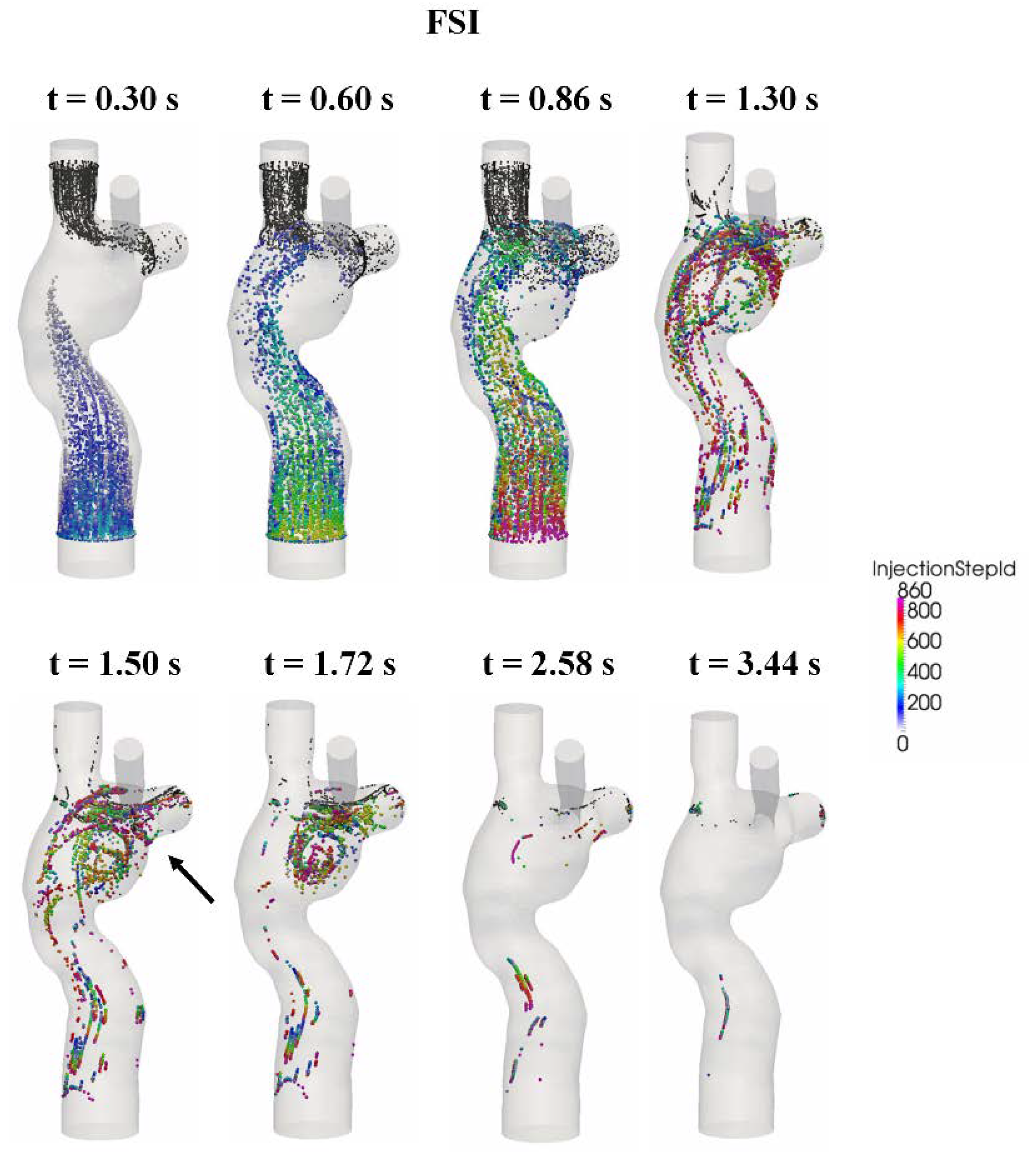
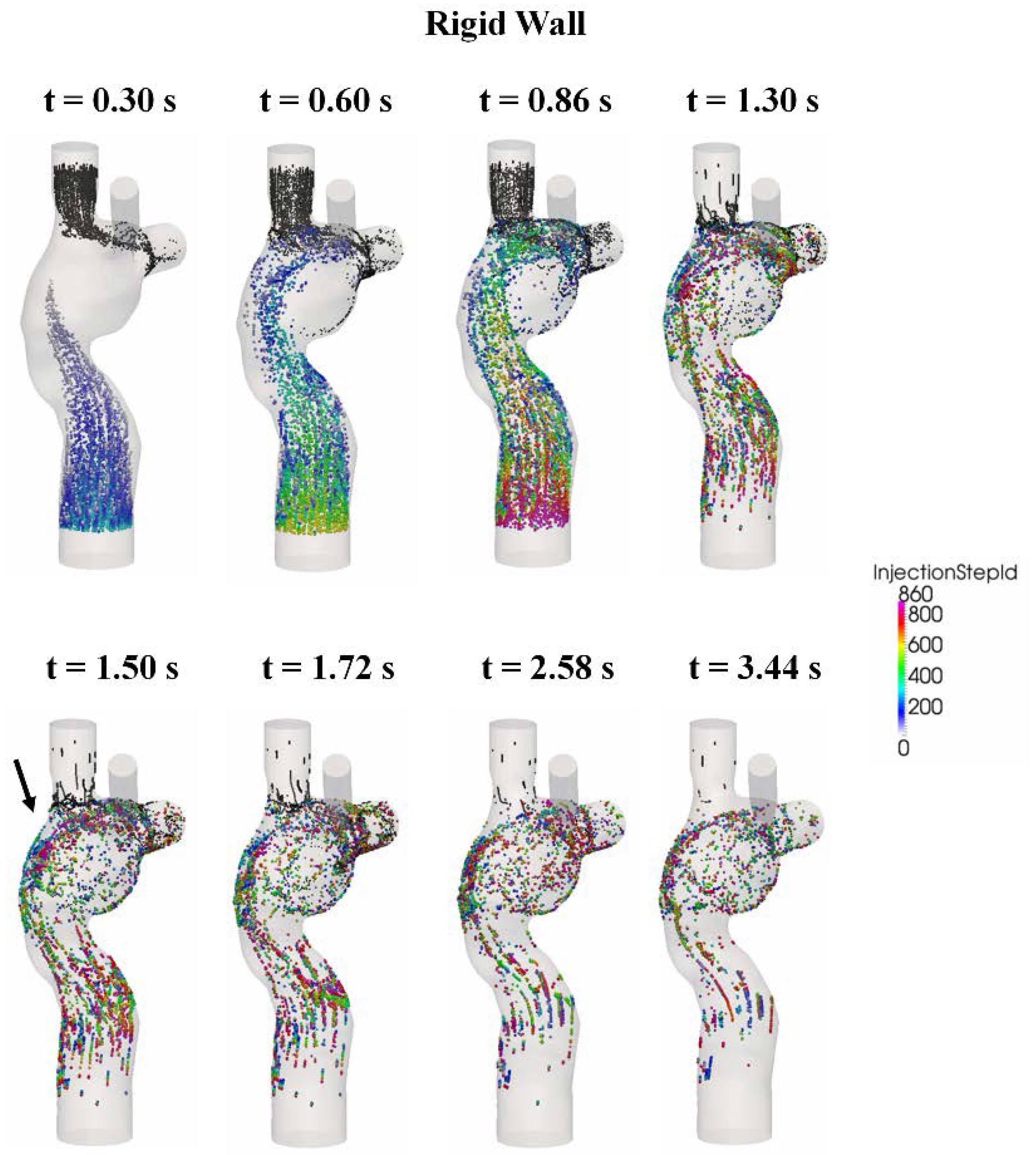
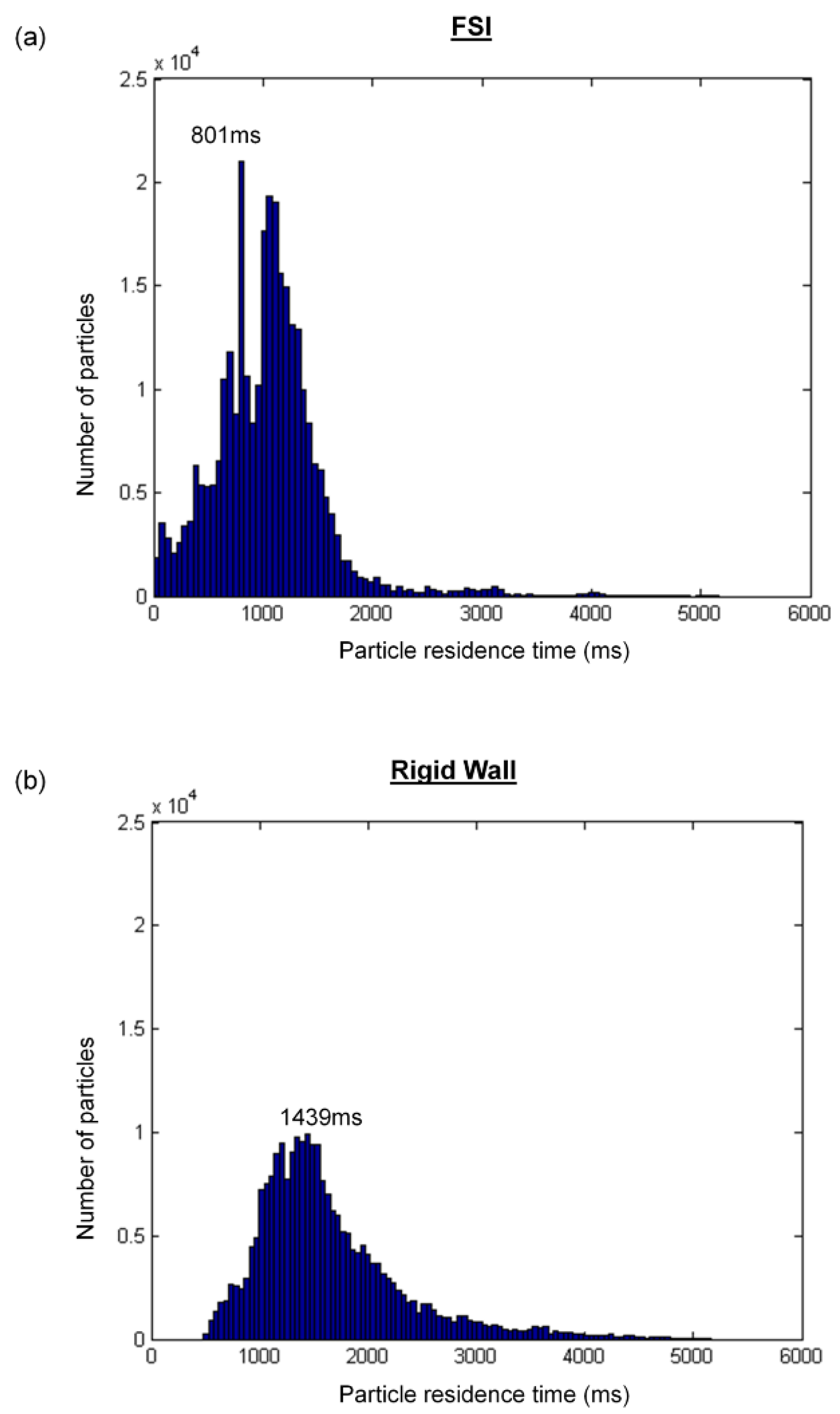
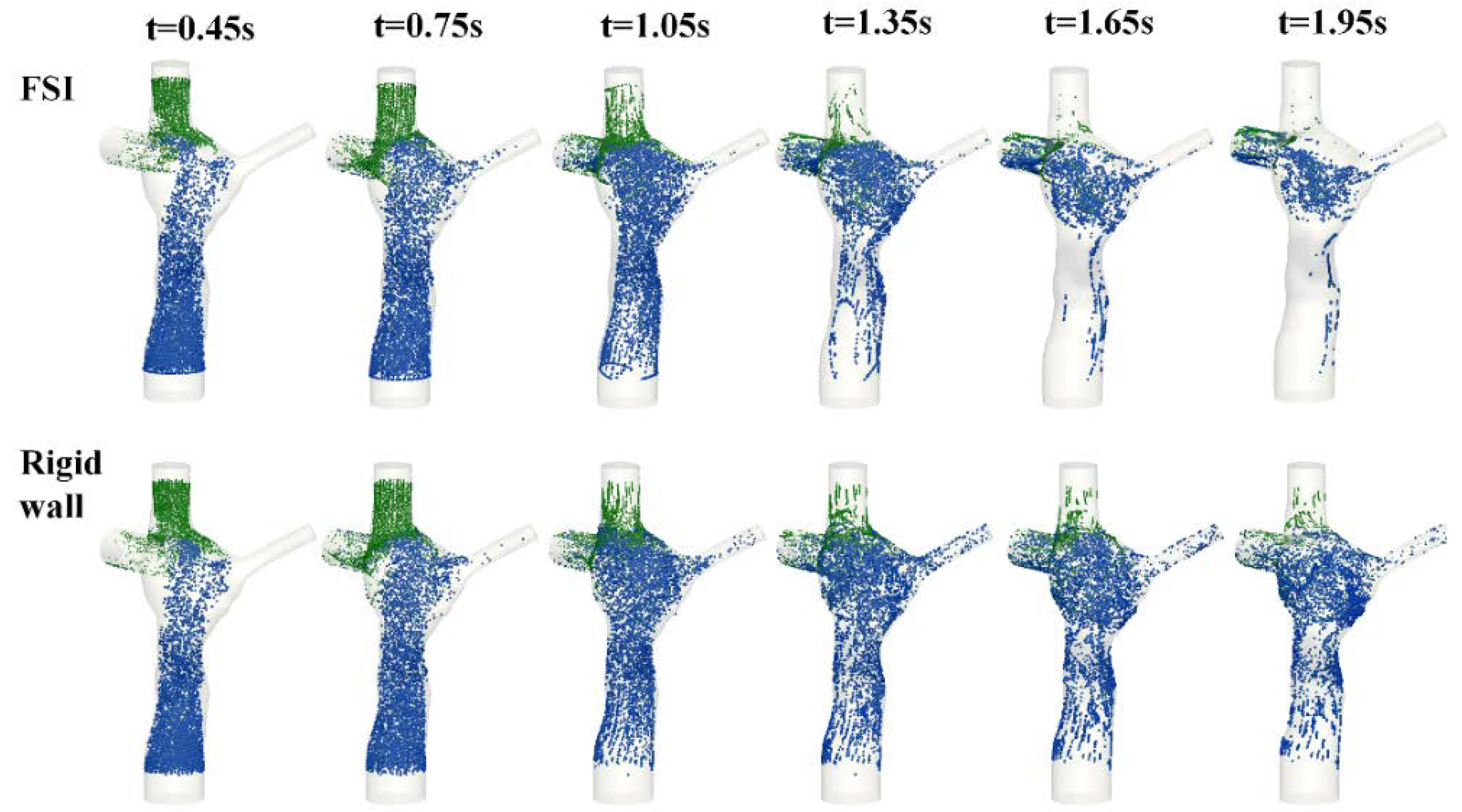
3.5. Particle Tracking
4. Discussion
Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
References
- Fontan, F.; Baudet, E. Surgical repair of tricuspid atresia. Thorax 1971, 26, 240–248. [Google Scholar] [CrossRef]
- de Leval, M.R.; Kilner, P.; Gewillig, M.; Bull, C. Total cavopulmonary connection: A logical alternative to atriopulmonary connection for complex Fontan operations. Experimental studies and early clinical experience. J. Thorac. Cardiovasc. Surg. 1988, 96, 682–695. [Google Scholar] [CrossRef]
- de Zelicourt, D.; Pekkan, K.; Wills, L.; Kanter, K.; Forbess, J.; Sharma, S.; Fogel, M.; Yoganathan, A.P. In vitro flow analysis of a patient-specific intraatrial total cavopulmonary connection. Ann. Thorac. Surg. 2005, 79, 2094–2102. [Google Scholar] [CrossRef] [PubMed]
- Amodeo, A.; Galletti, L.; Marianeschi, S.; Picardo, S.; Giannico, S.; Renzi, P.D.; Marcelletti, C. Extracardiac Fontan operation for complex cardiac anomalies: Seven years’ experience. J. Thorac. Cardiovasc. Surg. 1997, 114, 1020–1031. [Google Scholar] [CrossRef]
- Jayakumar, K.A.; Addonizio, L.J.; Kichuk-Chrisant, M.R.; Galantowicz, M.E.; Lamour, J.M.; Quaegebeur, J.M.; Hsu, D.T. Cardiac Transplantation After the Fontan or Glenn Procedure. J. Am. Coll. Cardiol. 2004, 44, 2065–2072. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, C.P.; Landzberg, M.J. The ‘failing’ Fontan circulation. Prog. Pediatr. Cardiol. 2002, 16, 105–114. [Google Scholar] [CrossRef]
- Sundareswaran, K.S.; Pekkan, K.; Dasi, L.P.; Whitehead, K.; Sharma, S.; Kanter, K.R.; Fogel, M.A.; Yoganathan, A.P. The total cavopulmonary connection resistance: A significant impact on single ventricle hemodynamics at rest and exercise. Am. J. Physiol. Circ. Physiol. 2008, 295, H2427–H2435. [Google Scholar] [CrossRef]
- Tree, M.; Wei, Z.A.; Trusty, P.M.; Raghav, V.; Fogel, M.; Maher, K.; Yoganathan, A. Using a Novel In Vitro Fontan Model and Condition-Specific Real-Time MRI Data to Examine Hemodynamic Effects of Respiration and Exercise. Ann. Biomed. Eng. 2018, 46, 135–147. [Google Scholar] [CrossRef]
- Tang, E.; Wei, Z.A.; Whitehead, K.K.; Khiabani, R.H.; Restrepo, M.; Mirabella, L.; Bethel, J.; Paridon, S.M.; Marino, B.S.; Fogel, M.A.; et al. Effect of Fontan geometry on exercise haemodynamics and its potential implications. Heart 2017, 103, 1806–1812. [Google Scholar] [CrossRef]
- Whitehead, K.K.; Pekkan, K.; Kitajima, H.D.; Paridon, S.M.; Yoganathan, A.P.; Fogel, M.A. Nonlinear power loss during exercise in single-ventricle patients after the Fontan: Insights from computational fluid dynamics. Circulation 2007, 116, I165–I171. [Google Scholar] [CrossRef]
- Pike, N.A.; Vricella, L.A.; Feinstein, J.A.; Black, M.D.; Reitz, B.A. Regression of severe pulmonary arteriovenous malformations after Fontan revision and "hepatic factor" rerouting. Ann. Thorac. Surg. 2004, 78, 697–699. [Google Scholar] [CrossRef]
- Srivastava, D.; Preminger, T.; Lock, J.E.; Mandell, V.; Keane, J.F.; Mayer, J.E., Jr.; Kozakewich, H.; Spevak, P.J. Hepatic venous blood and the development of pulmonary arteriovenous malformations in congenital heart disease. Circulation 1995, 92, 1217–1222. [Google Scholar] [CrossRef] [PubMed]
- Trusty, P.M.; Wei, Z.; Tree, M.; Kanter, K.R.; Fogel, M.A.; Yoganathan, A.P.; Slesnick, T.C. Local Hemodynamic Differences Between Commercially Available Y-Grafts and Traditional Fontan Baffles Under Simulated Exercise Conditions: Implications for Exercise Tolerance. Cardiovasc. Eng. Technol. 2017, 8, 390–399. [Google Scholar] [CrossRef] [PubMed]
- Trusty, P.M.; Wei, Z.; Rychik, J.; Russo, P.A.; Surrey, L.F.; Goldberg, D.J.; Fogel, M.A.; Yoganathan, A.P. Impact of hemodynamics and fluid energetics on liver fibrosis after Fontan operation. J. Thorac. Cardiovasc. Surg. 2018, 156, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Trusty, P.M.; Wei, Z.; Sales, M.; Kanter, K.R.; Fogel, M.A.; Yoganathan, A.P.; Slesnick, T.C. Y-graft modification to the Fontan procedure: Increasingly balanced flow over time. J. Thorac. Cardiovasc. Surg. 2020, 159, 652–661. [Google Scholar] [CrossRef]
- Trusty, P.; Wei, Z.; Fogel, M.; Maher, K.; Yoganathan, A.P.; Deshpande, S. Computational Modeling of a right-sided Fontan assist device: Effectiveness across patient anatomies and cannulations. J. Biomech. 2020, 109, 109917. [Google Scholar] [CrossRef] [PubMed]
- Trusty, P.M.; Wei, Z.; Rychik, J.; Graham, A.; Russo, P.A.; Surrey, L.F.; Goldberg, D.J.; Yoganathan, A.P.; Fogel, M.A. Cardiac Magnetic Resonance Derived Metrics are Predictive of Liver Fibrosis in Fontan Patients. Ann. Thorac. Surg. 2020, 109, 1904–1911. [Google Scholar] [CrossRef]
- Zhu, F.; Shi, G.; Wen, C.; Zhang, Q.; Fu, Q.; Liu, J.; Zhu, Z.; Chen, H. Hemodynamic Effects of A Simplified Venturi Conduit for Fontan Circulation: A Pilot, In Silico Analysis. Sci. Rep. 2020, 10, 817. [Google Scholar] [CrossRef] [PubMed]
- Kung, E.; Baretta, A.; Baker, C.; Arbia, G.; Biglino, G.; Corsini, C.; Schievano, S.; Vignon-Clementel, I.E.; Dubini, G.; Pennati, G.; et al. Predictive modeling of the virtual Hemi-Fontan operation for second stage single ventricle palliation: Two patient-specific cases. J. Biomech. 2013, 46, 423–429. [Google Scholar] [CrossRef]
- Yang, W.; Vignon-Clementel, I.E.; Troianowski, G.; Reddy, V.M.; Feinstein, J.A.; Marsden, A.L. Hepatic blood flow distribution and performance in conventional and novel Y-graft Fontan geometries: A case series computational fluid dynamics study. J. Thorac. Cardiovasc. Surg. 2012, 143, 1086–1097. [Google Scholar] [CrossRef]
- Long, C.C.; Hsu, M.C.; Bazilevs, Y.; Feinstein, J.A.; Marsden, A.L. Fluid-structure interaction simulations of the Fontan procedure using variable wall properties. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 513–527. [Google Scholar] [CrossRef]
- Liang, F.; Sughimoto, K.; Matsuo, K.; Liu, H.; Takagi, S. Patient-specific assessment of cardiovascular function by combination of clinical data and computational model with applications to patients undergoing Fontan operation. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 1000–1018. [Google Scholar] [CrossRef] [PubMed]
- Tang, E.; Wei, Z.A.; Trusty, P.M.; Whitehead, K.K.; Mirabella, L.; Veneziani, A.; Fogel, M.A.; Yoganathan, A.P. The effect of respiration-driven flow waveforms on hemodynamic metrics used in Fontan surgical planning. J. Biomech. 2019, 82, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.A.; Huddleston, C.; Trusty, P.M.; Singh-Gryzbon, S.; Fogel, M.A.; Veneziani, A.; Yoganathan, A.P. Analysis of Inlet Velocity Profiles in Numerical Assessment of Fontan Hemodynamics. Ann. Biomed. Eng. 2019, 47, 2258–2270. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.A.; Trusty, P.M.; Tree, M.; Haggerty, C.M.; Tang, E.; Fogel, M.; Yoganathan, A.P. Can time-averaged flow boundary conditions be used to meet the clinical timeline for Fontan surgical planning? J. Biomech. 2017, 50, 172–179. [Google Scholar] [CrossRef][Green Version]
- Wei, Z.; Singh-Gryzbon, S.; Trusty, P.M.; Huddleston, C.; Zhang, Y.; Fogel, M.A.; Veneziani, A.; Yoganathan, A.P. Non-Newtonian Effects on Patient-Specific Modeling of Fontan Hemodynamics. Ann. Biomed. Eng. 2020, 48, 2204–2217. [Google Scholar] [CrossRef]
- Schiavazzi, D.E.; Baretta, A.; Pennati, G.; Hsia, T.Y.; Marsden, A.L. Patient-specific parameter estimation in single-ventricle lumped circulation models under uncertainty. Int. J. Numer. Methods Biomed. Eng. 2017, 33, 1–34. [Google Scholar] [CrossRef]
- Marsden, A.L.; Vignon-Clementel, I.E.; Chan, F.P.; Feinstein, J.A.; Taylor, C.A. Effects of exercise and respiration on hemodynamic efficiency in CFD simulations of the total cavopulmonary connection. Ann. Biomed. Eng. 2007, 35, 250–263. [Google Scholar] [CrossRef]
- Siallagan, D.; Loke, Y.H.; Olivieri, L.; Opfermann, J.; Ong, C.S.; de Zelicourt, D.; Petrou, A.; Daners, M.S.; Kurtcuoglu, V.; Meboldt, M.; et al. Virtual surgical planning, flow simulation, and 3-dimensional electrospinning of patient-specific grafts to optimize Fontan hemodynamics. J. Thorac. Cardiovasc. Surg. 2018, 155, 1734–1742. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Benson, D.J.; Sankaran, S.; Marsden, A.L. Computational fluid–structure interaction: Methods and application to a total cavopulmonary connection. Comput. Mech. 2009, 45. [Google Scholar] [CrossRef]
- Orlando, W.; Shandas, R.; DeGroff, C. Efficiency differences in computational simulations of the total cavo-pulmonary circulation with and without compliant vessel walls. Comput. Methods Progr. Biomed. 2006, 81, 220–227. [Google Scholar] [CrossRef] [PubMed]
- Frakes, D.H.; Conrad, C.P.; Healy, T.M.; Monaco, J.W.; Fogel, M.; Sharma, S.; Smith, M.J.; Yoganathan, A.P. Application of an adaptive control grid interpolation technique to morphological vascular reconstruction. IEEE Trans. Biomed. Eng. 2003, 50, 197–206. [Google Scholar] [CrossRef] [PubMed]
- Frakes, D.H.; Smith, M.J.; Parks, J.; Sharma, S.; Fogel, M.; Yoganathan, A.P. New techniques for the reconstruction of complex vascular anatomies from MRI images. J. Cardiovasc. Magn. Reson. 2005, 7, 425–432. [Google Scholar] [CrossRef] [PubMed]
- Frakes, D.; Smith, M.; de Zelicourt, D.; Pekkan, K.; Yoganathan, A.P. Three-dimensional velocity field reconstruction. J. Biomech. Eng. 2004, 126, 727–735. [Google Scholar] [CrossRef] [PubMed]
- Sundareswaran, K.S.; Frakes, D.; Fogel, M.; Soerensen, D.; Oshinski, J.N.; Yoganathan, A. Optimum fuzzy filters for phase-contrast magnetic resonance imaging segmentation. J. Magn. Reson. Imaging 2009, 29, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.A.; Johnson, C.; Trusty, P.; Stephens, M.; Wu, W.; Sharon, R.; Srimurugan, B.; Kottayil, B.P.; Sunil, G.S.; Fogel, M.A.; et al. Comparison of Fontan Surgical Options for Patients with Apicocaval Juxtaposition. Pediatr. Cardiol. 2020, 41, 1021–1030. [Google Scholar] [CrossRef] [PubMed]
- Passerini, T.; Quaini, A.; Villa, U.; Veneziani, A.; Canic, S. Validation of an open source framework for the simulation of blood flow in rigid and deformable vessels. Int. J. Numer. Methods Biomed. Eng. 2013, 29. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J. Gmsh: A three-dimensional finite element mesh generator with built-in pre-and postprocessing facilities. Int. J. Numer. Methods Biomed. Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Tree, M.; Wei, Z.A.; Munz, B.; Maher, K.; Deshpande, S.; Slesnick, T.; Yoganathan, A. A Method for In Vitro TCPC Compliance Verification. J. Biomech. Eng. 2017, 139, 064502. [Google Scholar] [CrossRef]
- Bhatia, S.K. Biomaterials for Clinical Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Caro, C.G.; Pedley, T.J.; Schroter, R.C.; Seed, W.A.; Parker, K.H. The Mechanics of the Circulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Pedley, T.J. The Fluid Mechanics of Large Blood Vessels.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Ganong, W.F. Review of Medical Physiology, 21st ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Ling, L.H.; Oh, J.K.; Tei, C.; Click, R.L.; Breen, J.F.; Seward, J.B.; Tajik, A.J. Pericardial Thickness Measured With Transesophageal Echocardiography: Feasibility and Potential Clinical Usefulness. J. Am. Coll. Cardiol. 1997, 29, 1317–1323. [Google Scholar] [CrossRef]
- Wei, Z.A.; Tree, M.; Trusty, P.M.; Wu, W.; Singh-Gryzbon, S.; Yoganathan, A. The Advantages of Viscous Dissipation Rate over Simplified Power Loss as a Fontan Hemodynamic Metric. Ann. Biomed. Eng. 2018, 46, 404–416. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.A.; Trusty, P.M.; Zhang, Y.; Tang, E.; Whitehead, K.K.; Fogel, M.A.; Yoganathan, A.P. Impact of Free-Breathing Phase-Contrast MRI on Decision-Making in Fontan Surgical Planning. J. Cardiovasc. Transl. Res. 2019, 13, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Duvernois, V.; Marsden, A.L.; Shadden, S.C. Lagrangian analysis of hemodynamics data from FSI simulation. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 445–461. [Google Scholar] [CrossRef] [PubMed]
- Shadden, S.C.; Arzani, A. Lagrangian postprocessing of computational hemodynamics. Ann. Biomed. Eng. 2015, 43, 41–58. [Google Scholar] [CrossRef]
- Mirabella, L.; Haggerty, C.M.; Passerini, T.; Piccinelli, M.; Powell, A.J.; Del Nido, P.J.; Veneziani, A.; Yoganathan, A.P. Treatment planning for a TCPC test case: A numerical investigation under rigid and moving wall assumptions. Int. J. Numer. Methods Biomed. Eng. 2012, 29, 197–216. [Google Scholar] [CrossRef]
- Reuben, S.R. Compliance of the Human Pulmonary Arterial System in Disease. Circ. Res. 1971, 29, 40–50. [Google Scholar] [CrossRef]
- Khiabani, R.H.; Whitehead, K.K.; Han, D.; Restrepo, M.; Tang, E.; Bethel, J.; Paridon, S.M.; Fogel, M.A.; Yoganathan, A.P. Exercise capacity in single-ventricle patients after Fontan correlates with haemodynamic energy loss in TCPC. Heart 2015, 101, 139–143. [Google Scholar] [CrossRef]
- Toma, M.; Krdey, A.; Akagi, S.; Oshima, M. Strongly Coupled Fluid-Structure Interaction Cardiovascular Analysis with the Effect of Peripheral Network. Seisan Kenkyu 2011, 63, 339–344. [Google Scholar]
- Trusty, P.M.; Wei, Z.A.; Slesnick, T.C.; Kanter, K.R.; Spray, T.L.; Fogel, M.A.; Yoganathan, A.P. The first cohort of prospective Fontan surgical planning patients with follow-up data: How accurate is surgical planning? J. Thorac. Cardiovasc. Surg. 2019, 157, 1146–1155. [Google Scholar] [CrossRef]
- Trusty, P.M.; Slesnick, T.C.; Wei, Z.A.; Rossignac, J.; Kanter, K.R.; Fogel, M.A.; Yoganathan, A.P. Fontan Surgical Planning: Previous Accomplishments, Current Challenges, and Future Directions. J. Cardiovasc. Transl. Res. 2018, 11, 133–144. [Google Scholar] [CrossRef]
- van Bakel, T.M.J.; Lau, K.D.; Hirsch-Romano, J.; Trimarchi, S.; Dorfman, A.L.; Figueroa, C.A. Patient-Specific Modeling of Hemodynamics: Supporting Surgical Planning in a Fontan Circulation Correction. J. Cardiovasc. Transl. Res. 2018, 11, 145–155. [Google Scholar] [CrossRef]
- Carberry, T.; Murthy, R.; Hsiao, A.; Petko, C.; Moore, J.; Lamberti, J.; Hegde, S. Fontan Revision: Presurgical Planning Using Four-Dimensional (4D) Flow and Three-Dimensional (3D) Printing. World J. Pediatr. Congenit. Heart Surg. 2019, 10, 245–249. [Google Scholar] [CrossRef]
- Sundareswaran, K.S.; de Zelicourt, D.; Sharma, S.; Kanter, K.R.; Spray, T.L.; Rossignac, J.; Sotiropoulos, F.; Fogel, M.A.; Yoganathan, A.P. Correction of pulmonary arteriovenous malformation using image-based surgical planning. JACC Cardiovasc. Imaging 2009, 2, 1024–1030. [Google Scholar] [CrossRef]
- Pekkan, K.; Whited, B.; Kanter, K.; Sharma, S.; de Zelicourt, D.; Sundareswaran, K.; Frakes, D.; Rossignac, J.; Yoganathan, A.P. Patient-specific surgical planning and hemodynamic computational fluid dynamics optimization through free-form haptic anatomy editing tool (SURGEM). Med. Biol. Eng. Comput. 2008, 46, 1139–1152. [Google Scholar] [CrossRef]





| Maximum Displacement (mm) | (a) Very Fine | (b) Fine | (c) Coarse | Difference Between | |
|---|---|---|---|---|---|
| (a) & (b) | (b) & (c) | ||||
| Deceleration (at 0.02 s) | 2.448 | 2.450 | 2.457 | 0.002 | 0.007 |
| Low flow (at 0.03 s) | 4.334 | 4.342 | 4.342 | 0.008 | 0 |
| Acceleration (at 0.06 s) | 6.955 | 6.964 | 6.979 | 0.009 | 0.015 |
| High flow (at 0.09 s) | 6.886 | 6.917 | 6.962 | 0.031 | 0.045 |
| Hemodynamic Metrics | (a) Very Fine vs. (b) Fine | (b) Fine vs. (c) Coarse | |
|---|---|---|---|
| Pressure drop difference (mmHg) | Temporal average | 0.005 | 0.009 |
| Temporal maximum | 0.01 | 0.015 | |
| %difference in power loss | 0.29% | 0.66% | |
| Vessel Area | FSI Simulation | PC-MRI Data | ||
|---|---|---|---|---|
| FP | SVC | FP | SVC | |
| Average (cm2) | 3.74 | 1.99 | 6.81 | 1.94 |
| Change (cm2) | 0.20 | 0.07 | 0.37 | 0.14 |
| Deformation Index | 5.3% | 3.4% | 5.4% | 7.1% |
| Pressure Drop (mmHg) | TCPC Power Loss (mW) | |||||
|---|---|---|---|---|---|---|
| Minimum | Maximum | Average | Minimum | Maximum | Average | |
| Rigid wall | −0.60 | 2.35 | 0.60 | −4.46 | 17.33 | 2.89 |
| FSI | −0.07 | 1.13 | 0.61 | −0.82 | 9.34 | 2.99 |
| Particle Washout Time (s) | Particle Washout Time (No. of Cardiac Cycle) | Time-Average HFD(LPA) | |
|---|---|---|---|
| FSI | 1.77 | 2.06 | 19% |
| Rigid wall | 3.16 | 3.67 | 19% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, E.; Wei, Z.; Fogel, M.A.; Veneziani, A.; Yoganathan, A.P. Fluid-Structure Interaction Simulation of an Intra-Atrial Fontan Connection. Biology 2020, 9, 412. https://doi.org/10.3390/biology9120412
Tang E, Wei Z, Fogel MA, Veneziani A, Yoganathan AP. Fluid-Structure Interaction Simulation of an Intra-Atrial Fontan Connection. Biology. 2020; 9(12):412. https://doi.org/10.3390/biology9120412
Chicago/Turabian StyleTang, Elaine, Zhenglun (Alan) Wei, Mark A. Fogel, Alessandro Veneziani, and Ajit P. Yoganathan. 2020. "Fluid-Structure Interaction Simulation of an Intra-Atrial Fontan Connection" Biology 9, no. 12: 412. https://doi.org/10.3390/biology9120412
APA StyleTang, E., Wei, Z., Fogel, M. A., Veneziani, A., & Yoganathan, A. P. (2020). Fluid-Structure Interaction Simulation of an Intra-Atrial Fontan Connection. Biology, 9(12), 412. https://doi.org/10.3390/biology9120412