Stability of Signaling Pathways during Aging—A Boolean Network Approach
Abstract
:1. Introduction
2. Results
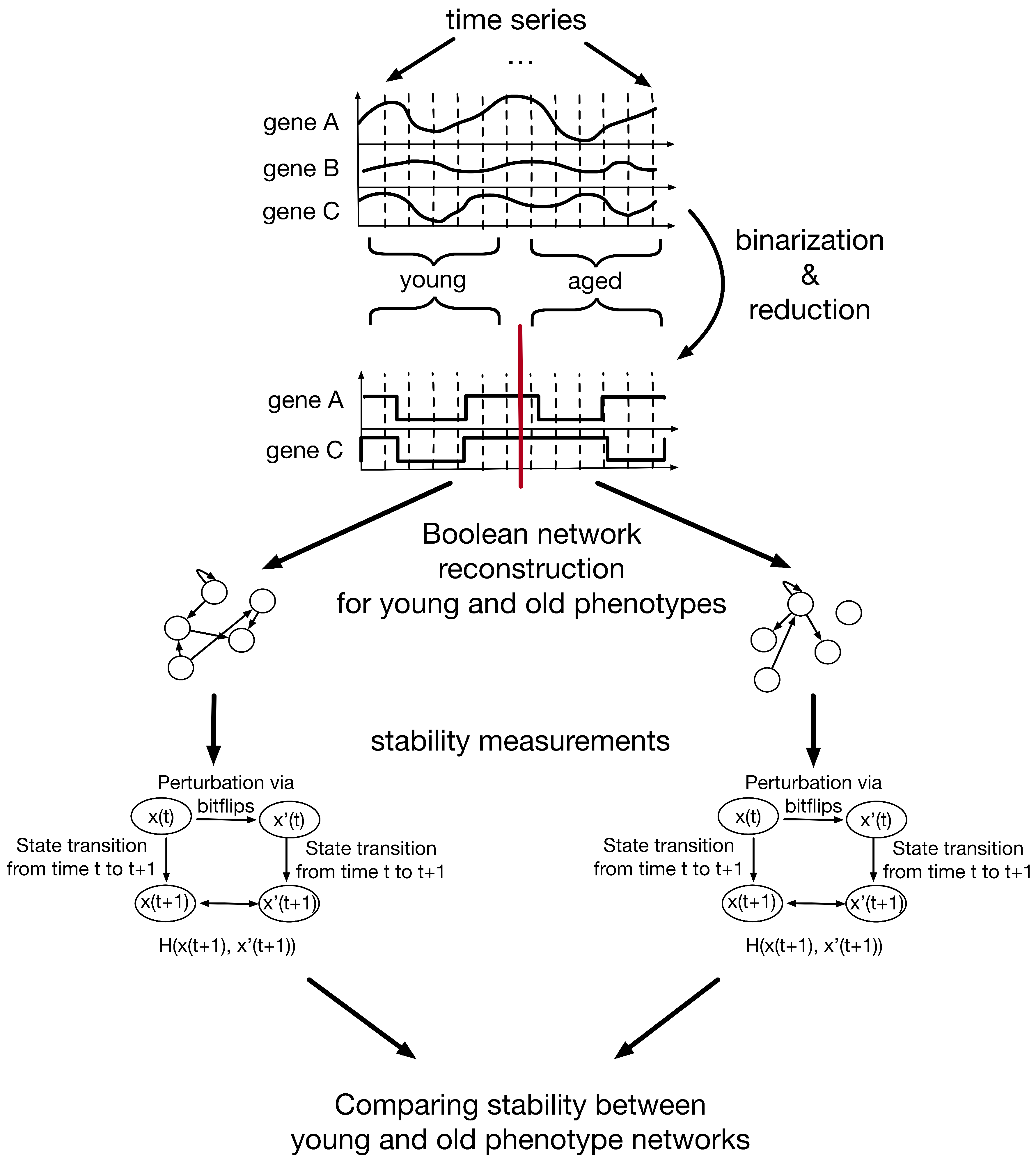
2.1. Experimental Settings
2.1.1. Data Processing
2.1.2. Inferring Boolean Networks from Binarized Time-Series Data
2.2. Stability Measure of Boolean Networks
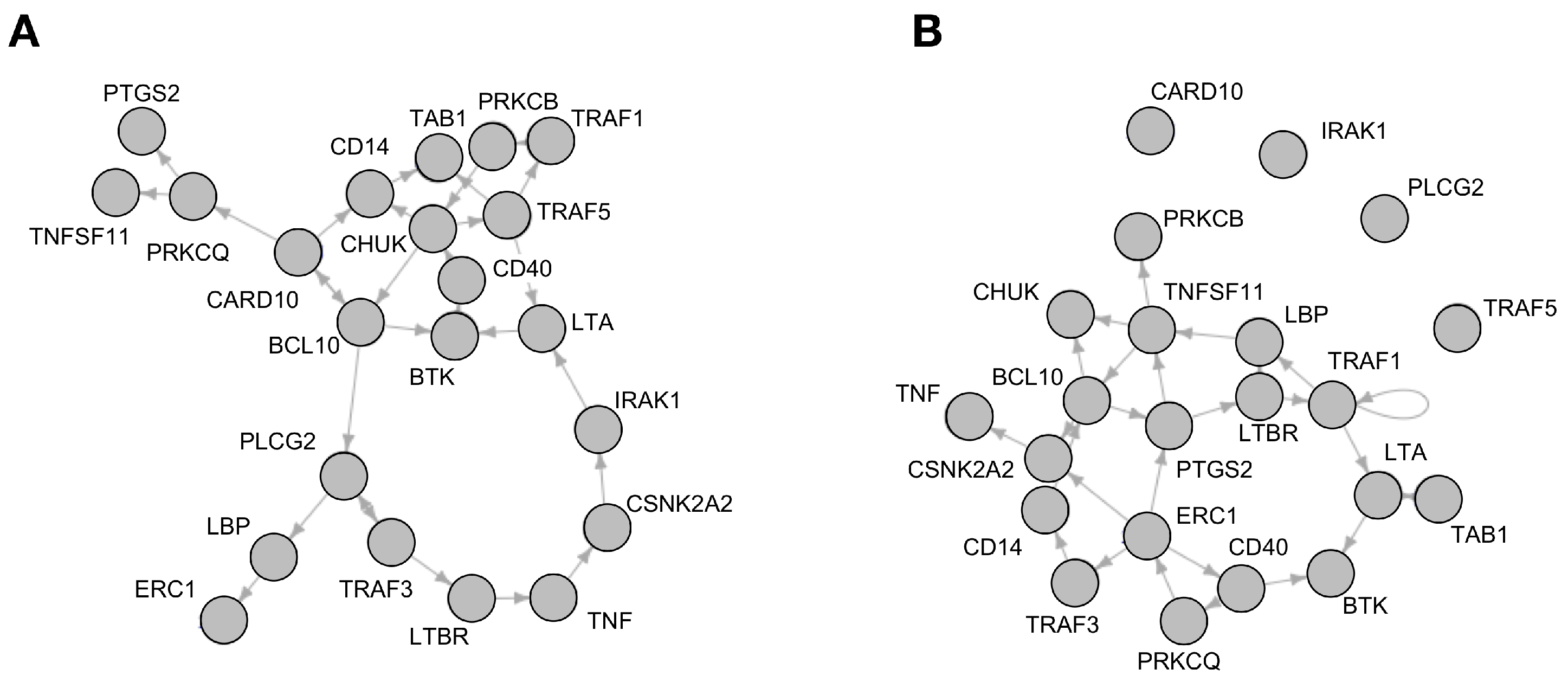
Analysis of Reconstructed Boolean Networks
2.3. Boolean Functions
2.4. Network Stability
3. Discussion
4. Conclusions
5. Materials and Methods
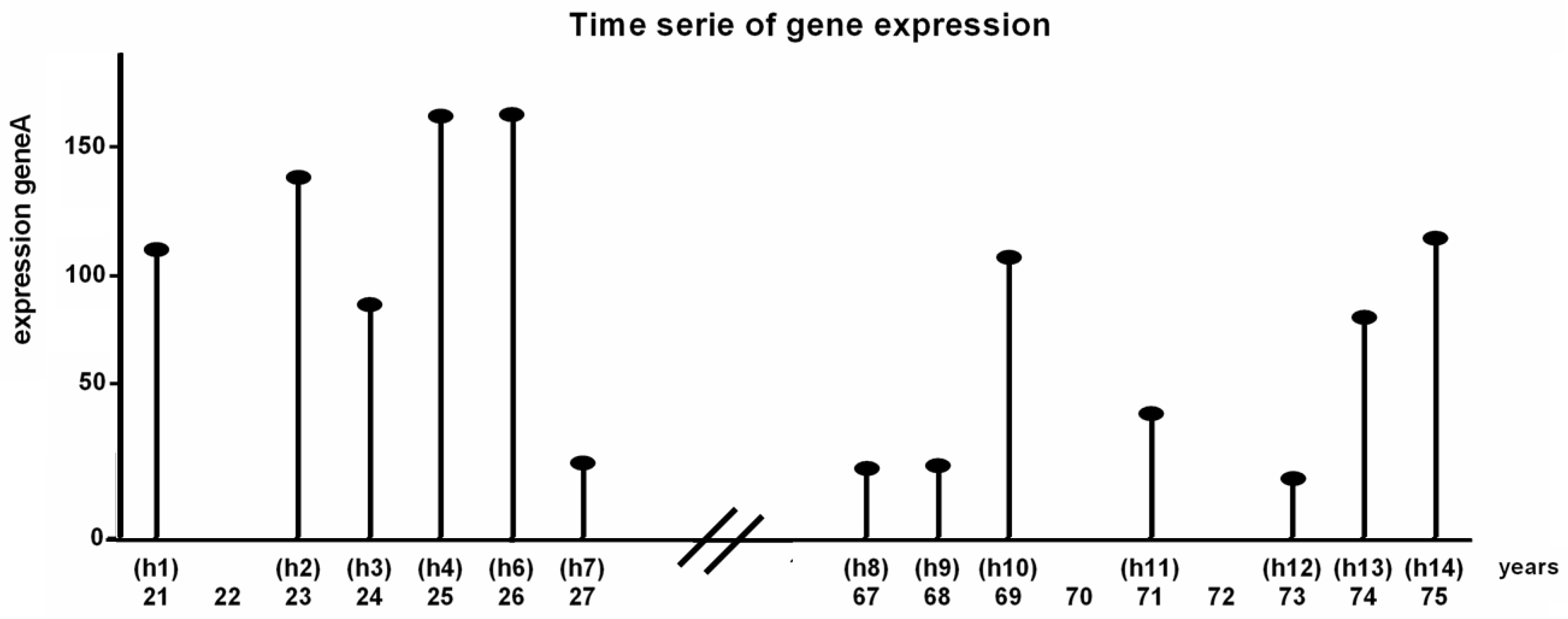
5.1. Data
5.2. Boolean Networks
5.3. Inferring Boolean Networks
5.3.1. Binarization of Time-Series Data
5.3.2. Inferring Boolean Functions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sauer, U.; Heinemann, M.; Zamboni, N. Genetics. Getting closer to the whole picture. Science 2007, 316, 550–551. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Naldi, A.; Monteiro, P.T.; Müssel, C.; Consortium for Logical Models and Tools; Kestler, H.A.; Thieffry, D.; Xenarios, I.; Saez-Rodriguez, J.; Helikar, T.; Chaouiya, C. Cooperative development of logical modelling standards and tools with CoLoMoTo. Bioinformatics 2015, 31, 1154–1159. [Google Scholar] [CrossRef] [PubMed]
- Tilstra, J.S.; Clauson, C.L.; Niedernhofer, L.J.; Robbins, P.D. NF-κB in Aging and Disease. Aging Dis. 2011, 2, 449–465. [Google Scholar] [PubMed]
- Manolagas, S.C.; Almeida, M. Gone with the Wnts: β-Catenin, T-Cell Factor, Forkhead Box O, and Oxidative Stress in Age-Dependent Diseases of Bone, Lipid, and Glucose Metabolism. Mol. Endocrinol. 2007, 21, 2605–2614. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Fergusson, M.M.; Castilho, R.M.; Liu, J.; Cao, L.; Chen, J.; Malide, D.; Rovira, I.I.; Schimel, D.; Kuo, C.J.; et al. Augmented Wnt signaling in a mammalian model of accelerated aging. Science 2007, 317, 803–806. [Google Scholar] [CrossRef] [PubMed]
- Kenyon, C. The first long-lived mutants: Discovery of the insulin/IGF-1 pathway for ageing. Philos. Trans. R. Soc. B Biol. Sci. 2010, 366, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.; Liu, F.; Adamo, M.L.; Remmen, H.V.; Nelson, J.F. The role of insulin and insulin-like growth factor-I in mammalian ageing. Best Pract. Res. Clin. Endocrinol. Metab. 2004, 18, 393–406. [Google Scholar] [CrossRef] [PubMed]
- Zs-Nagy, I.; Cutler, R.G.; Semsei, I. Dysdifferentiation hypothesis of aging and cancer: A comparison with the membrane hypothesis of aging. Ann. N. Y. Acad. Sci. 1988, 521, 215–225. [Google Scholar] [CrossRef] [PubMed]
- Gruber, J.; Yee, Z.; Tolwinski, N. Developmental Drift and the Role of Wnt Signaling in Aging. Cancers 2016, 8, 73. [Google Scholar] [CrossRef] [PubMed]
- Peterson, J.M.; Bakkar, N.; Guttridge, D.C. NF-κB Signaling in Skeletal Muscle Health and Disease. In Myogenesis; Elsevier: Amsterdam, The Netherlands, 2011; pp. 85–119. [Google Scholar]
- Salminen, A.; Kaarniranta, K. NF-kappaB signaling in the aging process. J. Clin. Immunol. 2009, 29, 397–405. [Google Scholar] [CrossRef] [PubMed]
- Adler, A.S.; Kawahara, T.L.A.; Segal, E.; Chang, H.Y. Reversal of aging by NFkappaB blockade. Cell Cycle 2008, 7, 556–559. [Google Scholar] [CrossRef] [PubMed]
- Osorio, F.G.; Soria-Valles, C.; Santiago-Fernández, O.; Freije, J.M.P.; López-Otín, C. NF-κB signaling as a driver of ageing. Int. Rev. Cell Mol. Biol. 2016, 326, 133–174. [Google Scholar] [PubMed]
- Welle, S.; Brooks, A.I.; Delehanty, J.M.; Needler, N.; Thornton, C.A. Gene expression profile of aging in human muscle. Physiol. Genom. 2003, 14, 149–159. [Google Scholar] [CrossRef] [PubMed]
- Harper, J.M.; Salmon, A.B.; Chang, Y.; Bonkowski, M.; Bartke, A.; Miller, R.A. Stress resistance and aging: Influence of genes and nutrition. Mech. Ageing Dev. 2006, 127, 687–694. [Google Scholar] [CrossRef] [PubMed]
- Durinck, S.; Spellman, P.T.; Birney, E.; Huber, W. Mapping identifiers for the integration of genomic datasets with the R/Bioconductor package biomaRt. Nat. Protoc. 2009, 4, 1184–1191. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Hopfensitz, M.; Müssel, C.; Wawra, C.; Maucher, M.; Kühl, M.; Neumann, H.; Kestler, H.A. Multiscale Binarization of Gene Expression Data for Reconstructing Boolean Networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 487–498. [Google Scholar] [CrossRef] [PubMed]
- Müssel, C.; Schmid, F.; Blätte, T.J.; Hopfensitz, M.; Lausser, L.; Kestler, H.A. BiTrinA—Multiscale binarization and trinarization with quality analysis. Bioinformatics 2015, 32, 465–468. [Google Scholar] [CrossRef] [PubMed]
- Müssel, C.; Hopfensitz, M.; Kestler, H.A. BoolNet—An R package for generation, reconstruction and analysis of Boolean networks. Bioinformatics 2010, 26, 1378–1380. [Google Scholar] [CrossRef] [PubMed]
- Lähdesmäki, H.; Shmulevich, I.; Yli-Harja, O. On Learning Gene Regulatory Networks Under the Boolean Network Model. Mach. Learn. 2003, 52, 147–167. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Franceschini, A.; Kuhn, M.; Simonovic, M.; Roth, A.; Minguez, P.; Doerks, T.; Stark, M.; Muller, J.; Bork, P.; et al. The STRING database in 2011: Functional interaction networks of proteins, globally integrated and scored. Nucleic Acids Res. 2010, 39, D561–D568. [Google Scholar] [CrossRef] [PubMed]
- Kitano, H. Biological robustness. Nat. Rev. Genet. 2004, 5, 826–837. [Google Scholar] [CrossRef] [PubMed]
- Peixoto, T.P.; Drossel, B. Noise in random Boolean networks. Phys. Rev. E 2009, 79, 036108. [Google Scholar] [CrossRef] [PubMed]
- Au, P.Y.B.; Yeh, W.C. Physiological Roles and Mechanisms of Signaling by TRAF2 and TRAF5. In TNF Receptor Associated Factors (TRAFs); Springer: New York, NY, USA, 2007; pp. 32–47. [Google Scholar]
- Schütze, S.; Potthoff, K.; Machleidt, T.; Berkovic, D.; Wiegmann, K.; Krönke, M. TNF activates NF-κB by phosphatidylcholine-specific phospholipase C-induced “Acidic” sphingomyelin breakdown. Cell 1992, 71, 765–776. [Google Scholar] [CrossRef]
- Liu, G.; Park, Y.J.; Abraham, E. Interleukin-1 receptor-associated kinase (IRAK)-1-mediated NF-kappaB activation requires cytosolic and nuclear activity. FASEB J. 2008, 22, 2285–2296. [Google Scholar] [CrossRef] [PubMed]
- Blonska, M.; Lin, X. NF-κB signaling pathways regulated by CARMA family of scaffold proteins. Cell Res. 2010, 21, 55–70. [Google Scholar] [CrossRef] [PubMed]
- Kitano, H. A robustness-based approach to systems-oriented drug design. Nat. Rev. Drug Discov. 2007, 5, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Kitano, H. Towards a theory of biological robustness. Mol. Syst. Biol. 2007, 3, 137. [Google Scholar] [CrossRef] [PubMed]
- Kriete, A. Robustness and aging—A systems-level perspective. Biosystems 2013, 112, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Othmer, H.G. The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster. J. Theor. Biol. 2003, 223, 1–18. [Google Scholar] [CrossRef]
- Herrmann, F.; Groß, A.; Zhou, D.; Kestler, H.A.; Kühl, M. A Boolean Model of the Cardiac Gene Regulatory Network Determining First and Second Heart Field Identity. PLoS ONE 2012, 7, e46798. [Google Scholar] [CrossRef] [PubMed]
- Karlebach, G.; Shamir, R. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 2008, 9, 770–780. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. The origins of order. Self-organization and selection in evolution. J. Evolut. Biol. 1994, 7, 518–519. [Google Scholar]
- Harvey, I.; Bossomaier, T. Time Out of Joint: Attractors in Asynchronous Random Boolean Networks. In Fourth European Conference on Artificial Life; Langton, C.G., Ed.; MIT Press: Cambridge, MA, USA, 1997; pp. 67–75. [Google Scholar]
- Shmulevich, I.; Dougherty, E.R.; Kim, S.; Zhang, W. Probabilistic Boolean networks: A rule-based uncertainty model for gene regulatory networks. Bioinformatics 2002, 18, 261–274. [Google Scholar] [CrossRef] [PubMed]
- Fauré, A.; Naldi, A.; Chaouiya, C.; Thieffry, D. Dynamical analysis of a generic Boolean model for the control of the mammalian cell cycle. Bioinformatics 2006, 22, e124–e131. [Google Scholar] [CrossRef] [PubMed]
- Dahlhaus, M.; Burkovski, A.; Hertwig, F.; Müssel, C.; Volland, R.; Fischer, M.; Debatin, K.M.; Kestler, H.A.; Beltinger, C. Boolean modeling identifies Greatwall/MASTL as an important regulator in the AURKA network of neuroblastoma. Cancer Lett. 2016, 371, 79–89. [Google Scholar] [CrossRef] [PubMed]
- García-Gómez, M.; Azpeitia, E.; Álvarez Buylla, E.R. A dynamic genetic-hormonal regulatory network model explains multiple cellular behaviors of the root apical meristem of Arabidopsis thaliana. PLoS Comput. Biol. 2017, 13, e1005488. [Google Scholar] [CrossRef] [PubMed]
- Meyer, P.; Maity, P.; Burkovski, A.; Schwab, J.; Müssel, C.; Singh, K.; Ferreira, F.F.; Krug, L.; Maier, H.J.; Wlaschek, M.; et al. A model of the onset of the senescence associated secretory phenotype after DNA damage induced senescence. PLoS Comput. Biol. 2017, 13, e1005741. [Google Scholar] [CrossRef] [PubMed]
- Thomas, R.; Kaufman, M. Multistationarity, the basis of cell differentiation and memory. II. Logical analysis of regulatory networks in terms of feedback circuits. Chaos Interdiscip. J. Nonlinear Sci. 2001, 11, 180. [Google Scholar] [CrossRef] [PubMed]
- Saadatpour, A.; Albert, R.; Reluga, T.C. A Reduction Method for Boolean Network Models Proven to Conserve Attractors. SIAM J. Appl. Dyn. Syst. 2013, 12, 1997–2011. [Google Scholar] [CrossRef]
- Schwab, J.; Burkovski, A.; Siegle, L.; Müssel, C.; Kestler, H.A. ViSiBooL-visualization and simulation of Boolean networks with temporal constraints. Bioinformatics 2017, 33, 601–604. [Google Scholar] [CrossRef] [PubMed]
- Dubrova, E.; Teslenko, M. A SAT-Based Algorithm for Finding Attractors in Synchronous Boolean Networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 1393–1399. [Google Scholar] [CrossRef] [PubMed]
- Klarner, H.; Bockmayr, A.; Siebert, H. Computing Symbolic Steady States of Boolean Networks. In Cellular Automata; Springer International Publishing: Cham, Switzerland, 2014; pp. 561–570. [Google Scholar]
- Zañudo, J.G.T.; Albert, R. An effective network reduction approach to find the dynamical repertoire of discrete dynamic networks. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 025111. [Google Scholar] [CrossRef] [PubMed]
- Steinway, S.N.; Biggs, M.B.; Loughran, T.P., Jr.; Papin, J.A.; Albert, R. Inference of Network Dynamics and Metabolic Interactions in the Gut Microbiome. PLoS Comput. Biol. 2015, 11. [Google Scholar] [CrossRef] [PubMed]
- Lavrova, A.I.; Postnikov, E.B.; Zyubin, A.Y.; Babak, S.V. Ordinary differential equations and Boolean networks in application to modelling of 6-mercaptopurine metabolism. R. Soc. Open Sci. 2017, 4, 160872. [Google Scholar] [CrossRef] [PubMed]
- Natalie Berestovsky, L.N. An Evaluation of Methods for Inferring Boolean Networks from Time-Series Data. PLoS ONE 2013, 8, e66031. [Google Scholar] [CrossRef] [PubMed]
- Maucher, M.; Kracher, B.; Kuhl, M.; Kestler, H.A. Inferring Boolean network structure via correlation. Bioinformatics 2011, 27, 1529–1536. [Google Scholar] [CrossRef] [PubMed]
- Maucher, M.; Kracht, D.V.; Schober, S.; Bossert, M.; Kestler, H.A. Inferring Boolean functions via higher-order correlations. Comput. Stat. 2012, 29, 97–115. [Google Scholar] [CrossRef]
- Akutsu, T.; Miyano, S.; Kuhara, S. Identification of genetic networks from a small number of gene expression patterns under the Boolean network model. Pac. Symp. Biocomput. 1999, 4, 17–28. [Google Scholar]
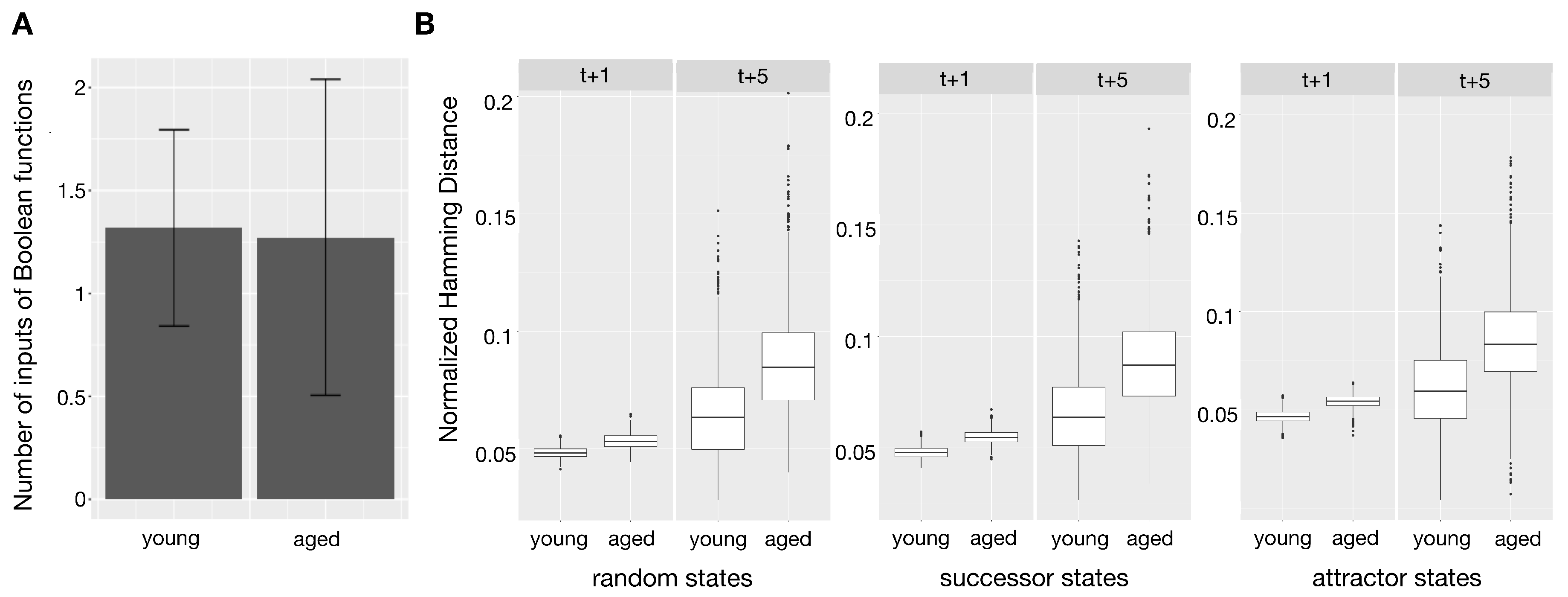
| After One State Transition | After Five State Transitions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Young Phenotype | Aged Phenotype | Young Phenotype | Aged Phenotype | |||||||||
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
| random initial state | 0.041 | 0.056 | 0.048 | 0.044 | 0.065 | 0.053 | 0.028 | 0.151 | 0.063 | 0.040 | 0.201 | 0.085 |
| random successor state | 0.041 | 0.057 | 0.048 | 0.045 | 0.067 | 0.055 | 0.027 | 0.143 | 0.064 | 0.034 | 0.209 | 0.087 |
| random attractor state | 0.036 | 0.057 | 0.047 | 0.037 | 0.064 | 0.054 | 0.004 | 0.144 | 0.060 | 0.007 | 0.211 | 0.083 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwab, J.D.; Siegle, L.; Kühlwein, S.D.; Kühl, M.; Kestler, H.A. Stability of Signaling Pathways during Aging—A Boolean Network Approach. Biology 2017, 6, 46. https://doi.org/10.3390/biology6040046
Schwab JD, Siegle L, Kühlwein SD, Kühl M, Kestler HA. Stability of Signaling Pathways during Aging—A Boolean Network Approach. Biology. 2017; 6(4):46. https://doi.org/10.3390/biology6040046
Chicago/Turabian StyleSchwab, Julian Daniel, Lea Siegle, Silke Daniela Kühlwein, Michael Kühl, and Hans Armin Kestler. 2017. "Stability of Signaling Pathways during Aging—A Boolean Network Approach" Biology 6, no. 4: 46. https://doi.org/10.3390/biology6040046
APA StyleSchwab, J. D., Siegle, L., Kühlwein, S. D., Kühl, M., & Kestler, H. A. (2017). Stability of Signaling Pathways during Aging—A Boolean Network Approach. Biology, 6(4), 46. https://doi.org/10.3390/biology6040046






