Evolutionary Stability of Small Molecular Regulatory Networks That Exhibit Near-Perfect Adaptation
Abstract
Simple Summary
Abstract
1. Introduction
- Integral Feedback Control. A feedback variable, Q(t), changes at a rate proportional to the difference between the adaptive response variable, R(t), and its desired steady-state value, Rss: ; i.e., . Q(t), which measures the deviation of the system from its setpoint, Rss, then feeds back on the network to cancel the disturbance. If the system comes to a steady state where Q(t) and R(t) are no longer changing in time, then , i.e., perfect adaptation. For examples, see Mechanisms 1, 2, 9, 10, 11 and 14 in the Catalogue. In all these cases, the degradation of Q is independent of the concentration of Q, which could be the result of enzymatic degradation, , in the limit KM → 0, as assumed by Barkai and Leibler for the enzyme CheR. Mechanism 14 in the Catalogue achieves perfect adaptation by assuming that the feedback variable is synthesized autocatalytically, , so that, at steady-state, regardless of the incoming signal.
- Balancing Controls. The signal S upregulates two proteins, P and Q, that have opposite effects on the response variable, R. The activation of R by P is canceled by the inhibition of R by Q. For examples, see Mechanisms 3, 4, 6, 7, 12, and 15 in the Catalogue. Mechanism 5 combines balancing and integral feedback controls.
- Antithetical Feedback. Two components, either P and R or P and Q, bind to make a complex that is removed from the system, thereby canceling the upregulation of R by S. See Mechanisms 8 and 13 in the Catalogue.
2. Methods: The Mathematical Model
3. Results
3.1. Classifying ‘Minimal’ Topologies That Might Exhibit Near-Perfect Adaption
3.2. Initial Exploration of Topology Space
3.3. Close Examination of IFFL and NFLB Topologies
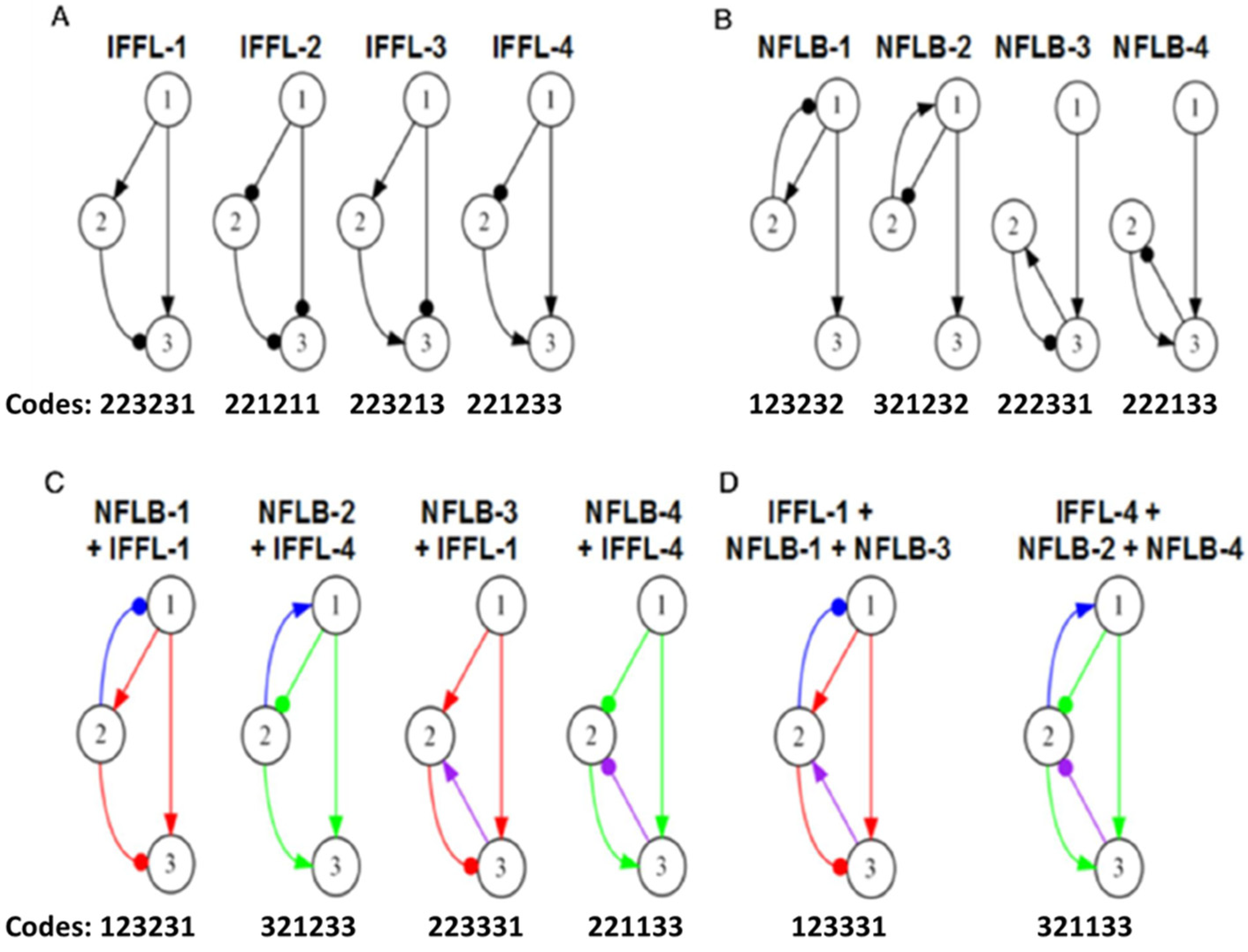
3.3.1. IFFL Topologies
3.3.2. NFLB Topologies
3.3.3. Evolution of IFFL-1 and IFFL-4 Topologies under Macro-Mutations
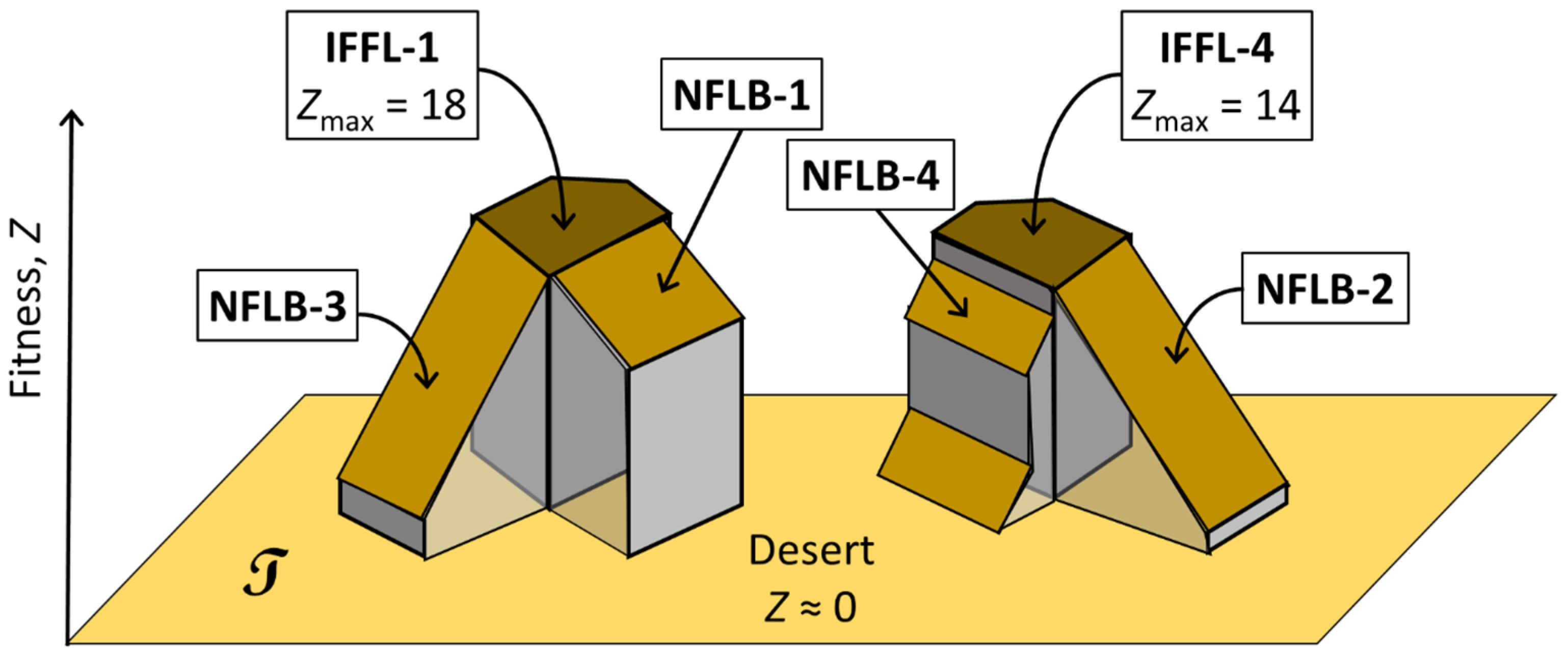
3.3.4. Why Are IFFL-1 Topologies Evolutionarily Stable?
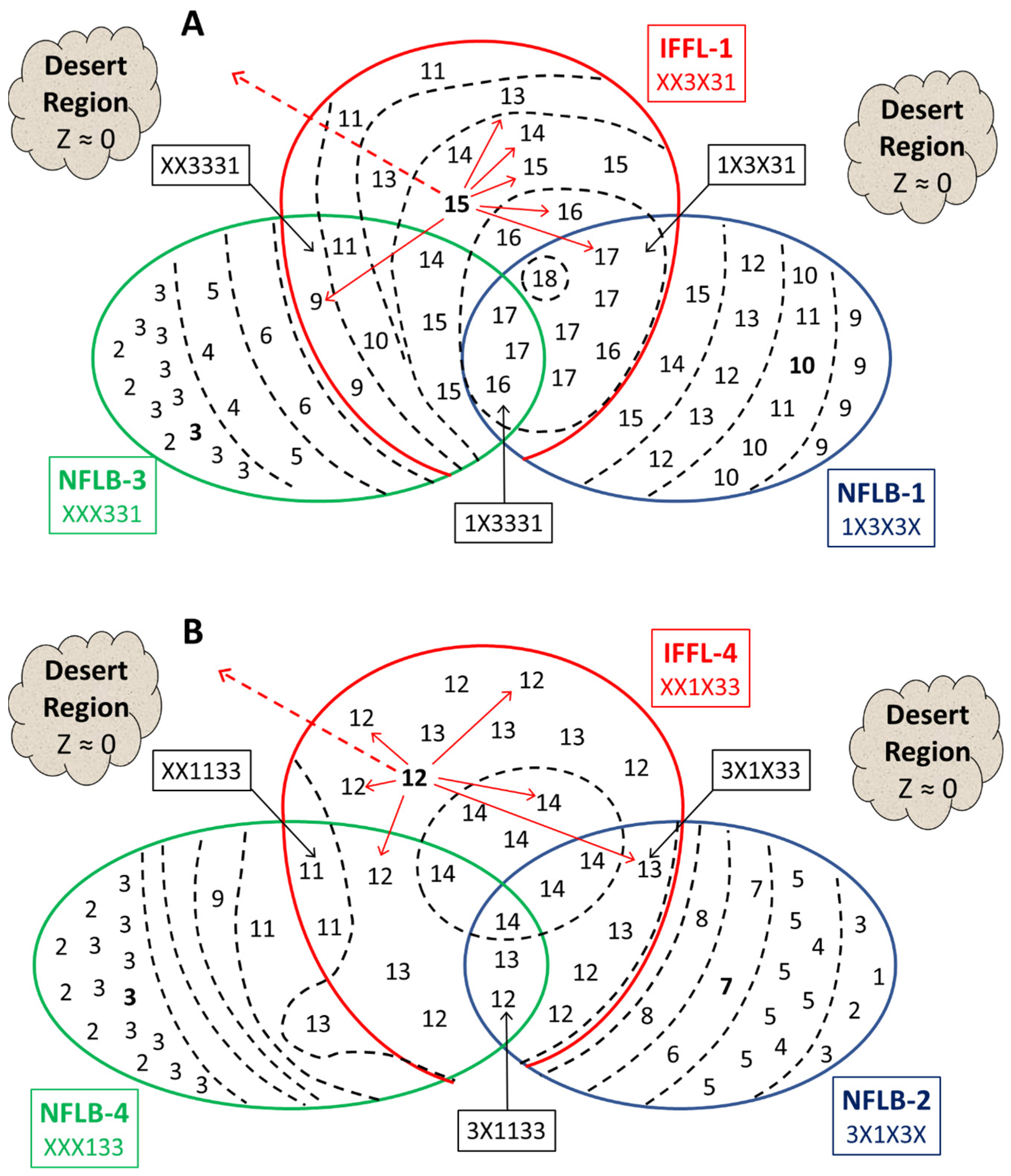
3.3.5. Examining the Interactions of IFFL and NFLB Topologies
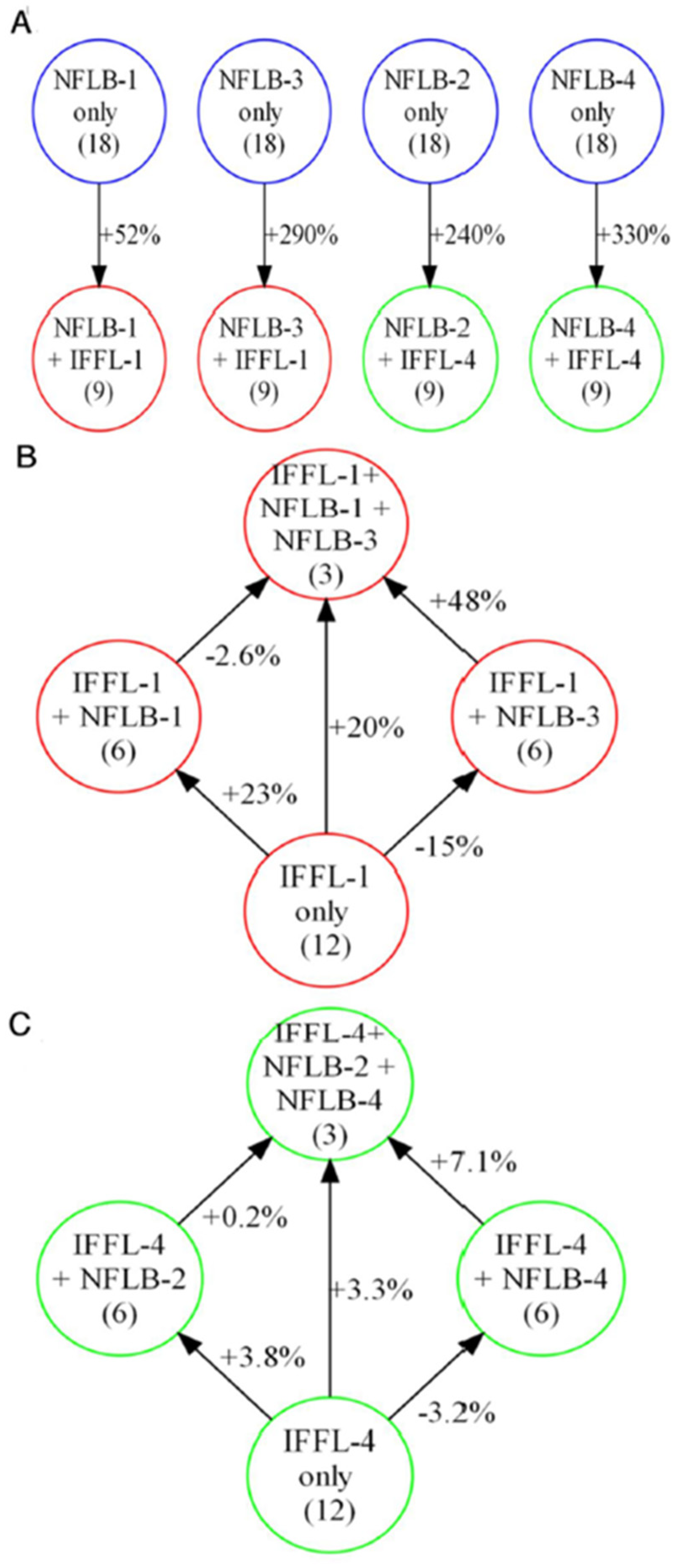
3.3.6. Interaction Coefficients Measure the Relative Contributions of NFLB and IFFL Motifs to High-Scoring Combination Topologies
4. Discussion
4.1. Summary of Results
4.2. Comparison with the Results of Ma et al. and Shi et al.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Methodological Details
Appendix A.1. Parameter Ranges
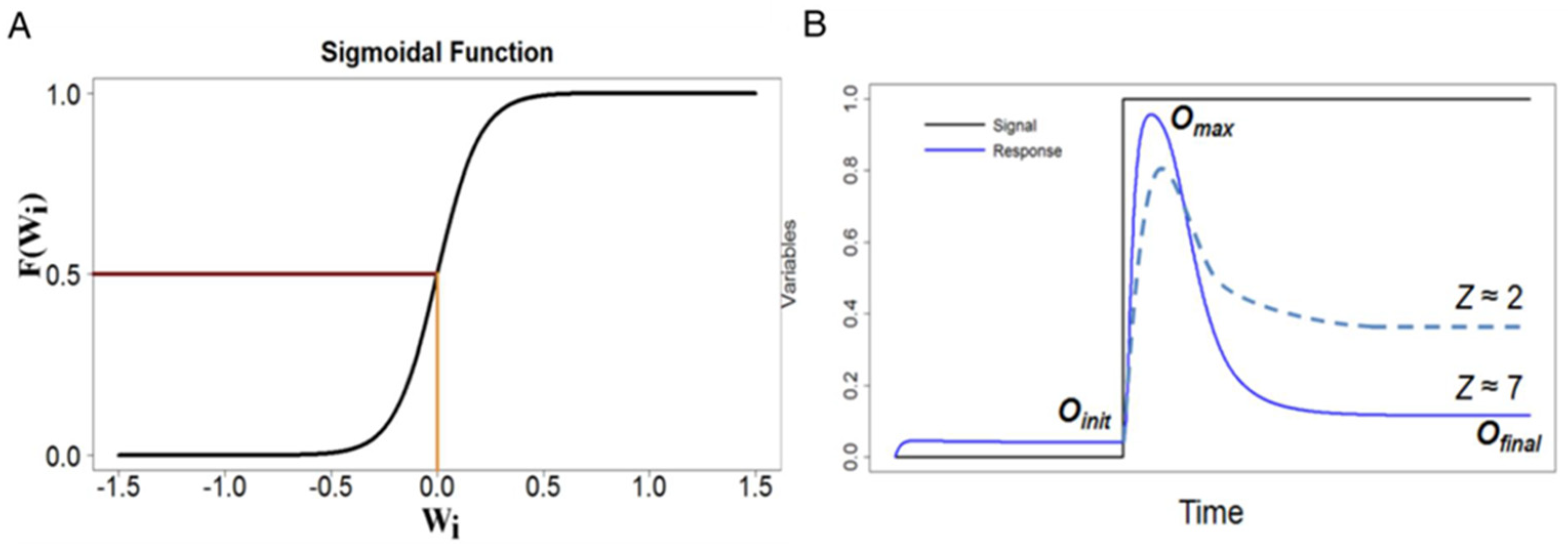
Appendix A.2. Scoring a Parameter Set
Appendix A.3. Evolutionary Algorithm
Appendix A.3.1. Generating Progeny Parameter Sets by Mutations
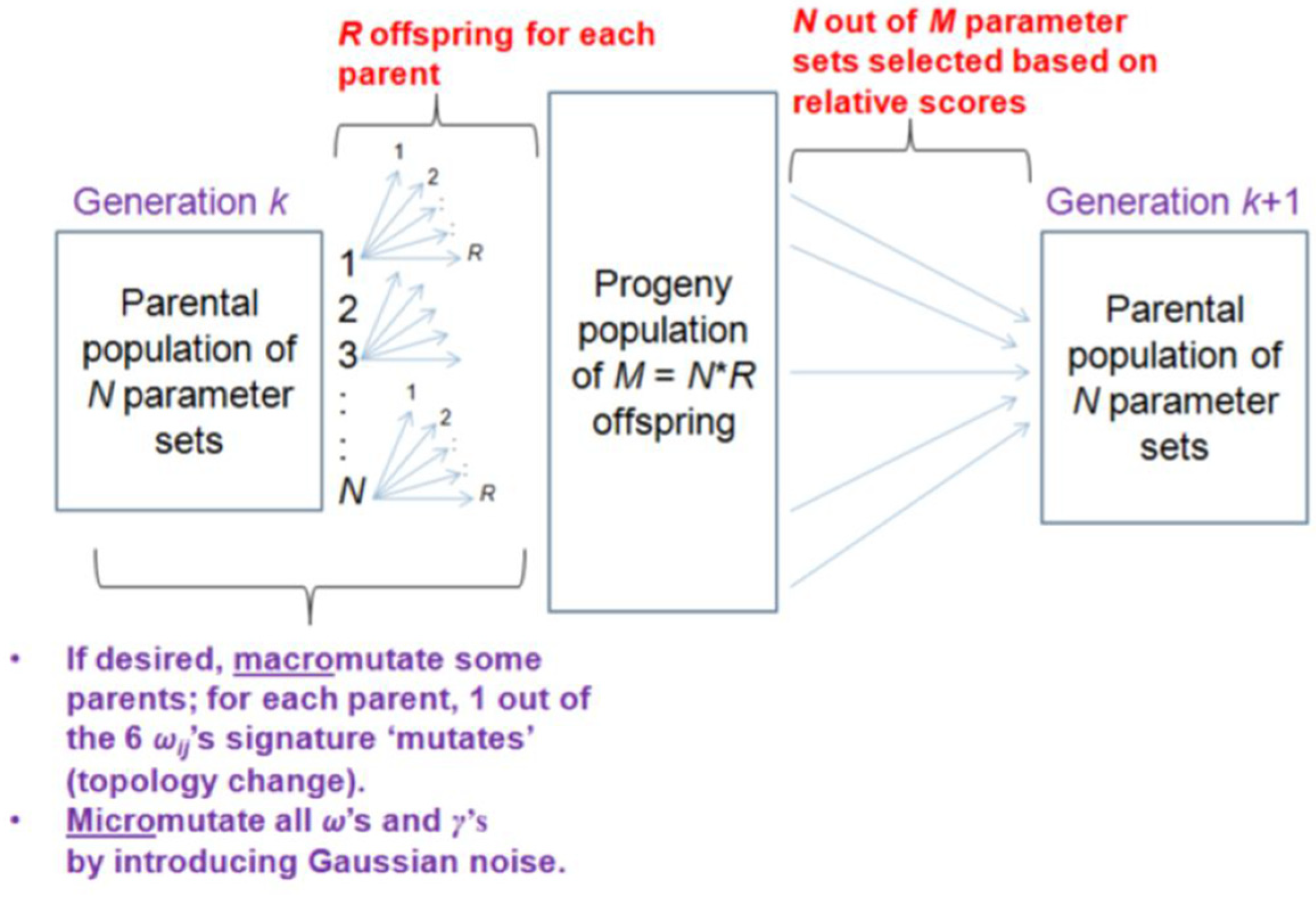
Appendix A.3.2. Selection Criterion
Appendix B. Comparison of Our Model to Ma et al. [14]
Appendix C. Fine-Tuning of Parameters
References
- Berg, H.C.; Brown, D.A. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 1972, 239, 500–504. [Google Scholar] [CrossRef] [PubMed]
- Macnab, R.M.; Koshland, D.E., Jr. The gradient-sensing mechanism in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 1972, 69, 2509–2512. [Google Scholar] [CrossRef] [PubMed]
- Takeda, K.; Shao, D.; Adler, M.; Charest, P.G.; Loomis, W.F.; Levine, H.; Groisman, A.; Rappel, W.J.; Firtel, R.A. Incoherent feedforward control governs adaptation of activated Ras in a eukaryotic chemotaxis pathway. Sci. Signal 2012, 5, ra2. [Google Scholar] [CrossRef] [PubMed]
- Dinauer, M.C.; Steck, T.L.; Devreotes, P.N. Cyclic 3′,5′-AMP relay in Dictyostelium discoideum V. Adaptation of the cAMP signaling response during cAMP stimulation. J. Cell Biol. 1980, 86, 554–561. [Google Scholar] [CrossRef] [PubMed]
- Muzzey, D.; Gomez-Uribe, C.A.; Mettetal, J.T.; van Oudenaarden, A. A systems-level analysis of perfect adaptation in yeast osmoregulation. Cell 2009, 138, 160–171. [Google Scholar] [CrossRef]
- Knox, B.E.; Devreotes, P.N.; Goldbeter, A.; Segel, L.A. A molecular mechanism for sensory adaptation based on ligand-induced receptor modification. Proc. Natl. Acad. Sci. USA 1986, 83, 2345–2349. [Google Scholar] [CrossRef]
- Hauri, D.C.; Ross, J. A model of excitation and adaptation in bacterial chemotaxis. Biophys. J. 1995, 68, 708–722. [Google Scholar] [CrossRef]
- Barkai, N.; Leibler, S. Robustness in simple biochemical networks. Nature 1997, 387, 913–917. [Google Scholar] [CrossRef]
- Yi, T.M.; Huang, Y.; Simon, M.I.; Doyle, J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA 2000, 97, 4649–4653. [Google Scholar] [CrossRef]
- Levchenko, A.; Iglesias, P.A. Models of eukaryotic gradient sensing: Application to chemotaxis of amoebae and neutrophils. Biophys. J. 2002, 82, 50–63. [Google Scholar] [CrossRef]
- Tyson, J.J.; Chen, K.C.; Novak, B. Sniffers, buzzers, toggles and blinkers: Dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003, 15, 221–231. [Google Scholar] [CrossRef] [PubMed]
- Mello, B.A.; Tu, Y. Quantitative modeling of sensitivity in bacterial chemotaxis: The role of coupling among different chemoreceptor species. Proc. Natl. Acad. Sci. USA 2003, 100, 8223–8228. [Google Scholar] [CrossRef] [PubMed]
- Francois, P.; Siggia, E.D. A case study of evolutionary computation of biochemical adaptation. Phys. Biol. 2008, 5, 026009. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Trusina, A.; El-Samad, H.; Lim, W.A.; Tang, C. Defining network topologies that can achieve biochemical adaptation. Cell 2009, 138, 760–773. [Google Scholar] [CrossRef]
- Ni, X.Y.; Drengstig, T.; Ruoff, P. The control of the controller: Molecular mechanisms for robust perfect adaptation and temperature compensation. Biophys. J. 2009, 97, 1244–1253. [Google Scholar] [CrossRef] [PubMed]
- Briat, C.; Gupta, A.; Khammash, M. Antithetic Integral Feedback Ensures Robust Perfect Adaptation in Noisy Biomolecular Networks. Cell Syst. 2016, 2, 15–26. [Google Scholar] [CrossRef]
- Shi, W.; Ma, W.; Xiong, L.; Zhang, M.; Tang, C. Adaptation with transcriptional regulation. Sci. Rep. 2017, 7, 42648. [Google Scholar] [CrossRef]
- Behar, M.; Hao, N.; Dohlman, H.G.; Elston, T.C. Mathematical and computational analysis of adaptation via feedback inhibition in signal transduction pathways. Biophys. J. 2007, 93, 806–821. [Google Scholar] [CrossRef]
- Drengstig, T.; Ueda, H.R.; Ruoff, P. Predicting perfect adaptation motifs in reaction kinetic networks. J. Phys. Chem. B 2008, 112, 16752–16758. [Google Scholar] [CrossRef]
- Hao, N.; Behar, M.; Elston, T.C.; Dohlman, H.G. Systems biology analysis of G protein and MAP kinase signaling in yeast. Oncogene 2007, 26, 3254–3266. [Google Scholar] [CrossRef]
- Xiong, L.; Shi, W.; Tang, C. Adaptation through proportion. Phys. Biol. 2016, 13, 046007. [Google Scholar] [CrossRef] [PubMed]
- Ferrell, J.E., Jr. Perfect and Near-Perfect Adaptation in Cell Signaling. Cell Syst. 2016, 2, 62–67. [Google Scholar] [CrossRef]
- Khammash, M.H. Perfect adaptation in biology. Cell Syst. 2021, 12, 509–521. [Google Scholar] [CrossRef]
- Wilson, H.R.; Cowan, J.D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Mjolsness, E.; Sharp, D.H.; Reinitz, J. A connectionist model of development. J. Theor. Biol. 1991, 152, 429–453. [Google Scholar] [CrossRef] [PubMed]
- Tyson, J.J.; Novak, B. Functional motifs in biochemical reaction networks. Annu. Rev. Phys. Chem. 2010, 61, 219–240. [Google Scholar] [CrossRef]
- Molinelli, E.J.; Korkut, A.; Wang, W.; Miller, M.L.; Gauthier, N.P.; Jing, X.; Kaushik, P.; He, Q.; Mills, G.; Solit, D.B.; et al. Perturbation biology: Inferring signaling networks in cellular systems. PLoS Comput. Biol. 2013, 9, e1003290. [Google Scholar] [CrossRef]
- Laomettachit, T.; Chen, K.C.; Baumann, W.T.; Tyson, J.J. A Model of Yeast Cell-Cycle Regulation Based on a Standard Component Modeling Strategy for Protein Regulatory Networks. PLoS ONE 2016, 11, e0153738. [Google Scholar] [CrossRef]
- Glass, L.; Kauffman, S.A. The logical analysis of continuous, non-linear biochemical control networks. J. Theor. Biol. 1973, 39, 103–129. [Google Scholar] [CrossRef]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 2007, 8, 450–461. [Google Scholar] [CrossRef]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; p. 301. [Google Scholar]
- Ma, H.W.; Kumar, B.; Ditges, U.; Gunzer, F.; Buer, J.; Zeng, A.P. An extended transcriptional regulatory network of Escherichia coli and analysis of its hierarchical structure and network motifs. Nucleic Acids Res. 2004, 32, 6643–6649. [Google Scholar] [CrossRef]
- Shen-Orr, S.S.; Milo, R.; Mangan, S.; Alon, U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 2002, 31, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Mangan, S.; Alon, U. Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. USA 2003, 100, 11980–11985. [Google Scholar] [CrossRef] [PubMed]
- Mangan, S.; Itzkovitz, S.; Zaslaver, A.; Alon, U. The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli. J. Mol. Biol. 2006, 356, 1073–1081. [Google Scholar] [CrossRef]
- Basu, S.; Mehreja, R.; Thiberge, S.; Chen, M.T.; Weiss, R. Spatiotemporal control of gene expression with pulse-generating networks. Proc. Natl. Acad. Sci. USA 2004, 101, 6355–6360. [Google Scholar] [CrossRef] [PubMed]
- Csikasz-Nagy, A.; Kapuy, O.; Toth, A.; Pal, C.; Jensen, L.J.; Uhlmann, F.; Tyson, J.J.; Novak, B. Cell cycle regulation by feed-forward loops coupling transcription and phosphorylation. Mol. Syst. Biol. 2009, 5, 236. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, K.A.; Wentzel, E.A.; Zeller, K.I.; Dang, C.V.; Mendell, J.T. c-Myc-regulated microRNAs modulate E2F1 expression. Nature 2005, 435, 839–843. [Google Scholar] [CrossRef]
- Vera, G.; Jansen, R.C.; Suppi, R.L. R/parallel—Speeding up bioinformatics analysis with R. BMC Bioinform. 2008, 9, 390. [Google Scholar] [CrossRef]
- Yao, X.; Heidebrecht, B.L.; Chen, J.; Tyson, J.J. Mathematical analysis of robustness of oscillations in models of the mammalian circadian clock. PLoS Comput. Biol. 2022, 18, e1008340. [Google Scholar] [CrossRef]



| Parameter | Role | Range |
|---|---|---|
| ωi0 | Offsets | [−2, 2] |
| ωij | Interaction Coefficients | [−1, −0.1] 0 [0.1, 1] |
| γ1, γ2 | Rate constants | [0.1, 3] |
| γ3−1 | Time scale | 1 |
| σ | Sigmoidicity | 10 |
| Code | < Z > | Code | < Z > | Code | < Z > |
|---|---|---|---|---|---|
| 123331 (1,3) | 14.18 | 113331 (1,3) | 10.40 | 113231 (1) | 7.81 |
| 133231 (1) | 13.84 | 233231 | 10.24 | 233331 (3) | 7.40 |
| 123231 (1) | 13.46 | 121333 | 10.07 | 121233 | 7.26 |
| 133331 (1,3) | 13.35 | 333331 (3) | 9.19 | 213331 (3) | 7.04 |
| 233131 | 13.31 | 333231 | 9.12 | 321233 (2) | 6.83 |
| 321133 (2) | 12.10 | 131233 | 9.06 | 323231 | 6.50 |
| 223131 | 11.42 | 223331 (3) | 8.79 | 221333 | 6.41 |
| 123131 (1) | 11.14 | 133131 (1) | 8.78 | 333131 | 6.07 |
| 131133 (4) | 11.11 | 223231 | 8.39 | ||
| 111233 | 10.50 | 113131 (1) | 8.08 |
| (A) IFFL-1 Topologies | (B) IFFL-4 Topologies | ||||
|---|---|---|---|---|---|
| Code | < Z > | FPT | Code | < Z > | FPT |
| 113131 | 16.87 | 118 | 111133 | 12.48 | 15 |
| 113231 | 16.26 | 27 | 111233 | 11.45 | 70 |
| 113331 | 16.10 | 20 | 111333 | 14.04 | 25 |
| 123131 | 16.92 | 17 | 121133 | 11.96 | 31 |
| 123231 | 17.15 | 28 | 121233 | 12.02 | 100 |
| 123331 | 16.76 | 16 | 121333 | 13.47 | 26 |
| 133131 | 17.68 | 11 | 131133 | 12.57 | 33 |
| 133231 | 17.03 | 24 | 131233 | 13.64 | 23 |
| 133331 | 16.77 | 22 | 131333 | 13.55 | 42 |
| 213131 | 11.43 | 34 | 211133 | 11.41 | 18 |
| 213231 | 13.19 | 49 | 211233 | 11.89 | 26 |
| 213331 | 10.93 | 38 | 211333 | 13.25 | 12 |
| 223131 | 15.18 | 7 | 221133 | 13.67 | 66 |
| 223231 | 15.25 | 26 | 221233 | 11.96 | 30 |
| 223331 | 9.34 | 17 | 221333 | 12.15 | 17 |
| 233131 | 13.88 | 53 | 231133 | 11.27 | 53 |
| 233231 | 14.38 | 69 | 231233 | 12.19 | 32 |
| 233331 | 14.99 | 10 | 231333 | 12.61 | 80 |
| 313131 | 13.14 | 28 | 311133 | 13.64 | 24 |
| 313231 | 14.73 | 6 | 311233 | 12.73 | 31 |
| 313331 | 10.33 | 134 | 311333 | 11.81 | 32 |
| 323131 | 10.80 | 48 | 321133 | 12.94 | 10 |
| 323231 | 15.62 | 5 | 321233 | 12.90 | 31 |
| 323331 | 14.91 | 25 | 321333 | 12.53 | 17 |
| 333131 | 15.49 | 21 | 331133 | 12.55 | 22 |
| 333231 | 14.40 | 8 | 331233 | 14.36 | 16 |
| 333331 | 9.19 | 41 | 331333 | 14.34 | 41 |
| (A) NFLB-1 | (B) NFLB-2 | (C) NFLB-3 | (D) NFLB-4 | ||||
|---|---|---|---|---|---|---|---|
| Code | < Z > | Code | < Z > | Code | < Z > | Code | < Z > |
| 133131 | 17.68 | 331233 | 14.36 | 123331 | 16.77 | 221133 | 13.67 |
| 123231 | 17.15 | 331333 | 14.34 | 133331 | 16.69 | 311133 | 13.64 |
| 133231 | 17.03 | 311133 | 13.64 | 113331 | 16.11 | 133133 | 13.20 |
| 123131 | 16.92 | 321133 | 12.94 | 233331 | 14.99 | 321133 | 12.94 |
| 113131 | 16.87 | 321233 | 12.90 | 323331 | 14.91 | 131133 | 12.57 |
| 123331 | 16.76 | 331133 | 12.55 | 213331 | 10.93 | 331133 | 12.55 |
| 133331 | 16.77 | 321333 | 12.53 | 313331 | 10.33 | 111133 | 12.48 |
| 113231 | 16.26 | 311333 | 11.81 | 223331 | 9.34 | 121133 | 11.96 |
| 113331 | 16.10 | 311233 | 10.40 | 333331 | 9.19 | 211133 | 11.41 |
| 133132 | 15.40 | 331332 | 8.20 | 122331 | 5.67 | 231133 | 11.27 |
| 133232 | 15.00 | 331132 | 7.58 | 132331 | 5.67 | 123133 | 10.46 |
| 133332 | 14.29 | 321132 | 7.39 | 112331 | 5.05 | 113133 | 8.63 |
| 133133 | 13.20 | 321232 | 7.10 | 321331 | 4.55 | 322133 | 3.25 |
| 133233 | 12.48 | 311132 | 6.23 | 121331 | 4.19 | 332133 | 3.22 |
| 123332 | 12.29 | 321231 | 5.09 | 131331 | 3.91 | 312133 | 2.90 |
| 123132 | 12.06 | 331232 | 4.78 | 212331 | 3.39 | 112133 | 2.74 |
| 133333 | 11.99 | 331231 | 4.76 | 322331 | 3.36 | 122133 | 2.68 |
| 123333 | 10.71 | 311232 | 4.74 | 312331 | 3.35 | 222133 | 2.64 |
| 113332 | 10.69 | 331131 | 4.73 | 222331 | 3.13 | 212133 | 2.64 |
| 123233 | 10.55 | 311231 | 4.55 | 332331 | 3.11 | 323133 | 2.63 |
| 123133 | 10.46 | 321331 | 4.55 | 232331 | 2.96 | 313133 | 2.60 |
| 113232 | 10.32 | 321332 | 4.42 | 311331 | 2.80 | 132133 | 2.59 |
| 123232 | 9.80 | 311332 | 4.30 | 331331 | 2.80 | 233133 | 2.43 |
| 113132 | 9.35 | 331331 | 2.80 | 231331 | 2.77 | 223133 | 2.27 |
| 113333 | 8.97 | 311331 | 2.79 | 221331 | 2.49 | 213133 | 2.24 |
| 113233 | 8.73 | 311131 | 1.64 | 211331 | 2.40 | 232133 | 2.12 |
| 113133 | 8.63 | 321131 | 1.33 | 111331 | 2.13 | 333133 | 1.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singhania, R.; Tyson, J.J. Evolutionary Stability of Small Molecular Regulatory Networks That Exhibit Near-Perfect Adaptation. Biology 2023, 12, 841. https://doi.org/10.3390/biology12060841
Singhania R, Tyson JJ. Evolutionary Stability of Small Molecular Regulatory Networks That Exhibit Near-Perfect Adaptation. Biology. 2023; 12(6):841. https://doi.org/10.3390/biology12060841
Chicago/Turabian StyleSinghania, Rajat, and John J. Tyson. 2023. "Evolutionary Stability of Small Molecular Regulatory Networks That Exhibit Near-Perfect Adaptation" Biology 12, no. 6: 841. https://doi.org/10.3390/biology12060841
APA StyleSinghania, R., & Tyson, J. J. (2023). Evolutionary Stability of Small Molecular Regulatory Networks That Exhibit Near-Perfect Adaptation. Biology, 12(6), 841. https://doi.org/10.3390/biology12060841








