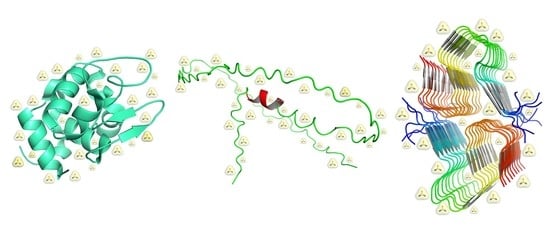
The Action of Chemical Denaturants: From Globular to Intrinsically Disordered Proteins
Abstract
Simple Summary
Abstract
1. Introduction
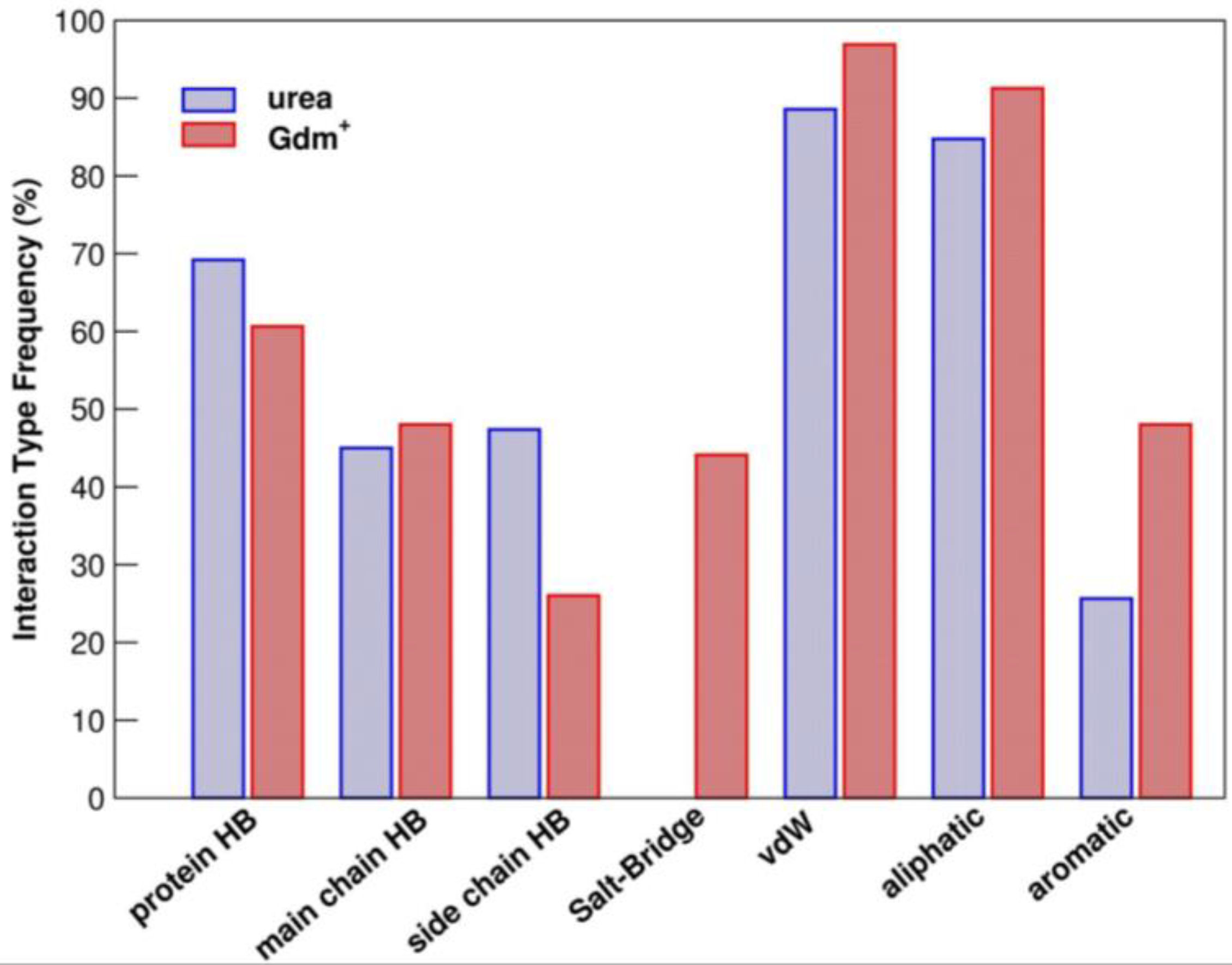
2. Molecular Mechanism(s) of Chemical Denaturation of Globular Proteins
3. Denatured and Native States in the Polymer Physics Perspective
4. Intrinsically Disordered Proteins: Conformational Preferences in Different Contexts
Effects of Chemical Denaturants on IDPs
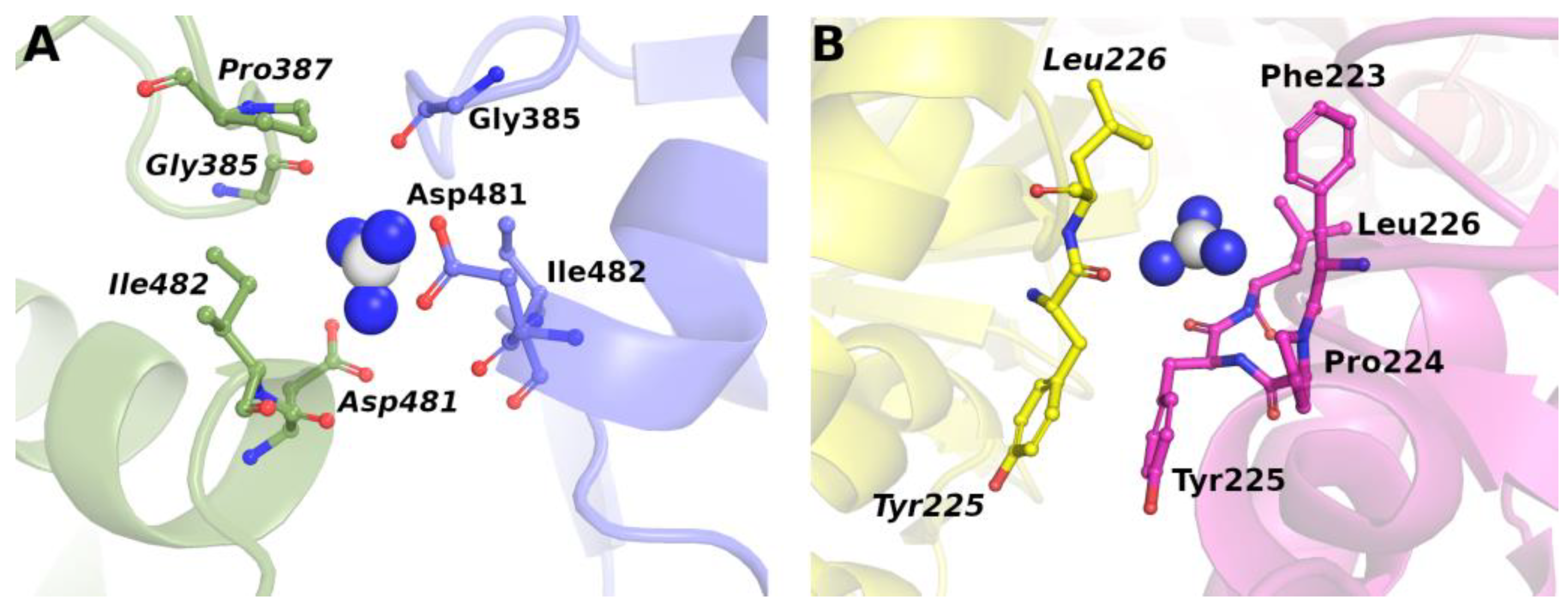
5. Effects of Chemical Denaturants on Amyloid-Like Aggregates
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tompa, P. Intrinsically Unstructured Proteins Evolve by Repeat Expansion. BioEssays 2003, 25, 847–855. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Intrinsically Disordered Proteins and Their Environment: Effects of Strong Denaturants, Temperature, PH, Counter Ions, Membranes, Binding Partners, Osmolytes, and Macromolecular Crowding. Protein J. 2009, 28, 305–325. [Google Scholar] [CrossRef]
- Sawaya, M.R.; Hughes, M.P.; Rodriguez, J.A.; Riek, R.; Eisenberg, D.S. The Expanding Amyloid Family: Structure, Stability, Function, and Pathogenesis. Cell 2021, 184, 4857–4873. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P. Intrinsically Unstructured Proteins. Trends Biochem. Sci. 2002, 27, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Dunker, A.K.; Babu, M.M.; Barbar, E.; Blackledge, M.; Bondos, S.E.; Dosztányi, Z.; Dyson, H.J.; Forman-Kay, J.; Fuxreiter, M.; Gsponer, J.; et al. What’s in a Name? Why These Proteins Are Intrinsically Disordered: Why These Proteins Are Intrinsically Disordered. Intrinsically Disord. Proteins 2013, 1, e24157. [Google Scholar] [CrossRef] [PubMed]
- Quaglia, F.; Mészáros, B.; Salladini, E.; Hatos, A.; Pancsa, R.; Chemes, L.B.; Pajkos, M.; Lazar, T.; Peña-Díaz, S.; Santos, J.; et al. DisProt in 2022: Improved Quality and Accessibility of Protein Intrinsic Disorder Annotation. Nucleic Acids Res. 2022, 50, D480–D487. [Google Scholar] [CrossRef]
- Otzen, D.; Riek, R. Functional Amyloids. Cold Spring Harb. Perspect. Biol. 2019, 11, a033860. [Google Scholar] [CrossRef]
- Bhatia, S.; Udgaonkar, J.B. Heterogeneity in Protein Folding and Unfolding Reactions. Chem. Rev. 2022, 122, 8911–8935. [Google Scholar] [CrossRef]
- Dill, K.A.; MacCallum, J.L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef]
- Gianni, S.; Dogan, J.; Jemth, P. Coupled Binding and Folding of Intrinsically Disordered Proteins: What Can We Learn from Kinetics? Curr. Opin. Struct. Biol. 2016, 36, 18–24. [Google Scholar] [CrossRef]
- Chiti, F.; Dobson, C.M. Protein Misfolding, Amyloid Formation, and Human Disease: A Summary of Progress Over the Last Decade. Annu. Rev. Biochem. 2017, 86, 27–68. [Google Scholar] [CrossRef] [PubMed]
- Lazar, T.; Martínez-Pérez, E.; Quaglia, F.; Hatos, A.; Chemes, L.B.; Iserte, J.A.; Méndez, N.A.; Garrone, N.A.; Saldaño, T.E.; Marchetti, J.; et al. PED in 2021: A Major Update of the Protein Ensemble Database for Intrinsically Disordered Proteins. Nucleic Acids Res. 2021, 49, D404–D411. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, M.; Wang, Y.; Ma, R.; Guo, C.; Feng, L.; Wu, J.; Yao, H.; Lin, D. Structural Basis for the Complete Resistance of the Human Prion Protein Mutant G127V to Prion Disease. Sci. Rep. 2018, 8, 13211. [Google Scholar] [CrossRef] [PubMed]
- Makhatadze, G.I.; Privalov, P.L. Energetics of Protein Structure. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1995; Volume 47, pp. 307–425. ISBN 978-0-12-034247-1. [Google Scholar]
- Robertson, A.D.; Murphy, K.P. Protein Structure and the Energetics of Protein Stability. Chem. Rev. 1997, 97, 1251–1268. [Google Scholar] [CrossRef] [PubMed]
- Rees, D.C.; Robertson, A.D. Some Thermodynamic Implications for the Thermostability of Proteins. Protein Sci. 2001, 10, 1187–1194. [Google Scholar] [CrossRef] [PubMed]
- Sawle, L.; Ghosh, K. How Do Thermophilic Proteins and Proteomes Withstand High Temperature? Biophys. J. 2011, 101, 217–227. [Google Scholar] [CrossRef] [PubMed]
- Pauling, L. The Nature of the Chemical Bond, 3rd ed.; The Cornell University Press: Ithaca, NY, USA, 1960; pp. 10–13. [Google Scholar]
- Shortle, D. The Denatured State (the Other Half of the Folding Equation) and Its Role in Protein Stability. FASEB J. 1996, 10, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Kawahara, K.; Tanford, C. Viscosity and Density of Aqueous Solutions of Urea and Guanidine Hydrochloride. J. Biol. Chem. 1966, 241, 3228–3232. [Google Scholar] [CrossRef]
- Kumar, A. Aqueous Guanidinium Salts: Part I. Densities, Ultrasonic Velocities, and Apparent Molar Properties. J. Solut. Chem. 2001, 30, 281–290. [Google Scholar] [CrossRef]
- Halonen, S.; Kangas, T.; Haataja, M.; Lassi, U. Urea-Water-Solution Properties: Density, Viscosity, and Surface Tension in an Under-Saturated Solution. Emiss. Control Sci. Technol. 2017, 3, 161–170. [Google Scholar] [CrossRef]
- Breslow, R.; Guo, T. Surface Tension Measurements Show That Chaotropic Salting-in Denaturants Are Not Just Water-Structure Breakers. Proc. Natl. Acad. Sci. USA 1990, 87, 167–169. [Google Scholar] [CrossRef] [PubMed]
- Soper, A.K.; Castner, E.W.; Luzar, A. Impact of Urea on Water Structure: A Clue to Its Properties as a Denaturant? Biophys. Chem. 2003, 105, 649–666. [Google Scholar] [CrossRef] [PubMed]
- Mason, P.E.; Neilson, G.W.; Enderby, J.E.; Saboungi, M.-L.; Dempsey, C.E.; MacKerell, A.D.; Brady, J.W. The Structure of Aqueous Guanidinium Chloride Solutions. J. Am. Chem. Soc. 2004, 126, 11462–11470. [Google Scholar] [CrossRef]
- Graziano, G. Contrasting the Denaturing Effect of Guanidinium Chloride with the Stabilizing Effect of Guanidinium Sulfate. Phys. Chem. Chem. Phys. 2011, 13, 12008. [Google Scholar] [CrossRef] [PubMed]
- Graziano, G. How Does Trimethylamine N-Oxide Counteract the Denaturing Activity of Urea? Phys. Chem. Chem. Phys. 2011, 13, 17689. [Google Scholar] [CrossRef] [PubMed]
- Graziano, G. On the Solubility of Aliphatic Hydrocarbons in 7 M Aqueous Urea. J. Phys. Chem. B 2001, 105, 2632–2637. [Google Scholar] [CrossRef]
- Trzesniak, D.; van der Vegt, N.F.A.; van Gunsteren, W.F. Computer Simulation Studies on the Solvation of Aliphatic Hydrocarbons in 6.9 M Aqueous Urea Solution. Phys. Chem. Chem. Phys. 2004, 6, 697. [Google Scholar] [CrossRef]
- Weerasinghe, S.; Smith, P.E. A Kirkwood−Buff Derived Force Field for Mixtures of Urea and Water. J. Phys. Chem. B 2003, 107, 3891–3898. [Google Scholar] [CrossRef]
- Weerasinghe, S.; Smith, P.E. A Kirkwood-Buff Derived Force Field for the Simulation of Aqueous Guanidinium Chloride Solutions. J. Chem. Phys. 2004, 121, 2180–2186. [Google Scholar] [CrossRef]
- Zangi, R.; Zhou, R.; Berne, B.J. Urea’s Action on Hydrophobic Interactions. J. Am. Chem. Soc. 2009, 131, 1535–1541. [Google Scholar] [CrossRef]
- Zheng, W.; Borgia, A.; Borgia, M.B.; Schuler, B.; Best, R.B. Empirical Optimization of Interactions between Proteins and Chemical Denaturants in Molecular Simulations. J. Chem. Theory Comput. 2015, 11, 5543–5553. [Google Scholar] [CrossRef] [PubMed]
- Cozzolino, S.; Balasco, N.; Vigorita, M.; Ruggiero, A.; Smaldone, G.; Del Vecchio, P.; Vitagliano, L.; Graziano, G. Guanidinium Binding to Proteins: The Intriguing Effects on the D1 and D2 Domains of Thermotoga Maritima Arginine Binding Protein and a Comprehensive Analysis of the Protein Data Bank. Int. J. Biol. Macromol. 2020, 163, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Paladino, A.; Balasco, N.; Graziano, G.; Vitagliano, L. A Protein Data Bank Survey of Multimodal Binding of Thiocyanate to Proteins: Evidence for Thiocyanate Promiscuity. Int. J. Biol. Macromol. 2022, 208, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Paladino, A.; Balasco, N.; Vitagliano, L.; Graziano, G. A Structure-Based Mechanism for the Denaturing Action of Urea, Guanidinium Ion and Thiocyanate Ion. Biology 2022, 11, 1764. [Google Scholar] [CrossRef]
- Makhatadze, G.I.; Privalov, P.L. Protein Interactions with Urea and Guanidinium Chloride. J. Mol. Biol. 1992, 226, 491–505. [Google Scholar] [CrossRef]
- Schellman, J.A. The Thermodynamics of Solvent Exchange. Biopolymers 1994, 34, 1015–1026. [Google Scholar] [CrossRef]
- Schellman, J.A. Protein Stability in Mixed Solvents: A Balance of Contact Interaction and Excluded Volume. Biophys. J. 2003, 85, 108–125. [Google Scholar] [CrossRef]
- Rembert, K.B.; Paterová, J.; Heyda, J.; Hilty, C.; Jungwirth, P.; Cremer, P.S. Molecular Mechanisms of Ion-Specific Effects on Proteins. J. Am. Chem. Soc. 2012, 134, 10039–10046. [Google Scholar] [CrossRef]
- Courtenay, E.S.; Capp, M.W.; Record, M.T. Thermodynamics of Interactions of Urea and Guanidinium Salts with Protein Surface: Relationship between Solute Effects on Protein Processes and Changes in Water-Accessible Surface Area. Protein Sci. 2009, 10, 2485–2497. [Google Scholar] [CrossRef]
- Record, M.T.; Guinn, E.; Pegram, L.; Capp, M. Introductory Lecture: Interpreting and Predicting Hofmeister Salt Ion and Solute Effects on Biopolymer and Model Processes Using the Solute Partitioning Model. Faraday Discuss 2013, 160, 9–44. [Google Scholar] [CrossRef]
- Pegram, L.M.; Record, M.T. Thermodynamic Origin of Hofmeister Ion Effects. J. Phys. Chem. B 2008, 112, 9428–9436. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved Side-Chain Torsion Potentials for the Amber Ff99SB Protein Force Field: Improved Protein Side-Chain Potentials. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. Monte Carlo Simulation of n-butane in Water. Conformational Evidence for the Hydrophobic Effect. J. Chem. Phys. 1982, 77, 5757–5765. [Google Scholar] [CrossRef]
- O’Brien, E.P.; Dima, R.I.; Brooks, B.; Thirumalai, D. Interactions between Hydrophobic and Ionic Solutes in Aqueous Guanidinium Chloride and Urea Solutions: Lessons for Protein Denaturation Mechanism. J. Am. Chem. Soc. 2007, 129, 7346–7353. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, E.P.; Ziv, G.; Haran, G.; Brooks, B.R.; Thirumalai, D. Effects of Denaturants and Osmolytes on Proteins Are Accurately Predicted by the Molecular Transfer Model. Proc. Natl. Acad. Sci. USA 2008, 105, 13403–13408. [Google Scholar] [CrossRef]
- Liu, Z.; Reddy, G.; Thirumalai, D. Theory of the Molecular Transfer Model for Proteins with Applications to the Folding of the Src-SH3 Domain. J. Phys. Chem. B 2012, 116, 6707–6716. [Google Scholar] [CrossRef]
- Liu, Z.; Reddy, G.; Thirumalai, D. Folding PDZ2 Domain Using the Molecular Transfer Model. J. Phys. Chem. B 2016, 120, 8090–8101. [Google Scholar] [CrossRef]
- Klimov, D.K.; Thirumalai, D. Mechanisms and Kinetics of β-Hairpin Formation. Proc. Natl. Acad. Sci. USA 2000, 97, 2544–2549. [Google Scholar] [CrossRef]
- Tanford, C. Protein Denaturation. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1968; Volume 23, pp. 121–282. ISBN 978-0-12-034223-5. [Google Scholar]
- Flory, P.J. Principles of Polymer Chemistry; The Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Chan, H.S.; Dill, K.A. Polymer Principles in Protein Structure and Stability. Annu. Rev. Biophys. Biophys. Chem. 1991, 20, 447–490. [Google Scholar] [CrossRef]
- Clark, P.L.; Plaxco, K.W.; Sosnick, T.R. Water as a Good Solvent for Unfolded Proteins: Folding and Collapse Are Fundamentally Different. J. Mol. Biol. 2020, 432, 2882–2889. [Google Scholar] [CrossRef] [PubMed]
- Graziano, G. On the Mechanism of Cold Denaturation. Phys. Chem. Chem. Phys. 2014, 16, 21755–21767. [Google Scholar] [CrossRef] [PubMed]
- Merlino, A.; Pontillo, N.; Graziano, G. A Driving Force for Polypeptide and Protein Collapse. Phys. Chem. Chem. Phys. 2017, 19, 751–756. [Google Scholar] [CrossRef] [PubMed]
- Graziano, G. Is Water a Good Solvent for the Denatured State of Globular Proteins? Chem. Phys. Lett. 2020, 759, 137949. [Google Scholar] [CrossRef]
- Dima, R.I.; Thirumalai, D. Asymmetry in the Shapes of Folded and Denatured States of Proteins. J. Phys. Chem. B 2004, 108, 6564–6570. [Google Scholar] [CrossRef]
- Holehouse, A.S.; Pappu, R.V. Collapse Transitions of Proteins and the Interplay Among Backbone, Sidechain, and Solvent Interactions. Annu. Rev. Biophys. 2018, 47, 19–39. [Google Scholar] [CrossRef]
- Best, R.B. Emerging Consensus on the Collapse of Unfolded and Intrinsically Disordered Proteins in Water. Curr. Opin. Struct. Biol. 2020, 60, 27–38. [Google Scholar] [CrossRef]
- Borgia, A.; Zheng, W.; Buholzer, K.; Borgia, M.B.; Schüler, A.; Hofmann, H.; Soranno, A.; Nettels, D.; Gast, K.; Grishaev, A.; et al. Consistent View of Polypeptide Chain Expansion in Chemical Denaturants from Multiple Experimental Methods. J. Am. Chem. Soc. 2016, 138, 11714–11726. [Google Scholar] [CrossRef]
- Zheng, W.; Borgia, A.; Buholzer, K.; Grishaev, A.; Schuler, B.; Best, R.B. Probing the Action of Chemical Denaturant on an Intrinsically Disordered Protein by Simulation and Experiment. J. Am. Chem. Soc. 2016, 138, 11702–11713. [Google Scholar] [CrossRef]
- Yu, L.; Brüschweiler, R. Quantitative Prediction of Ensemble Dynamics, Shapes and Contact Propensities of Intrinsically Disordered Proteins. PLoS Comput. Biol. 2022, 18, e1010036. [Google Scholar] [CrossRef]
- Merchant, K.A.; Best, R.B.; Louis, J.M.; Gopich, I.V.; Eaton, W.A. Characterizing the Unfolded States of Proteins Using Single-Molecule FRET Spectroscopy and Molecular Simulations. Proc. Natl. Acad. Sci. USA 2007, 104, 1528–1533. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Zerze, G.H.; Borgia, A.; Mittal, J.; Schuler, B.; Best, R.B. Inferring Properties of Disordered Chains from FRET Transfer Efficiencies. J. Chem. Phys. 2018, 148, 123329. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, I.C. Phase Transition Behavior of the Isolated Polymer Chain. Macromolecules 1979, 12, 980–988. [Google Scholar] [CrossRef]
- Hofmann, H.; Soranno, A.; Borgia, A.; Gast, K.; Nettels, D.; Schuler, B. Polymer Scaling Laws of Unfolded and Intrinsically Disordered Proteins Quantified with Single-Molecule Spectroscopy. Proc. Natl. Acad. Sci. USA 2012, 109, 16155–16160. [Google Scholar] [CrossRef]
- Aznauryan, M.; Delgado, L.; Soranno, A.; Nettels, D.; Huang, J.; Labhardt, A.M.; Grzesiek, S.; Schuler, B. Comprehensive Structural and Dynamical View of an Unfolded Protein from the Combination of Single-Molecule FRET, NMR, and SAXS. Proc. Natl. Acad. Sci. USA 2004, 108, 6564–6570. [Google Scholar] [CrossRef]
- O’Brien, E.P.; Morrison, G.; Brooks, B.R.; Thirumalai, D. How Accurate Are Polymer Models in the Analysis of Förster Resonance Energy Transfer Experiments on Proteins? J. Chem. Phys. 2009, 130, 124903. [Google Scholar] [CrossRef]
- Kohn, J.E.; Millett, I.S.; Jacob, J.; Zagrovic, B.; Dillon, T.M.; Cingel, N.; Dothager, R.S.; Seifert, S.; Thiyagarajan, P.; Sosnick, T.R.; et al. Random-Coil Behavior and the Dimensions of Chemically Unfolded Proteins. Proc. Natl. Acad. Sci. USA 2004, 101, 12491–12496. [Google Scholar] [CrossRef]
- Narayan, A.; Bhattacharjee, K.; Naganathan, A.N. Thermally versus Chemically Denatured Protein States. Biochemistry 2019, 58, 2519–2523. [Google Scholar] [CrossRef]
- Nettels, D.; Müller-Späth, S.; Küster, F.; Hofmann, H.; Haenni, D.; Rüegger, S.; Reymond, L.; Hoffmann, A.; Kubelka, J.; Heinz, B.; et al. Single-Molecule Spectroscopy of the Temperature-Induced Collapse of Unfolded Proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 20740–20745. [Google Scholar] [CrossRef]
- Tompa, P. Intrinsically Disordered Proteins: A 10-Year Recap. Trends Biochem. Sci. 2012, 37, 509–516. [Google Scholar] [CrossRef]
- Turoverov, K.K.; Kuznetsova, I.M.; Fonin, A.V.; Darling, A.L.; Zaslavsky, B.Y.; Uversky, V.N. Stochasticity of Biological Soft Matter: Emerging Concepts in Intrinsically Disordered Proteins and Biological Phase Separation. Trends Biochem. Sci. 2019, 44, 716–728. [Google Scholar] [CrossRef]
- Uversky, V.N. Intrinsically Disordered Proteins and Their “Mysterious” (Meta)Physics. Front. Phys. 2019, 7, 10. [Google Scholar] [CrossRef]
- Forman-Kay, J.D.; Mittag, T. From Sequence and Forces to Structure, Function, and Evolution of Intrinsically Disordered Proteins. Structure 2013, 21, 1492–1499. [Google Scholar] [CrossRef] [PubMed]
- Das, R.K.; Ruff, K.M.; Pappu, R.V. Relating Sequence Encoded Information to Form and Function of Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol. 2015, 32, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, P.; Bhattacharya, S.; Achuthan, S.; Behal, A.; Jolly, M.K.; Kotnala, S.; Mohanty, A.; Rangarajan, G.; Salgia, R.; Uversky, V. Intrinsically Disordered Proteins: Critical Components of the Wetware. Chem. Rev. 2022, 122, 6614–6633. [Google Scholar] [CrossRef] [PubMed]
- Gomes, G.-N.W.; Krzeminski, M.; Namini, A.; Martin, E.W.; Mittag, T.; Head-Gordon, T.; Forman-Kay, J.D.; Gradinaru, C.C. Conformational Ensembles of an Intrinsically Disordered Protein Consistent with NMR, SAXS, and Single-Molecule FRET. J. Am. Chem. Soc. 2020, 142, 15697–15710. [Google Scholar] [CrossRef]
- Shrestha, U.R.; Smith, J.C.; Petridis, L. Full Structural Ensembles of Intrinsically Disordered Proteins from Unbiased Molecular Dynamics Simulations. Commun. Biol. 2021, 4, 243. [Google Scholar] [CrossRef]
- Milles, S.; Salvi, N.; Blackledge, M.; Jensen, M.R. Characterization of Intrinsically Disordered Proteins and Their Dynamic Complexes: From in Vitro to Cell-like Environments. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 109, 79–100. [Google Scholar] [CrossRef]
- Ozenne, V.; Bauer, F.; Salmon, L.; Huang, J.; Jensen, M.R.; Segard, S.; Bernadó, P.; Charavay, C.; Blackledge, M. Flexible-Meccano: A Tool for the Generation of Explicit Ensemble Descriptions of Intrinsically Disordered Proteins and Their Associated Experimental Observables. Bioinformatics 2012, 28, 1463–1470. [Google Scholar] [CrossRef]
- Allison, J.R.; Varnai, P.; Dobson, C.M.; Vendruscolo, M. Determination of the Free Energy Landscape of α-Synuclein Using Spin Label Nuclear Magnetic Resonance Measurements. J. Am. Chem. Soc. 2009, 131, 18314–18326. [Google Scholar] [CrossRef]
- Ganguly, D.; Chen, J. Structural Interpretation of Paramagnetic Relaxation Enhancement-Derived Distances for Disordered Protein States. J. Mol. Biol. 2009, 390, 467–477. [Google Scholar] [CrossRef] [PubMed]
- Silvestre-Ryan, J.; Bertoncini, C.W.; Fenwick, R.B.; Esteban-Martin, S.; Salvatella, X. Average Conformations Determined from PRE Data Provide High-Resolution Maps of Transient Tertiary Interactions in Disordered Proteins. Biophys. J. 2013, 104, 1740–1751. [Google Scholar] [CrossRef] [PubMed]
- Schwalbe, M.; Ozenne, V.; Bibow, S.; Jaremko, M.; Jaremko, L.; Gajda, M.; Jensen, M.R.; Biernat, J.; Becker, S.; Mandelkow, E.; et al. Predictive Atomic Resolution Descriptions of Intrinsically Disordered HTau40 and α-Synuclein in Solution from NMR and Small Angle Scattering. Structure 2014, 22, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.-K.; Nodet, G.; Kim, H.-Y.; Jensen, M.R.; Bernado, P.; Fernandez, C.O.; Becker, S.; Blackledge, M.; Zweckstetter, M. Structural Characterization of α-Synuclein in an Aggregation Prone State: α-Synuclein in an Aggregation-Prone State. Protein Sci. 2009, 18, 1840–1846. [Google Scholar] [CrossRef]
- Bibow, S.; Ozenne, V.; Biernat, J.; Blackledge, M.; Mandelkow, E.; Zweckstetter, M. Structural Impact of Proline-Directed Pseudophosphorylation at AT8, AT100, and PHF1 Epitopes on 441-Residue Tau. J. Am. Chem. Soc. 2011, 133, 15842–15845. [Google Scholar] [CrossRef]
- Sibille, N.; Bernadó, P. Structural Characterization of Intrinsically Disordered Proteins by the Combined Use of NMR and SAXS. Biochem. Soc. Trans. 2012, 40, 955–962. [Google Scholar] [CrossRef]
- Cordeiro, T.N.; Herranz-Trillo, F.; Urbanek, A.; Estaña, A.; Cortés, J.; Sibille, N.; Bernadó, P. Small-Angle Scattering Studies of Intrinsically Disordered Proteins and Their Complexes. Curr. Opin. Struct. Biol. 2017, 42, 15–23. [Google Scholar] [CrossRef]
- Naudi-Fabra, S.; Tengo, M.; Jensen, M.R.; Blackledge, M.; Milles, S. Quantitative Description of Intrinsically Disordered Proteins Using Single-Molecule FRET, NMR, and SAXS. J. Am. Chem. Soc. 2021, 143, 20109–20121. [Google Scholar] [CrossRef]
- Shea, J.-E.; Best, R.B.; Mittal, J. Physics-Based Computational and Theoretical Approaches to Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol. 2021, 67, 219–225. [Google Scholar] [CrossRef]
- Mercadante, D.; Wagner, J.A.; Aramburu, I.V.; Lemke, E.A.; Gräter, F. Sampling Long- versus Short-Range Interactions Defines the Ability of Force Fields to Reproduce the Dynamics of Intrinsically Disordered Proteins. J. Chem. Theory Comput. 2017, 13, 3964–3974. [Google Scholar] [CrossRef]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [PubMed]
- Pesce, F.; Lindorff-Larsen, K. Refining Conformational Ensembles of Flexible Proteins against Small-Angle X-ray Scattering Data. Biophys. J. 2022, 121, 1576–1579. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Benton, L.A.; Singh, V.; Pielak, G.J. Disordered Protein Diffusion under Crowded Conditions. J. Phys. Chem. Lett. 2012, 3, 2703–2706. [Google Scholar] [CrossRef] [PubMed]
- Szasz, C.; Alexa, A.; Toth, K.; Rakacs, M.; Langowski, J.; Tompa, P. Protein Disorder Prevails under Crowded Conditions. Biochemistry 2011, 50, 5834–5844. [Google Scholar] [CrossRef]
- Soranno, A.; Koenig, I.; Borgia, M.B.; Hofmann, H.; Zosel, F.; Nettels, D.; Schuler, B. Single-Molecule Spectroscopy Reveals Polymer Effects of Disordered Proteins in Crowded Environments. Proc. Natl. Acad. Sci. USA 2014, 111, 4874–4879. [Google Scholar] [CrossRef]
- Zosel, F.; Soranno, A.; Buholzer, K.J.; Nettels, D.; Schuler, B. Depletion Interactions Modulate the Binding between Disordered Proteins in Crowded Environments. Proc. Natl. Acad. Sci. USA 2020, 117, 13480–13489. [Google Scholar] [CrossRef]
- Shillcock, J.C.; Thomas, D.B.; Ipsen, J.H.; Brown, A.D. Macromolecular Crowding Is Surprisingly Unable to Deform the Structure of a Model Biomolecular Condensate. Biology 2023, 12, 181. [Google Scholar] [CrossRef]
- Speer, S.L.; Stewart, C.J.; Sapir, L.; Harries, D.; Pielak, G.J. Macromolecular Crowding Is More than Hard-Core Repulsions. Annu. Rev. Biophys. 2022, 51, 267–300. [Google Scholar] [CrossRef]
- Fagerberg, E.; Lenton, S.; Nylander, T.; Seydel, T.; Skepö, M. Self-Diffusive Properties of the Intrinsically Disordered Protein Histatin 5 and the Impact of Crowding Thereon: A Combined Neutron Spectroscopy and Molecular Dynamics Simulation Study. J. Phys. Chem. B 2022, 126, 789–801. [Google Scholar] [CrossRef]
- Moses, D.; Yu, F.; Ginell, G.M.; Shamoon, N.M.; Koenig, P.S.; Holehouse, A.S.; Sukenik, S. Revealing the Hidden Sensitivity of Intrinsically Disordered Proteins to Their Chemical Environment. J. Phys. Chem. Lett. 2020, 11, 10131–10136. [Google Scholar] [CrossRef]
- Vancraenenbroeck, R.; Harel, Y.S.; Zheng, W.; Hofmann, H. Polymer Effects Modulate Binding Affinities in Disordered Proteins. Proc. Natl. Acad. Sci. USA 2019, 116, 19506–19512. [Google Scholar] [CrossRef] [PubMed]
- Longo, L.M.; Blaber, M. Prebiotic Protein Design Supports a Halophile Origin of Foldable Proteins. Front. Microbiol. 2014, 4, 418. [Google Scholar] [CrossRef] [PubMed]
- Reddy, G.; Thirumalai, D. Collapse Precedes Folding in Denaturant-Dependent Assembly of Ubiquitin. J. Phys. Chem. B 2017, 121, 995–1009. [Google Scholar] [CrossRef] [PubMed]
- Riback, J.A.; Bowman, M.A.; Zmyslowski, A.M.; Knoverek, C.R.; Jumper, J.M.; Hinshaw, J.R.; Kaye, E.B.; Freed, K.F.; Clark, P.L.; Sosnick, T.R. Innovative Scattering Analysis Shows That Hydrophobic Disordered Proteins Are Expanded in Water. Science 2017, 358, 238–241. [Google Scholar] [CrossRef]
- Yoo, T.Y.; Meisburger, S.P.; Hinshaw, J.; Pollack, L.; Haran, G.; Sosnick, T.R.; Plaxco, K. Small-Angle X-Ray Scattering and Single-Molecule FRET Spectroscopy Produce Highly Divergent Views of the Low-Denaturant Unfolded State. J. Mol. Biol. 2012, 418, 226–236. [Google Scholar] [CrossRef]
- Watkins, H.M.; Simon, A.J.; Sosnick, T.R.; Lipman, E.A.; Hjelm, R.P.; Plaxco, K.W. Random Coil Negative Control Reproduces the Discrepancy between Scattering and FRET Measurements of Denatured Protein Dimensions. Proc. Natl. Acad. Sci. USA 2015, 112, 6631–6636. [Google Scholar] [CrossRef]
- Abascal, J.L.F.; Vega, C. A General Purpose Model for the Condensed Phases of Water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Best, R.B. Computational and Theoretical Advances in Studies of Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef]
- Fuertes, G.; Banterle, N.; Ruff, K.M.; Chowdhury, A.; Mercadante, D.; Koehler, C.; Kachala, M.; Estrada Girona, G.; Milles, S.; Mishra, A.; et al. Decoupling of Size and Shape Fluctuations in Heteropolymeric Sequences Reconciles Discrepancies in SAXS vs. FRET Measurements. Proc. Natl. Acad. Sci. USA 2017, 114, E6342–E6351. [Google Scholar] [CrossRef]
- Song, J.; Gomes, G.-N.; Gradinaru, C.C.; Chan, H.S. An Adequate Account of Excluded Volume Is Necessary To Infer Compactness and Asphericity of Disordered Proteins by Förster Resonance Energy Transfer. J. Phys. Chem. B 2015, 119, 15191–15202. [Google Scholar] [CrossRef]
- Ke, P.C.; Zhou, R.; Serpell, L.C.; Riek, R.; Knowles, T.P.J.; Lashuel, H.A.; Gazit, E.; Hamley, I.W.; Davis, T.P.; Fändrich, M.; et al. Half a Century of Amyloids: Past, Present and Future. Chem. Soc. Rev. 2020, 49, 5473–5509. [Google Scholar] [CrossRef] [PubMed]
- Jahn, T.R.; Makin, O.S.; Morris, K.L.; Marshall, K.E.; Tian, P.; Sikorski, P.; Serpell, L.C. The Common Architecture of Cross-β Amyloid. J. Mol. Biol. 2010, 395, 717–727. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.I.P.; Staniforth, R.A. General Principles Underpinning Amyloid Structure. Front. Neurosci. 2022, 16, 878869. [Google Scholar] [CrossRef] [PubMed]
- Reches, M.; Gazit, E. Casting Metal Nanowires Within Discrete Self-Assembled Peptide Nanotubes. Science 2003, 300, 625–627. [Google Scholar] [CrossRef] [PubMed]
- Balasco, N.; Diaferia, C.; Morelli, G.; Vitagliano, L.; Accardo, A. Amyloid-Like Aggregation in Diseases and Biomaterials: Osmosis of Structural Information. Front. Bioeng. Biotechnol. 2021, 9, 641372. [Google Scholar] [CrossRef]
- Amit, M.; Yuran, S.; Gazit, E.; Reches, M.; Ashkenasy, N. Tailor-Made Functional Peptide Self-Assembling Nanostructures. Adv. Mater. 2018, 30, 1707083. [Google Scholar] [CrossRef]
- Buell, A.K.; Dobson, C.M.; Knowles, T.P.J. The Physical Chemistry of the Amyloid Phenomenon: Thermodynamics and Kinetics of Filamentous Protein Aggregation. Essays Biochem. 2014, 56, 11–39. [Google Scholar] [CrossRef]
- Baldwin, A.J.; Knowles, T.P.J.; Tartaglia, G.G.; Fitzpatrick, A.W.; Devlin, G.L.; Shammas, S.L.; Waudby, C.A.; Mossuto, M.F.; Meehan, S.; Gras, S.L.; et al. Metastability of Native Proteins and the Phenomenon of Amyloid Formation. J. Am. Chem. Soc. 2011, 133, 14160–14163. [Google Scholar] [CrossRef]
- Michaels, T.C.T.; Šarić, A.; Habchi, J.; Chia, S.; Meisl, G.; Vendruscolo, M.; Dobson, C.M.; Knowles, T.P.J. Chemical Kinetics for Bridging Molecular Mechanisms and Macroscopic Measurements of Amyloid Fibril Formation. Annu. Rev. Phys. Chem. 2018, 69, 273–298. [Google Scholar] [CrossRef]
- Arosio, P.; Knowles, T.P.J.; Linse, S. On the Lag Phase in Amyloid Fibril Formation. Phys. Chem. Chem. Phys. 2015, 17, 7606–7618. [Google Scholar] [CrossRef]
- Weiffert, T.; Meisl, G.; Curk, S.; Cukalevski, R.; Šarić, A.; Knowles, T.P.J.; Linse, S. Influence of Denaturants on Amyloid Β42 Aggregation Kinetics. Front. Neurosci. 2022, 16, 943355. [Google Scholar] [CrossRef]
- Khan, M.A.I.; Respondek, M.; Kjellström, S.; Deep, S.; Linse, S.; Akke, M. Cu/Zn Superoxide Dismutase Forms Amyloid Fibrils under Near-Physiological Quiescent Conditions: The Roles of Disulfide Bonds and Effects of Denaturant. ACS Chem. Neurosci. 2017, 8, 2019–2026. [Google Scholar] [CrossRef] [PubMed]
- Hamada, D.; Dobson, C.M. A Kinetic Study of β-Lactoglobulin Amyloid Fibril Formation Promoted by Urea. Protein Sci. 2009, 11, 2417–2426. [Google Scholar] [CrossRef] [PubMed]
- Vernaglia, B.A.; Huang, J.; Clark, E.D. Guanidine Hydrochloride Can Induce Amyloid Fibril Formation from Hen Egg-White Lysozyme. Biomacromolecules 2004, 5, 1362–1370. [Google Scholar] [CrossRef] [PubMed]
- Dueholm, M.S.; Petersen, S.V.; Sønderkaer, M.; Larsen, P.; Christiansen, G.; Hein, K.L.; Enghild, J.J.; Nielsen, J.L.; Nielsen, K.L.; Nielsen, P.H.; et al. Functional Amyloid in Pseudomonas: Functional Amyloid in Pseudomonas. Mol. Microbiol. 2010, 77, 1009–1020. [Google Scholar] [CrossRef]
- Buell, A.K. Stability Matters, Too–the Thermodynamics of Amyloid Fibril Formation. Chem. Sci. 2022, 13, 10177–10192. [Google Scholar] [CrossRef]
- Sulatsky, M.I.; Sulatskaya, A.I.; Stepanenko, O.V.; Povarova, O.I.; Kuznetsova, I.M.; Turoverov, K.K. Denaturant Effect on Amyloid Fibrils: Declasterization, Depolymerization, Denaturation and Reassembly. Int. J. Biol. Macromol. 2020, 150, 681–694. [Google Scholar] [CrossRef]
- Vettore, N.; Buell, A.K. Thermodynamics of Amyloid Fibril Formation from Chemical Depolymerization. Phys. Chem. Chem. Phys. 2019, 21, 26184–26194. [Google Scholar] [CrossRef]
- Chen, S.; Berthelier, V.; Hamilton, J.B.; O’Nuallai, B.; Wetzel, R. Amyloid-like Features of Polyglutamine Aggregates and Their Assembly Kinetics. Biochemistry 2002, 41, 7391–7399. [Google Scholar] [CrossRef]
- Sawaya, M.R.; Sambashivan, S.; Nelson, R.; Ivanova, M.I.; Sievers, S.A.; Apostol, M.I.; Thompson, M.J.; Balbirnie, M.; Wiltzius, J.J.W.; McFarlane, H.T.; et al. Atomic Structures of Amyloid Cross-β Spines Reveal Varied Steric Zippers. Nature 2007, 447, 453–457. [Google Scholar] [CrossRef]
- Pesce, F.; Newcombe, E.A.; Seiffert, P.; Tranchant, E.E.; Olsen, J.G.; Grace, C.R.; Kragelund, B.B.; Lindorff-Larsen, K. Assessment of Models for Calculating the Hydrodynamic Radius of Intrinsically Disordered Proteins. Biophys. J. 2023, 122, 310–321. [Google Scholar] [CrossRef] [PubMed]
- Thomasen, F.E.; Pesce, F.; Roesgaard, M.A.; Tesei, G.; Lindorff-Larsen, K. Improving Martini 3 for Disordered and Multidomain Proteins. J. Chem. Theory Comput. 2022, 18, 2033–2041. [Google Scholar] [CrossRef] [PubMed]


| ρ g L−1 | [H2O] M | ξ3 | γ Dyne cm−1 | |
|---|---|---|---|---|
| H2O | 997 | 55.3 | 0.383 | 72.8 |
| 2 M urea | 1029 | 50.4 | 0.413 | 72.9 |
| 4 M urea | 1059 | 45.4 | 0.442 | 73.3 |
| 6 M urea | 1088 | 40.4 | 0.471 | 74.4 |
| 2 M GdmCl | 1047 | 47.5 | 0.424 | 74.0 |
| 4 M GdmCl | 1095 | 39.6 | 0.465 | 74.8 |
| 6 M GdmCl | 1140 | 31.5 | 0.504 | 75.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paladino, A.; Vitagliano, L.; Graziano, G. The Action of Chemical Denaturants: From Globular to Intrinsically Disordered Proteins. Biology 2023, 12, 754. https://doi.org/10.3390/biology12050754
Paladino A, Vitagliano L, Graziano G. The Action of Chemical Denaturants: From Globular to Intrinsically Disordered Proteins. Biology. 2023; 12(5):754. https://doi.org/10.3390/biology12050754
Chicago/Turabian StylePaladino, Antonella, Luigi Vitagliano, and Giuseppe Graziano. 2023. "The Action of Chemical Denaturants: From Globular to Intrinsically Disordered Proteins" Biology 12, no. 5: 754. https://doi.org/10.3390/biology12050754
APA StylePaladino, A., Vitagliano, L., & Graziano, G. (2023). The Action of Chemical Denaturants: From Globular to Intrinsically Disordered Proteins. Biology, 12(5), 754. https://doi.org/10.3390/biology12050754