Computational Approach for Probing Redox Potential for Iron-Sulfur Clusters in Photosystem I
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
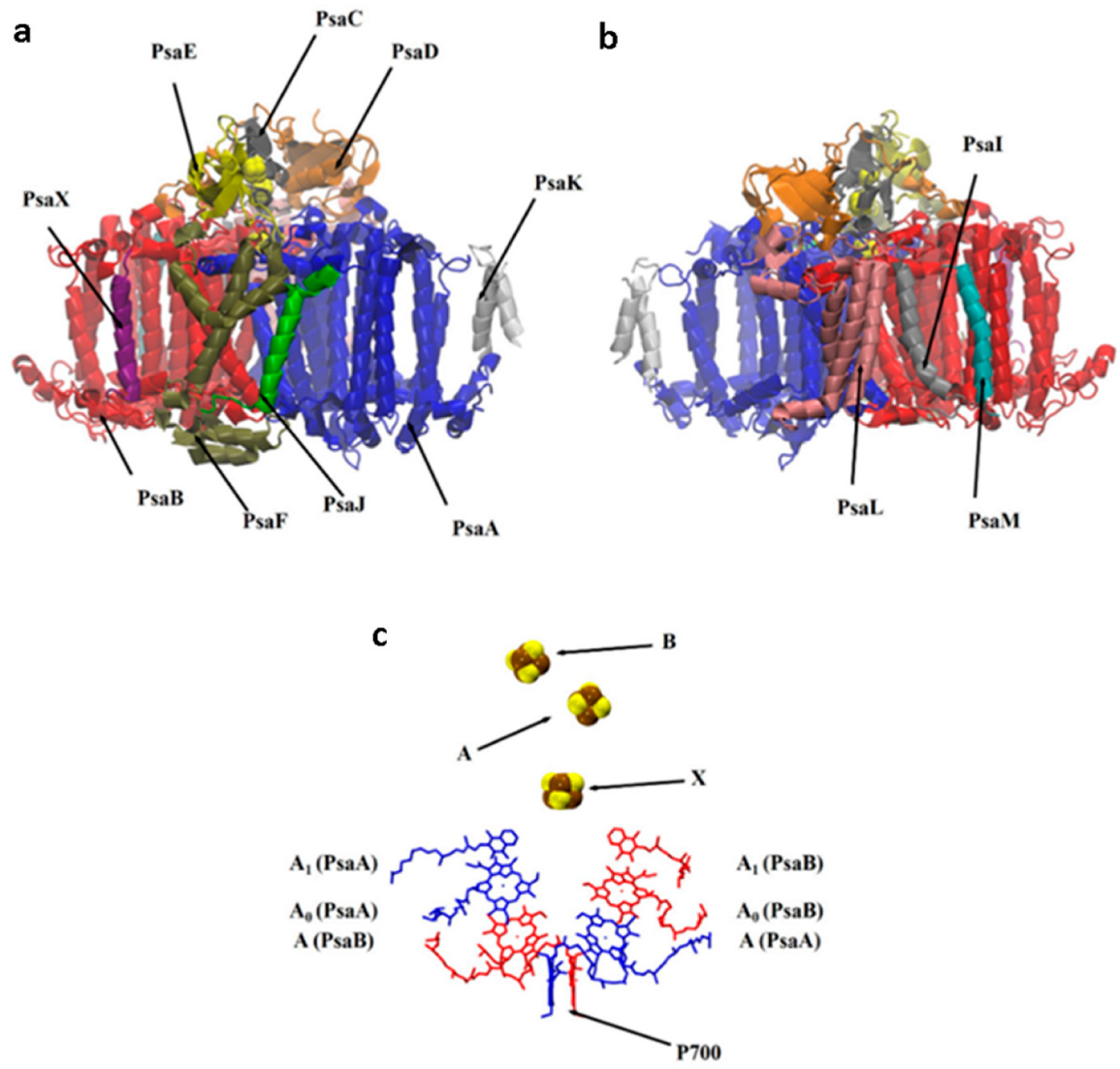
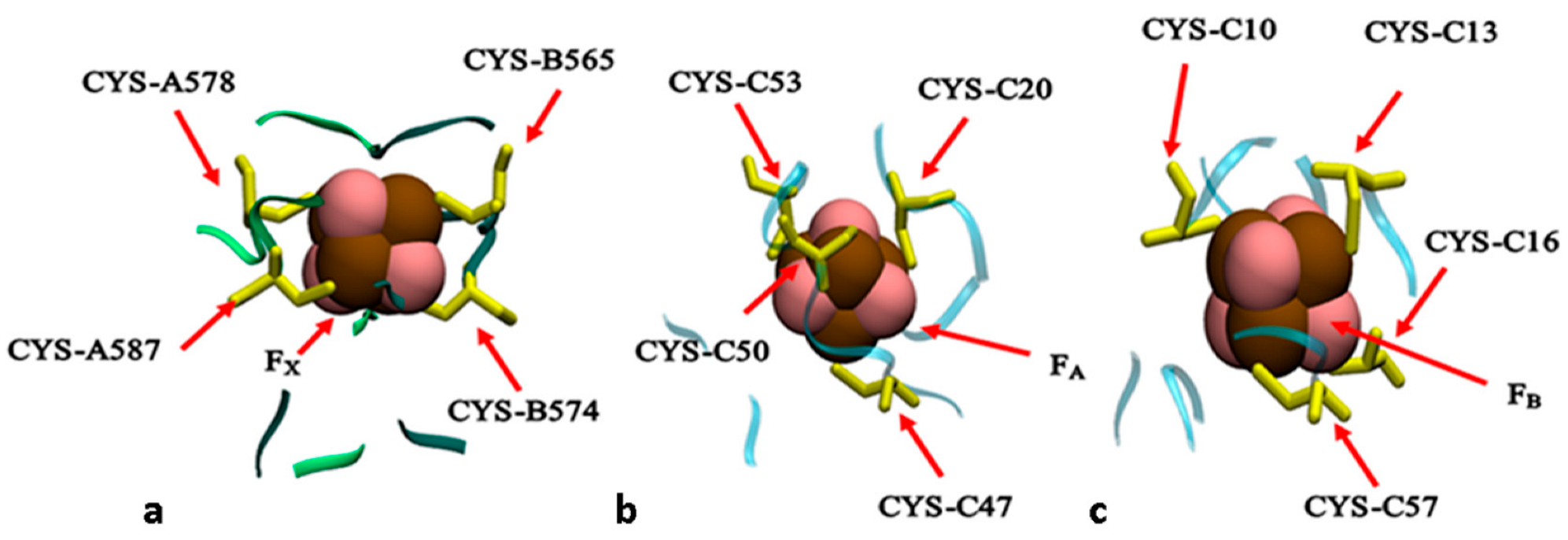
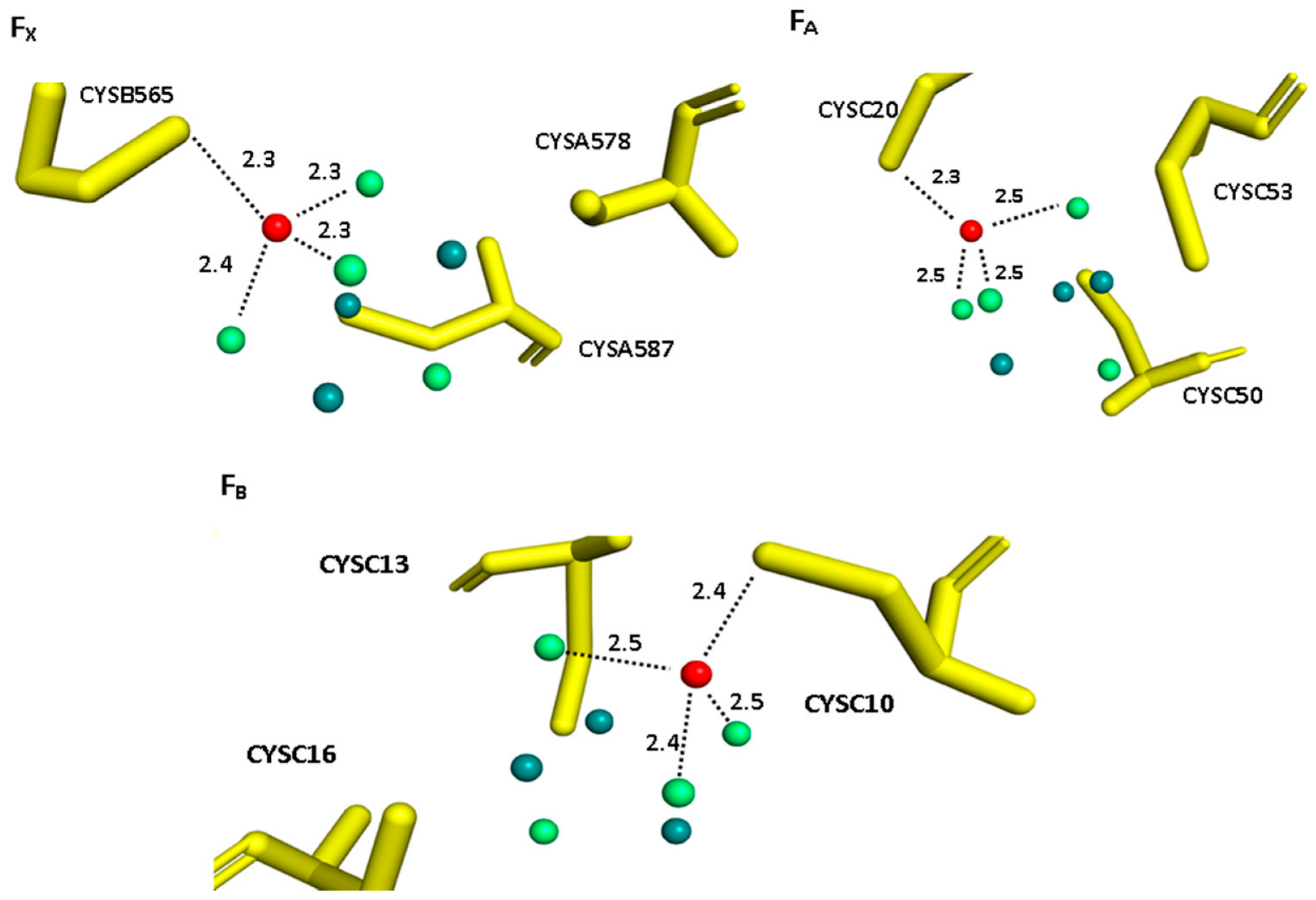
2.1. Structural Model
2.2. Multi-Conformer Continuum Electrostatics (MCCE) Calculations
2.3. Mean-Field Energy (MFE) Analysis
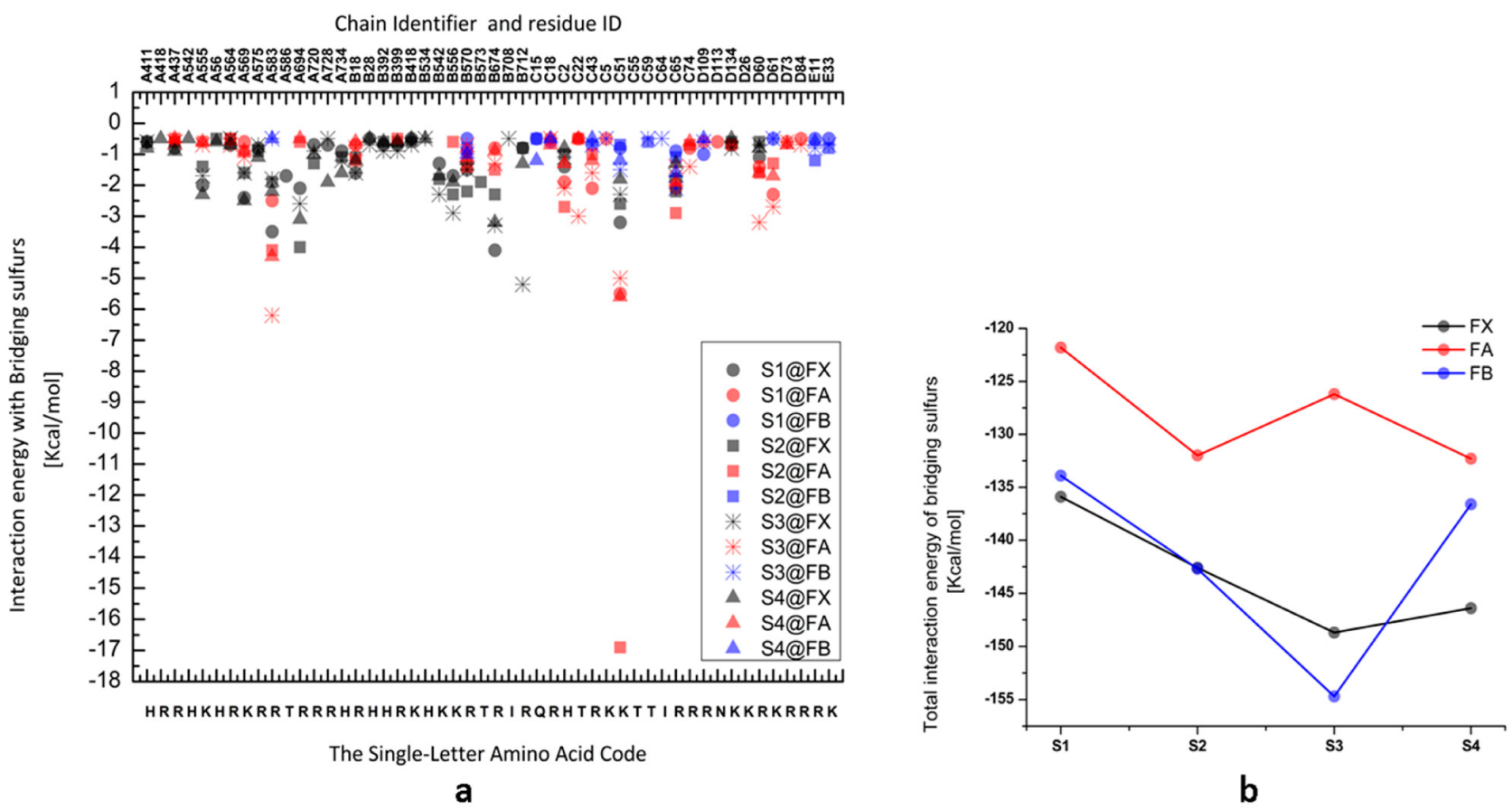
3. Results and Discussion
| DFT | XRD | |||||
|---|---|---|---|---|---|---|
| FX | FA | FB | FX | FA | FB | |
| Fe-S (Å) | 2.32 | 2.32 | 2.34 | 2.3 (×1) | 2.3 (×7) | 2.3 (×12) |
| 2.35 | 2.37 | 2.37 | 2.2 (×1) | 2.2 (×4) | ||
| 2.39 | 2.38 | 2.38 | 2.4 (×1) | |||
| 2.45 | 2.39 | 2.4 | ||||
| 2.46 | 2.4 | 2.4 | ||||
| 2.47 | 2.44 | 2.4 | ||||
| 2.49 | 2.46 | 2.44 | ||||
| 2.52 | 2.46 | 2.44 | ||||
| 2.52 | 2.47 | 2.49 | ||||
| 2.44 | 2.48 | 2.49 | ||||
| 2.44 | 2.52 | 2.5 | ||||
| 2.44 | 2.57 | 2.53 | ||||
| Fe-SG (Å) | 2.36 | 2.49 | 2.39 | 2.4 (×2) | 2.4 (×1) | 2.4 (×2) |
| 2.37 | 2.35 | 2.4 | 2.2 (×1) | 2.3 (×1) | 2.3 (×2) | |
| 2.35 | 2.34 | 2.35 | 2.3 (×1) | |||
| 2.34 | 2.34 | 2.36 | ||||
| Avg. | 2.42 | 2.45 | 2.45 | |||
| Fe-Fe (Å) | 2.96 | 3.16 | 3.05 | 2.7 (×6) | 2.7 (×4) | 2.7 (×6) |
| 2.97 | 3.02 | 3.14 | ||||
| 3.04 | 3.19 | 2.83 | ||||
| 3.18 | 2.95 | 3.15 | ||||
| 3.29 | 3.2 | 3.1 | ||||
| 3.15 | 2.97 | 3.02 | ||||
| EXAFS (Å) | ||||||
| Fe-S | Fe-Fe | |||||
| 2.27 | 2.7 | |||||
The Midpoint Potentials of FX, FB and FA
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gordon, R.B. Suggested Equations for the Photosynthetic Reaction. Ohio J. Sci. 1929, 29, 131–132. [Google Scholar]
- Barber, J.; Andersson, B. Revealing the blueprint of photosynthesis. Nature 1994, 370, 31–34. [Google Scholar] [CrossRef]
- Kiang, N.Y.; Siefert, J.; Govindjee; Blankenship, R.E. Spectral signatures of photosynthesis. I. Review of Earth organisms. Astrobiology 2007, 7, 222–251. [Google Scholar] [CrossRef]
- Blankenship, R.E. Origin and early evolution of photosynthesis. Photosynth. Res. 1992, 33, 91–111. [Google Scholar] [CrossRef]
- Nitschke, W.; William Rutherford, A. Photosynthetic reaction centres: Variations on a common structural theme? Trends Biochem. Sci. 1991, 16, 241–245. [Google Scholar] [CrossRef]
- Wolfe, G.R.; Hoober, J.K. Evolution of Thylakoid Structure. In Oxygenic Photosynthesis: The Light Reactions; Ort, D.R., Yocum, C.F., Heichel, I.F., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 31–40. ISBN 978-0-306-48127-7. [Google Scholar]
- Liebl, U.; Mockensturm-Wilson, M.; Trost, J.T.; Brune, D.C.; Blankenship, R.E.; Vermaas, W. Single core polypeptide in the reaction center of the photosynthetic bacterium Heliobacillus mobilis: Structural implications and relations to other photosystems. Proc. Natl. Acad. Sci. USA 1993, 90, 7124–7128. [Google Scholar] [CrossRef]
- Vassiliev, I.R.; Antonkine, M.L.; Golbeck, J.H. Iron-sulfur clusters in type I reaction centers. Biochim. Biophys. Acta Bioenerg. 2001, 1507, 139–160. [Google Scholar] [CrossRef]
- Croce, R.; van Amerongen, H. Light-harvesting in photosystem I. Photosynth. Res. 2013, 116, 153–166. [Google Scholar] [CrossRef]
- Trissl, H.-W.; Wilhelm, C. Why do thylakoid membranes from higher plants form grana stacks? Trends Biochem. Sci. 1993, 18, 415–419. [Google Scholar] [CrossRef]
- Srinivasan, N.; Golbeck, J.H. Protein-cofactor interactions in bioenergetic complexes: The role of the A1A and A1B phylloquinones in Photosystem I. Biochim. Biophys. Acta Bioenerg. 2009, 1787, 1057–1088. [Google Scholar] [CrossRef]
- Jordan, P.; Fromme, P.; Witt, H.T.; Klukas, O.; Saenger, W.; Krauß, N. Three-dimensional structure of cyanobacterial photosystem I at 2.5 Å resolution. Nature 2001, 411, 909–917. [Google Scholar] [CrossRef]
- Xu, W.; Tang, H.; Wang, Y.; Chitnis, P.R. Proteins of the cyanobacterial photosystem I. Biochim. Biophys. Acta Bioenerg. 2001, 1507, 32–40. [Google Scholar] [CrossRef]
- Nelson, N.; Yocum, C.F. Structure and Function of Photosystems I and II. Annu. Rev. Plant Biol. 2006, 57, 521–565. [Google Scholar] [CrossRef]
- Scheller, H.V.; Jensen, P.E.; Haldrup, A.; Lunde, C.; Knoetzel, J. Role of subunits in eukaryotic Photosystem I. Biochim. Biophys. Acta Bioenerg. 2001, 1507, 41–60. [Google Scholar] [CrossRef]
- Sétif, P.; Fischer, N.; Lagoutte, B.; Bottin, H.; Rochaix, J.-D. The ferredoxin docking site of photosystem I. Biochim. Biophys. Acta Bioenerg. 2002, 1555, 204–209. [Google Scholar] [CrossRef][Green Version]
- Sétif, P. Ferredoxin and flavodoxin reduction by photosystem I. Biochim. Biophys. Acta Bioenerg. 2001, 1507, 161–179. [Google Scholar] [CrossRef]
- Nelson, N.; Junge, W. Structure and Energy Transfer in Photosystems of Oxygenic Photosynthesis. Annu. Rev. Biochem. 2015, 84, 659–683. [Google Scholar] [CrossRef]
- Brettel, K. Electron transfer and arrangement of the redox cofactors in photosystem I. Biochim. Biophys. Acta Bioenerg. 1997, 1318, 322–373. [Google Scholar] [CrossRef]
- Shelaev, I.V.; Gostev, F.E.; Mamedov, M.D.; Sarkisov, O.M.; Nadtochenko, V.A.; Shuvalov, V.A.; Semenov, A.Y. Femtosecond primary charge separation in Synechocystis sp. PCC 6803 photosystem I. Biochim. Biophys. Acta Bioenerg. 2010, 1797, 1410–1420. [Google Scholar] [CrossRef]
- Vassiliev, I.R.; Jung, Y.-S.; Yang, F.; Golbeck, J.H. PsaC Subunit of Photosystem I Is Oriented with Iron-Sulfur Cluster FB as the Immediate Electron Donor to Ferredoxin and Flavodoxin. Biophys. J. 1998, 74, 2029–2035. [Google Scholar] [CrossRef][Green Version]
- Golbeck, J.H. A comparative analysis of the spin state distribution of in vitro and in vivo mutants of PsaC. A biochemical argument for the sequence of electron transfer in Photosystem I as FX → FA → FB → ferredoxin/flavodoxin. Photosynth. Res. 1999, 61, 107–144. [Google Scholar] [CrossRef]
- Díaz-Quintana, A.; Leibl, W.; Bottin, H.; Sétif, P. Electron Transfer in Photosystem I Reaction Centers Follows a Linear Pathway in Which Iron−Sulfur Cluster FB Is the Immediate Electron Donor to Soluble Ferredoxin. Biochemistry 1998, 37, 3429–3439. [Google Scholar] [CrossRef]
- Evans, M.; Reeves, S.; Cammack, R. Determination of the oxidation—Reduction potential of the bound iron-sulphur proteins of the primary electron acceptor complex of photosystem I in spinach chloroplasts. FEBS Lett. 1974, 49, 111–114. [Google Scholar] [CrossRef]
- Evans, M.C.; Sihra, C.; Bolton, J.R.; Cammack, R. Primary electron acceptor complex of photosystem I in spinach chloroplasts. Nature 1975, 256, 668–670. [Google Scholar] [CrossRef]
- Meyer, J. Iron-sulfur protein folds, iron-sulfur chemistry, and evolution. J. Biol. Inorg. Chem. 2008, 13, 157–170. [Google Scholar] [CrossRef]
- Cammack, R. Iron—Sulfur Clusters in Enzymes: Themes and Variations. In Advances in Inorganic Chemistry; Sykes, A.G., Ed.; Advances in inorganic chemistry; Academic Press: Cambridge, MA, USA, 1992; Volume 38, pp. 281–322. [Google Scholar]
- Venkateswara Rao, P.; Holm, R. Synthetic Analogues of the Active Sites of Iron-Sulfur Proteins. Chem. Rev. 2004, 104, 527–559. [Google Scholar] [CrossRef]
- Shinkarev, V.P.; Vassiliev, I.R.; Golbeck, J.H. A kinetic assessment of the sequence of electron transfer from F(X) to F(A) and further to F(B) in photosystem I: The value of the equilibrium constant between F(X) and F(A). Biophys. J. 2000, 78, 363–372. [Google Scholar] [CrossRef]
- Chamorovsky, S.; Cammack, R. Effect of temperature on the photoreduction of centres A and B in photosystem I, and the kinetics of recombination. Biochim. Biophys. Acta Bioenerg. 1982, 679, 146–155. [Google Scholar] [CrossRef]
- Parrett, K.G.; Mehari, T.; Warren, P.G.; Golbeck, J.H. Purification and properties of the intact P-700 and F x-containing Photosystem I core protein. Biochim. Biophys. Acta Bioenerg. 1989, 973, 324–332. [Google Scholar] [CrossRef]
- Golbeck, J.H. Comparison of in vitro and in vivo mutants of PsaC in photosystem I: Protocols for mutagenesis and techniques analysis. Methods Enzymol. 1998, 297, 95–123. [Google Scholar]
- Torres, R.A.; Lovell, T.; Noodleman, L.; Case, D.A. Density functional and reduction potential calculations of Fe4S4 clusters. J. Am. Chem. Soc. 2003, 125, 1923–1936. [Google Scholar] [CrossRef]
- Ptushenko, V.V.; Cherepanov, D.A.; Krishtalik, L.I.; Semenov, A.Y. Semi-continuum electrostatic calculations of redox potentials in photosystem I. Photosynth. Res. 2008, 97, 55–74. [Google Scholar] [CrossRef]
- Alexov, E.G.; Gunner, M.R. Incorporating protein conformational flexibility into the calculation of pH-dependent protein properties. Biophys. J. 1997, 72, 2075–2093. [Google Scholar] [CrossRef]
- Georgescu, R.E.; Alexov, E.G.; Gunner, M.R. Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins. Biophys. J. 2002, 83, 1731–1748. [Google Scholar] [CrossRef]
- Song, Y.; Mao, J.; Gunner, M.R. MCCE2: Improving protein pKa calculations with extensive side chain rotamer sampling. J. Comput. Chem. 2009, 30, 2231–2247. [Google Scholar] [CrossRef]
- Amin, M.; Mohamed, Z.; El-Sayed, M.; Samy, A.; Sultan, A.; Bassuoni, M.; Alkordi, M.H. Combined QM/MM and Monte Carlo study for redox leveling in Mn and Fe superoxide dismutase. JBIC J. Biol. Inorg. Chem. 2018, 23, 285–293. [Google Scholar] [CrossRef]
- Amin, M.; Vogt, L.; Vassiliev, S.; Rivalta, I.; Sultan, M.M.; Bruce, D.; Brudvig, G.W.; Batista, V.S.; Gunner, M.R. Electrostatic effects on proton coupled electron transfer in oxomanganese complexes inspired by the oxygen-evolving complex of photosystem II. J. Phys. Chem. B 2013, 117, 6217–6226. [Google Scholar] [CrossRef]
- Eastman, P.; Friedrichs, M.S.; Chodera, J.D.; Radmer, R.J.; Bruns, C.M.; Ku, J.P.; Beauchamp, K.A.; Lane, T.J.; Wang, L.-P.; Shukla, D.; et al. OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation. J. Chem. Theory Comput. 2013, 9, 461–469. [Google Scholar] [CrossRef]
- Zhang, L.; Silva, D.-A.; Yan, Y.; Huang, X. Force field development for cofactors in the photosystem II. J. Comput. Chem. 2012, 33, 1969–1980. [Google Scholar] [CrossRef]
- Carvalho, A.T.P.; Swart, M. Electronic Structure Investigation and Parametrization of Biologically Relevant Iron–Sulfur Clusters. J. Chem. Inf. Model. 2014, 54, 613–620. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09; revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Noodleman, L. Valence bond description of antiferromagnetic coupling in transition metal dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Rocchia, W.; Alexov, E.; Honig, B. Extending the Applicability of the Nonlinear Poisson−Boltzmann Equation: Multiple Dielectric Constants and Multivalent Ions. J. Phys. Chem. B 2001, 105, 6507–6514. [Google Scholar] [CrossRef]
- Nicholls, A.; Honig, B. A rapid finite difference algorithm, utilizing successive over-relaxation to solve the Poisson-Boltzmann equation. J. Comput. Chem. 1991, 12, 435–445. [Google Scholar] [CrossRef]
- Gilson, M.K.; Honig, B.H. The Dielectric Constant of a Folded Protein. Biopolym. Orig. Res. Biomol. 1986, 25, 2097–2119. [Google Scholar] [CrossRef] [PubMed]
- Sitkoff, D.; Sharp, K.A.; Honig, B. Accurate Calculation of Hydration Free Energies Using Macroscopic Solvent Models. J. Phys. Chem. 2002, 98, 1978–1988. [Google Scholar] [CrossRef]
- Alexov, E.; Miksovska, J.; Baciou, L.; Schiffer, M.; Hanson, D.K.; Sebban, P.; Gunner, M.R. Modeling the Effects of Mutations on the Free Energy of the First Electron Transfer from Q A—To Q B in Photosynthetic Reaction Centers †. Biochemistry 2000, 39, 5940–5952. [Google Scholar] [CrossRef]
- Gunner, M.R.; Mao, J.; Song, Y.; Kim, J. Factors influencing the energetics of electron and proton transfers in proteins. What can be learned from calculations. Biochim. Biophys. Acta Bioenerg. 2006, 1757, 942–968. [Google Scholar] [CrossRef]
- Alexov, E.G.; Gunner, M.R. Calculated protein and proton motions coupled to electron transfer: Electron transfer from Q(A)- to Q(B) in bacterial photosynthetic reaction centers. Biochemistry 1999, 38, 8253–8270. [Google Scholar] [CrossRef]
- Zhang, J.; Gunner, M.R. Multiconformation continuum electrostatics analysis of the effects of a buried asp introduced near heme a in rhodobacter sphaeroides cytochrome c Oxidase. Biochemistry 2010, 49, 8043–8052. [Google Scholar] [CrossRef]
- McDermott, A.E.; Yachandra, V.K.; Guiles, R.D.; Britt, R.D.; Dexheimer, S.L.; Sauer, K.; Klein, M.P. Low-potential iron-sulfur centers in photosystem I: An x-ray absorption spectroscopy study. Biochemistry 1988, 27, 4013–4020. [Google Scholar] [CrossRef]
- McDermott, A.E.; Yachandra, V.K.; Guiles, R.D.; Sauer, K.; Klein, M.P.; Parrett, K.G.; Golbeck, J.H. EXAFS structural study of FX, the low-potential iron-sulfur center in photosystem I. Biochemistry 1989, 28, 8056–8059. [Google Scholar] [CrossRef]
- Gong, X.M.; Hochman, Y.; Lev, T.; Bunker, G.; Carmeli, C. The structure of genetically modified iron-sulfur cluster Fx in photosystem I as determined by X-ray absorption spectroscopy. Biochim. Biophys. Acta Bioenerg. 2009, 1787, 97–104. [Google Scholar] [CrossRef][Green Version]
- Golbeck, J.H. Resolution and Reconstitution of the Photosystem I Reaction Center Complex in Green Plants and Cyanobacteria. In Current Research in Photosynthesis; Springer: Dordrecht, The Netherlands, 1990; Volume 468, pp. 1491–1498. ISBN 0167-4412. [Google Scholar]
- Chamorovsky, S.K.; Cammack, R. Direct determination of the midpoint potential of the acceptor X in chloroplast photosystem by electrochemical reduction and ESR spectroscopy. Photobiochem. Photobiophys. 1982, 4, 195–200. [Google Scholar]
- Brettel, K.; Leibl, W. Electron transfer in photosystem I. Biochim. Biophys. Acta Bioenerg. 2001, 1507, 100–114. [Google Scholar] [CrossRef]
- Golbeck, J.H.; Parrett, K.G.; McDermott, A.E. Photosystem I charge separation in the absence of center A and B. III. Biochemical characterization of a reaction center particle containing P-700 and FX. BBA Bioenerg. 1987, 893, 149–160. [Google Scholar] [CrossRef]
- Jordan, R.; Nessau, U.; Schlodder, E. Charge Recombination between the Reduced Iron-Sulphur Clusters and P700+. In Photosynthesis: Mechanisms and Effects; Garab, G., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 663–666. ISBN 978-94-011-3953-3. [Google Scholar]
- Zheng, Z.; Gunner, M. Analysis of the electrochemistry of hemes with Ems spanning 800 mV. Proteins 2009, 75, 719–734. [Google Scholar] [CrossRef]
- Zhu, Z.; Gunner, M.R. Energetics of quinone-dependent electron and proton transfers in Rhodobacter sphaeroides photosynthetic reaction centers. Biochemistry 2005, 44, 82–96. [Google Scholar] [CrossRef]
- Ke, B.; Hansen, R.E.; Beinert, H. Oxidation-Reduction Potentials of Bound Iron-Sulfur Proteins of Photosystem I. Proc. Natl. Acad. Sci. USA 1973, 70, 2941–2945. [Google Scholar] [CrossRef]
- Milanovsky, G.E.; Petrova, A.A.; Cherepanov, D.A.; Semenov, A.Y. Kinetic modeling of electron transfer reactions in photosystem I complexes of various structures with substituted quinone acceptors. Photosynth. Res. 2017, 133, 185–199. [Google Scholar] [CrossRef]

| Cal. Em | Exp. Em | |
|---|---|---|
| FA | −355 | −440 j, −53 0 i, −50 0m |
| FB | −346 | −465 j, −580 i, −550 m |
| FX | −715 | −650 m, −705 k, −670 l |
| 15.10 | 17.03 | 16.61 | |
| 79.99 | 75.70 | 76.27 | |
| −104.32 | −96.66 | −91.77 | |
| 12.81 | 4.35 | 4.14 |
| FX | FA | FB | ||||
|---|---|---|---|---|---|---|
| Residues | Energy | Residues | Energy | Residues | Energy | |
| 4Fe-4S | S1@Fx | −57.9 | S4@Fa | −49.38 | S3@Fb | −53.65 |
| S2@Fx | −56.31 | S3@Fa | −48.31 | S1@Fb | −49.47 | |
| S3@Fx | −55.31 | S1@Fa | −47.33 | S2@Fb | −47.19 | |
| C/B565 | −24.94 | C/C20 | −24.61 | C/C10 | −28.55 | |
| FE3@Fx | 40.98 | FE1@Fa | 34.44 | FE1@Fb | 54.62 | |
| FE2@Fx | 45.68 | FE3@Fa | 53.66 | FE2@Fb | 42.15 | |
| FE1@Fx | 60.88 | FE4@Fa | 36.45 | FE3@Fb | 35.66 | |
| Surrounding residues | C/B574 | −10.92 | S2@Fa | −22.32 | S4@Fb | −22.19 |
| C/A587 | −10.04 | C/C53 | −13.45 | C/C16 | −7.92 | |
| C/A578 | −9.33 | C/C47 | −7.89 | C/C57 | −7.67 | |
| S2@Fa | −3.01 | C/C50 | −7.7 | C/C13 | −5.56 | |
| D/A593 | −2.24 | C/C16 | −3.63 | S1@Fa | −2.78 | |
| S4@Fa | −1.97 | S3@Fb | −3.36 | S4@Fa | −2.1 | |
| S3@Fa | −1.86 | S4@Fb | −3.12 | C/C53 | −1.88 | |
| E/C54 | −1.83 | E/D62 | −2.73 | S2@Fa | −1.74 | |
| C/C50 | −1.73 | S1@Fb | −2.45 | S3@Fa | −1.37 | |
| E/A699 | −1.46 | E/C54 | −2.06 | E/C54 | −1.08 | |
| S1@Fa | −1.45 | D/C23 | −1.89 | C/C20 | −0.91 | |
| E/C71 | −1.29 | S1@Fx | −1.74 | S/C63 | −0.71 | |
| E/B679 | −1.19 | S2@Fb | −1.53 | C/C47 | −0.68 | |
| C/C53 | −0.94 | S2@Fx | −1.35 | |||
| C/C47 | −0.91 | C/C57 | −1.21 | |||
| E/B682 | −0.79 | S4@Fx | −1.08 | |||
| D/B566 | −0.77 | S3@Fx | −1.07 | |||
| E/D62 | −0.73 | D/C46 | −1.05 | |||
| D/B558 | −0.7 | C/B565 | −0.81 | |||
| D/B546 | −0.68 | C/A578 | −0.79 | |||
| D/B14 | −0.65 | E/C71 | −0.77 | |||
| S4@Fb | −0.64 | C/C10 | −0.75 | |||
| S3@Fb | −0.62 | E/D103 | −0.68 | |||
| D/B29 | −0.5 | D/B566 | −0.59 | |||
| C/A587 | −0.56 | |||||
| E/B679 | −0.53 | |||||
| E/B682 | −0.52 | |||||
| C/C13 | −0.51 | |||||
| FX | FA | FB | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | Tot.* | S1 | S2 | S3 | S4 | Tot.* | S1 | S2 | S3 | S4 | Tot.* | ||
| K | C51 | −3.2 | −2.6 | −2.3 | −1.8 | −9.9 | −5.5 | −16.9 | −5 | −5.6 | −33 | −0.8 | −0.7 | −1.5 | −1.2 | −4.2 |
| R | A583 | −3.5 | −1.9 | −1.8 | −2.2 | −9.4 | −2.5 | −4.1 | −6.2 | −4.3 | −17 | −0.5 | −0.5 | −1 | ||
| R | C65 | −1.8 | −2.2 | −1.7 | −1.3 | −7 | −2.1 | −2.9 | −1.4 | −1.9 | −8.3 | −0.9 | −1.1 | −2.1 | −1.6 | −5.7 |
| H | C2 | −1.4 | −1 | −1.1 | −0.8 | −4.3 | −1.9 | −2.7 | −2.1 | −1.3 | −8 | 0 | ||||
| R | D60 | −1.1 | −0.6 | −0.7 | −0.8 | −3.2 | −1.4 | −1.6 | −3.2 | −1.6 | −7.8 | 0 | ||||
| R | B674 | −4.1 | −2.3 | −3.3 | −3.2 | −13 | −0.8 | −1.5 | −1.3 | −0.9 | −4.5 | 0 | ||||
| R | B570 | −1.5 | −2.2 | −1.5 | −1.2 | −6.4 | −0.9 | −1.4 | −0.7 | −1.1 | −4.1 | −0.5 | −0.8 | −1 | −1 | −3.3 |
| K | D61 | 0 | −2.3 | −1.3 | −2.7 | −1.7 | −8 | −0.5 | −0.5 | −1 | ||||||
| R | B18 | −1.6 | −1.1 | −1.6 | −1.2 | −5.5 | −0.7 | −1.2 | −0.8 | −0.6 | −3.3 | 0 | ||||
| R | C43 | 0 | −2.1 | −1 | −1.6 | −1.2 | −5.9 | −0.7 | −0.7 | −0.5 | −1.9 | |||||
| K | A569 | −2.4 | −1.6 | −1.6 | −2.5 | −8.1 | −0.6 | −0.9 | −1.1 | −0.9 | −3.5 | 0 | ||||
| K | D134 | −0.7 | −0.6 | −0.8 | −0.5 | −2.6 | −0.7 | −0.7 | 0 | |||||||
| R | C74 | 0 | −0.8 | −0.7 | −1.4 | −0.6 | −3.5 | 0 | ||||||||
| R | A694 | −2.1 | −4 | −2.6 | −3.1 | −12 | −0.6 | −0.5 | −1.1 | 0 | ||||||
| K | A555 | −2 | −1.4 | −1.7 | −2.3 | −7.4 | −0.6 | −0.7 | −0.6 | −1.9 | 0 | |||||
| K | B556 | −1.7 | −2.3 | −2.9 | −1.9 | −8.8 | −0.6 | −0.6 | 0 | |||||||
| R | A437 | −0.8 | −0.6 | −0.6 | −0.9 | −2.9 | −0.5 | −0.6 | −0.5 | −1.6 | 0 | |||||
| R | A564 | −0.7 | −0.5 | −0.5 | −0.7 | −2.4 | −0.5 | −0.7 | −1.2 | 0 | ||||||
| R | B399 | −0.7 | −0.6 | −0.9 | −0.6 | −2.8 | −0.5 | −0.5 | 0 | |||||||
| T | C22 | 0 | −0.5 | −0.5 | −3 | −0.5 | −4.5 | 0 | ||||||||
| T | A586 | −1.7 | −1.7 | 0 | 0 | |||||||||||
| K | B542 | −1.3 | −1.8 | −2.3 | −1.7 | −7.1 | 0 | 0 | ||||||||
| H | A734 | −0.9 | −1.1 | −1.2 | −1.6 | −4.8 | 0 | 0 | ||||||||
| R | A575 | −0.8 | −0.9 | −0.7 | −1.1 | −3.5 | 0 | 0 | ||||||||
| R | B712 | −0.8 | −0.8 | −5.2 | −1.3 | −8.1 | 0 | 0 | ||||||||
| R | A720 | −0.7 | −1.3 | −0.9 | −1 | −3.9 | 0 | 0 | ||||||||
| R | A728 | −0.7 | −0.5 | −1.9 | −3.1 | 0 | 0 | |||||||||
| H | B392 | −0.7 | −0.6 | −0.9 | −0.6 | −2.8 | 0 | 0 | ||||||||
| H | A411 | −0.6 | −0.6 | −0.6 | −0.8 | −2.6 | 0 | 0 | ||||||||
| H | B28 | −0.5 | −0.7 | −0.5 | −1.7 | 0 | 0 | |||||||||
| K | B418 | −0.5 | −0.6 | −0.7 | −0.5 | −2.3 | 0 | 0 | ||||||||
| R | A418 | −0.5 | −0.5 | 0 | 0 | |||||||||||
| H | A542 | −0.5 | −0.5 | 0 | 0 | |||||||||||
| H | A56 | −0.5 | −0.6 | −1.1 | 0 | 0 | ||||||||||
| H | B534 | −0.5 | −0.5 | −1 | 0 | 0 | ||||||||||
| T | B573 | −1.9 | −1.9 | 0 | 0 | |||||||||||
| I | B708 | −0.5 | −0.5 | 0 | 0 | |||||||||||
| Q | C15 | 0 | 0 | −0.5 | −0.5 | −1.2 | −2.2 | |||||||||
| R | C18 | 0 | −0.5 | −0.5 | −0.7 | −1.7 | −0.6 | −0.5 | −1.1 | |||||||
| K | C5 | 0 | −0.5 | −0.5 | −0.5 | −0.5 | ||||||||||
| T | C55 | 0 | 0 | 0 | ||||||||||||
| T | C59 | 0 | 0 | −0.6 | −0.5 | −1.1 | ||||||||||
| I | C64 | 0 | 0 | −0.5 | −0.5 | |||||||||||
| R | D109 | 0 | −0.6 | −0.6 | −1 | −0.6 | −0.5 | −2.1 | ||||||||
| N | D113 | 0 | −0.6 | −0.6 | 0 | |||||||||||
| K | D26 | 0 | 0 | 0 | ||||||||||||
| R | D73 | 0 | −0.6 | −0.6 | −0.7 | −1.9 | 0 | |||||||||
| R | D84 | 0 | −0.5 | −0.7 | −1.2 | 0 | ||||||||||
| R | E11 | 0 | 0 | −0.5 | −1.2 | −0.8 | −0.6 | −3.1 | ||||||||
| K | E33 | 0 | 0 | −0.5 | −0.8 | −0.7 | −2 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, F.; Shafaa, M.W.; Amin, M. Computational Approach for Probing Redox Potential for Iron-Sulfur Clusters in Photosystem I. Biology 2022, 11, 362. https://doi.org/10.3390/biology11030362
Ali F, Shafaa MW, Amin M. Computational Approach for Probing Redox Potential for Iron-Sulfur Clusters in Photosystem I. Biology. 2022; 11(3):362. https://doi.org/10.3390/biology11030362
Chicago/Turabian StyleAli, Fedaa, Medhat W. Shafaa, and Muhamed Amin. 2022. "Computational Approach for Probing Redox Potential for Iron-Sulfur Clusters in Photosystem I" Biology 11, no. 3: 362. https://doi.org/10.3390/biology11030362
APA StyleAli, F., Shafaa, M. W., & Amin, M. (2022). Computational Approach for Probing Redox Potential for Iron-Sulfur Clusters in Photosystem I. Biology, 11(3), 362. https://doi.org/10.3390/biology11030362






