Aggregated Distribution as an Explanation for the Paradox of Plankton and Collective Animal Behavior
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. About ECA
- NumberOfCells: number of cells in which the habitat is divided.
- NumberOfRsrcsInEachCell: discrete quantity of resources in each cell.
- Distribution: type of structural distribution of the populations in the habitat.
- id: name of the species.
- NumberOfItems: size of the initial population.
- DirectOffspring: number of direct offspring of each species.
- Distribution: functional distribution of the species or vagility. If this variable is not defined for a species, the program selects the variable Distribution of the habitat variables by default.
- IndirectOffspring: number of indirect offspring.
2.2. Dispersion Strategies
2.3. Software
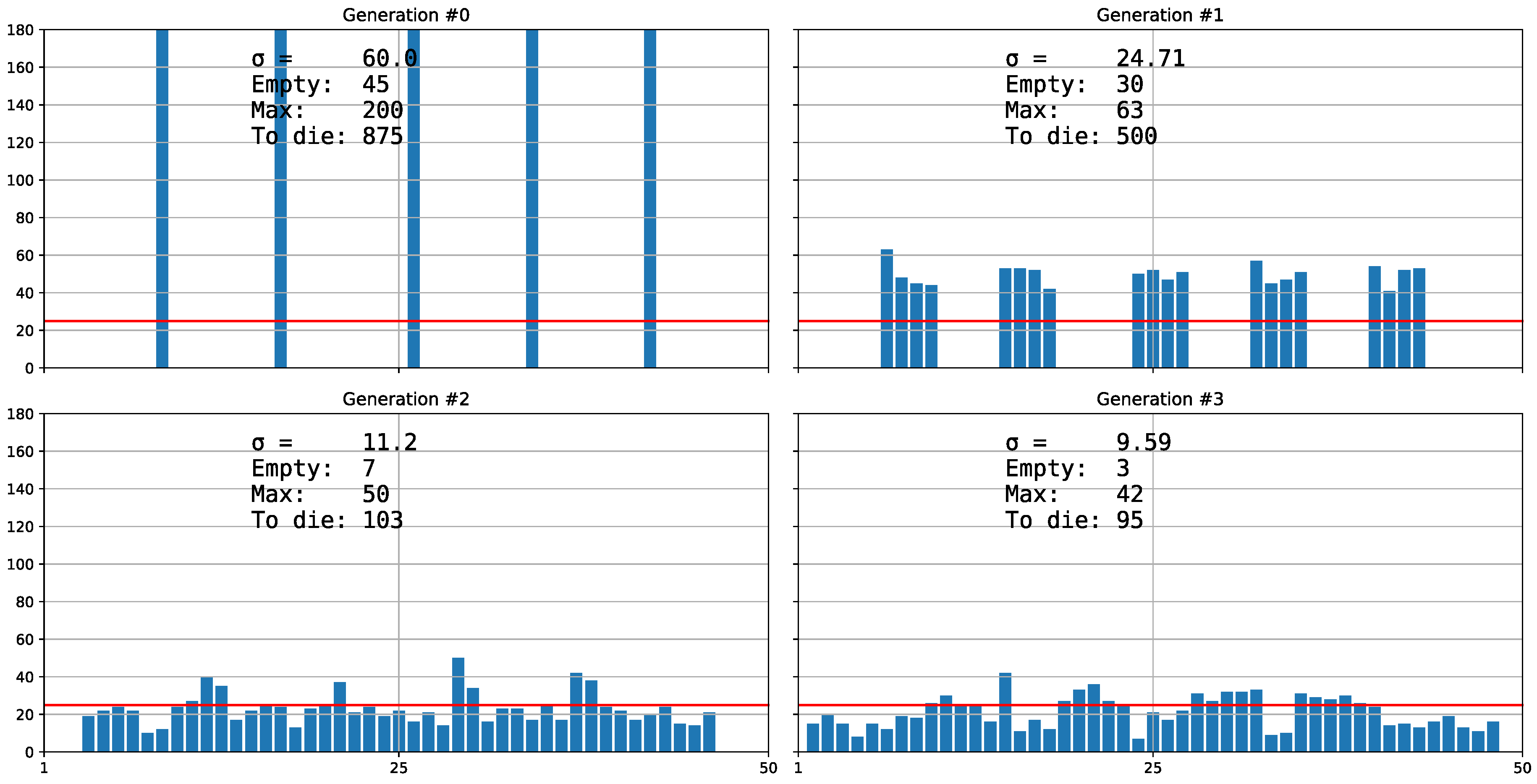
3. Results and Discussion
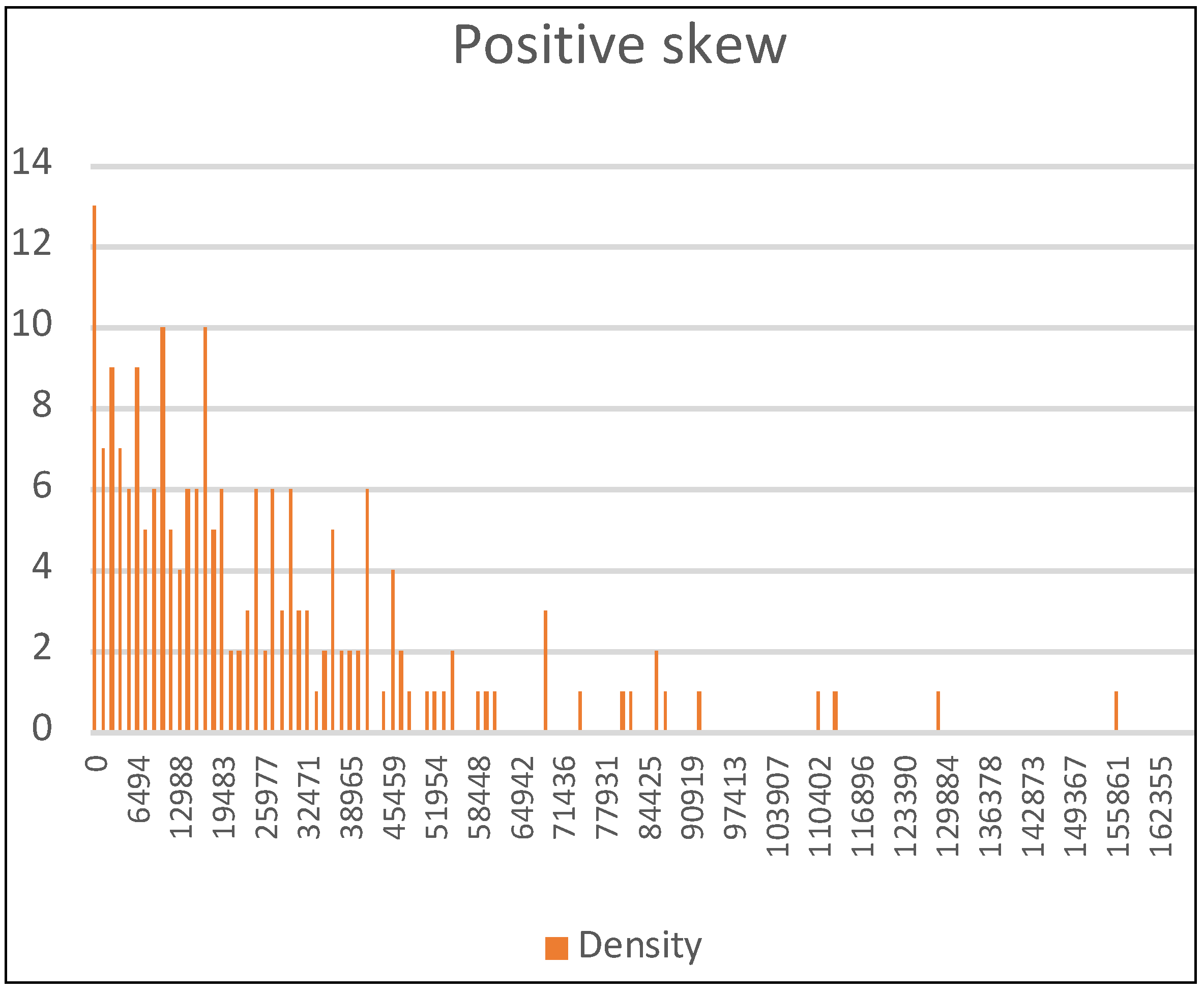
3.1. The Inefficiency of Aggregate Distribution
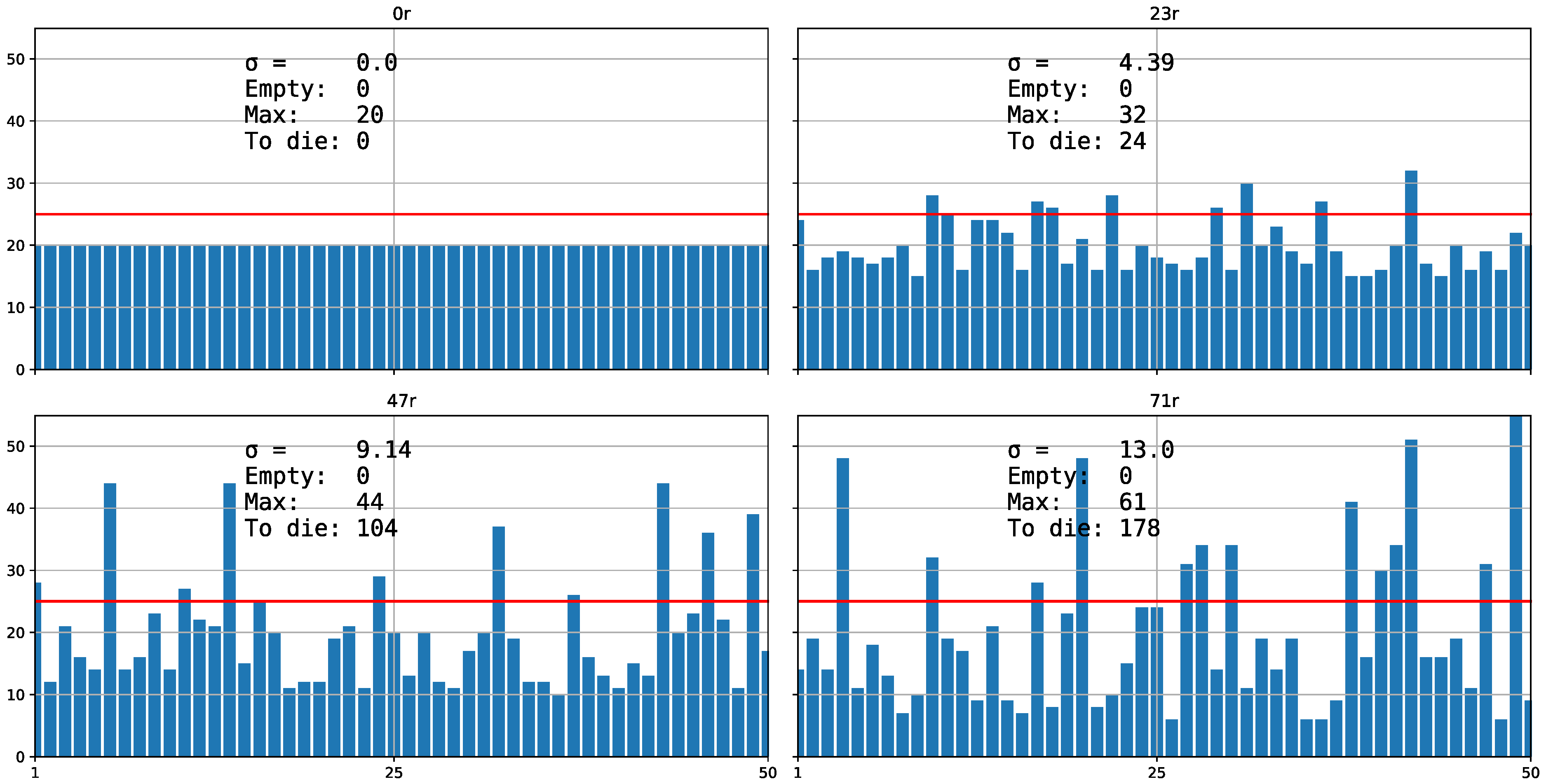
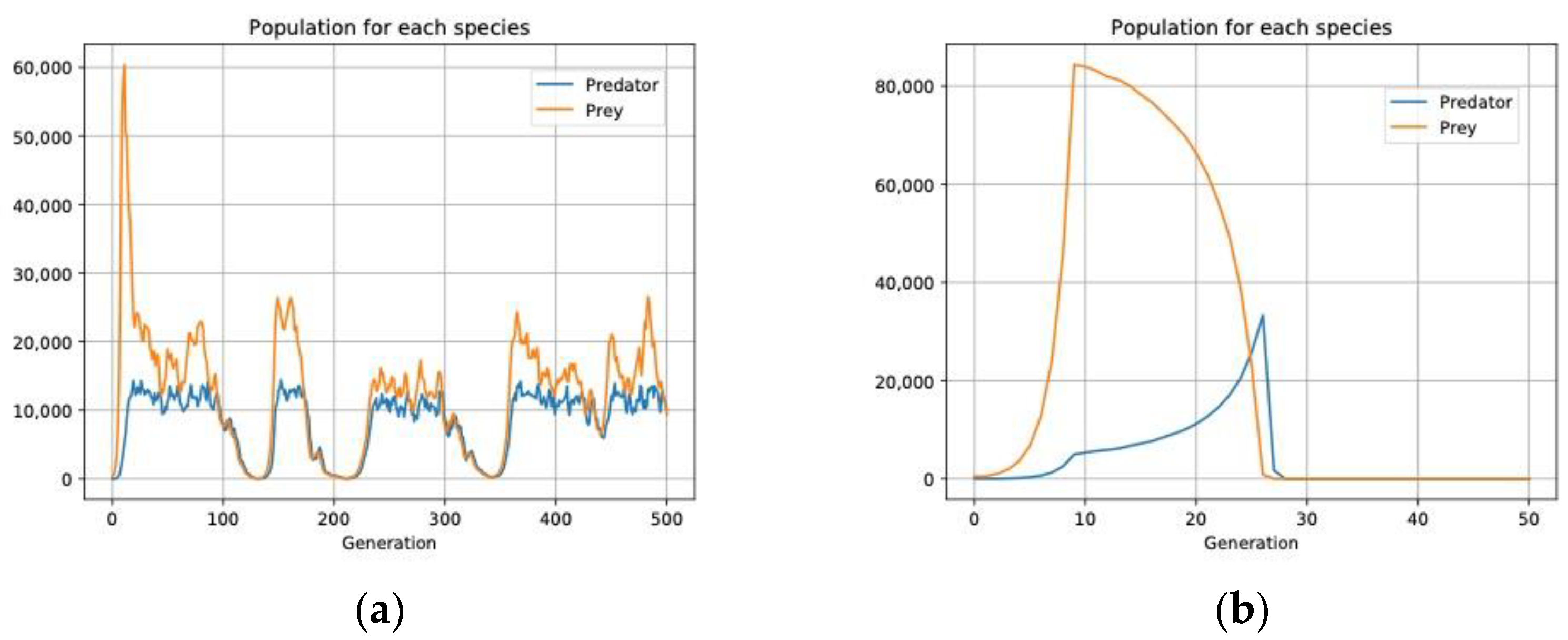
3.2. Aggregate Distribution Stabilizes Predator–Prey Interactions
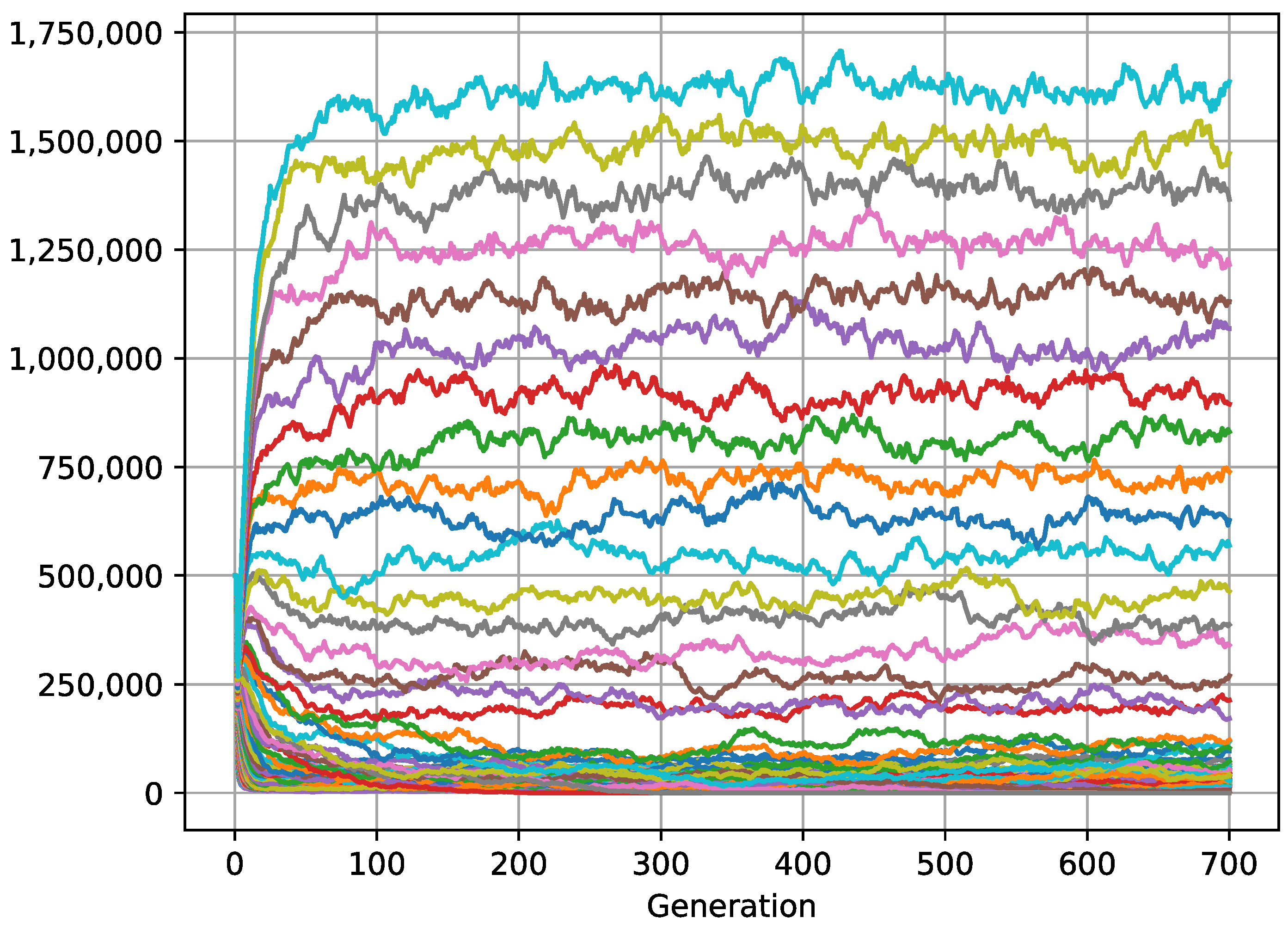
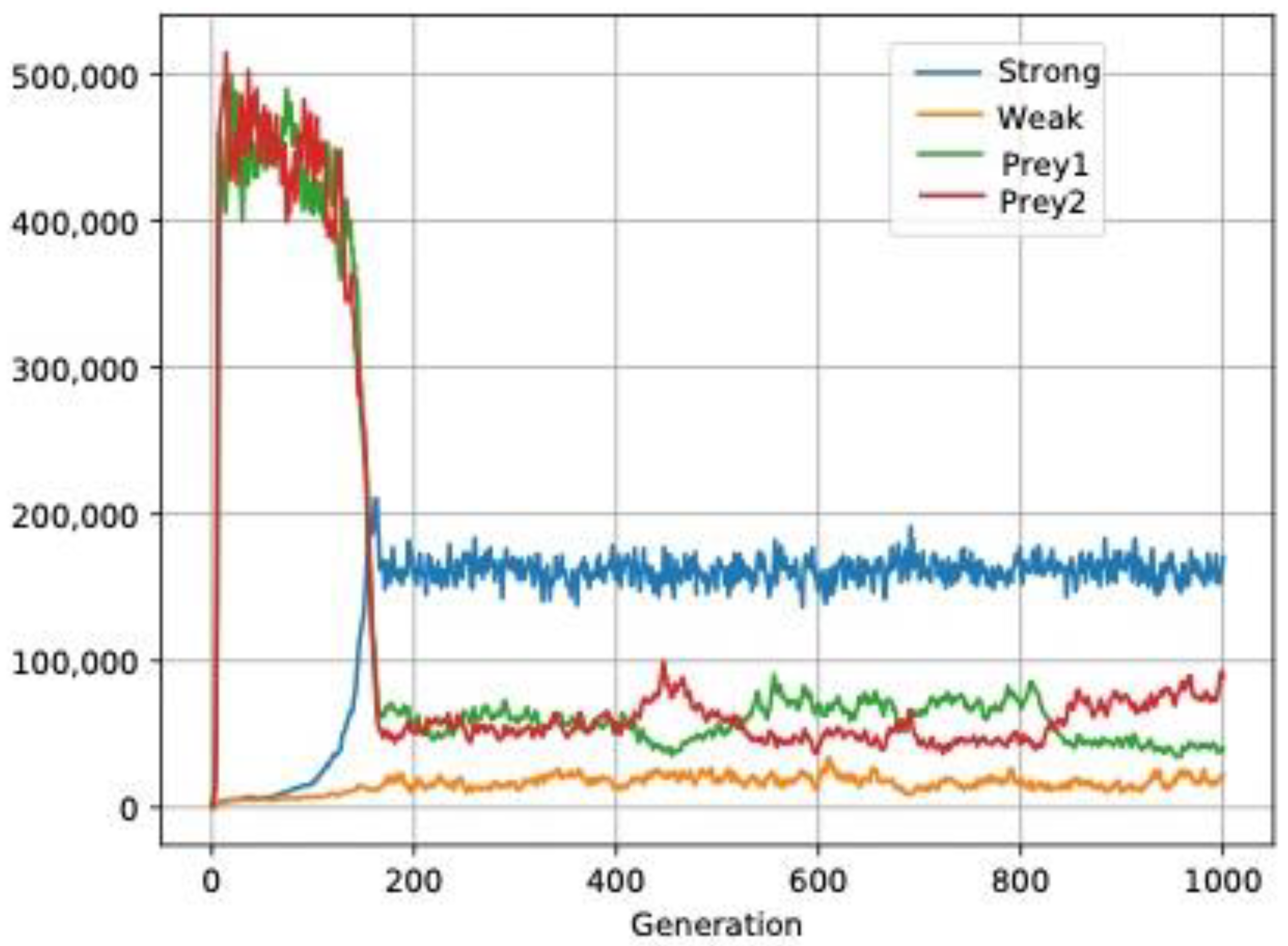
3.3. Aggregated Distribution: Another Explanation for the Paradox of the Plankton
3.4. An Explanation for Animal Aggregation
3.5. Interdemic Competition in Multilevel Selection Theory
3.6. The Selfish Herd
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hidasi-Neto, J.; Bini, L.M.; Siqueira, T.; Cianciaruso, M.V. Ecological similarity explains species abundance distribution of small mammal communities. Acta Oecol. 2020, 102, 103502. [Google Scholar] [CrossRef]
- Lowe, W.H.; McPeek, M.A. Is dispersal neutral? Trends Ecol. Evol. 2014, 29, 444–450. [Google Scholar] [CrossRef]
- Durrett, R.; Levin, S.A. Stochastic spatial models: A user’s guide to ecological applications. Philos. Trans. R. Soc. B Biol. Sci. 1994, 343, 329–350. [Google Scholar] [CrossRef]
- Chapman, D.S.; Dytham, C.; Oxford, G.S. Modelling population redistribution in a leaf beetle: An evaluation of alternative dispersal functions. J. Anim. Ecol. 2007, 76, 36–44. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Kot, M. Discrete-time growth-dispersal models with shifting species ranges. Theor. Ecol. 2011, 4, 13–25. [Google Scholar] [CrossRef]
- Radinger, J.; Wolter, C. Patterns and predictors of fish dispersal in rivers. Fish Fish. 2014, 15, 456–473. [Google Scholar] [CrossRef]
- Miller, T.E.X.; Shaw, A.K.; Inouye, B.D.; Neubert, M.G. Sex-biased dispersal and the speed of two-sex invasions. Am. Nat. 2011, 177, 549–561. [Google Scholar] [CrossRef] [PubMed]
- Baeumer, B.; Kovács, M.; Meerschaert, M.M. Fractional reproduction-dispersal equations and heavy tail dispersal kernels. Bull. Math. Biol. 2007, 69, 2281–2297. [Google Scholar] [CrossRef] [PubMed]
- Levins, R.; Culver, D. Regional Coexistence of Species and Competition between Rare Species. Proc. Natl. Acad. Sci. USA 1971, 68, 1246–1248. [Google Scholar] [CrossRef] [PubMed]
- Tilman, D. Competition and biodiversity in spatially structured habitats. Ecology 1994, 75, 2–16. [Google Scholar] [CrossRef]
- Leung, B. Aggregated parasite distributions on hosts in a homogeneous environment: Examining the Poisson null model. Int. J. Parasitol. 1998, 28, 1709–1712. [Google Scholar] [CrossRef]
- Rozsa, L.; Reiczigel, J.; Majoros, G. Quantifying Parasites in Samples of Hosts. J. Parasitol. 2000, 86, 228. [Google Scholar] [CrossRef]
- Dieckmann, U.; O’Hara, B.; Weisser, W. The evolutionary ecology of dispersal. In Trends in Ecology and Evolution; Elsevier Ltd.: Amsterdam, The Netherlands, 1999; Volume 14, pp. 88–90. [Google Scholar]
- Wright, S.J.; Biehl, C.C. Island Biogeographic Distributions: Testing for Random, Regular, and Aggregated Patterns of Species Occurrence. Am. Nat. 2015, 119, 345–357. [Google Scholar] [CrossRef]
- Ballerini, M.; Cabibbo, N.; Candelier, R.; Cavagna, A.; Cisbani, E.; Giardina, I.; Orlandi, A.; Parisi, G.; Procaccini, A.; Viale, M.; et al. Empirical investigation of starling flocks: A benchmark study in collective animal behaviour. Anim. Behav. 2008, 76, 201–215. [Google Scholar] [CrossRef]
- Muscatello, A.; Elith, J.; Kujala, H. How decisions about fitting species distribution models affect conservation outcomes. Conserv. Biol. 2021, 35, 1309–1320. [Google Scholar] [CrossRef]
- Lenormand, T. Gene flow and the limits to natural selection. Trends Ecol. Evol. 2002, 17, 183–189. [Google Scholar] [CrossRef]
- Keeling, M.J. Characteristic length scales of spatial models in ecology via fluctuation analysis. Philos. Trans. R. Soc. B Biol. Sci. 1997, 352, 1589–1601. [Google Scholar] [CrossRef]
- Falgueras-Cano, J.; Falgueras-Cano, J.A.; Moya, A. A study of the coevolution of digital organisms with an evolutionary cellular automaton. Biology 2021, 10, 1147. [Google Scholar] [CrossRef]
- van Veelen, M.; Allen, B.; Hoffman, M.; Simon, B.; Veller, C. Hamilton’s rule. J. Theor. Biol. 2017, 414, 176–230. [Google Scholar] [CrossRef]
- Nowak, M.A.; Tarnita, C.E.; Wilson, E.O. The evolution of eusociality. Nature 2010, 466, 1057–1062. [Google Scholar] [CrossRef]
- Atkinson, W.D.; Shorrocks, B. Competition on a Divided and Ephemeral Resource: A Simulation Model. J. Anim. Ecol. 1981, 50, 461. [Google Scholar] [CrossRef]
- Stoklosa, J.; Blakey, R.V.; Hui, F.K.C. An Overview of Modern Applications of Negative Binomial Modelling in Ecology and Biodiversity. Diversity 2022, 14, 320. [Google Scholar] [CrossRef]
- Holling, C.S. The Components of Predation as Revealed by a Study of Small-Mammal Predation of the European Pine Sawfly. Can. Entomol. 1959, 91, 293–320. [Google Scholar] [CrossRef]
- De Roos, A.M.; McCauley, E.; Wilson, W.G. Pattern formation and the spatial scale of interaction between predators and their prey. Theor. Popul. Biol. 1998, 53, 108–130. [Google Scholar] [CrossRef]
- Moskát, C.; Honza, M. Effect of nest and nest site characteristics on the risk of cuckoo Cuculus canorus parasitism in the great reed warbler Acrocephalus arundinaceus. Ecography 2000, 23, 335–341. [Google Scholar] [CrossRef]
- Takasu, F.; Kawasaki, K.; Nakamura, H.; Cohen, J.E.; Shigesada, N. Modeling the population dynamics of a cuckoo-host association and the evolution of host defenses. Am. Nat. 1993, 142, 819–839. [Google Scholar] [CrossRef]
- Benincà, E.; Jöhnk, K.D.; Heerkloss, R.; Huisman, J. Coupled predator-prey oscillations in a chaotic food web. Ecol. Lett. 2009, 12, 1367–1378. [Google Scholar] [CrossRef]
- Hardin, G. The competitive exclusion principle. Science 1960, 131, 1292–1297. [Google Scholar] [CrossRef]
- Gause, G.F. Experimental studies on the struggle for existence: I. Mixed population of two species of yeast. J. Exp. Biol. 1932, 9, 389–402. [Google Scholar] [CrossRef]
- Tilman, D. Resource Competition between Plankton Algae: An Experimental and Theoretical Approach. Ecology 1977, 58, 338–348. [Google Scholar] [CrossRef]
- Takeya, K.; Kuwata, A.; Yoshida, M.; Miyazaki, T. Effect of dilution rate on competitive interactions between the cyanobacterium Microcystis no vacekii and the green alga Scenedesmus quadricauda in mixed chemostat cultures. J. Plankton Res. 2004, 26, 29–35. [Google Scholar] [CrossRef]
- Kuwata, A.; Miyazaki, T. Effects of ammonium supply rates on competition between Microcystis novacekii (Cyanobacteria) and Scenedesmus quadricauda (Chlorophyta): Simulation study. Ecol. Modell. 2000, 135, 81–87. [Google Scholar] [CrossRef]
- Ogawa, Y.; Ichimura, S.E. Phytoplankton Diversity in Inland Waters of Different Trophic Status. Jpn. J. Limnol. 1984, 45, 173–177. [Google Scholar] [CrossRef]
- Ogawa, Y. Net increase rates and dynamics of phytoplankton populations under hypereutrophic and eutrophic conditions. Jpn. J. Limnol. 1988, 49, 261–268. [Google Scholar] [CrossRef]
- Hutchinson, G.E. The Paradox of the Plankton. Am. Nat. 1961, 95, 137–145. [Google Scholar] [CrossRef]
- Huisman, J.; Weissing, F.J. Biodiversity of plankton by species oscillations and chaos. Nature 1999, 402, 407–410. [Google Scholar] [CrossRef]
- Sommer, U. Comparison between steady state and non-steady state competition: Experiments with natural phytoplankton. Limnol. Oceanogr. 1985, 30, 335–346. [Google Scholar] [CrossRef]
- Levins, R. Coexistence in a variable environment. Am. Nat. 1979, 114, 765–783. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Bull. Math. Biol. 1990, 52, 153–197. [Google Scholar] [CrossRef]
- Malchow, H. Spatio-temporal pattern formation in nonlinear non-equilibrium plankton dynamics. Proc. R. Soc. B Biol. Sci. 1993, 251, 103–109. [Google Scholar] [CrossRef]
- Miyazaki, T.; Tainaka, K.I.; Togashi, T.; Suzuki, T.; Yoshimura, J. Spatial coexistence of phytoplankton species in ecological timescale. In Population Ecology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; Volume 48, pp. 107–112. [Google Scholar]
- Villarino, E.; Watson, J.R.; Jönsson, B.; Gasol, J.M.; Salazar, G.; Acinas, S.G.; Estrada, M.; Massana, R.; Logares, R.; Giner, C.R.; et al. Large-scale ocean connectivity and planktonic body size. Nat. Commun. 2018, 9, 1–13. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Doney, S.C.; Lima, I.; Boss, E.S.; Siegel, D.A. Annual cycles of ecological disturbance and recovery underlying the subarctic Atlantic spring plankton bloom. Glob. Biogeochem. Cycles 2013, 27, 526–540. [Google Scholar] [CrossRef]
- Navarro, G.; Almaraz, P.; Caballero, I.; Vázquez, Á.; Emma Huertas, I. Spatio-temporal variability of phytoplankton functional types in Alboran Sea from remote sensing images. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 963–966. [Google Scholar]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.W.; Bricaud, A.; Brotas, V.; Ciotti, A.M.; Clementson, L.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining phytoplankton diversity from ocean color: A scientific roadmap for future development. Front. Mar. Sci. 2017, 4, 55. [Google Scholar] [CrossRef]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Levin, D.A.; Kerster, H.W. An Analysis of Interspecific Pollen Exchange in Phlox. Am. Nat. 1967, 101, 387–399. [Google Scholar] [CrossRef]
- Hartley, S.; Shorrocks, B. A general framework for the aggregation model of coexistence. J. Anim. Ecol. 2002, 71, 651–662. [Google Scholar] [CrossRef]
- Sevenster, J.G. Aggregation and Coexistence. I. Theory and Analysis. J. Anim. Ecol. 1996, 65, 297. [Google Scholar] [CrossRef]
- Shorrocks, B.; Rosewell, J.; Edwards, K.; Atkinson, W. Interspecific competition is not a major organizing force in many insect communities. Nature 1984, 310, 310–312. [Google Scholar] [CrossRef]
- Iwao, S. Analysis of contagiousness in the action of mortality factors on the western tent caterpillar population by using the Mathematical expression relationshiprelationship. Res. Popul. Ecol. 1970, 12, 100–110. [Google Scholar] [CrossRef]
- Lloyd, M. ‘Mean Crowding’. J. Anim. Ecol. 1967, 36, 1. [Google Scholar] [CrossRef]
- Taylor, A.; Crizer, A. A Modified Lotka-Volterra Competition Model with a Non-Linear Relationship Between Species. Statistics 2005, 6, 8. [Google Scholar]
- Gavina, M.K.A.; Tahara, T.; Tainaka, K.I.; Ito, H.; Morita, S.; Ichinose, G.; Okabe, T.; Togashi, T.; Nagatani, T.; Yoshimura, J. Multi-species coexistence in Lotka-Volterra competitive systems with crowding effects. Sci. Rep. 2018, 8, 1198. [Google Scholar] [CrossRef]
- Tahara, T.; Gavina, M.K.A.; Kawano, T.; Tubay, J.M.; Rabajante, J.F.; Ito, H.; Morita, S.; Ichinose, G.; Okabe, T.; Togashi, T.; et al. Asymptotic stability of a modified Lotka-Volterra model with small immigrations. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Horgan, F.G. Aggregated distribution of resources creates competition refuges for rainforest dung beetles. Ecography 2005, 28, 603–618. [Google Scholar] [CrossRef]
- Ekaka-a, E.N.; Nafo, N.M. Stability analysis of predator-prey interaction with a crowding effect. Sci. Afr. 2013, 12, 23–27. [Google Scholar] [CrossRef]
- Hara, T.; Koike, F.; Matsui, K. Crowding effect in marine macrophytic algae populations. Bot. Mag. = Shokubutsu-gaku-zasshi 1986, 99, 319–321. [Google Scholar] [CrossRef]
- Suehiro, K.; Ogawa, H.; Hozumi, K. The crowding effect in an artificially mixed population of three species. Bot. Mag. = Shokubutsu-gaku-zasshi 1985, 98, 347–357. [Google Scholar] [CrossRef]
- Ghazal, A.M.; Avery, R.A. Population dynamics of Hymenolepis nana in mice: Fecundity and the ‘crowding effect. Parasitology 1974, 69, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Sumpter, D.T. Collective Animal Behavior; Princeton University Press: Princeton, NJ, USA, 2010; ISBN 9780691129631. [Google Scholar]
- Lion, S.; Baalen, M. Van Self-structuring in spatial evolutionary ecology. Ecol. Lett. 2008, 11, 277–295. [Google Scholar] [CrossRef]
- Chen, X.; Dong, X.; Be’er, A.; Swinney, H.L.; Zhang, H.P. Scale-Invariant Correlations in Dynamic Bacterial Clusters. Phys. Rev. Lett. 2012, 108, 148101. [Google Scholar] [CrossRef] [PubMed]
- Abrahams, M.V.; Colgan, P.W. Risk of predation, hydrodynamic efficiency and their influence on school structure. Environ. Biol. Fishes 1985, 13, 195–202. [Google Scholar] [CrossRef]
- Fish, F.E. Kinematics of ducklings swimming in formation: Consequences of position. J. Exp. Zool. 1995, 273, 1–11. [Google Scholar] [CrossRef]
- Partridge, B.L.; Johansson, J.; Kalish, J. The structure of schools of giant bluefin tuna in Cape Cod Bay. Environ. Biol. Fishes 1983, 9, 253–262. [Google Scholar] [CrossRef]
- Krause, J.; Ruxton, G.D.; Rubenstein, D. Is there always an influence of shoal size on predator hunting success? J. Fish Biol. 1998, 52, 494–501. [Google Scholar] [CrossRef]
- Turner, G.F.; Pitcher, T.J. Attack Abatement: A Model for Group Protection by Combined Avoidance and Dilution. Am. Nat. 1986, 128, 228–240. [Google Scholar] [CrossRef]
- Olson, R.S.; Knoester, D.B.; Adami, C. Critical interplay between density-dependent predation and evolution of the selfish herd. In Proceedings of the GECCO 2013—2013 Genetic and Evolutionary Computation Conference, Amsterdam, The Netherlands, 6–10 July 2013; ACM Press: New York, NY, USA, 2013; pp. 247–254. [Google Scholar]
- Hamilton, W.D. Geometry for the selfish herd. J. Theor. Biol. 1971, 31, 295–311. [Google Scholar] [CrossRef]
- Ioannou, C.C.; Tosh, C.R.; Neville, L.; Krause, J. The confusion effect—from neural networks to reduced predation risk. Behav. Ecol. 2007, 19, 126–130. [Google Scholar] [CrossRef]
- Biro, D.; Sumpter, D.J.T.; Meade, J.; Guilford, T. From Compromise to Leadership in Pigeon Homing. Curr. Biol. 2006, 16, 2123–2128. [Google Scholar] [CrossRef]
- Roberts, G. Why individual vigilance declines as group size increases. Anim. Behav. 1996, 51, 1077–1086. [Google Scholar] [CrossRef]
- Demšar, J.; Hemelrijk, C.K.; Hildenbrandt, H.; Bajec, I.L. Simulating predator attacks on schools: Evolving composite tactics. Ecol. Modell. 2015, 304, 22–33. [Google Scholar] [CrossRef]
- Krakauer, D.C. Groups confuse predators by exploiting perceptual bottlenecks: A connectionist model of the confusion effect. Behav. Ecol. Sociobiol. 1995, 36, 421–429. [Google Scholar] [CrossRef]
- Jeschke, J.M.; Tollrian, R. Prey swarming: Which predators become confused and why? Anim. Behav. 2007, 74, 387–393. [Google Scholar] [CrossRef]
- Milinski, M.; Heller, R. Influence of a predator on the optimal foraging behaviour of sticklebacks (Gasterosteus aculeatus L.). Nature 1978, 275, 642–644. [Google Scholar] [CrossRef]
- Partridge, B.L.; Pitcher, T.; Cullen, J.M.; Wilson, J. The three-dimensional structure of fish schools. Behav. Ecol. Sociobiol. 1980, 6, 277–288. [Google Scholar] [CrossRef]
- Loehle, C. Social Barriers to Pathogen Transmission in Wild Animal Populations. Ecology 1995, 76, 326–335. [Google Scholar] [CrossRef]
- Brown, C.R.; Brown, M.B. Ectoparasitism as a Cost of Coloniality in Cliff Swallows (Hirundo Pyrrhonota). Ecology 1986, 67, 1206–1218. [Google Scholar] [CrossRef]
- Alexander, R.D. The Evolution of Social Behavior. Annu. Rev. Ecol. Syst. 1974, 5, 325–383. [Google Scholar] [CrossRef]
- Pride, R.E. Optimal group size and seasonal stress in ring-tailed lemurs (Lemur catta). Behav. Ecol. 2005, 16, 550–560. [Google Scholar] [CrossRef]
- Da Silva, J.; Macdonald, D.W.; Evans, P.G.H. Net costs of group living in a solitary forager, the Eurasian badger (Meles meles). Behav. Ecol. 1994, 5, 151–158. [Google Scholar] [CrossRef]
- Sterck, E.H.M.; Watts, D.P.; Van Schaik, C.P. The evolution of female social relationships in nonhuman primates. Behav. Ecol. Sociobiol. 1997, 41, 291–309. [Google Scholar] [CrossRef]
- Eldridge, S. Adams Experimental analysis of territory size in a population of the fire ant Solenopsis invicta. Behav. Ecol. 2003, 14, 48–53. [Google Scholar] [CrossRef]
- Molvar, E.M.; Bowyer, R.T. Costs and Benefits of Group Living in a Recently Social Ungulate: The Alaskan Moose. J. Mammal. 1994, 75, 621–630. [Google Scholar] [CrossRef]
- Ford, J.R.; Swearer, S.E. Two’s company, three’s a crowd: Food and shelter limitation outweigh the benefits of group living in a shoaling fish. Ecology 2013, 94, 1069–1077. [Google Scholar] [CrossRef] [PubMed]
- Rossman, S.; Ostrom, P.H.; Stolen, M.; Barros, N.B.; Gandhi, H.; Stricker, C.A.; Wells, R.S. Individual specialization in the foraging habits of female bottlenose dolphins living in a trophically diverse and habitat rich estuary. Oecologia 2015, 178, 415–425. [Google Scholar] [CrossRef]
- Chapman, C.A.; Valenta, K. Costs and benefits of group living are neither simple nor linear. Proc. Natl. Acad. Sci. USA 2015, 112, 14751–14752. [Google Scholar] [CrossRef]
- Gomulkiewicz, R.; Holt, R.D. When does evolution by natural selection prevent extinction? Evolution 1995, 49, 201–207. [Google Scholar] [CrossRef]
- Fahrig, L.; Merriam, G. Conservation of fragmented populations. NCASI Tech. Bull. 1999, 8, 159–160. [Google Scholar] [CrossRef]
- Travis, J.M.J.; Dytham, C. Habitat persistence, habitat availability and the evolution of dispersal. Proc. R. Soc. B Biol. Sci. 1999, 266, 723–728. [Google Scholar] [CrossRef]
- Kéfi, S.; Rietkerk, M.; van Baalen, M.; Loreau, M. Local facilitation, bistability and transitions in arid ecosystems. Theor. Popul. Biol. 2007, 71, 367–379. [Google Scholar] [CrossRef]
- May, R.M.; Nowak, M.A. Superinfection, metapopulation dynamics, and the evolution of diversity. J. Theor. Biol. 1994, 170, 95–114. [Google Scholar] [CrossRef]
- ARTHUR, D.R. Parasitic Insects. Nature 1971, 233, 503–504. [Google Scholar] [CrossRef]
- Godfray, H.C.J.; Godfray, H.C.J. Parasitoids: Behavioral and Evolutionary Ecology; Princeton University Press: Princeton, NJ, USA, 1994; Volume 67, ISBN 0691000476. [Google Scholar]
- Nicholson, A.J.; Bailey, V.A. The Balance of Animal Populations—Part I. Proc. Zool. Soc. 1935, 105, 551–598. [Google Scholar] [CrossRef]
- May, R.M. Theoretical Ecology: Principles and Applications; Robert, M., McLean, A.R., Eds.; Oxford University Press: Oxford, UK, 2007; ISBN 9780199209989. [Google Scholar]
- Waters, C.M.; Bassler, B.L. Quorum sensing: Cell-to-cell communication in bacteria. Annu. Rev. Cell Dev. Biol. 2005, 21, 319–346. [Google Scholar] [CrossRef] [PubMed]
- Cornforth, D.M.; Foster, K.R. Competition sensing: The social side of bacterial stress responses. Nat. Rev. Microbiol. 2013, 11, 285–293. [Google Scholar] [CrossRef]
- Sidorovich, V. Analysis of Vertebrate Predator-Prey Community: Studies within the European Forest Zone in Terrains with Transitional Mixed Forest in Belarus; Tesey: Obninsk, Russia, 2011; ISBN 9854634566. [Google Scholar]
- Suarez, A.V.; Case, T.J. Bottom-up effects on persistence of a specialist predator: Ant invasions and horned lizards. Ecol. Appl. 2002, 12, 291–298. [Google Scholar] [CrossRef]
- Bonsall, M.B.; Hassell, M.P. The effects of metapopulation structure on indirect interactions in host-parasitoid assemblages. Proc. R. Soc. B Biol. Sci. 2000, 267, 2207–2212. [Google Scholar] [CrossRef]
- Bonsall, M.B.; Bull, J.C.; Pickup, N.J.; Hassell, M.P. Indirect effects and spatial scaling affect the persistence of multispecies metapopulations. Proc. R. Soc. B Biol. Sci. 2005, 272, 1465–1471. [Google Scholar] [CrossRef]
- Chesson, P.L.; Murdoch, W.W. Aggregation of risk: Relationships among host- parasitoid models. Am. Nat. 1986, 127, 696–715. [Google Scholar] [CrossRef]
- Pacala, S.W.; Hassell, M.P.; May, R.M. Host-parasitoid associations in patchy environments. Nature 1990, 344, 150–153. [Google Scholar] [CrossRef]
- Poulin, R. Explaining variability in parasite aggregation levels among host samples. Parasitology 2013, 140, 541–546. [Google Scholar] [CrossRef]
- Boots, M.; Sasaki, A. “Small worlds” and the evolution of virulence: Infection occurs locally and at a distance. Proc. R. Soc. B Biol. Sci. 1999, 266, 1933–1938. [Google Scholar] [CrossRef] [PubMed]
- De Vos, A.; O’Riain, M.J. Sharks shape the geometry of a selfish seal herd: Experimental evidence from seal decoys. Biol. Lett. 2010, 6, 48–50. [Google Scholar] [CrossRef] [PubMed]
- Boerlijst, M.C.; Hogeweg, P. Spiral wave structure in pre-biotic evolution: Hypercycles stable against parasites. Phys. D Nonlinear Phenom. 1991, 48, 17–28. [Google Scholar] [CrossRef]
- Heisler, I.L.; Damuth, J. A method for analyzing selection in hierarchically structured populations. Am. Nat. 1987, 130, 582–602. [Google Scholar] [CrossRef]
- Falgueras-Cano, J.; Carretero-Díaz, J.M.; Moya, A. Weighted fitness theory: An approach to symbiotic communities. Environ. Microbiol. Rep. 2017, 9, 44–46. [Google Scholar] [CrossRef][Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falgueras-Cano, J.; Falgueras-Cano, J.A.; Moya, A. Aggregated Distribution as an Explanation for the Paradox of Plankton and Collective Animal Behavior. Biology 2022, 11, 1477. https://doi.org/10.3390/biology11101477
Falgueras-Cano J, Falgueras-Cano JA, Moya A. Aggregated Distribution as an Explanation for the Paradox of Plankton and Collective Animal Behavior. Biology. 2022; 11(10):1477. https://doi.org/10.3390/biology11101477
Chicago/Turabian StyleFalgueras-Cano, Javier, Juan Antonio Falgueras-Cano, and Andrés Moya. 2022. "Aggregated Distribution as an Explanation for the Paradox of Plankton and Collective Animal Behavior" Biology 11, no. 10: 1477. https://doi.org/10.3390/biology11101477
APA StyleFalgueras-Cano, J., Falgueras-Cano, J. A., & Moya, A. (2022). Aggregated Distribution as an Explanation for the Paradox of Plankton and Collective Animal Behavior. Biology, 11(10), 1477. https://doi.org/10.3390/biology11101477






