SARS-CoV-2 and Rohingya Refugee Camp, Bangladesh: Uncertainty and How the Government Took Over the Situation
Abstract
Simple Summary
Abstract
1. Introduction
2. Methodology
2.1. Mathematical Model and Formulation
2.2. Equilibrium Points
2.3. Disease-Free Equilibrium Point
2.4. Basic Reproduction Number
2.5. Positivity and Boundedness of Solutions
3. Data
4. Results
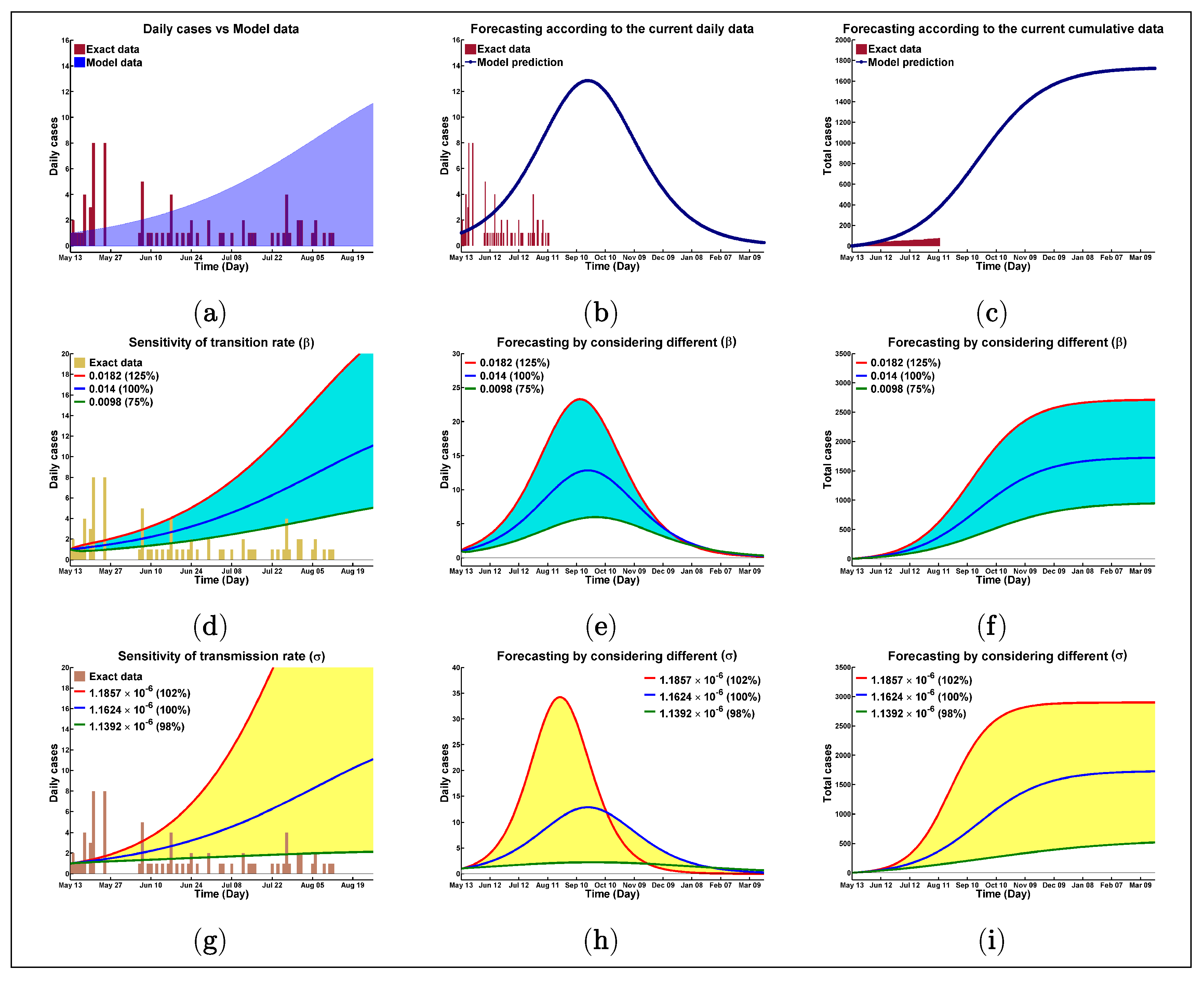
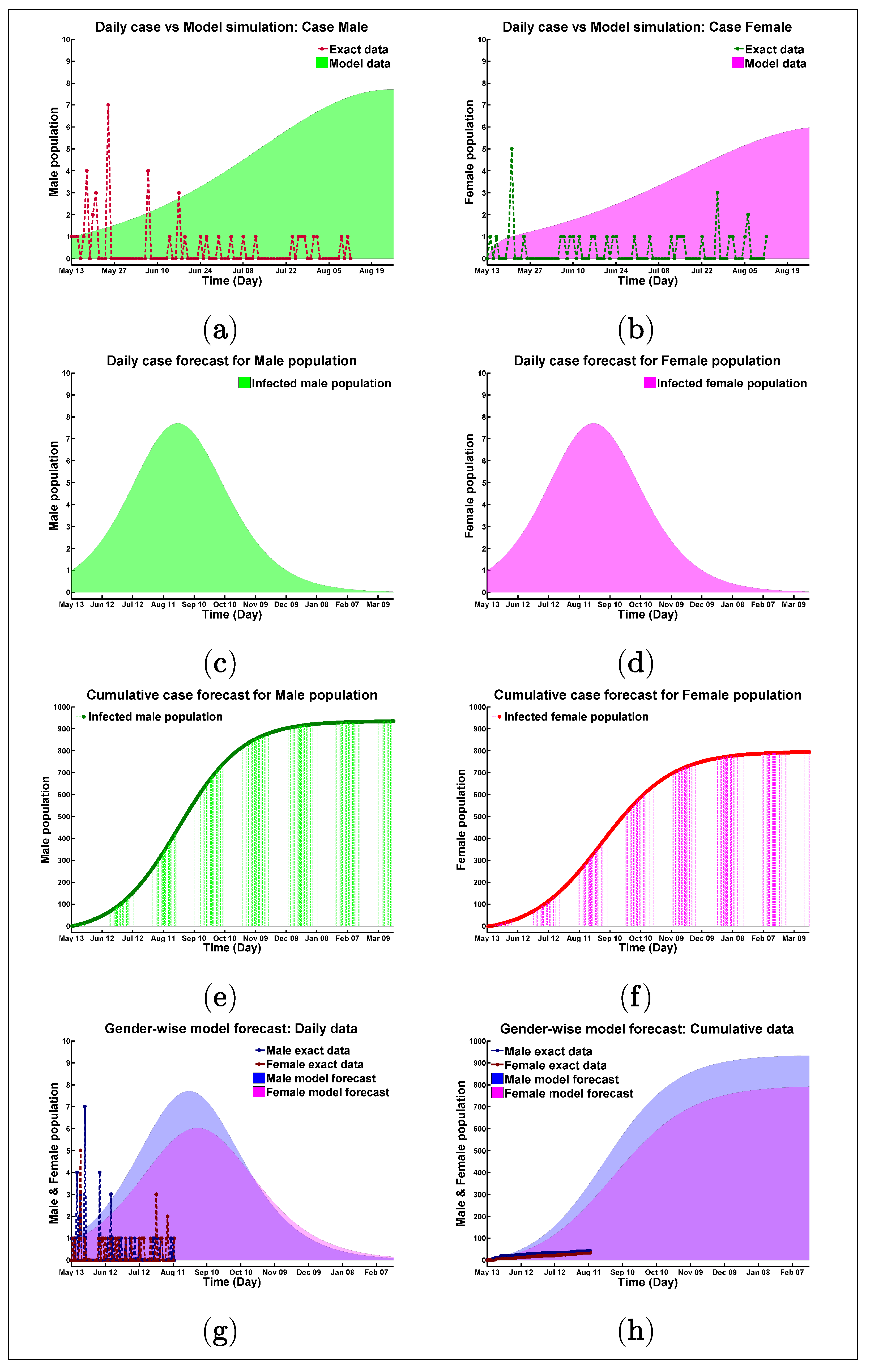
4.1. Numerical Illustrations, Data Fitting, and Model Validation
- First, we have tried our best to counterfeit the real data with the model generated forecast scenario.
- Then, we related the model result to be uninfluenced partially from the very fluctuating real data. These results warn about the worst scenario of this pandemic in this camp if initial strict initiatives were failed to be implemented or if the situation gets out of control for any other reason.
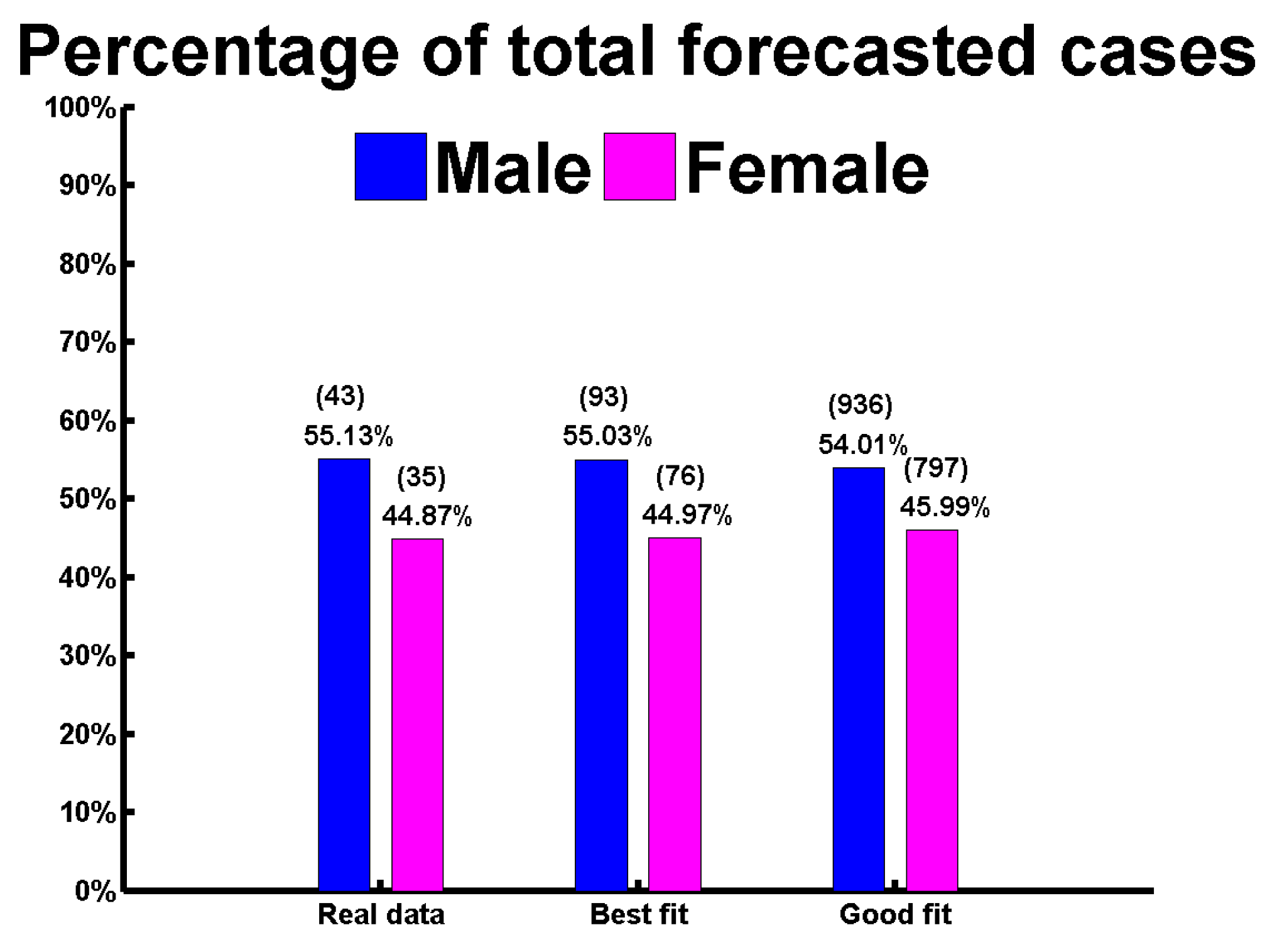
4.2. Best Fitting Data
4.3. Good Fitting Data
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| COVID-19 | Coronavirus diseases |
| SEIR | Susceptible-asymptomatically infected-infectious-recovered |
| SARS-CoV-2 | Severe acute respiratory syndrome coronavirus 2 |
| FDMN | Forcibly displaced Myanmar nationals |
| UNHCR | United Nations High Commissioner for Refugees |
| SARI | Severe acute respiratory illness |
| ITC | Isolation and treatment center |
| GAM | Global acute malnutrition |
| SIR | Susceptible-infectious-recovered |
| DFE | Disease-free equilibrium |
Appendix A
| Notation | Interpretations | Notation | Interpretations |
|---|---|---|---|
| Transition rate from E to I class | Natural death rate | ||
| Recruitment rate in S class | Disease induced death rate | ||
| Transmission rate from S to E & I classes | Recovery rate of E class | ||
| Initial population in S | Recovery rate of I class | ||
| Initial population in E | Initial population in I |
| Parameters | Description | Value (Best Fit) | Value (Good Fit) | References |
|---|---|---|---|---|
| Susceptible population | [3] | |||
| on 13 March 2020 (aprox.) | ||||
| asymptomatically infected | 100 | 30 | Assumed | |
| population on 13 March 2020 (aprox.) | ||||
| Infectious population on 13 March 2020 | 1 | 1 | [26] | |
| Recovered population on 13 March 2020 | 0 | 0 | [26] | |
| Per day average birth | 60 | 60 | [34] | |
| Per day transition rate from E to I | Assumed | |||
| Per day transmission rate | 1.1623 | 1.1624 | Estimated | |
| from S to E & I | ||||
| Per day recovery rate of E | Assumed | |||
| Per day recovery rate of I | Estimated | |||
| Per day natural death rate | 9.2997 | 9.3019 | [35] | |
| Per day disease induced death rate | Estimated | |||
| Average basic reproduction number | Estimated |
References
- Worldometer. Coronavirus Cases. 2020. Available online: https://www.worldometers.info/coronavirus/? (accessed on 21 September 2020).
- WHO. Archived: WHO Timeline—COVID-19. 27 April 2020. Available online: https://www.who.int/news-room/detail/27-04-2020-who-timeline—covid-19 (accessed on 21 September 2020).
- UNHCR. Situation Refugee Response in Bangladesh. Available online: https://data2.unhcr.org/en/situations/myanmar_refugees (accessed on 21 September 2020).
- Al Jazeera. First, Coronavirus Case Found in Bangladesh Rohingya Refugee Camps. Coronavirus Pandemic News. 15 May 2020. Available online: https://www.aljazeera.com/news/2020/05/coronavirus-case-bangladesh-rohingya-refugee-camps-200514143543211.html (accessed on 22 September 2020).
- WHO. Rohingya Crisis Situation Report # 18; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- WHO. Rohingya Crisis Situation Report # 37; WHO: Geneva, Switzerland, 2021. [Google Scholar]
- Chowdhury, M.; Billah, S.; Karim, F.; Khan, A.; Islam, S.; Arifeen, S. Report on Demographic Profiling and Needs Assessment of Maternal and Child Health (MCH) Care for the Rohingya Refugee Population in Cox’s Bazar, Bangladesh; Maternal and Child Health Division: 2018. Available online: http://dspace.icddrb.org/jspui/handle/123456789/9067 (accessed on 21 September 2020).
- Action Against Hunger. Emergency Nutrition Assessment: Final Report; Action against Hunger: Paris, France, 2019. [Google Scholar]
- Calafiore, G.C.; Novara, C.; Possieri, C. A modified sir model for the covid-19 contagion in italy. arXiv 2020, arXiv:2003.14391. [Google Scholar]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals 2020. [Google Scholar] [CrossRef] [PubMed]
- Peirlinck, M.; Linka, K.; Costabal, F.S.; Kuhl, E. Outbreak dynamics of COVID-19 in China and the United States. Biomech. Model. Mechanobiol. 2020, 19, 2179–2193. [Google Scholar] [CrossRef] [PubMed]
- Kamrujjaman, M.; Jubyrea, J.; Islam, M.S. Data analysis and mathematical model: Control measures and prediction to prevent COVID-19 outbreak. Arab. J. Med. Sci. 2020, 3, 5–9. [Google Scholar]
- Aràndiga, F.; Baeza, A.; Cordero-Carrión, I.; Donat, R.; Martí, M.C.; Mulet, P.; Yáñez, D.F. A Spatial-Temporal Model for the Evolution of the COVID-19 Pandemic in Spain Including Mobility. Mathematics 2020, 8, 1677. [Google Scholar] [CrossRef]
- Chowdhury, R.; Heng, K.; Shawon, M.S.R.; Goh, G.; Okonofua, D.; Ochoa-Rosales, C.; Gonzalez-Jaramillo, V.; Bhuiya, A.; Reidpath, D.; Prathapan, S.; et al. Dynamic interventions to control COVID-19 pandemic: A multivariate prediction modelling study comparing 16 worldwide countries. Eur. J. Epidemiol. 2020, 35, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R. Mathematical Modeling of Infectious Diseases Using Ordinary and Fractional Differential Equations. Ph.D. Thesis, Texas Tech University, Lubbock, TX, USA, 2020. [Google Scholar]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef]
- He, S.; Tang, S.; Rong, L. A discrete stochastic model of the COVID-19 outbreak: Forecast and control. Math. Biosci. Eng. 2020, 17, 2792–2804. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Owusu, M.A.; Jin, Z.; Oduro, F.T.; Abidemi, A.; Gyasi, E.O. Global stability and cost-effectiveness analysis of COVID-19 considering the impact of the environment: Using data from Ghana. Chaos Solitons Fractals 2020, 140, 110103. [Google Scholar] [CrossRef]
- Guo, Z.G.; Sun, G.Q.; Wang, Z.; Jin, Z.; Li, L.; Li, C. Spatial dynamics of an epidemic model with nonlocal infection. Appl. Math. Comput. 2020, 377, 125158. [Google Scholar] [CrossRef]
- Biswas, K.; Khaleque, A.; Sen, P. COVID-19 spread: Reproduction of data and prediction using a SIR model on Euclidean network. arXiv 2020, arXiv:2003.07063. [Google Scholar]
- Chang, S.L.; Harding, N.; Zachreson, C.; Cliff, O.M.; Prokopenko, M. Modelling transmission and control of the COVID-19 pandemic in Australia. Nat. Commun. 2020, 11, 5710. [Google Scholar] [CrossRef]
- Islam, M.S.; Ira, J.I.; Kabir, K.M.A.; Kamrujjaman, M. Effect of lockdown and isolation to suppress the COVID-19 in Bangladesh: An epidemic compartments model. J. Appl. Math. Comput. 2020, 4, 83–93. [Google Scholar] [CrossRef]
- Nabi, K.N. Forecasting COVID-19 pandemic: A data-driven analysis. Chaos Solitons Fractals 2020, 139, 110046. [Google Scholar] [CrossRef] [PubMed]
- Khan, I.M.; Haque, U.; Kaisar, S.; Rahman, M.S. A Computational Modeling Study of COVID-19 in Bangladesh. Am. J. Trop. Med. Hyg. 2020, 104, 66–74. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.M.; Yunus, M.Y. Rohingya refugees at high risk of COVID-19 in Bangladesh. Lancet Glob. Health 2020, 8, e993–e994. [Google Scholar] [CrossRef]
- Jubayer, F.; Kayshar, S.; Islam Limon, T. First, COVID-19 case in the Rohingya camp in Bangladesh: Needs proper attention. Public Health 2020. [Google Scholar] [CrossRef]
- Truelove, S.; Abrahim, O.; Altare, C.; Lauer, S.A.; Grantz, K.H.; Azman, A.S.; Spiegel, P. The potential impact of COVID-19 in refugee camps in Bangladesh and beyond: A modeling study. PLoS Med. 2020, 17, e1003144. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D. Mathematical Biology: I. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- WebMD. Latest Coronavirus News (Live Updates). 2020. Available online: https://www.webmd.com/lung/news/20200124/coronavirus-2020-outbreak-latest-updates (accessed on 18 September 2020).
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Kamrujjaman, M.; Mahmud, M.S.; Islam, M.S. Dynamics of a diffusive vaccination model with therapeutic impact and nonlinear incidence in epidemiology. J. Biol. Dyn. 2020, 1–29. [Google Scholar] [CrossRef]
- Cox’s Bazar Civil Surgeon Office, Chittagong, Bangladesh. 2020. Available online: http://facilityregistry.dghs.gov.bd/org_profile.php?org_code=10000750 (accessed on 18 September 2020).
- TIME. About 60 Rohingya Babies Are Born Every Day in Refugee Camps, the U.N. Says | TIME. 2018. Available online: https://time.com/5280232/myanmar-bangladesh-rohingya-babies-births/ (accessed on 18 September 2020).
- Guzek, J.; Siddiqui, R.; White, K. Health Survey in Kutupalong and Balukhali Refugee Settlements; Bangladesh Survey Report; Cox’s Bazar, Bangladesh. 2017. Available online: https://reliefweb.int/report/bangladesh/health-survey-kutupalong-and-balukhali-refugee-settlements-cox-s-bazar-bangladesh (accessed on 18 September 2020).
- China CDC Weekly. The Epidemiological Characteristics of an Outbreak of 2019 Novel Coronavirus Diseases (COVID-19)—China 2020. China CDC Wkly. 2020, 2, 113–122. [Google Scholar] [CrossRef]
- Chen, N.; Zhou, M.; Dong, X.; Qu, J.; Gong, F.; Han, Y.; Qiu, Y.; Wang, J.; Liu, Y.; Wei, Y.; et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. Lancet 2020, 395, 507–513. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, M.; Yang, L.; Li, Y.; Wang, L.; Huang, Z.; Wang, L.; Chen, Z.; Zhou, M. Prevalence and patterns of tobacco smoking among Chinese adult men and women: Findings of the 2010 national smoking survey. J. Epidemiol. Community Health 2017, 71, 154–161. [Google Scholar] [CrossRef]
- The Sentinel Project. The Bhasan Char Relocation Project—Implications for Rohingya Refugees in Bangladesh. Available online: https://reliefweb.int/report/bangladesh/bhasan-char-relocation-project\-implications-rohingya-refugees-bangladesh (accessed on 17 January 2020).
- The Guardian. Bangladesh Begins Moving Rohingya Families to Remote Island. Available online: https://www.theguardian.com/global-development/2020/dec/03/bangladesh-begins-moving-rohingya-families-to-remote-island (accessed on 4 December 2020).
- Truelove, S.A.; Keegan, L.T.; Moss, W.J.; Chaisson, L.H.; Macher, E.; Azman, A.S.; Lessler, J. Clinical and Epidemiological Aspects of Diphtheria: A Systematic Review and Pooled Analysis. Clin. Infect. Dis. 2020, 71, 89–97. [Google Scholar] [CrossRef]
- Davidson, H. First COVID-19 Case Happened in November, China Government Records Show—Report. The Guardian. 13 March 2020. Available online: https://www.theguardian.com/world/2020/mar/13/first-covid-19-case-happened-in-november-china-government-records-show-report (accessed on 4 December 2020).
- World Health Organization. Timeline of WHO’s Response to COVID-19. 31 July 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/interactive-timeline (accessed on 18 October 2020).
- The Business Standard. WHO Acknowledges ‘Evidence Emerging’ of Airborne Spread of COVID-19. 7 July 2020. Available online: https://www.reuters.com/article/us-health-coronavirus-who-airborne-idUSKBN2482AU (accessed on 18 October 2020).
- World Health Organization. Modes of Transmission of Virus Causing COVID-19: Implications for IPC Precaution Recommendations. 29 March 2020. Available online: https://www.who.int/news-room/commentaries/detail/modes-of-transmission-of-virus-causing-covid-19-implications-for-ipc-precaution-recommendations (accessed on 18 October 2020).
- Liu, J.; Liao, X.; Qian, S.; Yuan, J.; Wang, F.; Liu, Y.; Wang, Z.; Wang, F.S.; Liu, L.; Zhang, Z. Community transmission of severe acute respiratory syndrome Coronavirus 2, Shenzhen, China, 2020. Emerg. Infect. Dis. 2020, 26, 1320–1323. [Google Scholar] [CrossRef]
- van Doremalen, N.; Bushmaker, T.; Morris, D.H.; Holbrook, M.G.; Gamble, A.; Williamson, B.N.; Tamin, A.; Harcourt, J.L.; Thornburg, N.J.; Gerber, S.I.; et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N. Engl. J. Med. 2020, 382, 1564–1567. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.F.W.; Yuan, S.; Kok, K.H.; To, K.K.W.; Chu, H.; Yang, J.; Xing, F.; Liu, J.; Chik-Yan Yip, C.; Wing-Shan Poon, R.; et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: A study of a family cluster. Lancet 2020, 395, 514–523. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Mahmud, M.S.; Kamrujjaman, M.; Jubyrea, J.; Islam, M.S.; Islam, M.S. Quarantine vs Social Consciousness: A Prediction to Control COVID-19 Infection. J. Appl. Life Sci. Int. 2020, 23, 20–27. [Google Scholar] [CrossRef]
- Chatterjee, K.; Chatterjee, K.; Kumar, A.; Shankar, S. Healthcare impact of COVID-19 epidemic in India: A stochastic mathematical model. Med. J. Armed Forces India 2020, 76, 147–155. [Google Scholar] [CrossRef]
- Kamrujjaman, M.; Mahmud, M.S.; Islam, M.S. Coronavirus Outbreak and the Mathematical Growth Map of COVID-19. Annu. Res. Rev. Biol. 2020, 35, 72–78. [Google Scholar] [CrossRef]
- Boniol, M.; McIsaac, M.; Xu, L.; Wuliji, T.; Diallo, K.; Campbell, J. Gender Equity in the Health Workforce: Analysis of 104 Countries; WHO: Geneva, Switzerland, 2019. [Google Scholar]
- Wenham, C.; Smith, J.; Morgan, R. COVID-19: The gendered impacts of the outbreak. Lancet 2020, 395, 846–848. [Google Scholar] [CrossRef]
- Li, B.; Yang, J.; Zhao, F.; Zhi, L.; Wang, X.; Liu, L.; Bi, Z.; Zhao, Y. Prevalence and impact of cardiovascular metabolic diseases on COVID-19 in China. Clin. Res. Cardiol. 2020, 109, 531–538. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamrujjaman, M.; Mahmud, M.S.; Ahmed, S.; Qayum, M.O.; Alam, M.M.; Hassan, M.N.; Islam, M.R.; Nipa, K.F.; Bulut, U. SARS-CoV-2 and Rohingya Refugee Camp, Bangladesh: Uncertainty and How the Government Took Over the Situation. Biology 2021, 10, 124. https://doi.org/10.3390/biology10020124
Kamrujjaman M, Mahmud MS, Ahmed S, Qayum MO, Alam MM, Hassan MN, Islam MR, Nipa KF, Bulut U. SARS-CoV-2 and Rohingya Refugee Camp, Bangladesh: Uncertainty and How the Government Took Over the Situation. Biology. 2021; 10(2):124. https://doi.org/10.3390/biology10020124
Chicago/Turabian StyleKamrujjaman, Md., Md. Shahriar Mahmud, Shakil Ahmed, Md. Omar Qayum, Mohammad Morshad Alam, Md Nazmul Hassan, Md Rafiul Islam, Kaniz Fatema Nipa, and Ummugul Bulut. 2021. "SARS-CoV-2 and Rohingya Refugee Camp, Bangladesh: Uncertainty and How the Government Took Over the Situation" Biology 10, no. 2: 124. https://doi.org/10.3390/biology10020124
APA StyleKamrujjaman, M., Mahmud, M. S., Ahmed, S., Qayum, M. O., Alam, M. M., Hassan, M. N., Islam, M. R., Nipa, K. F., & Bulut, U. (2021). SARS-CoV-2 and Rohingya Refugee Camp, Bangladesh: Uncertainty and How the Government Took Over the Situation. Biology, 10(2), 124. https://doi.org/10.3390/biology10020124









