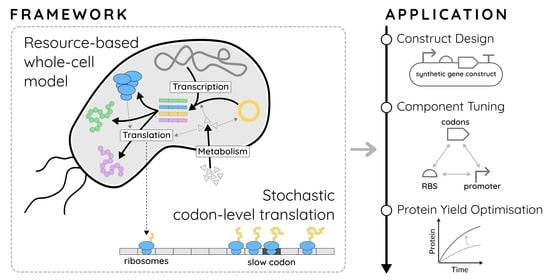
A Modelling Framework Linking Resource-Based Stochastic Translation to the Optimal Design of Synthetic Constructs
Abstract
Simple Summary
Abstract
1. Introduction
1.1. Whole-Cell Models in Synthetic Biology
1.2. Slow Codons and Ribosomal Queues
1.3. Biophysical Models of Translation
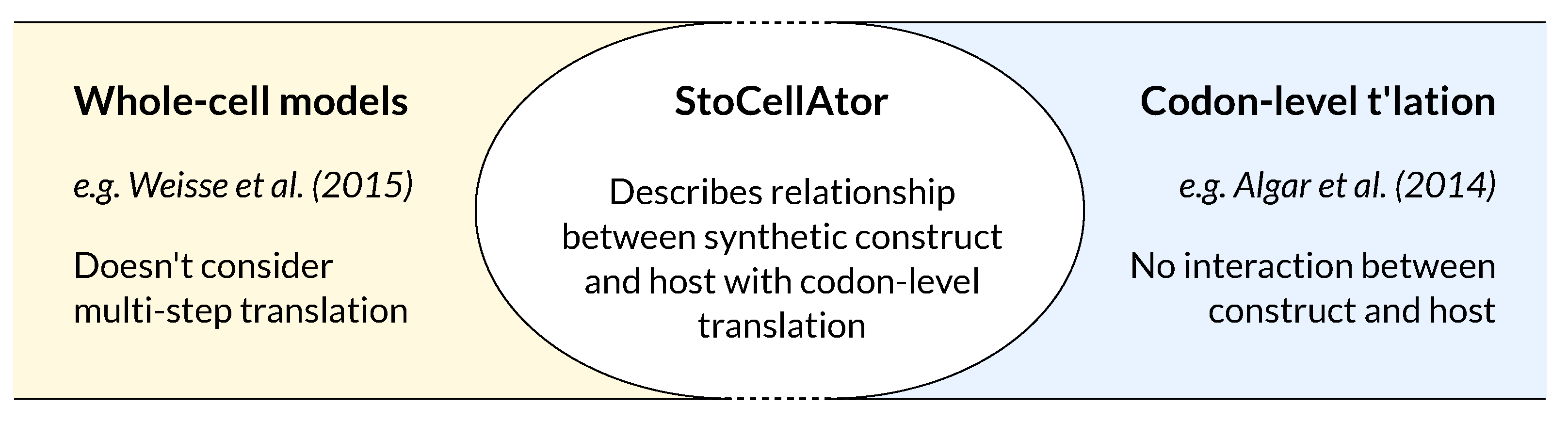
1.4. A Combined WCM-TASEP Framework
2. Materials and Methods
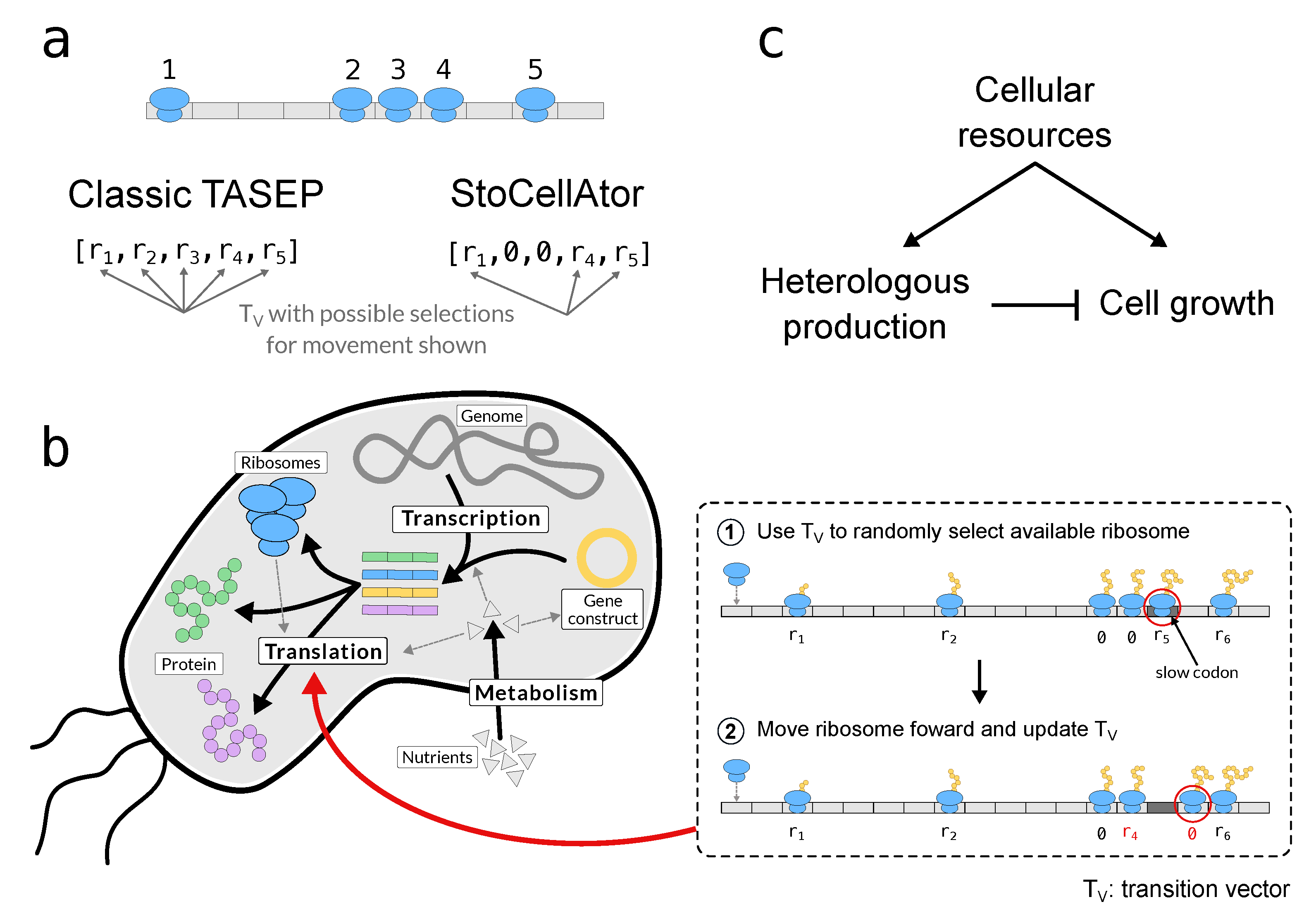
2.1. Whole-Cell Model
2.2. A Modified TASEP for Translation
2.3. Model Use Cases
2.4. Software
3. Results
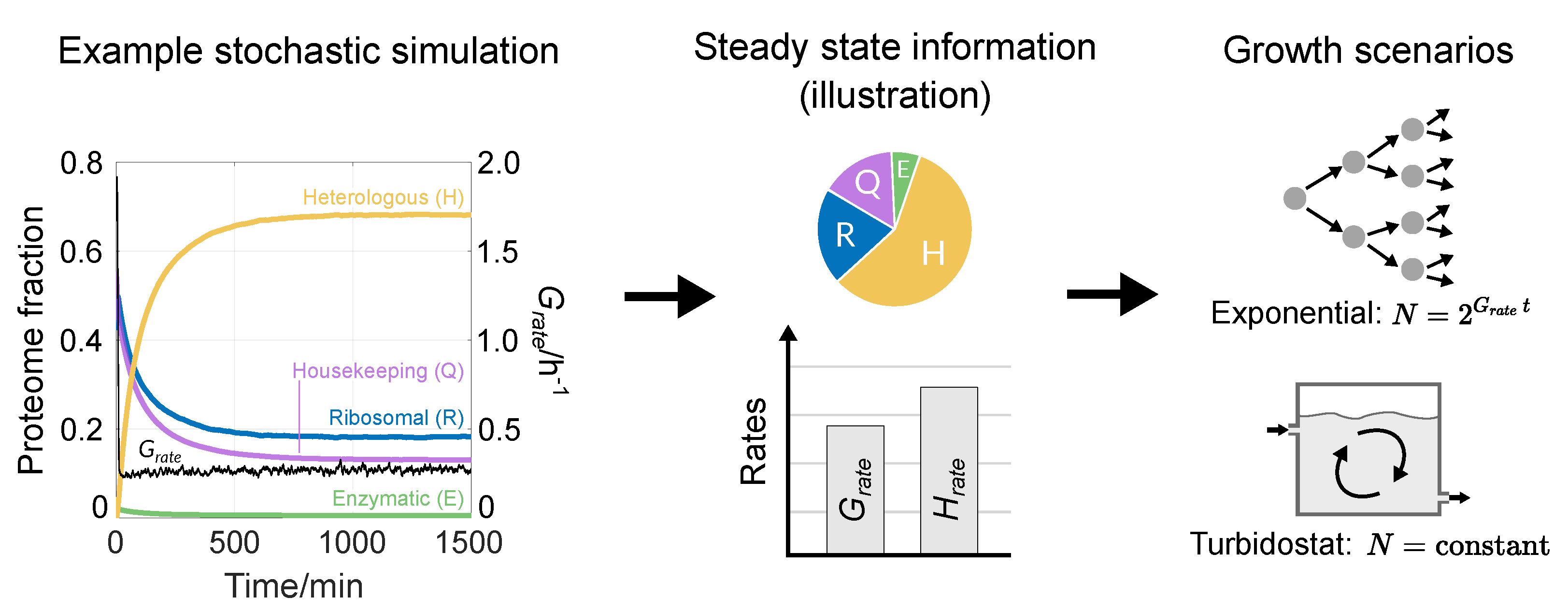
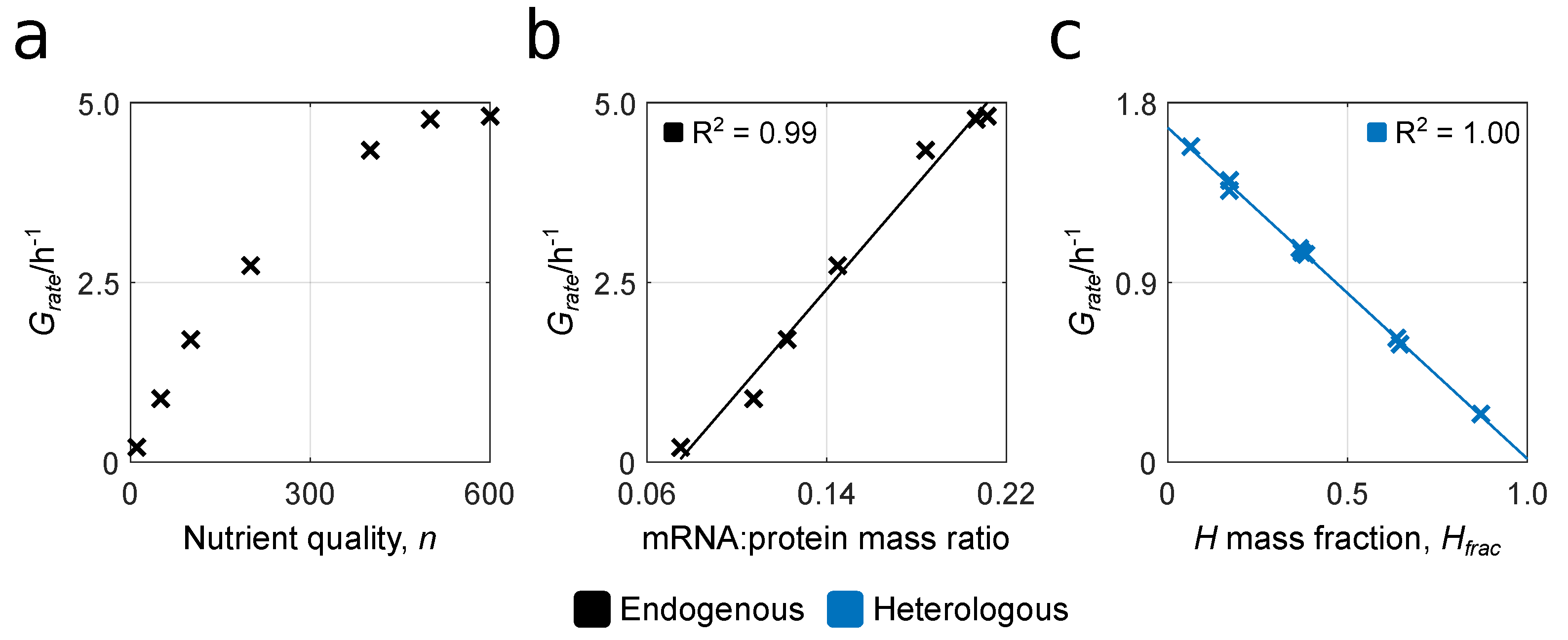
3.1. Reproducing Growth Laws
3.2. Optimising Construct Design
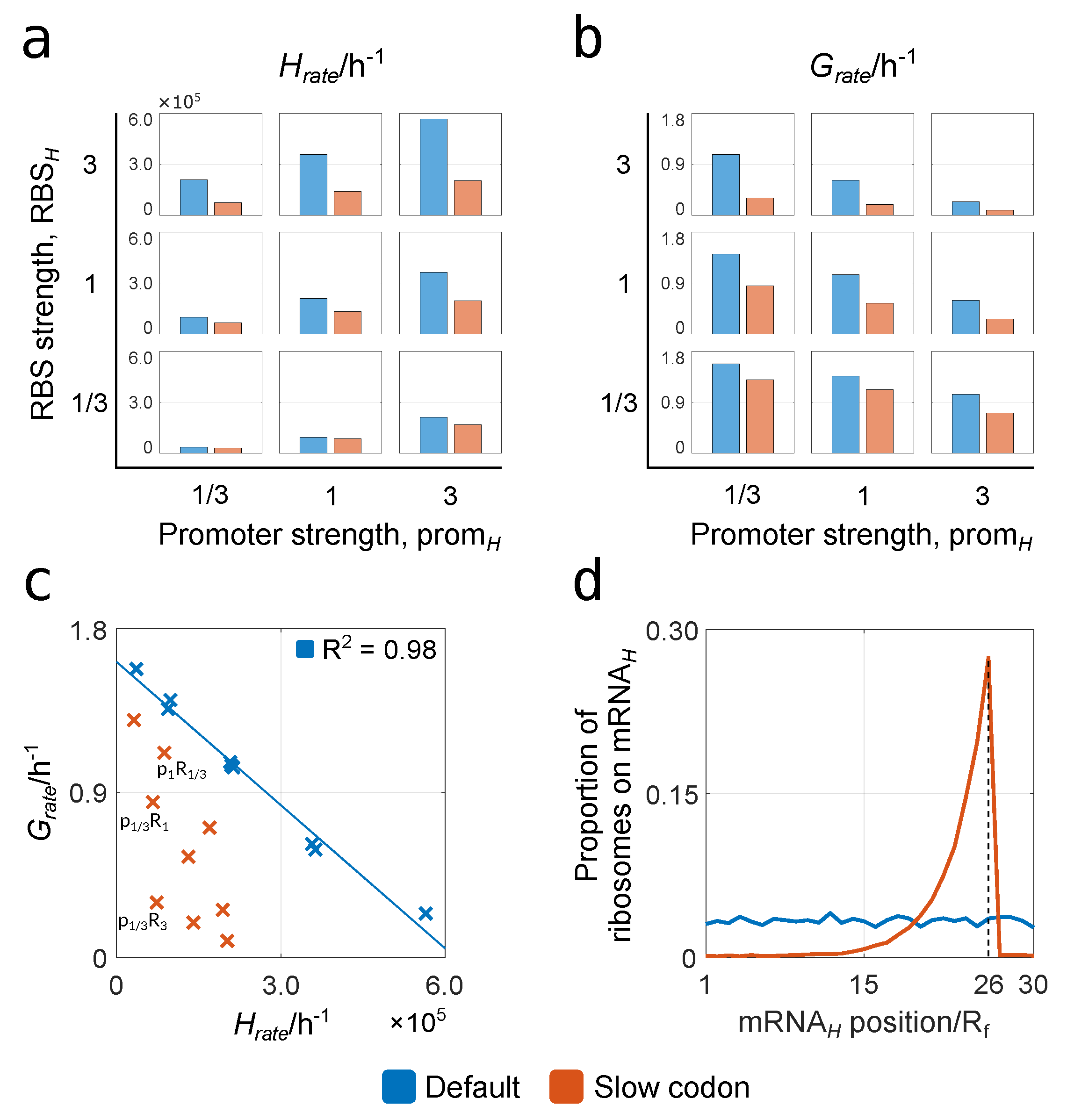
3.2.1. Relationships between Construct Design, Cell Growth and Heterologous Protein Yield
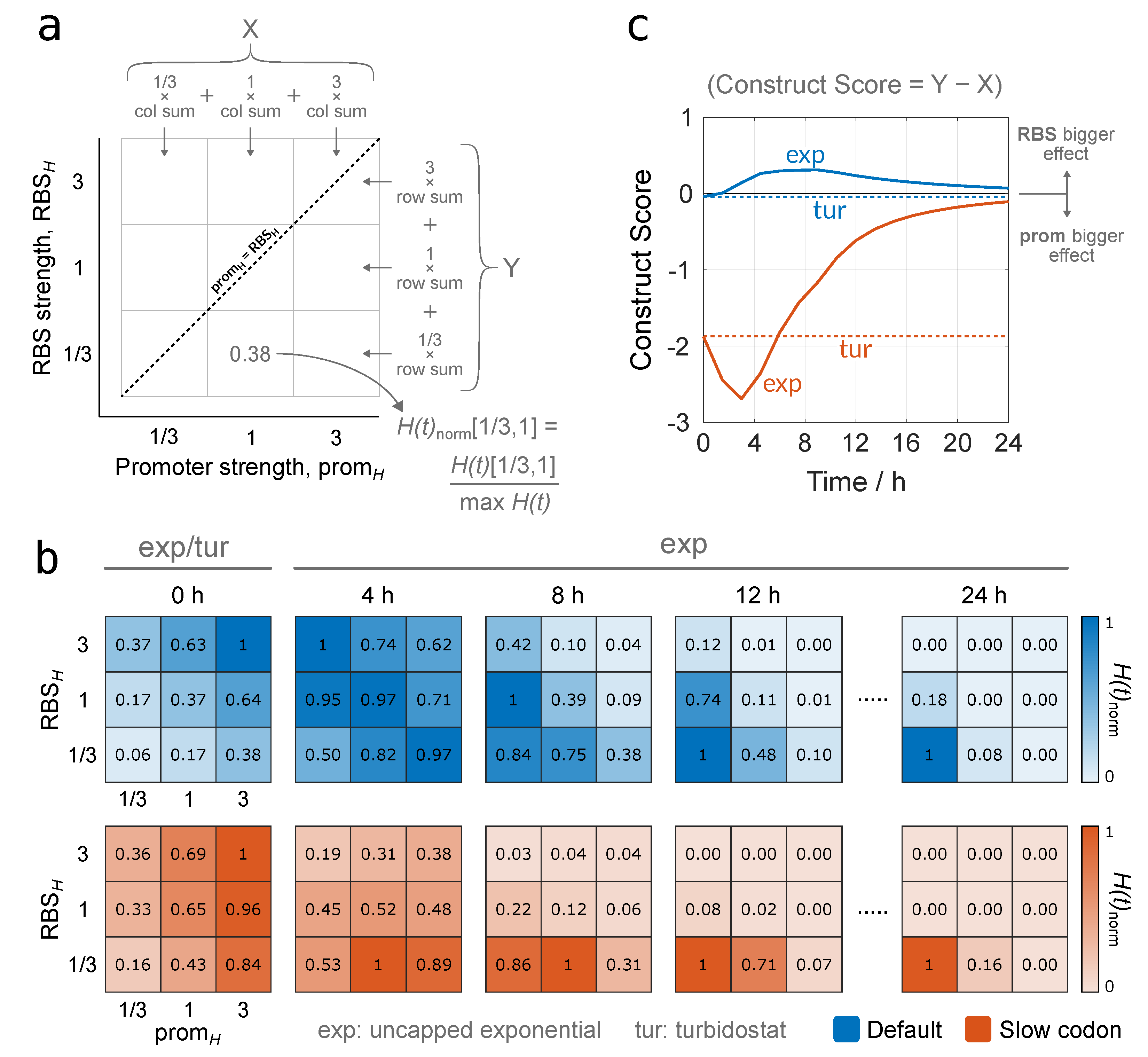
3.2.2. Identifying Optimal Gene Construct Designs by Quantifying Protein Production Yield Over Time
4. Discussion
4.1. Implications for Gene Construct Design
4.2. Future Applications of StoCellAtor
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WCM | whole-cell model |
| TASEP | totally asymmetric simple exclusion process |
| RBS | ribosome binding site |
References
- Ceroni, F.; Algar, R.; Stan, G.B.; Ellis, T. Quantifying cellular capacity identifies gene expression designs with reduced burden. Nat. Methods 2015, 12, 415–418. [Google Scholar] [CrossRef]
- Borkowski, O.; Ceroni, F.; Stan, G.B.; Ellis, T. Overloaded and stressed: Whole-cell considerations for bacterial synthetic biology. Curr. Opin. Microbiol. 2016, 33, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Scott, M.; Gunderson, C.W.; Mateescu, E.M.; Zhang, Z.; Hwa, T. Interdependence of cell growth and gene expression: Origins and consequences. Science 2010, 330, 1099–1102. [Google Scholar] [CrossRef] [PubMed]
- Weiße, A.Y.; Oyarzún, D.A.; Danos, V.; Swain, P.S. Mechanistic links between cellular trade-offs, gene expression, and growth. Proc. Natl. Acad. Sci. USA 2015, 112, E1038–E1047. [Google Scholar] [CrossRef] [PubMed]
- Erickson, D.W.; Schink, S.J.; Patsalo, V.; Williamson, J.R.; Gerland, U.; Hwa, T. A global resource allocation strategy governs growth transition kinetics of Escherichia coli. Nature 2017, 551, 119–123. [Google Scholar] [CrossRef]
- Liao, C.; Blanchard, A.E.; Lu, T. An integrative circuit—Host modelling framework for predicting synthetic gene network behaviours. Nat. Microbiol. 2017, 2, 1658–1666. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Huang, H.H.; Jiménez, J.I.; Del Vecchio, D. Resource competition shapes the response of genetic circuits. ACS Synth. Biol. 2017, 6, 1263–1272. [Google Scholar] [CrossRef]
- Nyström, A.; Papachristodoulou, A.; Angel, A. A Dynamic Model of Resource Allocation in Response to the Presence of a Synthetic Construct. ACS Synth. Biol. 2018, 7, 1201–1210. [Google Scholar] [CrossRef]
- Boo, A.; Ellis, T.; Stan, G.B. Host-aware synthetic biology. Curr. Opin. Syst. Biol. 2019, 14, 66–72. [Google Scholar] [CrossRef]
- Novoa, E.M.; de Pouplana, L.R. Speeding with control: Codon usage, tRNAs, and ribosomes. Trends Genet. 2012, 28, 574–581. [Google Scholar] [CrossRef]
- Quax, T.E.; Claassens, N.J.; Söll, D.; van der Oost, J. Codon bias as a means to fine-tune gene expression. Mol. Cell 2015, 59, 149–161. [Google Scholar] [CrossRef] [PubMed]
- Mitarai, N.; Sneppen, K.; Pedersen, S. Ribosome collisions and translation efficiency: Optimization by codon usage and mRNA destabilization. J. Mol. Biol. 2008, 382, 236–245. [Google Scholar] [CrossRef] [PubMed]
- Cannarozzi, G.; Schraudolph, N.N.; Faty, M.; von Rohr, P.; Friberg, M.T.; Roth, A.C.; Gonnet, P.; Gonnet, G.; Barral, Y. A role for codon order in translation dynamics. Cell 2010, 141, 355–367. [Google Scholar] [CrossRef] [PubMed]
- Tuller, T.; Carmi, A.; Vestsigian, K.; Navon, S.; Dorfan, Y.; Zaborske, J.; Pan, T.; Dahan, O.; Furman, I.; Pilpel, Y. An evolutionarily conserved mechanism for controlling the efficiency of protein translation. Cell 2010, 141, 344–354. [Google Scholar] [CrossRef]
- Mitarai, N.; Pedersen, S. Control of ribosome traffic by position-dependent choice of synonymous codons. Phys. Biol. 2013, 10, 056011. [Google Scholar] [CrossRef]
- Purvis, I.J.; Bettany, A.J.; Santiago, T.C.; Coggins, J.R.; Duncan, K.; Eason, R.; Brown, A.J. The efficiency of folding of some proteins is increased by controlled rates of translation in vivo: A hypothesis. J. Mol. Biol. 1987, 193, 413–417. [Google Scholar] [CrossRef]
- Zhou, M.; Guo, J.; Cha, J.; Chae, M.; Chen, S.; Barral, J.M.; Sachs, M.S.; Liu, Y. Non-optimal codon usage affects expression, structure and function of clock protein FRQ. Nature 2013, 495, 111–115. [Google Scholar] [CrossRef]
- Komar, A.A. A pause for thought along the co-translational folding pathway. Trends Biochem. Sci. 2009, 34, 16–24. [Google Scholar] [CrossRef]
- Angov, E. Codon usage: Nature’s roadmap to expression and folding of proteins. Biotechnol. J. 2011, 6, 650–659. [Google Scholar] [CrossRef]
- Rodriguez, A.; Wright, G.; Emrich, S.; Clark, P.L. %MinMax: A versatile tool for calculating and comparing synonymous codon usage and its impact on protein folding. Protein Sci. 2018, 27, 356–362. [Google Scholar] [CrossRef] [PubMed]
- Trösemeier, J.H.; Rudorf, S.; Loessner, H.; Hofner, B.; Reuter, A.; Schulenborg, T.; Koch, I.; Bekeredjian-Ding, I.; Lipowsky, R.; Kamp, C. Optimizing the dynamics of protein expression. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef]
- Zur, H.; Cohen-Kupiec, R.; Vinokour, S.; Tuller, T. Algorithms for ribosome traffic engineering and their potential in improving host cells’ titer and growth rate. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Kurland, C.; Ehrenberg, M. Growth-optimizing accuracy of gene expression. Annu. Rev. Biophys. Biophys. Chem. 1987, 16, 291–317. [Google Scholar] [CrossRef]
- Sharp, P.M.; Li, W.H. The codon adaptation index-a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 1987, 15, 1281–1295. [Google Scholar] [CrossRef] [PubMed]
- Carbone, A.; Zinovyev, A.; Képes, F. Codon adaptation index as a measure of dominating codon bias. Bioinformatics 2003, 19, 2005–2015. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, G.W.; Roth, D.A. Optimizing scaleup yield for protein production: Computationally Optimized DNA Assembly (CODA) and Translation Engineering™. Biotechnol. Annu. Rev. 2007, 13, 27–42. [Google Scholar] [PubMed]
- Moura, G.R.; Pinheiro, M.; Freitas, A.; Oliveira, J.L.; Frommlet, J.C.; Carreto, L.; Soares, A.R.; Bezerra, A.R.; Santos, M.A. Species-specific codon context rules unveil non-neutrality effects of synonymous mutations. PLoS ONE 2011, 6, e26817. [Google Scholar] [CrossRef] [PubMed]
- Chung, B.K.S.; Yusufi, F.N.; Yang, Y.; Lee, D.Y. Enhanced expression of codon optimized interferon gamma in CHO cells. J. Biotechnol. 2013, 167, 326–333. [Google Scholar] [CrossRef]
- Jack, B.R.; Leonard, S.P.; Mishler, D.M.; Renda, B.A.; Leon, D.; Suárez, G.A.; Barrick, J.E. Predicting the genetic stability of engineered DNA sequences with the EFM calculator. ACS Synth. Biol. 2015, 4, 939–943. [Google Scholar] [CrossRef]
- Zur, H.; Tuller, T. Predictive biophysical modeling and understanding of the dynamics of mRNA translation and its evolution. Nucleic Acids Res. 2016, 44, 9031–9049. [Google Scholar] [CrossRef]
- Heinrich, R.; Rapoport, T.A. Mathematical modelling of translation of mRNA in eucaryotes; steady states, time-dependent processes and application to reticulocytest. J. Theor. Biol.y 1980, 86, 279–313. [Google Scholar] [CrossRef]
- Shaw, L.B.; Zia, R.; Lee, K.H. Totally asymmetric exclusion process with extended objects: A model for protein synthesis. Phys. Rev. E 2003, 68, 021910. [Google Scholar] [CrossRef] [PubMed]
- Margaliot, M.; Tuller, T. Stability analysis of the ribosome flow model. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 1545–1552. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Wan, S.; Xu, Z.; Zheng, Y.; Feng, K.Y.; Li, H.P.; Kong, X.; Cai, Y.D. Analysis and prediction of translation rate based on sequence and functional features of the mRNA. PLoS ONE 2011, 6, e16036. [Google Scholar] [CrossRef]
- Welch, M.; Govindarajan, S.; Ness, J.E.; Villalobos, A.; Gurney, A.; Minshull, J.; Gustafsson, C. Design parameters to control synthetic gene expression in Escherichia coli. PLoS ONE 2009, 4, e7002. [Google Scholar] [CrossRef]
- Vogel, C.; de Sousa Abreu, R.; Ko, D.; Le, S.Y.; Shapiro, B.A.; Burns, S.C.; Sandhu, D.; Boutz, D.R.; Marcotte, E.M.; Penalva, L.O. Sequence signatures and mRNA concentration can explain two-thirds of protein abundance variation in a human cell line. Mol. Syst. Biol. 2010, 6, 400. [Google Scholar] [CrossRef]
- Ikemura, T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: A proposal for a synonymous codon choice that is optimal for the E. coli translational system. J. Mol. Biol. 1981, 151, 389–409. [Google Scholar] [CrossRef]
- Sabi, R.; Tuller, T. Modelling the efficiency of codon–tRNA interactions based on codon usage bias. DNA Res. 2014, 21, 511–526. [Google Scholar] [CrossRef]
- Tuller, T.; Kupiec, M.; Ruppin, E. Determinants of protein abundance and translation efficiency in S. cerevisiae. PLoS Comput. Biol. 2007, 3, e248. [Google Scholar] [CrossRef]
- Brockmann, R.; Beyer, A.; Heinisch, J.J.; Wilhelm, T. Posttranscriptional expression regulation: What determines translation rates? PLoS Comput. Biol. 2007, 3, e57. [Google Scholar] [CrossRef]
- Reuveni, S.; Meilijson, I.; Kupiec, M.; Ruppin, E.; Tuller, T. Genome-scale analysis of translation elongation with a ribosome flow model. PLoS Comput. Biol. 2011, 7, e1002127. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, C.T.; Gibbs, J.H.; Pipkin, A.C. Kinetics of biopolymerization on nucleic acid templates. Biopolym. Orig. Res. Biomol. 1968, 6, 1–25. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, C.T.; Gibbs, J.H. Concerning the kinetics of polypeptide synthesis on polyribosomes. Biopolym. Orig. Res. Biomol. 1969, 7, 707–725. [Google Scholar] [CrossRef]
- Ordon, R. Polyribosome dynamics at steady state. J. Theor. Biol. 1969, 22, 515–532. [Google Scholar] [CrossRef]
- Hiernaux, J. On some stochastic models for protein biosynthesis. Biophys. Chem. 1974, 2, 70–75. [Google Scholar] [CrossRef]
- Von der Haar, T. Mathematical and computational modelling of ribosomal movement and protein synthesis: An overview. Comput. Struct. Biotechnol. J. 2012, 1, e201204002. [Google Scholar] [CrossRef]
- Zhang, G.; Fedyunin, I.; Miekley, O.; Valleriani, A.; Moura, A.; Ignatova, Z. Global and local depletion of ternary complex limits translational elongation. Nucleic Acids Res. 2010, 38, 4778–4787. [Google Scholar] [CrossRef]
- Karr, J.R.; Sanghvi, J.C.; Macklin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B., Jr.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A whole-cell computational model predicts phenotype from genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef]
- Ciandrini, L.; Stansfield, I.; Romano, M.C. Ribosome traffic on mRNAs maps to gene ontology: Genome-wide quantification of translation initiation rates and polysome size regulation. PLoS Comput. Biol. 2013, 9, e1002866. [Google Scholar] [CrossRef]
- Shah, P.; Ding, Y.; Niemczyk, M.; Kudla, G.; Plotkin, J.B. Rate-limiting steps in yeast protein translation. Cell 2013, 153, 1589–1601. [Google Scholar] [CrossRef]
- Algar, R.; Ellis, T.; Stan, G.B. Modelling essential interactions between synthetic genes and their chassis cell. In Proceedings of the 2014 IEEE 53rd Annual Conference on Decision and Control (CDC), Los Angeles, CA, USA, 15–17 December 2014; pp. 5437–5444. [Google Scholar]
- Thomas, P.; Terradot, G.; Danos, V.; Weiße, A.Y. Sources, propagation and consequences of stochasticity in cellular growth. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Steitz, J.A. Polypeptide chain initiation: Nucleotide sequences of the three ribosomal binding sites in bacteriophage R17 RNA. Nature 1969, 224, 957–964. [Google Scholar] [CrossRef] [PubMed]
- Brandt, F.; Etchells, S.A.; Ortiz, J.O.; Elcock, A.H.; Hartl, F.U.; Baumeister, W. The native 3D organization of bacterial polysomes. Cell 2009, 136, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Keseler, I.M.; Collado-Vides, J.; Santos-Zavaleta, A.; Peralta-Gil, M.; Gama-Castro, S.; Muñiz-Rascado, L.; Bonavides-Martinez, C.; Paley, S.; Krummenacker, M.; Altman, T.; et al. EcoCyc: A comprehensive database of Escherichia coli biology. Nucleic Acids Res. 2010, 39, D583–D590. [Google Scholar] [CrossRef] [PubMed]
- Tuller, T.; Veksler-Lublinsky, I.; Gazit, N.; Kupiec, M.; Ruppin, E.; Ziv-Ukelson, M. Composite effects of gene determinants on the translation speed and density of ribosomes. Genome Biol. 2011, 12, R110. [Google Scholar] [CrossRef] [PubMed]
- Scott, M.; Hwa, T. Bacterial growth laws and their applications. Curr. Opin. Biotechnol. 2011, 22, 559–565. [Google Scholar] [CrossRef] [PubMed]
- Monod, J. The growth of bacterial cultures. Annu. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef]
- Schaechter, M.; Maaløe, O.; Kjeldgaard, N.O. Dependency on medium and temperature of cell size and chemical composition during balanced growth of Salmonella typhimurium. Microbiology 1958, 19, 592–606. [Google Scholar] [CrossRef]
- Scott, M.; Hwa, T. Anderson Promoter Collection. Available online: http://parts.igem.org/Promoters/Catalog/Anderson (accessed on 19 November 2020).
- Taylor, G.M.; Mordaka, P.M.; Heap, J.T. Start-Stop Assembly: A functionally scarless DNA assembly system optimized for metabolic engineering. Nucleic Acids Res. 2019, 47, e17. [Google Scholar] [CrossRef]
- Xiang, Y.; Dalchau, N.; Wang, B. Scaling up genetic circuit design for cellular computing: Advances and prospects. Nat. Comput. 2018, 17, 833–853. [Google Scholar] [CrossRef]
- Bartoli, V.; Meaker, G.A.; Di Bernardo, M.; Gorochowski, T.E. Tunable genetic devices through simultaneous control of transcription and translation. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ceroni, F.; Boo, A.; Furini, S.; Gorochowski, T.E.; Borkowski, O.; Ladak, Y.N.; Awan, A.R.; Gilbert, C.; Stan, G.B.; Ellis, T. Burden-driven feedback control of gene expression. Nat. Methods 2018, 15, 387–393. [Google Scholar] [CrossRef] [PubMed]
- Renda, B.A.; Hammerling, M.J.; Barrick, J.E. Engineering reduced evolutionary potential for synthetic biology. Mol. Biosyst. 2014, 10, 1668–1678. [Google Scholar] [CrossRef] [PubMed]
- Sleight, S.C.; Bartley, B.A.; Lieviant, J.A.; Sauro, H.M. Designing and engineering evolutionary robust genetic circuits. J. Biol. Eng. 2010, 4, 12. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarvari, P.; Ingram, D.; Stan, G.-B. A Modelling Framework Linking Resource-Based Stochastic Translation to the Optimal Design of Synthetic Constructs. Biology 2021, 10, 37. https://doi.org/10.3390/biology10010037
Sarvari P, Ingram D, Stan G-B. A Modelling Framework Linking Resource-Based Stochastic Translation to the Optimal Design of Synthetic Constructs. Biology. 2021; 10(1):37. https://doi.org/10.3390/biology10010037
Chicago/Turabian StyleSarvari, Peter, Duncan Ingram, and Guy-Bart Stan. 2021. "A Modelling Framework Linking Resource-Based Stochastic Translation to the Optimal Design of Synthetic Constructs" Biology 10, no. 1: 37. https://doi.org/10.3390/biology10010037
APA StyleSarvari, P., Ingram, D., & Stan, G.-B. (2021). A Modelling Framework Linking Resource-Based Stochastic Translation to the Optimal Design of Synthetic Constructs. Biology, 10(1), 37. https://doi.org/10.3390/biology10010037