Effect of the Structure Morphology on the Mechanical Properties of Crumpled Graphene Fiber
Abstract
:1. Introduction
2. Simulation Details
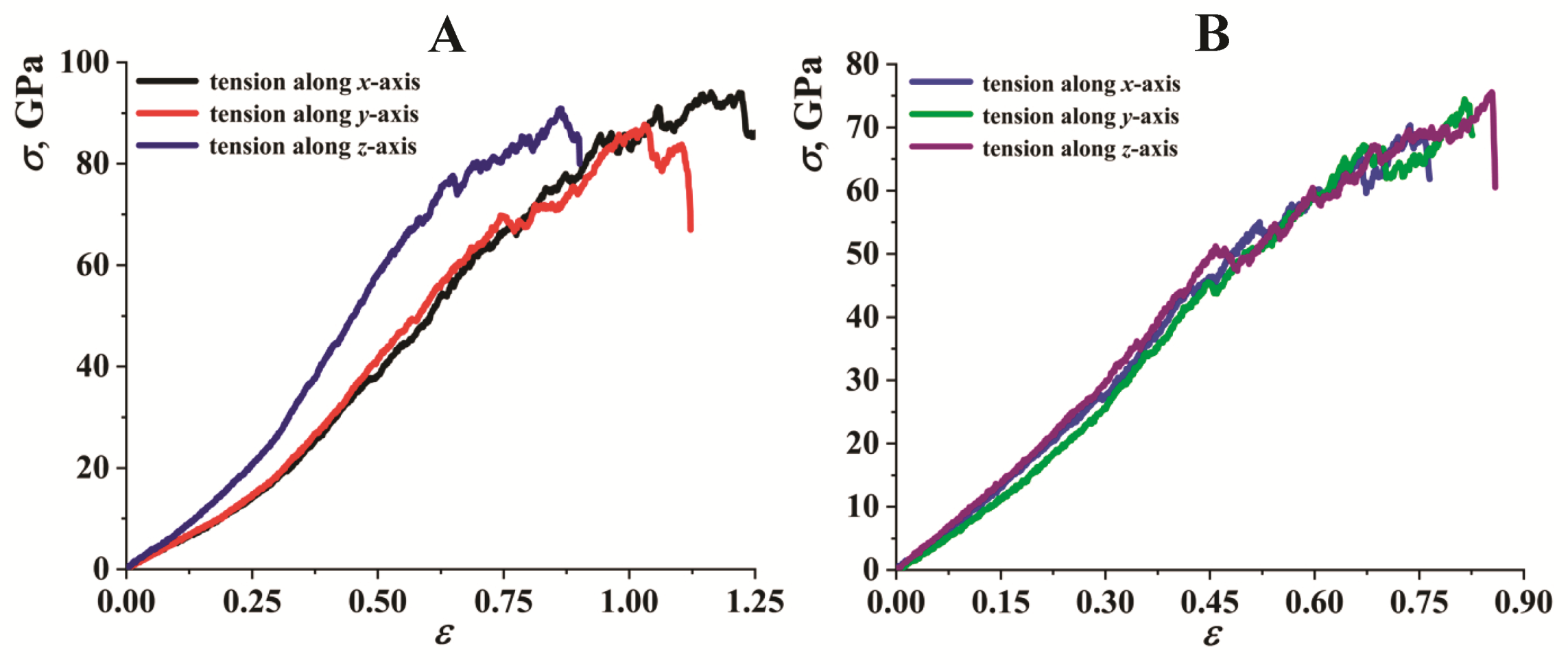
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bacon, R. Growth, Structure, and Properties of Graphite Whiskers. J. Appl. Phys. 1960, 31, 283–290. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, C. Graphene in Macroscopic Order: Liquid Crystals and Wet-Spun Fibers. Acc. Chem. Res. 2014, 47, 1267–1276. [Google Scholar] [CrossRef]
- Sagar, R.U.R.; Shabbir, B.; Hasnain, S.M.; Mahmood, N.; Zeb, M.H.; Shivananju, B.; Ahmed, T.; Qasim, I.; Malik, M.I.; Khan, Q.; et al. Large magnetotransport properties in mixed-dimensional van der Waals heterostructures of graphene foam. Carbon 2020, 159, 648–655. [Google Scholar] [CrossRef]
- Zeb, M.H.; Shabbir, B.; Sagar, R.U.R.; Mahmood, N.; Chen, K.; Qasim, I.; Malik, M.I.; Yu, W.; Hossain, M.M.; Dai, Z.; et al. Superior Magnetoresistance Performance of Hybrid Graphene Foam/Metal Sulfide Nanocrystal Devices. ACS Appl. Mater. Interfaces 2019, 11, 19397–19403. [Google Scholar] [CrossRef]
- Glukhova, O.; Mitrofanov, V.; Slepchenkov, M. The effect of the occurrence of a magnetic field of a current loop in hybrid graphene/C60 carbon systems. Lett. Mater. 2020, 10, 491–495. [Google Scholar] [CrossRef]
- Safina, L.; Baimova, J.; Krylova, K.; Murzaev, R.; Mulyukov, R. Simulation of metal-graphene composites by molecular dynamics: A review. Lett. Mater. 2020, 10, 351–360. [Google Scholar] [CrossRef]
- Holodova, O.; Prutsakova, N.; Zhdanova, T.; Lavrentyev, A.; Ershov, I.; Ilyasov, V. First principles study of the atomic and electronic structure in graphene-fullerene hybrid systems. Lett. Mater. 2020, 10, 365–370. [Google Scholar] [CrossRef]
- Shunaev, V.; Glukhova, O. Super square carbon nanotube networks: Mechanical properties and electric conductivity. Lett. Mater. 2019, 9, 136–141. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Z.; Gao, C. Multifunctional, Ultra-Flyweight, Synergistically Assembled Carbon Aerogels. Adv. Mater. 2013, 25, 2554–2560. [Google Scholar] [CrossRef]
- Kochaev, A.; Meftakhutdinov, R.; Sibatov, R.; Katin, K.; Maslov, M.; Efimov, V. Enhanced properties of covalently coupled borophene-graphene layers through fluorination and hydrogenation. Appl. Surf. Sci. 2021, 562, 150150. [Google Scholar] [CrossRef]
- Podlivaev, A.I.; Grishakov, K.S.; Katin, K.P.; Maslov, M.M. Stone–Wales Bilayer Graphene: Structure, Stability, and Interlayer Heat Transfer. JETP Lett. 2021, 114, 143–149. [Google Scholar] [CrossRef]
- Zhong, L.; Gao, H.; Li, X. Atomistic simulations of the tensile behavior of graphene fibers. Extrem. Mech. Lett. 2020, 37, 100699. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, C. Graphene fiber: A new trend in carbon fibers. Mater. Today 2015, 18, 480–492. [Google Scholar] [CrossRef]
- Rajabpour, S.; Mao, Q.; Gao, Z.; Talkhoncheh, M.K.; Zhu, J.; Schwab, Y.; Kowalik, M.; Li, X.; van Duin, A.C. Low-temperature carbonization of polyacrylonitrile/graphene carbon fibers: A combined ReaxFF molecular dynamics and experimental study. Carbon 2021, 174, 345–356. [Google Scholar] [CrossRef]
- Sagar, R.U.R.; Lifang, C.; Ali, A.; Khan, M.F.; Abbas, M.; Malik, M.I.; Khan, K.; Zeng, J.; Anwar, T.; Liang, T. Unusual magnetotransport properties in graphene fibers. Phys. Chem. Chem. Phys. 2020, 22, 25712–25719. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Song, L.; Zhang, Z.; Chen, N.; Feng, Z.; Qu, L. Tailored graphene systems for unconventional applications in energy conversion and storage devices. Energy Environ. Sci. 2015, 8, 31–54. [Google Scholar] [CrossRef]
- Meng, Y.; Jin, L.; Cai, B.; Wang, Z. Facile fabrication of flexible core–shell graphene/conducting polymer microfibers for fibriform supercapacitors. RSC Adv. 2017, 7, 38187–38192. [Google Scholar] [CrossRef] [Green Version]
- Zang, J.; Ryu, S.; Pugno, N.; Wang, Q.; Tu, Q.; Buehler, M.J.; Zhao, X. Multifunctionality and control of the crumpling and unfolding of large-area graphene. Nat. Mater. 2013, 12, 321–325. [Google Scholar] [CrossRef] [Green Version]
- Xin, G.; Yao, T.; Sun, H.; Scott, S.M.; Shao, D.; Wang, G.; Lian, J. Highly thermally conductive and mechanically strong graphene fibers. Science 2015, 349, 1083–1087. [Google Scholar] [CrossRef] [Green Version]
- Patil, S.P.; Shendye, P.; Markert, B. Molecular dynamics simulations of silica aerogel nanocomposites reinforced by glass fibers, graphene sheets and carbon nanotubes: A comparison study on mechanical properties. Compos. Part B Eng. 2020, 190, 107884. [Google Scholar] [CrossRef]
- Safina, L.R.; Baimova, J.A.; Mulyukov, R.R. Nickel nanoparticles inside carbon nanostructures: Atomistic simulation. Mech. Adv. Mater. Mod. Process. 2019, 5, 2. [Google Scholar] [CrossRef]
- Baimova, J.A.; Rysaeva, L.K.; Liu, B.; Dmitriev, S.V.; Zhou, K. From flat graphene to bulk carbon nanostructures. Phys. Status Solidi B 2015, 252, 1502–1507. [Google Scholar] [CrossRef]
- Rysaeva, L.K.; Korznikova, E.A.; Murzaev, R.T.; Abdullina, D.U.; Kudreyko, A.A.; Baimova, J.A.; Lisovenko, D.S.; Dmitriev, S.V. Elastic damper based on the carbon nanotube bundle. Facta Univ. Ser. Mech. Eng. 2020, 18, 001–012. [Google Scholar] [CrossRef]
- Baimova, Y.A.; Murzaev, R.T.; Dmitriev, S.V. Mechanical properties of bulk carbon nanomaterials. Phys. Solid State 2014, 56, 2010–2016. [Google Scholar] [CrossRef]
- Chae, H.G.; Minus, M.L.; Rasheed, A.; Kumar, S. Stabilization and carbonization of gel spun polyacrylonitrile/single wall carbon nanotube composite fibers. Polymer 2007, 48, 3781–3789. [Google Scholar] [CrossRef]
- Min, B.G.; Sreekumar, T.; Uchida, T.; Kumar, S. Oxidative stabilization of PAN/SWNT composite fiber. Carbon 2005, 43, 599–604. [Google Scholar] [CrossRef]
- Meng, F.; Lu, W.; Li, Q.; Byun, J.H.; Oh, Y.; Chou, T.W. Graphene-Based Fibers: A Review. Adv. Mater. 2015, 27, 5113–5131. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, H.; Zhao, X.; Gao, C. Ultrastrong Fibers Assembled from Giant Graphene Oxide Sheets. Adv. Mater. 2012, 25, 188–193. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Li, L.; Yu, M.; Ma, H.; Zhang, B. Flexible graphene fibers prepared by chemical reduction-induced self-assembly. J. Mater. Chem. A 2014, 2, 6359–6362. [Google Scholar] [CrossRef]
- Baimova, J.A.; Dmitriev, S.V.; Zhou, K.; Savin, A.V. Unidirectional ripples in strained graphene nanoribbons with clamped edges at zero and finite temperatures. Phys. Rev. B 2012, 86, 035427. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Pedram, Y.; Marsusi, F.; Yousefbeigi, S. Melting process of fluorinated graphene: A molecular dynamics study. Chem. Phys. Lett. 2021, 780, 138920. [Google Scholar] [CrossRef]
- Kim, J.C.; Wi, J.H.; Ri, N.C.; Ri, S.I. Thermal conductivity of graphene/graphane/graphene heterostructure nanoribbons: Non-equilibrium molecular dynamics simulations. Solid State Commun. 2021, 328, 114249. [Google Scholar] [CrossRef]
- Sarvestani, A.B.; Chogani, A.; Shariat, M.; Moosavi, A.; Kariminasab, H. The effect of nanopores geometry on desalination of single-layer graphene-based membranes: A molecular dynamics study. J. Mol. Liq. 2021, 339, 116749. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, C. Graphene chiral liquid crystals and macroscopic assembled fibres. Nat. Commun. 2011, 2, 571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shabbir, B.; Wang, X.; Ghorbani, S.R.; Shekhar, C.; Dou, S.; Srivastava, O.N. Hydrostatic pressure: A very effective approach to significantly enhance critical current density in granular iron pnictide superconductors. Sci. Rep. 2015, 5, 8213. [Google Scholar] [CrossRef] [Green Version]
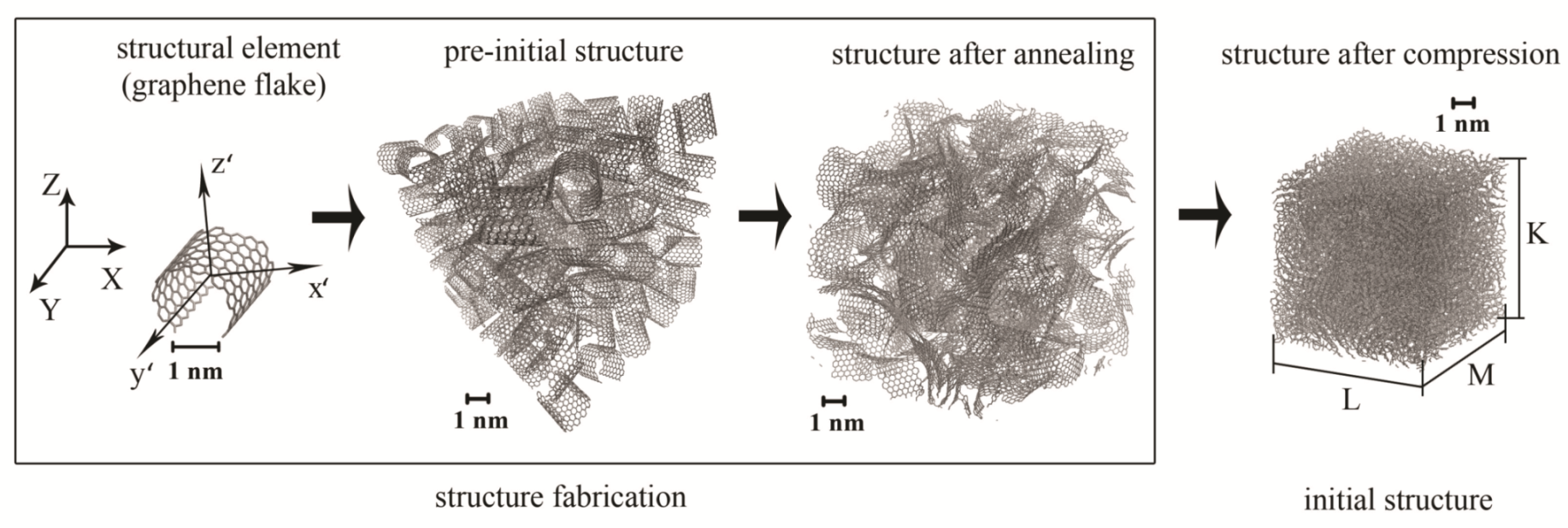


| Struct. | St. Element | Size of St. El. | N | , g/cm3 | V, cm3 | , cm |
|---|---|---|---|---|---|---|
| A | small GF | about 1 nm | 31,500 | 2.46 | 254,888.98 | 4.8 × 10 × 4.7 × 10 × 3.6 × 10 |
| B | GF of dif. size | 80 to 500 atoms | 10,960 | 2.18 | 99,936.7 | 6.1 × 10 × 6.1 × 10 × 5.9 × 10 |
| Structure | Young’s Modulus (GPa) | Tensile Strength (GPa) | ||||
|---|---|---|---|---|---|---|
| along x | along y | along z | along x | along y | along z | |
| A | 50.5 | 53.2 | 70.9 | 93.96 | 87.52 | 90.57 |
| B | 87.2 | 77.3 | 92.1 | 70.32 | 74.14 | 75.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baimova, J.; Polyakova, P.; Shcherbinin, S. Effect of the Structure Morphology on the Mechanical Properties of Crumpled Graphene Fiber. Fibers 2021, 9, 85. https://doi.org/10.3390/fib9120085
Baimova J, Polyakova P, Shcherbinin S. Effect of the Structure Morphology on the Mechanical Properties of Crumpled Graphene Fiber. Fibers. 2021; 9(12):85. https://doi.org/10.3390/fib9120085
Chicago/Turabian StyleBaimova, Julia, Polina Polyakova, and Stepan Shcherbinin. 2021. "Effect of the Structure Morphology on the Mechanical Properties of Crumpled Graphene Fiber" Fibers 9, no. 12: 85. https://doi.org/10.3390/fib9120085
APA StyleBaimova, J., Polyakova, P., & Shcherbinin, S. (2021). Effect of the Structure Morphology on the Mechanical Properties of Crumpled Graphene Fiber. Fibers, 9(12), 85. https://doi.org/10.3390/fib9120085







