Combining Experimental Data with Statistical Methods to Evaluate Hydrolyzed Reactive Dye Removal by α-Fe2O3 in a Cellulose-Based Membrane
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Dye Hydrolysis
2.3. Adsorption Experiments for hydRB5
2.4. Recyclability of a Membrane for hydRB5 Adsorption
2.5. Experimental Design, Statistical Analysis and Mathematical Modeling
3. Results and Discussion
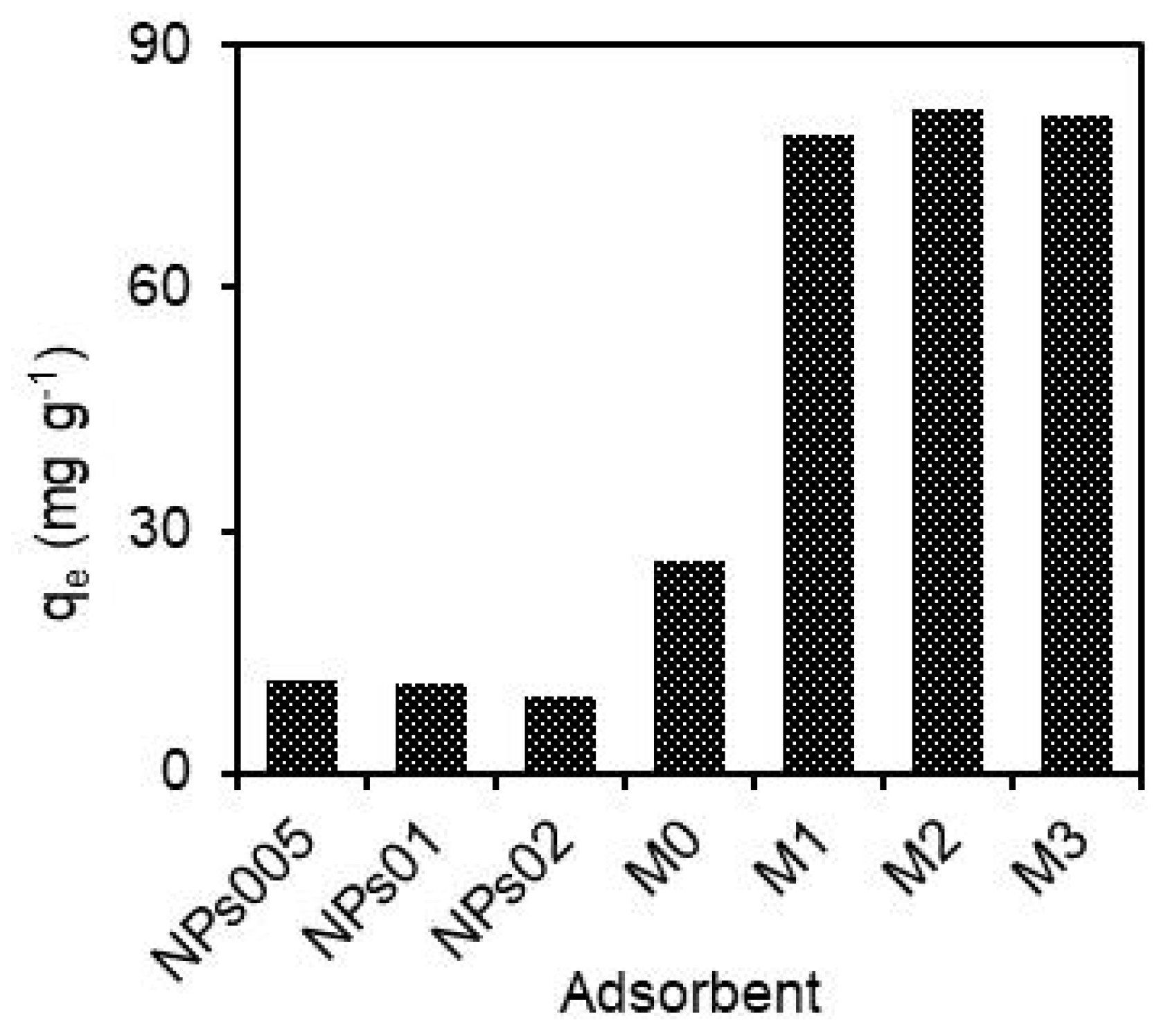
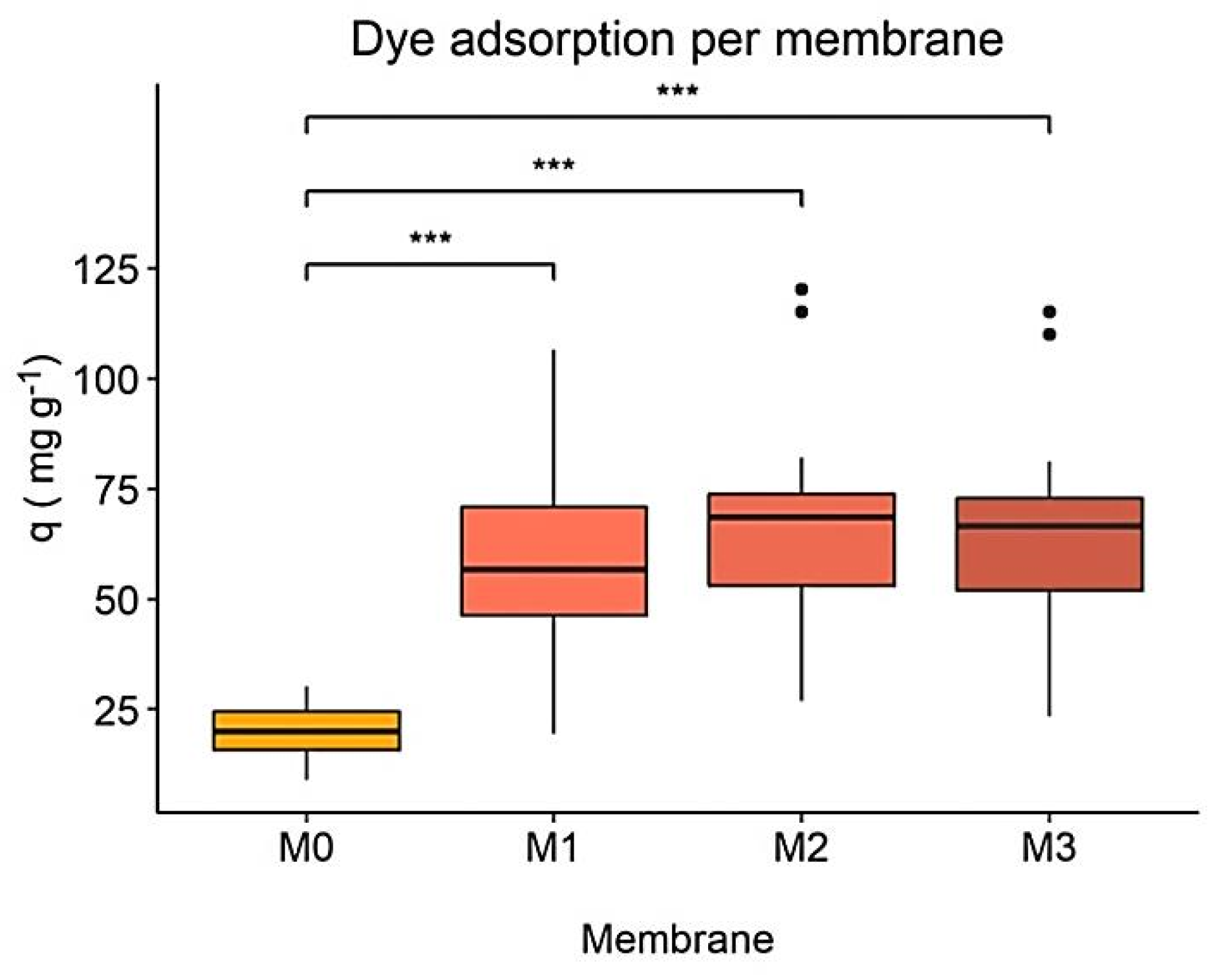
3.1. Comparison of hydRB5 Adsorption on Different Membranes
3.2. pH’s Effect on the Adsorption Capacity of Membranes
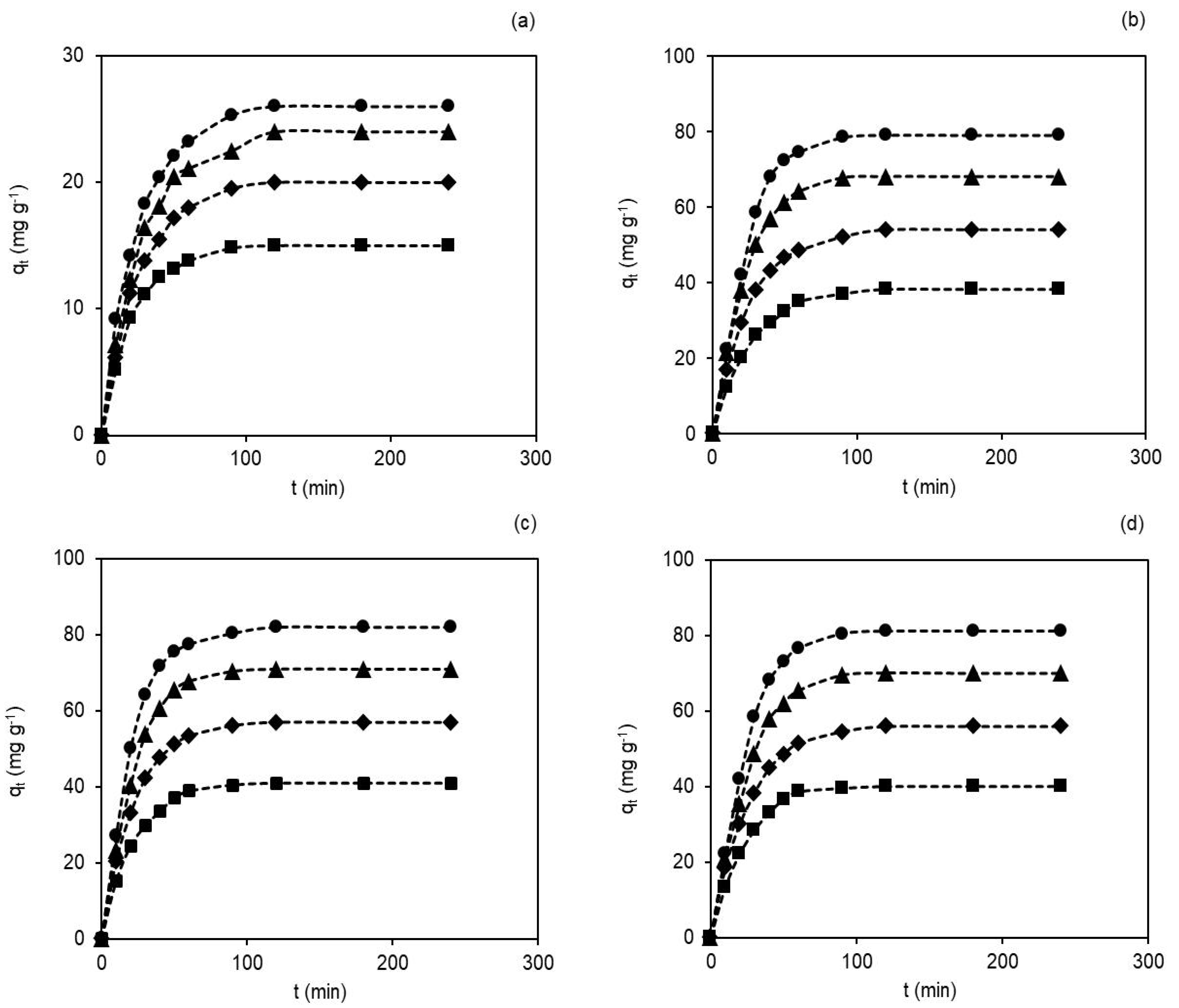
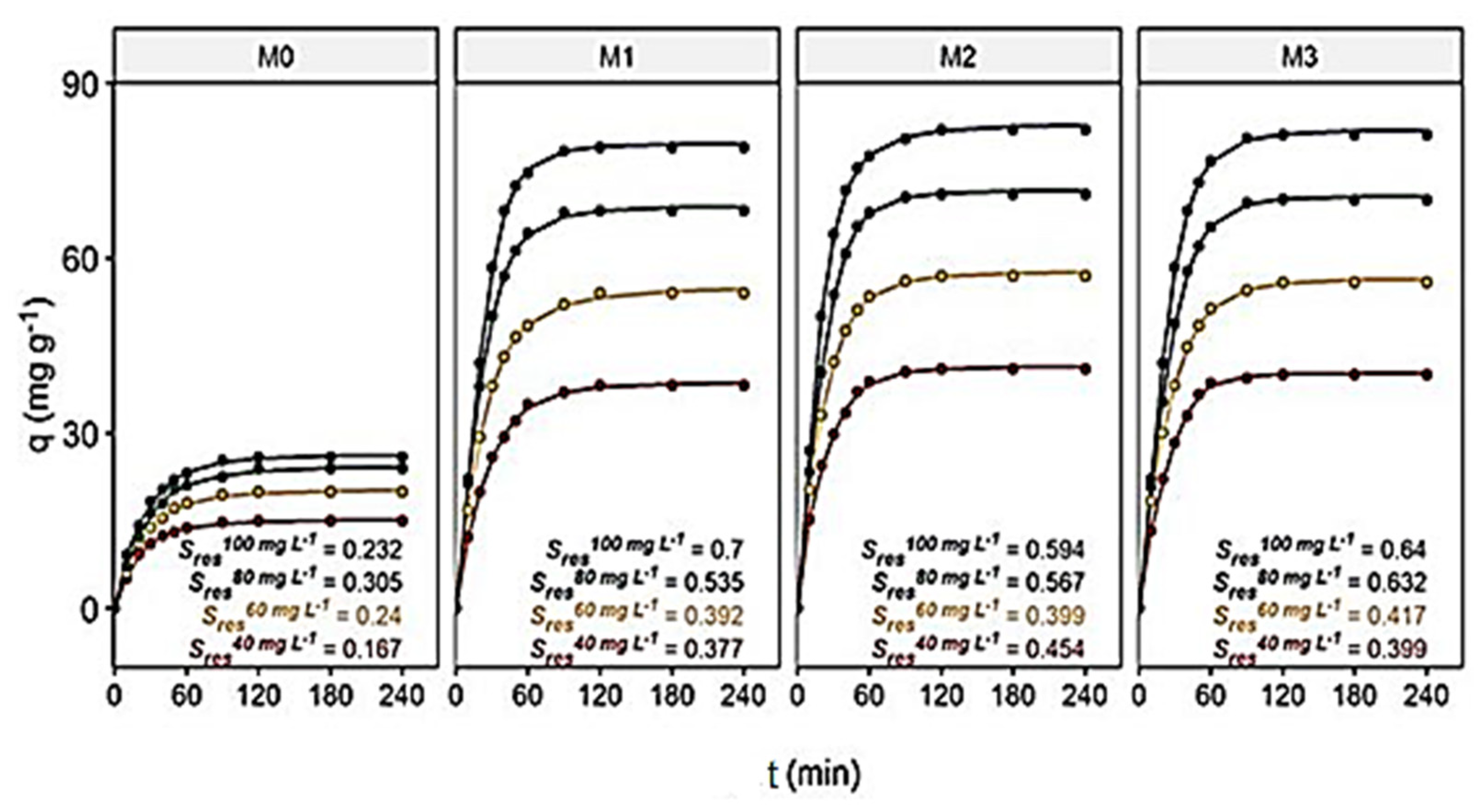
3.3. Contact Time and Initial Dye Concentration’ Effects on the Adsorption Capacity of Membranes
3.4. Adsorption Kinetic Studies
3.5. Adsorption Isotherms
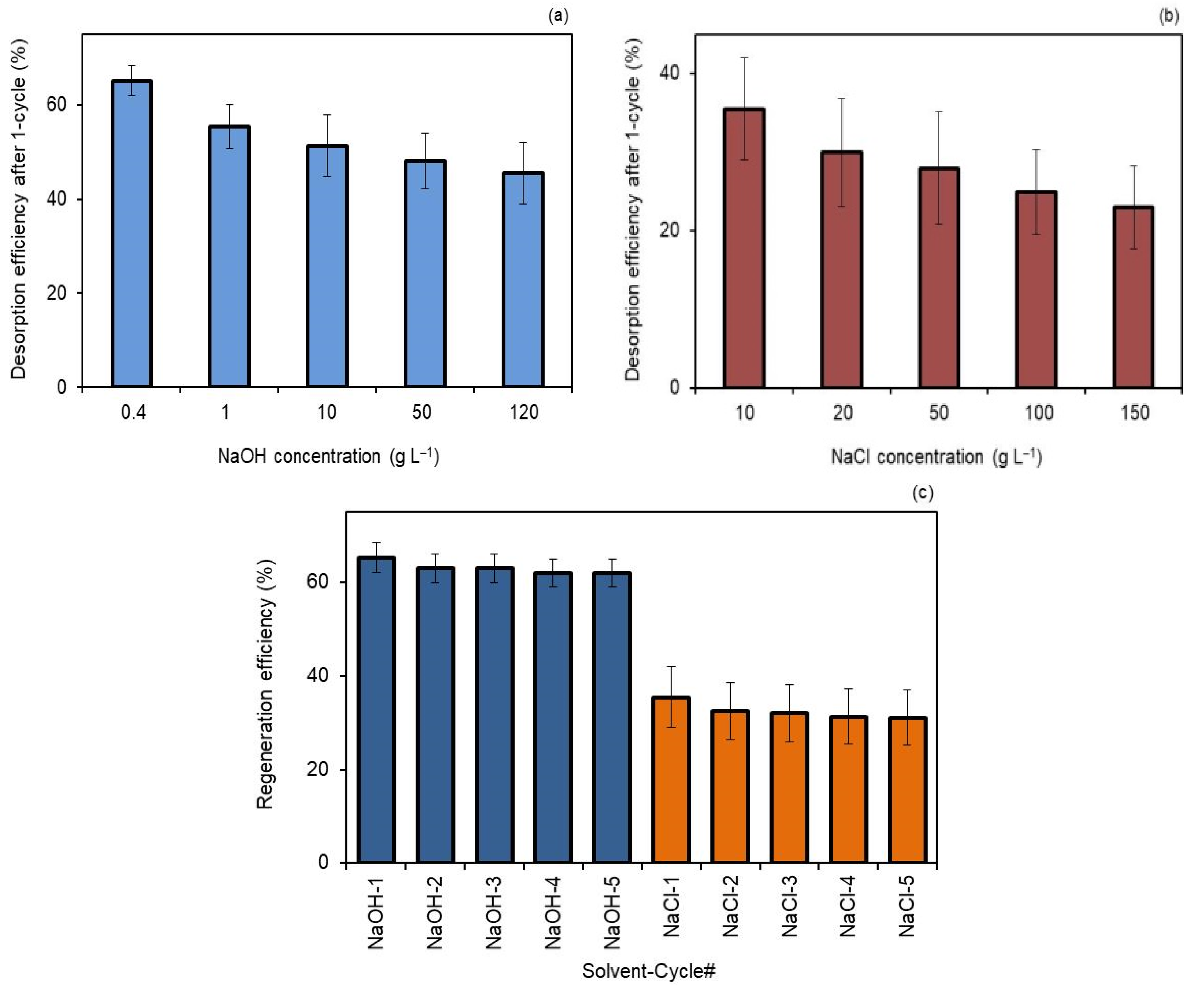
3.6. Recyclability of M2 Membrane in hydRB5 Adsorption
3.7. Experimental Design
3.7.1. Statistical Analyses
3.7.2. Influence of Factors on Dye Adsorption and Its Interactions
- pH effect
- 2.
- Dye concentration effect
- 3.
- Time effect
3.7.3. Optimization Process and Confirmation of Related Forecasts
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Gogate, P.R.; Pandit, A.B. A review of imperative technologies for wastewater treatment I: Oxidation technologies at ambient conditions. Adv. Environ. Res. 2018, 8, 501–551. [Google Scholar] [CrossRef]
- Sharma, S.K. Green Chemistry for Dyes Removal from Wastewater: Research Trends and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, C.; Ma, C.; Shen, Z.; Guo, J.; Sun, R. Studied on sonocatalytic degradation of Rhodamine B in aqueous solution. Ultrason. Sonochem. 2019, 58, 104691. [Google Scholar] [CrossRef] [PubMed]
- Yagub, M.T.; Sen, T.K.; Afroze, S.; Ang, H.M. Dye and its removal from aqueous solution by adsorption: A review. Adv. Colloid Interface Sci. 2014, 209, 172–184. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Gao, C.; Xu, W. Magnetic Dendritic Materials for Highly Efficient Adsorption of Dyes and Drugs. ACS Appl. Mater. Interfaces 2010, 2, 1483–1491. [Google Scholar] [CrossRef] [PubMed]
- Pierce, J. Colour in textile effluents-the origins of the problem. J. Soc. Dyers Colour. 1994, 110, 131–133. [Google Scholar] [CrossRef]
- Gottlieb, A.; Shaw, C.; Smith, A.; Wheatley, A.; Forsythe, S. The toxicity of textile reactive azo dyes after hydrolysis and decolourisation. J. Biotechnol. 2003, 101, 49–56. [Google Scholar] [CrossRef]
- Jalali Sarvestani, M.R.; Doroudi, Z. Removal of Reactive Black 5 from Waste Waters by Adsorption: A Comprehensive Review. J. Water Environ. Nanotechnol. 2020, 5, 180–190. [Google Scholar] [CrossRef]
- Bhaumik, M.; McCrindle, R.I.; Maity, A.; Agarwal, S.; Gupta, V.K. Polyaniline nanofibers as highly effective re-usable adsorbent for removal of reactive black 5 from aqueous solutions. J. Colloid Interface Sci. 2016, 466, 442–451. [Google Scholar] [CrossRef]
- Kumar, V. A review on the feasibility of electrolytic treatment of wastewater: Prospective and constraints. Arch. Agric. Environ. Sci. 2017, 2, 52–62. [Google Scholar]
- Devi, P.; Das, U.; Dalai, A.K. In-situ chemical oxidation: Principle and applications of peroxide and persulfate treatments in wastewater systems. Sci. Total Environ. 2016, 571, 643–657. [Google Scholar] [CrossRef]
- Zhao, W.-Y.; Zhou, M.; Yan, B.; Sun, X.; Liu, Y.; Wang, Y.; Xu, T.; Zhang, Y. Waste Conversion and Resource Recovery from Wastewater by Ion Exchange Membranes: State-of-the-Art and Perspective. Ind. Eng. Chem. Res. 2018, 18, 6025–6039. [Google Scholar] [CrossRef]
- Singh, R.L.; Singh, P.K.; Singh, R.P. Enzymatic decolorization and degradation of azo dyes—A review. Int. Biodeterior. Biodegrad. 2015, 104, 21–31. [Google Scholar] [CrossRef]
- Ahmed, S.N.; Haider, W. Heterogeneous photocatalysis and its potential applications in water and wastewater treatment: A review. Nanotechnology 2018, 34, 342001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buthiyappan, A.; Abdul Aziz, A.R.; Wan Daud, W.M.A. Recent advances and prospects of catalytic advanced oxidation process in treating textile effluents. Rev. Chem. Eng. 2016, 32, 1–47. [Google Scholar] [CrossRef]
- Crini, G.; Lichtfouse, E.; Wilson, L.; Morin-Crini, N. Conventional and nonconventional adsorbents for wastewater treatment. Environ. Chem. Lett. 2019, 17, 195–213. [Google Scholar] [CrossRef]
- Munagapati, V.S.; Wen, J.-C.; Pan, C.-L.; Gutha, Y.; Wen, J.-H.; Reddy, G.M. Adsorptive removal of anionic dye (Reactive Black 5) from aqueous solution using chemically modified banana peel powder: Kinetic, isotherm, thermodynamic, and reusability studies. Int. J. Phytorem. 2019, 22, 267–278. [Google Scholar] [CrossRef]
- Emik, S. Preparation and characterization of an IPN type chelating resin containing amino and carboxyl groups for removal of Cu(II) from aqueous solutions. React. Funct. Polym. 2014, 75, 63–74. [Google Scholar] [CrossRef]
- Anirudhan, T.S.; Rauf, T.A. Adsorption performance of amine functionalized cellulose grafted epichlorohydrin for the removal of nitrate from aqueous solutions. J. Ind. Eng. Chem. 2013, 19, 1659–1667. [Google Scholar] [CrossRef]
- Rashed, M.N.; Palanisamy, P.N. Introductory chapter: Adsorption and ion exchange properties of zeolites for treatment of polluted water. In Zeolites and Their Applications; Rashed, M.N., Ed.; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Kajjumba, G.W.; Emik, S.; Öngen, A.; Özcan, H.K.; Aydın, S. Modelling of adsorption kinetic processes—Errors, theory and application. In Advanced Sorption Process Applications; Edebali, S., Ed.; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.H.; Hwang, C.-H.; Kang, S.B.; Kim, S.; Park, S.W.; Yun, Y.-S.; Won, S.W. Removal of hydrolyzed Reactive Black 5 from aqueous solution using a polyethylenimine–polyvinyl chloride composite fiber. Chem. Eng. J. 2015, 280, 18–25. [Google Scholar] [CrossRef]
- Silva, M.; Rocha, C.; Gallo, J.; Felgueiras, H.; Amorim, M. Porous composites based on cellulose acetate and alfa-hematite with optical and antimicrobial properties. Carbohydr. Polym. 2020, 241, 116362. [Google Scholar] [CrossRef]
- Silva, M.; Hilliou, L.; Amorim, M. Fabrication of pristine-multiwalled carbon nanotubes/cellulose acetate composites for removal of methylene blue. Polym. Bull. 2020, 77, 623–653. [Google Scholar] [CrossRef]
- Ali, A.S.M.; El-Aassar, M.R.; Hashem, F.S.; Moussa, N.A. Surface Modified of Cellulose Acetate Electrospun Nanofibers by Polyaniline/β-cyclodextrin Composite for Removal of Cationic Dye from Aqueous Medium. Fibers Polym. 2019, 20, 2057–2069. [Google Scholar] [CrossRef]
- Khan, S.A.; Baksh, E.M.; Akhtar, K.; Khan, S.B. A template of cellulose acetate polymer-ZnAl layered double hydroxide composite fabricated with Ni NPs: Applications in the hydrogenation of nitrophenols and dyes degradation. Spectrochim. Acta Part A 2020, 241, 118671. [Google Scholar] [CrossRef]
- Parsaeian, M.R.; Dadfarnia, S.; Haji Shabani, A.M.; Hafezi Moghaddam, R. Green synthesis of a high capacity magnetic polymer nanocomposite sorbent based on the natural products for removal of Reactive Black 5. Int. J. Environ. Anal. Chem. 2020, 1–15. [Google Scholar] [CrossRef]
- Silva, M.A.; Felgueiras, H.P.; Amorim, M.T.P. Carbon based membranes with modified properties: Thermal, morphological, mechanical and antimicrobial. Cellulose 2020, 27, 1497–1516. [Google Scholar] [CrossRef]
- Askari, N.; Farhadian, M.; Razmjou, A. Simultaneous effects of pH, concentration, pressure on dye removal by a polyamide nanofilter membrane; optimization through response surface methodology. Environ. Nanotechnol. Monit. Manag. 2018, 10, 223–230. [Google Scholar] [CrossRef]
- Baneshi, M.M.; Ghaedi, A.M.; Vafaei, A.; Emadzadeh, D.; Lau, W.J.; Marioryad, H.; Jamshidi, A. A high-flux P84 polyimide mixed matrix membranes incorporated with cadmium-based metal organic frameworks for enhanced simultaneous dyes removal: Response surface methodology. Environ. Res. 2020, 183, 109278. [Google Scholar] [CrossRef] [PubMed]
- Pooralhossini, J.; Zanjanchi, M.A.; Ghaedi, M.; Asfaram, A.; Azqhandi, M.H.A. Statistical optimization and modeling approach for azo dye decolorization: Combined effects of ultrasound waves and nanomaterial-based adsorbent. Appl. Organomet. Chem. 2018, 32, e4205. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org (accessed on 6 May 2021).
- Team, R. R Studio: Integrated Development for R. Available online: http://www.rstudio.com (accessed on 6 May 2021).
- Ritz, C.; Baty, F.; Streibig, J.C.; Gerhard, D. Dose-Response Analysis Using R. PLoS ONE 2015, 10, e0146021. [Google Scholar] [CrossRef] [Green Version]
- Hadley, W. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Sievert, C. Interactive Web-Based Data Visualization with R, Plotly, and Shiny; Chapman and Hall/CRC: London, UK, 2020. [Google Scholar]
- Wilke, C.O. Streamlined Plot Theme and Plot Annotations for ‘ggplot2’. Available online: https://wilkelab.org/cowplot (accessed on 6 May 2021).
- Wilke, C.O. ggtext: Improved Text Rendering Support for ‘ggplot2’. Available online: https://wilkelab.org/ggtext/index.html (accessed on 6 May 2021).
- Ahmadi, M.; Hazrati Niari, M.; Kakavandi, B. Development of maghemite nanoparticles supported on cross-linked chitosan (γ-Fe2O3@CS) as a recoverable mesoporous magnetic composite for effective heavy metals removal. J. Mol. Liq. 2017, 248, 184–196. [Google Scholar] [CrossRef]
- Banerjee, S.; Chattopadhyaya, M.C. Adsorption characteristics for the removal of a toxic dye, tartrazine from aqueous solutions by a low cost agricultural by-product. Arabian J. Chem. 2017, 10, S1629–S1638. [Google Scholar] [CrossRef] [Green Version]
- Patil, H.; Shanmugam, V.; Marathe, K. Studies in synthesis and modification of PES membrane and its application for removal of reactive black 5 dye. Indian Chem. Eng. 2020. [Google Scholar] [CrossRef]
- Yan, H.; Yang, L.; Yang, Z.; Yang, H.; Li, A.; Cheng, R. Preparation of chitosan/poly (acrylic acid) magnetic composite microspheres and applications in the removal of copper (II) ions from aqueous solutions. J. Haz. Mat. 2012, 229, 371–380. [Google Scholar] [CrossRef]
- Mane, V.S.; Mall, I.D.; Srivastava, V.C. Use of bagasse fly ash as an adsorbent for the removal of brilliant green dye from aqueous solution. Dyes Pigm. 2007, 73, 269–278. [Google Scholar] [CrossRef]
- Asgher, M.; Bhatti, H.N. Evaluation of thermodynamics and effect of chemical treatments on sorption potential of Citrus waste biomass for removal of anionic dyes from aqueous solutions. Ecol. Eng. 2012, 38, 79–85. [Google Scholar] [CrossRef]
- Khosravi, I.; Eftekhar, M. Characterization and evaluation catalytic efficiency of NiFe2O4 nano spinel in removal of reactive dye from aqueous solution. Powder Technol. 2013, 250, 147–153. [Google Scholar] [CrossRef]
- Lagergren, S. Zur theorie der sogenannten adsorption geloster stoffe, Kungliga Svenska Vetenskapsakademiens. Handlingar 1898, 24, 1–39. [Google Scholar]
- Ho, Y.S.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Weber, W.J., Jr.; Morris, J.C. Kinetics of Adsorption on Carbon from Solution. J. Sanit. Eng. Div. 1963, 89, 31–59. [Google Scholar] [CrossRef]
- Xiao, Y.; Azaiez, J.; Hill, J.M. Erroneous Application of Pseudo-Second-Order Adsorption Kinetics Model: Ignored Assumptions and Spurious Correlations. Ind. Eng. Chem. Res. 2018, 57, 2705–2709. [Google Scholar] [CrossRef]
- Hubbe, M.A.; Azizian, S.; Douven, S. Implications of apparent pseudo-second-order adsorption kinetics onto cellulosic materials: A review. BioResources 2019, 14, 7582–7626. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surface of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef] [Green Version]
- Freundlich, H. Over the Adsorption in Solution. J. Phys. Chem. 1906, 57, 385–470. [Google Scholar]
- Temkin, M.; Pyzhev, V. Kinetics of Ammonia Synthesis on Promoted Iron Catalysts. Acta Physicochim. URSS 1940, 12, 217–222. [Google Scholar]
- Ghaedi, M.; Khafri, H.Z.; Asfaram, A.; Goudarzi, A. Response surface methodology approach for optimization of adsorption of Janus Green B from aqueous solution onto ZnO/Zn(OH)2-NP-AC: Kinetic and isotherm study. Spectrochim. Acta Part A 2016, 152, 233–240. [Google Scholar] [CrossRef]


 | Class | Anionic, diazo |
| Molecular formula | C26H23N5Na2O13S4 | |
| Molecular weight | 787.708 | |
| UV absorption maximum | 597 nm | |
| Reactive group | Sulfatoethylsulfone |
| Variables | Units | Levels | ||||
|---|---|---|---|---|---|---|
| Membrane | - | Mo | M1 | M2 | M3 | |
| Dye concentration | mg L−1 | 40 | 60 | 80 | 100 | |
| pH | - | 3 | 5 | 7 | 9 | 11 |
| Membrane | Models | Parameters | Dye Concentration at Initial Time Ci (mg L−1) | |||
|---|---|---|---|---|---|---|
| 40 | 60 | 80 | 100 | |||
| M0 | PFO | qe,exp (mg g−1) | 15.0 | 20.0 | 24.0 | 26.0 |
| q1 (mg g−1) | 15.8 | 20.8 | 21.5 | 26.0 | ||
| k1 × 10−2 (min−1) | 4.62 | 4.04 | 3.19 | 3.91 | ||
| R2 | 0.990 | 0.997 | 0.980 | 0.997 | ||
| PSO | q2 (mg g−1) | 17.7 | 24.7 | 29.7 | 31.25 | |
| k2 × 10−4 (g mg−1 min−1) | 29.8 | 16.3 | 12.6 | 14.4 | ||
| h (mg g−1 min−1) | 0.94 | 1.0 | 1.1 | 1.4 | ||
| R2 | 0.995 | 0.994 | 0.994 | 0.998 | ||
| IPD | ki (mg g−1 min−0.5) | 1.82 | 2.11 | 2.47 | 2.57 | |
| C (mg g−1) | 0.430 | 1.35 | 1.42 | 2.88 | ||
| R2 | 0.943 | 0.924 | 0.912 | 0.937 | ||
| M1 | PFO | qe,exp (mg g−1) | 38.2 | 54.0 | 68.1 | 79.0 |
| q1 (mg g−1) | 39.1 | 51.6 | 94.3 | 97.8 | ||
| k1 × 10−2 (min−1) | 3.90 | 3.74 | 5.85 | 5.46 | ||
| R2 | 0.996 | 0.998 | 0.971 | 0.993 | ||
| PSO | q2 (mg g−1) | 47.4 | 66.2 | 83.3 | 99.0 | |
| k2 × 10−4 (g mg−1 min−1) | 8.31 | 6.34 | 5.52 | 4.23 | ||
| h (mg g−1 min−1) | 1.92 | 2.84 | 3.85 | 4.14 | ||
| R2 | 0.995 | 0.994 | 0.974 | 0.987 | ||
| IPD | ki (mg g−1 min−0.5) | 4.41 | 5.83 | 7.92 | 9.96 | |
| C (mg g−1) | 0.672 | 5.01 | 4.84 | 1.28 | ||
| R2 | 0.989 | 0.964 | 0.960 | 0.928 | ||
| M2 | PFO | qe,exp (mg g−1) | 41.0 | 57.0 | 71.0 | 82.0 |
| q1 (mg g−1) | 44.7 | 58.7 | 82.0 | 75.2 | ||
| k1 × 10−2 (min−1) | 4.92 | 4.63 | 5.44 | 4.58 | ||
| R2 | 0.995 | 0.998 | 0.998 | 0.987 | ||
| PSO | q2 (mg g−1) | 48.5 | 67.6 | 85.5 | 97.1 | |
| k2 × 10−4 (g mg−1 min−1) | 11.1 | 7.84 | 5.97 | 5.76 | ||
| h (mg g−1 min−1) | 2.64 | 3.62 | 4.31 | 5.44 | ||
| R2 | 0.995 | 0.994 | 0.987 | 0.987 | ||
| IPD | ki (mg g−1 min−0.5) | 5.23 | 6.21 | 7.65 | 8.37 | |
| C (mg g−1) | 0.412 | 7.12 | 7.27 | 16.0 | ||
| R2 | 0.982 | 0.967 | 0.875 | 0.929 | ||
| M3 | PFO | qe,exp (mg g−1) | 40.0 | 55.9 | 70.1 | 81.2 |
| q1 (mg g−1) | 45.5 | 57.7 | 90.9 | 102.8 | ||
| k1 × 10−2 (min−1) | 5.17 | 4.18 | 5.24 | 5.32 | ||
| R2 | 0.984 | 0.999 | 0.984 | 0.992 | ||
| PSO | q2 (mg g−1) | 48.8 | 68.5 | 88.5 | 103.1 | |
| k2 × 10−4 (g mg−1 min−1) | 9.65 | 6.23 | 4.44 | 3.76 | ||
| h (mg g−1 min−1) | 2.36 | 2.92 | 3.45 | 3.91 | ||
| R2 | 0.988 | 0.994 | 0.983 | 0.973 | ||
| IPD | ki (mg g−1 min−0.5) | 4.33 | 5.92 | 6.66 | 7.42 | |
| C (mg g−1) | 3.12 | 4.12 | 11.5 | 16.1 | ||
| R2 | 0.901 | 0.925 | 0.876 | 0.855 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, M.A.; Belmonte-Reche, E.; de Amorim, M.T.P. Combining Experimental Data with Statistical Methods to Evaluate Hydrolyzed Reactive Dye Removal by α-Fe2O3 in a Cellulose-Based Membrane. Fibers 2021, 9, 61. https://doi.org/10.3390/fib9100061
Silva MA, Belmonte-Reche E, de Amorim MTP. Combining Experimental Data with Statistical Methods to Evaluate Hydrolyzed Reactive Dye Removal by α-Fe2O3 in a Cellulose-Based Membrane. Fibers. 2021; 9(10):61. https://doi.org/10.3390/fib9100061
Chicago/Turabian StyleSilva, Mónica A., Efres Belmonte-Reche, and Maria T. P. de Amorim. 2021. "Combining Experimental Data with Statistical Methods to Evaluate Hydrolyzed Reactive Dye Removal by α-Fe2O3 in a Cellulose-Based Membrane" Fibers 9, no. 10: 61. https://doi.org/10.3390/fib9100061
APA StyleSilva, M. A., Belmonte-Reche, E., & de Amorim, M. T. P. (2021). Combining Experimental Data with Statistical Methods to Evaluate Hydrolyzed Reactive Dye Removal by α-Fe2O3 in a Cellulose-Based Membrane. Fibers, 9(10), 61. https://doi.org/10.3390/fib9100061







