Abstract
The aim of this research was to determine the optimum twist equation for ring-spun yarns. The yarn twist can be calculated by different equations. With the research, we tried to find the appropriate equation to determine the yarn twist, which is determined by the values of yarn strength and hairiness. In the research, yarns from long staple combed cotton rovings and of different fineness (10 tex, 11.8 tex, 20 tex and 29.4 tex) were analyzed. The yarn twist was calculated using the equations of Koechlin and Laetsch. The analyzed yarns were produced in the spinning mill on the laboratory ring spinning machine Spinntester. In the second part of the investigation, yarn strength and hairiness were analyzed as a function of yarn twist. The results showed that Laetsch’s equation is suitable for determining the twist for yarns with a fineness of 10 tex, 11.8 tex, 20 tex and 29.4 tex, since, in this case, the calculated number of yarn threads is higher and thus the strength and elongation at break are also higher. The yarn hairiness is higher in analyzed samples for yarns with the twist calculated according to the Koechlin’s equation.
Keywords:
ring-spun yarn; Koechlin’s equation; Laetsch’s equation; twist; evenness; strength; hairiness 1. Introduction
The twisting of yarn leads to a change in its structure and, thus, to a change in various parameters and properties of the fiber in the yarn structure. In addition to the measuring conditions and material properties, the inclination of the fibers to the linear axis of the yarn is one of the most important factors influencing the mechanical and physical properties of the yarn (the shape of the tensile stress–strain curve, the strength and the breaking elongation of the yarn).
In the present study, we have determined the optimum twist equation (Koechlin’s and Laetsch’s equations) for long staple combed cotton ring-spun yarns. The yarns analyzed were produced in a spinning mill. During the investigation, yarn strength and hairiness were analyzed as a function of yarn twist.
We compared yarns of different fineness (10 tex, 11.8 tex, 20 tex and 29.4 tex), whereby the twist was calculated using two equations (Koechlin’s and Laetsch’s equations). Finally, we tried to find out which of these is suitable for calculating the yarn twist before producing the analyzed yarns. Based on the measured properties (tensile properties, hairiness), we determined the optimum equation for calculating the yarn twist. The ring-spun yarn for the research was produced from long staple combed cotton rovings with a fineness of 0.58 ktex. The yarn produced was measured on the basis of parameters that can be influenced by the yarn twist, namely yarn fineness, tenacity and elongation at break, as well as thin and thick places, neps and hairiness of the yarn.
Ring spinning machines represent one of the most widely used yarn production technologies worldwide. The ring spinning machine is used in the textile industry to simultaneously twist staple fibers into a yarn structure and then wind it onto cops for storage. The yarn loop rotating rapidly around a fixed axis creates a surface called a “balloon”. The settings of the ring spinning machine are selected to reduce the hairiness of the yarn and the risk of the fiber vitrifying or melting. Koechlin’s equation is a basic equation which assumes that the yarn is a linear formation in the form of a cylinder [1,2].
Koechlin’s equation is also the oldest and forms the basis for the derivation of all other equations developed by various scientists. When calculating the yarn twist, Koechlin’s equation assumes that the yarn forms the shape of a cylinder. The twist angle (helix angle) is an important parameter of the filaments, which determines the degree and shape of deformations that occur along their length. It is generally accepted that the twist in yarns of different fineness (linear density) is comparable if the helix angle (and twist factor) is constant. Koechlin’s equation was first proposed by Mr. Koechlin in 1828 and represents an objective method for determining the twist level in yarn. According to Koechlin, the yarn twist is a product of the twist multiplier and the square root of the yarn count, expressed in an indirect system of yarn count. This expression was very simple, but, unfortunately, did not provide sufficiently accurate results [2,3,4,5]. Later, many researchers corrected Koechlin’s expression empirically [2]. However, there is still hardly any theoretical expression for determining yarn twist. The balance of action and reaction forces determines the final diameter of the yarn. The relationships between twist, fineness and diameter of the yarn cannot be resolved by definitions alone. This was the main reason for deriving Koechlin’s equation. Koechlin’s assumptions assume that all yarns are made from the same material, spun with the same spinning technology and designed for the same purpose. The traditional equation of Koechlin’s theoretical concept is very simple, so it could be used in various practical applications worldwide, but it is not too precise. This is the reason why some authors suggest different spin exponents. In practice, finer yarns are twisted slightly more than coarser yarns in order to obtain good properties. In contrast to the twist exponent resulting from the Koechlin concept (q = 0.5), the authors recommend various modified values of this exponent. This is very interesting because all authors recommend twist exponents greater than 0.5, usually by 0.66 (q = 2/3). The twist exponent mentioned above is also recommended by Mr. Laetsch [2,3,4,5].
1.1. Theoretical Part
Equations for Calculating Yarn Twist
Yarn twist and the direction of twist of the yarn influence various important properties of yarn, such as strength, elasticity, fullness, smoothness, softness and evenness.
The first equation for calculating yarn twist was introduced in France almost 200 years ago. The equation was introduced by Mr. Koechlin in the first quarter of the 19th century [2,5] under the assumption that all yarns are made from the same material, with the same technology and for the same purpose [2].
In practice, finer yarns are twisted slightly more than coarser yarns in order to obtain optimum properties. This was the reason why several authors proposed an empirical generalization of the basic Koechlin’s equation. In contrast to the twist exponent resulting from Koechlin’s concept (q = 0.5, see Table 1), the authors recommended various modified values for the twist exponent (Table 1). They are usually not too far from the value 0.6.

Table 1.
Developing equations for calculating the number of turns per meter of yarn ([2], p. 28).
Later, various scientists looked for solutions to improve Koechlin’s equation. They concentrated on changing the exponent of the twist. Table 1 shows a large number of empirical values for the exponent of rotation by Koechlin’s determination of different scientists based on equation calculations and experimental work [2,6,7].
1.2. Koechlin’s Equation for Calculating Yarn Twist
Koechlin was a French engineer who was still working on yarn twists and was able to establish the optimum equation for calculating the number of twists per unit length of yarn. All further investigations of the equations for optimum winding were based on his assumptions. [2,3,4,5,6,7,8].
Koechlin assumes that yarn is a linear formation having the shape of a circular cylinder, as shown in Figure 1 [2].
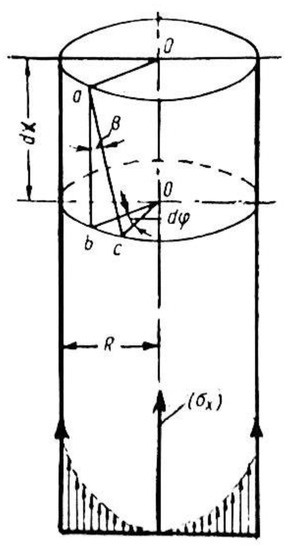
Figure 1.
Principle of cylindrical yarn shape.
As the yarn is passed on, each individual fiber in the yarn is twisted through an angle around the axis of the yarn. The fiber ab with the length dx, which is parallel to the yarn axis in the yarn before twisting, tilts by an angle of β and rotates by an angle of dφ around the yarn axis.
As a result of the intervention in the yarn, the fiber ab is displaced by an angle of β and lengthened to the length (ac). [2,3,4,5,6,7].
The derivation of Koechlin‘s equation is presented with following Equations (1)–(16) [5,9].
The intensity of the yarn twist Tm is defined by Equation (3):
If one turn is transmitted at length dx = ab (length of fiber in yarn), the fiber (ab) is rotated about the axis of the yarn by:
From Equation (2), the angle dφ is expressed:
From Equations (4) and (5) is seen, that the angle dφ amounts to 360 °.
If an ideal model for yarn presented a smooth cylinder, then the weight of the unit length of the yarn and diameter of yarn would be shown by Equations (7) and (9).
The mass of yarn, dm, is expressed as the product of the volume, dV, and density, γ, of yarn, assuming the yarn cross section has the shape of a circle. The volume of the yarn, dV, presents the product between the cross-sectional area of the yarn, s, and the length of the fibre in the yarn, dx (dV = s·dx) (Equation (7)).
The quotient between the mass, dm, and the length of the single fibre in the yarn, dx (see Figure 1), is expressed as a fineness of the yarn, Ttyarn.
The cross-sectional area, s, of the circular shape of the cylinder is expressed with Equation (9):
From Equations (7) and (9), Equation (10), which express the diameter of the yarn, d, is derived:
If the finennes, Ttyarn, in Equation (10) is presented as metric number, Nmyarn, Equation (11) is derived.
From Equation (10), the expression is calculated and presented in Equation (12).
when Equation (10) for the yarn diameter is inserted into Equation (3) for the intensity of the yarn, it is as follows:
The unit of yarn twist is turns per meter of yarn. Because of this, we have to convert the yarn density unit γ (g/cm3) to g/m3, resulting in the following change in Equation (14) for yarn twist:
Finally, we express the expression as the coefficient of twist, , in the Koechlin’s Equations (15) and (16):
where Yarn radius (mm); the rotation of the fiber ab about the axis of the yarn (radians); d-yarn diameter (mm); Nm-yarn fineness (m/g); Tt-yarn fineness (tex); αm is the coefficient of twist; Tm is the number of turns in the yarn according to Koechlin’s equation (T/m).
1.3. Laetsch’s Equation for Calculating the Twist of the Yarn
Koechlin’s equation has the disadvantage of assuming that all yarns are made of the same material, with the same technology and for the same purpose of end-use [2,3,4,5,6,7]. That is the reason to modify the twist exponent (see Table 1). As a result, other equations have been introduced, the most famous of which is Laetsch‘s equation for calculating yarn twist. [7,10].
Laetsch’s Equation (17) for calculating the number of turns per inch depends on the twist coefficient and the fineness of the yarn. In Laetsch’s Equation (17) the English cotton number, Ne, is converted into a metric number, Nm, and finally, the number of turns per meter, Tm, is calculated. The twist coefficient is determined on the basis of the raw material (combed cotton yarn) from which the yarn is made and its intended use: αe = 1.75 [11].
The calculation of yarn twist using Laetsch’s equation [2]:
Determination of the twist factor of the yarn with fineness 29.4 tex using Koechlin’s Equation (18):
where Ne is the English yarn numbering for Laetsch’s equation [yard/libra]; αm is the coefficient of twists per inch; Te is the number of turns in the yarn according to Koechlin’s equation [T/inch].
The twist coefficient, αe, is derived according to the English measuring system. For yarn made of cotton, the values given in Table 2 are determined and depend on the purpose of further use of the yarn [10,11,12].

Table 2.
Coefficient of twist, αe, according to the useful properties of the yarn produced [9].
Typical cotton yarns have a twist factor, αe, of 3 to 8, while worsted yarns have a twist factor, αe, of 1.4 to 2.5, when twist is measured in turns per inch. Cotton yarn with a twist factor of 3 feels soft and docile, while yarn with a twist factor of 8 feels hard and lively [12,13].
2. Materials and Methods
2.1. Calculation of the Number of Turns Per Meter in the Yarn
With the presented investigations, we wanted to find the optimum equation for determining yarn twist. We used two equations, Koechlin’s and Laetsch’s equations, to calculate the number of turns per meter in the yarn. The equations differ in their twist exponents. Koechlin’s equation is used to calculate the twist with the metric measuring system, while Laetsch’s equation is used to calculate the twist using the English measuring system. The twist coefficient, αe, was determined in a spinning mill for ring-spun yarn made of long staple cotton fibers with a length of 25 to 60 mm, taking into account that the analyzed samples were produced on a laboratory spinning machine spinning tester (SERMSTES), which allows the production of ring-spun yarns with a fineness between 10 and 30 tex and a twist count between 500 and 1200 turns per meter. Given the fineness and the number of twists per meter of the analyzed yarn that can be spun on the spinning tester, they determined the optimum twist coefficient, αe, in the spinning mill before spinning.
According to Laetsch’s equation, the twist coefficient for combed long staple cotton fibers is αe = 1.75.
To calculate of the number of twists according to Laetsch’s equation, the fineness in the English measurement system, Ne, is converted into the metric measurement system, Nm. Consequently, the number of twists according to the Laetsch equation is expressed in turns per meter (T/m) instead of turns per inch (T/inch). We have, therefore, represented the number of turns per meter (T/m) (metric number system) with the transformation of Te (English measuring system) (see Equation (18)).
In order to simplify the calculation of the number of turns per meter of yarn according to Koechlin’s and Laetsch’s equations, we have taken, as a starting point, the number of turns per meter calculated according to Koechlin’s and Laetsch’s equations for the coarsest analyzed yarn with a fineness of 29.4 tex (Te = Tm).
The equation for the number of turns per meter at 29.4 tex according to Laetsch’s and Koechlin’s equations, for the calculation of the alphabet according to the Koechlin’s equation, is represented by Equation (19):
In Table 3, calculations of the number of turns per meter according to both equations are given.

Table 3.
Calculation of the number of turns per meter in yarn.
2.2. Production of Yarn on a Ring Spinning Machine
The analyzed yarn was produced from long staple cotton fibres in a combing process. Long staple cotton has a length of 25 to 60 mm and is therefore one of the highest quality cotton types for processing. The roving had 25 turns per meter. The analyzed ring-spun yarns were produced on the laboratory spinning machine Spinntester (SERMSTES). The analyzed yarns had different finenesses of 29.4, 20, 11.8 and 10 tex.
The Spinntester (Figure 2) has six spindles and a three-roller double-apron drawing frame (La Blan Roth draw frame). The diameter of the ring is 38–60 mm, it can reach a speed of 3500 to 25,000 rpm and it is suitable for the use of cops with a height of 200 to 240 mm.

Figure 2.
Laboratory Spinntester.
Based on the processed raw material, the yarn fineness and the yarns produced, we determined, for each of the machines, separately, the type of travellers and spacers for the Spinntester. The settings on the machines and other data are given in Table 4.

Table 4.
Settings on the Laboratory Spinntester.
2.3. Method
For the present research, we have to determine the optimum equation for determining yarn twist. Yarn twist has an important influence on some physical and mechanical properties of yarn, such as yarn strength, hairiness, evenness, etc. Yarns with different finenesses (10 tex, 11.8 tex, 20 tex and 29.4 tex) were analyzed with different numbers of turns per meter, calculated using the equations of Koechlin and Laetsch.
To find the optimum equation for determining yarn twist (Koechlin’s and Laetsch’s equations), the following properties were analyzed on the ring yarn produced:
Fineness of the yarn;
- Yarn twist and twist direction;
- Tenacity and breaking extension;
- Hairiness, neps and thin and thick places of ring-spun yarn.
2.4. Fineness of Yarn in Tex and Metric Systems
The fineness of yarn is defined as mass per unit length and is expressed in tex (g/km).
The yarn fineness was determined directly and gravimetrically based on ISO 2060 (Textiles—Yarn from packages—Determination of linear density (mass per unit length, 1996)) by the skein method [14] (Table 5, Figure 3).

Table 5.
Measured fineness of the analyzed yarns.
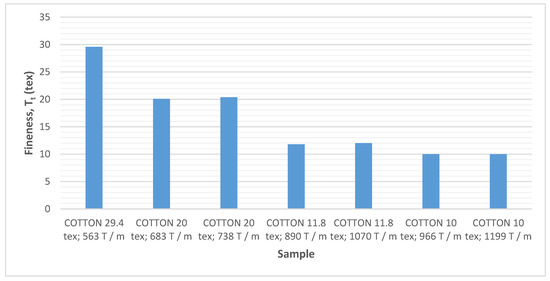
Figure 3.
Average fineness of the analyzed yarns.
2.5. Number of Turns Per Meter and Direction of Twist
The yarn produced on the Laboratory Spinntester is a single yarn that is twisted in a Z-direction. Twisting yarn allows the fibers to be combined into a yarn and affects properties of the yarn, such as strength, elasticity, elongation and softness of the yarn.
The number of turns per meter in a single yarn was determined indirectly by an apparatus for measuring the number of turns per meter of the so-called torsiometer on the basis of the standard ISO 2061 (Textiles. Determining the turns per meter of the yarn. Direct counting method, 2010) [15].

Table 6.
Measured number of turns per meter of analyzed yarns.
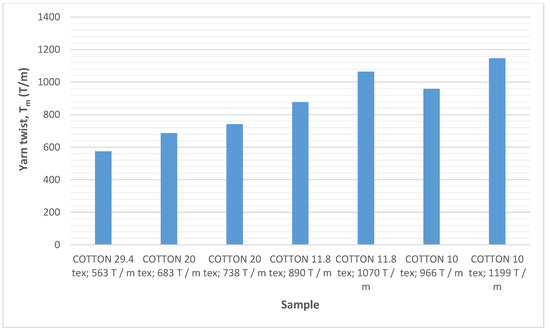
Figure 4.
Average yarn twist of the analyzed yarns.
2.6. The Tenacity and the Elongation at Break of the Yarn
Tensile properties, such as tenacity and elongation at break of a single yarn, were measured on the tensile testing machine Statimat, based on ISO 2062 (Textiles. Yarns from windings. Determination of breaking force and breaking elongation on devices with constant expansion rate (CRE), 2009) [16]. We took ten measurements from each cop, so we performed 50 measurements altogether. Table 7 gives the results of the measurements for single yarns of different fineness and number of turns per meter; for each measured cop, the average value of ten measurements is given. Figure 5 presents the average tenacity and elongation at break of samples analyzed.

Table 7.
Measured tensile properties of the yarn analyzed with different numbers of turns per meter.
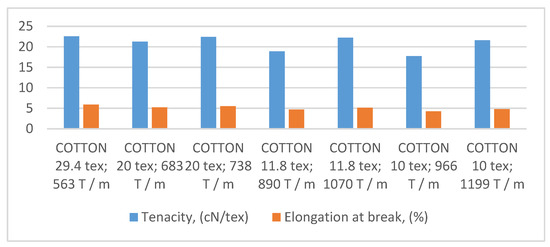
Figure 5.
Average tenacity and elongation at break of the samples analyzed.
2.7. Hairiness, Neps, Thin and Thick Places of Analyzed Yarn
Hairiness, neps and thin and thick places of the analyzed yarns were determined by Uster Tester using a capacitive sensor. The results of the measured properties of the yarns are listed in Table 8. Figure 6 presents the average hairiness of the analyzed yarns.

Table 8.
Hairiness, neps, thin and thick places analyzed yarn.
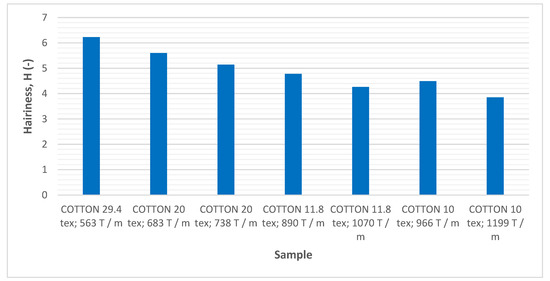
Figure 6.
Average hairiness of the analyzed yarns.
2.8. Statistical Analysis
The significance of yarn twist, which was determined with the equations of Koechlin and Laetsch, for strength, elongation at break and hairiness was tested with the one-factor variance analysis (ANOVA).
The basis of the one-factor ANOVA is represented by the division of the square sums of the squares into intermediate classes (SSb) and within classes (SSw). This technique makes it possible to compare all classes with each other simultaneously, rather than individually. This method also assumes that the samples are normally distributed. The one-factor analysis is calculated in three steps. The sums of the squares are determined for all samples and then for cases within and between classes. For each step, the degrees of freedom (df) are also determined, where df is the number of independent pieces of information involved in estimating a parameter. These calculations are used in Fisher statistics to analyze the null hypothesis. The null hypothesis states that there are no differences between the means of different classes, which suggests that the variance of the samples within the classes should be identical to the variance of the samples between the classes. If F ≥ 1, then differences are likely to exist between the means of the classes. These results are then tested for statistical significance, or p-value, where the p-value is the probability that a variation takes on a value that is greater than or equal to the strictly randomly observed value. If the p-value is low (e.g., p ≤ 0.05 or p ≤ 5%), then the null hypothesis is rejected, indicating that differences exist between classes and that these differences are statistically significant. If the p-value is greater than 0.05 (e.g., p ≥ 0.05 or p ≥ 5%), then the null hypothesis is accepted, indicating that the differences between the classes are random. [17]
The results of the statistical analysis of the influence of yarn twist (determined using Koechlin’s and Laetsch’s equations) on strength and hairiness are given in Table 9 and Table 10.

Table 9.
The results of the statistical analysis of the influence of yarn twist on tenacity.

Table 10.
The results of the statistical analysis of the influence of yarn twist on hairiness.
3. Discussion of the Results
The research focused on determining the optimal equation for calculating the twist of long staple cotton ring-spun yarns with a fineness of 29.4 tex, 20 tex, 11.8 tex and 10 tex.
To determine the optimum equation for calculating yarn twist, we focused on the influence of yarn twist on the tensile properties of yarn (tensile strength and elongation at break) and hairiness; thin and thick places and neps were also analyzed.
3.1. Tenacity of Analyzed Yarns
The results of tenacity of the analyzed showed that ring-spun yarn with 29.4 tex with the same number of calculated turns per meter had a tenacity of 22.56 cN/tex according to both equations (Figure 7). For ring-spun yarn with 20 tex, with the number of turns per meter calculated according to the Koechlin equation (683 T/m), the tenacity amounted to 21.25 cN/tex, and for Laetsch’s equation (the number of turns per meter is 738 T/m), to 22.41 cN/tex. For ring-spun yarns with 11.8 tex (number of turns per meter is 890 T/m, Koechlin’s equation) there was a tenacity of 18.88 cN/tex, and for the yarn twist calculated with Laetsch’s equation (1070 T/m), it was 22.23 cN/tex. The yarn with a number of turns per meter higher than 180 T/m also had a higher tenacity of 3.35 cN/tex. For ring-spun yarns with 10 tex at 966 T/m, calculated according to Koechlin’s equation, the tenacity was 17.72 cN/tex, while at 1199 T/m, calculated according to Laetsch’s equation, it was 21.58 cN/tex. The yarn, which had a higher twist of 233 T/m, also had a higher tenacity by 3.86 cN/tex.
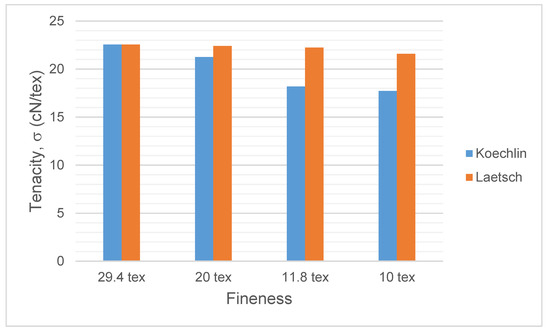
Figure 7.
Tenacity as a function of the number of turns per meter and fineness of yarn.
The results of measuring tenacity show that tenacity decreases with the decreasing fineness and twist of yarns (see Figure 3). For yarns where the twist was calculated according to Koechlin’s equation, the decrease in tenacity was higher.
From the available results, it is evident that the tenacity was higher for yarns examined with a fineness of 10 tex to 20 tex, for which the twist was calculated according to Laetsch’s equation. The statistical analysis ANOVA showed significant differences in tenacity (Table 9) between the samples analyzed (p-value < 0.05).
3.2. Elongation at Break of Analyzed Yarns
The results of measuring elongation at break showed that the elongation at break of the yarn with 29.4 tex was 5.91% (Figure 8). The elongation at break of the yarn with 20 tex at 683 T/m, calculated according to Koechlin’s equation, was 5.23%. The results showed that when Laetsch’s equation was used, the twist of the yarn with 20 tex at 738 T/m was higher, thus, the elongation at break of the yarn was mentioned (5.48%). The yarn with a higher twist (approx. 55 T/m) also expressed a higher elongation at break (by 0.25%).
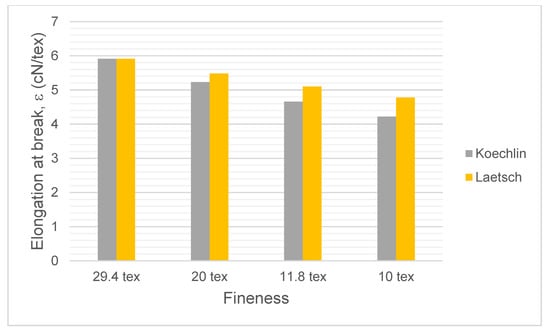
Figure 8.
Elongation at break as a function of the number of turns per meter and yarn fineness.
The elongation at break of the yarn with 11.8 tex at 890 T/m, calculated according to Koechlin’s equation, was 4.66%. The results showed that, using the Laetsch’s equation, the twist of the yarn with 11.8 tex at 1070 T/m was higher, and thus the elongation at break of the yarn was also mentioned (5.10%). The yarn with a higher twist (approx. 180 T/m) also expressed a higher elongation at break (by 0.44%).
The elongation at break of the yarn with 10 tex at 966 T/m, calculated according to Koechlin’s equation, was 4.22%. The results showed that, using Laetsch’s equation, the twist of the yarn with 10 tex at 1199 T/m was higher, thus, the elongation at break of the yarn was mentioned (4.78%). The yarn with a higher twist (approx. 233 T/m) also expressed a higher elongation at break (by 0.56%).
The results of the elongation at break showed that the elongation at break also decreased with decreasing fineness and twist of the yarns. The decrease in elongation at break was higher for yarns for which the twist was calculated according to the Koechlin equation (see Figure 9).
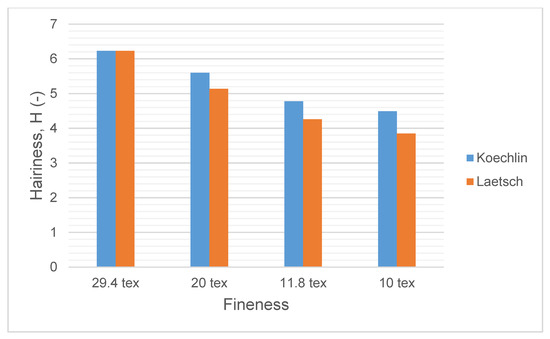
Figure 9.
Yarn hairiness as a function of number of turns per meter and yarn fineness.
The results indicated that the elongation at break was higher for yarns with a fineness of 10 tex to 20 tex, for which the twist was calculated according to Laetsch’s equation. Statistical analysis ANOVA showed significant differences in elongation at break between the samples analyzed (p-value < 0.05).
3.3. Yarn Hairiness
The hairiness results showed that the hairiness of the yarn with 29.4 tex was 6.23 (Figure 9).
The hairiness of the yarn with 20 tex at 683 T/m, calculated using Koechlin’s equation, was 5.60. The results showed that, when using Laetsch’s equation, the twist of the yarn with 20 tex at 738 T/m was higher, but the hairiness of the yarn mentioned was lower (5.14). The yarn with a higher twist (approx. 55 T/m) also expressed a lower hairiness (by 0.46).
The hairiness of the yarn 11.8 tex at 890 T/m, calculated according to the Koechlin’s equation, was 4.78. The results showed that, when the Laetsch’s equation was used, the twist of the yarn with 11.8 tex was higher at 1070 T/m and, consequently, the hairiness of the yarn mentioned was lower (4.26). The yarn with a higher twist (approx. 180 T/m) also expressed a lower hairiness (by 0.52).
The hairiness of the yarn with 10 tex at 966 T/m, calculated according to Koechlin’s equation, was 4.50. The results showed that, when Laetsch’s equation was used, the twist of the yarn with 10 tex was higher at 1199 T/m and, consequently, the hairiness of the yarn mentioned was lower (3.85). The yarn with a higher twist (approx. 233 T/m) also expressed a lower hairiness (by 0.65).
From the given results of the hairiness (Figure 9), it can be concluded that the hairiness of yarn is not directly influenced by the fineness of the yarn, but only by the number of turns per meter, which depends on the fineness of the yarn. Figure 9 shows that the hairiness of yarn decreases as the number of turns per meter in the yarn increases. However, since the optimum number of turns per meter in the yarn is determined for a given yarn count, it is a fact that coarser yarns are also hairier than finer yarns, as coarser yarns cannot obtain as many turns per meter.
The yarn hairiness showed exactly the opposite of the results for tenacity and yarn elongation (Figure 7 and Figure 8), i.e., the hairiness of the analyzed yarns was lower for the yarns for which the twist was calculated according to the Laetsch equation. Statistical analysis ANOVA showed significant differences in hairiness (Table 10) between the analyzed samples (p-value = 0.05).
Yarn hairiness can occur in the area of the spinning triangle, where certain fibers do not fit into the yarn alone. In the area of the spinning triangle, the adhesion between the fibers is minimal. The fibers on the surface of and inside the triangle have different tensions and cannot, therefore, twist at the same time. The geometry of the spinning triangle influences different properties of yarn and depends on the spinning geometry and the intensity of the yarn conveyed. It can, therefore, be assumed that yarns with higher turns per meter have a shorter spinning triangle than yarns with lower turns per meter. In general, yarn hairiness is greater in the shorter spinning triangle because the edge fibers in the spinning triangle crimp at a greater angle around the yarn axis, therefore, some edge fibers avoid the twist effect and leave the spinning triangle. Otherwise, the yarn hairiness results (Figure 9) show that yarn hairiness is higher for yarns with lower turns per meter. Since the differences in yarn hairiness are so small, and the difference in the number of turns per meter in the yarn is not so great, it can be assumed that for yarns with lower turns per meter and, thus, somewhat larger spinning triangles, all shorter fibers in the wick leave the fiber bundle due to the smaller spinning triangle and do not twist into the yarn, but appear as protruding fibers on the yarn.
3.4. Future Research Perspectives
The determination of an appropriate equation for calculating yarn twist before yarn production is very important, since the optimum yarn twist has a considerable influence on the mechanical properties and the evenness of the yarn. The research presented is also very important for future research in the field of determining the optimum equation for calculating yarn twist and its influence on the mechanical properties and evenness of the yarn.
In fact, the results of our research have shown that Laetsch’s equation is more optimal for calculating yarn twist than Koechlin’s equation, which is mentioned several times in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13].
The present study shows that the tenacity and elongation at break were higher for the combed ring yarns of long staple cotton with a fineness of 10 tex to 20 tex, for which the twist was calculated using Laetsch’s equation rather than those calculated the Koechlin equation.
The tenacity and the reduction in elongation at break were also higher for yarns where the twist was calculated using Koechlin’s equation.
The yarn hairiness showed exactly the opposite in the results for tenacity and elongation, i.e., the hairiness of the analyzed yarns was lower for yarns where the twist was calculated according to the Laetsch’s equation.
4. Conclusions
Based on the research work to determine the optimum equation for calculating the twist of ring-spun yarn made of combed long staple cotton yarn, we can state the following:
- Ring-spun yarns of combed long staple cotton with a fineness of 10 tex to 20 tex have a higher strength and elongation at break when the twist is calculated according to Laetsch’s equation.
- The decrease in strength and elongation at break as a function of decreasing yarn fineness (from 20 tex to 10 tex) is higher for yarns for which the twist has been calculated using Koechlin’s equation.
- Yarn hairiness showed exactly the opposite in the results for tenacity and elongation, i.e., the hairiness of the analyzed yarns was lower for yarns for which the twist was calculated using the Laetsch equation.
Based on the results of the most important properties of strength, elongation at break and hairiness, we propose to use Laetsch’s equation to calculate yarn twist.
Author Contributions
Conceptualization, D.Š.G and N.S.; methodology, D.Š.G and N.S.; validation, D.Š.G and N.S; formal analysis, D.Š.G and N.S; investigation, D.Š.G and N.S; data curation, D.Š.G and N.S; writing—original draft preparation, D.Š.G.; writing—review and editing, D.Š.G.; supervision, D.Š.G and N.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lawrence, C.A. Advances in Yarn Spinning Technology; Woodhead Publishing: Cambridge, UK, 2010; pp. 42–77. [Google Scholar]
- Neckár, B.; Das, D. Theory of Structure and Mechanics of Yarns; Woodhead Publishing: New Delhi, India, 2018; pp. 24–31. [Google Scholar]
- Gregory, J. Cotton yarn structure; Part 1: Micro yarn structure. J. Text. Inst. 1950, 41, T1–T13. [Google Scholar] [CrossRef]
- Hearle, J.W.S.; Merchant, V.B. Relations between Specific Volume, Count, and Twist of Spun Nylon Yarns. Text. Res. J. 1963, 33, 417–424. [Google Scholar] [CrossRef]
- Hearle, J.W.S.; Grosberg, P.; Backer, S. Structural Mechanics of Fibres, Yarns, and Fabrics; Wiley-Interscience: Hoboken, NJ, USA, 1969; Volume 1, 469p. [Google Scholar]
- Takajima, T. Advanced Fiber Spinning Technology; Woodhead Publishing: Tokio, Japan, 1996; p. 268. [Google Scholar]
- Neckář, B.; Das, D. Computational methodology for determination of yarn twist and diameter. J. Text. Inst. 2019, 110, 1660–1671. [Google Scholar] [CrossRef]
- Mertová, I.; Moučková, E.; Neckář, B.; Vyšanská, M. Influence of twist on selected properties of multifilament yarn. Autex Res. J. 2018, 18, 110–120. [Google Scholar] [CrossRef]
- Lawrence, C.A. Fundamentals of Spun Yarn Technology; CRC Press: London, UK, 2003; p. 32. [Google Scholar]
- Senthil Kumar, R. Process Management in Spinning; CRC Press: London, UK, 2015; pp. 157–216. [Google Scholar]
- Nikolic, M.; Lesjak, F.; Stritof, A. The future of ring spinning = The future of ring spinning. Tekstilec 2000, 43, 188–195. [Google Scholar]
- Saville, B.P. Physical Testing of Textiles; Woodhead Publishing Limited: Manchester, UK, 1999; p. 89. [Google Scholar]
- Klein, W. The Rieter Manual of Spinning-Volume 1: Technology of Short-Staple Spinning; Rieter Holding: Winterthur, Switzerland, 2018; pp. 1–52. [Google Scholar]
- ISO 2060. Textiles–Yarn from Packages—Determination of Linear Density (Mass per unit Length) by the Skein Method; BSI: London, UK, 1996; p. 13. [Google Scholar]
- ISO 2061. Textiles–Determining the Turns per Meter of the Yarn. Direct Counting Method; BSI: London, UK, 2010; p. 12. [Google Scholar]
- ISO 2062. Textiles–Yarns from Windings. Determination of Breaking force and Breaking Elongation on Devices with Constant Expansion Rate (CRE); BSI: London, UK, 2009; p. 3. [Google Scholar]
- Clarke, D.M.; Cooke, D. A Basic Course of Statistics; John Wiley & Sons: London, UK, 2004; pp. 571–593. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).