Abstract
The use of fiber-reinforced polymer (FRP) composite materials are continuously growing in civil infrastructure due to their high strength, low weight, and manufacturing flexibility. However, FRP is characterized by sudden failure and lacks ductility. When used in construction, gradual failure of FRP components is desired to avoid catastrophic structural collapse. Due to its mechanical orthotropy, the behavior of FRP relies significantly on fiber orientation and stacking sequence. In this paper, a novel multi-angled glass fiber reinforced polymer (GFRP) composite laminate showing pseudo ductile behavior is produced using 3D-printing. This is accomplished by varying fiber orientation angles, stacking sequence, and thickness of lamina. Single-angled GFRP composite specimens were 3D-printed with different fiber orientation angles of 0°, 12°, 24°, 30°, 45°, and 90° using continuous and fused filament techniques. The tension test results of the single-angled specimens were then used to aid the design of multi-angled laminate for potential progressive failure behavior. A 3D finite element (FE) model was developed to predict the response of the experimental results and to provide insight into the failure mechanism of the multi-angled laminate. The experimental observations and the FE simulations show the possibility of producing pseudo ductile FRP-by-design composite using 3D-printing technology, which leads the way to fabricate next-generation composites for civil infrastructure.
1. Introduction
Steel is widely used in the construction, automotive, and airplane industries due to its remarkable ductility. However, steel corrosion is a multi-billion-dollar challenge that creates a vicious cycle of maintenance, repair, and replacement in infrastructure. Fiber-reinforced polymers (FRP) are high-strength materials that were introduced in the middle of the 20th century for aerospace applications. Despite its relatively high initial cost, FRP found their way to construction industries due to its lightweight, durability, and immunity to corrosion [1,2,3,4]. However, the mechanical behavior of FRP composites is typically anisotropic, which results in a variety of complex failures [5]. The structural design of components is based on a ‘fail-safe’ concept that requires elements to give a warning prior to failure to prevent catastrophes. FRP composites with monotype fibers do not address this criterion and, thus, abrupt structural failure with little to no warning can occur. The lack of ductility in FRP hinders their widespread use in civil infrastructure.
To overcome such shortcomings, hybrid FRP composites incorporating two or more fibers have been studied. The tensile properties of hybrid FRP composites were reported, which were created using glass, carbon, and Kevlar fibers arranged in an interlayer or layer-by-layer, intralayer, yarn-by-yarn and intra-yarn, or fiber-by-fiber [6]. Characteristic load drops obtained from experimental testing were reported in hybrid FRP composites [7]. Several efforts were also made to achieve a pseudo-ductile behavior in hybrid composites to obtain a gradual load drop instead of multiple sharp load drops [6,8,9,10,11,12,13]. However, the degree of dispersion of fibers governed the performance and failure strain of hybrid FRP [6,7]. Alternative ways to achieve high failure strain were investigated by combining brittle and ductile fibers. High strains up to 18% were achieved at very low load-carrying capacities due to the sudden failure of the brittle fibers [14]. Additionally, the fabrication methods were very challenging.
The current study demonstrates the possibility of achieving characteristic progressive failure in FRP composites consisting of the monotype fiber by controlling the shared stiffness between the different layers. Engineering the shared stiffness is achieved by designing fiber layer thickness, fiber orientations, and stacking sequence that allow specific stiffness distribution within the FRP composite. Controlling and fabricating FRP composites with different fiber orientations and varying layer thickness is cumbersome when using traditional fabrication methods such as hand layup technique, compression molding, injection molding, and vacuum-assisted methods [15,16,17]. Therefore, 3D-printing with continuous fiber printing technology at different orientations is used to produce the new design of FRP composites in this study.
3D-printing technology or additive manufacturing has been in use extensively to fabricate non-reinforced and reinforced polymer composites [18,19,20,21,22,23,24,25,26,27,28,29]. Alternatively known as Rapid Prototyping (RP), the manufacturing process in 3D-printing involves producing components created from computer-aided design (CAD). Several categories in 3D-printing exist such as Fused Deposition Modeling (FDM), Stereolithography (STL), Selective Laser Melting (SLM), and Laminated Object Manufacturing (LOM) [30]. FDM is a leading technique achieved through the layer-by-layer deposition of material in the form of a filament extruded through a nozzle [26]. The layer-by-layer approach in 3D-printing allows component building with complex tailor-made geometries for wide applications [27]. For improved mechanical performance and excellent functionality, polymer matrix components are 3D-printed with fiber reinforcement [28]. Demand for such high performing fiber-reinforced 3D-printed parts has led to advancements in 3D-printing technology toward continuous filament fabrication (CFF) [19] for printing fiberglass filament and fused filament fabrication (FFF) [31]. Improved mechanical performance was achieved with an increased volume of fiber reinforcement in 3D-printed specimens with continuous fiber reinforcement [30]. In this study, the mechanical behavior of 3D-printed glass fiber reinforced polymer (GFRP) composites with multiple fiber orientations and varying layer thickness is evaluated experimentally. 3D-printing slicing software allows controlling the placement of fiber, fiber orientation, and sequence of the FRP laminate, which is needed for this study. Failure mechanics and tensile behavior are further studied by developing a 3D finite element (FE) model. Comparisons between the FE model and experimental data were performed to aid further understanding of progressive failure.
2. Experimental Procedures
2.1. Materials
FRP composites with discrete fiber orientation were 3D-printed using fiberglass and a thermoplastic filament. The fiberglass spool used was 150 cc with a melting temperature of 229 °C. A 50 cc Nylon-based thermoplastic spool was used with a melting temperature of 273 °C, and it was printed with 100% infill density to minimize voids. Markforged™ 3D-printer and filament spools were used. The thermoplastic material was used for printing one layer of floor and roof along with wall supports, which are necessary to ensure stability during 3D-printing. Fiberglass filaments were used for printing intermediate layers with discrete fiber orientations in the 3D-printed FRP composite laminate. The complete printing process, including part preparation, 3D model import from AutoCAD and slicing, was controlled using the 3D-printing software. Eiger™ is reported by others [30].
2.2. 3D-Printing and Specimen Preparation
Two sets of 3D-printed specimens reinforced with glass fibers were produced. The first set, ‘single-angled 3D-printed GFRP composite’, consisted of GFRP specimens 3D-printed at each discrete fiber orientation of 0°, 12°, 24°, 30°, 45°, and 90° following ASTM D3039 test standards [32]. The single-angled composites were 3D-printed with a 140-mm gauge length and 15-mm width as 10-layer symmetric balanced layers, i.e., eight layers of glass fiber and two layers of thermoplastic as floor and roof of the composite. The symmetrically balanced layup is utilized to eliminate in-plane and out-of-plane coupling and eliminate in-plane tension-shear coupling during tensile testing [33]. The second set, ‘multi-angled 3-D printed GFRP composites’, consisted of GFRP tension test specimens 3D-printed with a stacking sequence of multiple fiber orientations and thicknesses. The multi-angled composites were 3D-printed with a 140-mm gauge length and a 15-mm width as 23 layers of glass fiber and two layers of thermoplastic as floor and roof of the composites. The printing process is illustrated in Figure 1.
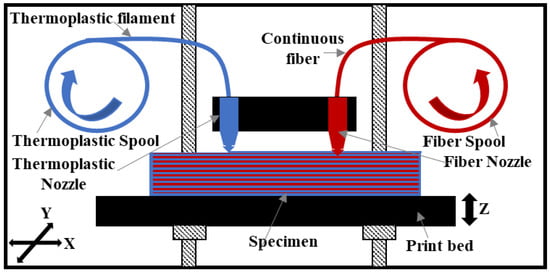
Figure 1.
Schematic of the 3D-printing process.
The printer operates at a fixed layer height of 0.1 mm for fiber-reinforced parts. Therefore, for the single-angled 3D-printed GFRP composites (Set 1), the thickness rounds up to 1 mm, and for the multi-angled 3D-printed GFRP composites (Set 2), the thickness rounds up to 2.5 mm. The layup of single-angled 3D-printed GFRP composites (Set 1) is shown in Table 1.

Table 1.
3D-printing sequence in the single-angled 3D-printed glass fiber reinforced polymer (GFRP) composites (Set 1).
In Table 1, the layer numbers indicate a printing sequence during manufacturing. Layer 1 is the first layer that is printed on the bed and then layer 2 and so on. In addition to the two sets of GFRP specimens, five thermoplastic specimens were also prepared according to the ASTM D638 test standard. Type IV specimen dimensions were used [34]. The internal view of 3D-printing patterns of thermoplastic specimens and fiber orientations are shown in Figure 2.
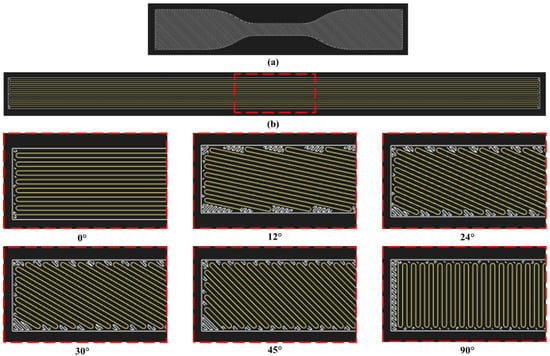
Figure 2.
Internal view of 3D-printed layers (a) thermoplastic specimen (b) fiber orientations.
For the multi-angled 3D-printed GFRP composites (Set 2), the layer thickness for each fiber orientation was selected based on axial stiffness analysis to maintain appropriate load sharing ratios among all layers at different load levels. The axial stiffness for different layers was obtained from single-angled 3D-printed GFRP composites (Set 1) tension test results. Appropriate load sharing ratios, as shown in Equations (1) and (2), guarantee gradual load transfer between different layers and could subsequently result in progressive failure of the multi-angled composite.
The length of the layer, is constant for all layers, which brings Equations (1) and (2) to their final form, as shown in Equations (3) and (4).
In the above equations, is the initial modulus, is the secant modulus, is the area of cross-section, the product is the axial stiffness, is the total number of layers, and is the layer number. To maintain the appropriate axial stiffness ratio at different load levels, the initial modulus was used to calculate the axial stiffness ratio in the initial stage, while the secant modulus was used to calculate the axial stiffness at the peak load stage [35]. Using the above approach, one multi-angled 3D-printed GFRP composites (Set 2) design was used with the following stacking sequence for fiberglass layers: Fiber orientation (number of laminas): ±45° (7)/±30° (2)/±24° (2)/12° (1)/±24° (2)/±30° (2)/±45° (7), as schematically shown in Figure 3. Laminate nomenclature is based on Reference [36]. The load sharing analysis for the multi-angled 3D-printed GFRP composite (Set 2) is presented in the Results section. The stacking sequence is selected to achieve the gradual transition of fiber orientation through-thickness of the composite plate while maintaining the symmetry of the composite plate. The printing sequence is listed in Table 2 and the layup is schematically presented in Figure 3.
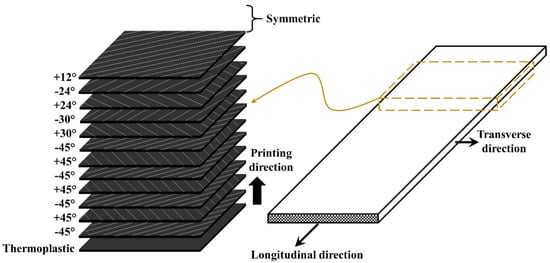
Figure 3.
Schematic of 3D-printing sequence of multi-angled 3D-printed glass fiber reinforced polymer (GFRP) composites (Set 2).

Table 2.
3D-printing sequence in the multi-angled 3D-printed glass fiber reinforced polymer (GFRP) composites (Set 2).
Prior to printing, the print bed was cleaned of any debris, and the area to be used for printing was prepared with glue to stick the printed laminates to the bed. To 3D-print, the two sets of GFRP specimens, the nozzle for thermoplastic filaments was first heated to 273 °C, and then the thermoplastic material was extruded onto the printer bed to serve as the floor for subsequent layers. This step was followed by the extrusion of the fiberglass filaments after heating the nozzle for fiberglass filaments to 229 °C. The fiberglass filaments were extruded continuously onto the thermoplastic floor with mild pressure applied by the nozzle. For the printing of the thermoplastic specimens, a similar process was used without printing any layers of fiberglass. The specimens were detached from the print bed with a flat spatula post completion of the printing.
Upon printing, end tabs were attached to the single-angled 3D-printed GFRP composite (Set 1) specimens, and the multi-angled 3D-printed GFRP composite (Set 2) specimens to ensure failures take place in the gauge section and to minimize potential damage due to gripping, as recommended by ASTM D3039 [32]. The tab material was obtained from a composite plate manufactured using a vacuum-assisted hand layup technique with two layers of carbon fiber-reinforced polymer that was made of woven fabric impregnated with epoxy matrix. After 24 h of hardening time and 48 h of the heat curing process, 56-mm long, 15-mm wide tabs were cut from the plate. This geometry was chosen to suit the specimen dimensions based on the ASTM D3039 [32]. The tabs were bonded to specimens using high-strength super glue generously applied with a uniform bond line. The pressure was applied on the tabs with steel plates to ensure a good bond, which was removed after 24 h to begin testing. No tabs were attached to the thermoplastic specimens as per ASTM D638 [34].
2.3. Static Tension Tests
Static tension tests were guided by ASTM D3039 [32]. Five specimens for each fiber orientation angle were tested for single-angled 3D-printed GFRP composites (Set 1) and five specimens were tested for multi-angled 3D-printed GFRP composite (Set 2). Static tension tests were guided by ASTM D638 [34] for five thermoplastic specimens. Specimen width and thickness were measured prior to testing to obtain an accurate cross-sectional area for the calculation of stress. Strain in the specimens was recorded using a contact extensometer with a 25.4-mm gauge length. Loading was applied using MTS® Minnesota Bionex servo-hydraulic system with mechanical grips under a displacement-control protocol at a rate of 1 mm/min and a sampling rate of 1 Hz. Upon failure, the extensometer was removed, and pictures were taken to record failure modes.
2.4. Finite Element Modeling
A 3D finite element model was developed using ANSYS® Pennsylvania Parametric Design Language (APDL) modeling environment to simulate the mechanical behavior of the single-angled 3D-printed GFRP composite (Set 1), the thermoplastic specimens, and the multi-angled 3D-printed GFRP composite (Set 2). The FE model is established to provide insight of the mechanical response observed experimentally and to explain the mechanics involved in the progressive failure of a multi-angled 3D-printed GFRP composite (Set 2). The FE model was 50 mm in length, 12 mm in width, and 2.5 mm in thickness. The mesh size was 0.5 mm. The model and mesh sizes were selected to achieve both accuracy and computational efficiency and to avoid possible termination of the simulation due to element distortion. The composite layers were modeled using eight-node 3D SOLID45 brick elements. One element was assigned for each layer through-thickness corresponding to the specific fiber orientation. The element type was selected to enable incorporating both linear and nonlinear material behaviors using an elastic orthotropic material model and Hill yield criteria for the fiberglass layers, respectively. The material nonlinearity for the fiberglass layers represents inter-fiber damage due to matrix micro-cracking and/or fiber/matrix interface debonding. In addition, a multilinear isotropic hardening material model (MISO) was used to define the material response for thermoplastic layers to account for the gradual damage due to matrix micro-cracking in the form of plasticity.
In order to capture a complete failure of composite laminas, birth and death features in APDL were utilized. In this approach, the displacement was applied in small increments, and all the elements were evaluated against a maximum stress failure criterion. Any element that meets the failure criterion was considered as a dead element, and its contribution to the FE simulation was minimized by reducing the stiffness by a factor of 10−6. The stress and failure criterion in all neighboring elements were checked to ensure they did not reach the failure stress level. The updated status for all elements was fed to the following displacement increment. In the finite element model, a small displacement increment of 0.012 mm was utilized by specifying a displacement step of 0.06 mm and five sub-steps for every displacement step. The specified small displacement increments were necessary to ensure that failure of an element is evaluated very frequently. Moreover, overestimation of the failure stress and ductility was minimized. In addition, a maximum of 1000 iterations were specified for every displacement increment to minimize numerical error for predicting nodal forces and deformations. To simulate the tensile tests, a vertical displacement was applied on the top surface extremity of the finite element model, and the opposite extremity at the bottom surface was restrained in all directions. To avoid early failure at ends due to stress singularity at displacement constrains, 3-mm long end regions were modeled as failure-free zones. The FE model was divided through thicknesses into multiple layers. One SOLID45 element was considered for each layer through thickness. Each layer was assigned a specific thickness and fiber orientation, θ. A perfect bond was assumed between adjacent layers. The geometry of the FE model and the multiple layers with respective thickness for the laminated composites are shown in Figure 4.
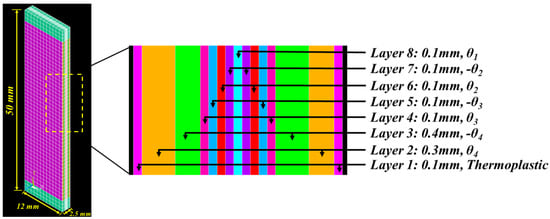
Figure 4.
Finite element model and fiber layup for the multi-angled laminate.
The thermoplastic was modeled as an isotropic material. The elastic modulus (E11) was obtained directly from the experimental median stress-strain values of 3D-printed thermoplastic specimens. Poisson’s ratio () was assumed to be that of typical Nylon material. Failure stresses (S11F) and (S22F) were assumed from the manufacturer’s datasheet [37], and shear failure stress (S12F) was obtained from experimental data of 3D-printed thermoplastic specimens in accordance with the ASTM 3518 [38] test standard. Fiberglass was modeled as nonlinear transversely isotropic material with elastic, plastic, and strength properties that were determined from the experimental test results of 3D-printed single angled laminates (Set 1). In particular, the elastic modulus in the fiber direction (E11) and in the transverse direction (E22) was determined from experimental data of the single-angled 3D-printed GFRP composite (Set 1) at 0° and 90° fiber orientation in accordance with the ASTM D3039 test standard [32]. Shear modulus (G12) was calculated from the experimental data of the single-angled 3D-printed GFRP composite (Set 1) at 45° fiber orientation in accordance with the ASTM 3518 test standard [38]. Poisson’s ratio () for fiberglass was assumed to be of typical GFRP material [35]. Hill yield criterion was used to define the nonlinear behavior of fiberglass material in the fiber, transverse, and shear directions. No yield stress (S11Y) and tangent modulus (E11Y) were assumed in the fiber direction due to the linearity of the stress-strain curves. Idealized bilinear curves were produced for experimental data with 90° fiber orientation to obtain yield stress (S22Y) and tangent modulus (E22Y) in the transverse direction. Shear yield stress (S12Y) and tangent modulus (E12Y) were determined from bilinear curves produced for shear stress-shear strain data obtained from 45° experimental data. Failure stresses in the fiber direction (S11F) and transverse direction (S22F) were determined from the experimental data of the single-angled 3D-printed GFRP composite (Set 1) at 0° and 90° fiber orientation. Shear stress at failure was calculated from the experimental data of single-angled 3D-printed GFRP composite (Set 1) at 45° fiber orientation in accordance with the ASTM 3518 test standard [38]. All the mechanical properties used in the finite element model are listed in Table 6.
All properties are determined after eliminating the contribution of thermoplastic layers. Since all the single angled 3D-printed GFRP composite specimens (Set 1) had two layers of thermoplastic already included, properties for the model were calculated by eliminating the contribution of these two thermoplastic layers. This modified data ensured that elastic, yield, shear, and failure properties provided in the model are solely for the glass fiber layers at different angles. This method is outlined using Equations (5)–(10).
where is the displacement, is the strain reading from extensometer, is the gauge length measured, is the force at specific displacement in the single-angled composite, is the stress at the specific displacement, is the force at specific displacement in the thermoplastic specimen, is the new force evaluation after eliminating the thermoplastic contribution, and is the new stress calculated with the new area by eliminating the two thermoplastic layers.
3. Results and Discussion
Single-angled 3D-printed GFRP composite specimens (Set 1) and 3D-printed thermoplastic specimens were tested up to failure under static tensile loading. The median stress-strain curves for these specimens are shown in Figure 5. A summary of the experimental results is presented in Table 3. The thermoplastic specimens had high nonlinearity, and lateral failure was observed in the gauge area near the middle location. In the GFRP specimens, an apparent decrease in strength and elastic modulus with the increase in fiber orientation angle is observed. Similar behavior has been reported in the past [39,40] for GFRP composites with some fiber orientations. GFRP specimens with 0° and 12° fiber orientation showed high linearity to failure. Nonlinearity in the tensile behavior of GFRP specimens increases with fiber orientation. The median stress-strain curves are shown in Figure 6 and a summary of the experimental results is presented in Table 3.
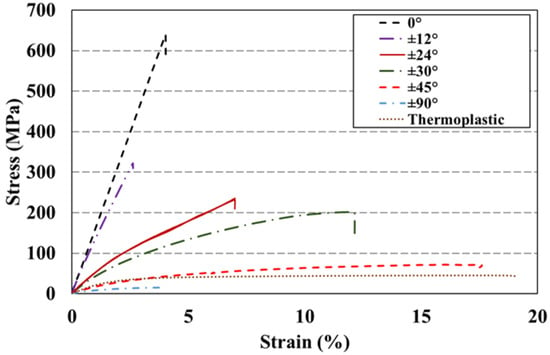
Figure 5.
Median tensile stress-strain curves (out of five specimens) for single-angled 3D-printed GFRP composite specimens (Set 1) and 3D-printed thermoplastic specimen.

Table 3.
Tensile properties of single-angled 3D-printed GFRP composite specimens (Set 1) and 3D-printed thermoplastic specimens.

Figure 6.
Failure mode for 3D-printed thermoplastic specimen and single-angled 3D-printed GFRP composite specimens (Set 1).
Failure modes of the GFRP specimens were described per ASTM D3039 [32] as explosive failure in the gauge area in the middle location (XGM) for 0° fiber orientation specimens, which represented typical broom-like failure due to the weak interfacial bond between glass fibers and the thermoplastic matrix [41,42]. Lateral failure in the gauge area in the middle location (LGM) was observed for 45° fiber orientation specimens showing fiber rupture in multiple superimposed ±45° angled planes. The increasing ductility of 45° fiber orientation specimens can be explained by the homogeneous share of the applied tensile load between the fibers and the matrix. The thermoplastic layer seemed to be peeling off, which indicates fiber-matrix interface debonding. Conical structures and pockets in the middle portion showed evidence of accumulation of damage in the center and consequent crack formation by pulling out the fibers [39]. Lateral failure in the gauge area in the bottom location (LGB) for 90° fiber orientation showed a straight rupture edge pulling out of the transverse fibers through the cross-section of the specimen. Finally, angled failure in the gauge area in the middle location (AGM) was observed in the specimen with 12° fiber orientation. Minor broom-like failure was observed, which indicated a limited degree of fiber-matrix interface debonding before fiber fracture occurs. Fiber rupture was observed with angled failure in the gauge area in the top location (AGT) for 24° fiber orientation and AGM was observed for 30° fiber orientation. Figure 6 presents the failure modes of the 3D-printed thermoplastic specimens and all the single-angled 3D-printed GFRP composite specimens (Set 1).
With the results obtained from experimental testing of single-angled 3D-printed GFRP composites (Set 1) and thermoplastic specimens, axial stiffness ratios for the design of the multi-angled 3D-printed GFRP composites (Set 2) were evaluated using Equations (3) and (4). Table 4 presents the initial axial stiffness (EA) ratios varying between a minimum value of 22.3% for 12° fiber orientation and a maximum value of 48.0% for 24° fiber orientation. On the other hand, the axial stiffness ratios at peak load varied between 20.0% for 12° fiber orientation and 35.3% for 24° fiber orientation. The initial axial stiffness ratios showed a coefficient of variation of 31% between the different orientations, and the axial stiffness ratios at peak load showed a coefficient of variation of 29% at the peak load. The limited variation between the axial stiffness ratios is meant to enable gradual load transfer among the layers and promote progressive failure in the multi-angled 3D-printed GFRP composite specimens (Set 2). Axial stiffness ratios are presented in Table 4.

Table 4.
Axial stiffness ratios as a percentage for layers with different fiber orientations in the multi-angled 3D-printed GFRP composite specimens (Set 2).
The stress-strain behavior and failure modes of the multi-angled 3D-printed GFRP composite specimens (Set 2) are shown in Figure 7. Three distinct drops can be observed, and the damage corresponding to every stress drop is illustrated in Figure 7a,b. At drop 1, a considerable loss in capacity was observed in the specimen with partial damage at the top and middle locations of the specimens. The sudden loss in capacity at the first drop could be attributed to the high strain rate effect in load transfer between layers, which results in multiple layers failing together rather than failing sequentially. At drop 2, excessive damage occurred, which led to drop 3 where complete specimen failure was observed. It is evident from Figure 7 that the behavior of the multi-angled 3D-printed GFRP composite differs from the single-angled 3D-printed GFRP composite. In particular, the strength and strains at the failure of discrete fiber orientations are different when tested individually than when tested in a composite with other fibers at other discrete angles. The multi-angled 3D-printed GFRP composite does not achieve high strength and high stiffness when compared to traditional GFRP composites. It is the goal of this study to show the possibility of achieving pseudo-ductility in 3D-printed FRP composites and lead the way to future directions for improvements in strength and stiffness. A summary of the results of the multi-angled 3D-printed GFRP composite specimens (Set 2) is presented in Table 5. The stress-strain behavior and failure modes of the multi-angled 3D-printed GFRP composite specimens (Set 2) are shown in Figure 7.
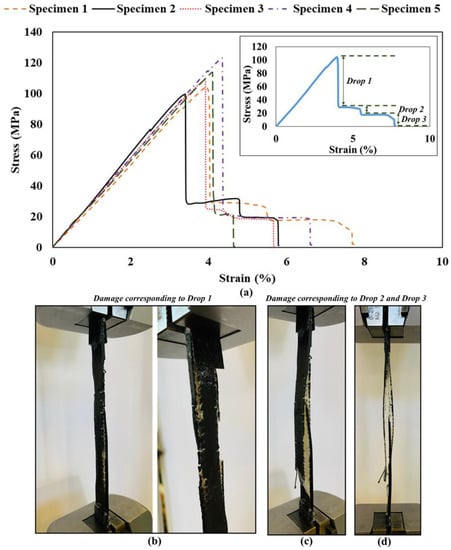
Figure 7.
Multi-angled 3D-printed GFRP composite specimens (Set 2). (a) Tensile stress-strain behavior of all five specimens. (b) Damage corresponding to each stress Drop 1. (c) Damage corresponding to each stress Drop 2. (d) Damage corresponding to each stress Drop 3.

Table 5.
Tensile properties of multi-angled 3D-printed GFRP composite specimens (Set 2).
The material’s elastic, plastic, and ultimate strength properties for the FE model were obtained from the experimental data of the single-angled 3D-printed GFRP composite specimens with discrete fiber orientations of 0°, 90°, and 45°, and thermoplastic specimens. The test results for 0° fiber orientation specimens were used to determine the mechanical properties in the fiber direction (1-direction) while the test results for 90° fiber orientation specimens were used to determine the mechanical properties in the transverse direction (2-direction). Shear properties were obtained from test results for the 45° fiber orientation single-angled 3D-printed GFRP composite specimen. All the mechanical properties used in the FE model are listed in Table 6.

Table 6.
Material properties used in the finite element (FE) model.
To validate the FE model, the simulation results for the 0°, 90°, and 45° single-angled 3D-printed GFRP composite specimens and thermoplastic specimens were compared to their experimental results, as shown in Figure 8.
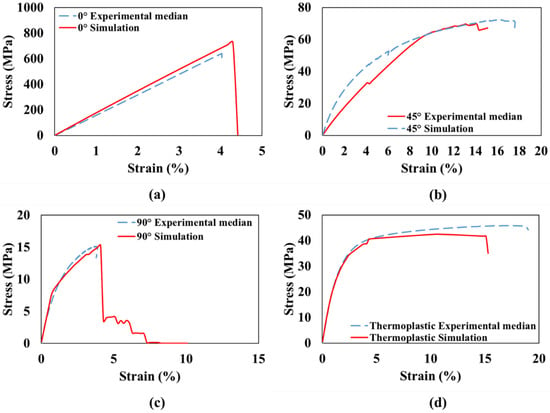
Figure 8.
Comparison of stress-strain curves from the experiment and simulation for single-angled 3D-printed GFRP composite with (a) ±0°, (b) ±45°, (c) ±90°, and (d) thermoplastic.
Failure modes of single-angled 3D-printed GFRP specimens with a fiber orientation of 0°, 90°, and 45° were analyzed. This analysis was performed by considering the middle layer of the model and observing stress contours at strains before and at failure attributing to their respective mechanical response. In the composite with 0° fiber orientation, the tensile stress contour in the fiber direction at 4.3% strain shows that the stress slightly exceeds the specified tensile strength in the fiber direction (S11F) by 2%. Following this step, uniform failure is observed throughout the composite layer. In the case of a composite with 90° fiber orientation, at 4.1% strain, tensile stress contours in the transverse direction show that the stress slightly exceeds the specified tensile strength in the transverse direction (S22F) by 3.8%. Following this step, uniform failure is observed throughout the composite layer. The shear (XY) component of stress was analyzed for the composite with 45° fiber orientation. At 8% strain, some elements located on a 45° plane experienced high shear stresses slightly exceed the specified shear strength (S12F) by 0.75%. The failure pattern is observed in the +45° direction. The stress contours and failure patterns of the middle layer for the 0°, 90°, and 45° single-angled composite models are shown in Figure 9.
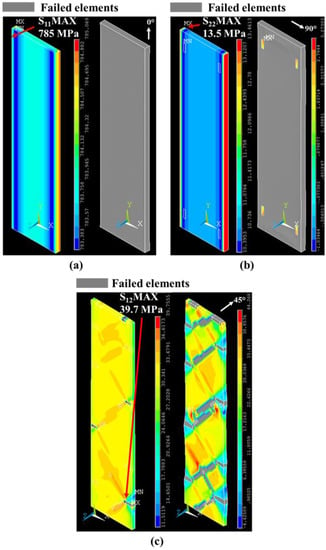
Figure 9.
Failure modes of the finite element model simulations of single-angled 3D-printed GFRP specimens with (a) 0°, (b) 90°, and (c) 45° fiber orientations.
To gain confidence in the FE model, comparisons were made for the other single-angled 3D-printed GFRP composite specimens (i.e., at 12°, 24°, and 30° fiber orientation), as depicted by Figure 10. The comparisons demonstrate the ability of the model to reasonably predict the mechanical response of the single-angled 3D-printed GFRP composite based on angle rotation for different angles.
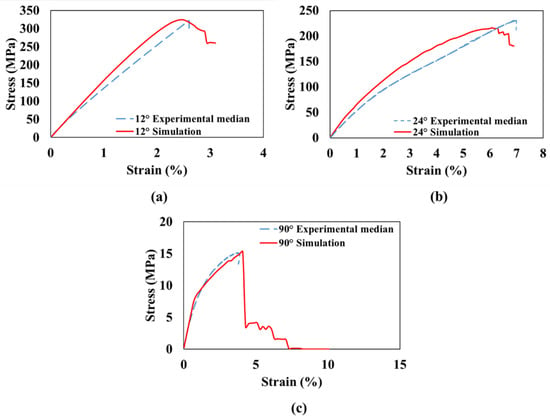
Figure 10.
Comparison of stress-strain curves from the experiment and simulation for single-angled 3D-printed GFRP composite with (a) ±12°, (b) ±24°, and (c) ±30°.
The multi-angled 3D-printed GFRP composite model was developed with the thickness and fiber orientations as presented earlier in Figure 4 with θ1 = 12°, θ2 = 24°, θ3 = 30°, and θ4 = 45°. The stress-strain curves obtained from the simulation and the experiment of the multi-angled 3D-printed GFRP composite are shown in Figure 11. It is evident that, prior to the peak, the behavior of multi-angled 3D-printed GFRP composite is similar in both simulation and experimental testing. The elastic modulus and the ultimate strength of the multi-angled 3D-printed GFRP composite model are fairly similar to the experimental observation. This shows that the load share between the layers of the discrete fiber orientations meets the load share assumed in designing the composite. Therefore, the concept of load share used in this study for design works well in the linear elastic range.
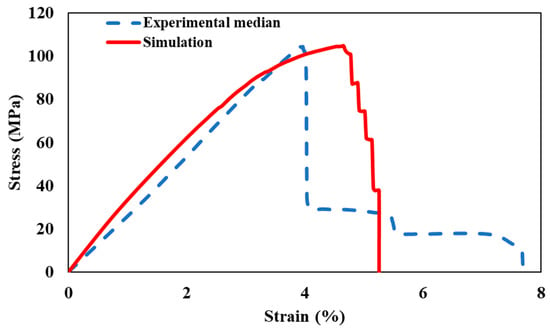
Some yield-like plateau was observed in the simulation toward the ultimate strength, which was not observed in the test. The simulation also showed progressive sequential failure, whereas the experiment showed one sudden large drop in capacity at a strain level lower than that predicted by the model, which was followed by two other small progressive drops. The difference between the experimental observations and the FE model could be attributed to the high strain rate effect in load transfer between layers, which results in multiple layers failing together rather than failing sequentially. This is not simulated in the FE model. The absence of yield, such as plateau in the experiment, can be due to layer failure dynamics on adjacent layers and the debonding/delamination between layers. These effects can result in an early loss in the load capacity of the composite when compared to the simulation. After drop 1, the higher angled layers such as the 45° layers observed some debonding from the remaining composite, as shown in Figure 7. This leads to the 45° layers behaving as a single-angled composite, which allows them to sustain the remaining load capacity for a considerable strain. This resulted in drop 2 and drop 3. Further investigations are necessary by implementing transient analysis and considering interface elements to introduce high strain rate effects between layers.
The strength and strains at the failure of single-angled 3D-printed GFRP composites at discrete fiber orientations are different when tested individually than when tested in a composite with other fibers, which is the case of multi-angled 3D-printed GFRP composites. To understand the mechanics behind these differences, the FE model was utilized for comparing the stress state of layers with the same fiber orientation in the single-angled and multi-angled composite models at the same strain levels. Such a comparison reveals that the stress contours in a single-angled composite at the same strain levels are different when compared to the multi-angled composite. For example, layer 4 with a 30° fiber orientation in the single-angled composite was observed to have very different axial stress contours in the loading direction (i.e., Y component of stress) at 4.5% strain, when compared with the multi-angled composite, as demonstrated in Figure 12a,b. The difference in stress contours explains the difference in the behavior between single-angled 3D-printed GFRP composites and multi-angled 3D-printed GFRP composites, as observed experimentally. The maximum axial stresses observed in each layer with specific fiber orientation in single-angled composite and multi-angled composite are presented in Table 7.
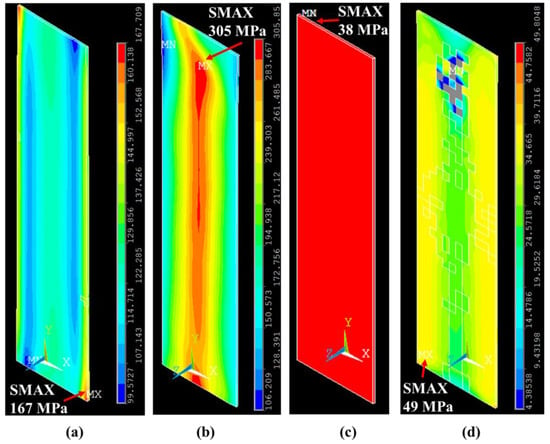
Figure 12.
Contours for the Y-component of stress for 30° fiber orientation layer at 4.5% strain in a (a) single-angled GFRP composite and (b) multi-angled GFRP composite and thermoplastic layer at 3.2% strain in a (c) single-angled GFRP composite and (d) multi-angled GFRP composite, as revealed using the finite element method.

Table 7.
Axial stresses in single-angled vs. multi-angled composite models for each layer.
Similarly, for the thermoplastic layer, non-uniform stress contours were observed in a multi-angled composite with failure observed in some elements. However, in the single-angled composite, uniform stress was observed in the thermoplastic layer. The strain at failure for the thermoplastic layer reached 15% based on the FE model result shown in Figure 5. However, in the multi-angled composite, failure initiation is captured as early as 3.3%, as demonstrated in Figure 12d. The difference in stress contours for the thermoplastic layer between single-angled and multi-angled composites could be attributed to the difference in the adjacent layers. In the case of a single-angled composite, all layers were thermoplastic and behaved similarly under uniaxial load. On the other hand, in the case of a multi-angled composite, the adjacent layers were fiberglass with fibers oriented at 45°, which behave differently under a uniaxial load. The mismatch in deformations between the two layers (i.e., thermoplastic layer and its adjacent layer) due to layer orthotropy and fiber orientation results in developing interlaminar stresses, which impose additional non-uniform stresses on the two layers. This causes the thermoplastic layer to fail at a relatively low strain level. Understanding interlaminar stresses could explain the excessive delamination observed in the multi-angled composite and explains why the experiment showed a sudden drop in capacity at lower strain compared with the FE model. This observation suggests that a ductile behavior could be obtained experimentally if interlaminar strength between layers was engineered to enable separate failure for layers that have different fiber orientations. Stress contours are shown in Figure 12.
Detailed analysis of the failed elements and layers attributed to the progressive drops in the stress-strain curve of the multi-angled 3D-printed GFRP composite is performed and presented. A complete overview of the failure is shown in Figure 13. The stress contours of the different layers are shown in Figure 13c. In these contours, the grey color represents failed elements at the corresponding drops illustrated in Figure 13a. The polymer layer observed complete failure at a 3.8% strain with a negligible drop in capacity. At about 4.75% strain, about one-third of the elements in layer 8 with 12° fiber orientation failed to lead to the second drop in capacity, which occurred after the peak load. Extensive failures of layer 7 with −24° fiber orientation and layer 6 with +24° fiber orientation occurred at about 4.92% strain, which results in the third drop in capacity. Layer 5 with −30° fiber orientation observed failure of some elements at the 5.00% strain, which causes the fourth drop. Combined failure for elements in layer 4 with +30° fiber orientation and layer 3 with −45° fiber orientation occurred at 5.16% strain, which results in the fifth drop. Finally, considerable failure in layer 2 with +45° fiber orientation took place at 5.26% strain, which leads to the last drop in capacity and concluding failure of the entire composite. Figure 13b shows a complete set of failed elements in specific layers corresponding to that of the fiber orientation. The failure of layers with different fiber orientations was successive due to the assumed perfect bond and ideal load transfer between layers. Considering delamination in modeling could disturb load transfer between layers and, therefore, could lead to a separation between the load drops, as observed experimentally.
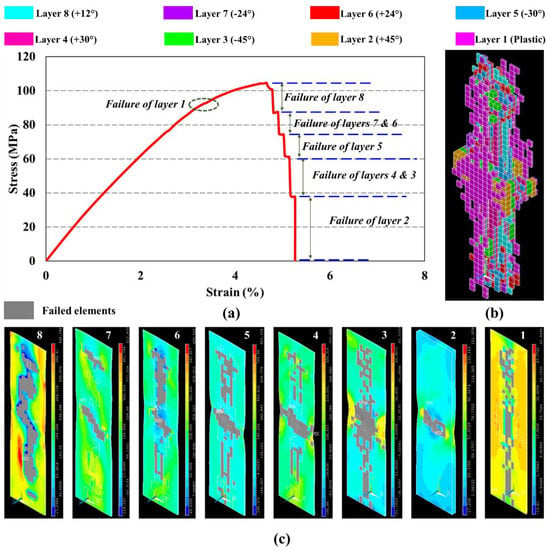
Figure 13.
(a) Progressive failure in multi-angled 3D-printed GFRP composite, (b) all failed elements in composite, and (c) failure in each layer after corresponding drops.
It is evident from the above investigation that the combination of fibers at discrete orientations designed to meet a specific axial stiffness sharing ratio can lead to progressive failure and, thus, demonstrate a pseudo ductile behavior. It is also evident that this concept can be accomplished using 3D-printing technology. The study also shows that the high strain rate effects in load transfer between layers could result in losing a considerable load capacity of the composite at an early stage of damage. This might be controlled if load transfer between the layers is dampened and an alternative bond between layers is achieved. Limitations of the above study include the limited number of design parameters used such as the stacking sequence of the multi-angled 3D-printed GFRP composites. Additionally, the FE model assumed a perfect bond between layers, which may be further developed to include the strain rate effect in load transfer between layers. Further research is warranted to investigate the use of 3D-printed technology to produce ductile FRP composites.
4. Conclusions
It is demonstrated that GFRP composites can show progressive failure and pseudo ductility using 3D-printing technology. This is achieved by integrating a combination of discrete fiber orientations and stacking sequence using monotype fibers. Tension tests of single-angled 3D-printed GFRP composite specimens with 0°, 12°, 24°, 30°, 45°, and 90° discrete fiber orientations were carried out and analyzed. The test data of single-angled 3D-printed GFRP composites were then used to design multi-angled 3D-printed GFRP composites to achieve a desired axial load sharing ratio. Tension tests of multi-angled 3D-printed GFRP composites demonstrated progressive failure and pseudo ductile behavior through multiple drops in load capacity at different strain levels. The first drop represented a relatively large drop in capacity. The premature drop in the tension test is attributed to the high strain rate effects in load transfer between layers. FE analysis was used to provide insight into the behavior of 3D-printed GFRP composites. Nonlinear orthotropic models with birth and kill approach were used to simulate the behavior of the 3D-printed GFRP composite with discrete fiber orientations. The elastic modulus and the ultimate strength of the multi-angled 3D-printed GFRP composite model were fairly similar to the experimental observation. The FE model for the multi-angled 3D-printed GFRP composite demonstrated successive drops in load capacity and gradual load transfer between layers. The main difference between the experimental and computational simulation is attributed to the fact that the model does not include the high strain rate effect and assumes a perfect bond between the layers. Nevertheless, the model shows that the load share between the layers meets the design concept and illustrates that a pseudo ductile behavior is attainable. Future investigations on the effect of interlaminar bond strength controlled via 3-D printing and on possible control of load transfer dynamics are suggested to improve the ductility of the multi-angled 3D-printed GFRP composites.
5. Patents
The current study is based on US patent No. US 10,337,186 B2 entitled Ductile Fiber Reinforced Polymer Plates and Bars Using Monotype Fibers [6].
Author Contributions
S.V. fabricated and tested all the specimens. S.V. and E.S. developed the FE models. S.V., E.S., and M.R.T. participated in data analysis and interpretation of the test results. All three authors participated in writing the manuscript. M.R.T. led the team’s efforts. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by Internal funds from the University of New Mexico and the Air Force Research Laboratory (AFRL) grant to the University of New Mexico partially funded this work in the summer of 2019.
Acknowledgments
The authors would like to extend their thanks to the Air Force Research Laboratory (AFRL) grant to the University of New Mexico for their support and their time when conducting this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bakis, C.E.; Bank, L.C.; Brown, V.; Cosenza, E.; Davalos, J.; Lesko, J.; Machida, A.; Rizkalla, S.; Triantafillou, T. Fiber-reinforced polymer composites for construction—State-of-the-art review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef]
- Hollaway, L. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties. Constr. Build. Mater. 2010, 24, 2419–2445. [Google Scholar] [CrossRef]
- Pendhari, S.S.; Kant, T.; Desai, Y.M. Application of polymer composites in civil construction: A general review. Compos. Struct. 2008, 84, 114–124. [Google Scholar] [CrossRef]
- Zhao, X.-L.; Zhang, L. State-of-the-art review on FRP strengthened steel structures. Eng. Struct. 2007, 29, 1808–1823. [Google Scholar] [CrossRef]
- Banakar, P.; Shivananda, H.; Niranjan, H. Influence of fiber orientation and thickness on tensile properties of laminated polymer composites. Int. J. Pure Appl. Sci. Technol. 2012, 9, 61. [Google Scholar]
- Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Fibre hybridisation in polymer composites: A review. Compos. Part A Appl. Sci. Manuf. 2014, 67, 181–200. [Google Scholar] [CrossRef]
- Bakis, C.E.; Nanni, A.; Terosky, J.; Koehler, S. Self-monitoring, pseudo-ductile, hybrid FRP reinforcement rods for concrete applications. Compos. Sci. Technol. 2001, 61, 815–823. [Google Scholar] [CrossRef]
- Bunsell, A.; Harris, B. Hybrid carbon and glass fibre composites. Composites 1974, 5, 157–164. [Google Scholar] [CrossRef]
- Czél, G.; Wisnom, M. Demonstration of pseudo-ductility in high performance glass/epoxy composites by hybridisation with thin-ply carbon prepreg. Compos. Part A Appl. Sci. Manuf. 2013, 52, 23–30. [Google Scholar] [CrossRef]
- Jones, K.D.; DiBenedetto, A.T. Fiber fracture in hybrid composite systems. Compos. Sci. Technol. 1994, 51, 53–62. [Google Scholar] [CrossRef]
- Liang, Y.; Sun, C.; Ansari, F. Acoustic emission characterization of damage in hybrid fiber-reinforced polymer rods. J. Compos. Constr. 2004, 8, 70–78. [Google Scholar] [CrossRef]
- Somboonsong, W.; Ko, F.K.; Harris, H.G. Ductile hybrid fiber reinforced plastic reinforcing bar for concrete structures: Design methodology. Mater. J. 1998, 95, 655–666. [Google Scholar]
- Swolfs, Y.; Gorbatikh, L.; Hine, P.; Ward, I.; Verpoest, I. Toughening of Carbon Fibre Composites By Hybridisation with Self-Reinforced Polypropylene. In Proceedings of the 9th International Conference on Composite Science and Technology, Sorrento, Italy, 24–26 April 2013. [Google Scholar]
- Taketa, I.; Ustarroz, J.; Gorbatikh, L.; Lomov, S.V.; Verpoest, I. Interply hybrid composites with carbon fiber reinforced polypropylene and self-reinforced polypropylene. Compos. Part A Appl. Sci. Manuf. 2010, 41, 927–932. [Google Scholar] [CrossRef]
- Ramnath, B.V.; Rajesh, S.; Elanchezhian, C.; Shankar, A.S.; Pandian, S.P.; Vickneshwaran, S.; Rajan, R.S. Investigation on mechanical behaviour of twisted natural fiber hybrid composite fabricated by vacuum assisted compression molding technique. Fibers Polym. 2016, 17, 80–87. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, M.; Kumar, S.; Mohapatra, S. Properties of glass-fiber hybrid composites: A review. Polym. Plast. Technol. Eng. 2017, 56, 455–469. [Google Scholar] [CrossRef]
- Tanwer, A.K. Mechanical properties testing of uni-directional and bi-directional glass fibre reinforced epoxy based composites. Int. J. Res. Advent Technol. 2014, 2, 34–39. [Google Scholar]
- Agarwal, K.; Kuchipudi, S.K.; Girard, B.; Houser, M. Mechanical properties of fiber reinforced polymer composites: A comparative study of conventional and additive manufacturing methods. J. Compos. Mater. 2018, 52, 3173–3181. [Google Scholar] [CrossRef]
- Araya-Calvo, M.; López-Gómez, I.; Chamberlain-Simon, N.; León-Salazar, J.L.; Guillén-Girón, T.; Corrales-Cordero, J.S.; Sánchez-Brenes, O. Evaluation of compressive and flexural properties of continuous fiber fabrication additive manufacturing technology. Addit. Manuf. 2018, 22, 157–164. [Google Scholar] [CrossRef]
- Carey, J.P.; Melenka, G.W.; Schofield, J.; Dawson, M.R.; Cheung, B.O. Evaluation and Prediction of the Tensile Properties of Continuous Fiber-Reinforced 3D Printed Structures. 2016. Available online: https://era.library.ualberta.ca/items/c6f65e7d-3fd0-487d-8bf9-fc0cd8210e9e (accessed on 15 June 2020).
- Elsayed, Y.; Elkholy, A.; Melenka, G.; Kempers, R. Continuous Fiber Polymer Composites for Thermal Applications. In Proceedings of the Canadian Society for Mechanical Engineering International Congress, Toronto, Canada, 27–30 May 2018. [Google Scholar]
- Frketic, J.; Dickens, T.; Ramakrishnan, S. Automated manufacturing and processing of fiber-reinforced polymer (FRP) composites: An additive review of contemporary and modern techniques for advanced materials manufacturing. Addit. Manuf. 2017, 14, 69–86. [Google Scholar] [CrossRef]
- Goh, G.D.; Yap, Y.L.; Agarwala, S.; Yeong, W.Y. Recent progress in additive manufacturing of fiber reinforced polymer composite. Adv. Mater. Technol. 2019, 4, 1800271. [Google Scholar] [CrossRef]
- Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.-H.; Lee, J.-W.; Choi, K.H. 3D printing for soft robotics—A review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, C.; Cormier, D. 3D printing of carbon fiber composites with preferentially aligned fibers. In Proceedings of the IIE Annual Conference, Nashville, TN, USA, 30 May–2 June 2015; p. 2953. [Google Scholar]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Almutairi, M.D.; Aria, A.I.; Thakur, V.K.; Khan, M.A. Self-Healing Mechanisms for 3D-Printed Polymeric Structures: From Lab to Reality. Polymers 2020, 12, 1534. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Yang, C.; Tian, X.; Liu, T.; Cao, Y.; Li, D. 3D printing for continuous fiber reinforced thermoplastic composites: Mechanism and performance. Rapid Prototyp. J. 2017, 23, 209–215. [Google Scholar] [CrossRef]
- Melenka, G.W.; Cheung, B.K.; Schofield, J.S.; Dawson, M.R.; Carey, J.P. Evaluation and prediction of the tensile properties of continuous fiber-reinforced 3D printed structures. Compos. Struct. 2016, 153, 866–875. [Google Scholar] [CrossRef]
- Tanikella, N.G.; Wittbrodt, B.; Pearce, J.M. Tensile strength of commercial polymer materials for fused filament fabrication 3D printing. Addit. Manuf. 2017, 15, 40–47. [Google Scholar] [CrossRef]
- ASTM International. D3039/D3039M-14 Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Daniel, I.M.; Ishai, O.; Daniel, I.M.; Daniel, I. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 1994; Volume 3. [Google Scholar]
- ASTM International. D638-14 Standard Test Method for Tensile Properties of Plastics; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Taha, M.R.; Soliman, E.M. Ductile Fiber Reinforced Polymer Plates and Bars Using Monotype Fibers. Google Patents. U.S. Patent 10,337,186, 2 July 2019. [Google Scholar]
- Hyer, M.W.; White, S.R. Stress Analysis of Fiber-Reinforced Composite Materials; DEStech Publications, Inc.: Lancaster, PA, USA, 2009. [Google Scholar]
- Markforged Composite Data Sheet. Available online: http://static.markforged.com/downloads/composites-data-sheet.pdf (accessed on 24 April 2020).
- ASTM International. D3518/D3518M-18 Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- Godara, A.; Raabe, D. Influence of fiber orientation on global mechanical behavior and mesoscale strain localization in a short glass-fiber-reinforced epoxy polymer composite during tensile deformation investigated using digital image correlation. Compos. Sci. Technol. 2007, 67, 2417–2427. [Google Scholar] [CrossRef]
- Mei, H.; Ali, Z.; Yan, Y.; Ali, I.; Cheng, L. Influence of mixed isotropic fiber angles and hot press on the mechanical properties of 3D printed composites. Addit. Manuf. 2019, 27, 150–158. [Google Scholar] [CrossRef]
- Genedy, M.; Daghash, S.; Soliman, E.; Taha, M.M.R. Improving fatigue performance of GFRP composite using carbon nanotubes. Fibers 2015, 3, 13–29. [Google Scholar] [CrossRef]
- Chennareddy, R.; Tuwair, H.; Kandil, U.F.; ElGawady, M.; Taha, M.R. UV-resistant GFRP composite using carbon nanotubes. Constr. Build. Mater. 2019, 220, 679–689. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).