A Moving Interface Finite Element Formulation to Predict Dynamic Edge Debonding in FRP-Strengthened Concrete Beams in Service Conditions
Abstract
1. Introduction
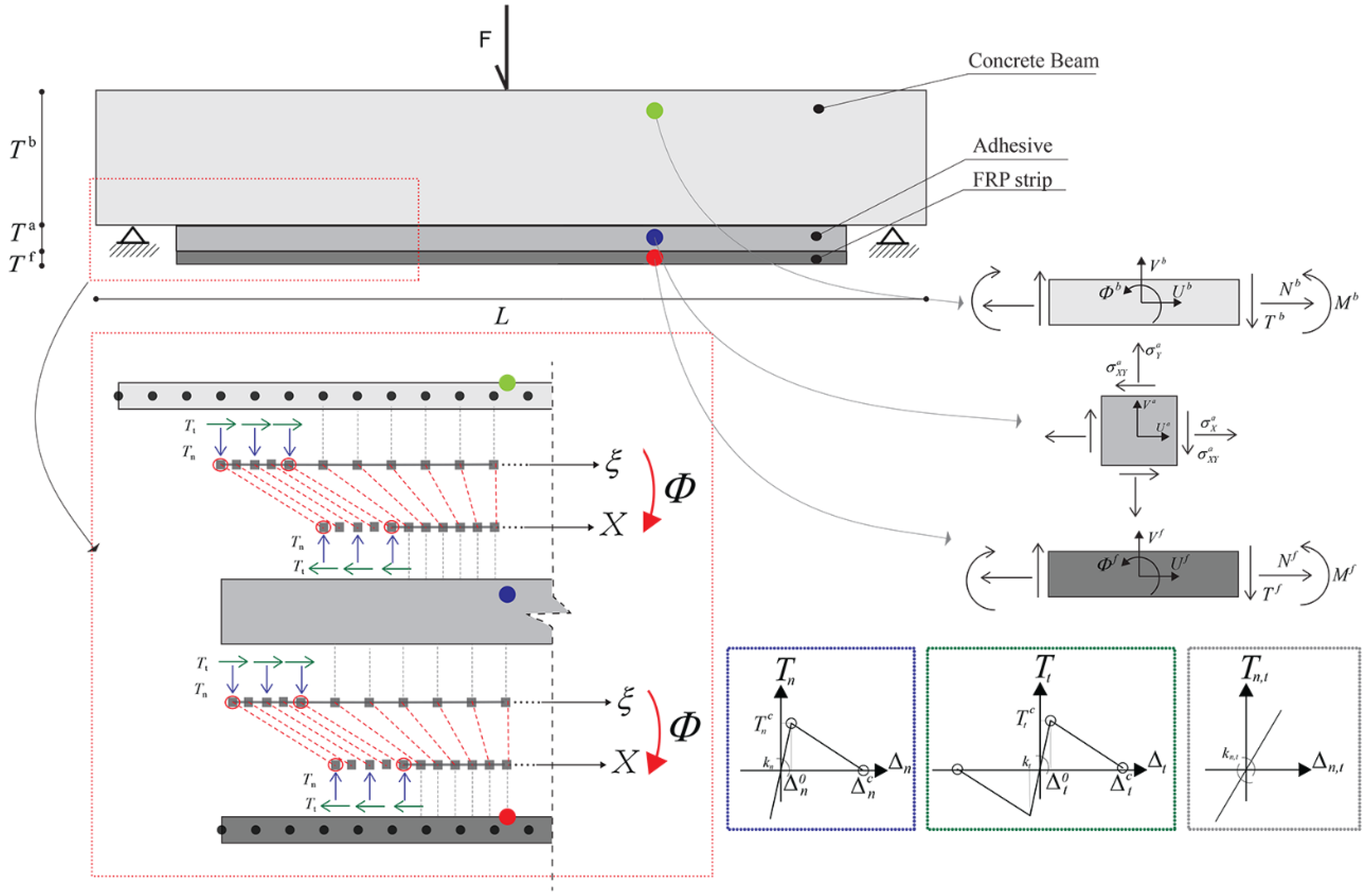
2. Formulation of the Model
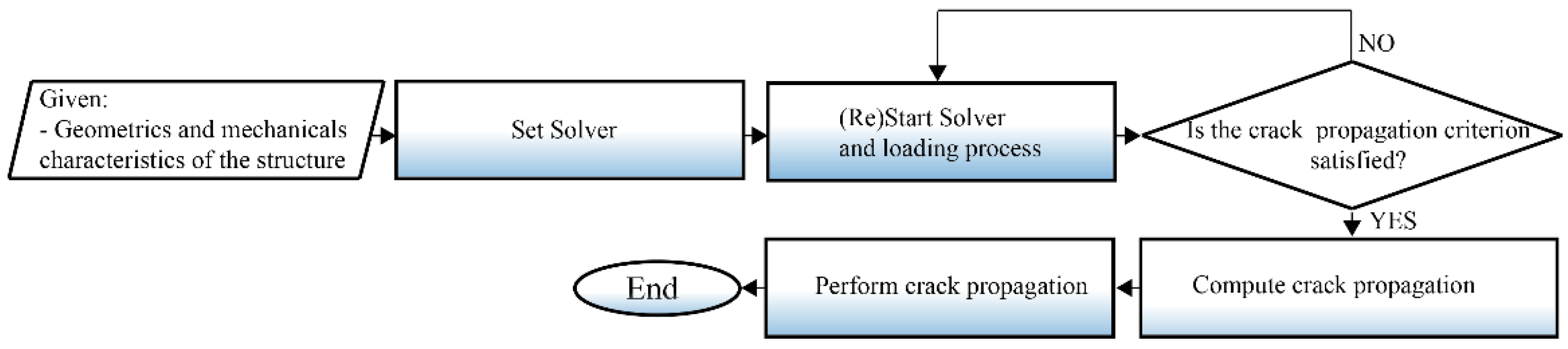
3. Numerical Implementation
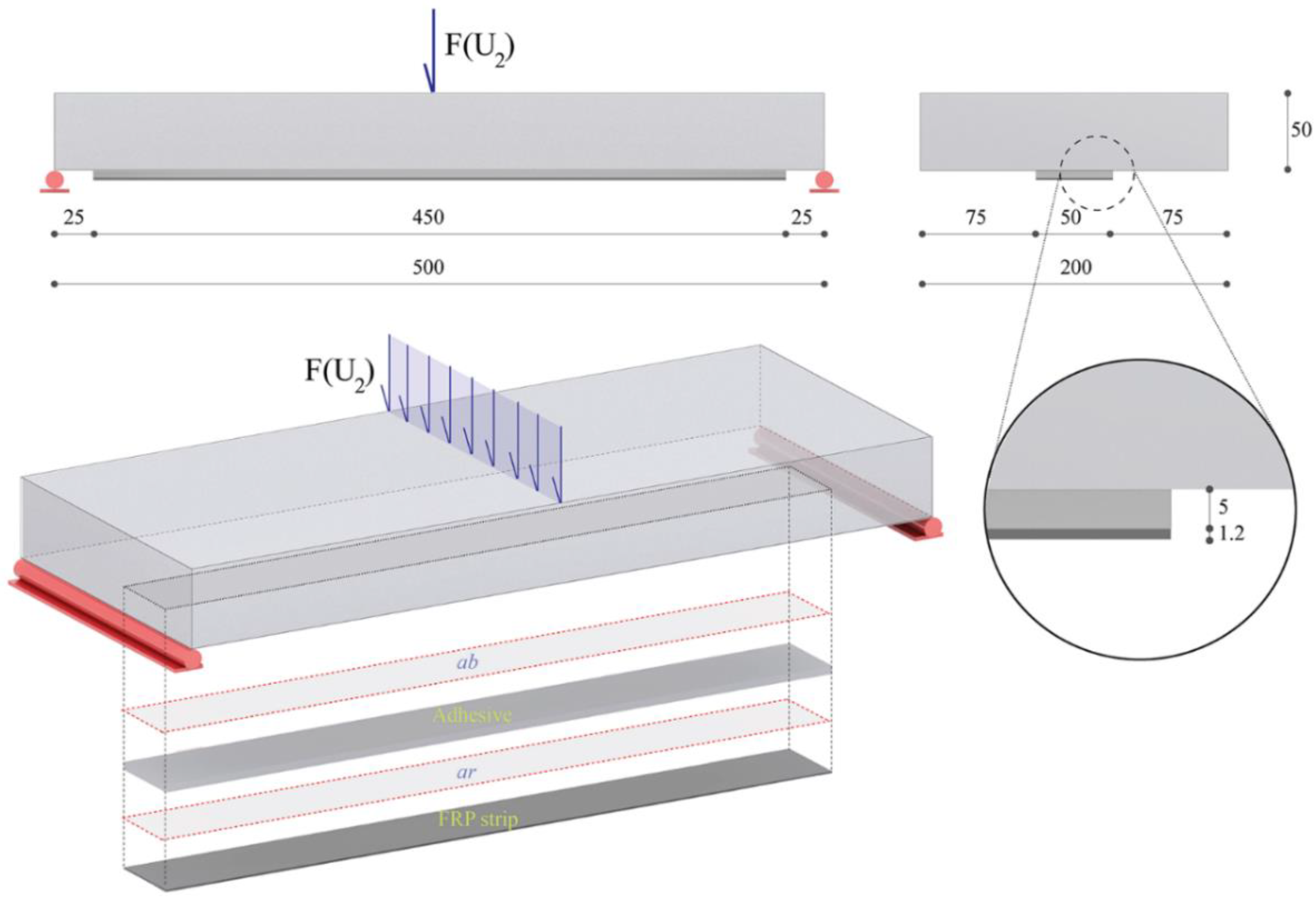
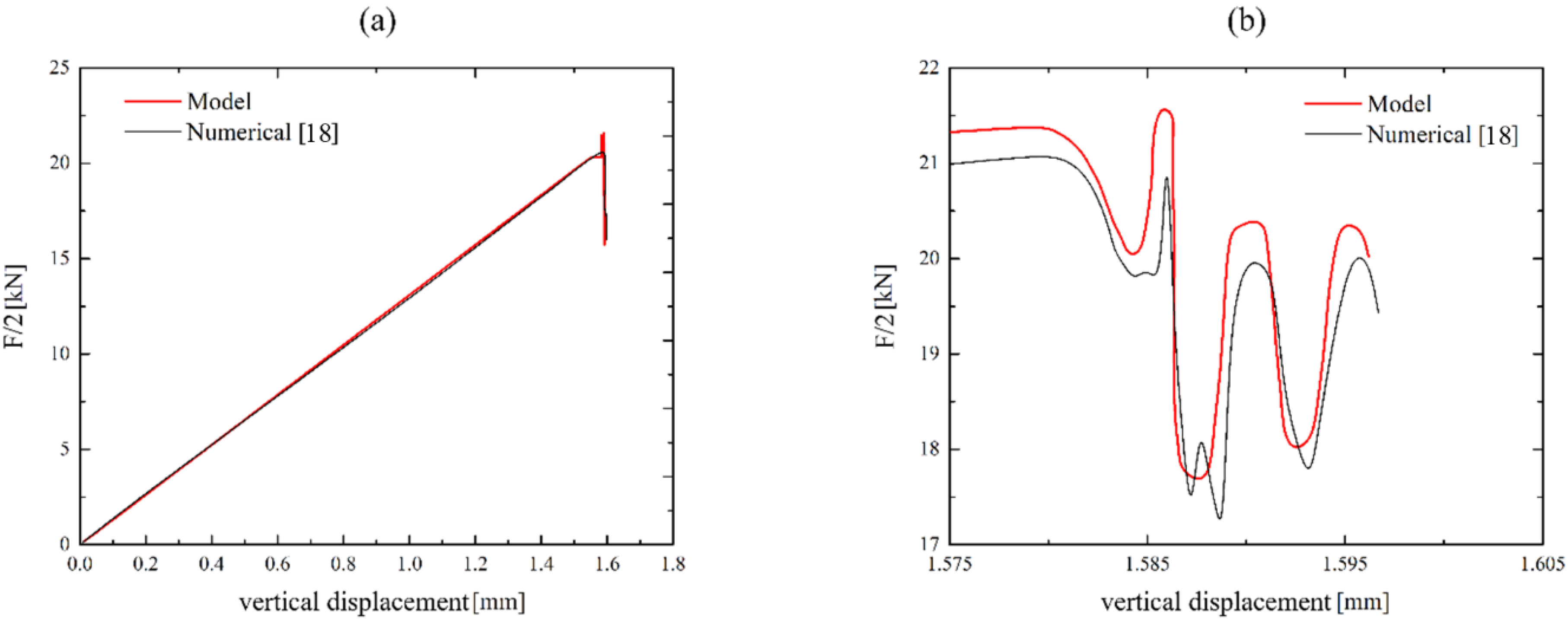
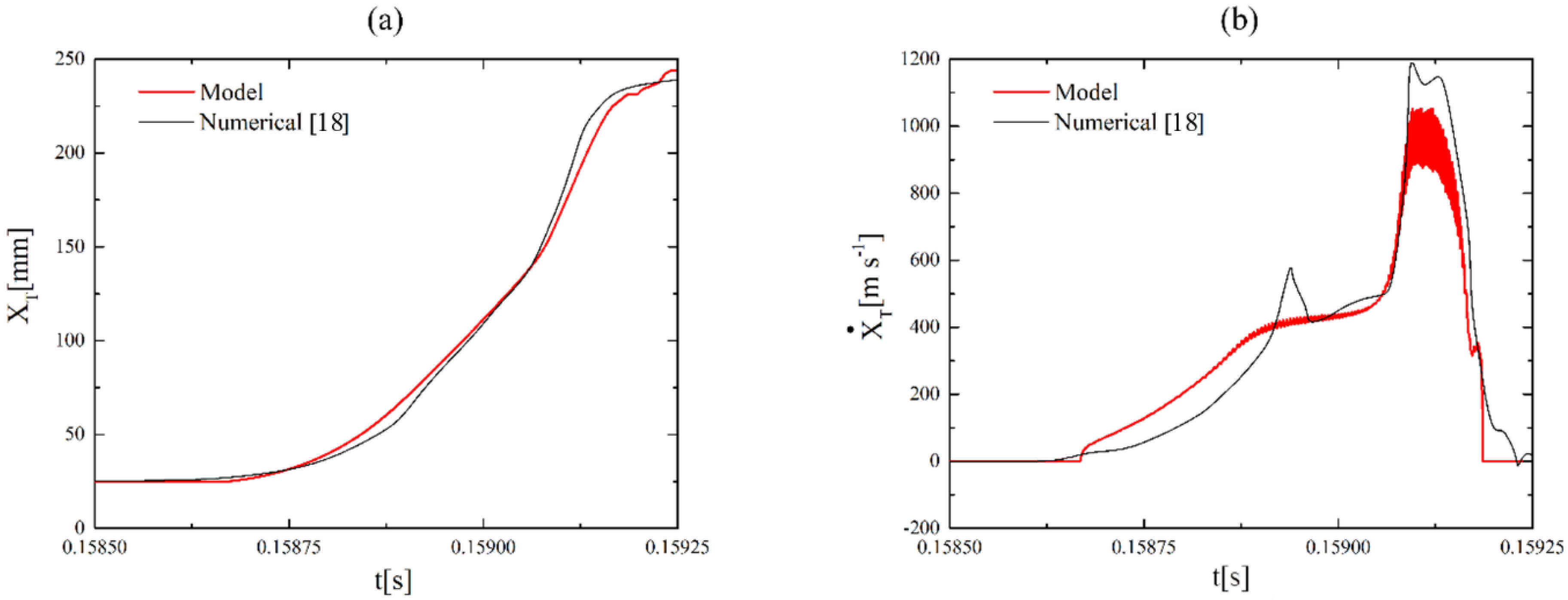
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barbero, E.J. Introduction to Composite Materials Design; CRC Press: Boca raton, FL, USA, 2017. [Google Scholar]
- Barbero, E.; Lonetti, P. An Inelastic Damage Model for Fiber Reinforced Laminates. J. Compos. Mater. 2002, 36, 941–962. [Google Scholar] [CrossRef]
- Ascione, L.; Razaqpur, A.G.; Spadea, S. Effectiveness of FRP stirrups in concrete beams subject to shear. In Proceedings of the 7th International Conference on FRP Composites in Civil Engineering, CICE, Vancouver, BC, Canada, 20–22 August 2014. [Google Scholar]
- Spadea, S.; Orr, J.; Ivanova, K. Bend-strength of novel filament wound shear reinforcement. Compos. Struct. 2017, 176, 244–253. [Google Scholar] [CrossRef]
- Spadea, S.; Orr, J.; Nanni, A.; Yang, Y. Wound FRP Shear Reinforcement for Concrete Structures. J. Compos. Constr. 2017, 21. [Google Scholar] [CrossRef]
- Ascione, L.; Berardi, V.P.; Giordano, A.; Spadea, S. Macro-scale analysis of local and global buckling behavior of T and C composite sections. Mech. Res. Commun. 2014, 58, 105–111. [Google Scholar] [CrossRef]
- Rosa, I.C.; Firmo, J.P.; Correia, J.R.; Mazzuca, P. Influence of elevated temperatures on the bond behaviour of GFRP bars to concrete—Pull-out tests. In IABSE Symposium, Guimaraes 2019: Towards a Resilient Built Environment Risk and Asset Management—Report; International Union of Laboratories and Experts in Construction Materials, Systems and Structures: Guimarães, Portugal, 2019; pp. 861–868. [Google Scholar]
- Odessa, I.; Rabinovitch, O.; Frostig, Y. High-order crack propagation in compressed sandwich panels. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Funari, M.F.; Greco, F.; Lonetti, P. A coupled ALE-Cohesive formulation for interfacial debonding propagation in sandwich structures. Procedia Struct. Integr. 2018, 9, 92–100. [Google Scholar] [CrossRef]
- Ascione, L.; Berardi, V.P.; Giordano, A.; Spadea, S. Pre-buckling imperfection sensitivity of pultruded FRP profiles. Compos. Part B Eng. 2015, 72, 206–212. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Ascione, F.; Lamberti, M.; Spadea, S.; Malagic, M. GFRP hollow column to built-up beam adhesive connection: Mechanical behaviour under quasi-static, cyclic and fatigue loading. Compos. Struct. 2019, 224. [Google Scholar] [CrossRef]
- Ascione, F.; Lamberti, M.; Razaqpur, A.G.; Spadea, S.; Malagic, M. Pseudo-ductile failure of adhesively joined GFRP beam-column connections: An experimental and numerical investigation. Compos. Struct. 2018, 200, 864–873. [Google Scholar] [CrossRef]
- Ombres, L.; Iorfida, A.; Mazzuca, S.; Verre, S. Bond Analysis of Thermally Conditioned FRCM-Masonry Joints; International Measurement Confederation (IMEKO): Budapest, Hungary, 2019. [Google Scholar]
- Cascardi, A.; Micelli, F.; Aiello, M.A. FRCM-confined masonry columns: Experimental investigation on the effect of the inorganic matrix properties. Constr Build Mater 2018, 186, 811–825. [Google Scholar] [CrossRef]
- Cascardi, A.; Dell’Anna, R.; Micelli, F.; Lionetto, F.; Aiello, M.A.; Maffezzoli, A. Reversible techniques for FRP-confinement of masonry columns. Constr Build Mater 2019, 225, 415–428. [Google Scholar] [CrossRef]
- Cascardi, A.; Aiello, M.A.; Triantafillou, T. Analysis-oriented model for concrete and masonry confined with fiber reinforced mortar. Mater Struct 2017, 50. [Google Scholar] [CrossRef]
- Ombres, L.; Verre, S. Flexural Strengthening of RC Beams with Steel-Reinforced Grout: Experimental and Numerical Investigation. J. Compos. Constr. 2019, 23. [Google Scholar] [CrossRef]
- Rabinovitch, O. Dynamic edge debonding in FRP strengthened beams. Eur. J. Mech. A Solids 2014, 47, 309–326. [Google Scholar] [CrossRef]
- Bruno, D.; Greco, F.; Lonetti, P. A fracture-ALE formulation to predict dynamic debonding in FRP strengthened concrete beams. Compos. Part B Eng. 2013, 46, 46–60. [Google Scholar] [CrossRef]
- Rabinovitch, O.; Frostig, Y. Experiments and analytical comparison of RC beams strengthened with CFRP composites. Compos. Part B Eng. 2003, 34, 663–677. [Google Scholar] [CrossRef]
- Funari, M.F.; Greco, F.; Lonetti, P.; Spadea, S. A numerical model based on ALE formulation to predict crack propagation in sandwich structures. Frat. Ed Integrita Strutt. 2019, 13, 277–293. [Google Scholar] [CrossRef]
- Fabbrocino, F.; Funari, M.F.; Greco, F.; Lonetti, P.; Luciano, R.; Penna, R. Dynamic crack growth based on moving mesh method. Compos. Part B Eng. 2019, 174. [Google Scholar] [CrossRef]
- Fortunato, G.; Funari, M.F.; Lonetti, P. Survey and seismic vulnerability assessment of the Baptistery of San Giovanni in Tumba (Italy). J. Cult. Herit. 2017, 26, 64–78. [Google Scholar] [CrossRef]
- Olivito, R.S.; Porzio, S. A new multi-control-point pushover methodology for the seismic assessment of historic masonry buildings. J. Build. Eng. 2019, 26, 100926. [Google Scholar] [CrossRef]
- Funari, M.F.; Spadea, S.; Lonetti, P.; Fabbrocino, F.; Luciano, R. Visual programming for structural assessment of out-of-plane mechanisms in historic masonry structures. J. Build. Eng. 2020, 31. [Google Scholar] [CrossRef]
- Rabinovitch, O. Cohesive interface modeling of debonding failure in FRP strengthened beams. J. Eng. Mech. ASCE 2008, 134, 578–588. [Google Scholar] [CrossRef]
- Bruno, D.; Fabbrocino, F.; Funari, M.F.; Greco, F.; Lonetti, P.; Spadea, S. An experimental and numerical study to evaluate the crack path under mixed mode loading on pvc foams. In Lecture Notes in Mechanical Engineering; Springer, Cham: Berlin, Gemany, 2020; pp. 378–388. [Google Scholar] [CrossRef]
- Funari, M.F.; Lonetti, P.; Spadea, S. A crack growth strategy based on moving mesh method and fracture mechanics. Appl. Fract. Mech. 2019, 102, 103–115. [Google Scholar] [CrossRef]
- Lonetti, P. Dynamic propagation phenomena of multiple delaminations in composite structures. Comput. Mater. Sci. 2010, 48, 563–575. [Google Scholar] [CrossRef]
- Funari, M.F.; Greco, F.; Lonetti, P. Sandwich panels under interfacial debonding mechanisms. Compos. Struct. 2018, 203, 310–320. [Google Scholar] [CrossRef]
- Funari, M.F.; Greco, F.; Lonetti, P. A moving interface finite element formulation for layered structures. Compos. Part B Eng. 2016, 96, 325–337. [Google Scholar] [CrossRef]
- Xu, X.P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Volokh, K.Y.; Needleman, A. Buckling of sandwich beams with compliant interfaces. Comput. Struct. 2002, 80, 1329–1335. [Google Scholar] [CrossRef]
- Funari, M.F.; Greco, F.; Lonetti, P. A cohesive finite element model based ALE formulation for z-pins reinforced multilayered composite beams. Procedia Struct. Integr. 2016, 2, 452–459. [Google Scholar] [CrossRef]
- COMSOL. COMSOL Multiphysics®, v. 5.2; COMSOL AB: Stockholm, Sweden, 2015; Available online: www.comsol.com (accessed on 14 June 2020).
- Funari, M.F.; Lonetti, P. Initiation and evolution of debonding phenomena in layered structures. Appl. Fract. Mech. 2017, 92, 133–145. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Pugno, N. Edge debonding in FRP strengthened beams: Stress versus energy failure criteria. Eng. Struct. 2009, 31, 2436–2447. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Funari, M.F.; Spadea, S.; Fabbrocino, F.; Luciano, R. A Moving Interface Finite Element Formulation to Predict Dynamic Edge Debonding in FRP-Strengthened Concrete Beams in Service Conditions. Fibers 2020, 8, 42. https://doi.org/10.3390/fib8060042
Funari MF, Spadea S, Fabbrocino F, Luciano R. A Moving Interface Finite Element Formulation to Predict Dynamic Edge Debonding in FRP-Strengthened Concrete Beams in Service Conditions. Fibers. 2020; 8(6):42. https://doi.org/10.3390/fib8060042
Chicago/Turabian StyleFunari, Marco Francesco, Saverio Spadea, Francesco Fabbrocino, and Raimondo Luciano. 2020. "A Moving Interface Finite Element Formulation to Predict Dynamic Edge Debonding in FRP-Strengthened Concrete Beams in Service Conditions" Fibers 8, no. 6: 42. https://doi.org/10.3390/fib8060042
APA StyleFunari, M. F., Spadea, S., Fabbrocino, F., & Luciano, R. (2020). A Moving Interface Finite Element Formulation to Predict Dynamic Edge Debonding in FRP-Strengthened Concrete Beams in Service Conditions. Fibers, 8(6), 42. https://doi.org/10.3390/fib8060042






