1. Introduction
Fiber-reinforced polymer composites are widely used in different sectors of industry and technology. In recent years, significant growth has been observed in the manufacture of composite materials based on basalt continuous fibers (BCFs). They can successfully replace traditional construction materials, and can also be applied to conditions that exclude the use of metals [
1]. Basalt fibers exhibit good adhesion to various polymeric binders: epoxy [
2], polycarbonate [
3], poly(butylene succinate) [
4], etc. Therefore, the prospect of their use in fiber-reinforced polymer composites instead of E-glass fibers is very high. Basalt fibers show better alkali resistance than E-glass fibers. They are a promising reinforcing component for concrete reinforcement [
5,
6].
Basalt continuous fiber production technology consists of several stages: glass melting, melt homogenization, formation, sizing, and winding. Most works in this area are devoted to the study of the dependence of different physicochemical properties of basalt melts, glasses, and fibers on their chemical composition. Glasses based on basalts are multicomponent systems with the following composition, in mass. %: SiO
2 43–58, Al
2O
3 11–20, CaO 7–13, FeO + Fe
2O
3 8–16, MgO 4–12, R
2O ≤ 4. The effects of both glass-forming oxides [
7,
8] and modifier oxides have been studied [
9]. Researchers have mostly paid attention to the effects of iron oxides [
10,
11].
Although the first continuous glass fibers based on rocks were obtained in the middle of the 20th century, the development of the BCF production technology is still hampered. The process of basalt continuous fiber production is quite complicated. It is influenced by various factors, such as melt viscosity, melt surface tension, and crystallization ability. In addition to that, external factors such as winding speed, flow rate, external cooling condition, and thermal uniformity play a role. The first group of parameters is primarily defined by the chemical composition of the raw materials. The second group can be conventionally attributed to the technological parameters [
12]. The effect of technological parameters (winding speed, melt temperature, nozzle diameter, etc.) on the properties of basalt continuous fibers has been insufficiently studied.
The influence of the basalt and E-glass melt viscosity, cooling rate, structural heterogeneity, and technological defects on mechanical and thermal properties have been thoroughly studied by Yue et al. [
13,
14,
15,
16]. For E-glass fibers, the effects of parameters such as the length and diameter of the nozzle, winding speed, and temperature of the melt were studied [
17,
18]. In contrast to the composition of E-glass melt, basalt melts have a significantly higher ability to crystallize. As a result, basalt melt has a narrow production temperature range, which leads to a catastrophically large number of fiber breaks. This dramatically affects the capacity of the technological plants.
The bushing for basalt and glass fibers is made of a platinum–rhodium alloy, which makes studying the effects of shape and size of the nozzles on the filament formation process and the properties of continuous fibers very expensive. Due to low thermal conductivity and viscosity, the basalt melt flowing through the nozzle plate has a high temperature gradient [
16,
19]. Due to its high crystallization ability, this can have a significant effect on the stability of the fiber-forming process as well as the mechanical properties of the fibers [
20]. The diameter of the nozzle can have a significant impact on this process.
A crucible of platinum–rhodium alloy with four nozzles of different diameters (1.5, 2.5, 3.5 and 4.5 mm) was specially designed and made for the purpose of this work. During fiber formation, we varied both the preparation temperature (from 1370 to 1450 °C) and the winding speed (from 300 to 1200 m/min). The melt flow through the nozzles, diameter of fibers, and influence of technological parameters on the strength of continuous basalt fibers for all series of samples were studied.
3. Results
Basalt continuous fibers were produced using a laboratory-scale system [
21]. BCFs were drawn from melts and wound onto a take-up reel. According to X-ray diffraction, all obtained samples were amorphous. The chemical composition was determined by X-ray fluorescence analysis and contained (in wt.%): 55.6% SiO
2, 1.1% TiO
2, 15.8% Al
2O
3, 10.5% Fe
2O
3, 3.7% MgO, 9.2% CaO, 2.2% Na
2O, and 1.8% K
2O. All the iron is reported as Fe
2O
3.
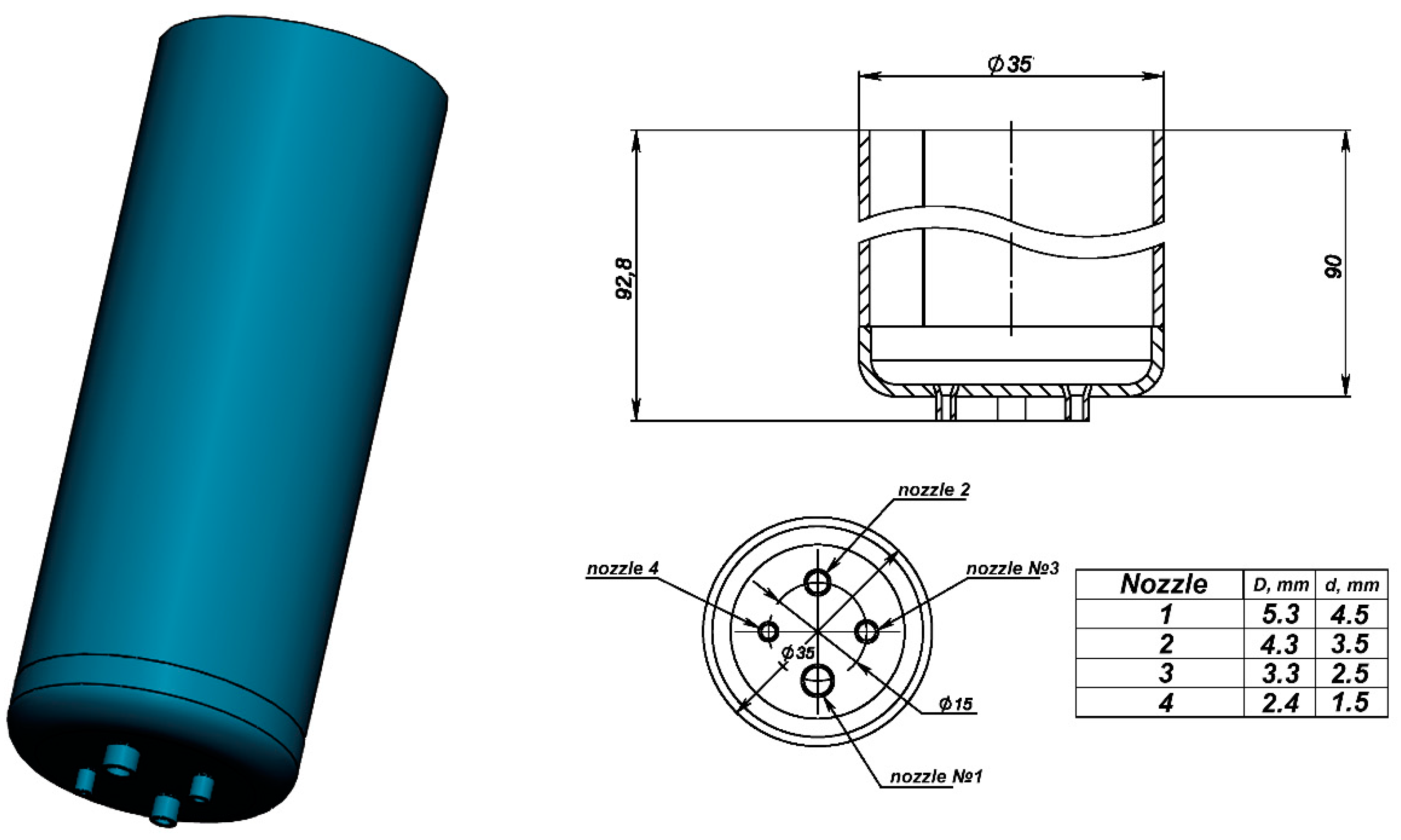
A special crucible was designed To investigate the effect of the nozzle diameter on the strength properties of the basalt continuous fibers and the basalt melt flow (
Figure 1). The crucible was made of a platinum–rhodium alloy (90/10). The scheme and dimensions of the crucible are presented in
Figure 1. At the bottom of the crucible there were four nozzles with inner diameters of 1.5, 2.5, 3.5, and 4.5 mm. The length of each nozzle was 2.8 mm.
In order to obtain the fiber, previously prepared basalt glass was added to the crucible. Then, the melt was heated to the formation temperature. Basalt continuous fibers were obtained at temperatures corresponding to the lower, middle, and upper limits of the formation temperature range (1370, 1410, and 1450 °C, respectively). During the experiments, the winding speed of the take-up reel was varied from 300 to 1200 m/min.
The experiment was carried out so that the level of the melt for each obtained sample differed by no more than 10%. The melt level was calculated based on the mass of the obtained sample and the geometric dimensions of the crucible.
In order to determine the possibility of using nozzles with the given diameters in industrial-scale plants, the number of filament breaks within 20 minutes of drawing was calculated. It was possible to achieve a stable process of fiber formation for the experiments with nozzles having diameters of 2.5, 3.5, and 4.5 mm. For the 1.5-mm diameter nozzle, it was not possible to obtain fibers steadily.
The diameter and tensile strength were measured for all obtained fibers. The melt flow rate was determined by calculation based on the measured diameters and density.
Table 1,
Table 2,
Table 3 and
Table 4 present the obtained results.
4. Discussion
One of the key stages of the basalt continuous fiber production technology is fiber formation. Basalt melt flows through the nozzles that are placed on the bottom of the bushing. The bushing is usually made of platinum alloyed with rhodium (up to 10 mass. %). The fiberization process takes place within a definite temperature range (usually 70–100 °C for basalt systems). The drawing cone (or gob) is formed at the end of the nozzle that forms the fiber by winding on a rotating cylinder (winding machine). Although this technology has been known since the last century, there are not many papers devoted to the influence of the shape and dimensions of the nozzle on the melt flow and fiber properties.
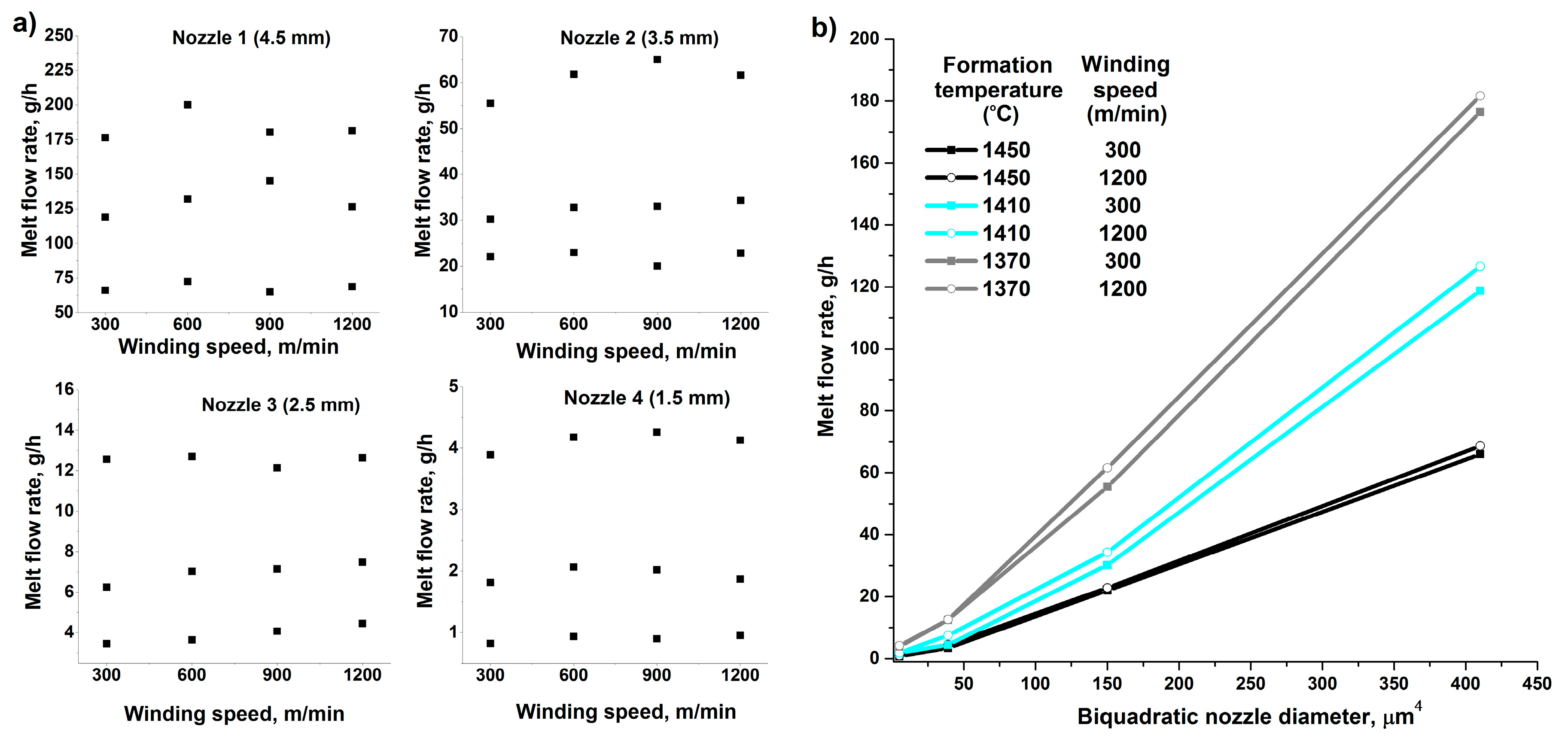
Figure 2a shows the dependence of the melt flow rate on the winding speed. The melt flow rate was almost independent of the winding speed, which indicates a laminar flow of the melt through the nozzles and a Newtonian nature of the liquid. The dependence of the melt flow rate correlated well with the biquadratic nozzle diameter (
Figure 2b). Pearson’s correlation coefficients for all cases were greater than 0.99. This confirms the possibility of applying the Hagen–Poiseuille equation to the basalt system. This result correlates with the data obtained previously for E-glass fibers [
17,
18].
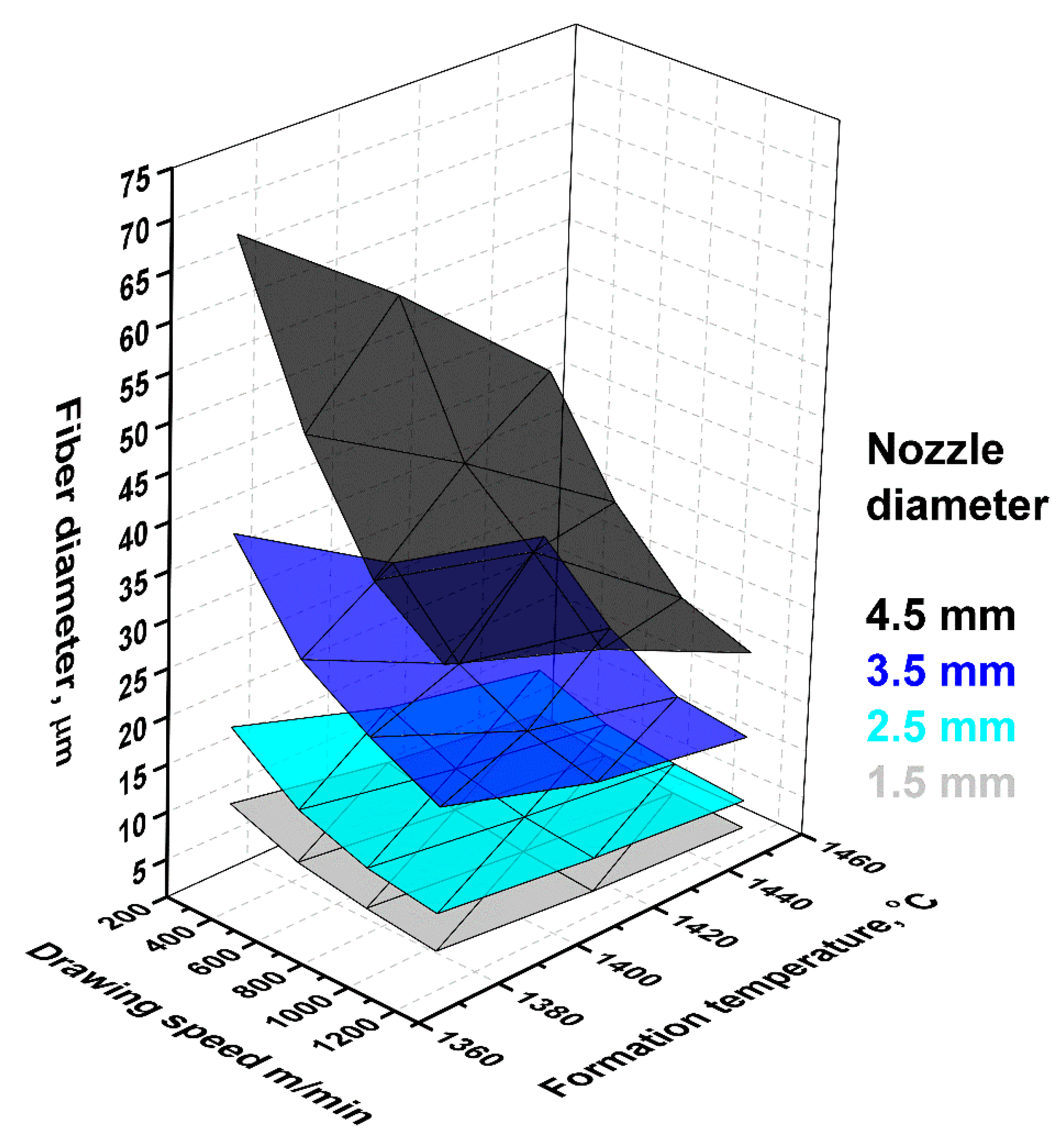
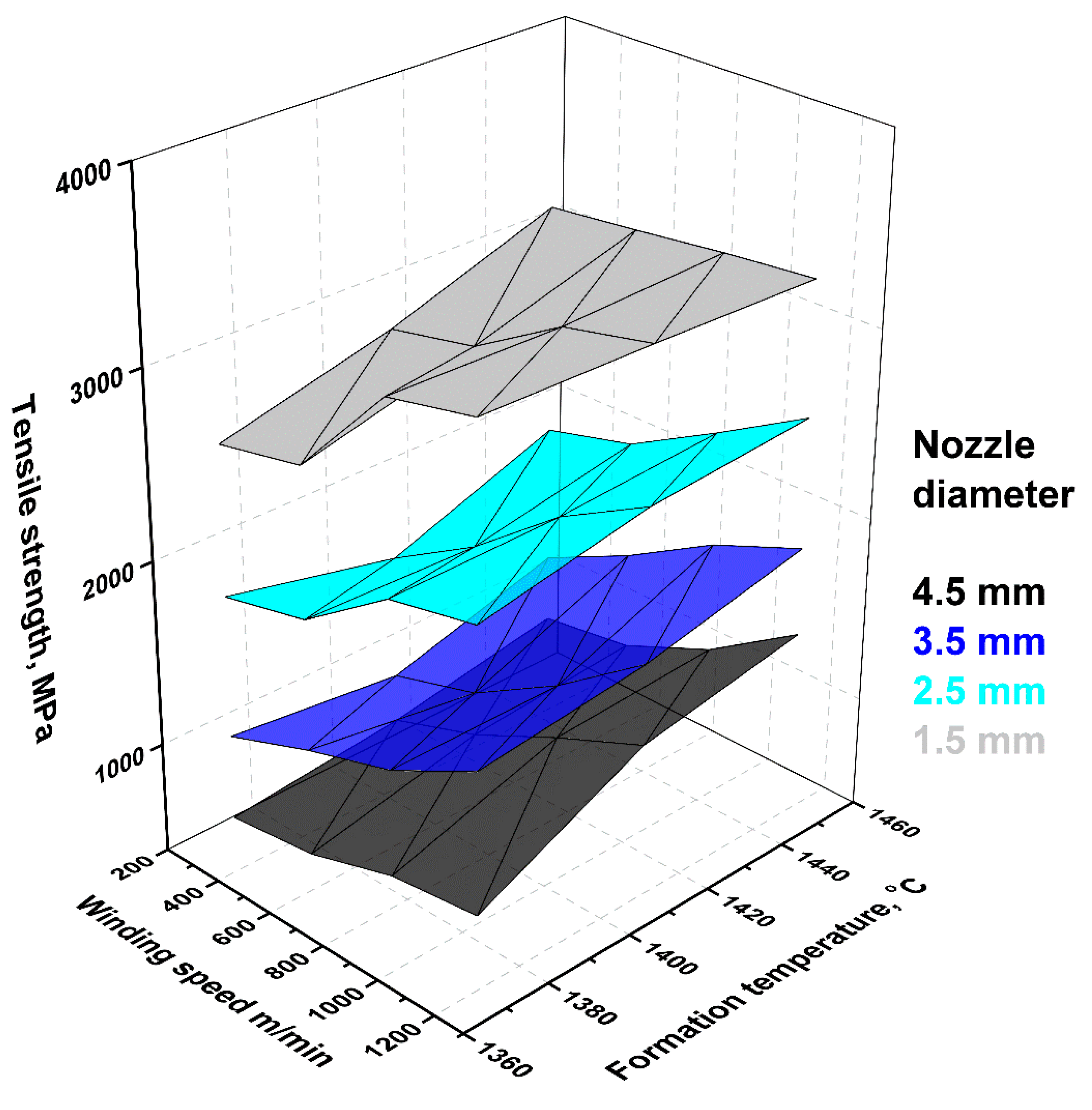
Figure 3 shows the dependence of the diameter of the obtained basalt continuous fibers on the winding speed and formation temperature. With an increase in the nozzle diameter from 1.5 to 4.5 mm, the fiber diameter increased by 6.5–9 times (for the same conditions). An increase in winding speed led to a decrease in fiber diameter. For nozzles with a large diameter this dependence was more explicit. For example, with an increase of winding speed from 300 to 1200 m/min, fiber diameter increased from 7 to 12.8 μm (nozzle diameter 2.5 mm, formation temperature 1410 °C), and with an increase of winding speed from 300 to 1200 m/min, fiber diameter increased from 28.8 to 58.8 μm (nozzle diameter 4.5 mm, formation temperature 1410 °C)—these represent respective increases of 83% and 104%. In a rough approximation at a definite formation temperature, this dependence can be estimated by a linear approximation.
The formation temperature had a less-significant effect on fiber diameter under otherwise equal conditions. For example, with an increase of formation temperature from 1370 to 1450 °C the fiber diameter decreased from 10.3 to 6 μm (nozzle diameter 2.5 mm, winding speed 900 m/min) and with an increase from 1370 to 1450 °C the fiber diameter decreased from 39.7 to 23.8 μm (nozzle diameter 4.5 mm, winding speed 900 m/min)—decreases of 72% and 67%, respectively. This dependence can be well estimated by a linear approximation.
In order to explain the obtained results, the theory of basalt melt flow through a nozzle should be taken into account. In the 19th century, Poiseuille proposed the use of an empirical formula for calculating the flow rate of viscous liquids flowing through tubes with small diameter:
where K is a constant (m/s
2), H is the head pressure (melt level) in meters, L is the inner tube length (nozzle length) in meters, d is the inner tube diameter (nozzle diameter) in meters, and
is the kinematic viscosity of the liquid in stokes.
Subsequently, this formula was clarified by Hagen, yielding the following form:
Reynolds showed that this formula is valid not only for capillaries, but also for tubes with small diameter (Reynolds numbers of the order of 10−2).
For basalt continuous fiber production technology, the Reynolds numbers are rather small, on the order of approximately 6 × 10
−6 [
18]. Thus, many authors believe that the Hagen–Poiseuille equation may be applicable to the process of glass and basalt fiber formation [
17,
19,
22]. Most researchers believe that basalt melt flow in the spinning zone usually follows a Newtonian behavior [
18,
23,
24]. The influence of the basalt and E-glass melt viscosity, cooling rate, structural heterogeneity, and technological defects on mechanical and thermal properties were studied in detail by Yue et al. [
13,
14,
15,
16]. The authors suggest the existence of non-Newtonian extensional thinning flow in a fibrous stream [
12]. This can indirectly confirm the fact that many experiments have shown that the melt flow rate through nozzles for E-glass exceeds the theoretical one by several times [
17,
25]. This is because the Hagen–Poiseuille equation ignores the nonisothermal nature of the melt in nozzles. This effect should be greatly enhanced for continuous basalt fibers, which have a high crystallization capacity [
11,
20].
The assumption that the length of the nozzles were not sufficient to establish laminar flow are not supported by calculations. The effect of winding tension on increasing melt flow rate has not been confirmed practically [
17,
18]. Many authors have shown [
17,
19,
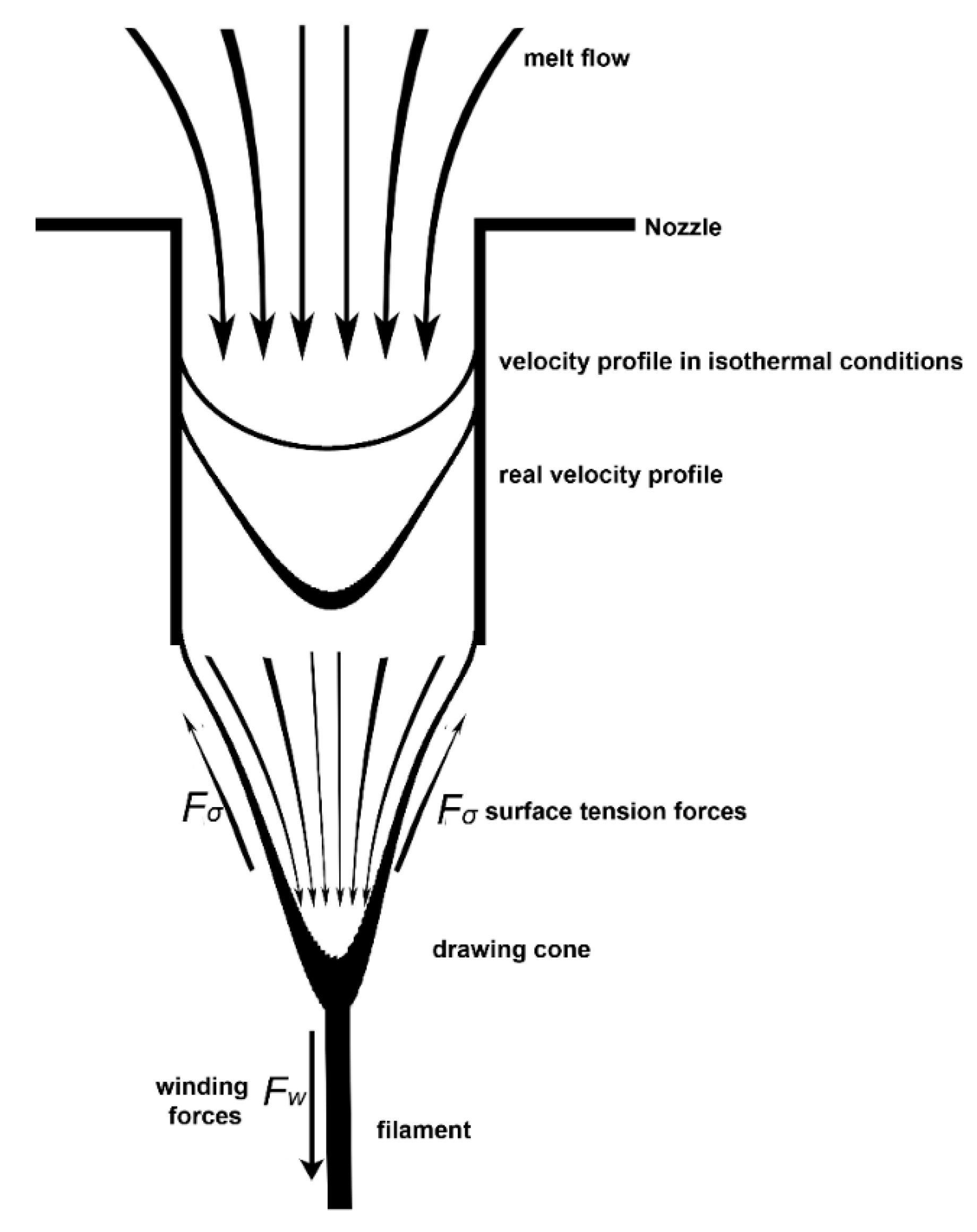
26] that the melt flow rate during a drip flow is significantly less than that during winding. This can be explained by the fact that the downward-directed forces arising from the gob formation (
Fw) reduce the surface forces (
Fσ) directed upwards. In this case, the smaller the diameter of the nozzle, the higher the value of these forces (
Figure 4). Due to the significant difference between the speed of the glass melt near the edge of the flow and in its center, the melt temperature at these points can differ significantly. This leads not only to different values of melt viscosity, but also to different contents of crystalline inclusions.
The melt viscosity of the basalt, hydrostatic pressure, diameter and length of the nozzle, and winding speed are the most important parameters determining the diameter of basalt fiber being drawn out. For a stable melt flow rate (i.e., a constant amount of molten basalt to draw the fibers flowing out of the nozzle per unit of time), the fiber diameter will be determined by winding speed. This fact stems from the conditions of the process of drawing the fiber (i.e., the continuous drawing of the molten basalt from the nozzle into a filament of a given diameter). Thus, a change in the nozzle diameter with a given stabilized winding speed will lead to a change in the diameter of the fiber. Changes in the basalt melt viscosity during the formation lead to high crystallization ability, which significantly affects the strength of the fiber.
The effect of the nozzle diameter and the conditions of obtaining fiber on its strength were studied in this work. Fiber strength is affected by a very large number of factors, including structure anisotropy [
15], high crystallization ability [
20], chemical composition fluctuations [
21], ambient temperature and quenching speed [
23], axial stress [
14], etc. Thus, it is very difficult to isolate the influence of one factor in any study of this issue.
The obtained results are in good agreement with the literature data on the effect of the diameter of basalt and glass fibers on their strength [
1,
3].
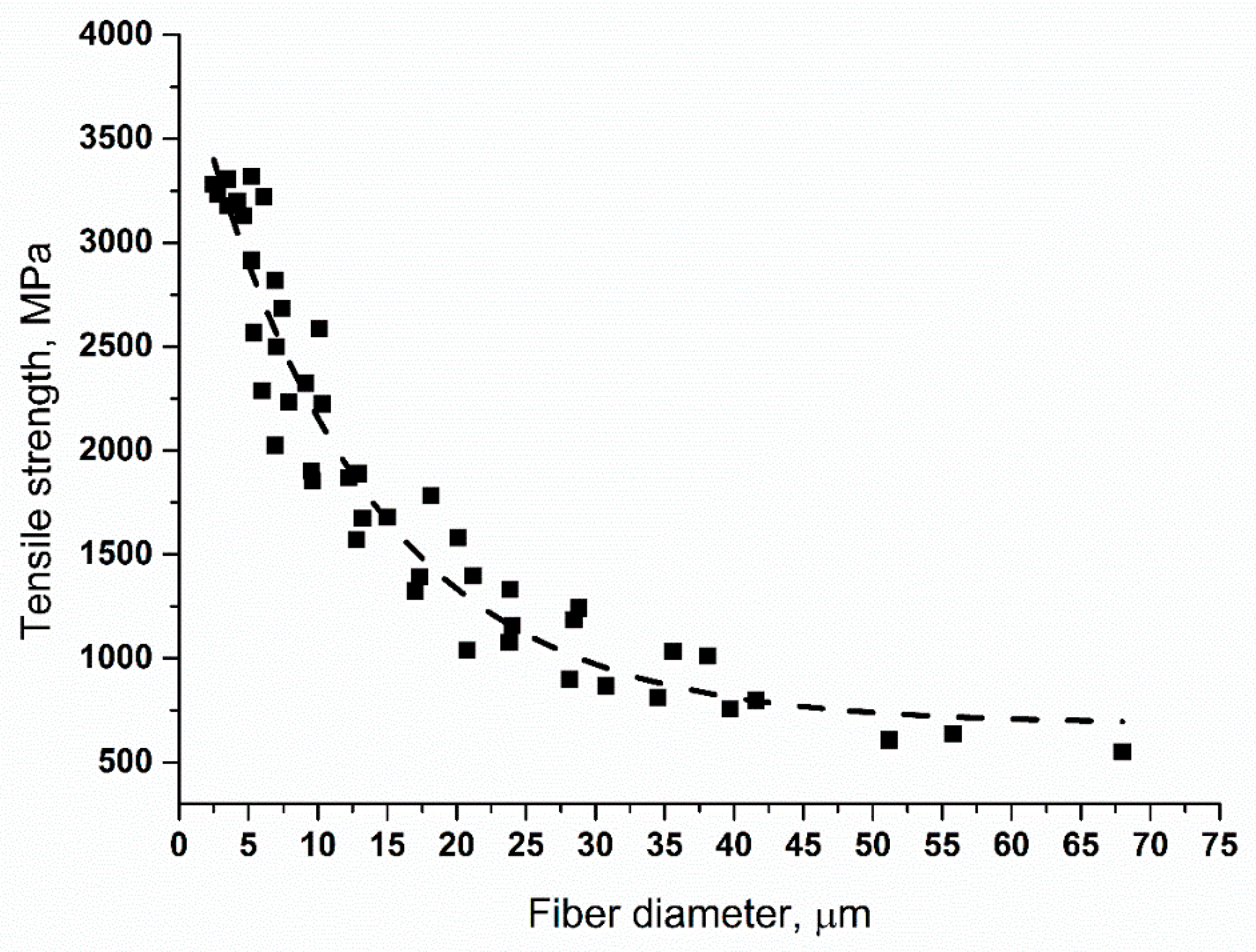
Figure 5 shows this dependence for all obtained fibers.
This dependence is described in many papers devoted to glass fibers [
27] and basalt fibers [
14]. Many authors place importance on the fact that the strength of the fibers reaches an asymptote at a certain diameter, due to the influence of axial stress. Considering the dependence of the optical birefringence on axial stress, authors decided that the structural anisotropy induced by the axial stress plays an important role in determining the tensile strength of the continuous fibers. It was found that an increase of the axial stress resulted in a linear increase of the degree of structural anisotropy. Thus, it can be inferred that increases of structural anisotropy enhance the tensile strength of glass fibers. However, unlike the anisotropy, tensile strength reaches a plateau or maximum above a certain axial stress value.
Surface defects (crystals, cracks, immiscibility) appear due to the high crystallization ability of the melt and the tension arising in the basalt melt under the action of the winding forces. The degree of influence of these parameters depends on the cooling rate of the basalt melt in the forming zone. Increasing the cooling rate while reducing the nozzle diameter slows down the process of phase separation and crystal growth, thereby reducing the formation of defects on the surface of the fibers and increasing their strength (
Figure 6). However, an increase in the cooling rate of the melt entails an increase in tensions in the basalt melt, which leads to an increase in the damageability of the fibers during formation and a decrease in strength. Thus, the dependence of the strength of the fibers on the conditions of their production has a more complex correlation. As one would expect, the diameter of the fibers has a significant effect on the strength thereof. That is due to the nature of the strength of glass basalt fibers. In fact, the strength of the fiber is determined by the probability of finding a defect of critical size in the fiber surface. On the other hand, as the formation temperature of the fiber increases, the probability of crystal formation decreases. Due to the difficulty of experimental determination of the upper limit of the crystallization temperature range, every 10 °C becomes critical. Thus, we can observe that the effect of formation temperature is particularly important for the case of basalt fibers. The drawing speed in this case probably affected the strength of the fibers indirectly according to their diameters. However, one should always consider that a high quenching rate also allows for a more homogeneous structure, which directly affects the strength.
The results of this work could be useful not only for scientists, but also for technologists that choose the optimal conditions for technological processes.