1. Introduction
Projectile nose shape is an important parameter that dominates the ballistic performance of a high-performance fiber [
1,
2,
3]. The projectile striking velocity that causes instantaneous rupture on a yarn under transverse impact is defined as critical velocity [
2,
3]. Upon impact below the critical velocity, the transverse waves developed in the yarn deform according to the Smith theory [
3,
4,
5]. Such transverse speed can be determined analytically using the projectile’s striking velocity and the axial mechanical properties of the yarn [
3,
4,
5]. On the other hand, if the projectile strikes above the critical velocity, the transverse displacement of the yarn is insignificant [
2,
6]. Additionally, even though the Smith theory is capable of predicting the critical velocity, the predicted results are always overestimated compared to those obtained from experiments [
2,
6,
7,
8].
A factor that causes the overestimation of the predicted critical velocity by the Smith theory is the projectile’s nose shape [
1,
2]. Hudspeth et al. [
2] shot a razor blade, a 0.30-cal fragmented simulation projectile (FSP) and a 0.30-cal round onto high-performance yarns and found out that the 0.30-cal round had the highest critical velocity, followed by the 0.30-cal FSP and the razor blade. The failure surface of the recovered specimens indicated that the yarns impacted by the razor blade failed in shear and the 0.30-cal round failed in fibrillation [
2]. Multi-axial load developed in the yarn during transverse impact caused stress concentration and ultimately influenced the critical velocity [
9].
Carr [
10] shot a spherical steel projectile with a mass of 0.68 g onto para-aramid yarns and Dyneema
® yarn. The failure surfaces of para-aramid yarns showed fibrillation irrespective of projectile’s striking velocity [
10]. However, for Dyneema
® yarn, the failure was caused by shear when impacted below the critical velocity [
10]. The failure surfaces for Dyneema
® yarn revealed melting when impacted above the critical velocity which was similar to those observed by Hudspeth et al. [
2,
10].
Utomo et al. [
7,
11] performed single fiber aramid and ultra-high weight molecular Polyethylene (UHMWPE) impact experiments using saddle and cylindrical projectiles impacted to obtain the mechanical behavior. The results showed that the tensile modulus was independent of the projectile’s striking velocity. The failure strains determined from the saddle projectile were higher than those obtained from the cylindrical projectile. However, both failure strains were lower than the quasi-static ultimate tensile strain [
7].
Phoenix et al. [
1] performed ballistic experiments on Dyneema
® SK76 yarns with various initial pretension using two types of projectiles (flat and saddle noses). The results showed that as the initial pretension increased, the Young’s modulus also increased. The critical velocity for the flat nosed projectile was lower compared to that of the saddle nose projectile. A wave-propagation model was developed to predict the critical velocity for a flat nose projectile impacted onto yarns with various initial pretension.
To the best of our knowledge, the circular nose shape projectiles (round, saddle or spherical) used in most of the transverse impact experiments contained only one radius of curvature [
1,
7,
8,
10,
11]. The only exception was the experimental work done by Hudspeth et al. [
2] where a razor blade and a 0.30-cal round projectile were used. The razor blade used in their study can be considered as a round projectile with a radius of curvature of 1.15 µm [
2]. The difference in radius of curvature between the razor blade and the 0.30-cal round was at least 3 orders of magnitude. To understand the effect of projectile radius of curvature on the critical velocity, we performed ballistic experiments to determine the critical velocity of an aramid yarn transversely impacted by round projectiles with different radii of curvatures.
2. Materials and Methods
The aramid yarn specimens used in this study were strands of Twaron
® 2040 yarns (Teijin Aramid, Conyers, GA, USA) extracted from plain weave single ply CT 709 Twaron
® (Teijin Aramid, Conyers, GA, USA) in the warp direction. According to the manufacturer, this yarn consists of 1000 filaments with an average diameter of 9 µm. The quasi-static axial mechanical properties of the yarn were determined in a previous study [
12]. The average Young’s modulus, ultimate tensile strength and ultimate tensile strain were 92.55 ± 1.66 GPa, 2.47 ± 0.08 GPa and 2.71 ± 0.08%, respectively [
12].
Ballistic Experiments
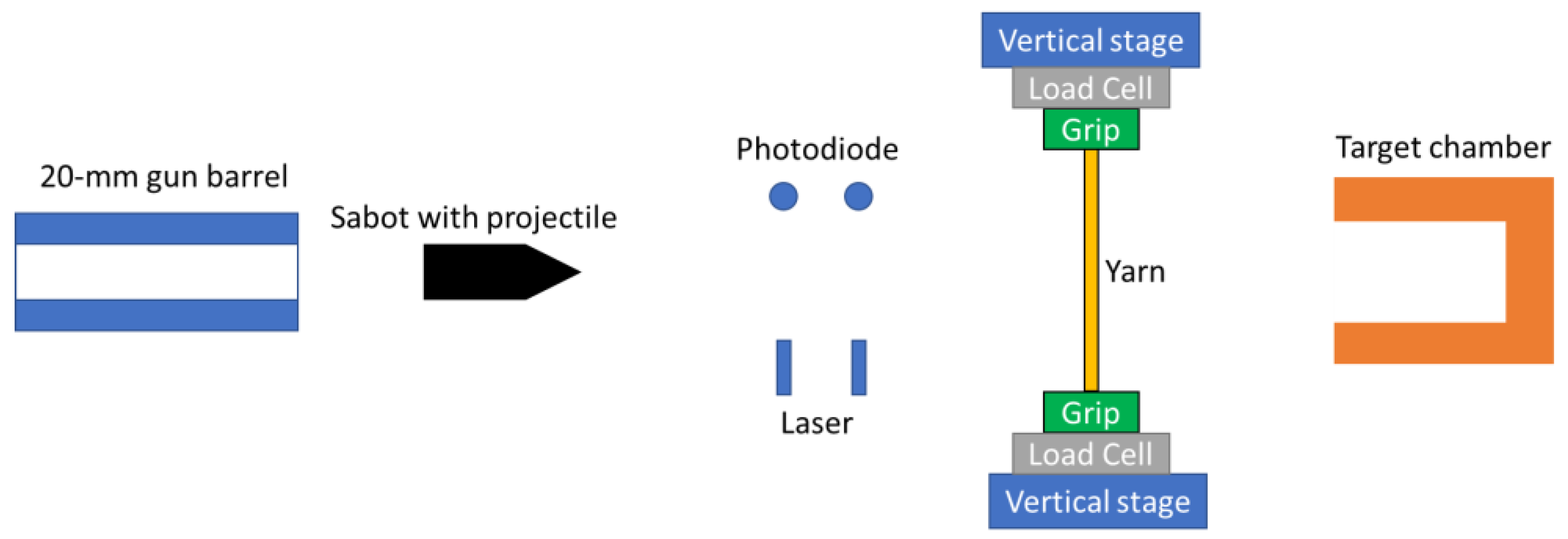
A gas/powder gun setup was utilized to perform the ballistic experiments to determine the critical velocity of the yarn, as shown in
Figure 1.
The detail of the experimental setup, including the method to attach the yarn, was presented in previous studies [
6,
12]. The load cells were mounted to the grips to measure the load history. Four different types of round projectiles were used in this study. These were razor blades, 20-µm, 200-µm, and 2-mm round projectiles. The razor blades used were commercially available razor blades. In the previous study, scanning electron microscopy (SEM) images revealed that the average radius of curvature of the razor blade was 2 µm [
12]. The remaining three projectiles were custom-made projectiles. The inner diameter of the gun barrel was larger than the projectiles. To fit these projectiles into the barrel, sabots were used, as shown in
Figure 2.
The sabots were made by polyurethane cast into a mold. An insert with a 9-mm hex shape was placed on top of the mold to fit different size projectiles except for the razor blade, as shown in
Figure 2. A slot was cut at the top of each sabot using a precision wafering saw. For the razor blade, the purpose of this slot was to allow the razor blade to be placed on top of the sabot, as shown in
Figure 2a. For the other types of projectiles, this slot was used to align the projectile to the sabot. These projectiles were then secured on the sabot with cyanoacrylate adhesive. Another parallel cut was made at the rear end of the sabot to assist in alignment of the sabot inside the gun barrel and to ensure the contact angle between the blade and the yarn was perpendicular. The combination of sabot and projectile yielded an average mass of 29 g for razor blade and 39 g for the other three types of projectiles. To observe the failure process of the yarn under transverse impact, a high-speed camera was integrated into the experimental setup.
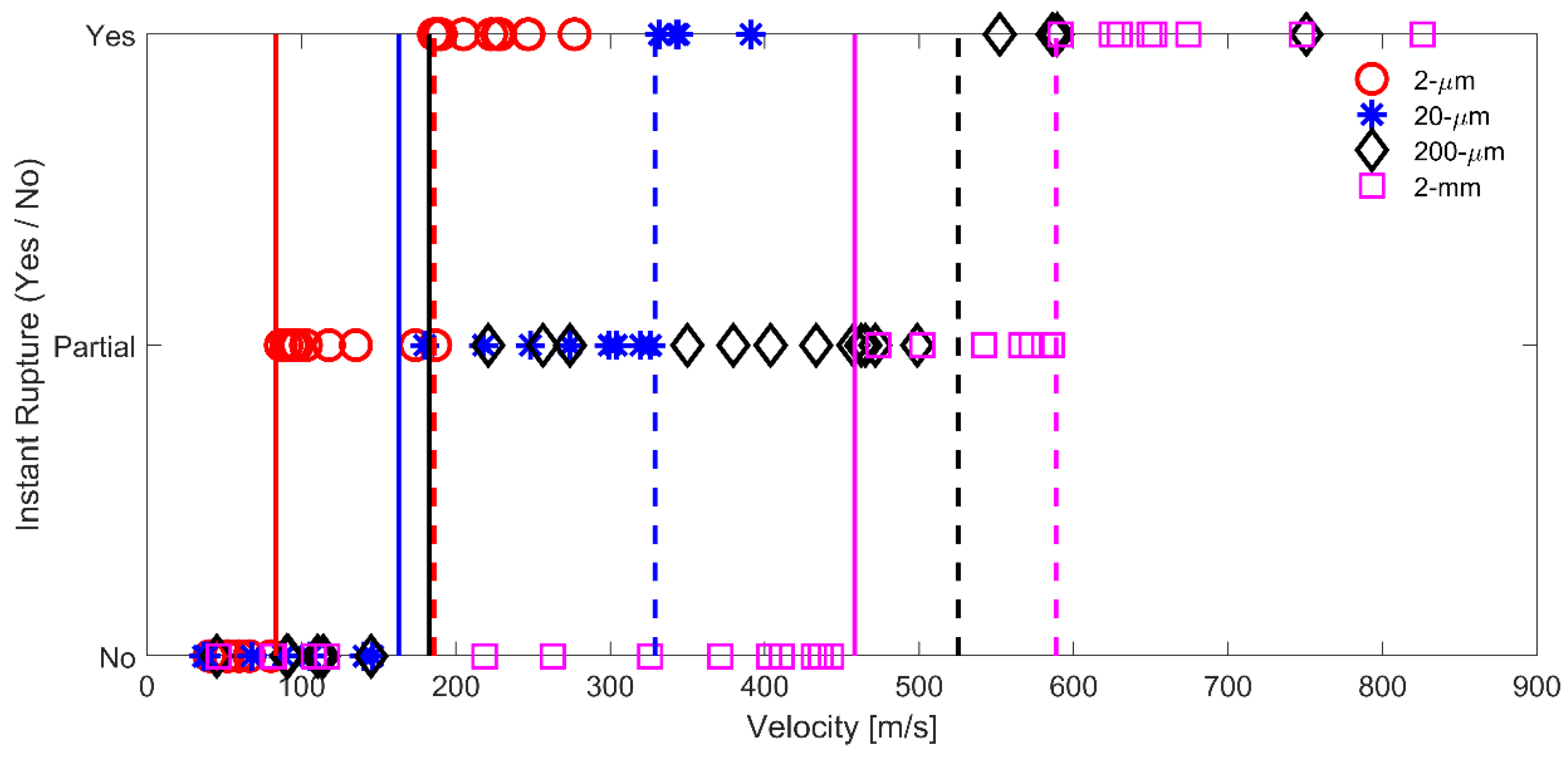
3. Results
The critical velocities of Twaron 2040 yarns upon transverse impact by four round projectiles were obtained via ballistic experiments. It is important to emphasize that for a given case, the critical velocity has a range. If the impact of the projectile on the yarn was below the lower limit of the critical velocity, the transverse waves would develop and propagate in the yarn, causing it to deform according to Smith theory [
3,
6]. On the other hand, if impacted above the upper limit, the yarn would rupture instantaneously [
2,
6]. When impacted within the range of the critical velocity, some of the fibers would rupture upon impact and the remaining fibers would deform into a triangular shape as describe by Smith theory [
2,
3,
6]. Therefore, when a yarn is transversely impacted by a projectile, the initial deformation of the yarn falls into one of the three possible cases: (i) no rupture, (ii) partial rupture, and (iii) instantaneous rupture [
2,
6].
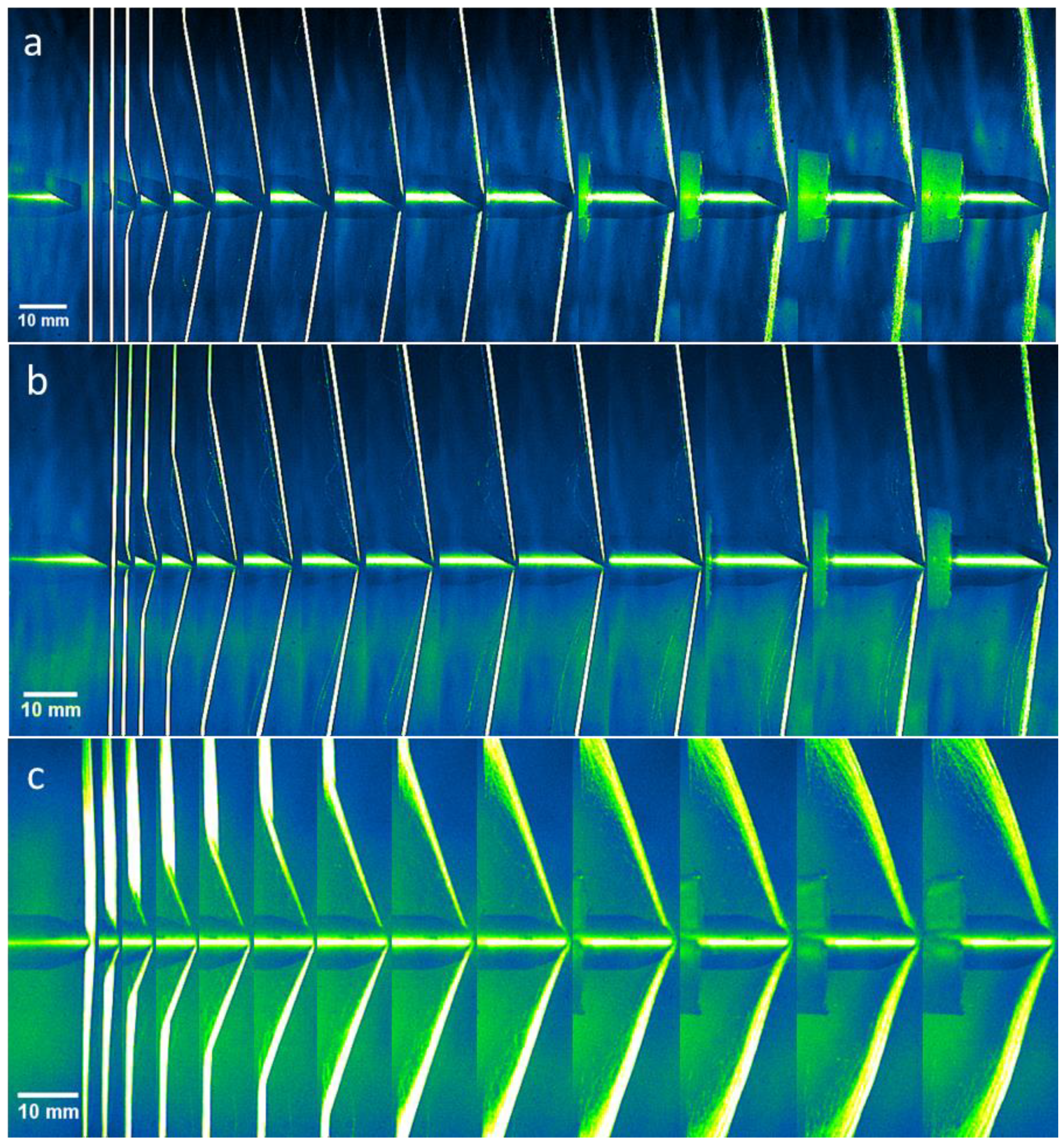
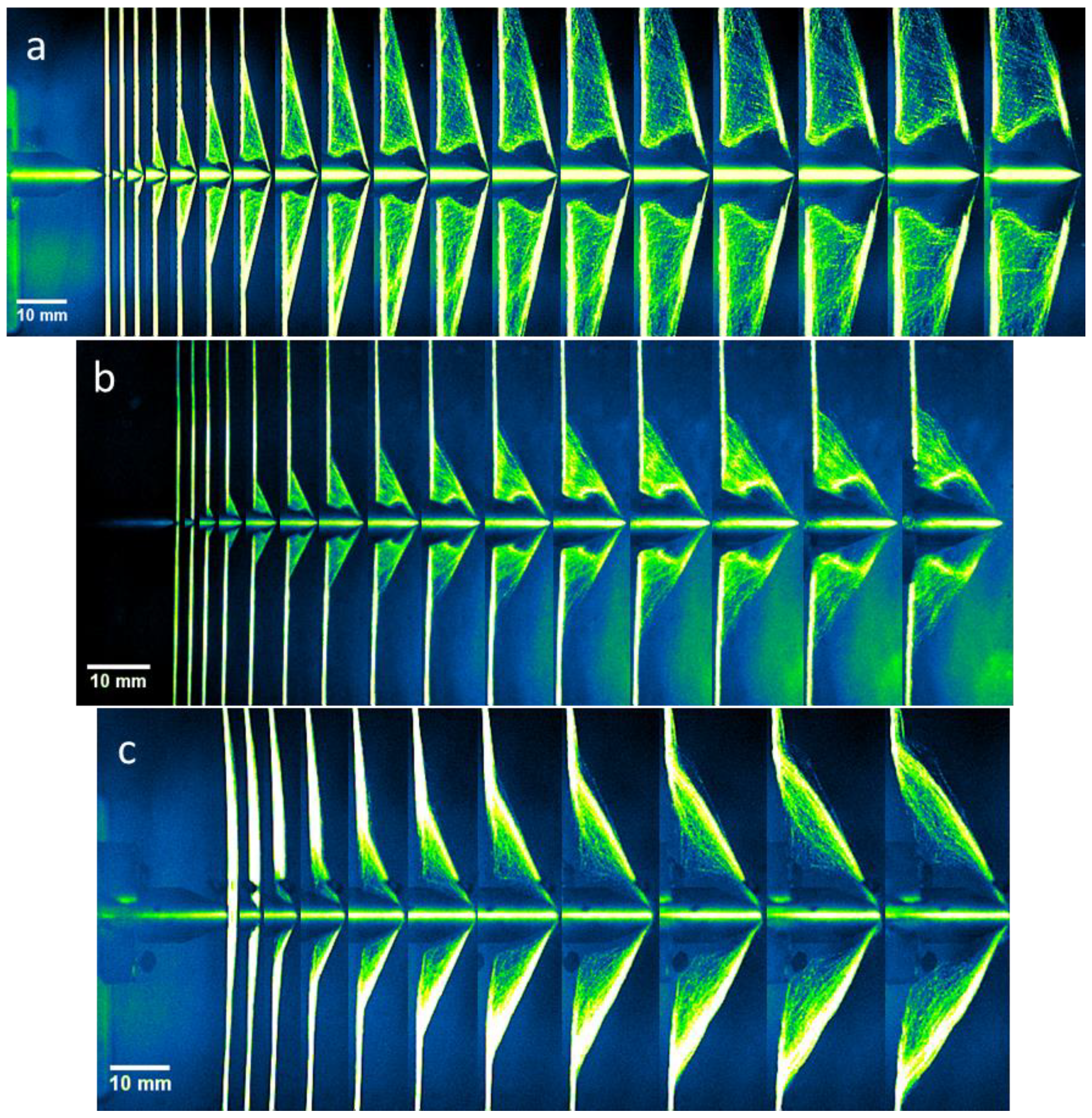
Figure 3,
Figure 4 and
Figure 5 show the high-speed images when impacted below, between and above the critical velocities by 20 µm, 200 µm and 2 mm round projectiles. For those yarns impacted by the 2 µm round projectile, the high-speed images can be found in [
6].
From
Figure 3,
Figure 4 and
Figure 5, it was observed that as the radius of curvature of the projectile increased, the initial deformation of the yarn appeared to follow the contour of the projectile, as opposed to triangular-shape deformation as described by Smith [
3]. In addition, upon impact above the critical velocity, prior to rupture, the transverse displacement of the yarn increased as the projectile’s radius of curvature increased, as shown in
Figure 5. From
Figure 5a, the transverse displacement of the yarn at failure was small and occurred at the point of impact. Subsequently, as shown in
Figure 5c, when impacted by a 2-mm round projectile, the transverse displacement of the yarn was larger than those impacted by smaller radius of curvature projectiles. Furthermore, the failure also initiated from a point away from the tips of the projectile as pointed by the arrows in
Figure 5c.
Figure 6 presents the initial deformation of the yarn at various projectile striking velocity for all four cases.
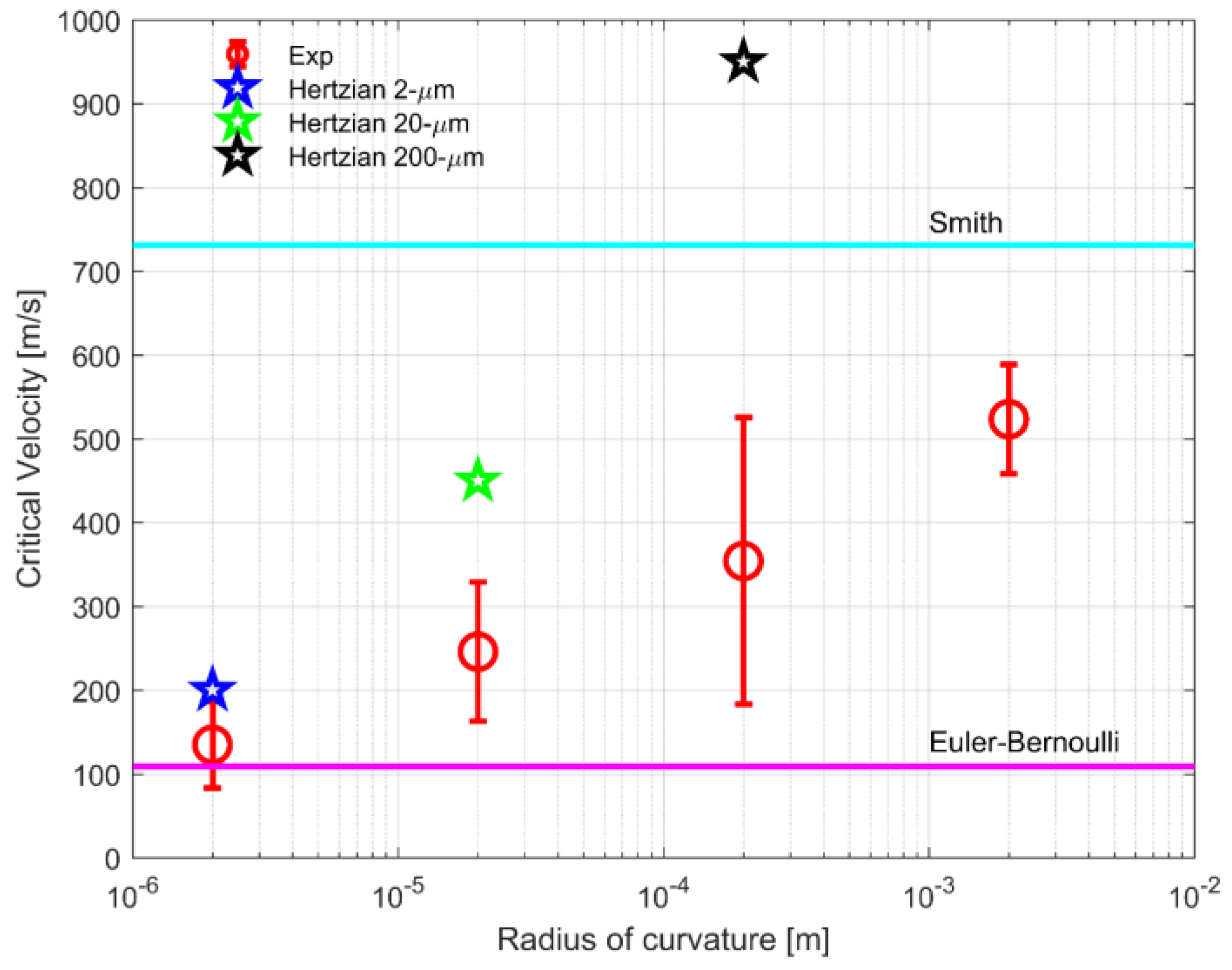
The range of critical velocities for Twaron
® 2040 yarns transversely impacted by round projectiles possessing a radius of curvature of 2 µm, 20 µm, 200 µm and 2 mm were 83–186 m/s, 163–329 m/s, 183–525 m/s and 458–589 m/s, respectively. As pointed out in the previous study, the critical velocity predicted by Smith theory was around 731 m/s [
3,
6]. Such a discrepancy between the predicted and experimental critical velocities for all cases agreed with the results reported in the literature [
1,
2,
7,
8]. The load cells mounted to the grips allowed the force to be measured when the yarn specimen was subjected to transverse impact.
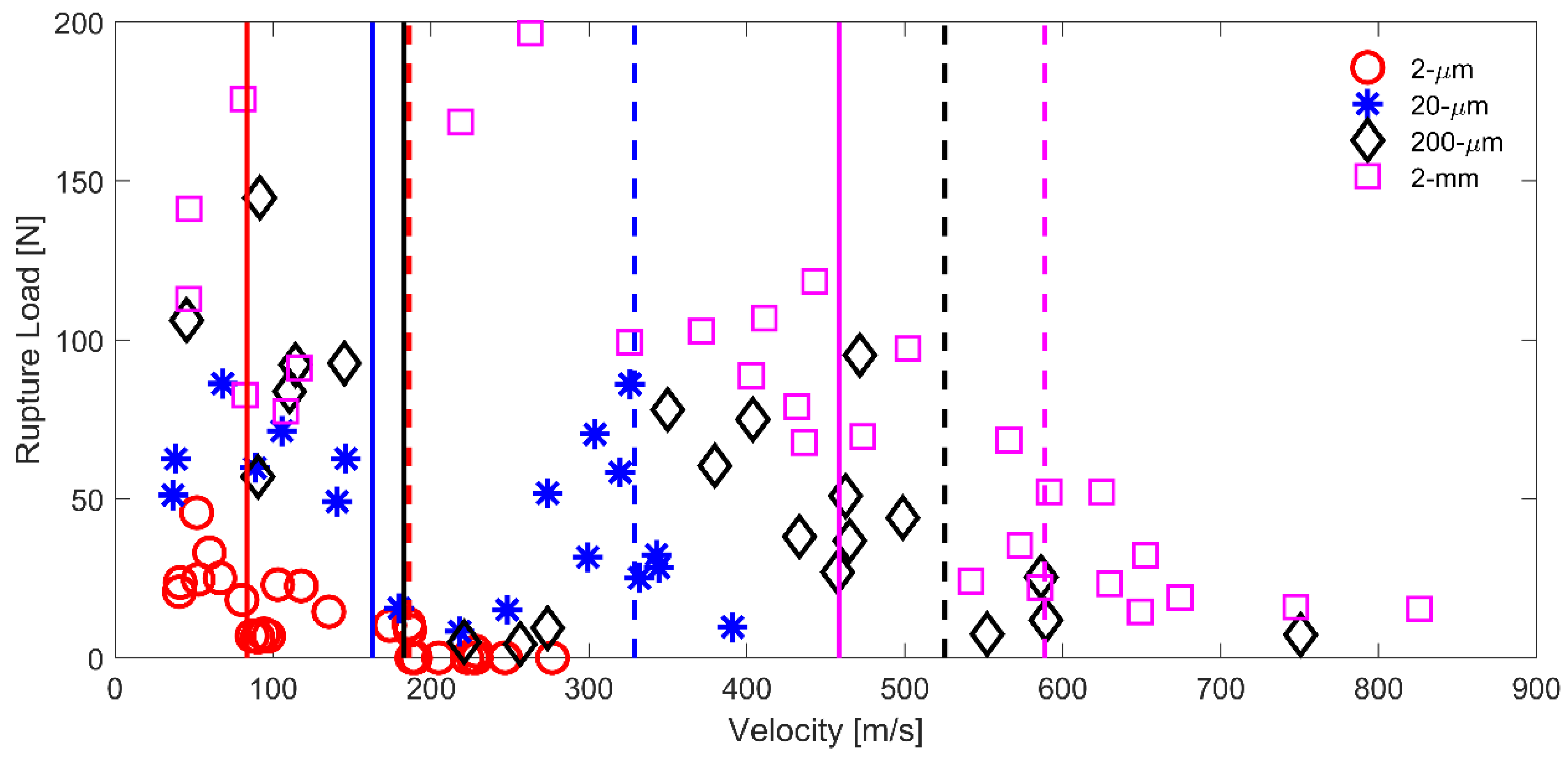
Figure 7 plots the axial force at rupture versus the projectile striking velocity for Twaron
® yarn impacted by 2 µm, 20 µm, 200 µm and 2 mm round projectiles. Such rupture load was obtained by averaging the loads from both load cells at failure.
From
Figure 7, it was observed that for a given striking velocity, the rupture load increased as the radius of curvature of the projectile increased. It is important to note that such rupture load is not equivalent to the axial load of the yarn when impacted below the lower limit of the critical velocity. The reason is that, upon transverse impact below the critical velocity, the yarn deformed into triangular shape causing the axial load in the yarn to have both vertical and horizontal components. Since the load cells were only capable of measuring the vertical force, the axial force in the yarn was underestimated. For 2 µm and 20 µm cases, the rupture loads decreased as the projectile striking velocity approached its respective lower limit of the critical velocity. A possible reason is that these small projectiles were able to shear through the yarns, causing them to fail progressively at the point of impact from projectile end toward the other free end. However, such failure process was not observed when impacted by larger round projectiles. The 2-mm round projectile was unable to shear through the yarn at low velocity, suggesting that the yarn failed due to stretching which caused the axial rupture load to be highest among all cases.
Unlike the previous case, when impacted above the upper limit of the critical velocity, the transverse displacement of the yarn was small. In addition, the yarn remained vertical away from the point of impact. Therefore, the measured loads represented the axial load in the yarn. The rupture load showed a demonstrative reduction when impacted above the critical velocity. This suggested that the load generated at the point of impact was unable to be transferred out by the stress waves, causing stress concentration to develop in the yarn and ultimately leading to premature failure [
2,
12,
13,
14].