Abstract
We report on a passively mode-locked oscillator based on an erbium-doped dual concentric core fiber combining high normal dispersion and large mode area. This large normal dispersion laser generates long pulses with 30 ps duration and 0.17 nm spectral width at 1530 nm wavelength. The source delivers an average power of 64 mW at a repetition rate of 16 MHz, corresponding to 4 nJ energy. This concept opens up new degrees of freedom in the design of mode-locked fiber lasers.
1. Introduction
Ultrafast lasers based on optical fibers are increasingly exploited in scientific and industrial applications. This success is primarily based on the unique features inherent to optical fiber technology such as the good spatial beam quality, compactness, stability, and ease of use. Stimulated by several industrial and scientific applications, the performance of ultrashort pulse fiber laser systems has grown phenomenally over the last decade. This outstanding growth mainly concerned ytterbium-doped fiber lasers operating at 1 μm. The extension of these developments to the spectral region of ocular safety centered at 1.5 μm could find new opportunities in industry, metrology, and medicine.
One of the advantages of lasers operating at wavelengths below 1.3 μm is that the dispersion of silica fibers is normal, thus allowing a better management of nonlinear effects which constitute a fundamental issue in the ultrashort-pulse regime. Indeed, it is now well-established that nonlinear pulse propagation in normal dispersion fibers favors energy scaling. This is the case of self-similar pulse lasers characterized by the generation of parabolic pulses, which are more resistant to nonlinearities [1]. In particular, the performances of these sources have been significantly improved by exploiting all-normal dispersion (ANDI) cavities, leading to the generation of highly-chirped dissipative solitons [2,3,4]. The implementation of ANDI lasers using low nonlinearity large mode area fibers combined with a strong mode-locking mechanism resulted in the generation of ultrashort pulses with multi-MW peak powers and more than 1 µJ energy [5,6,7,8]. The implementation of this concept with erbium-doped fiber lasers operating around 1.55 μm has allowed energies of more than 20 nJ with sub-picosecond pulses to be reached [9,10,11,12,13,14]. Unfortunately, commercially available normal dispersion active fibers exhibit a small effective area for moderate dispersion values, thus limiting the energy scaling potential of this concept.
However, the theoretical analysis of ultrashort pulse propagation in normal dispersion gain media indicates that energy scaling is governed not only by the fiber nonlinearity, which should be lowered, but also by the magnitude of its second-order dispersion [15,16]. Thus, the development of active fibers with large normal dispersion and large mode area constitutes an interesting alternative for energy scaling in mode-locked lasers, which has not yet been explored. It worth noting that fibers with W-profile cores, also known as dual concentric core fibers (DCCF), have been studied early in the 1970s, mostly for dispersion compensation purposes [17]. However, it is also well-known that a W-profile can act as a low-pass filter. Indeed, in contrast to conventional step-index fibers, the fundamental mode of a W-type fiber can exhibit a nonzero cutoff. Revealed theoretically in the 1980s [18], this untypical feature has been largely exploited for laser applications using rare-earth doped DCCFs [19,20]. The enhanced dispersion tailoring capabilities of DCCFs allow positive or negative dispersion to be reached at almost any wavelength in the transparency window of glass [21]. Indeed, the use of a passive DCCFs with anomalous dispersion has permitted the realization of a soliton ytterbium fiber laser at 1 µm wavelength where standard fibers exhibit normal dispersion [22]. Moreover, normal dispersion DCCFs are routinely used to manage dispersion in high-energy dissipative soliton oscillators delivering several nanojoules of energy [9,12]. Thus, the development of active DCCFs with engineered dispersion properties is very promising for energy scaling in mode-locked lasers.
In this paper, we reported a passively mode-locked oscillator exploiting an active DCCF designed to provide a large normal dispersion around 1530 nm for the first time to our knowledge. Robust and self-starting mode-locking was achieved by combining nonlinear polarization evolution with a semiconductor saturable absorber mirror (SESAM). The laser subsequently generated 4 nJ pulses at 16 MHz repetition rate.
2. Materials and Methods
2.1. Fiber Structure and Dispersion Properties
Very large dispersion, in excess of −1800 ps/nm/km at 1550 nm wavelength, can be achieved with the triple-clad fiber design, also referred to as dual concentric core fiber (DCCF) [23]. However, such a large value comes at the cost of (a) reduced bandwidth, and therefore large third-order dispersion, and (b) ultra-small mode area about 10 µm2, which are detrimental to energy scaling in the mode-locked regime. Guided by numerical simulations, we selected a set of opto-geometrical parameters that lead to a tradeoff between normal dispersion, dispersion slope, and effective mode area. Then, a fiber was fabricated by the modified chemical vapor deposition process associated to the solution-doping process for Er3+ doping. The refractive index profile (RIP) of the fiber is shown in Figure 1a.
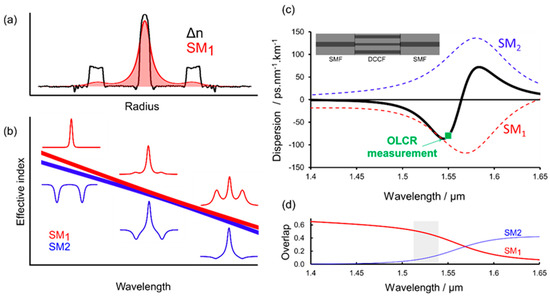
Figure 1.
(a) Index profile of the dual concentric core fiber and electric field distribution of the first supermode of the structure computed at 1530 nm. (b) Effective index curves versus wavelength computed for the refractive index profile shown in (a). Insets show the electric field distributions for the two supermodes (SM1 and SM2). (c) Chromatic dispersion curve of the device shown in inset. Green dot shows the value measured by means of the optical low coherence interferometry at 1550 nm. (d) Overlap factor between the field distributions of the two supermodes with the gain region. The preferred spectral range for laser oscillation is shown in grey and is centered on 1530 nm. SMF: Single-mode fiber; DCCF: Dual concentric core fiber; OLCR: Optical low coherence reflectometry.
The RIP incorporated a single-mode central core surrounded by a broad high-index ring. By properly tailoring the thicknesses and refractive indices of the fiber, electromagnetic coupling between the fundamental modes of the two isolated cores yielded two supermodes with bent effective index curves around the phase-matching wavelength, as shown by numerical simulation in Figure 1b. As dispersion is related to the second derivative of the effective index versus wavelength, these two supermodes, labelled SM1 and SM2, exhibited large second-order dispersion with opposite signs (see Figure 1c, dashed lines). As this fiber is inherently bimode, the overall behavior depends on the weights of the super-modes, which depend on the launching conditions [24,25]. In the following, we considered that light was launched into and collected from the central core of the DCCF by means of standard single-mode fibers (SMF) according to the schematic shown in inset to Figure 1c. Under these conditions, light was preferentially launched into SM1 at short wavelengths, while SM2 was predominantly excited at long wavelengths (see spatial distributions of light in both modes in insets to Figure 1b).
The chromatic dispersion of the DCCF (inserted between two centered SMFs) has a characteristic symmetric shape and changes its sign when increasing the wavelength, as shown in Figure 1c. Therefore, it retains the features of both supermodes: large normal dispersion at short wavelengths and large anomalous dispersion at long wavelengths (see Figure 1c, thick black line). The computed chromatic dispersion of the device was expected to be large and negative (−85 ps/nm/km) at 1543 nm. The fabricated fiber consisted in a high-index inner core with a diameter of 5 µm, surrounded by a broad lower-index ring with a radius of 15 µm. Then, the chromatic dispersion of the device was measured at 1550 nm by the optical low coherence interferometry technique described in [26]. A value of −80 ps/nm/km was measured, which was in excellent agreement with the computation. In the fabricated fiber, the central core was doped with Er3+ to reach core absorption of 23 dB/m at 976 nm. The overlap factors between the electric field distribution of both supermodes and the doped region were computed and plotted in Figure 1d. These computations confirmed that the supermode SM1 with large normal dispersion will experience higher gain at short wavelengths. Despite the inherent bimodal nature of the system, laser oscillation should occur on the fundamental supermode with large normal dispersion in the wavelength range highlighted by the grey box in Figure 1d. In particular, lasing on the first supermode was expected around 1530 nm a wavelength, which was untypical and more difficult to generate from mode-locked erbium fiber lasers. Furthermore, the effective area of the SM1 was relatively large (73 µm2 at 1530 nm) and comparable to that of standard single-mode fiber at this wavelength. This large effective area would allow the generation of high-energy ultrashort pulses in the C-band.
2.2. Laser Experimental Setup
The experimental setup of the mode-locked oscillator based on the active dual concentric core fiber is schematically depicted in Figure 2. The basic structure was a σ-cavity, of which the unidirectional transmission of light was guaranteed by a polarization sensitive isolator (PS-ISO). A resonant-type semiconductor saturable absorber mirror (R-SAM) was used to ensure mode-locking [9]. The R-SAM absorption band was centered at 1543 nm, with a bandwidth of 40 nm. Its nonlinear characteristics were measured using a commercial laser delivering 1.2 ps pulses at 1550 nm. At this wavelength, the R-SAM presented a low-intensity reflectivity of 14%, a modulation depth of 40%, and a saturation fluence of 1 μJ/cm2. Time-resolved pump-probe experiments revealed a relaxation time of 5 ps [27]. The nonlinear polarization evolution (NPE) effect was also employed to assist mode-locking by inserting waveplates into the cavity. The 10-m-long Er-doped DCCF was pumped through a 976/1550 WDM by a laser diode emitting at 980 nm. A 10/90 coupler was used to extract the signal from the cavity through the 90% port. The fiber segments of the WDM and coupler in the cavity were 0.5 m Nufern 980 fiber and 1 m standard singlemode fiber (SMF28), respectively. The group velocity dispersion (GVD) of these fibers was 8.6 ps/nm/km and 17 ps/nm/km, respectively. The total length of the cavity, including the free space, was about 13.5 m, corresponding to a free spectral range of 16 MHz. Stable mode-locking regimes could be retrieved by properly setting the focus on the SESAM and by adjusting the waveplates angles. The single-pulse operation of the oscillator was confirmed by temporal measurements using a fast oscilloscope (5 GHz bandwidth) and a large span auto-correlator (AC) with 200 ps scan range. An external-cavity stage was added after the oscillator to nonlinearly compress the output pulses. The nonlinear compression stage consisted of a 30/70 coupler to extract 30% of the pulse energy, an erbium-doped fiber amplifier, 20 m of dispersion-shifted passive fiber (DSF) to broaden the spectrum through SPM, and a pair of transmission gratings used to recompress the pulse.
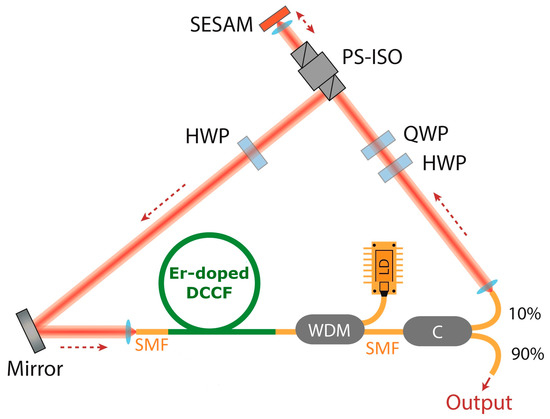
Figure 2.
Schematic diagram of the experimental setup of the laser cavity. HWP: Half-wave plate; QWP: Quarter-wave plate; SAM: Saturable absorber mirror; WDM: Wavelength-division multiplexer; SMF: Single-mode fiber; PS-ISO: Polarization-sensitive isolator; C: Coupler.
3. Experimental and Numerical Results
The characteristics of the output pulses generated in a typical operation regime of this cavity are shown in Figure 3. The pulse exhibited very narrow spectrum (0.17 nm in terms of FWHM) and long temporal duration (29 ps of FWHM assuming a Gaussian pulse shape). The oscillator delivered 65 mW average power at 16 MHz repetition rate, corresponding to about 4 nJ. Two reasons can cause the laser to mode-lock in regimes exhibiting very narrow spectrum. On the one hand, the mismatch between the peak values in the gain profile and that of the dispersion causes the laser to operate around a wavelength where high-order dispersion is significant. On the other hand, the mode coupling between the core and the ring modes effectively enlarges the supermode field area, which leads to a weak broadening effect through self-phase modulation (SPM).
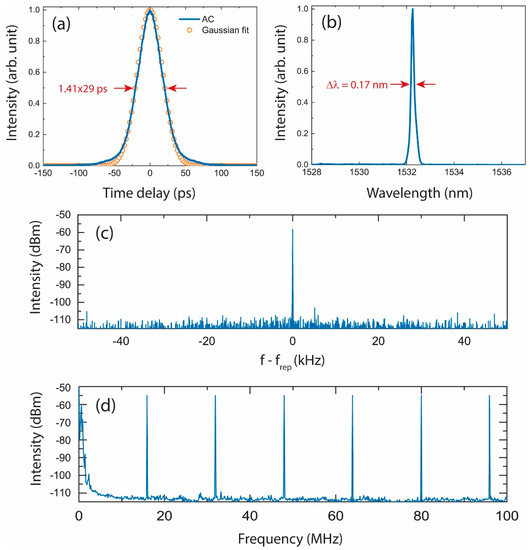
Figure 3.
Laser outputs for 4 nJ pulse energy: (a) Autocorrelation trace of the pulse from the oscillator. (b) Corresponding optical spectrum. Radio-frequency spectra recorded at spans of 100 kHz (c) and 100 MHz (d).
The mode-locking operation was self-starting and remained stable for hours. The quality of the mode-locking pulse train was evaluated by radiofrequency (RF) measurements using the power spectra obtained with a microwave spectrum analyzer (Rohde & Schwarz, Munich, Germany, 7 GHz bandwidth) via a high-speed photodetector (8-GHz bandwidth). Spectra were taken at different frequency ranges from 50 kHz to 200 MHz. The RF spectrum, shown in Figure 3c, revealed a high signal-to-noise ratio of the fundamental beat note at 16 MHz. It showed very good stability, with a contrast of more than 60 dB between the fundamental harmonic and the background. This indicates that the mode-locked laser operation was very stable and free from any Q-switching instability. The slowly decreasing amplitude of the inter-mode frequency harmonics, shown in Figure 3d, also confirmed stability of the CW mode-locking regime.
The output pulses were then nonlinearly compressed through the extra-cavity stage introduced in Part 2. The dispersion of the DSF was about −2 ps/nm/km at 1530 nm. The spectrum and alternating current (AC) trace of the nonlinearly compressed pulses are depicted in Figure 4.
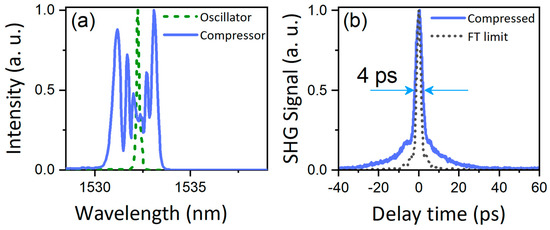
Figure 4.
Optical spectrum (a) and alternating current (AC) trace of the output pulses measured after nonlinear compression (b). The dashed and dotted curves correspond, respectively, to the spectrum measured at the oscillator output and the Fourier transform (FT) limited AC-trace inferred from the SPM-broadened spectrum.
As the spectrum of the pulse is broadened to a FWHM of 2.33 nm from the original 0.17 nm, its temporal shape experienced little stretching in this process to reach 32 ps duration. The Fourier transformation of the spectrum assuming a zero-phase relation led to a duration of 1.43 ps. Using a pair of polarization independent transmission gratings (PING model from Ibsen photonics), the output pulses were dechirped down to a width of 2.3 ps, which was about 1.6-times the transform limit. The relatively large pedestal on the AC trace of the compressed pulses, combined with the small deviation of the pulse width from its transform-limited value, indicate that the output pulses suffered from nonlinear chirp, which could be attributed to the mismatch between the dispersion characteristics of the DSF and the gratings-based compressor. Nevertheless, the results of the external-cavity compression confirm the coherent nature of the pulse generated by the DCCF-based oscillator, which negates the possibility of noise-like pulse operation and highlights the potential of this new type of fiber laser if the fiber and the cavity parameters are correctly optimized.
To better understand the pulse dynamics along this cavity, we numerically investigated this system using the standard split-step method with the cavity elements arrangement provided in Figure 2. Pulse propagation along the gain fiber was described by the extended nonlinear Schrödinger equation (NLSE), including second- and third-order dispersion terms, Kerr nonlinearity, and saturated gain with a finite bandwidth of 30 nm around 1530 nm [6,12,28,29]. Propagation along the fibers was assumed to be single-mode, and only the dispersion and nonlinearity parameters inferred from their structures were considered. The linear and nonlinear parameters of the intracavity fibers are summarized in Table 1. The action of the mode-locking mechanism was modeled by a high-contrast effective saturable absorption effect with an instantaneous response [6]. We used the well-known transmission equation given by [28]:
where ΔR and Psat correspond to the modulation depth and the saturation power, respectively. An ideal saturable absorber with a modulation depth of 90% was considered in this study. The saturation power was increased with pump power to maintain a constant saturation ratio of about 10 [29].

Table 1.
Fiber parameters used in the simulation.
The evolution of the pulse parameters inside the cavity shows that the pulse dynamics were dominated by the interplay between the high dispersion of the gain fiber and the saturable absorption mechanism, as shown in Figure 5. The temporal lengthening endured within the gain fiber was completely compensated by the saturable absorber effect. We note that the spectral broadening along the cavity was moderate at this energy level, indicating a quasi-linear propagation regime. The simulated pulse characteristics are shown in Figure 5, with a spectrum of 220 pm FWHM and pulse duration of 34.3 ps, which are comparable with the experimental measurements.
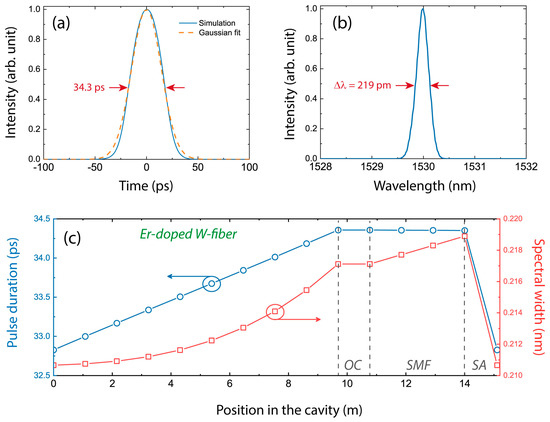
Figure 5.
Laser outputs calculated for 4 nJ pulse energy: Pulse temporal profile (a) and corresponding spectrum (b), intracavity pulse dynamics (c). OC: Output coupler; SMF: Single-mode fiber; SA: Saturable absorber.
It is worth noting that these results are retrievable only in the case that the effective supermode area is much larger than the actual core diameter of the fiber. This fact confirms that the mode-field distortion caused by the mode coupling plays an important role in the dynamics and is studying further. Interestingly, numerical simulations showed that stable pulsed solutions were obtained for output pulse energies higher than 100 nJ, indicating that this concept is very promising for energy scaling. The laser outputs predicted for 110 nJ pulse energy are shown in Figure 6. The pulsed solution presented a spectral width of 6.3 nm and a pulse duration of 100 ps. As expected, the linearly chirped output pulses could be compressed down to a duration of 870 fs which is close to the Fourier limit, calculated by Fourier transformation of the optical spectrum assuming a zero-phase relation (see Figure 6). We note that the calculated solution exhibited a quasi-parabolic profile and a linear chirp, thus suggesting that self-similar pulse propagation occurred in the normal dispersion DCCF segment.
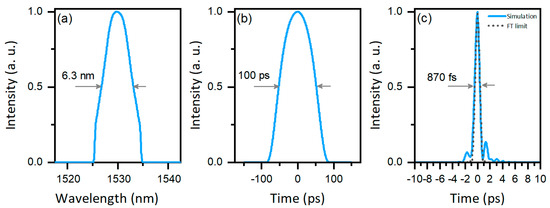
Figure 6.
Numerical results obtained for 110 nJ output energy: Optical spectrum (a) and temporal pulse profile before (b) and after extra-cavity dechirping (c).
4. Discussion
In summary, we demonstrated a passively mode-locked laser featuring an erbium-doped dual concentric core fiber combining a high normal dispersion and a large mode area. This laser generated picosecond pulses with several nanojoules energy, which were nonlinearly compressed down to 2.3 ps externally to the cavity. The numerical simulations showed good agreement with experimental results and revealed that self-similar pulse propagation can occur in the normal dispersion active DCCF, thus paving the way for energy scaling. Indeed, simulations showed that several tens of nanojoules energy can be reached in this laser platform. From these calculations, it appears that third-order dispersion did not constitute a fundamental limit for the generation of sub-picoseconds pulses with few nanometers of spectral width. However, the stabilization of higher energy pulses with broader spectra could be compromised by the higher-order dispersion terms. More work is needed to identify the upper limits of this concept and to improve the fiber design to better match the dispersion curve with the gain profile. Moreover, the fabrication of a double-clad version of the DCCF is also desired to overcome the power limitation of the passive fiber components.
Author Contributions
Conceptualization and coordination, A.H. and S.F.; fiber design and fabrication, S.F., M.L., D.G. and G.G.; fiber characterization, Y.J. and R.G.; SESAM design, fabrication and characterization, J.-L.O., M.T. and C.L.; experimental investigation, F.L., H.W., K.Q. and C.L.; numerical study, M.T.; T.G. and A.H.; initial draft writing, M.T., T.G., A.H. and S.F.; results discussion and manuscript comment, all authors.
Funding
This research was funded by French national research agency (ANR-13-BS09-0018 UBRIS2 Ultra-high brightness sources at 2 µm, ANR-16-CE08-0031 BISCOT Broadband infrared supercontinuum); Conseil regional de Nouvelle Aquitaine (FLOWA); European Union with the European Regional Development Fund (FEDER); Regional Council of Normandie.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ilday, F.Ö.; Buckley, J.R.; Clark, W.G.; Wise, F.W. Self-Similar Evolution of Parabolic Pulses in a Laser. Phys. Rev. Lett. 2004, 92, 213902. [Google Scholar] [CrossRef] [PubMed]
- Chong, A.; Renninger, W.H.; Wise, F.W. All-Normal-Dispersion femtosecond fiber laser with pulse energy above 20 nJ. Opt. Lett. 2007, 32, 2408. [Google Scholar] [CrossRef] [PubMed]
- Nie, B.; Pestov, D.; Wise, F.W.; Dantus, M. Generation of 42-fs and 10-nJ pulses from a fiber laser with self-similar evolution in the gain segment. Opt. Express 2011, 19, 12074. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Ziegler, Z.M.; Wright, L.G.; Wise, F.W. Megawatt peak power from a Mamyshev oscillator. Optica 2017, 4, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Lefrançois, S.; Kieu, K.; Deng, Y.; Kafka, J.D.; Wise, F.W. Scaling of dissipative soliton fiber lasers to megawatt peak powers by use of large-area photonic crystal fiber. Opt. Lett. 2010, 35, 1569–1571. [Google Scholar] [CrossRef]
- Lecaplain, C.; Baumgartl, M.; Schreiber, T.; Hideur, A. On the mode-locking mechanism of a dissipative- soliton fiber oscillator. Opt. Express 2011, 19, 26742–26751. [Google Scholar] [CrossRef]
- Baumgartl, M.; Lecaplain, C.; Hideur, A.; Limpert, J.; Tünnermann, A. 66 W average power from a microjoule-class sub-100 fs fiber oscillator. Opt. Lett. 2012, 37, 1640–1642. [Google Scholar] [CrossRef]
- Liu, W.; Liao, R.; Zhao, J.; Cui, J.; Song, Y.; Wang, C.; Hu, M. Femtosecond Mamyshev oscillator with 10-MW-level peak power. Optica 2019, 6, 194–197. [Google Scholar] [CrossRef]
- Cabasse, A.; Ortaç, B.; Martel, G.; Hideur, A.; Limpert, J. Dissipative solitons in a passively mode-locked Er-doped fiber with strong normal dispersion. Opt. Express 2008, 16, 19322. [Google Scholar] [CrossRef]
- Chichkov, N.B.; Hausmann, K.; Wandt, D.; Morgner, U.; Neumann, J.; Kracht, D. High-Power dissipative solitons from an all-normal dispersion erbium fiber oscillator. Opt. Lett. 2010, 35, 2807. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Z.; Lamb, E.S.; Wise, F. Self-Similar erbium-doped fiber laser with large normal dispersion. Opt. Lett. 2014, 39, 1019. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Wang, H.; Becheker, A.; Gaponov, D.; Oudar, J.-L.; Godin, T.; Hideur, A. High-Energy dissipative solitons generation from a large normal dispersion Er-fiber laser. Opt. Lett. 2015, 40, 1414. [Google Scholar] [CrossRef] [PubMed]
- Kharenko, D.S.; Zhdanov, I.S.; Bednyakova, A.E.; Podivilov, E.V.; Fedoruk, M.P.; Apolonski, A.; Turitsyn, S.K.; Babin, S.A. All-Fiber highly chirped dissipative soliton generation in the telecom range. Opt. Lett. 2017, 42, 3221–3224. [Google Scholar] [CrossRef] [PubMed]
- Olivier, M.; Boulanger, V.; Guilbert-Savary, F.; Sidorenko, P.; Wise, F.W.; Piché, M. Femtosecond fiber Mamyshev oscillator at 1550 nm. Opt. Lett. 2019, 44, 851–854. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Peacock, A.C.; Harvey, J.D.; Dudley, J.M. Self-Similar propagation of parabolic pulses in normal-dispersion fiber amplifiers. J. Opt. Soc. Am. B 2002, 19, 461–469. [Google Scholar] [CrossRef]
- Deng, Y.; Chien, C.-Y.; Fidric, B.G.; Kafka, J.D. Generation of sub-50 fs pulses from a high-power Yb-doped fiber amplifier. Opt. Lett. 2009, 34, 3469–3471. [Google Scholar] [CrossRef]
- Nishida, S.K.S. Characteristics of a double clad optical fiber with a low-index inner cladding. IEEE J. Quantum Electron. 1974, 10, 879–887. [Google Scholar]
- Monerie, M. Propagation in doubly clad single-mode fibers. IEEE J. Quantum Electron. 1982, 18, 535–542. [Google Scholar] [CrossRef]
- Soh, D.; Yoo, S.; Nilsson, J.; Sahu, J.; Oh, K.; Baek, S.; Jeong, Y.; Codemard, C.; Dupriez, P.; Kim, J.; et al. Neodymiumdoped cladding-pumped aluminosilicate fiber laser tunable in the 0.9-µm wavelength range. IEEE J. Quantum Electron. 2004, 40, 1275–1282. [Google Scholar] [CrossRef]
- Yang, L.-G.; Jyu, S.-S.; Chow, C.-W.; Yeh, C.-H.; Lai, Y. S-Band pulse generation by polarization additive-pulse mode-locking in an erbium-doped all-fiber ring laser. Las. Phys. Lett. 2013, 11, 015105. [Google Scholar] [CrossRef]
- Grüner-Nielsen, L.; Knudsen, N.; Edvold, B.; Veng, T.; Magnussen, D.; Larsen, C.; Damsgaard, H. Dispersion Compensating Fibers. Opt. Fiber Technol. 2000, 6, 164–180. [Google Scholar] [CrossRef]
- Ramachandran, S.; Ghalmi, S.; Nicholson, J.W.; Yan, M.F.; Wisk, P.; Monberg, E.; Dimarcello, F.V. Anomalous dispersion in a solid, silica-based fiber. Opt. Lett. 2006, 31, 2532–2534. [Google Scholar] [CrossRef] [PubMed]
- Auguste, J.-L.; Jindal, R.; Blondy, J.-M.; Clapeau, M.; Marcou, J.; Dussardier, B.; Monnom, G.; Ostrowsky, D.; Pal, B.; Thyagarajan, K. −1800 ps nm km chromatic dispersion at 1 55 µm in a dual concentric core fibre. Electron. Lett. 2000, 36, 1689. [Google Scholar] [CrossRef]
- Gérôme, F.; Auguste, J.L.; Février, S.; Maury, J.; Blondy, J.M.; Gasca, L.; Provost, L. Dual concentric core dispersion compensating fibre optimized for WDM application. Electron. Lett. 2005, 41, 116. [Google Scholar] [CrossRef]
- Gérôme, F.; Auguste, J.-L.; Maury, J.; Blondy, J.-M.; Marcou, J. Theoretical and Experimental Analysis of a Chromatic Dispersion Compensating Module Using a Dual Concentric Core Fiber. J. Lightwave Technol. 2006, 24, 442. [Google Scholar] [CrossRef]
- Hamel, P.; Jaouën, Y.; Gabet, R.; Ramachandran, S. Optical low-coherence reflectometry for complete chromatic dispersion characterization of few-mode fibers. Opt. Lett. 2007, 32, 1029. [Google Scholar] [CrossRef]
- Cabasse, A.; Gaponov, D.; Ndao, K.; Khadour, A.; Oudar, J.-L.; Martel, G. 130 mW average power, 4.6 nJ pulse energy, 10.2 ps pulse duration from an Er3+ fiber oscillator passively mode locked by a resonant saturable absorber mirror. Opt. Lett. 2011, 36, 2620–2622. [Google Scholar] [CrossRef]
- Ankiewicz, N.N.A.A.; Luther-Davies, M.J.L.B. Ultrashort pulses generated by mode-locked lasers with either a slow or a fast saturable-absorber response. Opt. Lett. 1998, 23, 280. [Google Scholar]
- Schreiber, T.; Ortaç, B.; Limpert, J.; Tünnermann, A. On the study of pulse evolution in ultra-short pulse mode-locked fiber lasers by numerical simulations. Opt. Express 2007, 15, 8252–8262. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).