Reinforced Concrete Beams with Carbon-Fiber-Reinforced Polymer Bars—Experimental Study
Abstract
1. Introduction
2. Experimental Work
2.1. Specimen Description
2.2. Material Properties
2.3. Test Setup and Instrumentation
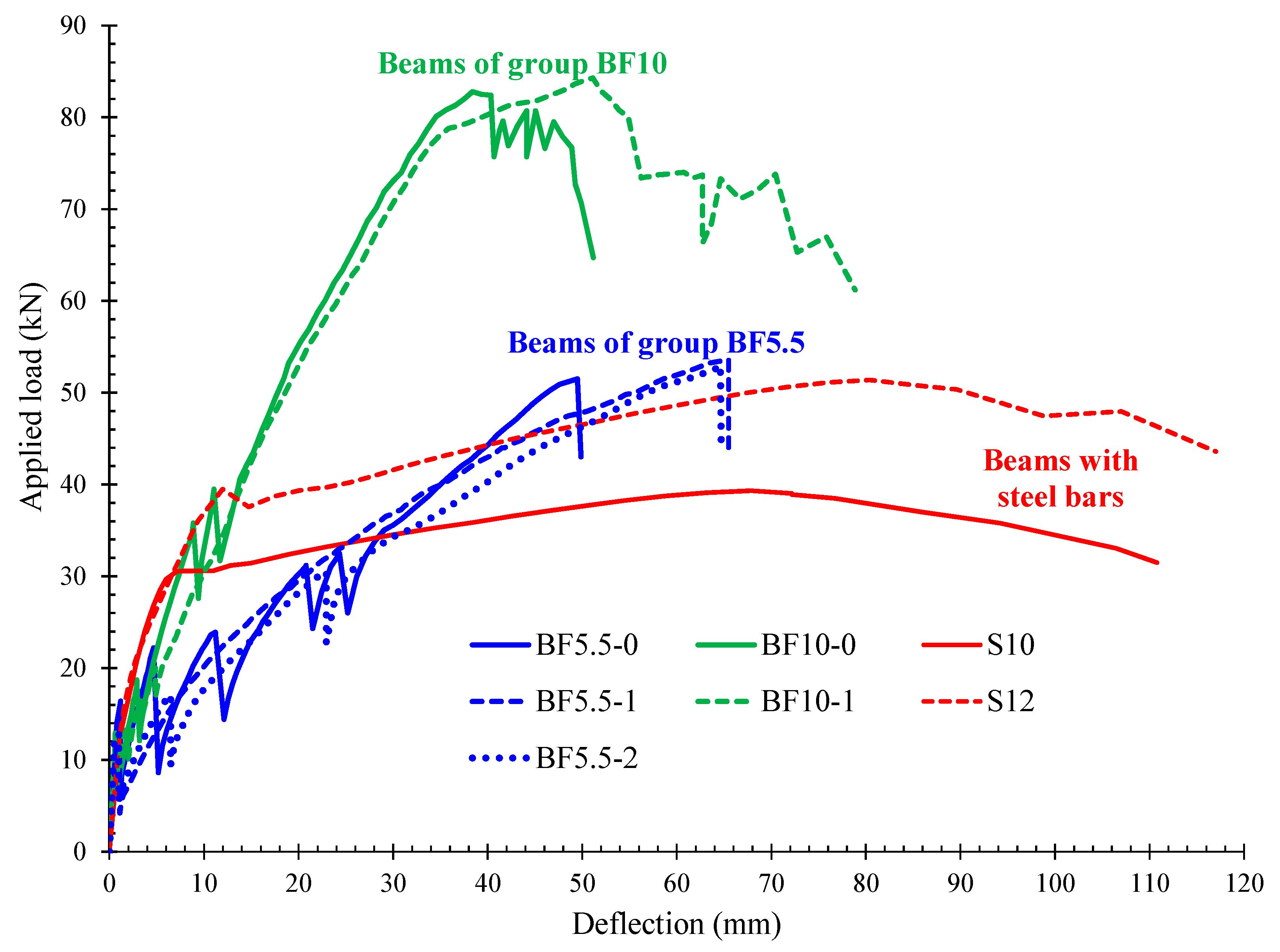
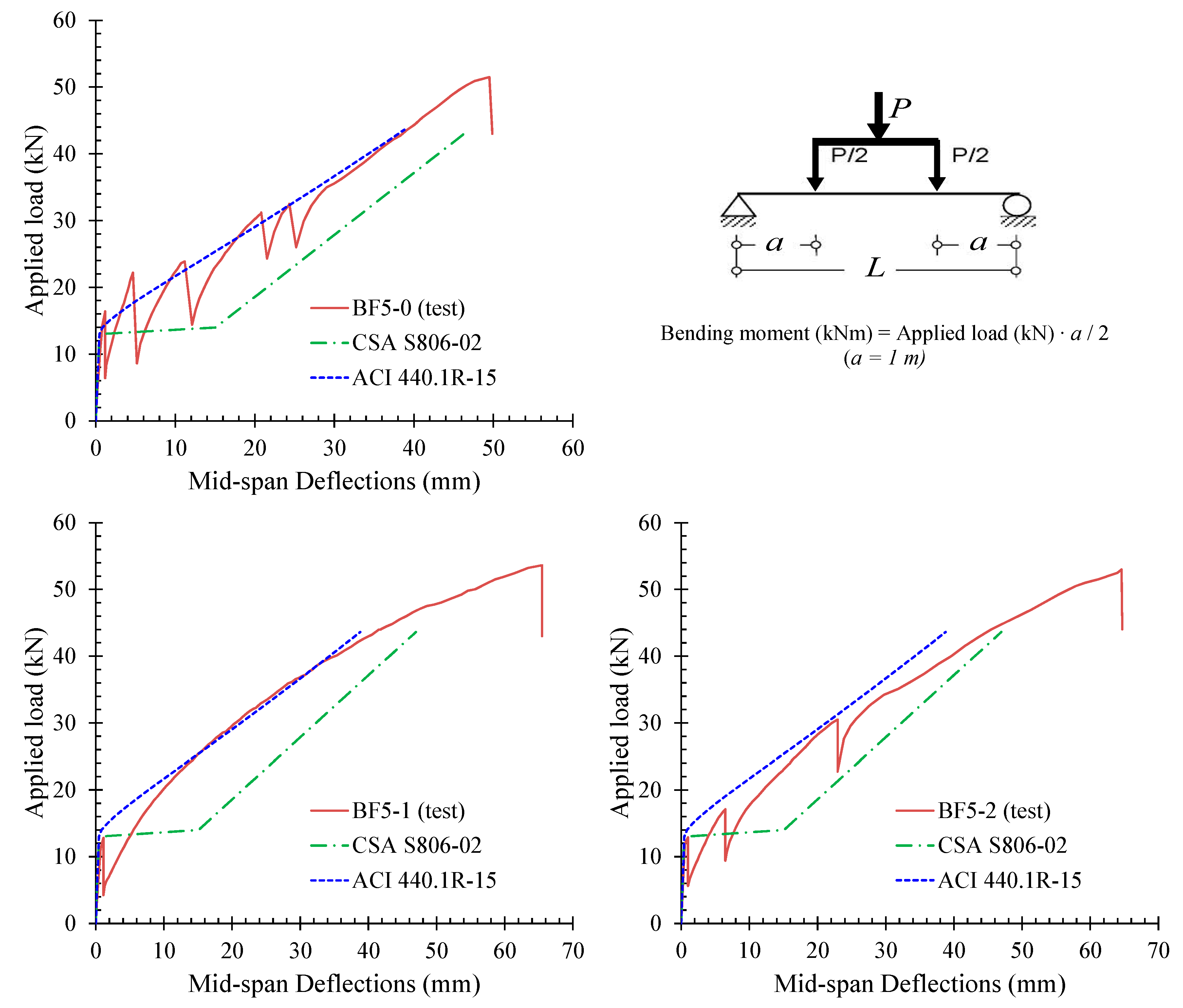
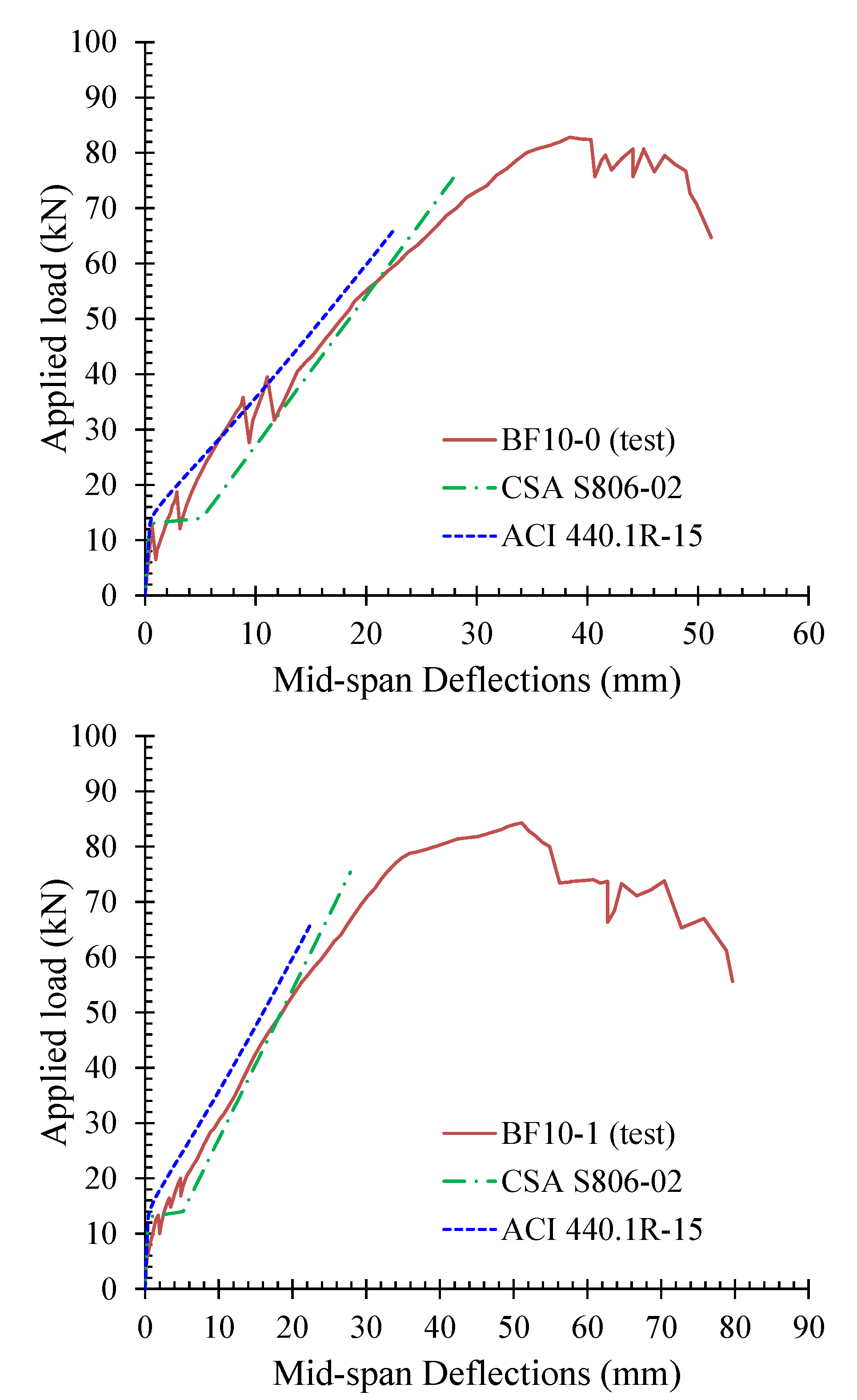
3. Deflections
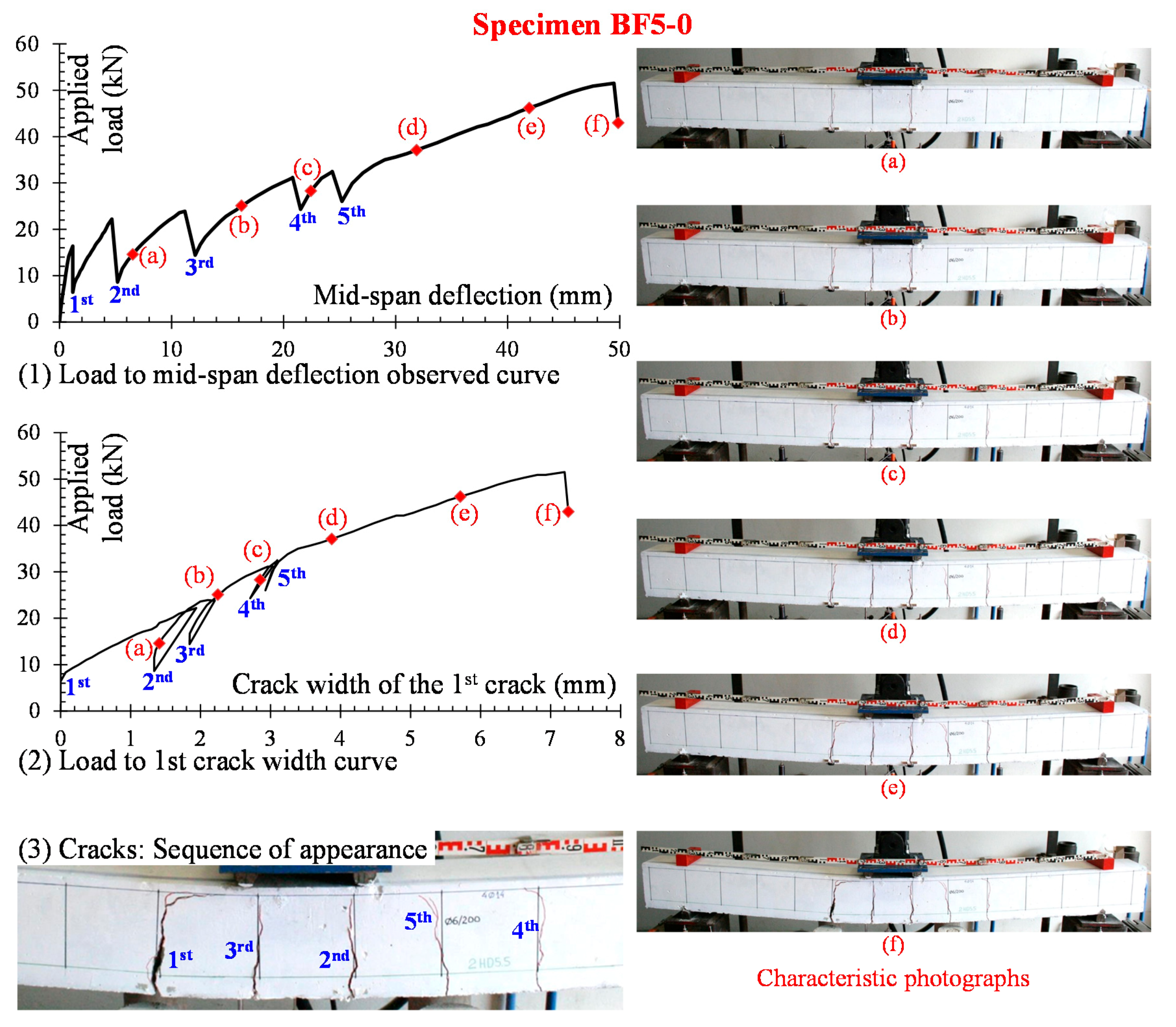
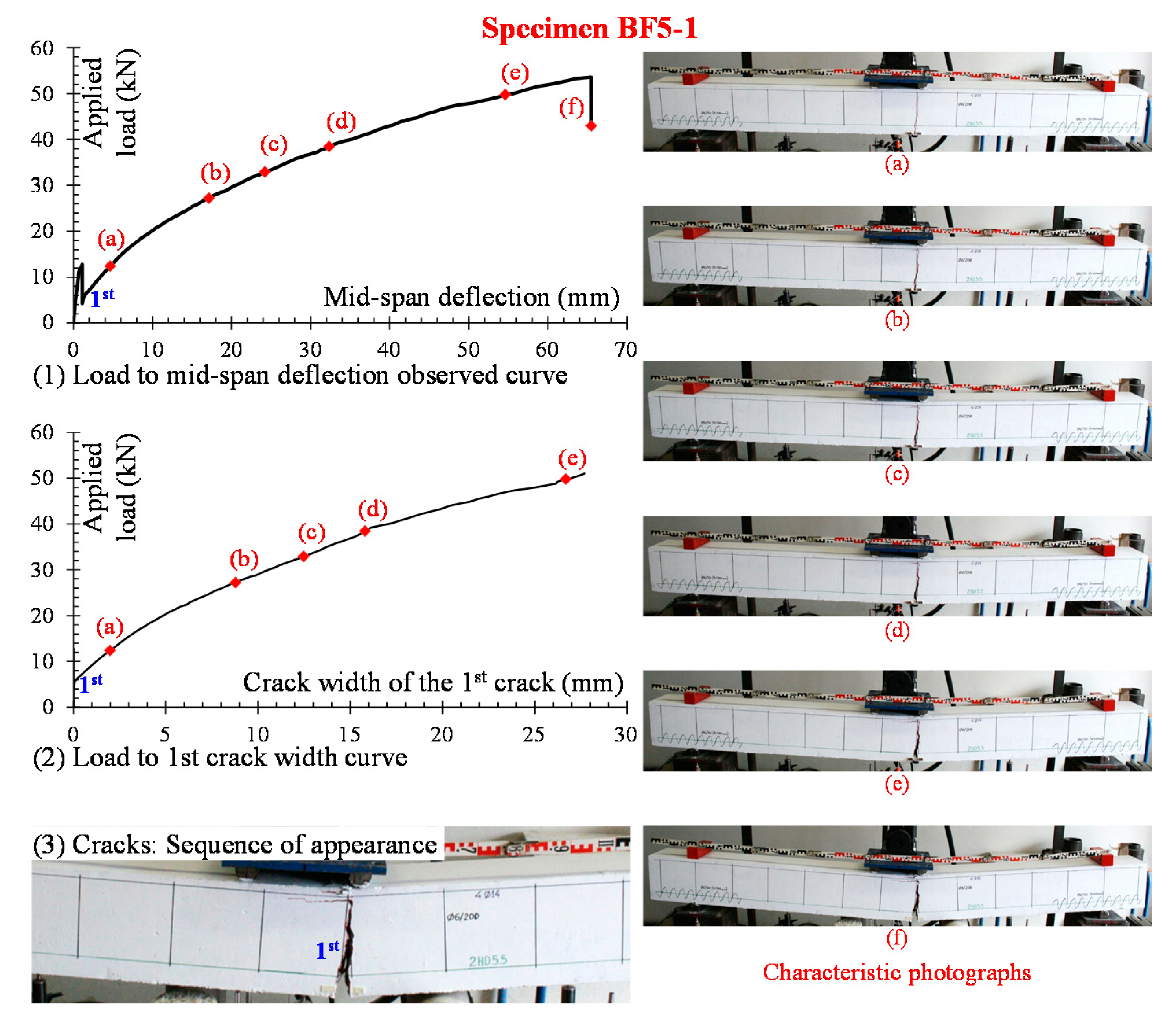
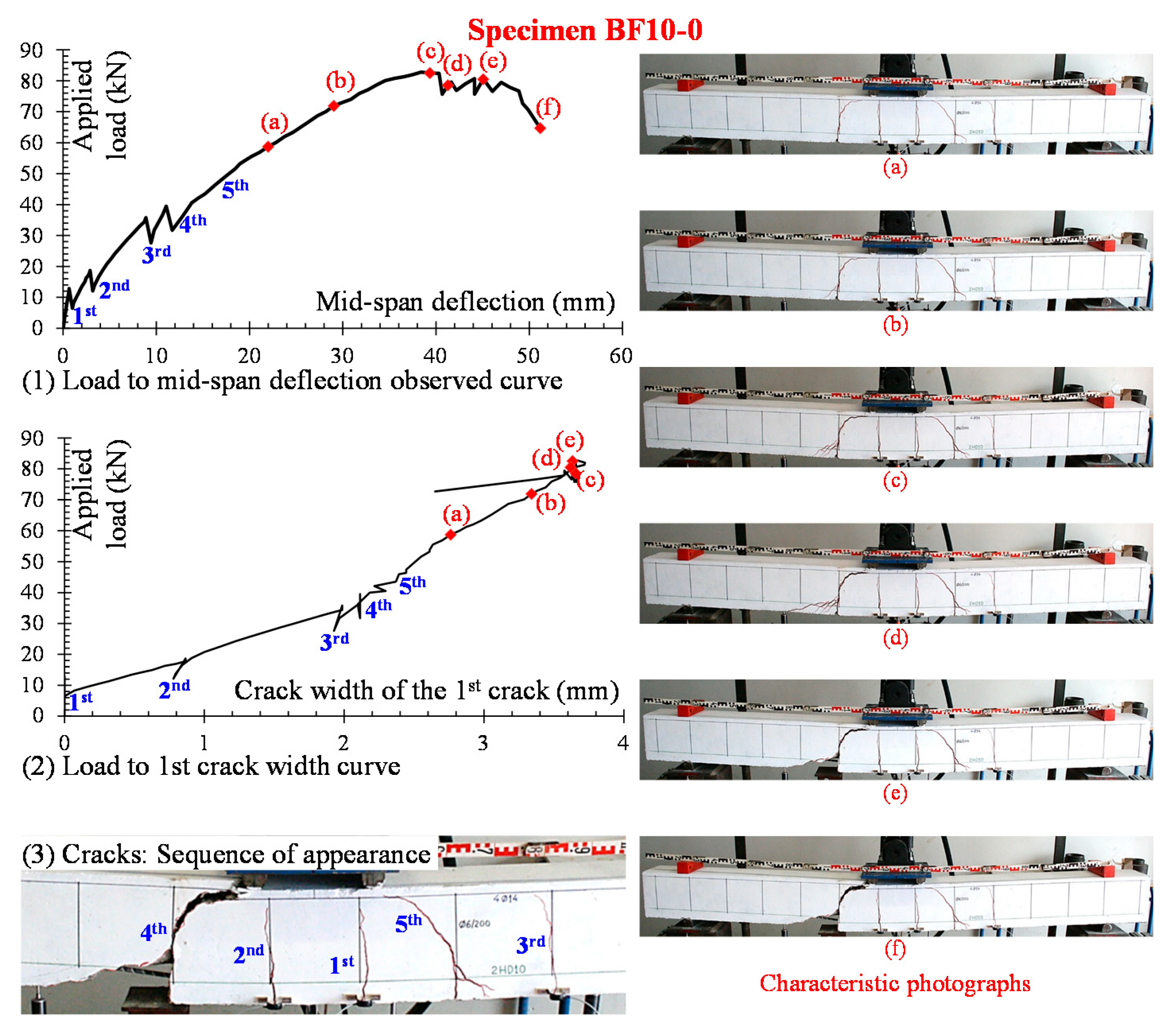
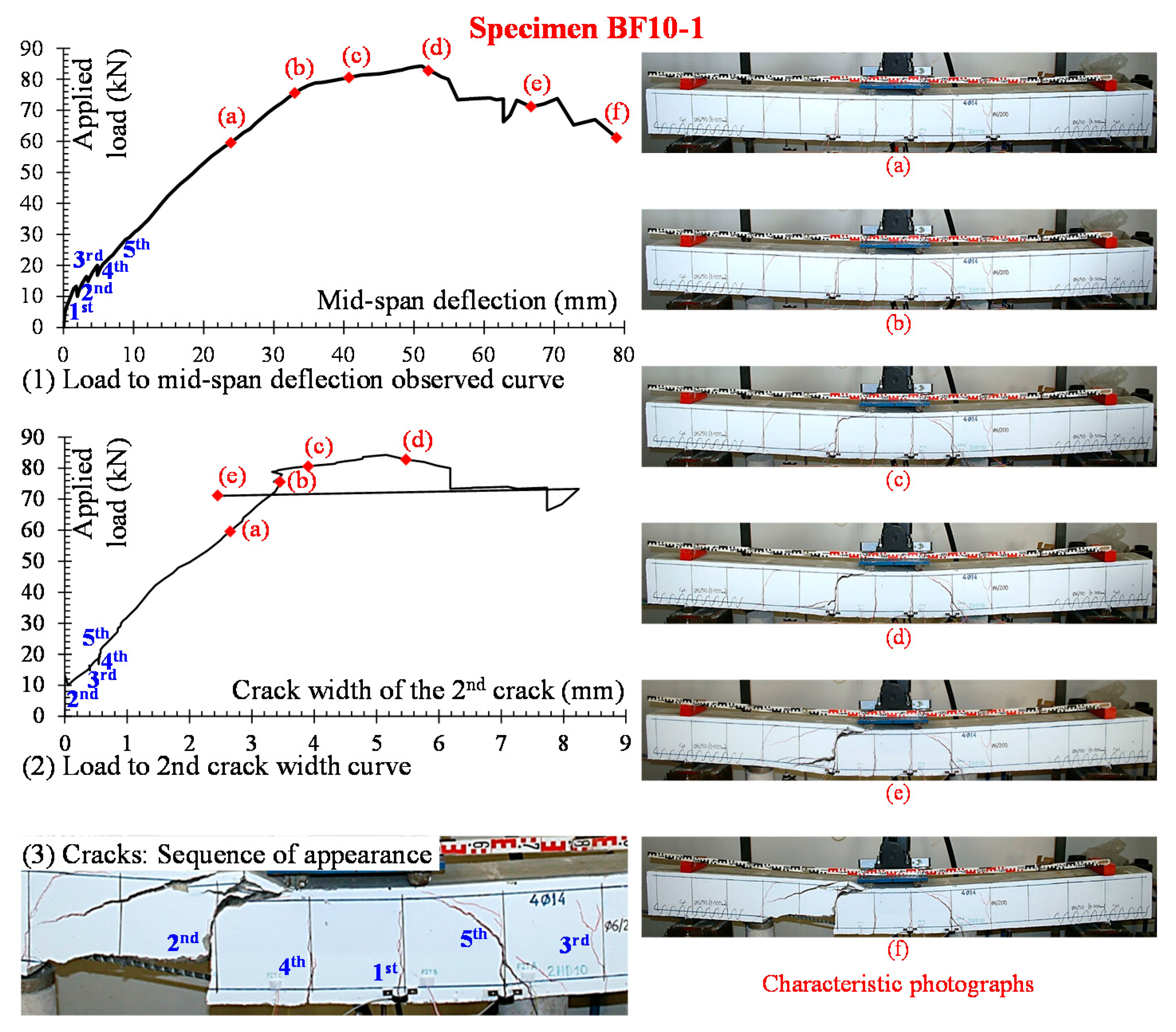
3.1. Deflection Curves
3.2. Loading Drops
4. Crack Shapes and Failure Modes
4.1. “BF5” Series
4.1.1. Beam BF5-0
4.1.2. Beam BF5-1
4.1.3. Beam BF5-2
4.2. “BF10” Series
4.2.1. Beam BF10-0
4.2.2. Beam BF10-1
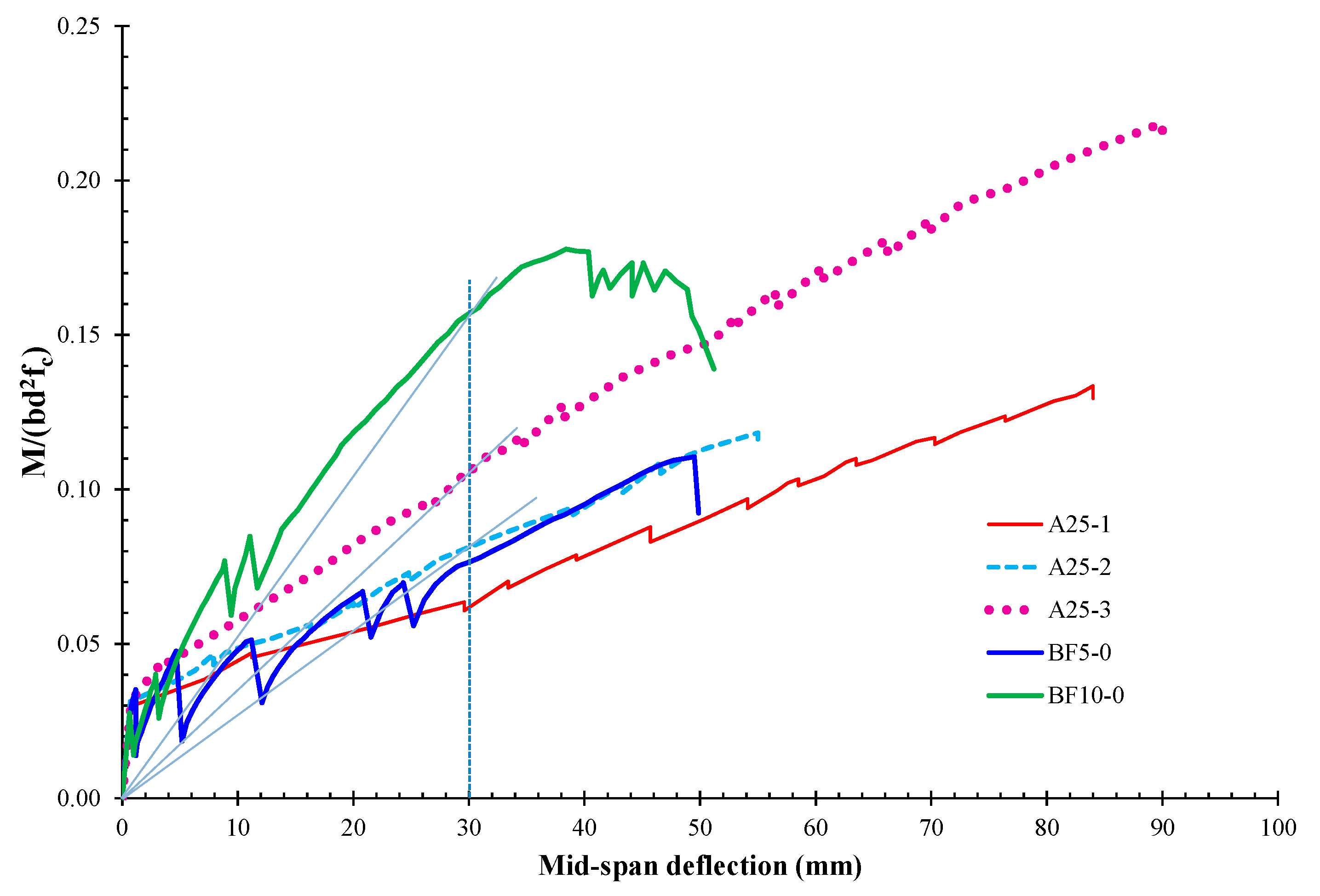
5. Comparisons of Deflections with G-FRP Reinforced Beams
- 40% higher flexural chord stiffness than the one of the beam A25-3 [40] although the mechanical reinforcement ratio ωf = ρfffu/fc in both beams are equal (ωf = 0.24) and
- 78% higher flexural chord stiffness than the one of the beam A25-2 [40] although the cross section areas of the FRP bars in both beams are almost alike (approximately 160 mm2)
6. Calculations of Strength and Deflections—Modern Codes
6.1. Flexural Strength
6.2. Shear Strength
6.3. Deflections and Comparisons with Test Results
- -
- Pre-cracking deflection
- -
- Post-cracking deflection
7. Concluding Remarks
- The observed load versus midspan deflection curves include first a small pre-cracking part that exhibits high flexural stiffness while the main part of these curves is the post-cracking response that exhibits substantially lower stiffness than the one of the uncracked first part.
- A general observation from the deflection curves is that each time a crack appears in the concrete beams reinforced with C-FRP bars a sudden load drop is simultaneously occurred. It can be attributed to the fact that a local decrease of the stiffness undergo at the cracked section of the beam due to formation of long flexural cracks in combination with the low normalized reinforcement ratio of the C-FRP bars.
- Increasing of the C-FRP reinforcement ratio can possibly change the nature of the failure from pure flexural (series “BF5”) to a response with final failure in shear (series “BF10”).
- The application of the local spiral confinement conditions along the anchorage lengths of the C-FRP bars in some specimens (beams BF5-1, BF5-2, and BF10-1) seems to influence the development of the cracking system of these specimens. This influence appeared to be more intense in the case of the specimen BF5-1. The deflection at peak load of these beams seems also to be increased with regards to the corresponding beams without spirals. Nevertheless, more research is required in this direction.
- Comparisons of experimental results for C-FRP beams with beams reinforced with G-FRP bars extracted from recent literature have been presented and beams with C-FRP exhibited higher flexural stiffness than the beams with G-FRP bars.
- Comparisons of the experimental results with the predictions according to ACI 440.1R-15 and to CSA S806-12 have been also presented. The codes provisions successfully predicted the failure mode and seemed to be rather conservative.
Author Contributions
Funding
Conflicts of Interest
References
- Karayannis, C.G.; Sirkelis, G.M. Strengthening and rehabilitation of RC beam—Column joints using carbon—FRP jacketing and epoxy resin injection. Earthq. Eng. Struct. Dyn. 2008, 37, 769–790. [Google Scholar] [CrossRef]
- Tsonos, A.G. Ultra-high-performance fiber reinforced concrete: An innovative solution for strengthening old R/C structures and for improving the FRP strengthening method. WIT Trans. Eng. Sci. 2009, 64, 273–284. [Google Scholar]
- Tsonos, A.G. Effectiveness of CFRP jackets in post-earthquake and pre-earthquake retrofitting of beam-column subassemblages. Struct. Eng. Mech. 2007, 27, 393–408. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Tourtouras, I.S. RC columns of square section—Passive and active confinement with composite ropes. Compos. Part B Eng. 2014, 58, 573–581. [Google Scholar] [CrossRef]
- Kakaletsis, D. Comparison of CFRP and alternative seismic retrofitting techniques for bare and infilled RC frames. J. Compos. Constr. 2011, 15, 565–577. [Google Scholar] [CrossRef]
- Spyrakos, C.C.; Maniatakis, C.A.; Psycharis, I.N.; Smyarou, E.; Asteris, P.G. Validation of analytical models for the assessment of brick-infilled RC frames strengthened with FRPs. In Proceedings of the ECCOMAS Thematic Conference-COMPDYN, Kos Island, Greece, 12–14 June 2013; pp. 2978–2996. [Google Scholar]
- Chalioris, C.E. Analytical model for the torsional behaviour of reinforced concrete beams retrofitted with FRP materials. Eng. Struct. 2007, 29, 3263–3276. [Google Scholar] [CrossRef]
- Gopinath, S.; Murthy, A.R.; Patrawala, H. Near surface mounted strengthening of RC beams using basalt fiber reinforced polymer bars. Constr. Build. Mater. 2016, 111, 1–8. [Google Scholar] [CrossRef]
- Jabr, A.; El-Ragaby, A.; Ghrib, F. Effect of the fiber type and axial stiffness of FRCM on the flexural strengthening of RC beams. Fibers 2017, 5, 2. [Google Scholar] [CrossRef]
- Gribniak, V.; Tamulenas, V.; Ng, P.-L.; Arnautov, A.K.; Gudonis, E.; Misiunaite, I. Mechanical behavior of steel fiber-reinforced concrete beams bonded with external carbon fiber sheets. Materials 2017, 10, 666. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Kosmidou, P.-M.K.; Papadopoulos, N.A. Investigation of a new strengthening technique for RC deep beams using carbon FRP ropes as transverse reinforcements. Fibers 2018, 6, 52. [Google Scholar] [CrossRef]
- Abdel-Mohti, A.; Shen, H. Strengthening of corroded reinforced SCC-RAP members with CFRP. Fibers 2016, 4, 3. [Google Scholar] [CrossRef]
- Napoli, A.; Matta, F.; Martinelli, E.; Nanni, A.; Realfonzo, R. Modelling and verification of response of RC slabs strengthened in flexure with mechanically fastened FRP laminates. Mag. Concr. Res. 2010, 62, 593–605. [Google Scholar] [CrossRef]
- Bellakehal, H.; Zaidi, A.; Masmoudi, R.; Bouhicha, M. Behavior of FRP bars-reinforced concrete slabs under temperature and sustained load effects. Polymers 2014, 6, 873–889. [Google Scholar] [CrossRef]
- Seyhan, E.C.; Goksu, C.; Uzunhasanoglu, A.; Ilki, A. Seismic behavior of substandard RC columns retrofitted with embedded Aramid Fiber Reinforced Polymer (AFRP) reinforcement. Polymers 2015, 7, 2535–2557. [Google Scholar] [CrossRef]
- Gouda, A.; El-Salakawy, E. Finite Element modeling of GFRP-reinforced concrete interior slab-column connections subjected to moment transfer. Fibers 2015, 3, 411–431. [Google Scholar] [CrossRef]
- Gouda, A.; El-Salakawy, E. Punching Shear Strength of GFRP-RC Interior Slab-Column Connections Subjected to Moment Transfer. J. Compos. Constr. 2016, 20, 04015037. [Google Scholar] [CrossRef]
- Gribniak, V.; Kaklauskas, G.; Torres, L.; Daniunas, A.; Timinskas, E.; Gudonis, E. Comparative analysis of deformations and tension-stiffening in concrete beams reinforced with GFRP or steel bars and fibers. Compos. Part B Eng. 2013, 50, 158–170. [Google Scholar] [CrossRef]
- Ju, M.; Park, L.; Park, C. Punching shear behavior of two-way concrete slabs reinforced with Glass-Fiber-Reinforced Polymer (GFRP) bars. Polymers 2018, 10, 893. [Google Scholar] [CrossRef]
- Toutanji, A.H.; Saafi, M. Flexural behavior of concrete beams reinforced with glass fiber-reinforced polymer (GFRP) bars. ACI Struct. J. 2000, 97, 712–719. [Google Scholar]
- Ovitigala, T.; Ibrahim, M.A.; Issa, M.A. Serviceability and ultimate load behavior of concrete beams reinforced with basalt fiber-reinforced polymer bars. ACI Struct. J. 2016, 113, 757–768. [Google Scholar] [CrossRef]
- ACI 440 Committee. Guide for the Design and Construction of Concrete Reinforced with FRP Bars (ACI440.1R-15); American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Zadeh, H.J.; Nanni, A. Reliability analysis of concrete beams internally reinforced with fiber-reinforced polymer bars. ACI Struct. J. 2013, 110, 1023–1031. [Google Scholar]
- Tureyen, A.K.; Frosch, R.J. Concrete shear strength: Another perspective. ACI Struct. J. 2003, 100, 609–615. [Google Scholar]
- Gopinath, S.; Meenu, S.; Murthy, A.R. Shear strength evaluation of concrete beams reinforced with BFRP bars and steel fibers without stirrups. Comput. Mater. Cont. 2016, 51, 81–103. [Google Scholar]
- El-Sayed, A.K.; Soudki, K. Evaluation of shear design equations of concrete beams with FRP reinforcement. J. Compos. Constr. 2011, 15, 9–20. [Google Scholar] [CrossRef]
- Marí, A.; Cladera, A.; Oller, E.; Bairán, J. Shear design of FRP reinforced concrete beams without transverse reinforcement. Compos. Part B Eng. 2014, 57, 228–241. [Google Scholar] [CrossRef]
- Herwig, A.; Motavalli, M. Load-carrying capacity of GFRP bars under combined axial force–transverse force loading. Compos. Part B Eng. 2013, 44, 167–171. [Google Scholar] [CrossRef]
- Achillides, Z.; Pilakoutas, K. Bond behaviour of fiber reinforced polymer bars under direct pullout conditions. J. Compos. Constr. 2004, 8, 173–181. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y.X. Bond–slip behaviour of FRP-reinforced concrete beams. Constr. Build. Mater. 2013, 44, 110–117. [Google Scholar] [CrossRef]
- Akbas, T.; Celik, O.; Yalcin, C.; Ilki, A. Monotonic and cyclic bond behavior of deformed CFRP bars in high strength concrete. Polymers 2016, 8, 211. [Google Scholar] [CrossRef]
- Lau, D.; Pam, H.J. Experimental study of hybrid FRP reinforced concrete beams. Eng. Struct. 2010, 32, 3857–3865. [Google Scholar] [CrossRef]
- Qin, R.; Zhou, A.; Lau, D. Effect of reinforcement ratio on the flexural performance of hybrid FRP reinforced concrete beams. Compos. Part B Eng. 2017, 108, 200–209. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A.; Ombres, L. Numerical and analytical modeling of concrete beams with steel, FRP and hybrid FRP-steel reinforcements. Compos. Struct. 2016, 140, 53–65. [Google Scholar] [CrossRef]
- Ascione, L.; Mancusi, G.; Spadea, S. Flexural behaviour of concrete beams reinforced with GFRP bars. Strain 2010, 46, 460–469. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.; Karayannis, C. Flexural behaviour of concrete beams reinforced with FRP bars. Adv. Compos. Lett. 1998, 7, 133–137. [Google Scholar]
- Vijay, P.; GangaRao, H.V. Bending behaviour and deformability of glass fiber-reinforced polymer reinforced concrete members. ACI Struct. J. 2001, 98, 834–842. [Google Scholar]
- Mota, C.; Alminar, S.; Svecova, D. Critical review of deflection formulas for FRP-RC members. J. Compos. Constr. 2006, 10, 183–194. [Google Scholar] [CrossRef]
- Issa, M.; Metwally, I.; Elzeiny, S. Influence of fibers on flexural behaviour and ductility of concrete beams reinforced with GFRP fibers. Eng. Struct. 2011, 33, 1754–1763. [Google Scholar] [CrossRef]
- Adam, M.; Said, M.; Mahmoud, A.; Shanour, A. Analytical and experimental flexural behaviour of concrete beams reinforced with glass fiber reinforced polymers bars. Constr. Build. Mater. 2015, 84, 354–366. [Google Scholar] [CrossRef]
- Maranan, G.B.; Manalo, A.C.; Benmokrane, B.; Karunasena, W.; Mendis, P.; Nguyen, T.Q. Shear behaviour of geopolymer-concrete beams transversely reinforced with continuous rectangular GFRP composite spirals. Compos. Struct. 2018, 187, 454–465. [Google Scholar] [CrossRef]
- Goldston, M.W.; Remennikov, A.; Sheikh, M.N. Experimental investigation of the behaviour of concrete beams reinforced with GFRP bars under static and impact loading. Eng. Struct. 2016, 113, 220–232. [Google Scholar] [CrossRef]
- Goldston, M.W.; Remennikov, A.; Sheikh, M.N. Flexural behaviour of GFRP reinforced high strength and ultra high strength concrete beams. Constr. Build. Mater. 2017, 131, 606–617. [Google Scholar] [CrossRef]
- CSA Standard. Design and Construction of Building Structures with Fibre-Reinforced Polymers (CSA S806–S12); Canadian Standards Association: Mississauga, ON, Canada, 2012. [Google Scholar]
- Tsonos, A.G. An innovative solution for strengthening of old R/C structures and for improving the FRP strengthening method. Struct. Monit. Maint. 2014, 1, 323–338. [Google Scholar] [CrossRef]
- Bischoff, P.H.; Gross, S.P. Equivalent moment of inertia based on integration of curvature. J. Compos. Constr. 2011, 15, 263–273. [Google Scholar] [CrossRef]
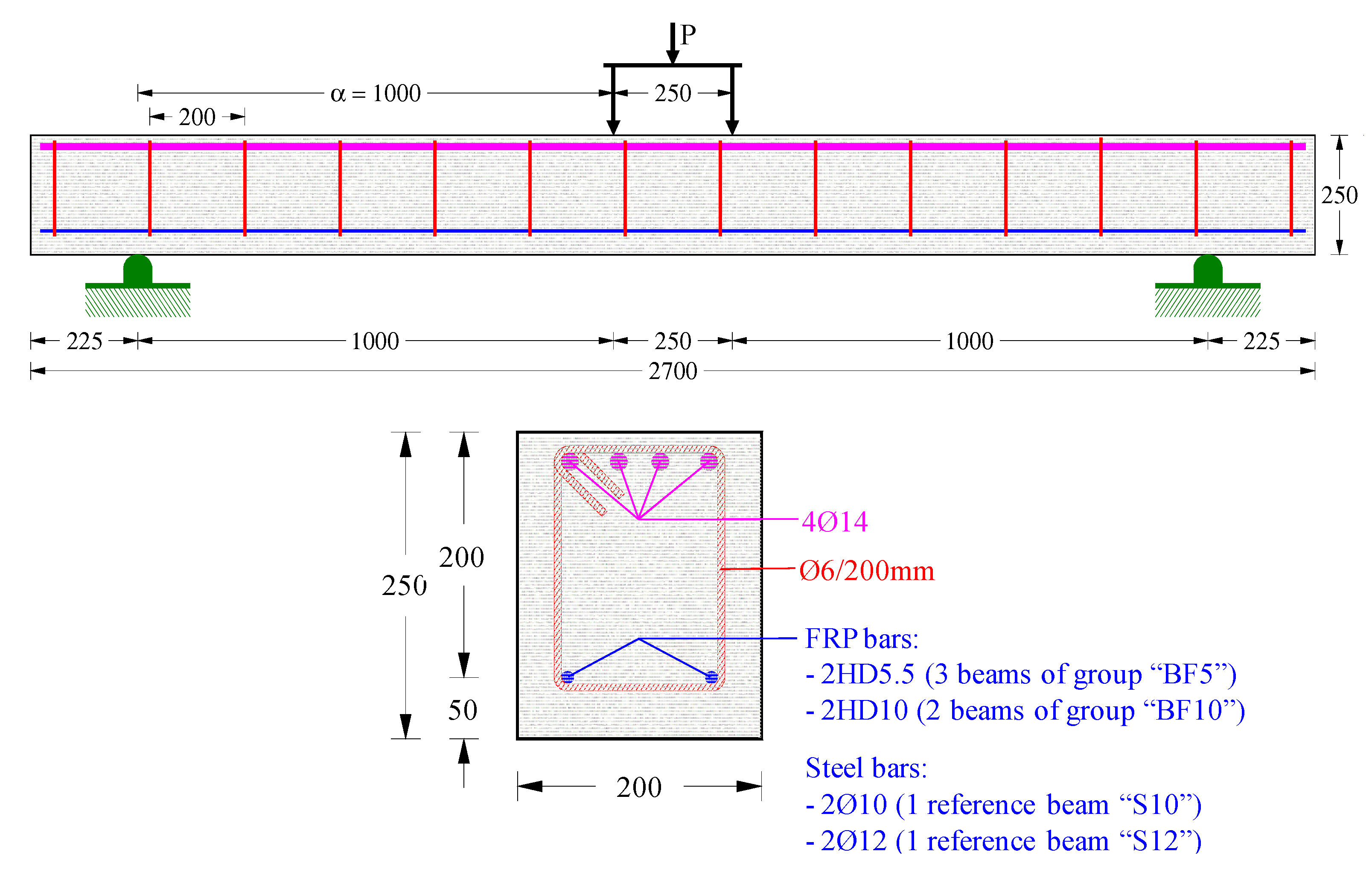
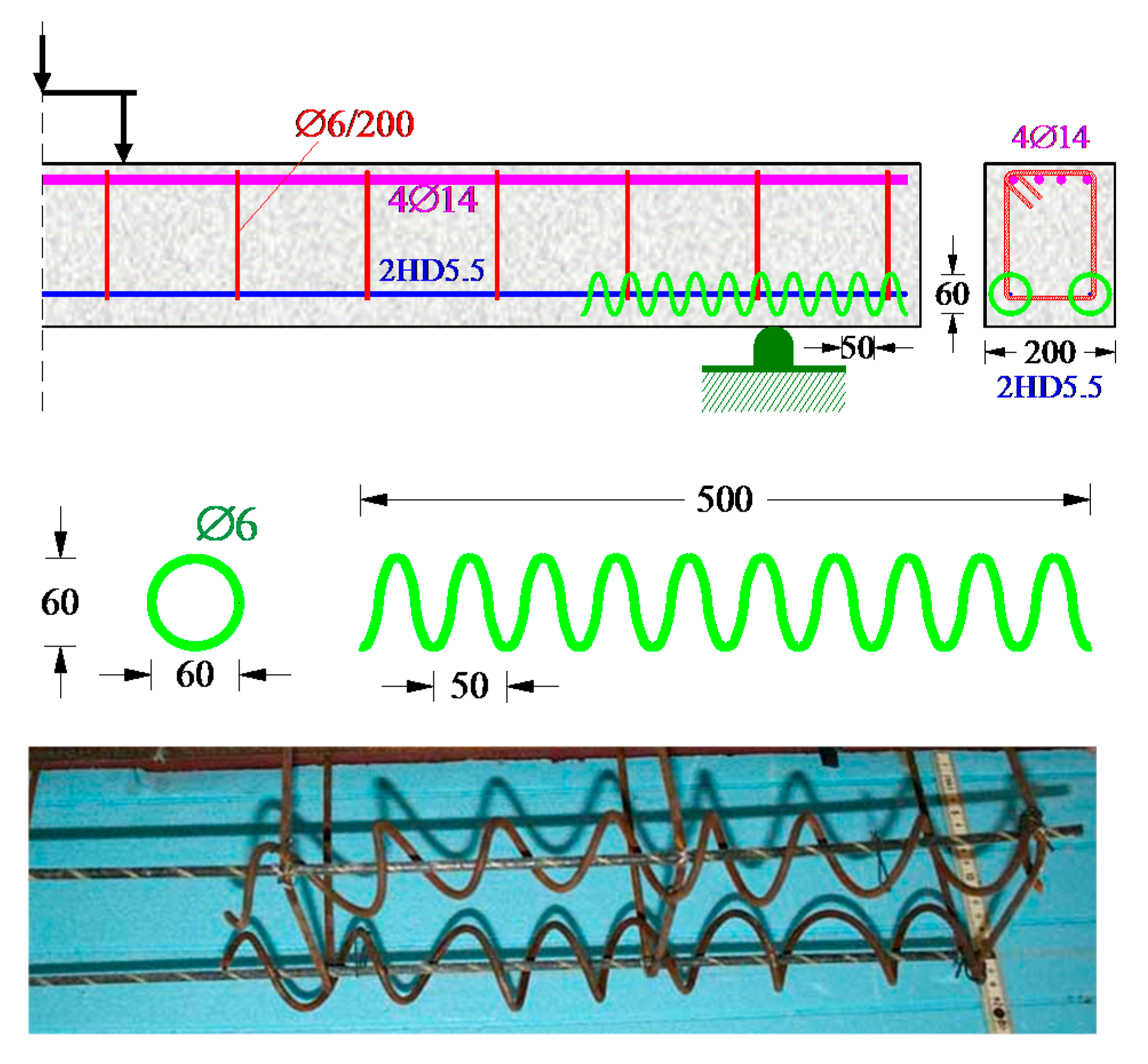


| Group | Beam Name | Type and Diameter | Tensional Bars | Experimental Results | |||||
|---|---|---|---|---|---|---|---|---|---|
| ρ 1 (%) | ρf 2 (MPa) | ω 3 | Pexp (kN) | Vexp = Mexp (kN) or (kNm) | δpeak (mm) | Observed Failure 4 | |||
| “S” | S10 | 2∅10 | 0.39 | 2.16 | 0.07 | 30.6 * 35.0 | 15.3 * 17.5 | 6.0 * 62.8 | Y |
| S12 | 2∅12 | 0.57 | 3.11 | 0.11 | 45.2 * 53.6 | 22.6 * 26.8 | 11.1 * 63.8 | Y | |
| “BF5” | BF5-0 | 2HD5.5 | 0.12 | 2.14 | 0.07 | 51.6 | 25.8 | 49.5 | F-R |
| BF5-1 | 2HD5.5 | 0.12 | 2.14 | 0.07 | 53.6 | 26.8 | 65.5 | F-R | |
| BF5-2 | 2HD5.5 | 0.12 | 2.14 | 0.07 | 52.4 | 26.2 | 64.6 | F-R | |
| “BF10” | BF10-0 | 2HD10 | 0.39 | 7.07 | 0.24 | 82.8 | 41.4 | 38.4 | S-T |
| BF10-1 | 2HD10 | 0.39 | 7.07 | 0.24 | 84.4 | 42.2 | 51.1 | S-T | |
| Group | Beam Name | Flexural Strength | Shear Strength | Predicted Failure 1,2 | Comparisons with Tests 2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mn,ACI (kNm) | Mn,CSA (kNm) | Vn,ACI (kN) | Vn,CSA (kN) | Pn,ACI (kN) | Pn,CSA (kN) | |||||
| “BF5” | BF5-0 | 21.8 | N/A | 26.5 | 31.0 | F-R | 43.6 | 0.84 | N/A | N/A |
| BF5-1 | 21.8 | N/A | 26.5 | 31.0 | F-R | 43.6 | 0.81 | N/A | N/A | |
| BF5-2 | 21.8 | N/A | 26.5 | 31.0 | F-R | 43.6 | 0.83 | N/A | N/A | |
| “BF10” | BF10-0 | 58.9 | 65.8 | 33.1 | 37.7 | S-T | 66.2 | 0.80 | 75.4 | 0.91 |
| BF10-1 | 58.9 | 65.8 | 33.1 | 37.7 | S-T | 66.2 | 0.78 | 75.4 | 0.89 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
G. Karayannis, C.; K. Kosmidou, P.-M.; E. Chalioris, C. Reinforced Concrete Beams with Carbon-Fiber-Reinforced Polymer Bars—Experimental Study. Fibers 2018, 6, 99. https://doi.org/10.3390/fib6040099
G. Karayannis C, K. Kosmidou P-M, E. Chalioris C. Reinforced Concrete Beams with Carbon-Fiber-Reinforced Polymer Bars—Experimental Study. Fibers. 2018; 6(4):99. https://doi.org/10.3390/fib6040099
Chicago/Turabian StyleG. Karayannis, Chris, Parthena-Maria K. Kosmidou, and Constantin E. Chalioris. 2018. "Reinforced Concrete Beams with Carbon-Fiber-Reinforced Polymer Bars—Experimental Study" Fibers 6, no. 4: 99. https://doi.org/10.3390/fib6040099
APA StyleG. Karayannis, C., K. Kosmidou, P.-M., & E. Chalioris, C. (2018). Reinforced Concrete Beams with Carbon-Fiber-Reinforced Polymer Bars—Experimental Study. Fibers, 6(4), 99. https://doi.org/10.3390/fib6040099







