1. Introduction
A new form of silica hollow-core fiber consisting of a single ring of touching or non-touching antiresonant elements (ARE) surrounding a central hollow-core has emerged in recent years. This antiresonant fiber (ARF) has been investigated as a result of the discovery of the importance of core wall shape in the attenuation reduction in Kagome-structured hollow-core fiber in 2010 [
1]. Accordingly, it was possible to reduce the Kagome cladding to just one single glass layer of ARE without significantly increasing fiber attenuation [
2]. Thereafter, different hollow core fibers comprising a single ring of touching capillaries in the cladding void have been proposed and studied. It was proven that ARFs, with an inverted optical core boundary, possess large transmission bandwidth and low attenuations in the mid-infrared spectral region due to both low leakage losses and weak coupling of air-core modes with the cladding structure [
3,
4,
5]. This type of design was extended to shorter wavelength transmission in the near-infrared and visible spectrum [
6,
7]. A modified form of the basic design with contactless capillaries has also been proposed and fabricated in order to remove the additional optical resonances in the transmission bands related to nodes between cladding elements [
8]. In this way, the loss level can be further decreased in the mid-infrared wavelength range [
8,
9]. Recently, greatly reduced transmission loss at 750 nm in similar fiber was reported by Debord et al. [
10]. By adding one or more nested capillaries within the node-less cladding structure, numerical simulations predicted leakage losses reduction by roughly two orders of magnitude in the middle and near infrared spectral regions [
11,
12]. Up to now, the fabrication of at least two fibers with nested antiresonant node-less elements (NANFs) has been reported for low loss operation. The fibers have been manufactured both with different [
13] and closely identical [
14] wall thicknesses between the inner and outer cladding capillaries. The wall thickness of the large capillaries was greater than a micrometer. According to performances of theses fabricated fibers, the positive effect of the nested capillaries on the loss is limited by their small hole diameter and the distinction between the wall thicknesses of the large and small capillaries. However, a minimum optical loss of 74 dB/km at 1.8
m was obtained in a NANF with a 25
m core diameter and a 2.3
m average wall thickness of all the capillaries [
14]. The leakage loss in the ARFs, as in the NANFs, is inversely proportional to the fourth power of core diameter [
15], so lower losses are much easier to achieve at larger core diameters. For large core diameters (>25
m), the ARFs and NANFs are however multimoded [
11] and therefore not ideal for applications where a high modal purity is desirable, for example in high-power pulse delivery or in gas cells. To suppress HOMs while preserving low confinement loss for the fundamental core mode, a technique has already been proposed for different designs of ARFs with touching and non-touching capillaries [
16,
17,
18]. It exploits resonant coupling between the higher-order core modes and the air-capillary modes. The approach is analogous to using defect modes in HC-PCFs [
19,
20]; however, there is no need to create defects in this case, since the capillaries that create cladding structure can also provide the resonant coupling. Specifically Uebel et al. [
17] showed the importance of the dimensionless parameter
, with the inner capillary diameter
d and the inner core diameter
D, in order to achieve optimal suppression of HOMs over all wavelength bands where the ARF guides with low loss. For 6- and 7-capillary designs [
17,
18], an avoided crossing between TM
, TE
, and HE
core modes and fundamental air-capillary mode is observed at
which leads to high leakage losses of those HOMs and hence, provides robust single-mode guidance at all wavelengths within the main transmission window, independent of the absolute core size of the structure. This condition on the capillary-to-core diameter can also be verified for any ARF structures composed of a smaller number of capillaries. However, a number of capillaries less than six would lead to a pronounced gap between capillaries that can affect the fundamental mode loss.
The purpose of this work is to study the impact that the nested elements can have on the avoided crossing between the higher-order core modes and the air-capillary modes, in order to verify that the condition of HOM suppression established for the ARFs could be applied or not to NANFs. We show computationally that it is also possible to suppress the HOMs in NANFs; however, the optimal value, for which the leakage losses of HOMs are maximum, is strongly dependent on the geometric dimension of nested capillaries. The numerical results are also interpreted and verified by extending an already proposed analytical model based on coupled capillaries.
2. Design and Numerical Analysis
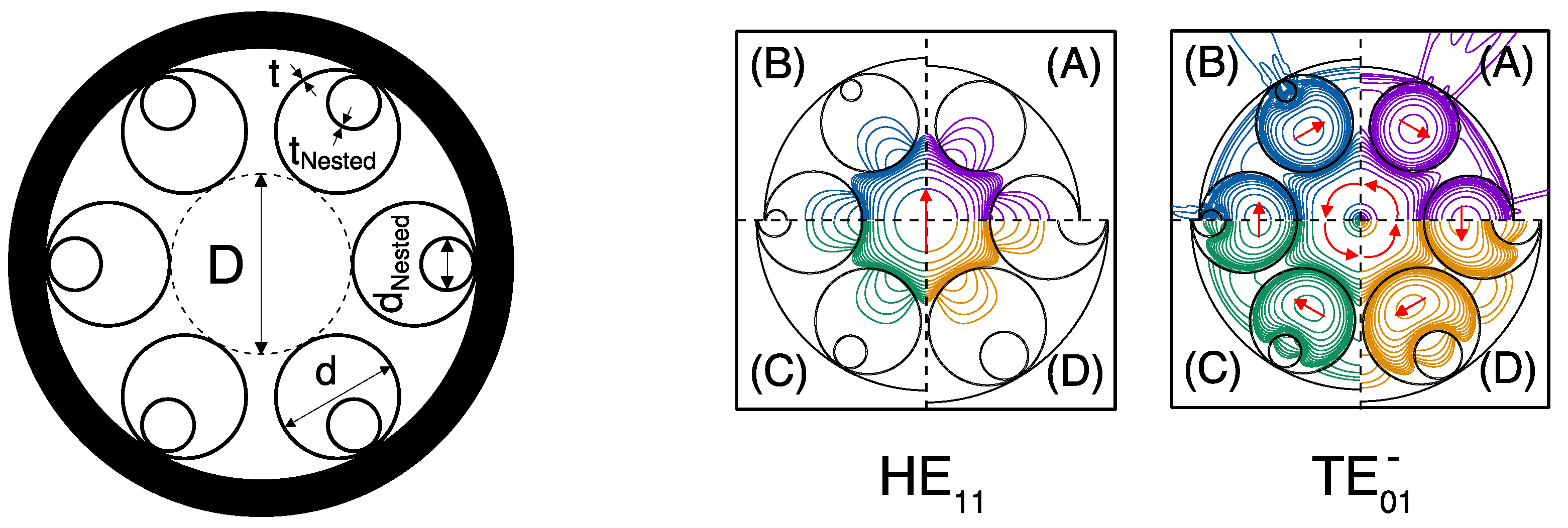
In order to analyze the influence of nested elements on the modal properties of ARFs, we propose in this work to maintain the six node-less capillary lattice structure described in [
17] and add nested capillaries of inner diameter
with the same wall thickness
as the outer ones and attached to the cladding at the same azimuthal position, as shown in the left panel of
Figure 1. Considering the fact that both the transmission band positions [
11,
12,
16,
17] and the leakage losses [
13] are dependent on the wall thickness of the capillaries, the choice of setting
allows for avoiding additional effects on the present study.
All numerical simulations reported here are based on a commercial full-vector finite-element based modal solver (Comsol Multiphysics). A circular Perfectly Matched Layer (PML) surrounding the simulated area is used to calculate the mode leakage losses. Only a quarter of the geometry is used in modeling fibers because of the symmetry of the modes [
21]. As in [
17], we adopted a core diameter
30
m, a silica wall thickness
0.30
m and a wavelength
1.50
m, in such a way that the ratios
and
are equal to 0.01 and 20, respectively. The glass refractive index was set a constant value of 1.45 and the hollow regions were taken to be vacuum. The material loss is neglected since the material absorption is quite low at this wavelength [
22].
In order to model NANF accurately, great care was taken to optimize both mesh and PML parameters. Typically, a maximum element size of
was used in the air regions while a rather dense mesh with a maximum element size of
in the thin glass regions was found to be essential to obtain reliable results. To ensure convergence of the numerical results, we first checked our model by reproducing the results of the [
17] (
= 0), and afterward the modal properties for the first guided modes were simulated for
ratio respectively equal to 0.20, 0.30 and 0.40.
Figure 2a shows the effective index for the fundamental HE
core mode, the TE
core mode, and the ARE
air-capillary mode as a function of the radio
. The TE
mode is the higher-order core mode that has the lowest loss, and also the lowest effective index difference with the fundamental HE
mode. Note that, according to the polarization profile of the guided modes, the core modes are indicated using the designation of vector modes HE
, EH
, TE
and TM
with
n and
m integers and the air-capillary mode of the node-less cladding structure is labeled ARE
with
l and
m integers, based on the notation of the linearly polarized modes.
Figure 2b shows the corresponding confinement loss of the core modes.
For
= 0, we find again in
Figure 2a the discontinuity of the TE
core mode effective index for 0.62
0.75 as in [
17], typical of an avoided crossing between the core localized mode (herein the TE
mode) and a cladding leaky mode (herein the ARE
mode) [
23]. In this region of
values, the TE
core mode splits into two hybrid modes labelled TE
and TE
, which evolve asymptotically in toward uncoupled ARE
and TE
modes. Indeed for largest values of effective index, the TE
core mode gradually changes its nature to become an ARE
air-capillary mode and conversely for smaller values of effective index, the ARE
air-capillary mode progressively converges toward a TE
core mode. For non-zero values of the ratio
, the evolution of the TE
core mode effective index as a function of
is similar. However, we observe an increasing shift in the position of the discontinuity in relation to
when the ratio
rises. As with the
parameter, these numerical results show the importance of the nested capillaries’s diameter on avoided crossing between the TE
core mode and the ARE
air-capillary mode, and the scalability of this phenomenon through the dimensionless parameter
. On the other hand, the effective index of the HE
core mode remains independent of
, regardless of the
value.
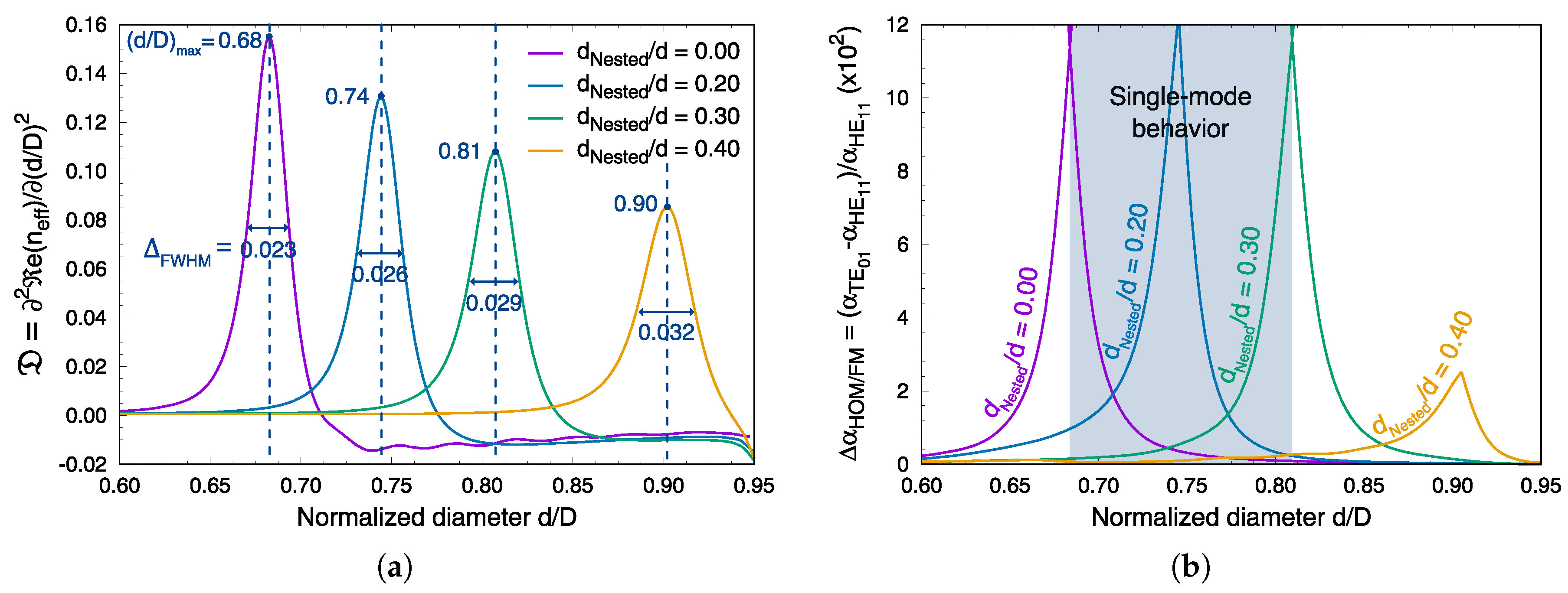
To quantify the avoided crossing properties, we introduce the quantity
. By analogy with chromatic dispersion, we can associate this quantity with the effective index dispersion of a mode in relation to
. In
Figure 3a, we plotted the obtained curves for the four values of the parameter
. For each transition region, we observe that the effective index dispersion curve exhibits a concave profile and large positive coefficient around a specific
value corresponding at the phase-matching to resonance point
. These values are summarized in
Table 1. The numerical result presented for
is in good agreement with that of the [
17], and thus ensures the validity of the optimal values for the ratio
for which an avoided crossing between the TE
core mode and the
air-capillary mode exists. Similarly to what was already described in [
24], the strength of the interaction between the core mode and the air-capillary mode or, in other words, the degree of overlap between the fields of the two modes is proportional to the magnitude of the
range over which the transformation takes place, and is conversely in proportion to the peak value that is smoothed. As a result, we can deduce that an increase of the nested capillary’s diameter induces a stronger coupling between these modes because the full width at half maximum
of the curves increases slightly with the
parameter and the peak value at
decreases. This increased interaction is related to the nested capillaries which increasingly squeeze the air-capillary modes towards the fiber core when their sizes increase (see
Figure 1 at the right).
In terms of confinement loss, we observe in each case that the loss of the two hybrid modes strongly increases up to the avoided crossing point and then slowly varies beyond the
value. Conversely, the HE
core mode has a weakly fluctuating low loss over the value range of
, independently of the set value of the
ratio. We thus find the same performances in the evolution of the losses in respect to
as described in [
17] for the HE
11 and hybrid TE
modes, which makes it possible to consider finding NANF designs with a strong degree of HOM suppression compared to the fundamental mode, defined as [
17]
where
and
are the losses of the HE
and hybrid TE
modes (in dB/m), respectively. This relation can give an indication of the single-modeness of the given fiber. However, the addition of nested capillaries decreases the overall losses for all guided modes between one to two orders of magnitude depending on the size of the nested AREs. For NANFs consisting of six nested elements with a ratio
, the suppression of higher-order core modes while satisfying the condition on the parameter
can become problematic. This is due to the fact that the nested capillaries and the narrow inter-capillary distance effectively shield the electric field leaking into the silica outer cladding (see
Figure 1 on the right hand side). A sufficiently large loss level cannot hence be reached for the higher-order TE
mode. In
Figure 3b the calculated degree of HOM suppression strongly increases at the anti-crossing position, peaking at the values around 1200 for the first three values of
. When
, this value drops at ∼250. The degree of HOM suppression for
is similar to that without nested capillaries, whereas the loss is almost two orders of magnitude smaller for the two core modes. Whatever the value of
, the single-mode or multimode behavior of NANF can only be defined with respect to the length of fiber needed to develop new applications, such as light-sources/lasers emitting in the deep-UV/UV or the mid-infrared. If only a few meters of fiber are sufficient so that the losses of the HE
and TE
core modes are practically negligible over this length (as for
), in spite of the fact the TE
mode presents 1000 times higher loss, it will not actually be effectively suppressed. Thus, in order to verify the single-mode behavior of NANFs over a specified wavelength interval, estimating the degree of HOM suppression is a necessary but not sufficient criteria and the lowest loss estimation of higher-order core modes is most important.
3. Analytical Model
To understand and predict the avoided crossings in ARFs with touching or non-touching capillaries, an analytical model in which the core and the cladding of AREs are treated as two coupled capillaries has been proposed in the [
16,
17]. We propose here to apply this analytical model to NANFs depicted in
Figure 1. Generally, the effective index of guided modes in the inner region of capillary with infinite wall thickness can be estimated by the Marcatili-Schmeltzer formula [
25], rewritten as
where the exponents
and
indicate the capillary linked to the core and the cladding, respectively;
the refractive index of inner medium made of air (
=
= 1) ; the coefficient
is the m-th zero of the Bessel function
, with
for vector modes and
for linearly polarized modes. The effective diameter
or
is the inner diameter of the capillary. The coefficients
and
are used to adjust the value of diameters
d and
D in order to match the analytical values from Equation (
2) to the numerical results of finite-element simulations. In
Figure 2a, are plotted the fitted values for each
air-capillary mode (red dashed curves) calculated using Equation (
2) with the fitting coefficients
reported in
Table 1. Analytical and numerical computed values are in excellent agreement. The dependence of the coefficient
with respect to the dimensionless parameter
can be related to the space filling rate of the nested capillaries inside the outer ones. Indeed we observe in
Figure 2a that the more the nested capillary diameter increases, the more the effective index of the
air-capillary mode decreases with both parameters
D and
d held constant. According to (
2), the combination of two nested capillaries can then be defined by a single capillary with an effective diameter of smaller size. For the HE
core mode, the effective index value showing a very low variation at constant core diameter (
m), the application of Equation (
2) allows by taking the average of the effective indices for each value of
to find a constant value of the fitting coefficient
equal to 1.07. We verified that this increase in core diameter by
can be applied to the first four higher-order core modes and found that the effective indices of the HE
, TM
and TE
core modes in NANFs match the effective indices of the modes in the corresponding capillary with a precision of order to
. At the avoided crossing point of the coupled modes, the equivalence of effective indices between the TE
core mode and ARE
air-capillary mode by using Equation (
2) allows to derive a simple expression for the
parameter:
in which the value of coefficient
depends on the value of the ratio
. The calculated theoretical values of
from Equation (
3) are summarized in
Table 1 and are in good agreement with the
values obtained from finite-element modeling. Thus, the analytical model based on coupled capillaries can be extended to NANFs and allows a simple prediction of the avoided crossing between the higher-order core modes and the air-capillary modes.