Development of Touch Probing System Using a Fiber Stylus
Abstract
:1. Introduction
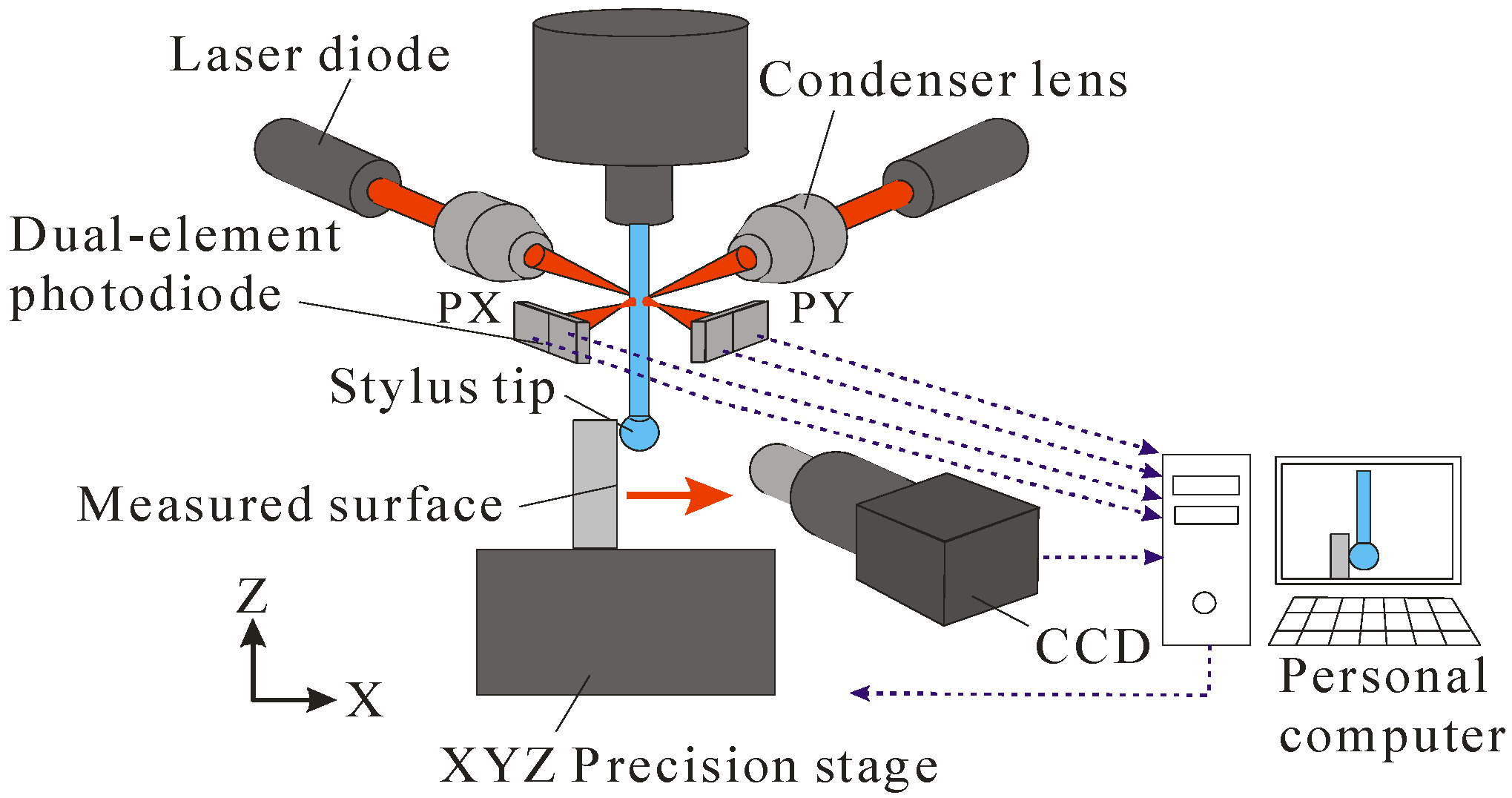
2. Measurement Principle
3. Optical Analysis to Determine the Relationship between Stylus Tip Displacement and the Output Signal
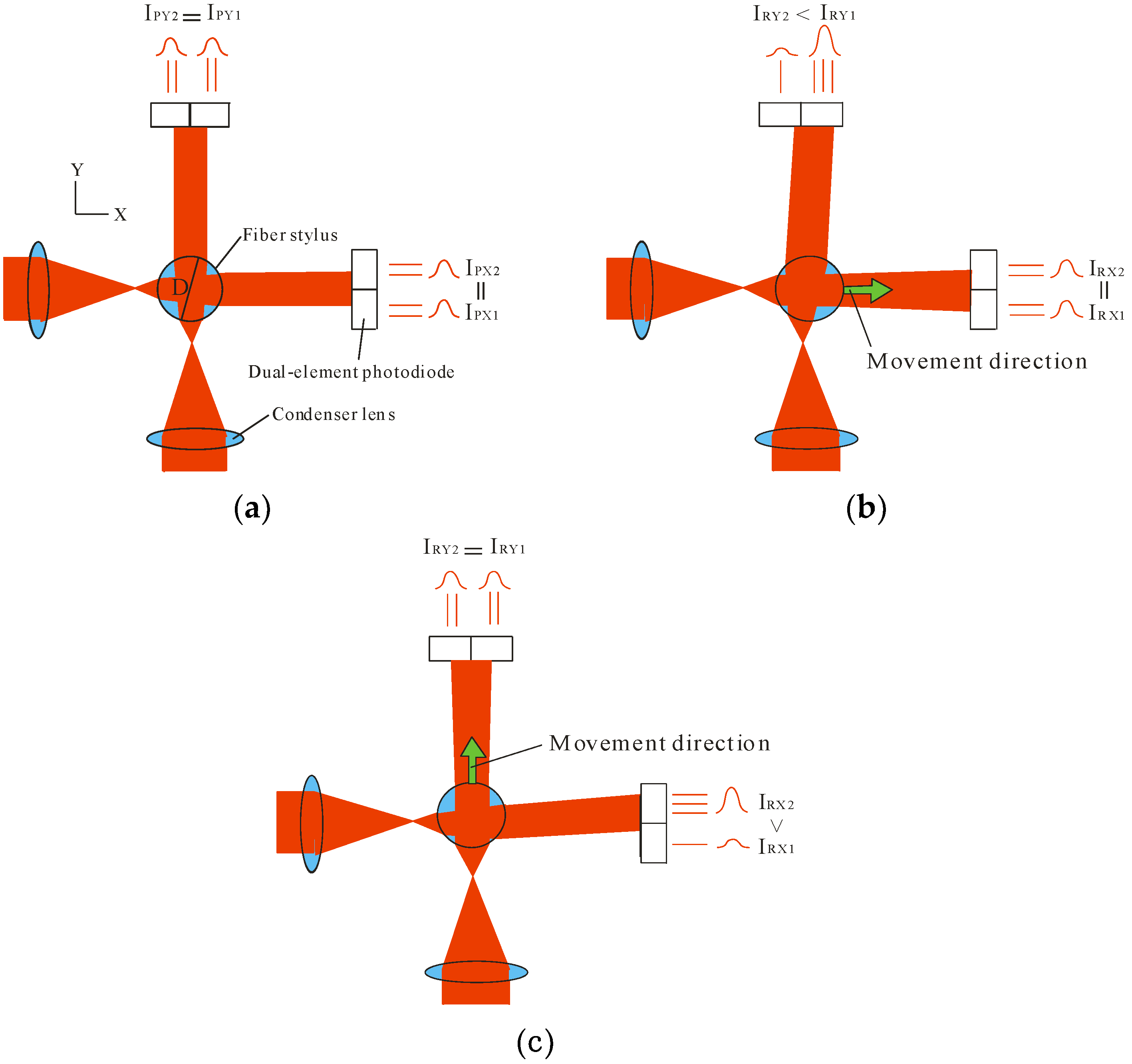
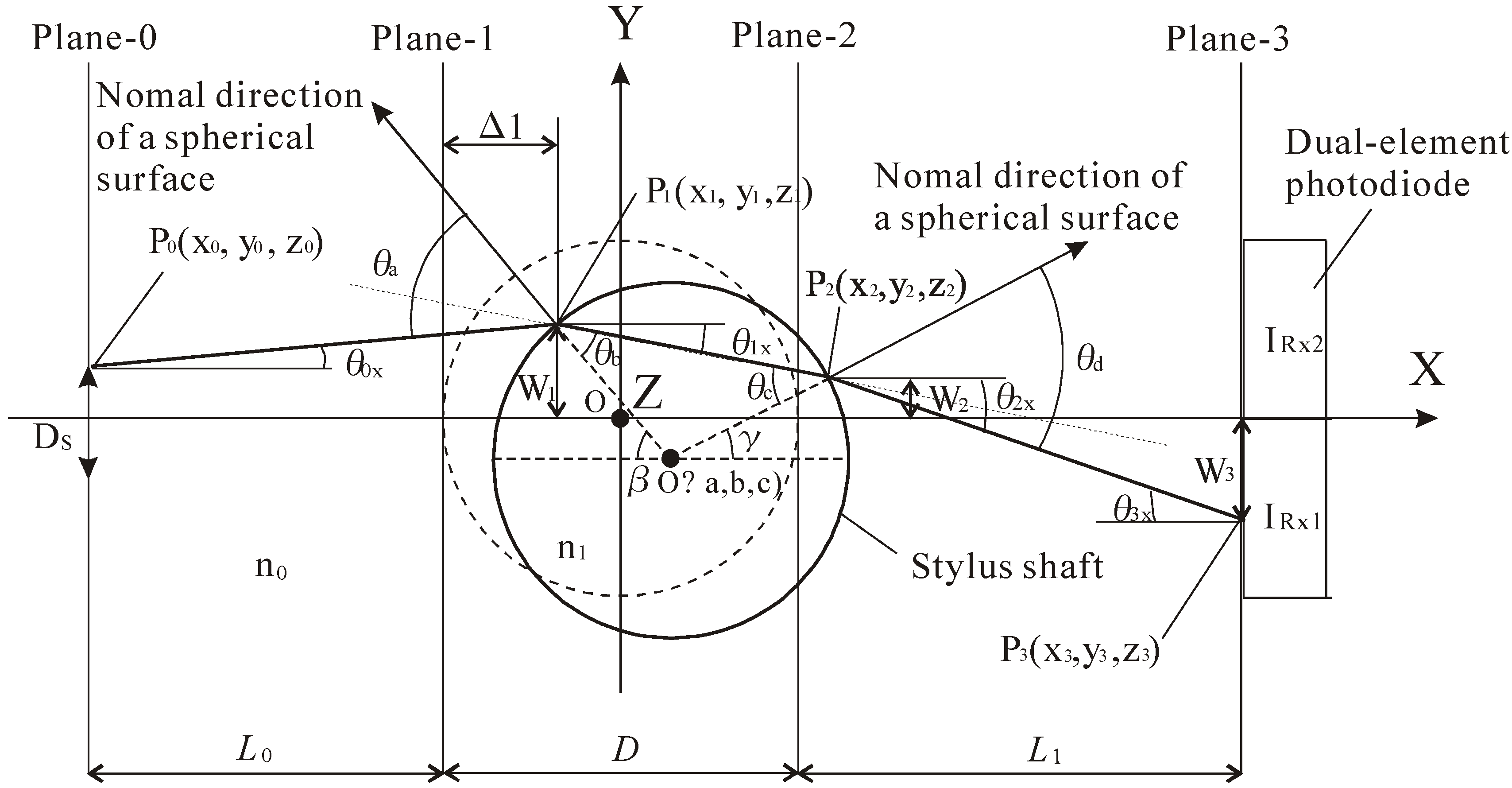
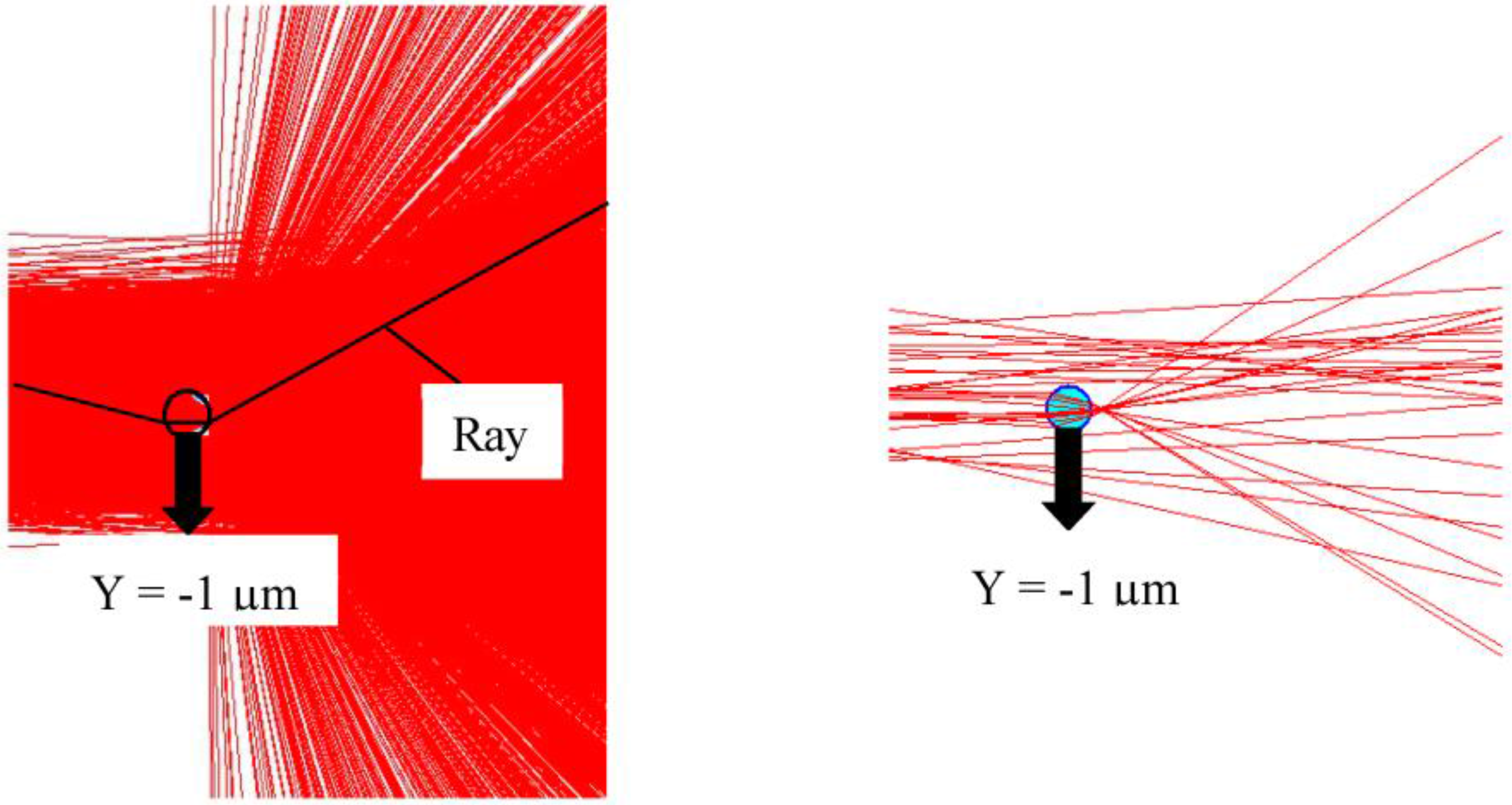
3.1. Analysis Method
3.2. Conversion to Stylus Tip Displacement
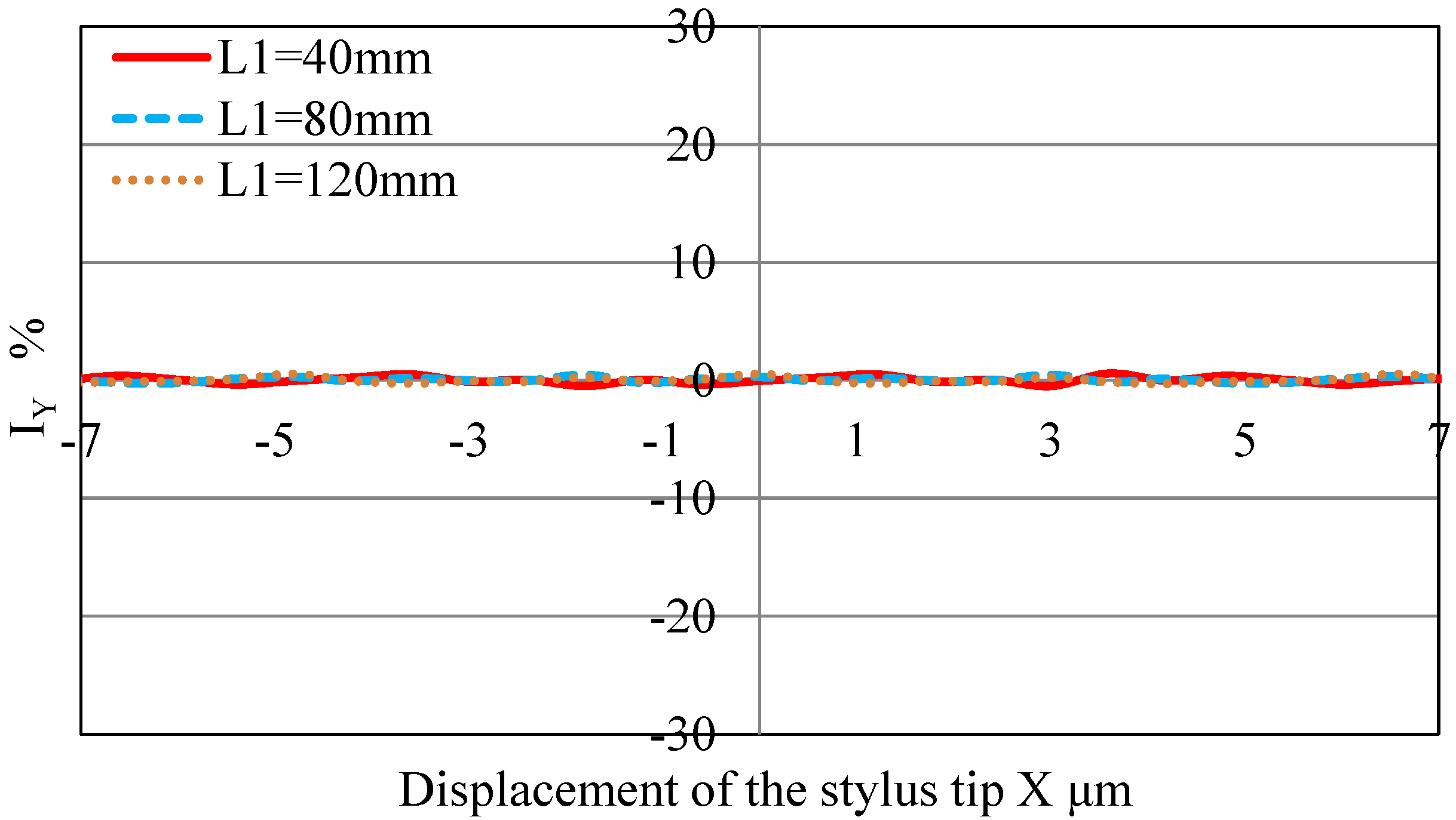
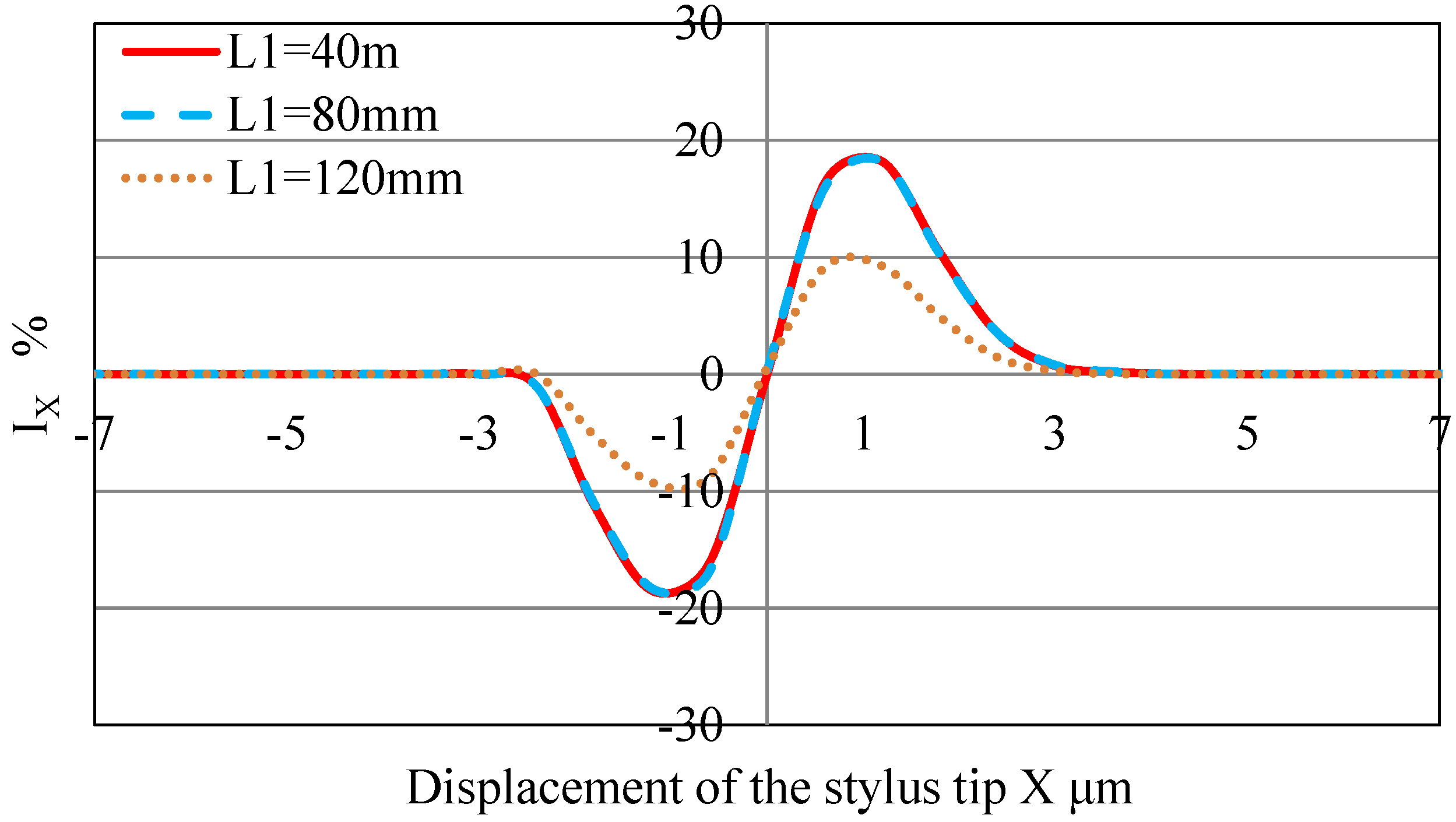
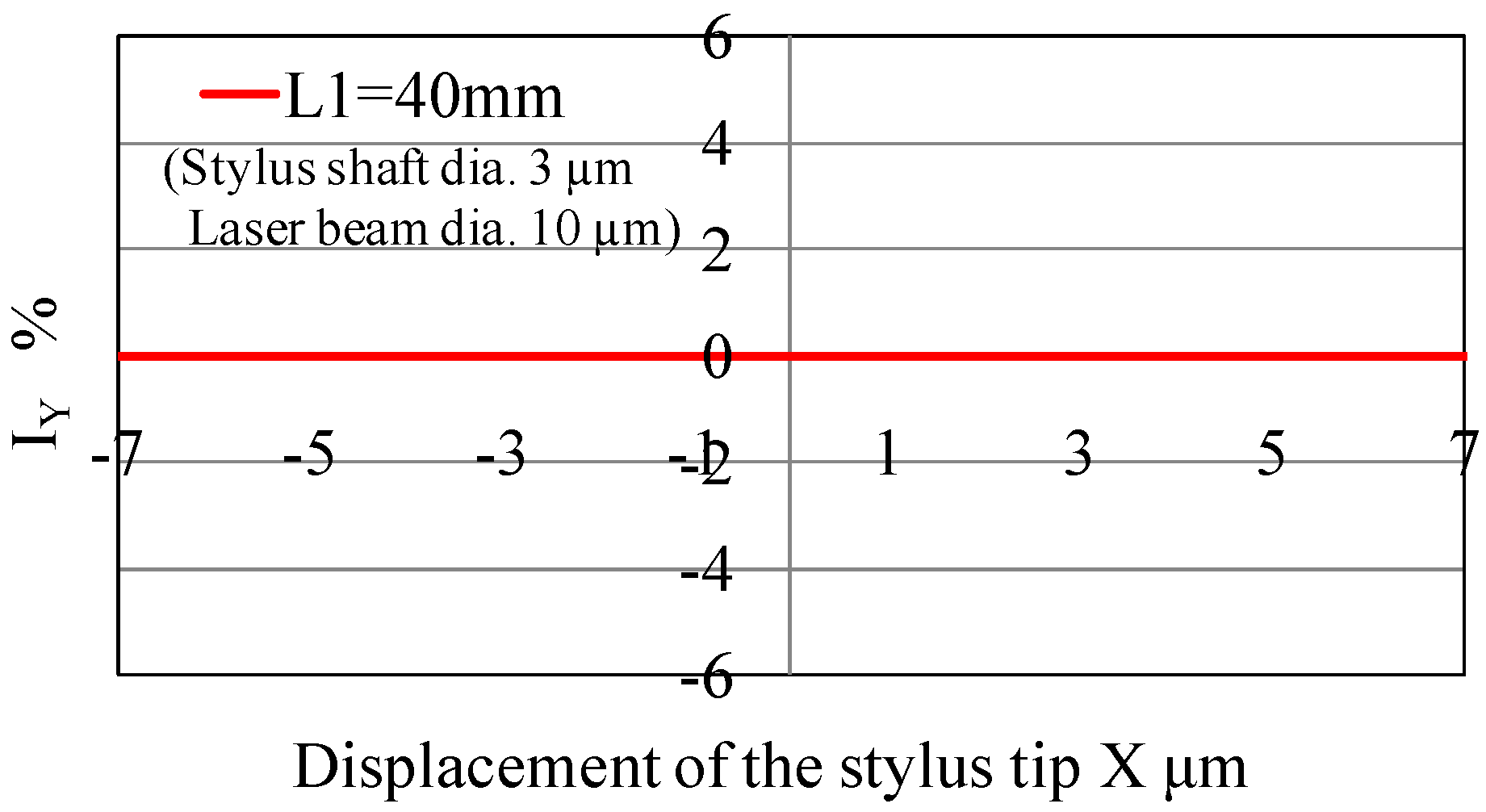
3.3. Simulation Results
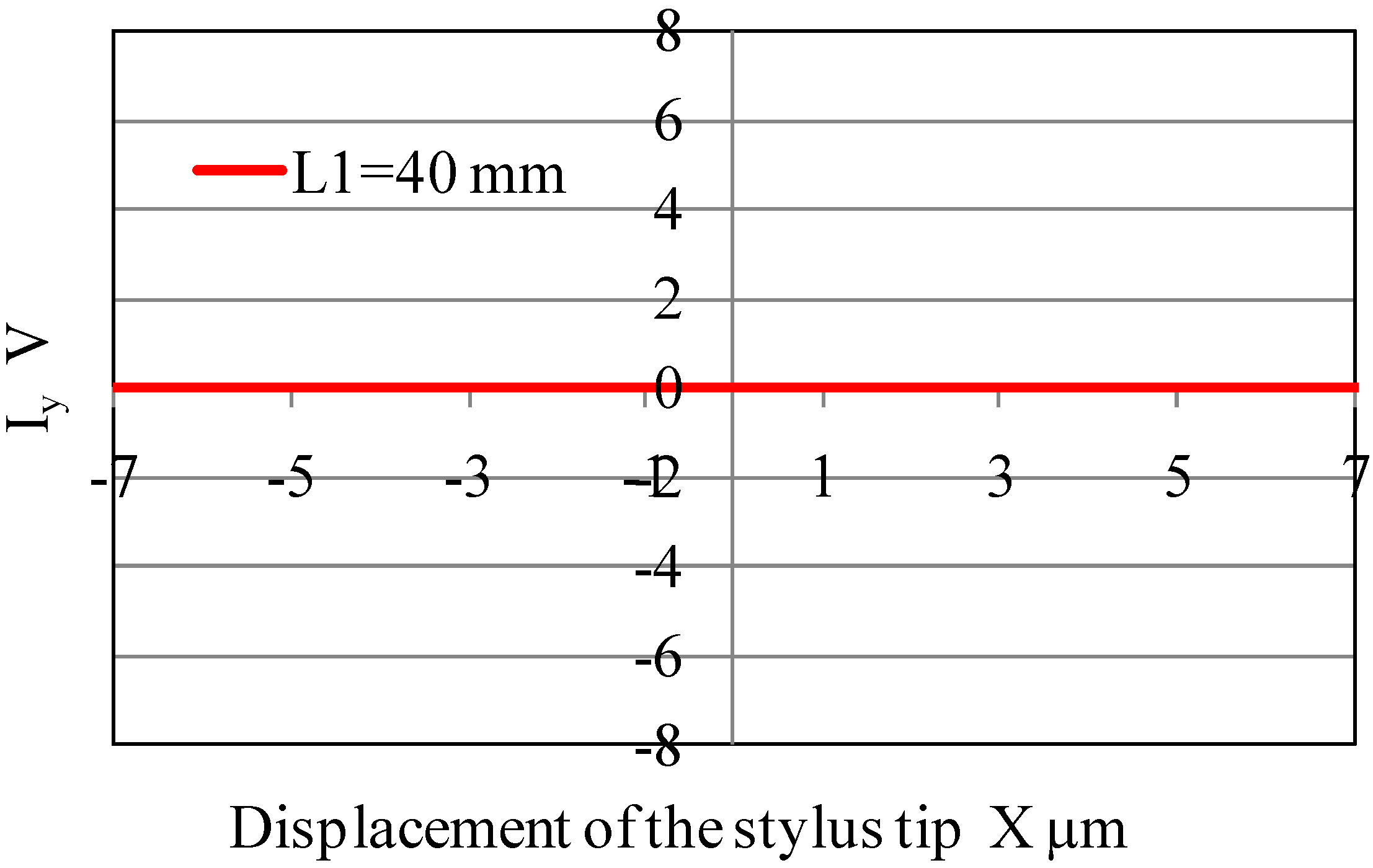
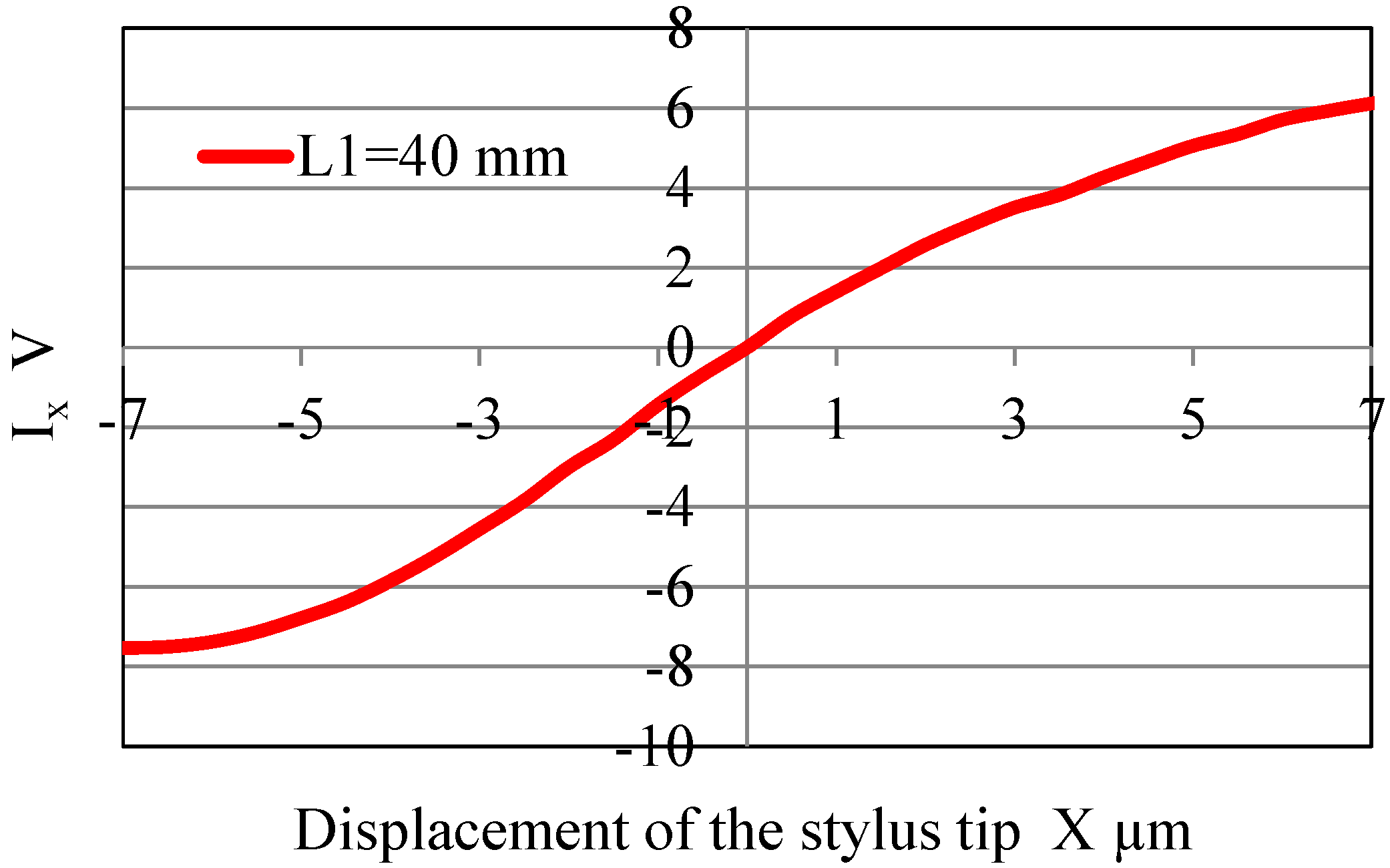
4. Characteristics of the Stylus during Displacement Detection
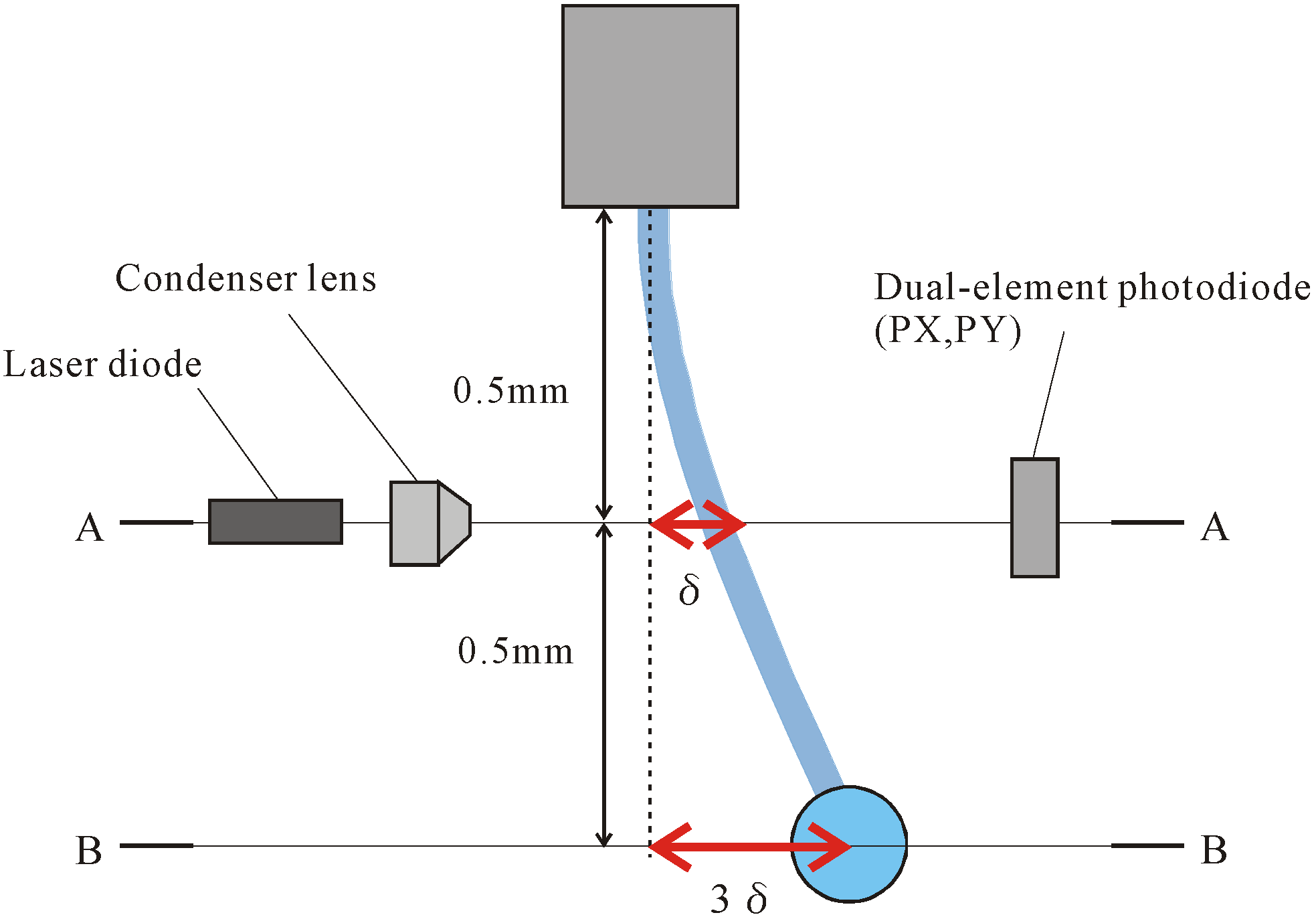
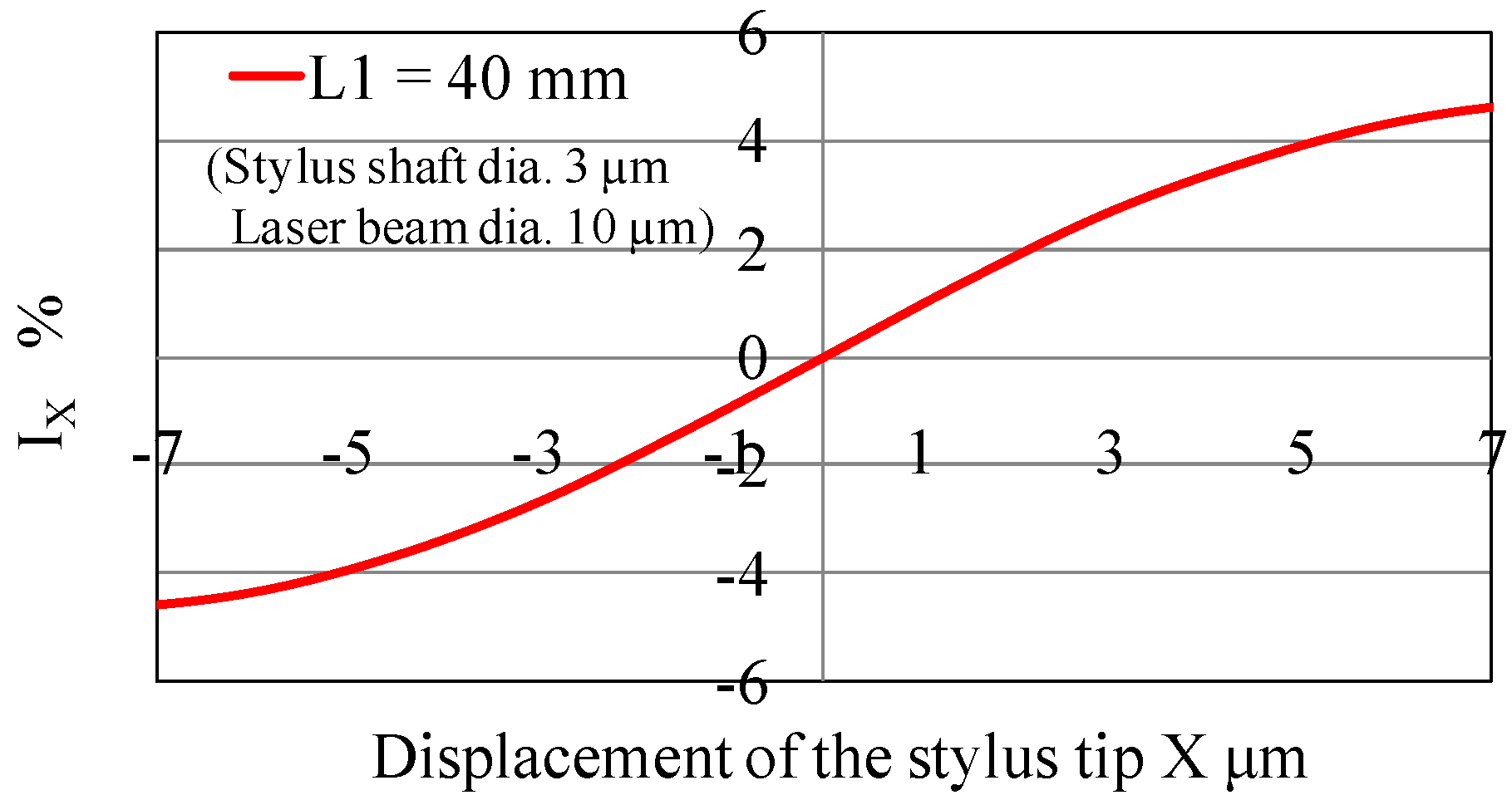
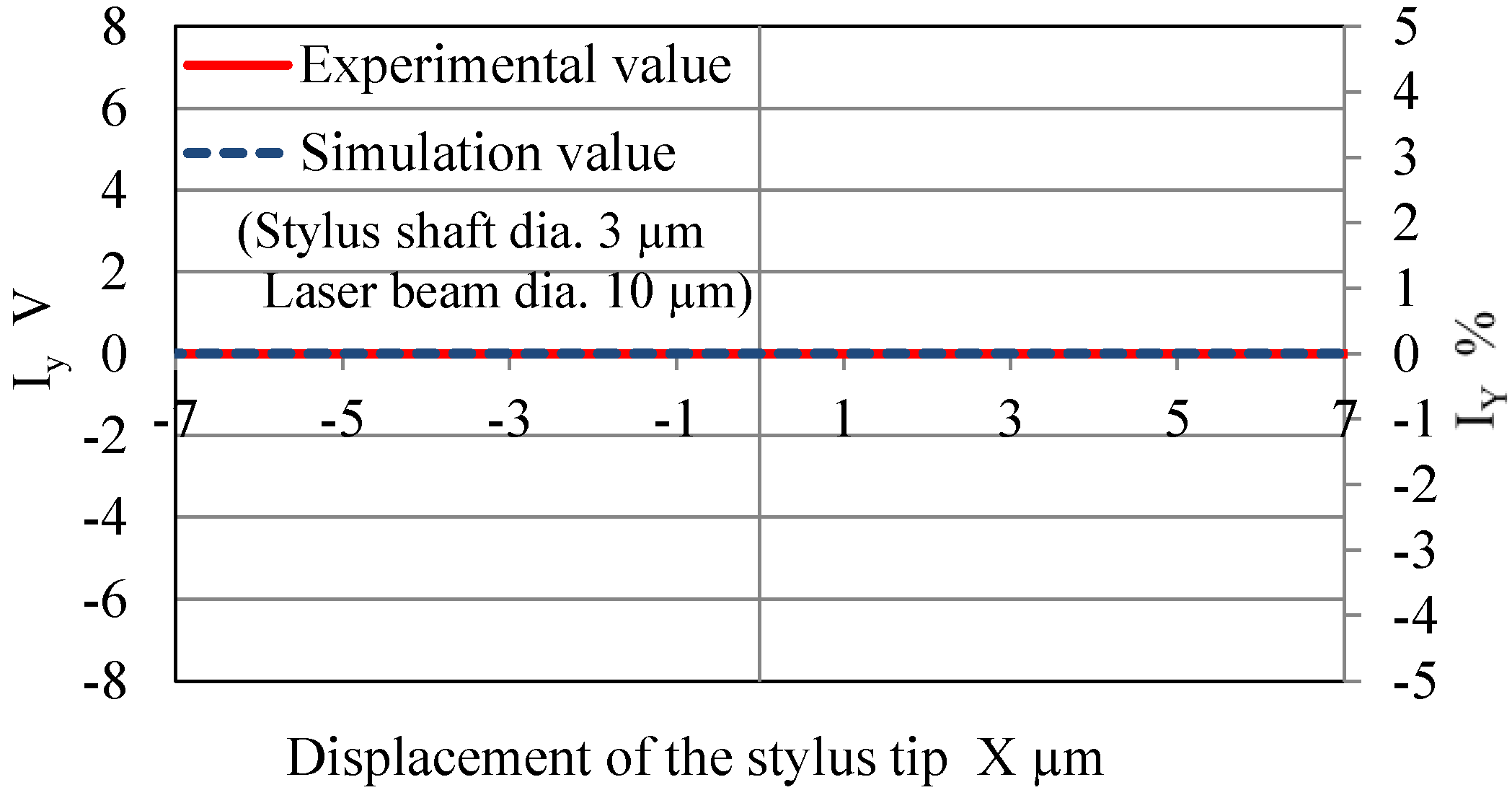
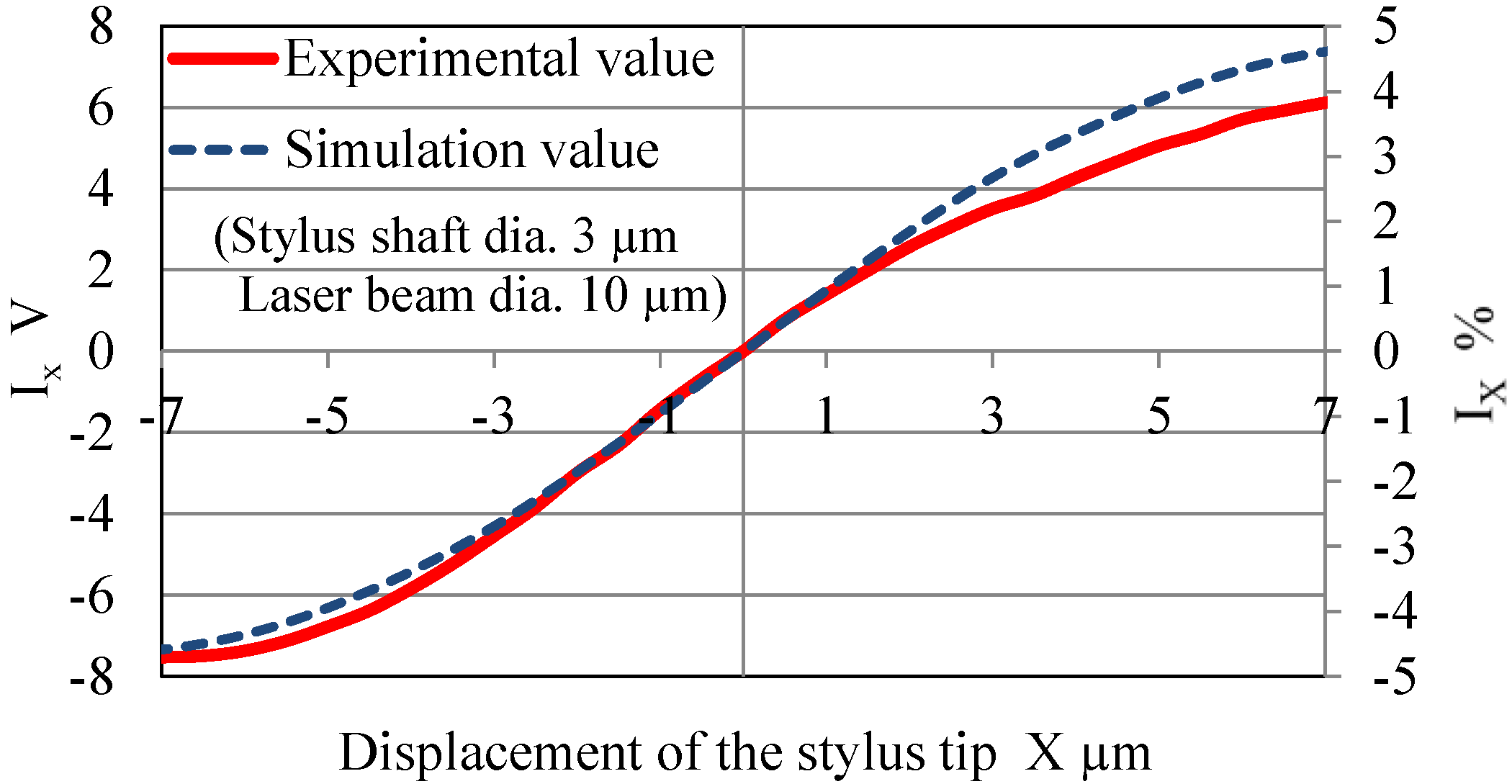
5. Optical Analysis Taking Laser Beam Size into Consideration
5.1. Analysis Method
5.2. Simulation Results
6. Evaluation of Measurement Resolution
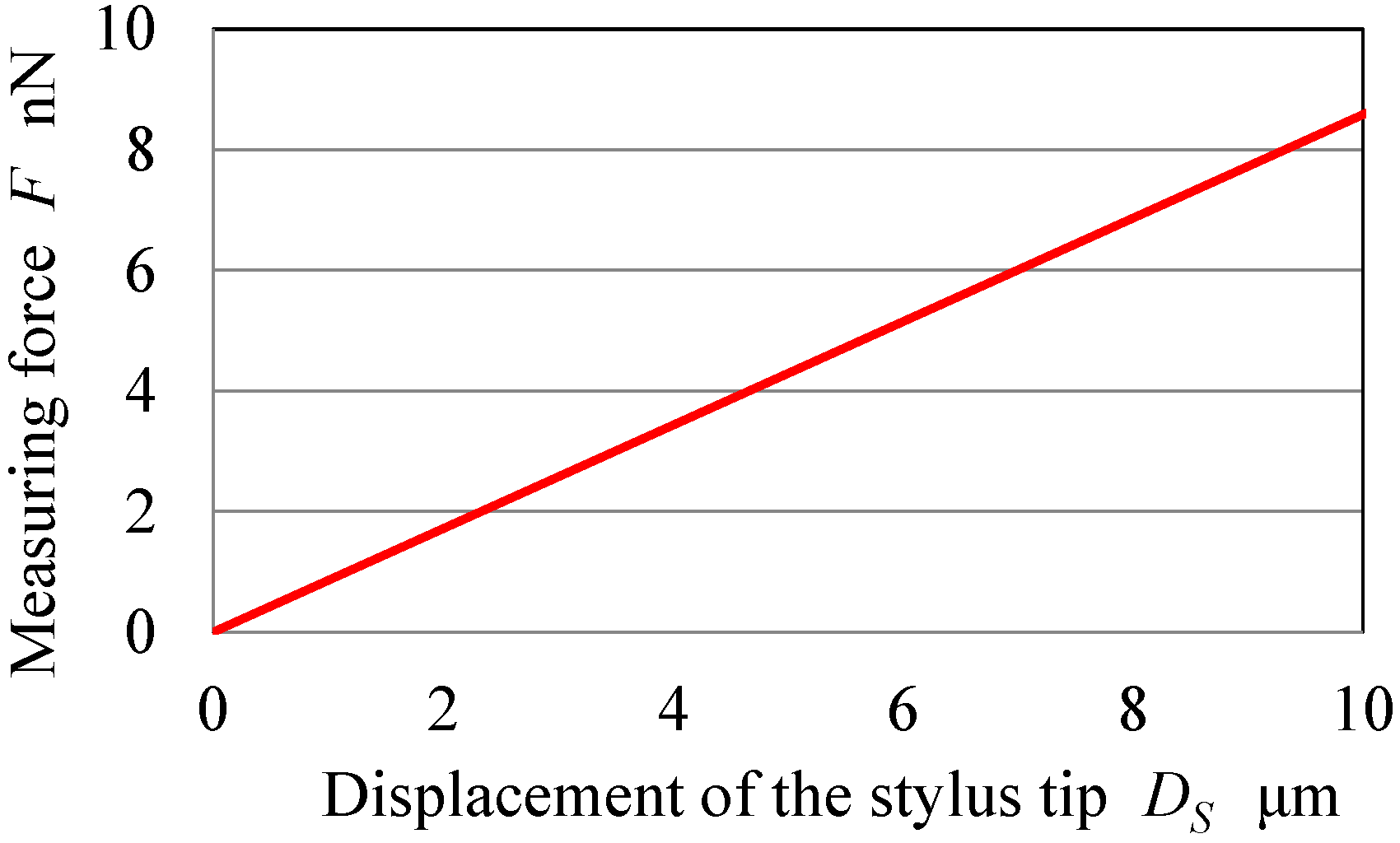
7. Force Measurement
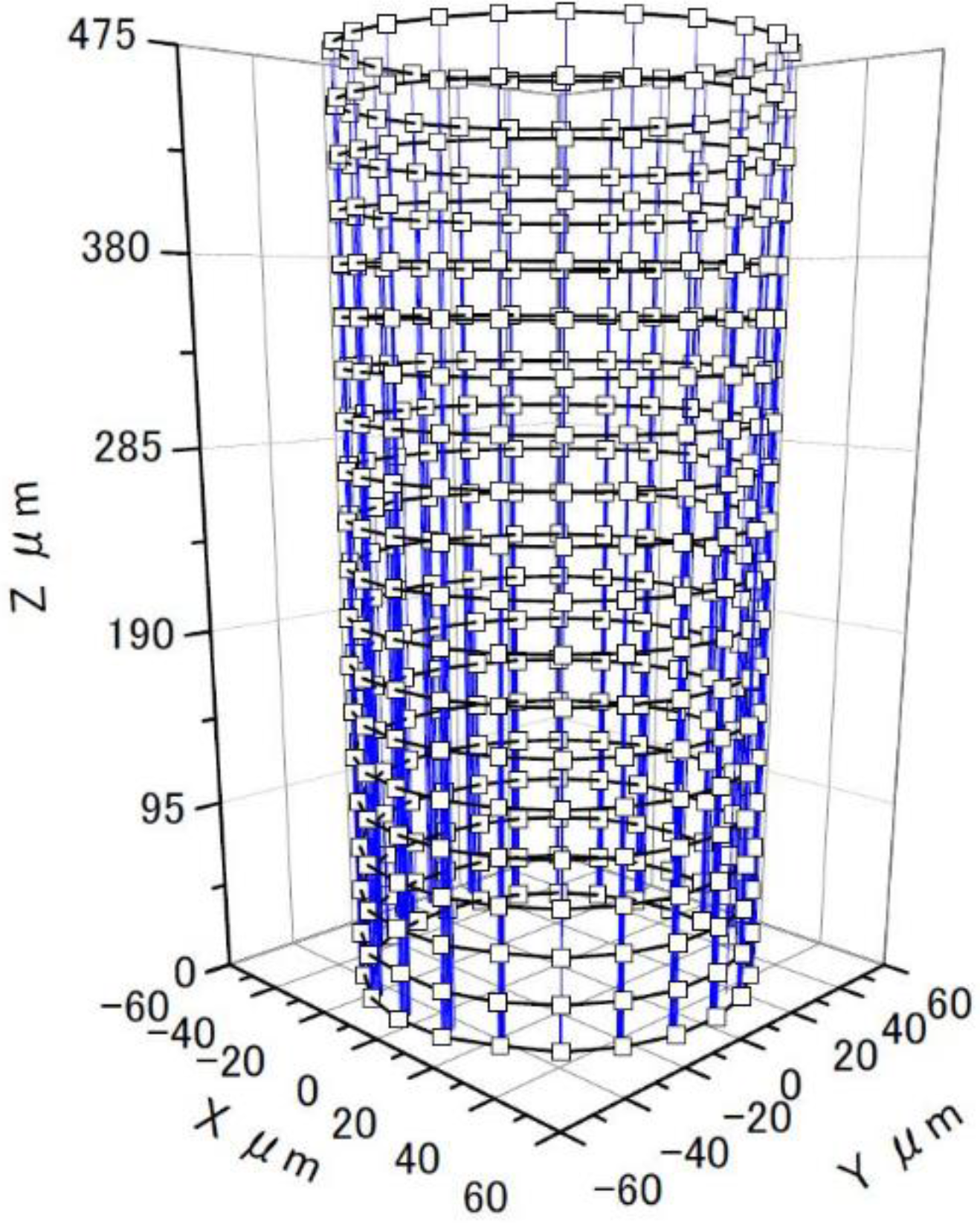
8. Micro-Hole Measurement
9. Conclusions
- (1)
- The design parameters of the optical system were determined using a ray-tracing method.
- (2)
- Optical analysis reveals that the ray-tracing simulation values agree in terms of the inclination at the origin relative to the experimental values when the laser beam size is taken into consideration. Therefore, the utility of the proposed simulation method was confirmed.
- (3)
- The resolution of the measurement system using this shaft was found to be approximately 3 nm.
- (4)
- The practicality of this system was confirmed by measuring the shape of a micro-hole 100 µm in diameter and 475 µm in depth.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Maruyama, M.; Osaka, H.; Ono, M.; Kasei, S. Development of optical apparatus for measuring small hole diameter. J. Jpn. Soc. Precis. Eng. 1996, 62, 145–149. (In Japanese) [Google Scholar] [CrossRef]
- Akiyama, N.; Kitano, A.; Yoshida, M.; Fujimoto, E.; Kohira, H.; Fukushima, T. Development of an optical measurement equipment for diameter of small and deep hole. J. Jpn. Soc. Precis. Eng. 1996, 62, 584–588. (In Japanese) [Google Scholar] [CrossRef]
- Onikura, H.; Kuwabara, Y.; Nakamura, T.; Sajima, T.; Imazeki, Y.; Katsuki, A.; Yamada, S. Development of an optical hole-diameter measurement instrument—Optical analysis, fundamental experiment, trial manufacture and performance test. J. Jpn. Soc. Precis. Eng. 1995, 61, 248–252. (In Japanese) [Google Scholar] [CrossRef]
- Masuzawa, T.; Hamasaki, Y.; Fujino, M. Vibroscanning method for nondestructive measurement of small holes. CIRP Ann. 1993, 42, 589–592. [Google Scholar] [CrossRef]
- Masuzawa, T.; Kim, B.J.; Bergaud, C.; Fujino, M. Twin-probe vibroscanning method for dimensional measurement of microholes. CIRP Ann. 1997, 46, 437–440. [Google Scholar] [CrossRef]
- Claverley, J.D.; Leach, R.K. Development of a three-dimensional vibrating tactile probe for miniature CMMs. Precis. Eng. 2013, 37, 491–499. [Google Scholar] [CrossRef]
- Hidaka, K. Study of a small-sized ultrasonic probe. CIRP Ann. 2006, 55, 567–570. [Google Scholar] [CrossRef]
- Hidaka, K.; Saito, A.; Koga, S. Study of a micro-roughness probe with ultrasonic sensor. CIRP Ann. Manuf. Technol. 2008, 57, 489–492. [Google Scholar] [CrossRef]
- Bauza, M.B.; Hocken, R.J.; Smith, S.T.; Woody, S.C. Development of a virtual probe tip with an application to high aspect ratio microscale features. Rev. Sci. Instrum. 2005, 76, 095112. [Google Scholar] [CrossRef]
- Claverley, J.; Leach, R. Three-dimensional characterisation of a novel vibrating tactile probe for miniature CMMs. In Presented at the Laser Metrology and Machine Performance X (LAMBDAMAP 2013), Chichley, UK, 20–21 March 2013.
- Ito, S.; Kikuchi, H.; Chen, Y.; Shimizu, Y.; Gao, W.; Takahashi, K.; Kanayama, T.; Arakawa, K.; Hayashi, A. A micro-coordinate measurement machine (CMM) for large-scale dimensional measurement of micro-slits. Appl. Sci. 2016, 6. [Google Scholar] [CrossRef]
- Shiraishi, T.; Mitsui, K. Development of three dimensional profile measuring apparatus for microparts—Measuring principle and measuring results. J. Jpn. Soc. Precis. Eng. 1998, 64, 1395–1399. (In Japanese) [Google Scholar] [CrossRef]
- Shiramatsu, T.; Kitano, K.; Kawata, M.; Mitsui, K. Development of a measuring method for shape and dimension of micro-components—Modification to the original measuring system, calibration of the probes and the results of dimensional measurements. J. Jpn. Soc. Precis. Eng. Ser. C 2002, 68, 267–274. (In Japanese) [Google Scholar] [CrossRef]
- Schwenke, H.; Wäldele, F.; Weiskrich, C.; Kunzmann, H. Opto-tactile sensor for 2D and 3D measurement of small structures on coordinate measuring machines. CIRP Ann. 2001, 50, 361–364. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Stone, J.A.; Stoup, J.R. Fiber deflection probe for small hole metrology. Precis. Eng. 2006, 30, 154–164. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Sajima, T.; Suematsu, T. Study of a vibrating fiber probing system for 3-D micro-structures: Performance improvement. Meas. Sci. Technol. 2014, 25, 094010. [Google Scholar] [CrossRef]
- Michihata, M.; Takaya, Y.; Hayashi, T. Development of the nano-probe system based on the laser-trapping technique. CIRP Ann. 2008, 57, 493–496. [Google Scholar] [CrossRef]
- Li, R.-J.; Fan, K.-C.; Huang, Q.-X.; Zhou, H.; Gong, E.-M.; Xiang, M. A long-stroke 3D contact scanning probe for micro/nano coordinate measuring machine. Precis. Eng. 2016, 43, 220–229. [Google Scholar] [CrossRef]
- Boris, G.; Lothar, D.; Martin, H. Design and characterization of a resonant triaxial microprobe. J. Micromech. Microeng. 2015, 25, 125011. [Google Scholar]
- Spaan, H.A.M.; Donker, R.L.; Widdershoven, I. Isara 400: Development of an ultra-precision CMM for 3D measurement for large parts. In Proceedings of the ASPE Spring Topical Meeting, Chicago, IL, USA, 6–7 April 2009.
- Meli, F.; Bieri, M.; Thalmann, R.; Fracheboud, M.; Breguet, J.-M.; Clavel, R.; Bottinelli, S. Novel 3D analogue probe with a small sphere and low measurement force. In Proceedings of the ASPE Summer Topical Meeting, Charlotte, NC, USA, 25–26 June 2003.
- Pril, W.O. Development of High Precision Mechanical Probes for Coordinate Measuring Machines. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2002. [Google Scholar]
- Liebrich, T.; Knapp, W. New concept of a 3D-probing system for micro-components. CIRP Ann. 2010, 59, 513–516. [Google Scholar] [CrossRef]
- Yang, S.; Li, S.; Kaiser, M.J.; Eric, F.H.K. A probe for the measurement of diameters and form errors of small holes. Meas. Sci. Technol. 1998, 9, 1365–1368. [Google Scholar] [CrossRef]
- Bütefisch, S.; Büttgenbach, S.; Kleine-Besten, T.; Brand, U. Micromechanical three-axial tactile force sensor for micromaterial characterization. Microsyst. Technol. 2001, 7, 171–174. [Google Scholar] [CrossRef]
- Lewis, A.J. Fully traceable miniature CMM with submicrometer uncertainty. Proc. SPIE 5190 Recent Dev. Traceable Dimens. Meas. II 2003, 265. [Google Scholar] [CrossRef]
- Bos, E.J.C. Aspects of tactile probing on the micro scale. Precis. Eng. 2011, 35, 228–240. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Onikura, H.; Sajima, T.; Kawagoishi, N.; Kondo, E. Development of a system for measuring micro hole accuracy using an optical fiber probe. J. Adv. Mech. Des. Syst. Manuf. 2010, 5, 995–1004. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1988; p. 216. [Google Scholar]
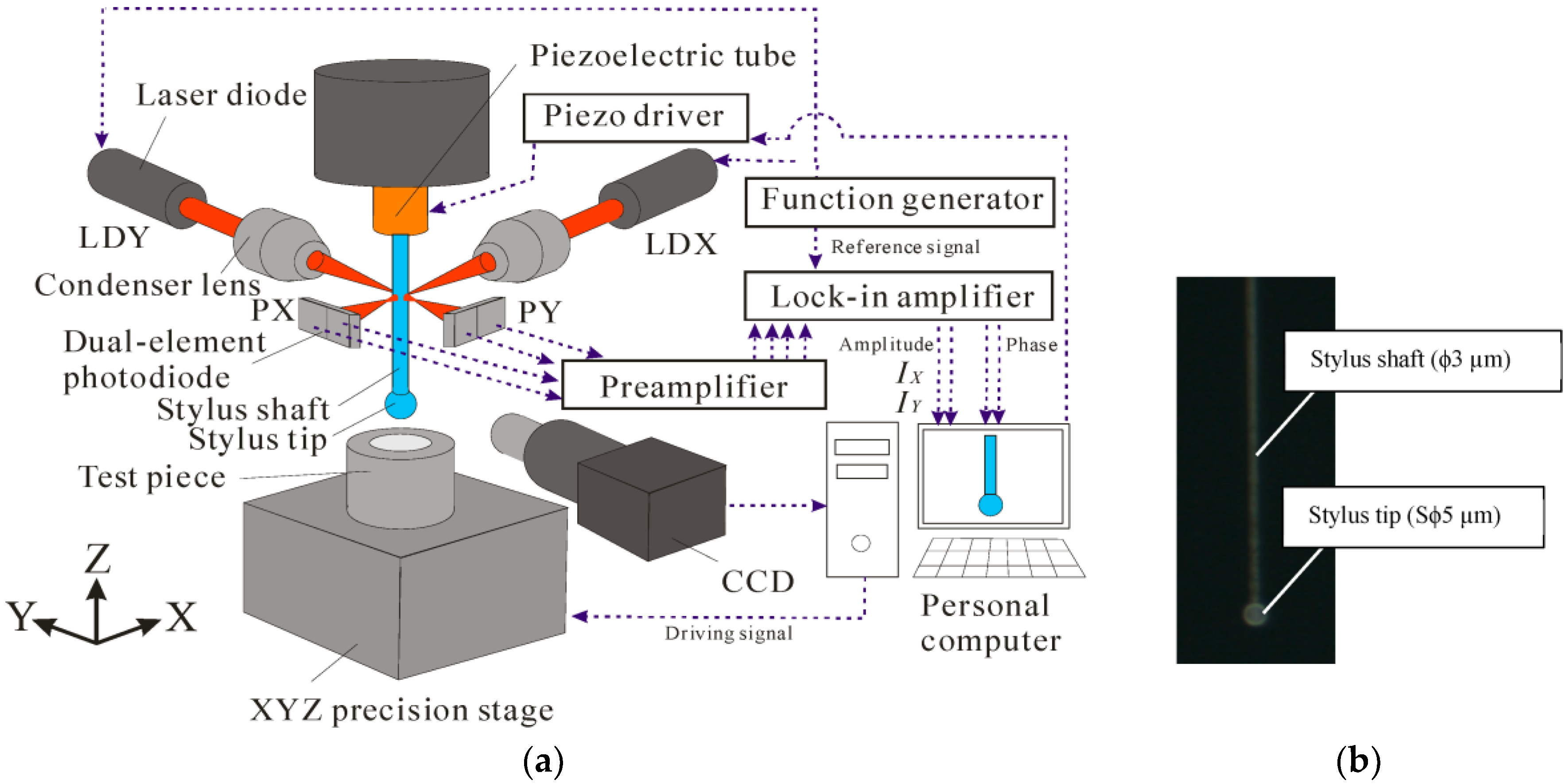



| Laser source | Wavelength: 650 nm |
| Stylus shaft diameter, D | 3 µm |
| Refractive index of the stylus shaft | 1.457 |
| Distance between planes 0 and 1, L0 | 10 µm |
| Distance between planes 2 and 3, L1 | 40, 80, 120 mm |
| Numerical aperture of the condenser lens | 0.13 |
| Displacement, X | −1.0 to 1.0 µm, −7.0 to 7.0 µm |
| Area of the dual-element photodiode | 5 × 10 mm |
| X, Y, Z | Coordinates of the optical system |
| D | Diameter of the stylus shaft |
| L0, L1 | Distances between plane 0 and plane 1, plane 2 and plane 3 |
| n0, n1 | Refractive indices of the target planes |
| W1, W2, W3 | Beam heights of the target planes |
| , , , | Tilt angles for the optic axis (X-direction) |
| , , | Tilt angles for the optic axis (Z-direction) |
| , | Angles between the normal line drawn on the spherical surface and the optic axis |
| , | Angles of incidence |
| , | Angles of refraction |
| Offset of a laser spot on the fiber surface from plane-1 |
| Laser Source | Wavelength: 650nm |
| Stylus shaft diameter, D | 3 µm |
| Refractive index of the stylus shaft | 1.457 |
| Distance between planes 0 and 1, L0 | 10 µm |
| Distance between planes 2 and 3, L1 | 40 mm |
| Numerical aperture of the condenser lens | 0.13 |
| Displacement, X | −7.0 to 7.0 µm |
| Laser beam diameter, DL | 10 µm |
| Area of the dual-element photodiode | 5 × 10 mm |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murakami, H.; Katsuki, A.; Sajima, T. Development of Touch Probing System Using a Fiber Stylus. Fibers 2016, 4, 24. https://doi.org/10.3390/fib4030024
Murakami H, Katsuki A, Sajima T. Development of Touch Probing System Using a Fiber Stylus. Fibers. 2016; 4(3):24. https://doi.org/10.3390/fib4030024
Chicago/Turabian StyleMurakami, Hiroshi, Akio Katsuki, and Takao Sajima. 2016. "Development of Touch Probing System Using a Fiber Stylus" Fibers 4, no. 3: 24. https://doi.org/10.3390/fib4030024
APA StyleMurakami, H., Katsuki, A., & Sajima, T. (2016). Development of Touch Probing System Using a Fiber Stylus. Fibers, 4(3), 24. https://doi.org/10.3390/fib4030024






