Structure Design by Knitting: Combined Wicking and Drying Behaviour in Single Jersey Fabrics Made from Polyester Yarns
Abstract
Highlights
- Eight samples of single jersey knitted fabrics made from polyester yarns with different levels of texturisation and fibre diameters were examined in a combined wicking and drying experiment.
- The quantitative measures extracted from these experiments show that texturised and non-texturised yarns behave significantly differently.
- The wicking and drying properties of fabrics are highly affected by their structure and can be well correlated with the fabrics’ porous properties.
- The mechanisms observed in this study suggest ways to optimise drying behaviour by combining yarns and knitted fabric structures.
Abstract
1. Introduction
2. Theoretical Background: Liquid Transport and Drying in Knitted Fabrics
2.1. Wetting and Wicking
2.2. Horizontal Wicking
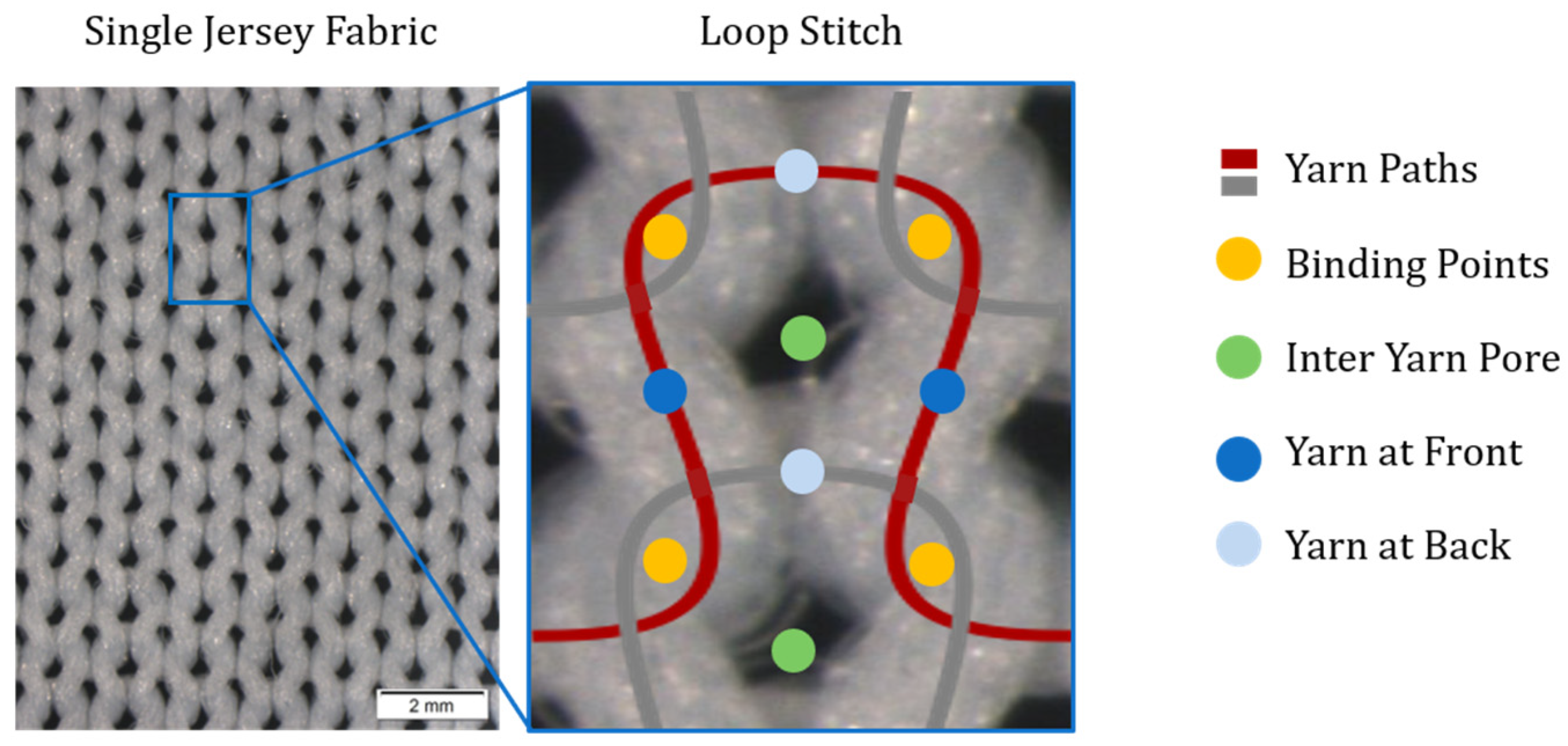
2.3. Capillary Transport in Knitted Fabrics
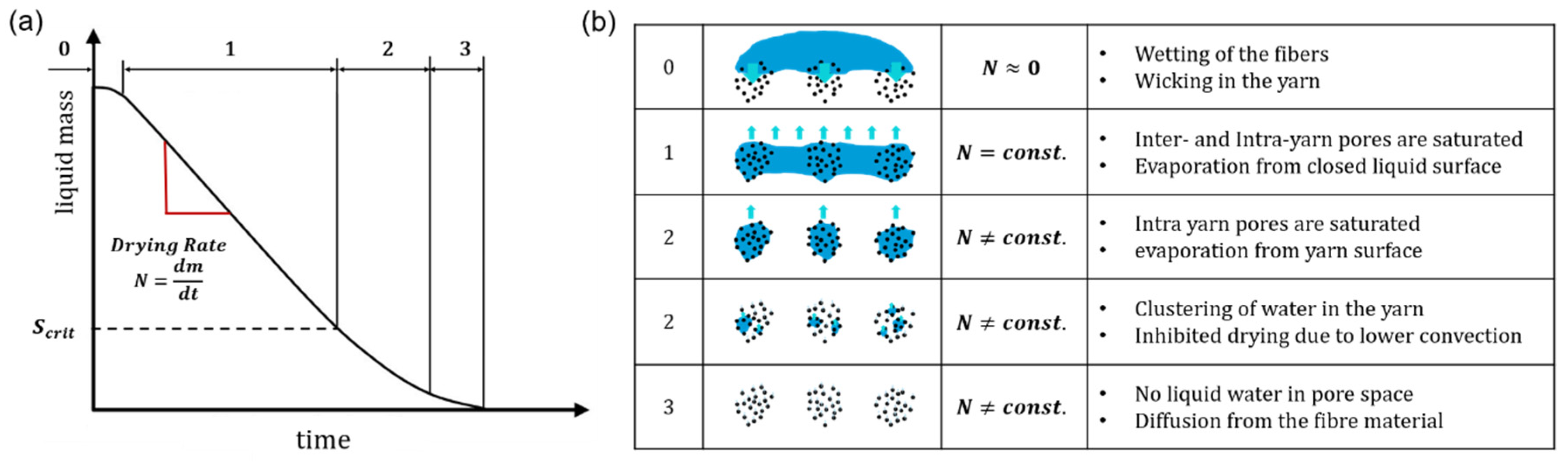
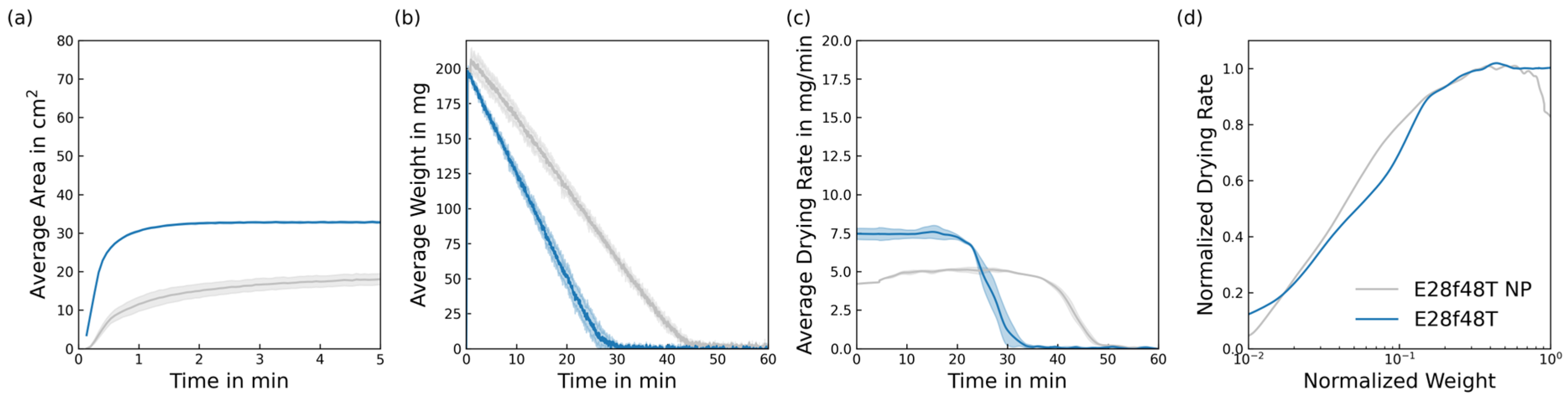
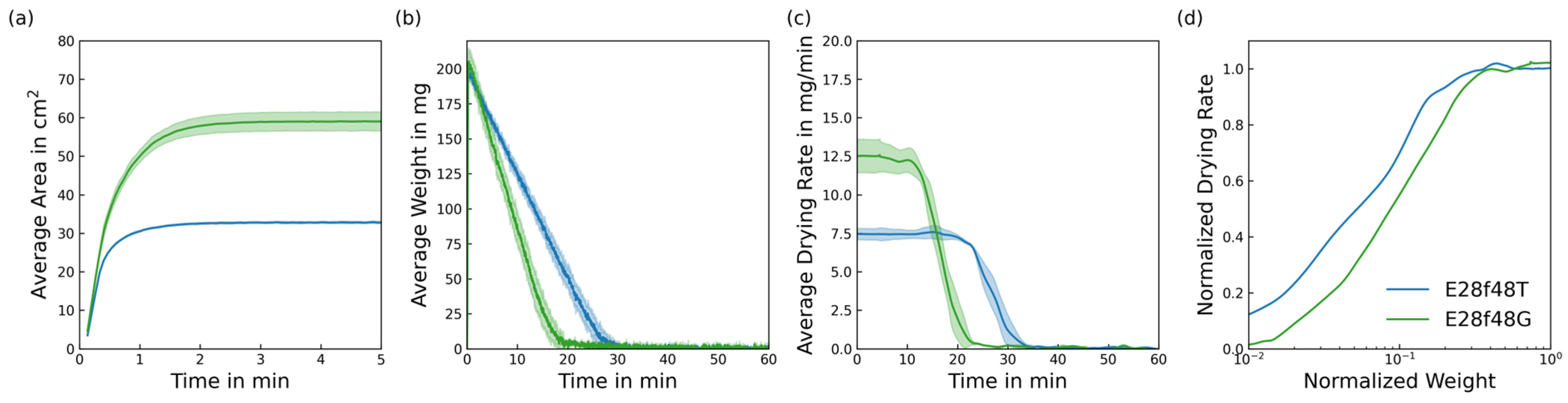
2.4. Drying of Porous Media
2.5. Drying of Knitted Fabrics
2.6. Conclusion and Research Gap
3. Materials and Methods
3.1. Materials
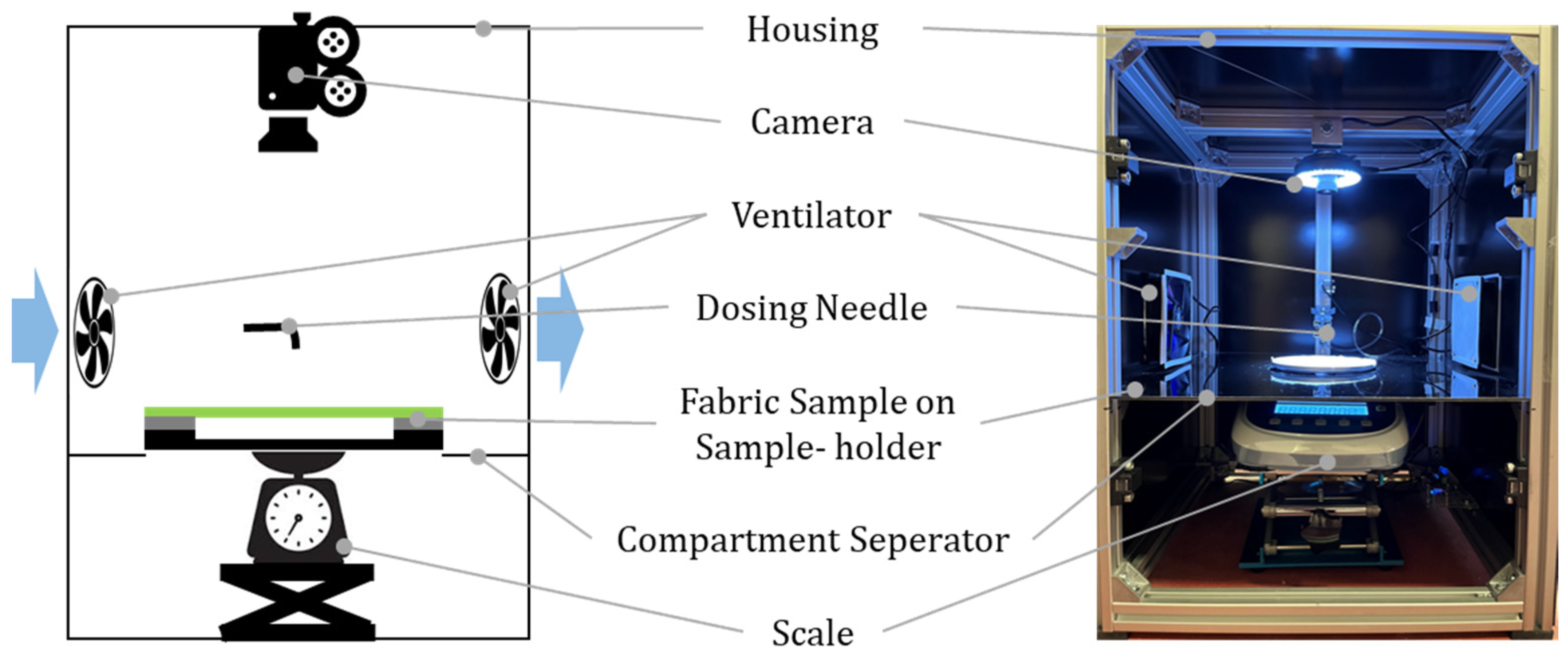
3.2. Sample Preparation and Experimental Setup
4. Results
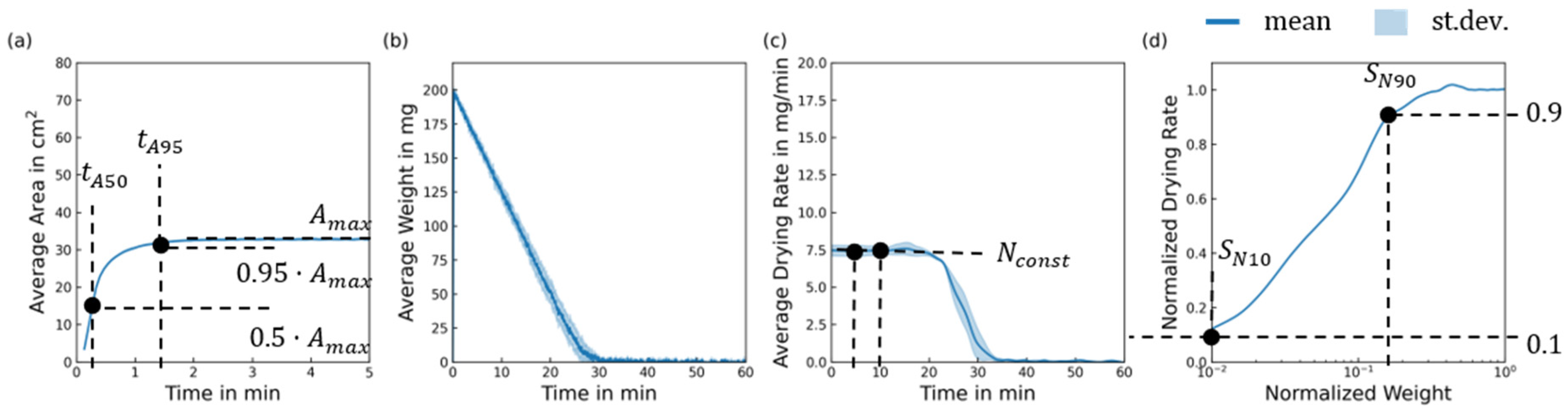
4.1. Quantitative Analysis
4.2. Qualitative Analysis of Wicking Fronts and Local Saturation
5. Discussion
5.1. Wetting Behaviour
5.2. Yarn Texturisation and Fabric Structure
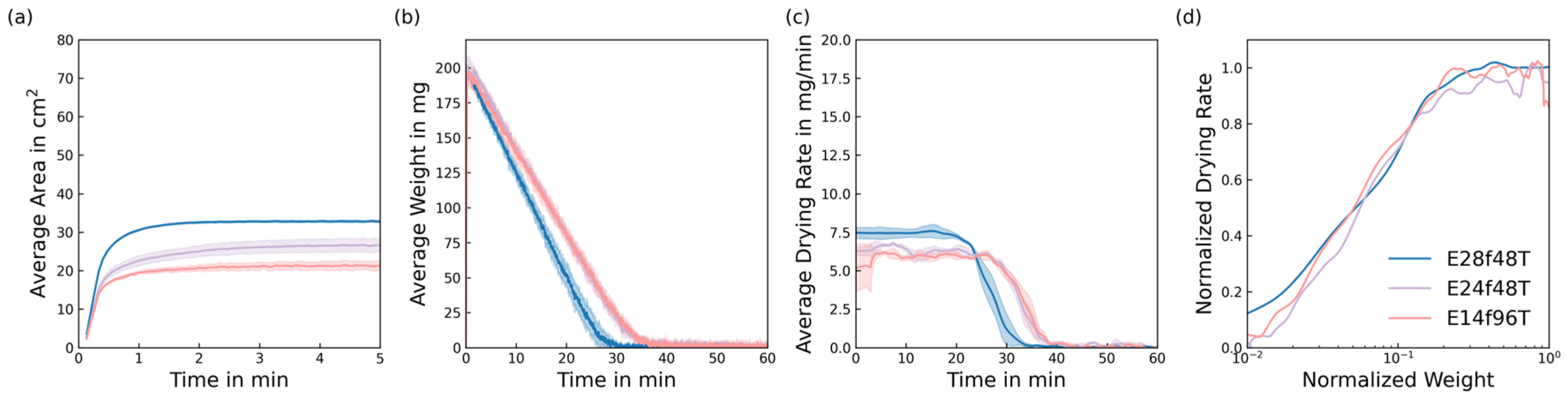
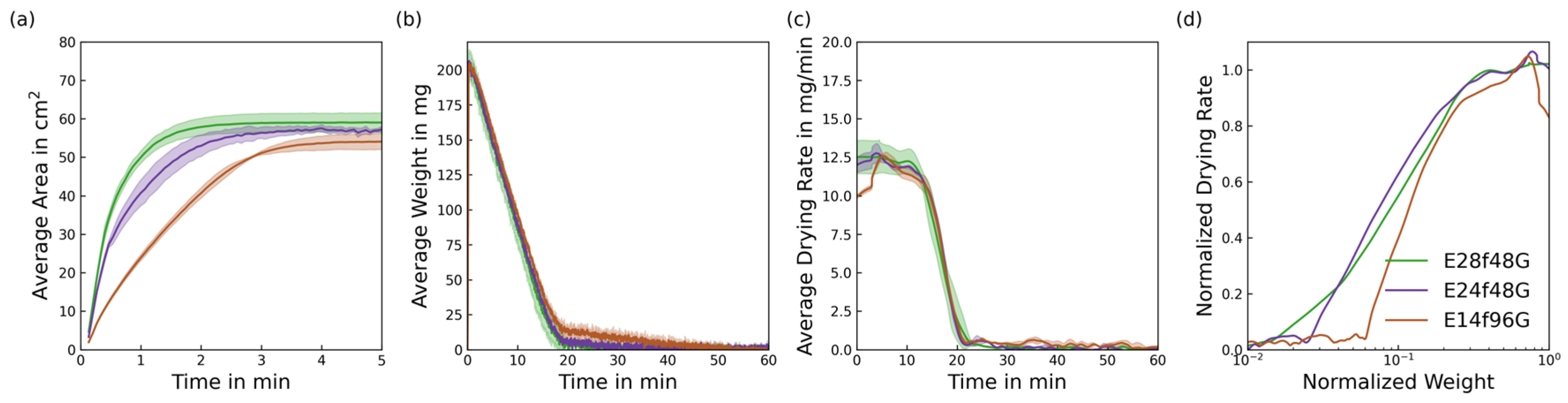
5.3. Fibre Diameter
5.4. Machine Gauge
6. Conclusions
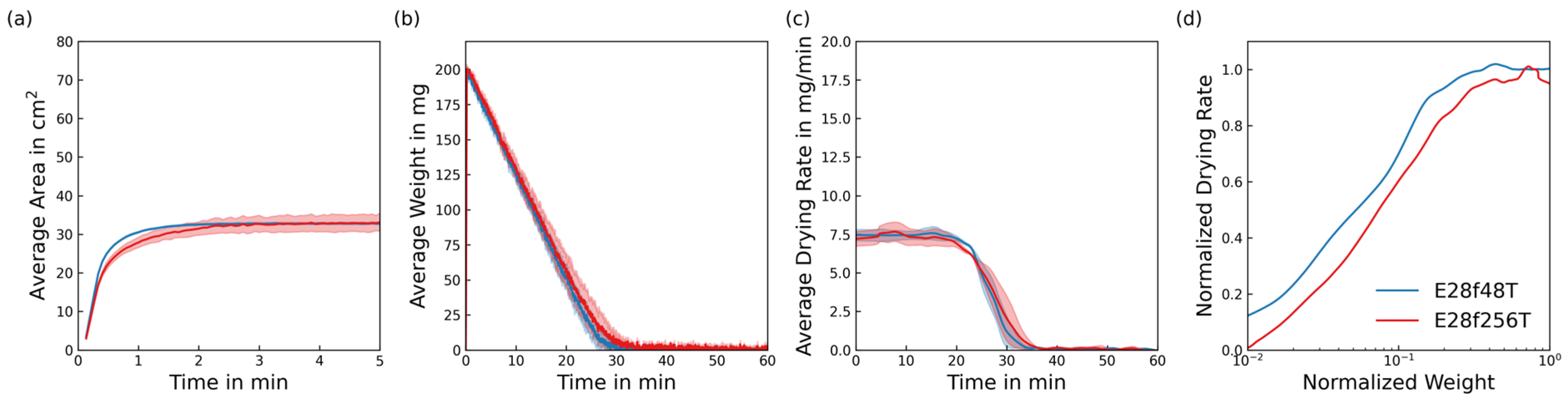
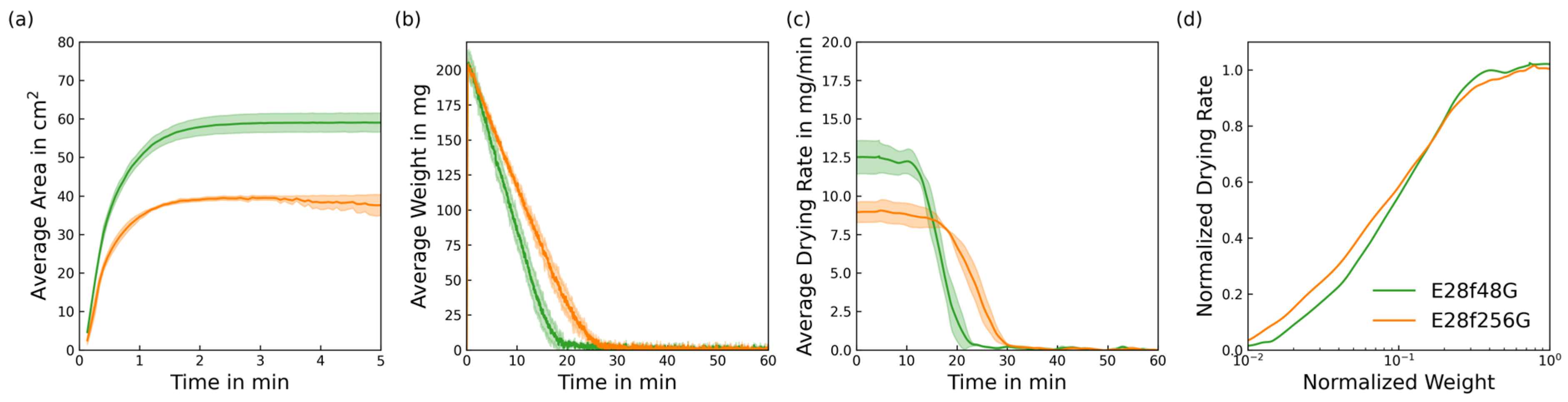
- Good wettability increases spreading dynamics and maximum spread in the CRP. The spread area determines the effective drying rate in the CRP and the absolute drying time.
- Fine filaments inhibit the spread of liquid in the fabric and therefore reduce the drying rate in the CRP. However, fine filaments seem to have a contrary impact on the FRP depending on the yarn structure.
- Fabrics made from textured yarns exhibit the classic FRP behaviour of a constantly falling drying rate, as reported in previous studies on this topic.
- Fabrics made from non-textured yarns show two phases of constant drying rate. The latter has a significantly lower rate, resulting in long drying times for the final few percentages of residual liquid. The yarn diameter significantly affects the appearance of this phase.
- The inter-yarn pores have a significant impact on the orientation and size of the macroscopic spread of liquid in knitted fabrics, as liquid cannot pass through inter-yarn pores larger than a certain size, and must follow the tortuous yarn path. This can be observed in fabrics with different yarn structures and machine gauges.
- Intra-yarn pore sizes affect the liquid spreading dynamics and the late drying stages of the FRP.
- Ultimately, the structure of the fabric and its combined wicking and drying behaviour are affected by the parameters of the material, the yarn-forming process and the knitting process. It was found that the structural measures of intra-yarn and inter-yarn pore radii assist the comprehension of liquid transport mechanisms in knitted fabrics. Therefore, the mechanisms observed in this study motivate the optimisation of drying behaviour by combining different structures to achieve the desired properties.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pauly, L.; Maier, L.; Schmied, S.; Dinkelmann, A.; Nieken, U.; Gresser, G.T. Modelling Pore Size Distribution Function of Twist-Texturized Yarns and Single-Jersey Knitted Fabrics. Fibers 2025, 13, 48. [Google Scholar] [CrossRef]
- Fischer, R.; Schlepütz, C.M.; Rossi, R.M.; Derome, D.; Carmeliet, J. Wicking through Complex Interfaces at Interlacing Yarns. J. Colloid Interface Sci. 2022, 626, 416–425. [Google Scholar] [CrossRef]
- Das, B.; Das, A.; Kothari, V.K.; Fangueiro, R.; de Araújo, M. MOISTURE TRANSMISSION THROUGH TEXTILES Part II: Evaluation Methods and Mathematical Modelling. AUTEX Res. J. 2007, 7, 194–216. [Google Scholar] [CrossRef]
- Patnaik, A.; Rengasamy, R.S.; Kothari, V.K.; Ghosh, A. Wetting and Wicking in Fibrous Materials. Text. Prog. 2006, 38, 1–105. [Google Scholar] [CrossRef]
- Jhanji, Y.; Gupta, D.; Kothari, V.K. Moisture Management and Wicking Properties of Polyester- Cotton Plated Knits. Indian J. Fibre Text. Res. 2017, 42, 183–188. [Google Scholar]
- Hussainn, S.; Glombikova, V.; Akhtar, N.; Mazari, A.; Mansoor, T.; Khan, K.A.H. Liquid Moisture Transportation Properties of Functional Underwears: Part 1. Autex Res. J. 2019, 19, 97–103. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, L.; Naveed, T.; Zhang, P.; Farooq, A. Influence of Fabric Structure and Finishing Pattern on the Thermal and Moisture Management Properties of Unidirectional Water Transport Knitted Polyester Fabrics. Text. Res. J. 2019, 89, 1983–1996. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Ishtiaque, S.M.; Uttam, D. Impact of Structural Variations in Hollow Yarn on Heat and Moisture Transport Properties of Fabrics. J. Text. Inst. 2011, 102, 700–712. [Google Scholar] [CrossRef]
- Onofrei, E.; Rocha, A.M.; Catarino, A. The Influence of Knitted Fabrics’ Structure on the Thermal and Moisture Management Properties. J. Eng. Fibers Fabr. 2011, 6, 10–22. [Google Scholar] [CrossRef]
- Choudhary, A.K. Ramratan the Influence of Yarn and Knit Structure on Moisture Management Properties of Sportswear Fabric. J. Inst. Eng. India Ser. E 2020, 101, 77–90. [Google Scholar] [CrossRef]
- Kim, H.; Michielsen, S.; DenHartog, E. Wicking in Textiles at Rates Comparable to Human Sweating. Colloids Surf. A Physicochem. Eng. Asp. 2021, 622, 126726. [Google Scholar] [CrossRef]
- Parada, M.; Vontobel, P.; Rossi, R.M.; Derome, D.; Carmeliet, J. Dynamic Wicking Process in Textiles. Transp. Porous Med. 2017, 119, 611–632. [Google Scholar] [CrossRef]
- Birrfelder, P.; Dorrestijn, M.; Roth, C.; Rossi, R.M. Effect of Fiber Count and Knit Structure on Intra- and Inter-Yarn Transport of Liquid Water. Text. Res. J. 2013, 83, 1477–1488. [Google Scholar] [CrossRef]
- Gurudatt, K.; Nadkarni, V.M.; Khilar, K.C. A Study on Drying of Textile Substrates and a New Concept for the Enhancement of Drying Rate. J. Text. Inst. 2010, 101, 635–644. [Google Scholar] [CrossRef]
- Onal, L.; Arslan, C.; Pasayev, N. Relation Between Structural Parameters and Drying Properties of Cotton Knitted Fabrics. Tekst. Ve Konfeksiyon 2013, 23, 357–363. [Google Scholar]
- Cay, A.; Gurlek, G.; Oglakcioglu, N. Analysis and Modeling of Drying Behavior of Knitted Textile Materials. Dry. Technol. 2017, 35, 509–521. [Google Scholar] [CrossRef]
- Chen, Q.; Tang, K.-P.M.; Ma, P.; Jiang, G.; Xu, C. Thermophysiological Comfort Properties of Polyester Weft-Knitted Fabrics for Sports T-Shirt. J. Text. Inst. 2017, 108, 1421–1429. [Google Scholar] [CrossRef]
- Kissa, E. Wetting and Wicking. Text. Res. J. 1996, 66, 660–668. [Google Scholar] [CrossRef]
- Kumar, A.; Kleinen, J.; Venzmer, J.; Trybala, A.; Starov, V.; Gambaryan-Roisman, T. Spreading and Imbibition of Vesicle Dispersion Droplets on Porous Substrates. Colloids Interfaces 2019, 3, 53. [Google Scholar] [CrossRef]
- Liu, Y.; Kang, Y.; Luo, M.; Ma, P. Unidirectional Wettability Performances of Weft-Knitted Fabric Based on Yarn Structure. Fibers Polym. 2022, 23, 827–835. [Google Scholar] [CrossRef]
- Gillespie, T. The Spreading of Low Vapor Pressure Liquids in Paper. J. Colloid Sci. 1958, 13, 32–50. [Google Scholar] [CrossRef]
- Kawase, T.; Sekoguchi, S.; Fuj, T.; Minagawa, M. Spreading of Liquids in Textile Assemblies. Text. Res. J. 1986, 56, 409–414. [Google Scholar] [CrossRef]
- Gonçalves, M.; Kim, J.Y.; Kim, Y.; Rubab, N.; Jung, N.; Asai, T.; Hong, S.; Weon, B.M. Droplet Evaporation on Porous Fabric Materials. Sci. Rep. 2022, 12, 1087. [Google Scholar] [CrossRef]
- Rahimi, A.; Metzger, T.; Kharaghani, A.; Tsotsas, E. Interaction of droplets with porous structures: Pore network simulation of wetting and drying. Dry. Technol. 2016, 34, 1129–1140. [Google Scholar] [CrossRef]
- Kharaghani, A. Drying and Wetting of Capillary Porous Materials: Insights from Imaging and Physics-Based Modeling. Ph.D. Thesis, Otto-von-Guericke-University, Magdeburg, Germany, 2020. [Google Scholar]
- Sampath, M.; Mani, S.; Nalankilli, G. Effect of Filament Fineness on Comfort Characteristics of Moisture Management Finished Polyester Knitted Fabrics. J. Ind. Text. 2011, 41, 160–173. [Google Scholar] [CrossRef]
- Fei, L.; Qin, F.; Zhao, J.; Derome, D.; Carmeliet, J. Pore-Scale Study on Convective Drying of Porous Media. Langmuir 2022, 38, 6023–6035. [Google Scholar] [CrossRef]
- Steele, R. Part I: Drying Behavior. Text. Res. J. 1958, 28, 136–144. [Google Scholar] [CrossRef]
- Hassan, M.M.; Leighs, S.J. Quick Dry Ability of Various Quick Drying Polyester and Wool Fabrics Assessed by a Novel Method. Dry. Technol. 2017, 35, 585–592. [Google Scholar] [CrossRef]
- Chau, K.-H.; Tang, K.-P.M.; Kan, C.-W. Constant Temperature Drying Rate Tester: Real-Time Water Evaporation Measurement of Fabrics. IEEE Trans. Instrum. Meas. 2018, 67, 2635–2648. [Google Scholar] [CrossRef]
- Guidoin, R.; King, M.; Marceau, D.; Cardou, A.; De La Faye, D.; Legendre, J.; Blais, P. Textile Arterial Prostheses: Is Water Permeability Equivalent to Porosity? J. Biomed. Mater. Res. 1987, 21, 65–87. [Google Scholar] [CrossRef]
- DIN EN ISO 13934-1; Textiles-Tensile Properties of Fabrics-Part 1: Determination of Maximum Force and Elongation at Maximum Force Using the Strip Method. ISO: Geneva, Switzerland, 2013.
- Pauly, L.; Maier, L.; Nieken, U.; Gresser, G.T. Physics-Based Modeling of the Effective Gas Transport Properties of Single Jersey Knitted Fabrics Based on Images. Text. Res. J. 2024, 94, 2543–2561. [Google Scholar] [CrossRef]
- Python Software Foundation Python Language Reference, Release 3.12. Available online: https://www.python.org (accessed on 28 July 2025).
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools 2000, 120, 122–125. [Google Scholar]



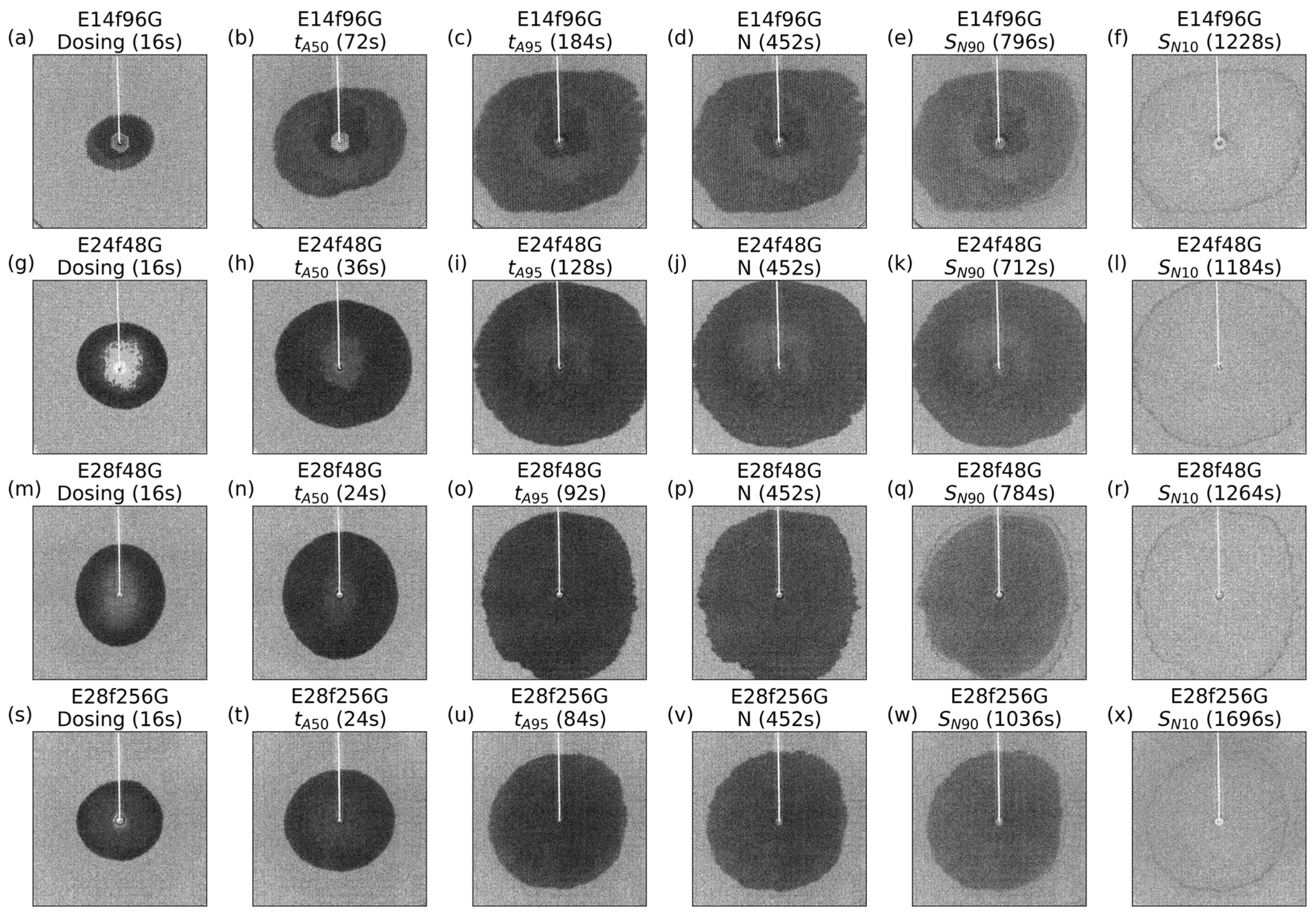
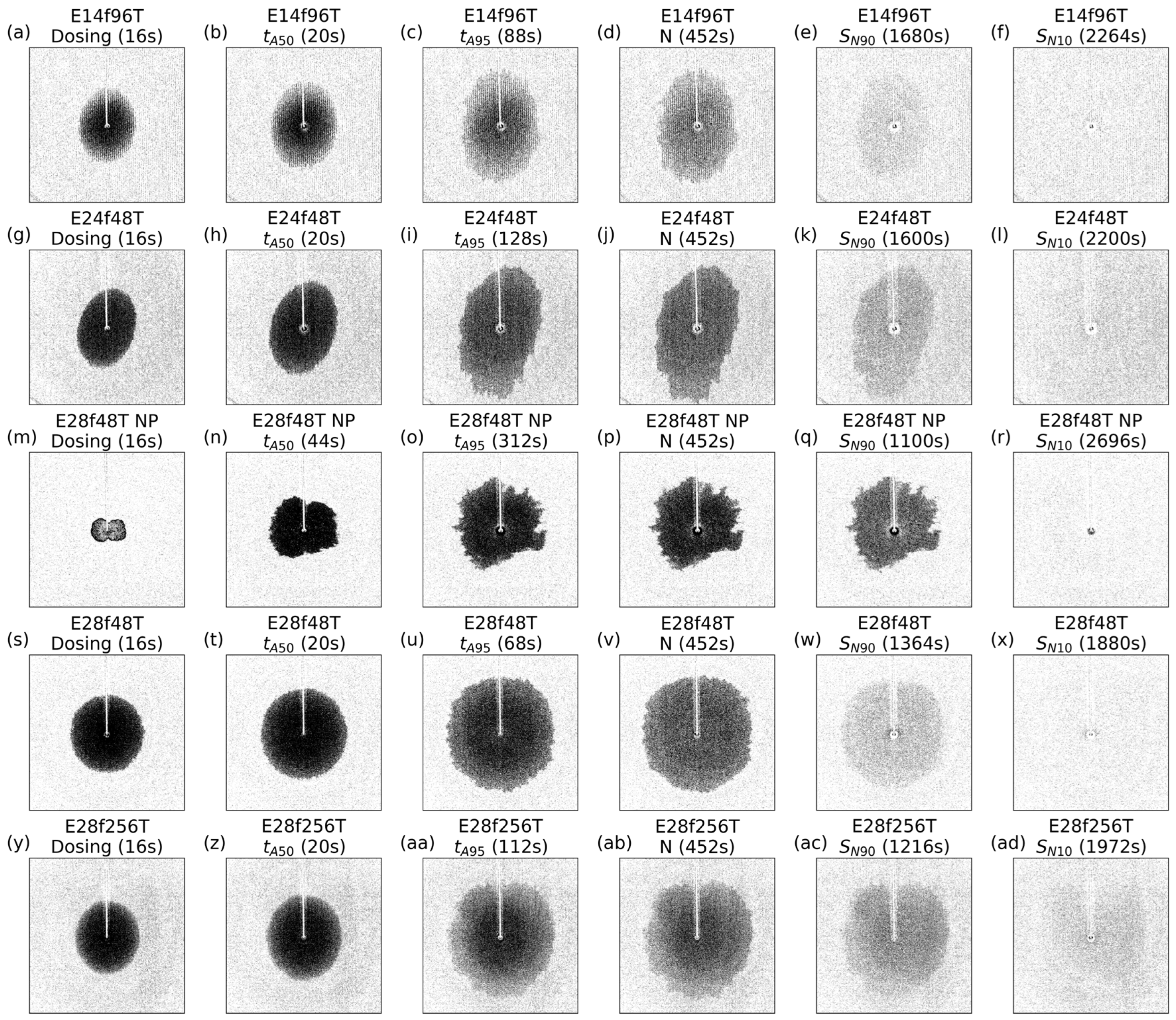
| Sample Name | Yarn | [mm] | [g/m2] | [-] | [µm] | [µm] |
|---|---|---|---|---|---|---|
| E28f48T E28f48T NP | PES dtex 196 f48/1 | 0.68 | 148 | 0.83 | 30 | 142 |
| E24f48T | PES dtex 196 f48/1 | 0.79 | 144 | 0.87 | 22 | 169 |
| E14f96T | PES dtex 196 f48/2 | 1.01 | 196 | 0.86 | 37 | 215 |
| E28f48G | PES dtex 184 f48/1 | 0.36 | 129 | 0.73 | 9 | 190 |
| E24f48G | PES dtex 186 f48/1 | 0.35 | 111 | 0.77 | 11 | 208 |
| E14f96G | PES dtex 186 f48/2 | 0.47 | 126 | 0.81 | 11 | 383 |
| E28f256T | PES dtex 180 f256/1 | 0.61 | 128 | 0.86 | 15 | 153 |
| E28f256G | PES dtex 180 f256/1 | 0.36 | 135 | 0.73 | 6 | 178 |
| Sample Name | ||||||||
|---|---|---|---|---|---|---|---|---|
| E28f48T NP | 5.08 | 19.0 | 0.27 | 44 | 312 | 0.15 | 0.013 | 5.7 |
| E28f48T | 7.44 | 32.8 | 0.23 | 20 | 68 | 0.16 | 0.008 | 5.3 |
| E24f48T | 6.63 | 26.5 | 0.25 | 20 | 128 | 0.19 | 0.018 | 4.5 |
| E14f96T | 6.03 | 21.2 | 0.28 | 20 | 88 | 0.17 | 0.015 | 5.1 |
| E28f48G | 12.27 | 59.0 | 0.21 | 24 | 92 | 0.24 | 0.021 | 3.6 |
| E24f48G | 11.98 | 56.9 | 0.21 | 32 | 132 | 0.23 | 0.029 | 3.9 |
| E14f96G | 12.01 | 54.0 | 0.22 | 72 | 184 | 0.29 | 0.065 | 3.6 |
| E28f256T | 7.59 | 32.8 | 0.23 | 20 | 112 | 0.27 | 0.017 | 3.2 |
| E28f256G | 8.92 | 39.5 | 0.23 | 24 | 84 | 0.27 | 0.016 | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pauly, L.; Maier, L.; Schmied, S.; Nieken, U.; Gresser, G.T. Structure Design by Knitting: Combined Wicking and Drying Behaviour in Single Jersey Fabrics Made from Polyester Yarns. Fibers 2025, 13, 103. https://doi.org/10.3390/fib13080103
Pauly L, Maier L, Schmied S, Nieken U, Gresser GT. Structure Design by Knitting: Combined Wicking and Drying Behaviour in Single Jersey Fabrics Made from Polyester Yarns. Fibers. 2025; 13(8):103. https://doi.org/10.3390/fib13080103
Chicago/Turabian StylePauly, Leon, Lukas Maier, Sibylle Schmied, Ulrich Nieken, and Götz T. Gresser. 2025. "Structure Design by Knitting: Combined Wicking and Drying Behaviour in Single Jersey Fabrics Made from Polyester Yarns" Fibers 13, no. 8: 103. https://doi.org/10.3390/fib13080103
APA StylePauly, L., Maier, L., Schmied, S., Nieken, U., & Gresser, G. T. (2025). Structure Design by Knitting: Combined Wicking and Drying Behaviour in Single Jersey Fabrics Made from Polyester Yarns. Fibers, 13(8), 103. https://doi.org/10.3390/fib13080103







