Advanced Vibration of Functionally Graded Material Coupled Plates and Circular Shells with Four Layers
Abstract
Highlights
- Thermal vibration of FGM plate–cylindrical shells with four constituent layers is computed
- Nonlinear TSDT was used to obtain the GDQ results
- Advanced varied shear correction, environmental temperature, and FGM power law are considered
Abstract
1. Introduction
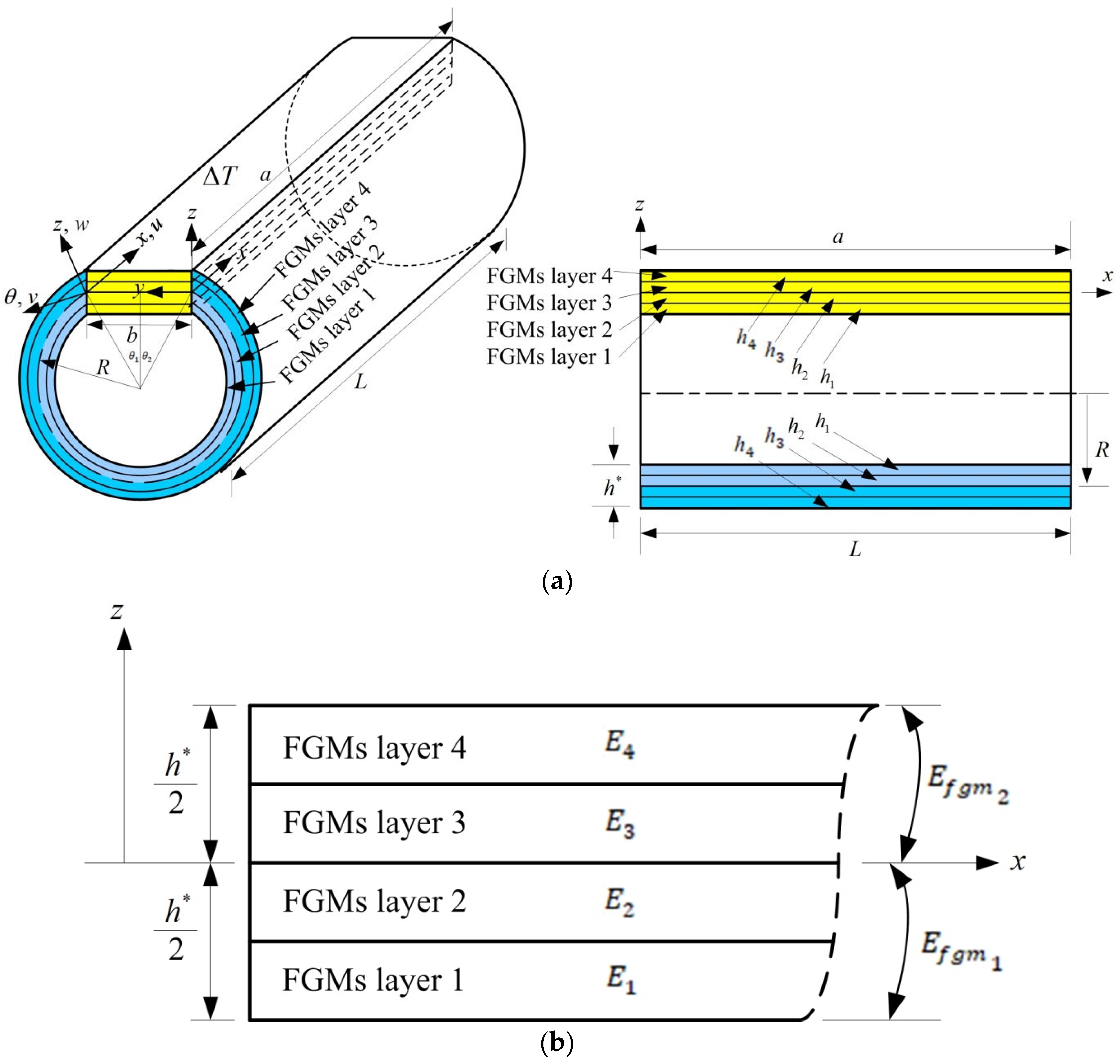
2. Formulation
2.1. Stiffness and
2.2. Stiffness Integrals for , …, and , …,
3. Numerical Results
3.1. Dynamic Convergence
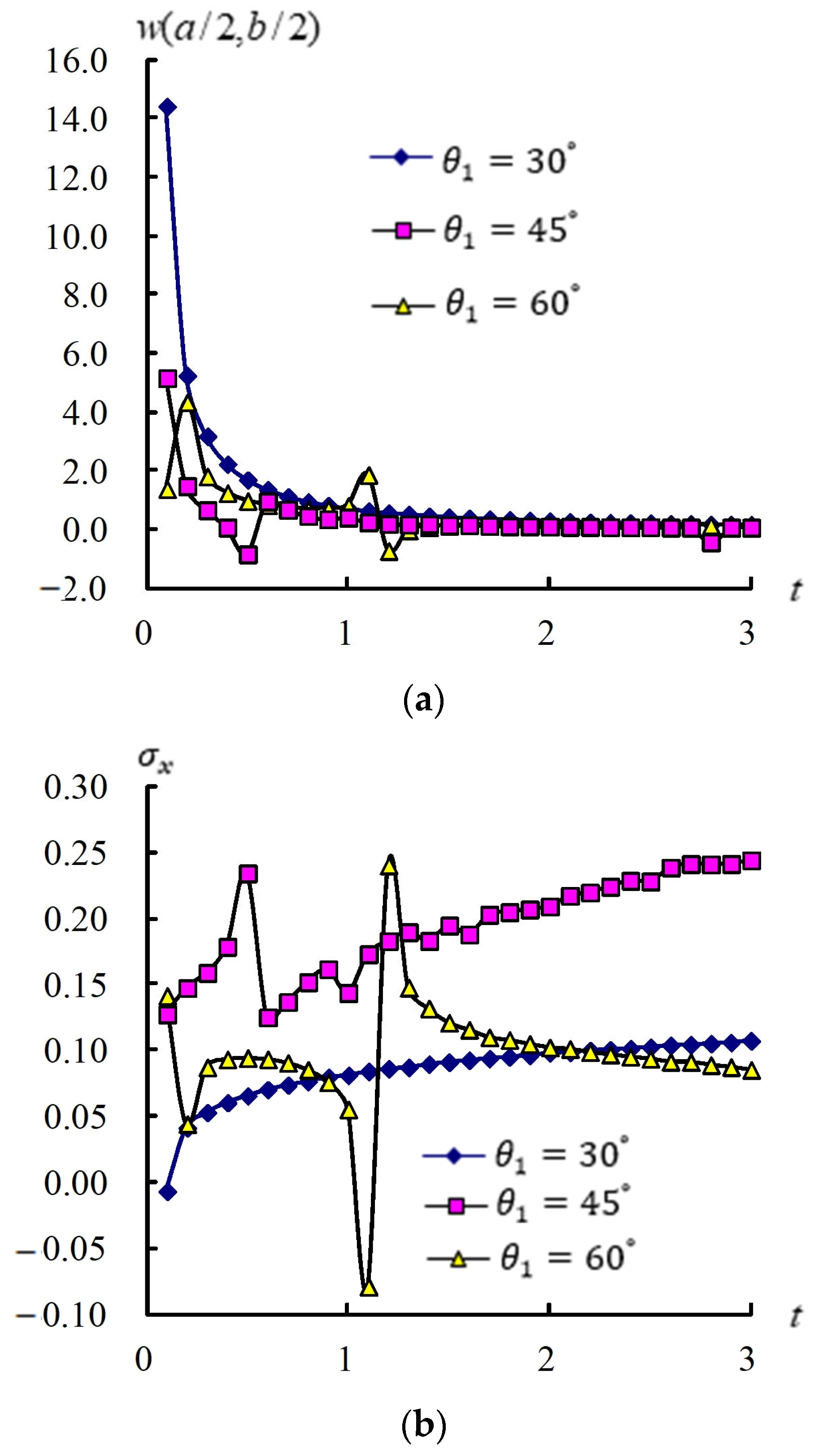
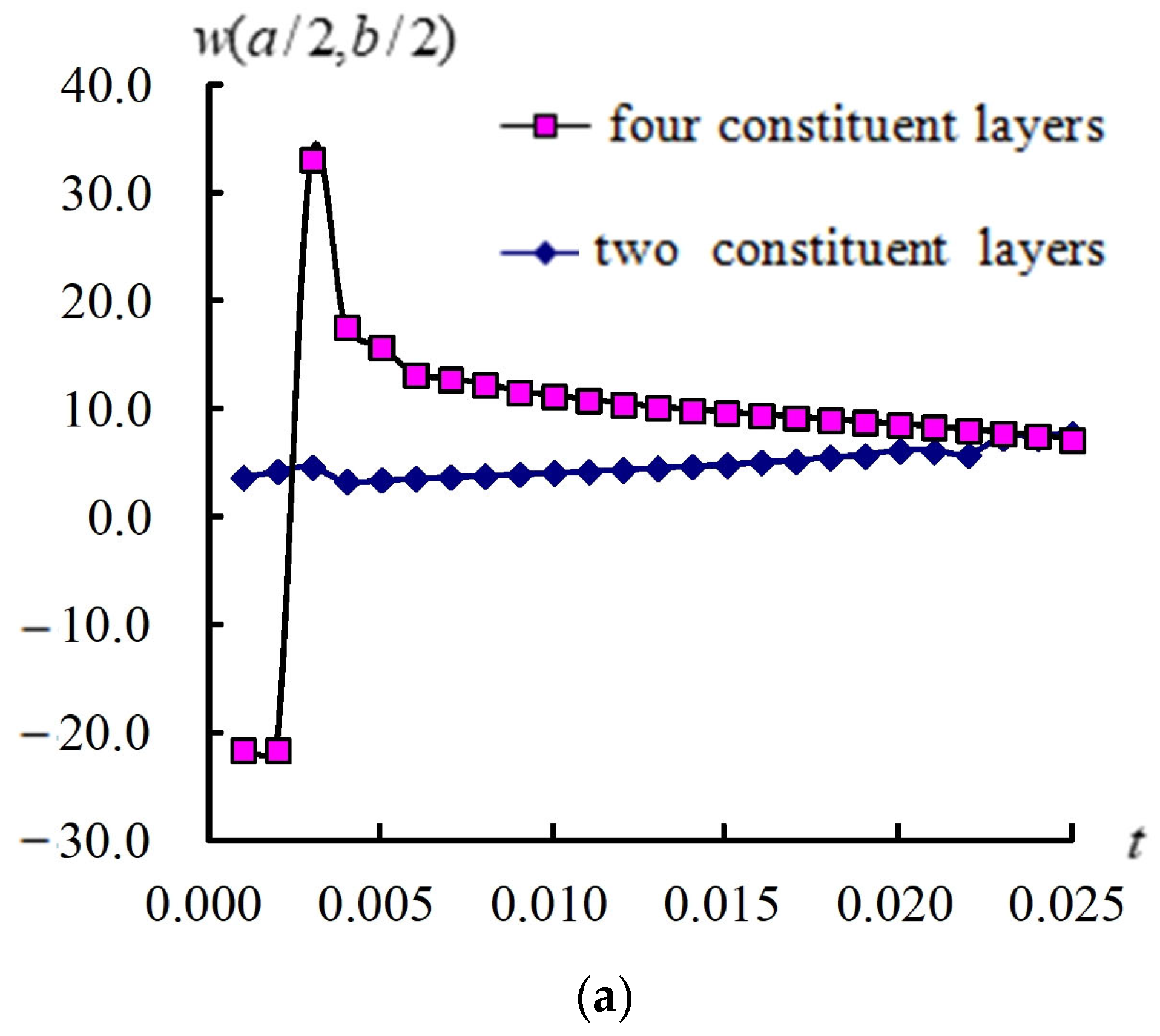
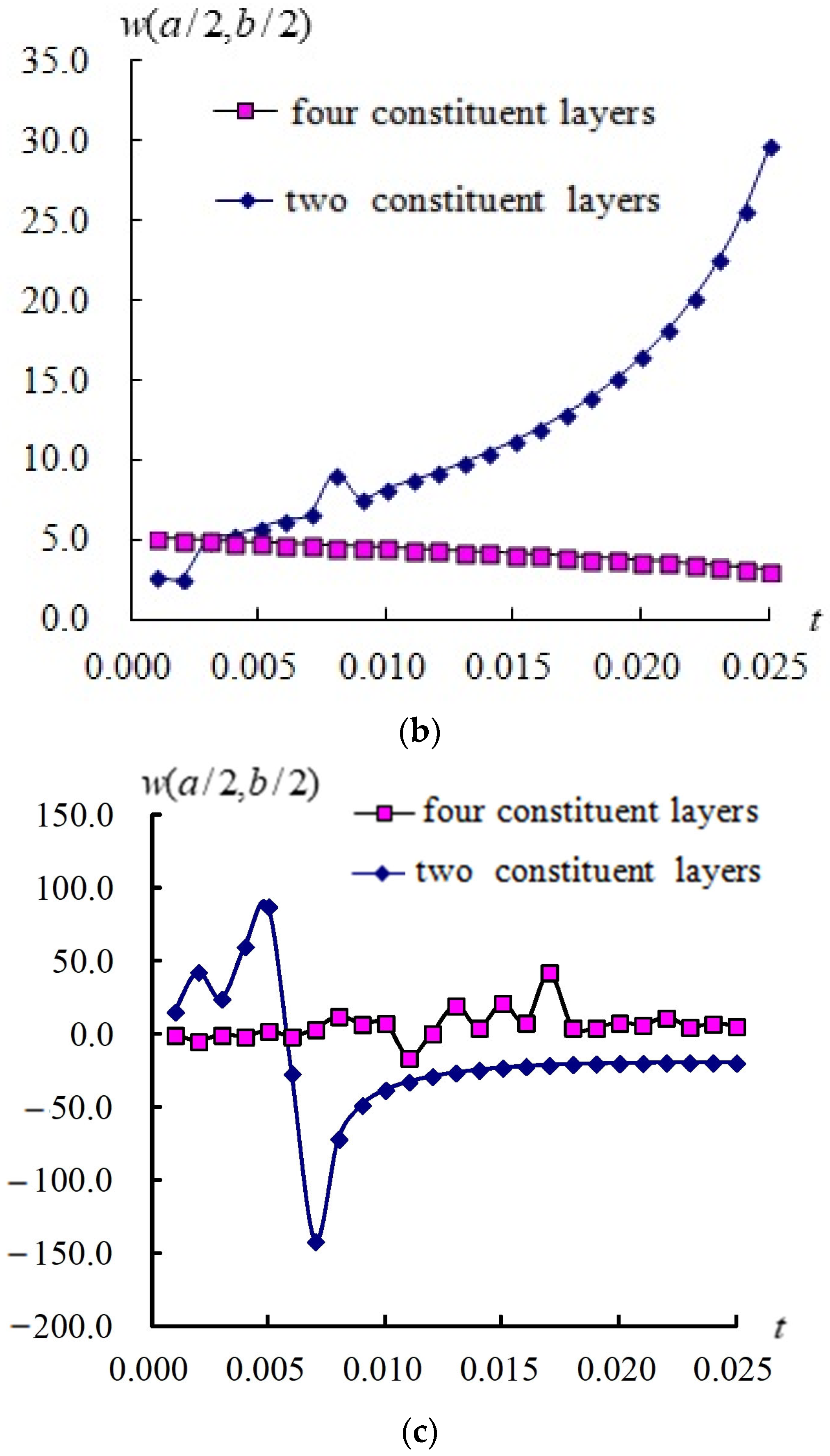
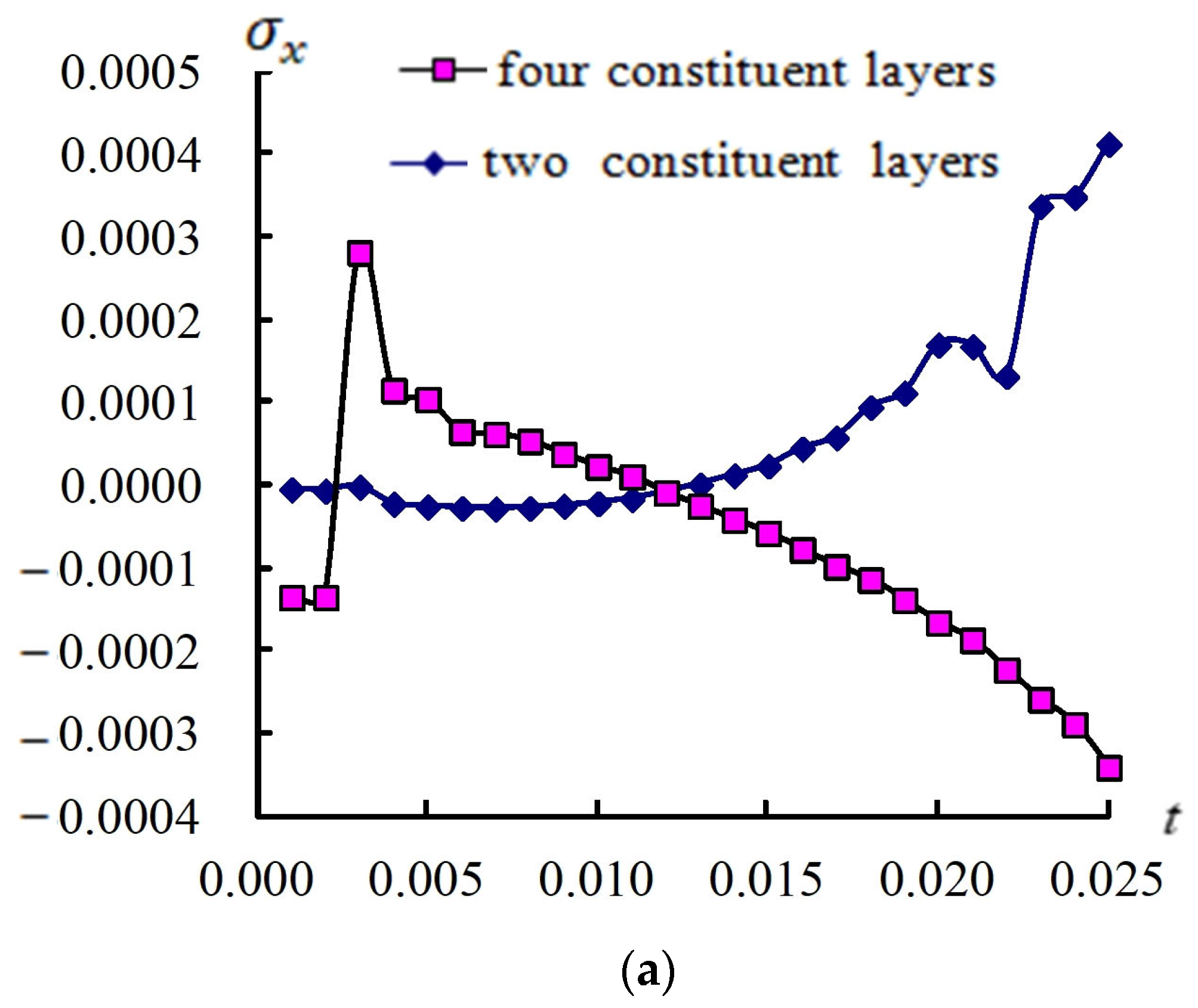
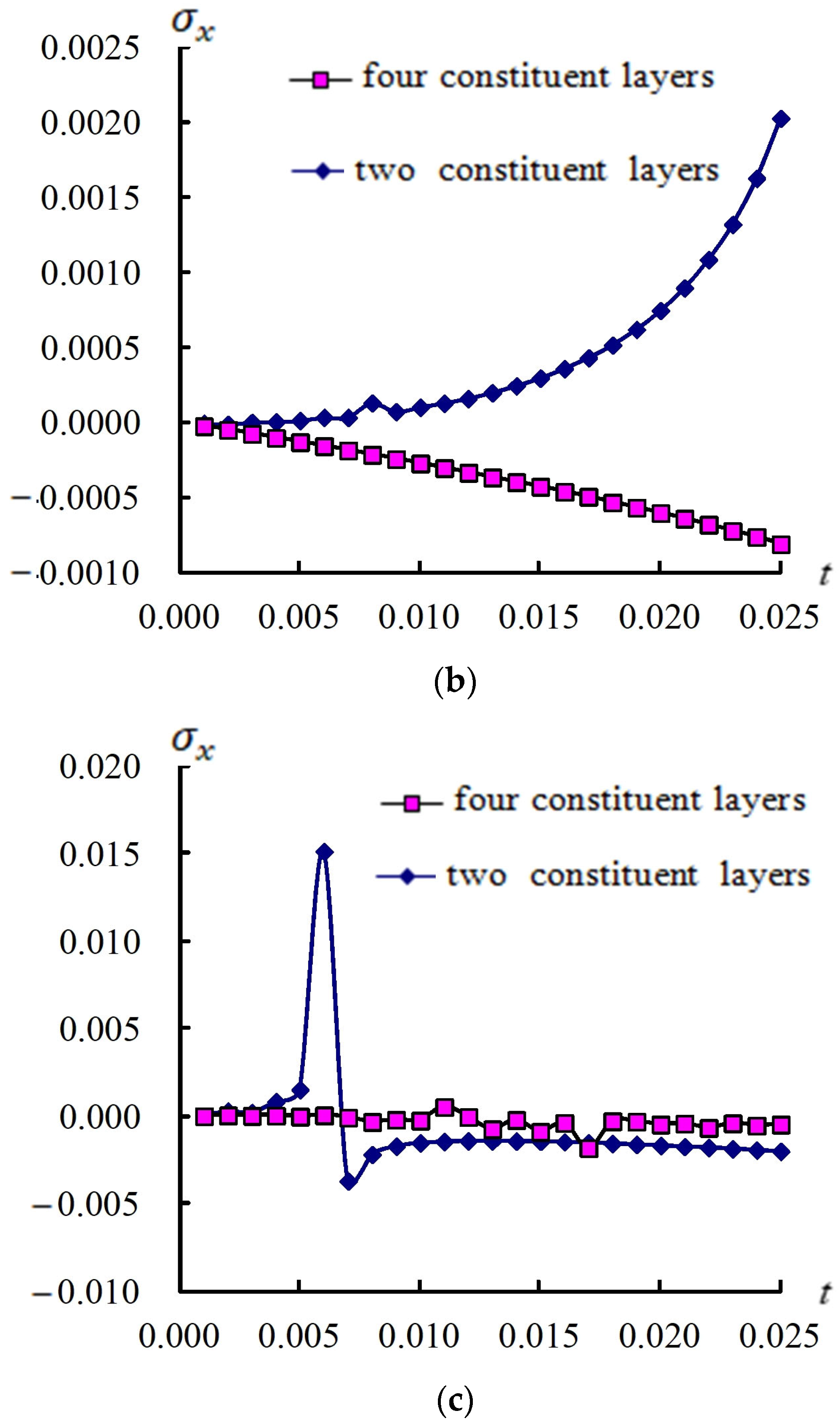
3.2. Responses for (a/2, b/2) and Stress
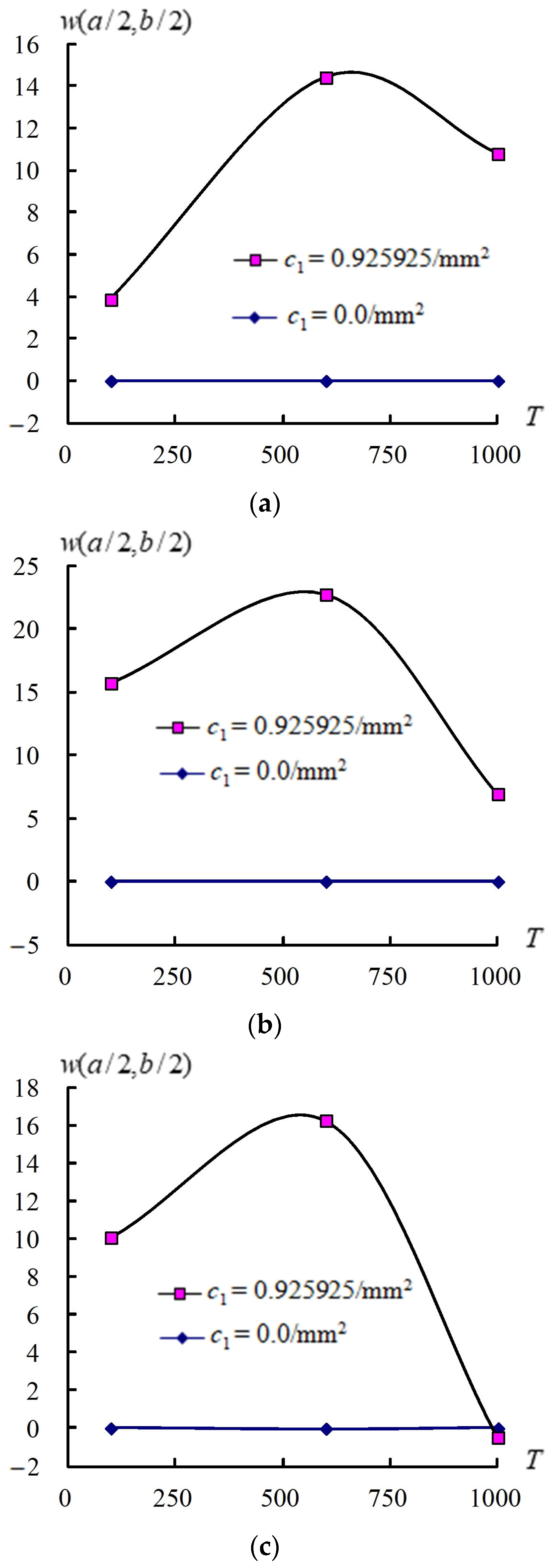
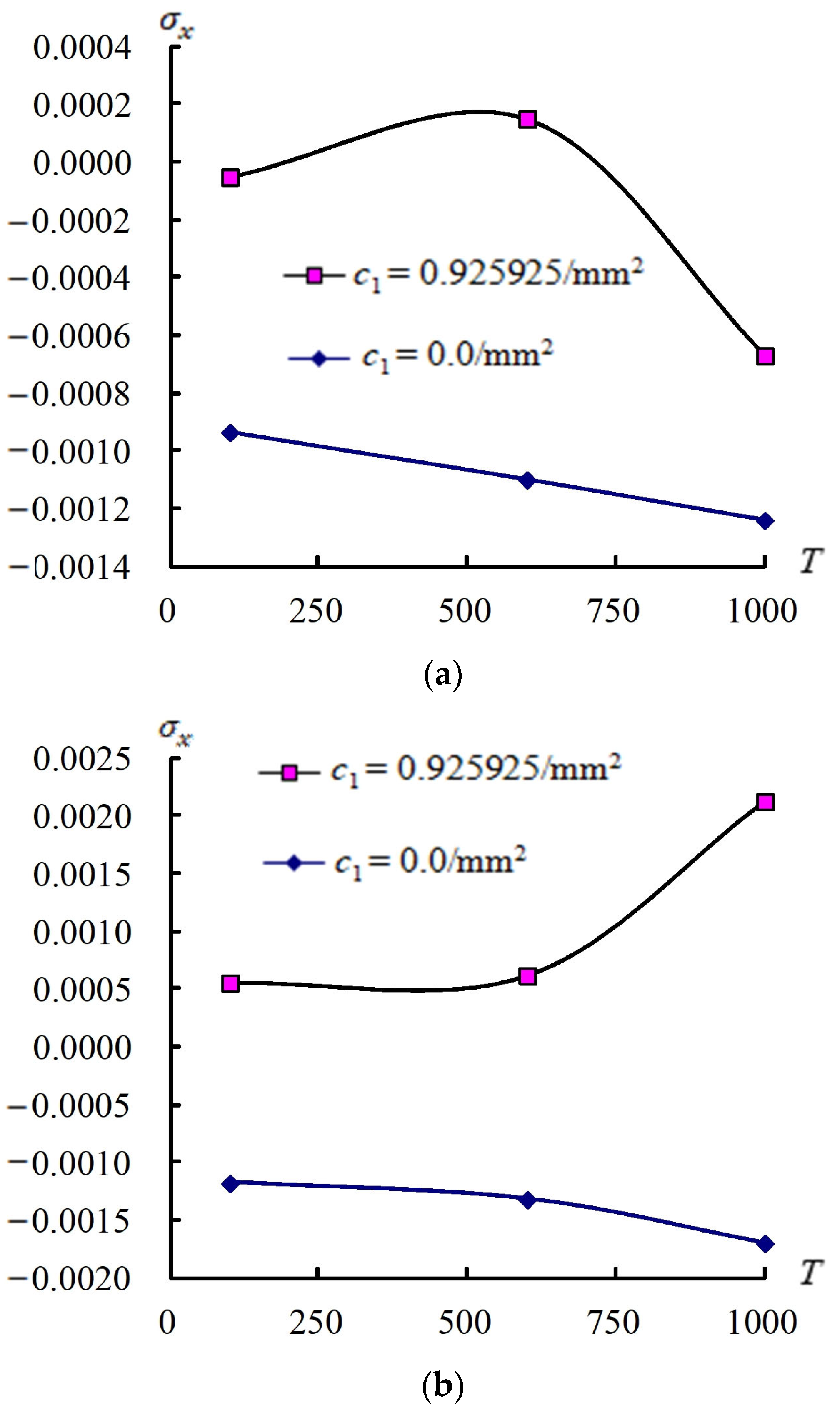
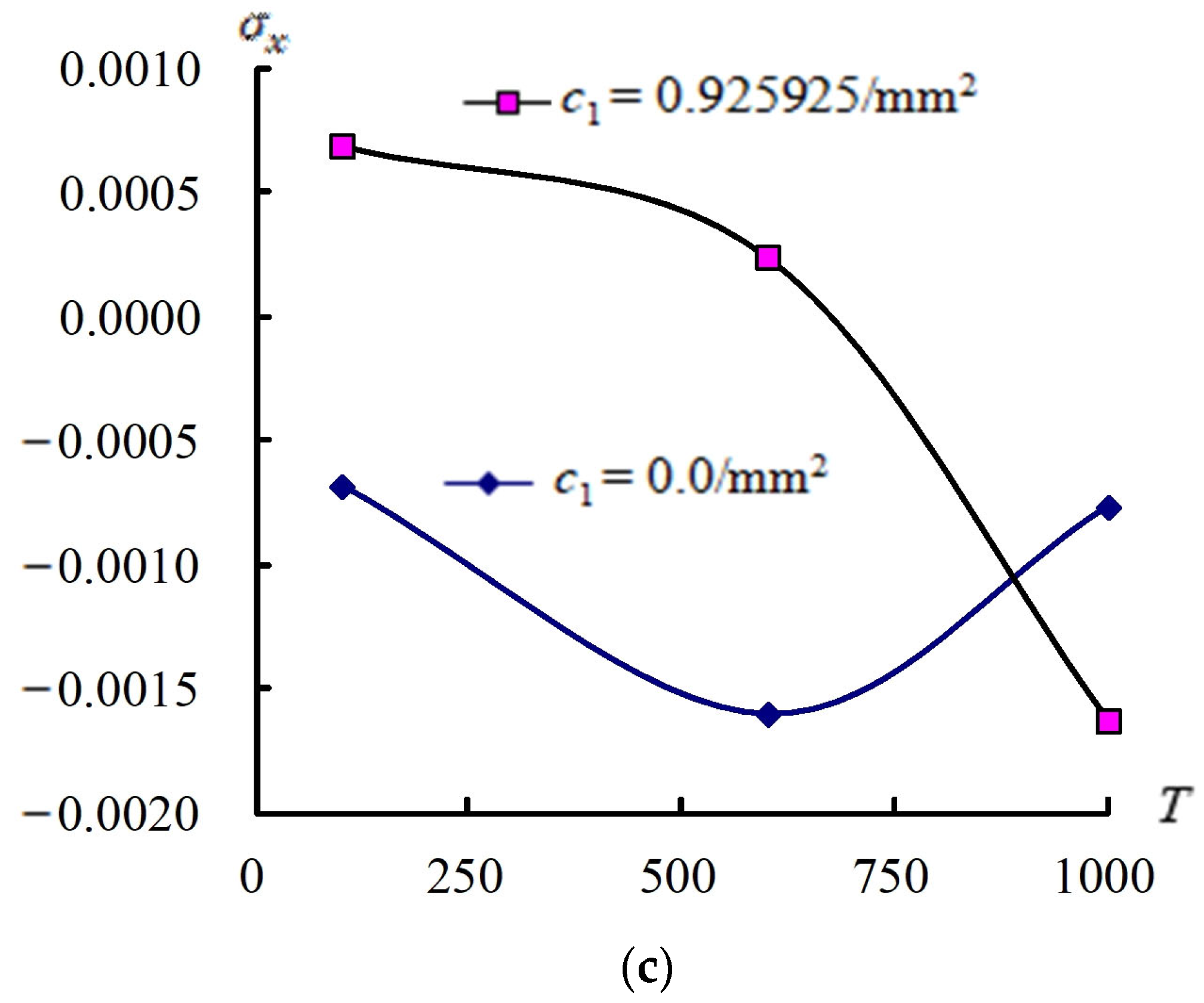
3.3. Responses of (a/2, b/2) and Versus T
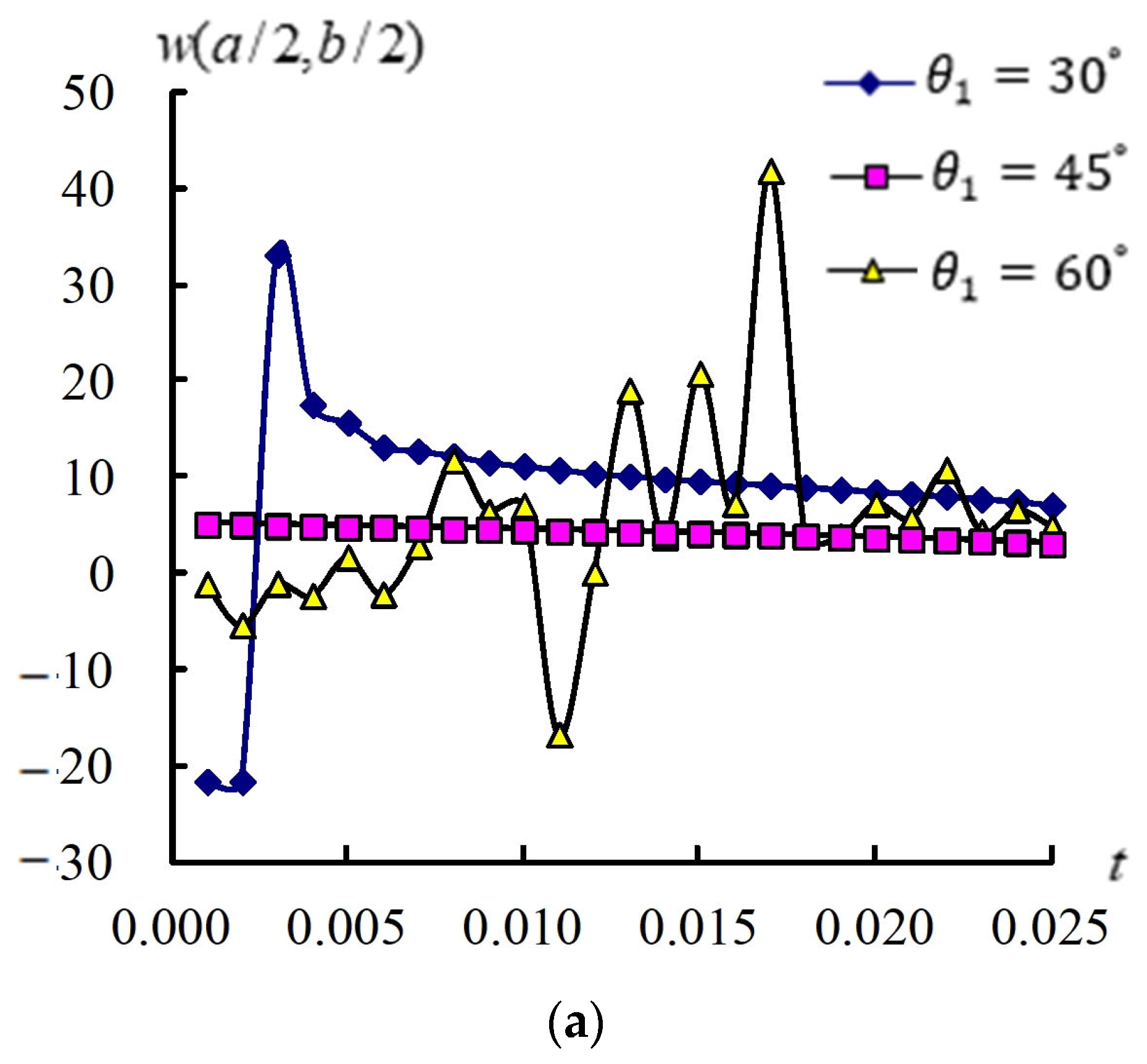
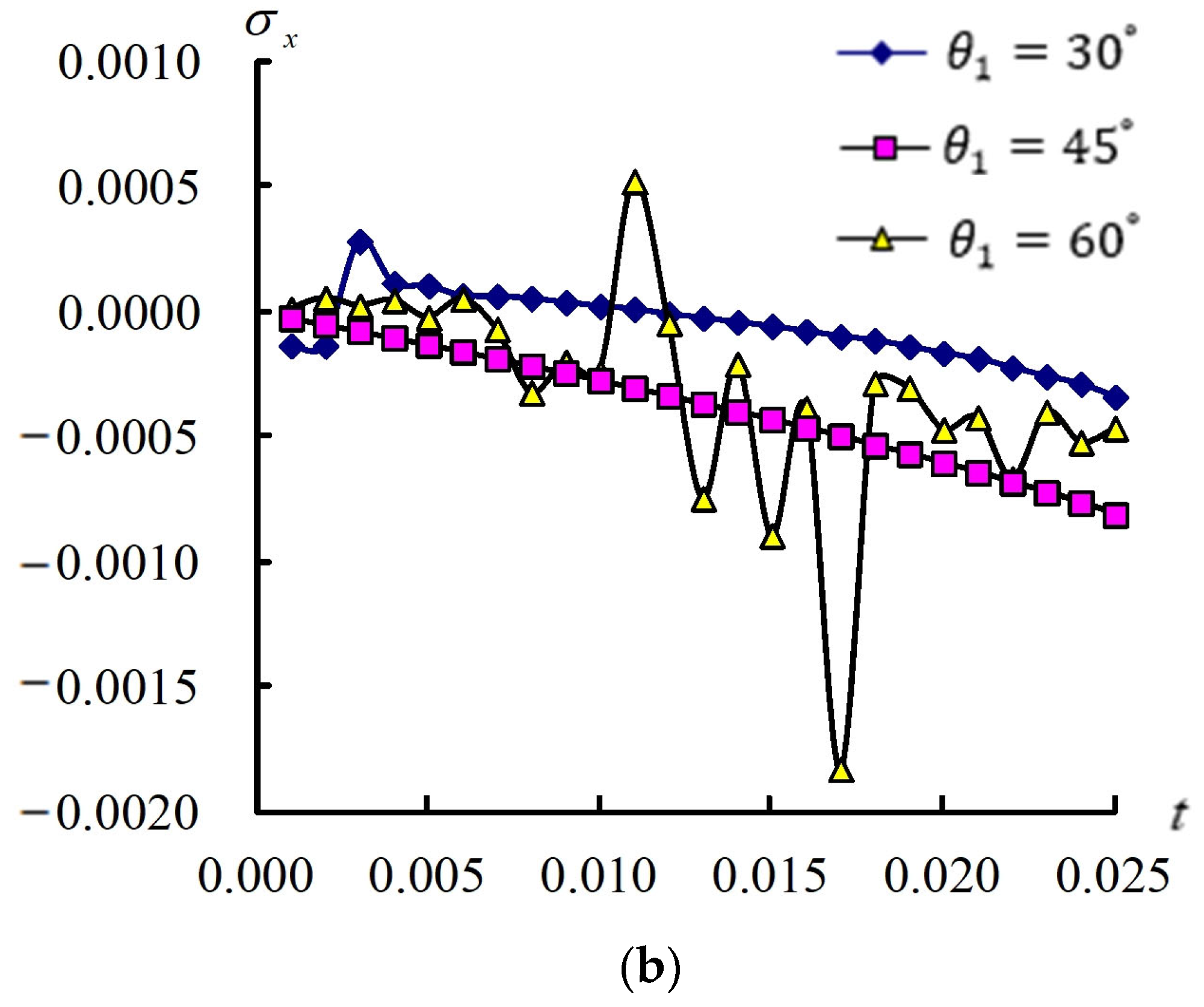
3.4. Transient Responses of (a/2, b/2) and
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Li, Z.; Jin, G.; Ye, T.; Yang, T.J.; Zhong, S.; Tian, L. A unified vibration modeling of open cylindrical shell-rectangular plate coupling structures based on the dynamic stiffness method. J. Sound Vib. 2023, 53, 117870. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, Y. Study on the influence of the internal elastic constraint stiffness on the vib-acoustic performance of a coupled plate-cylindrical shell system. Shock. Vib. 2023, 6668089, 1–11. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, A.; Qin, B.; Wang, Q.; Zhong, R. Investigation on vibration of the functionally graded material–stepped cylindrical shell coupled with annular plate in thermal environment. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 85–111. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, D.; He, D. Vibration characteristics of a laminated composite double-cylindrical shell system coupled with a variable number of annular plates. Materials 2022, 15, 4246. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.Y.; Yan, K.; Li, H.W.; Wang, X. Study on theoretical modeling and vibration performance of an assembled cylindrical shell-plate structure with whirl motion. Appl. Math. Model. 2022, 110, 618–632. [Google Scholar] [CrossRef]
- Zhao, Z.; Sheeng, M.; Yang, Y. Vibration transmission of a cylindrical shell with an interior rectangular plate with the receptance method. Adv. Acoust. Vib. 2012, 2012, 5817691. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.H.; Xing, J.T.; Price, W.G. A study of power flow in a coupled plate–cylindrical shell system. J. Sound Vib. 2004, 271, 863–882. [Google Scholar] [CrossRef]
- Messina, A.; Soldatos, K.P. Vibration of completely free composite plates and cylindrical shell panels by a higher-order theory. Int. J. Mech. Sci. 1999, 41, 891–918. [Google Scholar] [CrossRef]
- Hong, C.C. GDQ computation for thermal vibration of thick FGM plates by using third-order shear deformation theory. Mater. Sci. Eng. B 2023, 1294, 116208. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced dynamic thermal vibration of thick FGM plates-cylindrical shells. Ocean. Eng. 2022, 266, 112701. [Google Scholar] [CrossRef]
- Babaee, A.; Jelovica, J. Nonlinear transient thermoelastic response of FGM plate under sudden cryogenic cooling. Ocean. Eng. 2021, 226, 108875. [Google Scholar] [CrossRef]
- Lee, S.J.; Reddy, J.N.; Rostam-Abadi, F. Transient analysis of laminated composite plates with embedded smart-material layers. Finite Elem. Anal. Des. 2004, 40, 463–483. [Google Scholar] [CrossRef]
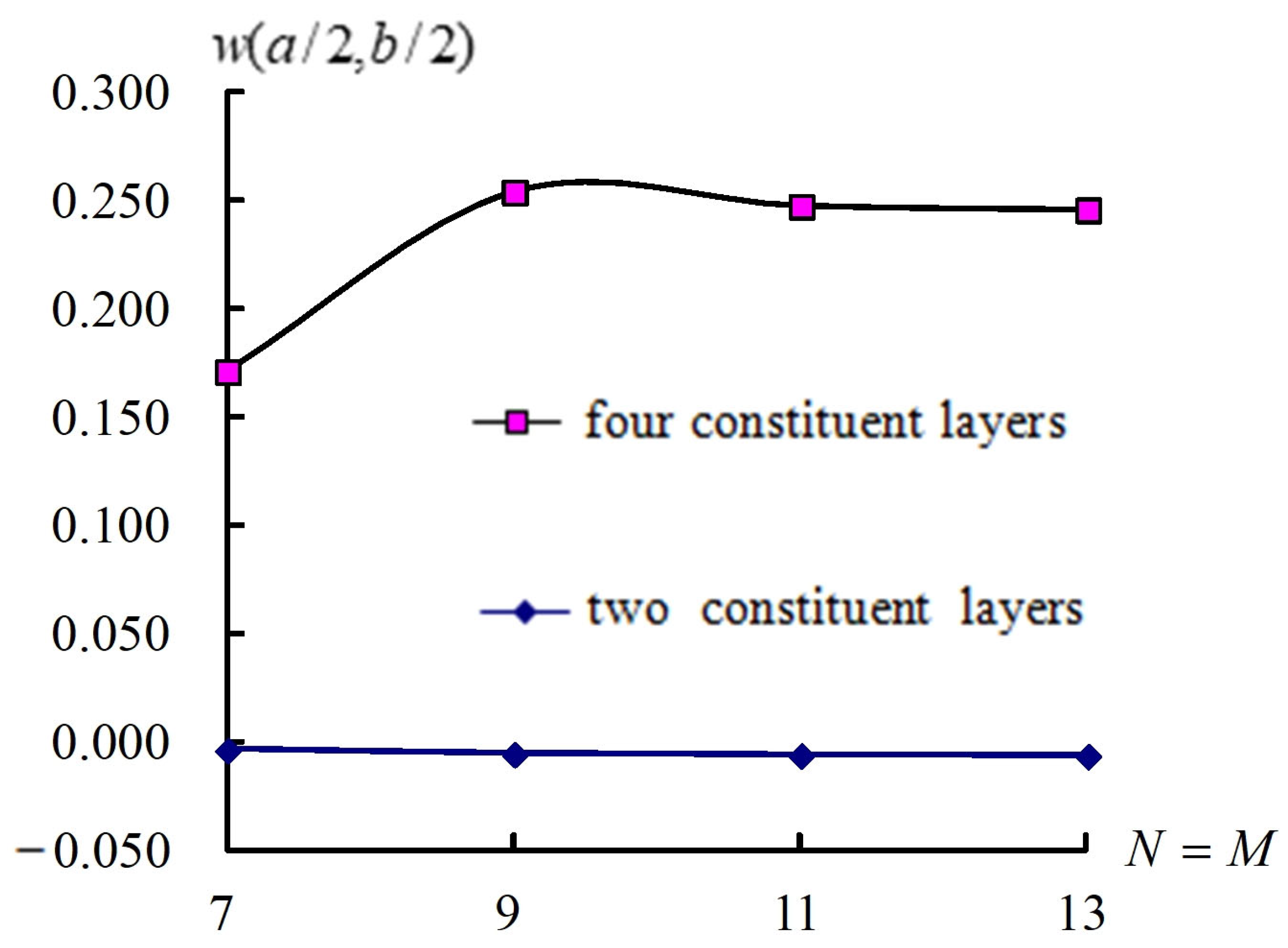
| L/ | GDQ Grids | (a/2, b/2) (mm) at t = 6 s | |||
|---|---|---|---|---|---|
| N × M | = 1 | = 2 | = 3 | ||
| 5 | 7 × 7 | 0.029018 | 0.170753 | 0.177768 | |
| 9 × 9 | 0.079825 | 0.253681 | −0.208156 | ||
| 11 × 11 | 0.034491 | 0.247196 | −0.184317 | ||
| 13 × 13 | 0.041132 | 0.245420 | −0.209937 | ||
| 7 × 7 | 0.011518 | 0.313653 | 0.071740 | ||
| 9 × 9 | 0.055920 | 0.332697 | 0.050863 | ||
| 11 × 11 | −0.001323 | 0.375168 | −0.093123 | ||
| 13 × 13 | 0.049634 | 0.387151 | −0.148491 | ||
| 7 × 7 | 0.006889 | 0.081579 | −0.054453 | ||
| 9 × 9 | 0.072284 | 0.320733 | 0.186224 | ||
| 11 × 11 | 0.162171 | 0.470269 | −0.065824 | ||
| 13 × 13 | 0.057590 | 0.976272 | −0.079881 | ||
| Number of Layers | (1/mm2) | T (K) | ||||
|---|---|---|---|---|---|---|
| = 1 | = 2 | |||||
| 4 | 0.925925 | 100 | −0.343867 | −0.207462 | −0.123929 | |
| 600 | −0.353743 | −0.222928 | −0.134674 | |||
| 1000 | −0.219714 | −0.137416 | −0.078338 | |||
| 2 | 100 | −0.619957 | −0.366153 | −0.214343 | ||
| 0 | 600 | −0.646208 | −0.398133 | −0.233597 | ||
| 1000 | −0.370177 | −0.231584 | −0.132588 | |||
| 100 | −0.922719 | 9.852628 | 1.273259 | |||
| 0.925925 | 600 | −3.535402 | 1.560071 | 0.855717 | ||
| 1000 | −0.252506 | −0.532898 | −1.614390 | |||
| 0 | 100 | 1.273499 | 1.317037 | 1.278385 | ||
| 600 | 1.20086 | 1.232039 | 1.199164 | |||
| 1000 | 1.516531 | 1.61682 | 1.563072 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.-C. Advanced Vibration of Functionally Graded Material Coupled Plates and Circular Shells with Four Layers. Fibers 2025, 13, 32. https://doi.org/10.3390/fib13030032
Hong C-C. Advanced Vibration of Functionally Graded Material Coupled Plates and Circular Shells with Four Layers. Fibers. 2025; 13(3):32. https://doi.org/10.3390/fib13030032
Chicago/Turabian StyleHong, Chih-Chiang. 2025. "Advanced Vibration of Functionally Graded Material Coupled Plates and Circular Shells with Four Layers" Fibers 13, no. 3: 32. https://doi.org/10.3390/fib13030032
APA StyleHong, C.-C. (2025). Advanced Vibration of Functionally Graded Material Coupled Plates and Circular Shells with Four Layers. Fibers, 13(3), 32. https://doi.org/10.3390/fib13030032






