Geometric Characterisation of Stochastic Fibrous Networks: A Comprehensive Review
Abstract
Highlights
- This study provides a comprehensive review of the geometrical characterization of stochastic fibrous networks, combining results from the literature with original research findings.
- This review focuses on the main parameters used to describe such networks, including basis weight, orientation distribution function, crimp, porosity, spatial distribution of fibres, and fibre intersections.
Abstract
1. Introduction
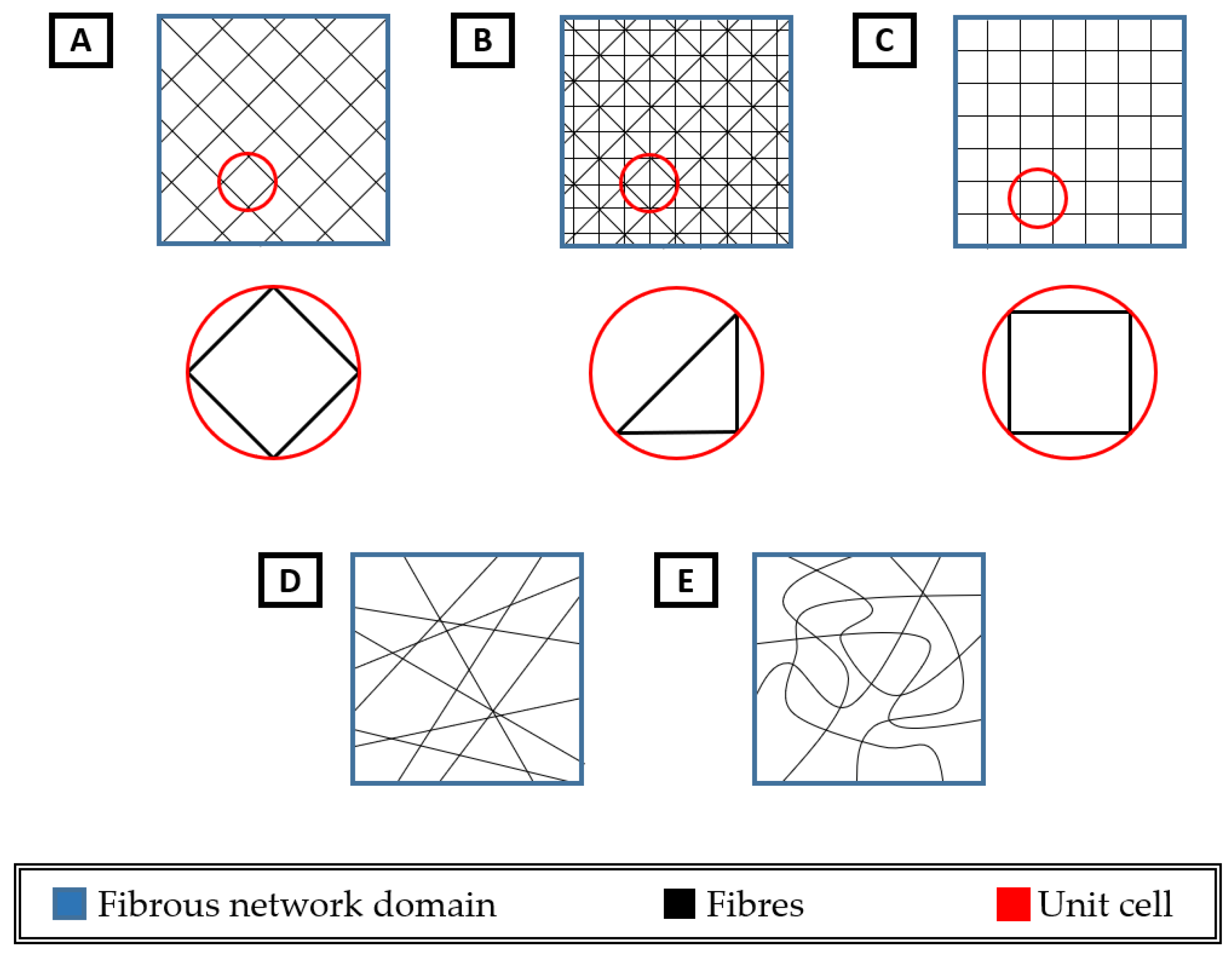
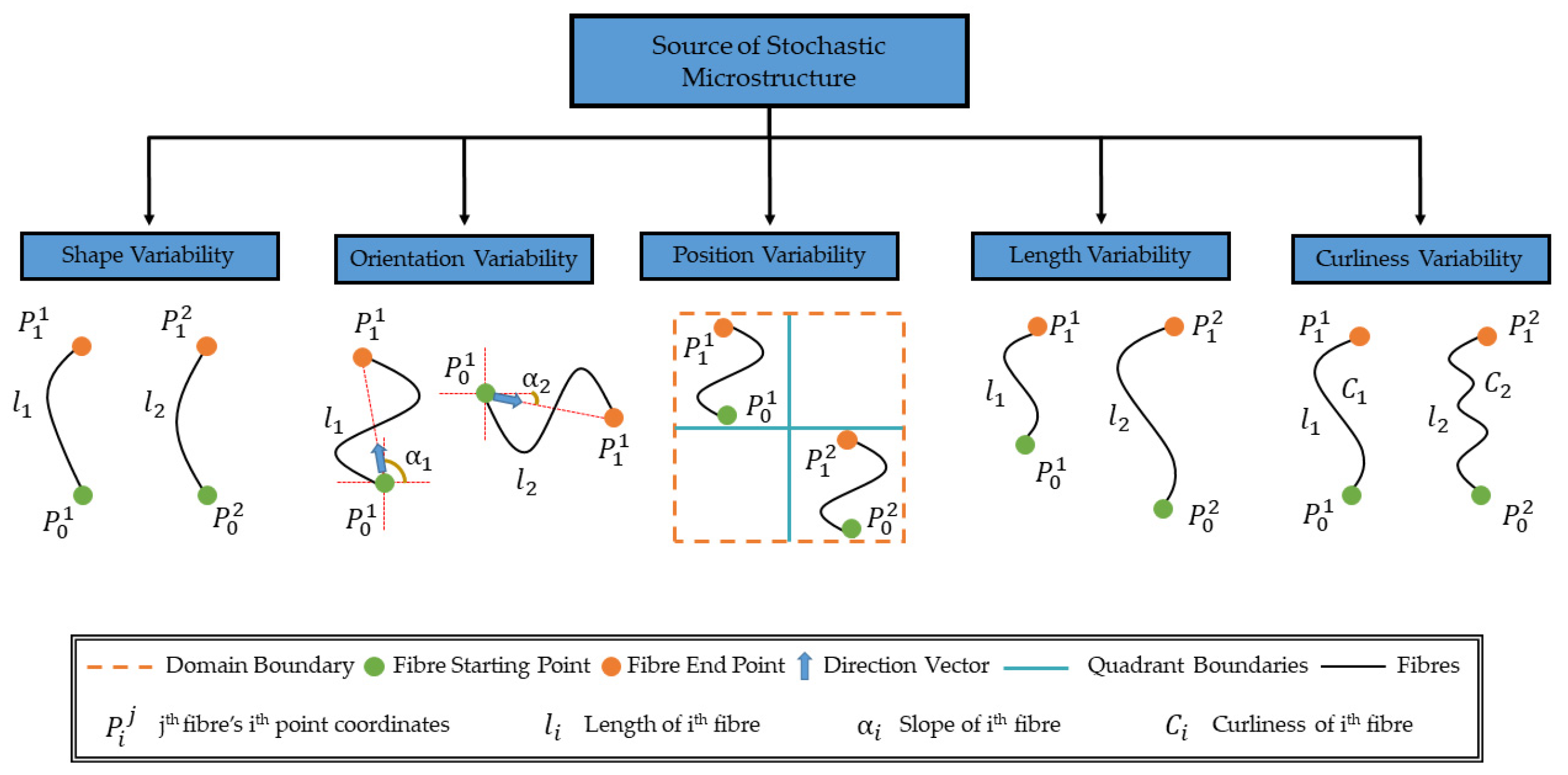
2. Regular Versus Random Microstructures
3. Geometric Characterisation Parameters
3.1. Basis Weight
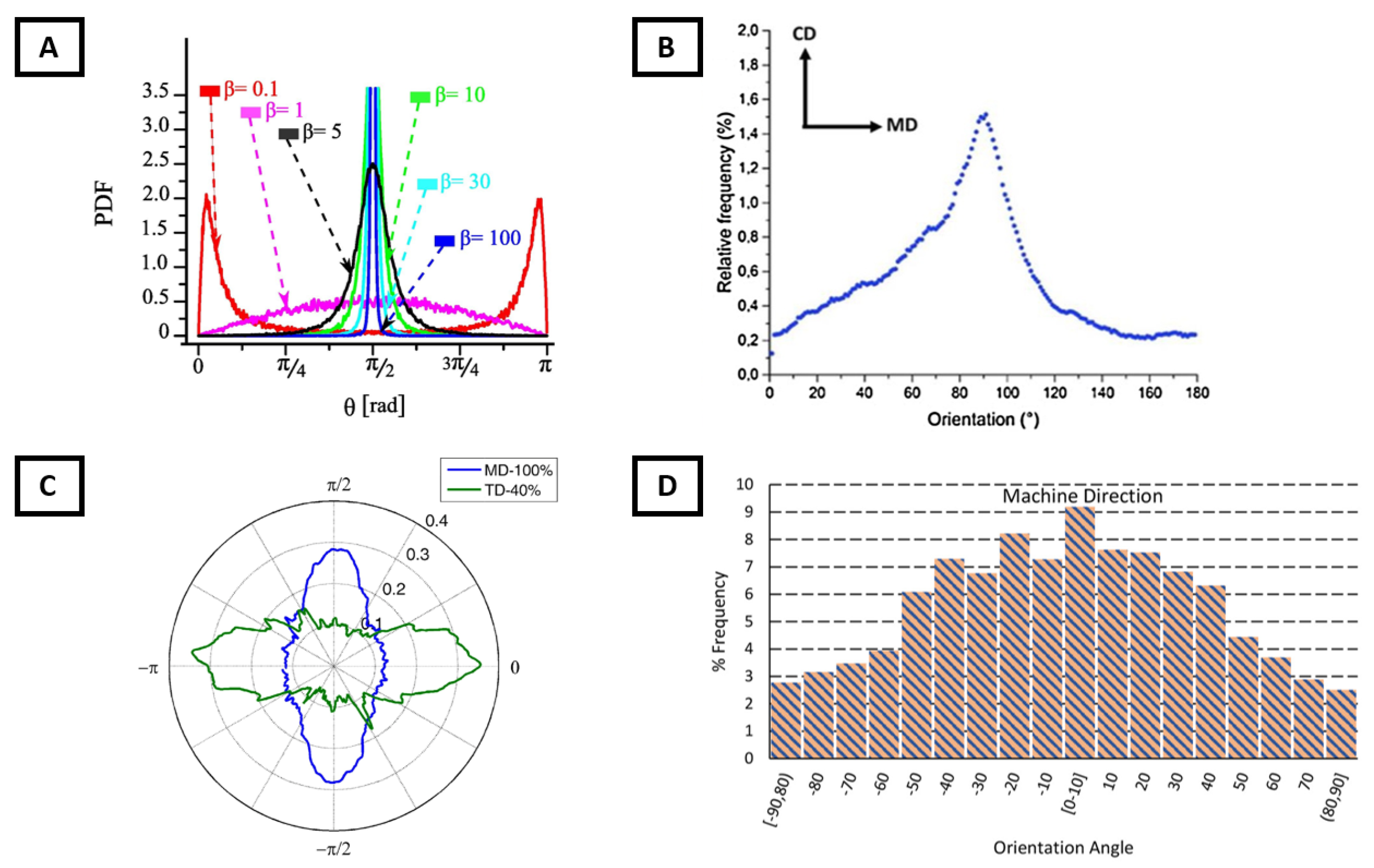
3.2. Orientation Distribution Function
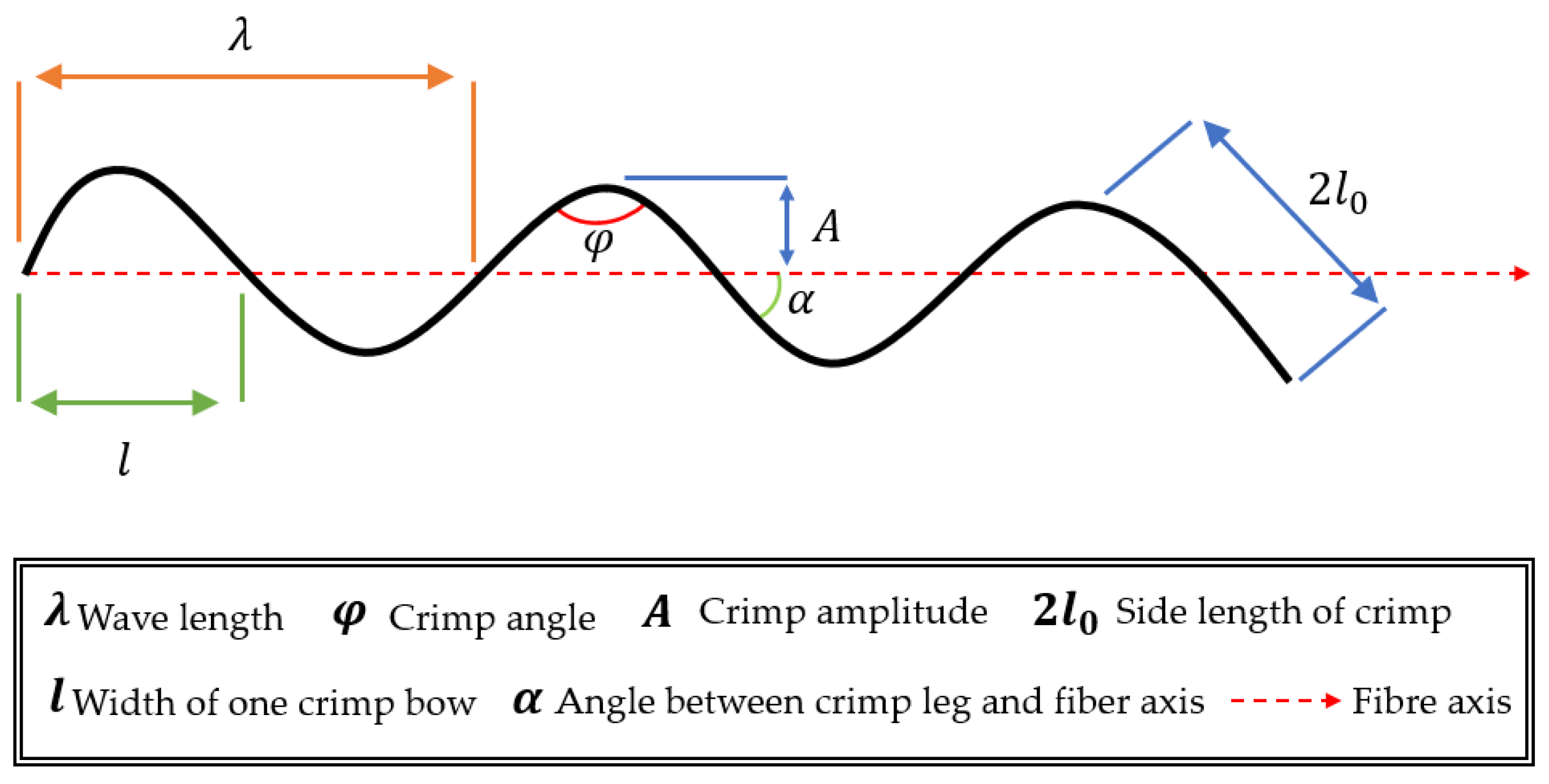
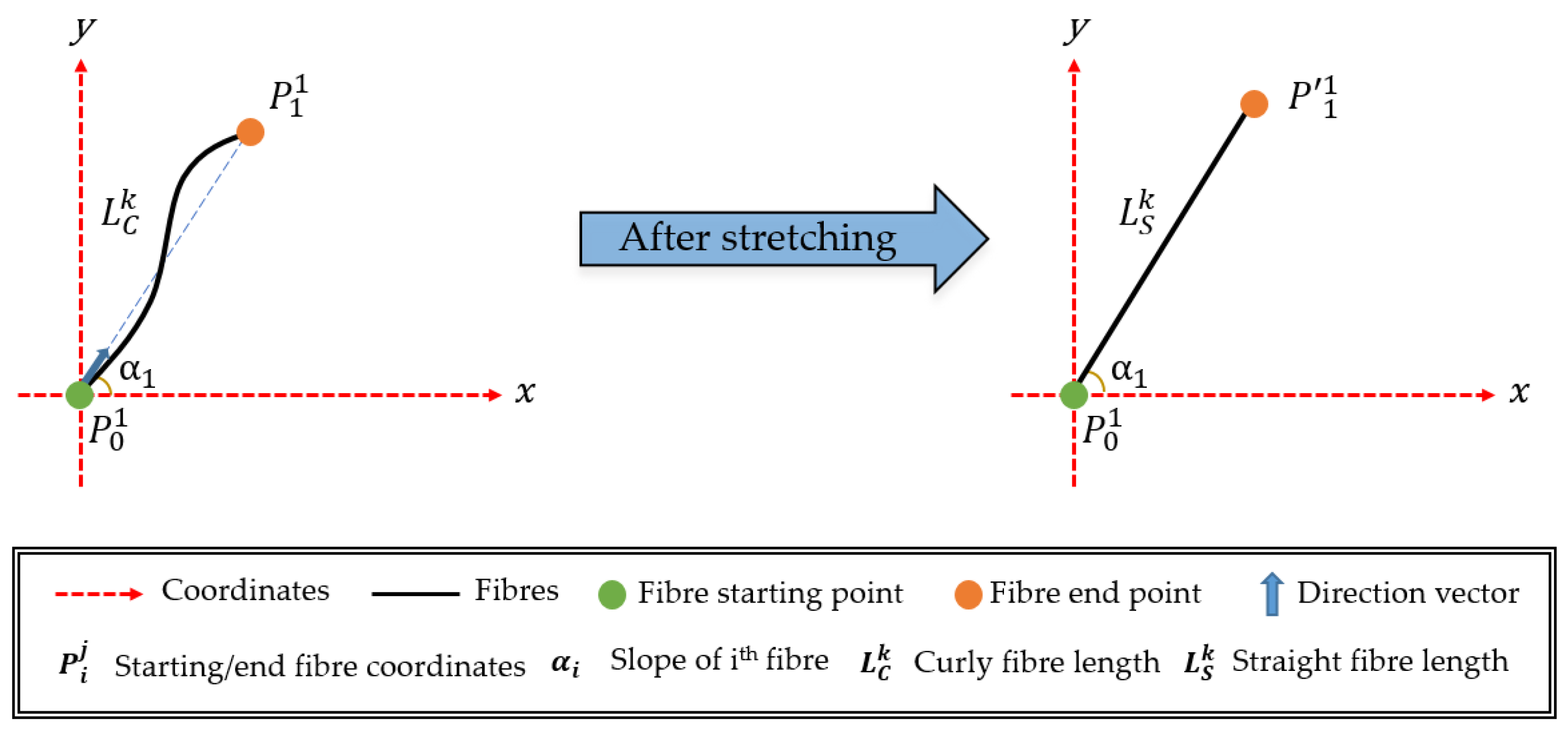
3.3. Crimp
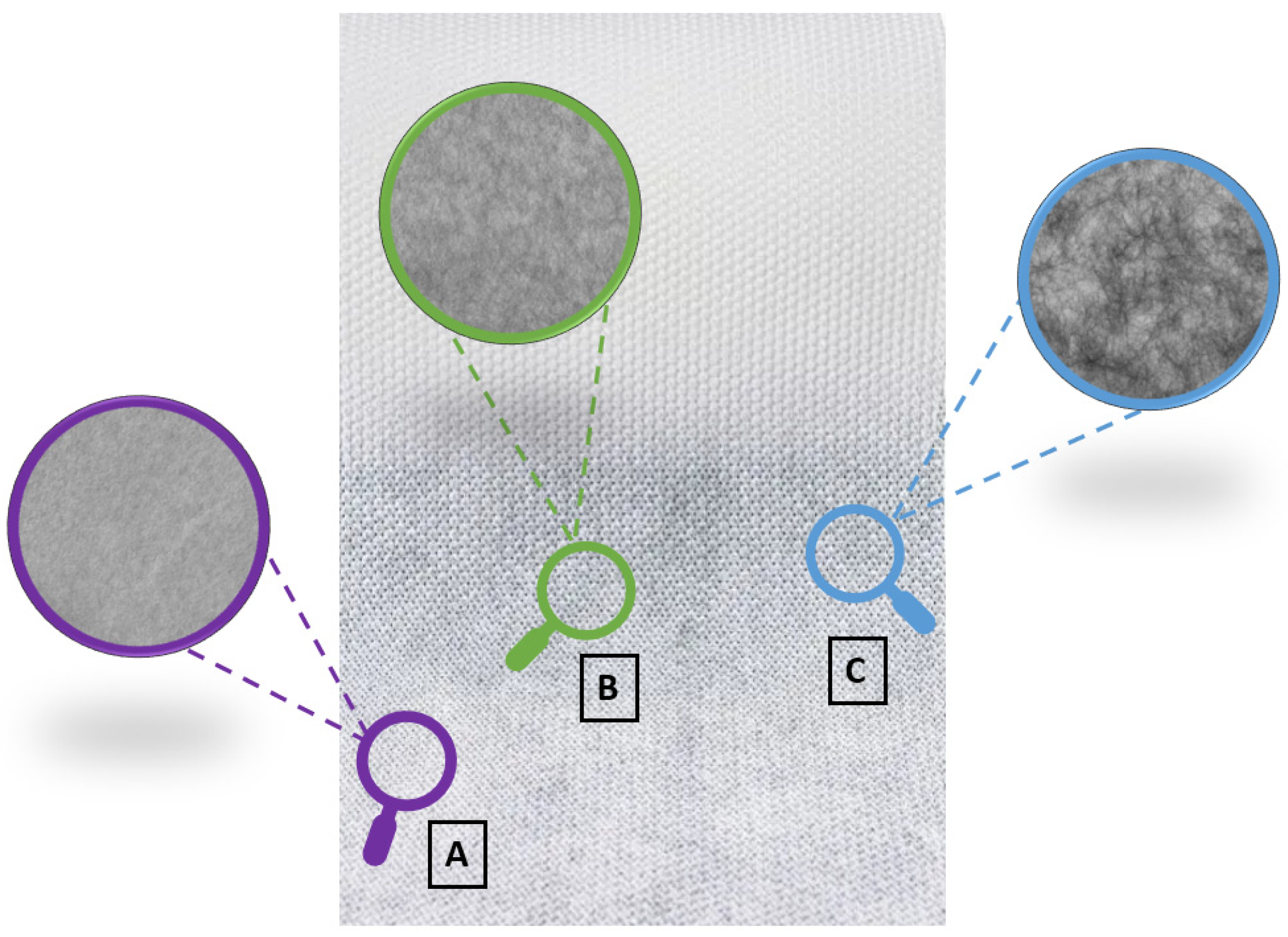
3.4. Spatial Distribution of Fibres
- The uniformity index based on grey-value images developed by Amirnasr et al. has challenges with consistency in the medium range of the index.
- Similar to the uniformity index developed by Amirnasr et al., Chhabra’s method, i.e., the standardised index, is also inconsistent in the medium range.
- On the other hand, the uniformity index developed by Pourdeyhimi and Kohel has a resolution problem; for example, it cannot differentiate between highly uniform fibrous networks.
- The quadrant-based coefficient of variation developed by Tascan and Nohut is the most reliable method compared with the other alternatives owing to its consistently high resolution and robustness, which prevent errors generated due to the influence of basis weight, thickness, and fibre-material-related parameters.
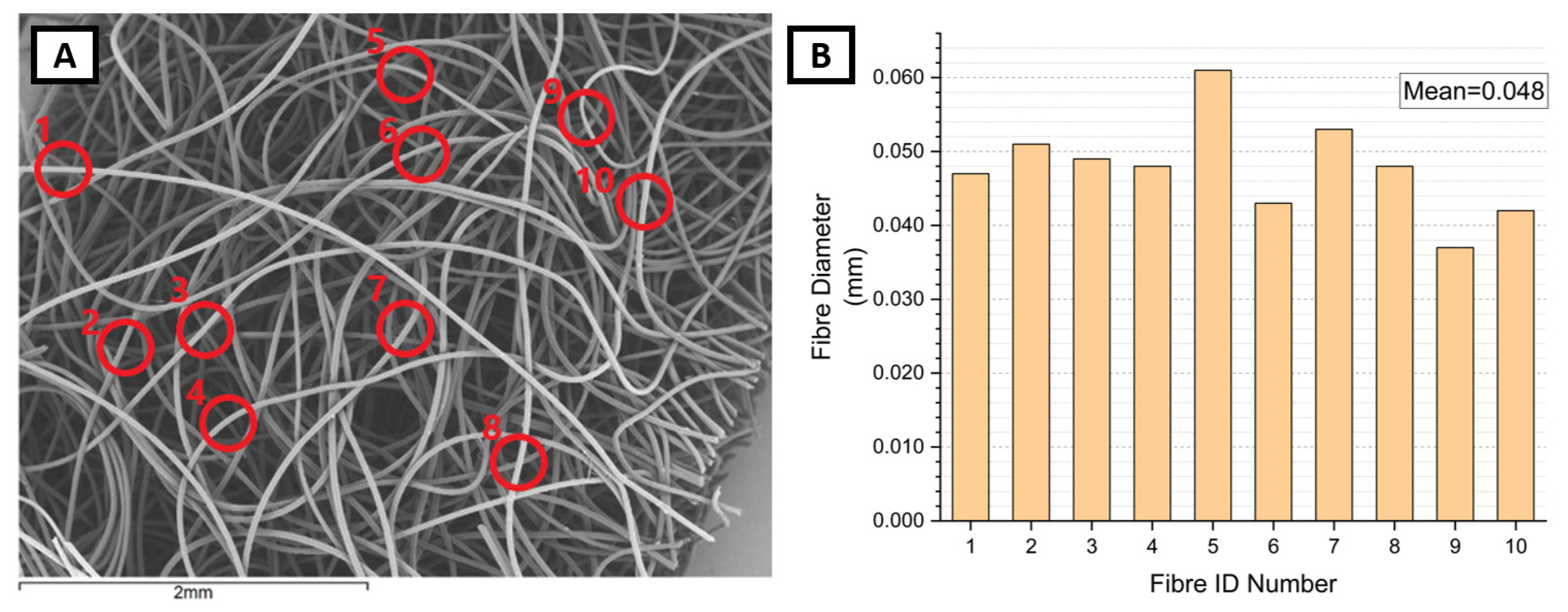
3.5. Fibre Diameter
3.6. Porosity and Pore Size Distribution
3.7. Fibre-to-Fibre Interactions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Schaible, E.; Stewart, P.; Ritchie, R.O.; Meyers, M.A. On the Tear Resistance of Skin. Nat. Commun. 2015, 6, 6649. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Ovaska, M.; Bertalan, Z.; Miksic, A.; Sugni, M.; Di Benedetto, C.; Ferrario, C.; Leggio, L.; Guidetti, L.; Alava, M.J.; La Porta, C.A.M.; et al. Deformation and Fracture of Echinoderm Collagen Networks. J. Mech. Behav. Biomed. Mater. 2017, 65, 42–52. [Google Scholar] [CrossRef]
- Jin, K.; Qin, Z.; Buehler, M.J. Molecular Deformation Mechanisms of the Wood Cell Wall Material. J. Mech. Behav. Biomed. Mater. 2015, 42, 198–206. [Google Scholar] [CrossRef]
- Youssefian, S.; Rahbar, N. Molecular Origin of Strength and Stiffness in Bamboo Fibrils. Sci. Rep. 2015, 5, 11116. [Google Scholar] [CrossRef]
- Domaschke, S.; Zündel, M.; Mazza, E.; Ehret, A.E. A 3D Computational Model of Electrospun Networks and Its Application to Inform a Reduced Modelling Approach. Int. J. Solids Struct. 2019, 158, 76–89. [Google Scholar] [CrossRef]
- Xue, J.; Wu, T.; Dai, Y.; Xi, Y. Electrospinning and Electrospun Nanofibers: Methods, Materials, and Applications. Chem. Rev. 2019, 119, 5298–5415. [Google Scholar] [CrossRef]
- Moon, J.; Bui, T.T.; Jang, S.; Ji, S.; Park, J.T.; Kim, M.-G. A Highly Efficient Nanofibrous Air Filter Membrane Fabricated Using Electrospun Amphiphilic PVDF-g-POEM Double Comb Copolymer. Sep. Purif. Technol. 2021, 279, 119625. [Google Scholar] [CrossRef]
- Borojeni, I.A.; Gajewski, G.; Riahi, R.A. Application of Electrospun Nonwoven Fibers in Air Filters. Fibers 2022, 27, 15. [Google Scholar] [CrossRef]
- Albrecht, W.; Fuchs, H.; Kittelmann, W. Nonwoven Fabrics: Raw Materials, Manufacture, Applications, Characteristics, Testing Processes; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar] [CrossRef]
- Chapman, R. Applications of Nonwovens in Technical Textiles; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Ajmeri, J.R.; Ajmeri, C.J. Developments in Nonwovens as Agrotextiles. In Advances in Technical Nonwovens; Kellie, G., Ed.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Sawston, UK, 2016; pp. 365–384. ISBN 978-0-08-100575-0. [Google Scholar]
- Guhados, G.; Wan, W.; Hutter, J.L. Measurement of the Elastic Modulus of Single Bacterial Cellulose Fibers Using Atomic Force Microscopy. Langmuir 2005, 21, 6642–6646. [Google Scholar] [CrossRef]
- Torres, F.; Commeaux, S.; Troncoso, O. Biocompatibility of Bacterial Cellulose Based Biomaterials. J. Funct. Biomater. 2012, 3, 864–878. [Google Scholar] [CrossRef]
- Gao, X.; Sözümert, E.; Shi, Z.; Yang, G.; Silberschmidt, V.V. Mechanical Modification of Bacterial Cellulose Hydrogel under Biaxial Cyclic Tension. Mech. Mater. 2020, 142, 103272. [Google Scholar] [CrossRef]
- Xu, F.; Du, X.; Liu, H.; Mai, Y.; Wang, X. Interlaminar Toughening Effects and Mechanisms of Non-Woven Carbon Fiber Tissue on CFRP Laminates. Fuhe Cailiao Xuebao Acta Mater. Compos. Sin. 2015, 32, 1784–1790. [Google Scholar] [CrossRef]
- Tse, B.; Yu, X.; Gong, H.; Soutis, C. Flexural Properties of Wet-Laid Hybrid Nonwoven Recycled Carbon and Flax Fibre Composites in Poly-Lactic Acid Matrix. Aerospace 2018, 5, 120. [Google Scholar] [CrossRef]
- Xu, F.; Huang, D.; Du, X. Improving the Delamination Resistance of Carbon Fiber/Epoxy Composites by Brushing and Abrading of the Woven Fabrics. Constr. Build. Mater. 2018, 158, 257–263. [Google Scholar] [CrossRef]
- Dhanakodi, A.K.P.; Hemamalini, T.; Navamithra, A.B.; Arun, T.; Swetha, G.; Giri Dev, V.R. Effect of Carbon Fillers as Fibres on the Flexural and Impact Performance of Wet Laid Polypropylene Nonwoven Composites. J. Text. Inst. 2022, 113, 589–594. [Google Scholar] [CrossRef]
- Yang, L.; Wang, H.; Leng, D.; Fang, S.; Yang, Y.; Du, Y. Machine Learning Applications in Nanomaterials: Recent Advances and Future Perspectives. Chem. Eng. J. 2024, 500, 156687. [Google Scholar] [CrossRef]
- Soszyn’ski, R.M. Simulation of Two-Dimensional Random Fiber Networks. Nord. Pulp Pap. Res. J. 1992, 7, 160–162. [Google Scholar] [CrossRef]
- Lavrykov, S.; Ramarao, B.; Lindström, S.; Singh, K. 3D Network Simulations of Paper Structure. Nord. Pulp Pap. Res. J. 2012, 27, 256–263. [Google Scholar] [CrossRef]
- Considine, J.M.; Vahey, D.W.; Evans, J.W.; Turner, K.T.; Rowlands, R.E. Evaluation of Strength-Controlling Defects in Paper by Stress Concentration Analyses. J. Compos. Mater. 2012, 46, 1323–1334. [Google Scholar] [CrossRef]
- Moreno-Arotzena, O.; Meier, J.G.; Del Amo, C.; García-Aznar, J.M. Characterization of Fibrin and Collagen Gels for Engineering Wound Healing Models. Materials 2015, 8, 1636–1651. [Google Scholar] [CrossRef]
- Gültekin, E.; Çelik, H.İ.; Nohut, S.; Elma, S.K. Predicting Air Permeability and Porosity of Nonwovens with Image Processing and Artificial Intelligence Methods. J. Text. Inst. 2020, 111, 1641–1651. [Google Scholar] [CrossRef]
- Zobel, S.; Gries, T. The Use of Nonwovens as Filtration Materials. In Applications of Nonwovens in Technical Textiles; Chapman, R.A., Ed.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Sawston, UK, 2010; pp. 160–183. ISBN 978-1-84569-437-1. [Google Scholar]
- Mu, J.; Pei, X.; Dai, W.; Zhang, J.; Luo, T.; He, Y.; Luo, W. A Novel Biodegradable Fibrous Membrane with Remarkable Filtration and Antibacterial Properties. J. Polym. Environ. 2021, 29, 4040–4047. [Google Scholar] [CrossRef]
- Wang, P.; Cutts, W.D.; Ning, H.; Pillay, S.; Liu, S. Effects of Chemical and Autoclave Sterilization Treatments on Medical Personal Protective Equipment Made of Nonwoven Polypropylene Fibers for Recycling. J. Polym. Res. 2022, 29, 360. [Google Scholar] [CrossRef]
- Adanur, S.; Jayswal, A. Filtration Mechanisms and Manufacturing Methods of Face Masks: An Overview. J. Ind. Text. 2020, 51, 3683S–3717S. [Google Scholar] [CrossRef]
- Karmacharya, M.; Kumar, S.; Gulenko, O.; Cho, Y.-K. Advances in Facemasks during the COVID-19 Pandemic Era. ACS Appl. Bio Mater. J. 2021, 4, 3891–3908. [Google Scholar] [CrossRef]
- Fereiduni, E.; Yakout, M.; Elbestawi, M. Laser-Based Additive Manufacturing of Lightweight Metal Matrix Composites. In Additive Manufacturing of Emerging Materials; AlMangour, B., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 55–109. ISBN 978-3-319-91713-9. [Google Scholar]
- Li, Y.; Xiao, Y.; Yu, L.; Ji, K.; Li, D. A Review on the Tooling Technologies for Composites Manufacturing of Aerospace Structures: Materials, Structures and Processes. Compos. Part A Appl. Sci. Manuf. 2022, 154, 106762. [Google Scholar] [CrossRef]
- Jeon, H.Y.; Kim, S.H.; Chung, Y.I.; Park, Y.M.; Chung, C.G. Analysis of the Drainage Performance of Geotextile Composites under Confined Loads. Polym. Test. 2004, 23, 239–244. [Google Scholar] [CrossRef]
- Rawal, A.; Anandjiwala, R. Comparative Study between Needlepunched Nonwoven Geotextile Structures Made from Flax and Polyester Fibres. Geotext. Geomembr. 2007, 25, 61–65. [Google Scholar] [CrossRef]
- Rawal, A.; Anand, S.; Shah, T. Optimization of Parameters for the Production of Needlepunched Nonwoven Geotextiles. J. Ind. Text. 2008, 37, 341–356. [Google Scholar] [CrossRef]
- Michielsen, S.; Pourdeyhimi, B.; Desai, P. Review of Thermally Point-Bonded Nonwovens: Materials, Processes, and Properties. J. Appl. Polym. Sci. 2006, 99, 2489–2496. [Google Scholar] [CrossRef]
- Picu, R. Mechanics of Random Fiber Networks—A Review. Soft Matter 2011, 7, 6768–6785. [Google Scholar] [CrossRef]
- Horoshenkov, K.V. A Review of Acoustical Methods for Porous Material Characterisation. Int. J. Acoust. Vib. 2017, 22, 92–103. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Leary, M.; Tang, H.P.; Song, T.; Qian, M. Selective Electron Beam Manufactured Ti-6Al-4V Lattice Structures for Orthopedic Implant Applications: Current Status and Outstanding Challenges. Curr. Opin. Solid State Mater. Sci. 2018, 22, 75–99. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical Performance of Additively Manufactured Meta-Biomaterials. Acta Biomater. 2019, 85, 41–59. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM Lattice Structures: Properties, Performance, Applications and Challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Kayali, Y.; Ding, M.; Hamdallah, S.; Qi, S.; Bibb, R.; Gleadall, A. Effect of Printing Parameters on Microscale Geometry for 3D Printed Lattice Structures. Mater. Today Proc. 2022, 70, 31–37. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.; Lu, J. Design and Optimization of Lattice Structures: A Review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- Fratzl, P. (Ed.) Collagen: Structure and Mechanics; Springer: New York, NY, USA, 2008; ISBN 978-0-387-73905-2. [Google Scholar]
- Sherman, V.R.; Tang, Y.Z.; Zhao, S.T.; Yang, W.; Meyers, M.A. Structural Characterization and Viscoelastic Constitutive Modeling of Skin. Acta Biomater. 2017, 53, 460–469. [Google Scholar] [CrossRef]
- Coradin, T.; Wang, K.; Law, T.; Trichet, L. Type I Collagen-Fibrin Mixed Hydrogels: Preparation, Properties and Biomedical Applications. Gels 2020, 6, 36. [Google Scholar] [CrossRef]
- Russell, S. Handbook of Nonwovens; Woodhead Publishing: Sawston, UK, 2006. [Google Scholar]
- ISO 9073-1:2023; Nonwovens—Test Methods—Part 1: Determination of Mass per Unit Area. International Organization for Standardization: Geneva, Switzerland, 2023.
- ISO 186:2002; Sampling to Determine Average Quality. International Organization for Standardization: Geneva, Switzerland, 2022.
- Cox, H.L. The Elasticity and Strength of Paper and Other Fibrous Materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Martínez-Hergueta, F.; Ridruejo, A.; Gálvez, F.; González, C.; LLorca, J. Influence of Fiber Orientation on the Ballistic Performance of Needlepunched Nonwoven Fabrics. Mech. Mater. 2016, 94, 106–116. [Google Scholar] [CrossRef]
- Ivars, J.; Labanieh, A.R.; Soulat, D. Effect of the Fibre Orientation Distribution on the Mechanical and Preforming Behaviour of Nonwoven Preform Made of Recycled Carbon Fibres. Fibers 2021, 9, 82. [Google Scholar] [CrossRef]
- Sozumert, E.; Cucumazzo, V.; Silberschmidt, V.V. Deformation and Damage of Random Fibrous Networks. In Mechanics of Fibrous Networks; Silberschmidt, V.V., Ed.; Elsevier Series in Mechanics of Advanced Materials; Elsevier: Amsterdam, The Netherlands, 2022; pp. 203–219. ISBN 978-0-12-822207-2. [Google Scholar]
- Kallel, H.; Joulain, K. Design and Thermal Conductivity of 3D Artificial Cross-Linked Random Fiber Networks. Mater. Des. 2022, 220, 110800. [Google Scholar] [CrossRef]
- Kayali, Y.; Balci, M.N.; Gleadall, A.; Silberschmidt, V.V.; Demirci, E. Numerical Characterisation of Uniformity of Fibrous Networks. Powder Technol. 2022, 408, 117783. [Google Scholar] [CrossRef]
- Kayali, Y.; Gleadall, A.; Silberschmidt, V.V.; Demirci, E. Advance Algorithm for Two-Dimensional Fibrous-Network Generation. J. Comput. Des. Eng. 2023, 10, 1790–1803. [Google Scholar] [CrossRef]
- Hearle, J.; Stevenson, P. Nonwoven Fabric Studies: Part III: The Anisotropy of Nonwoven Fabrics. Text. Res. J. 1963, 33, 877–888. [Google Scholar] [CrossRef]
- Chudleigh, P. Image Formation by Fibers and Fiber Assemblies. Text. Res. J. 1984, 54, 813–820. [Google Scholar] [CrossRef]
- Xu, B.; Ting, Y.-L. Measuring Structural Characteristics of Fiber Segments in Nonwoven Fabrics. Text. Res. J. 1995, 65, 41–48. [Google Scholar]
- Kim, H.S.; Pourdeyhimi, B.; Desai, P.; Abhiraman, A.S. Anisotropy in the Mechanical Properties of Thermally Spot-Bonded Nonwovens: Experimental Observations. Text. Res. J. 2001, 71, 965–976. [Google Scholar] [CrossRef]
- Yu, B.; Zhao, X.; Zeng, Y.; Qi, D. The Influence of Process Parameters on Needle Punched Nonwovens Investigated Using Image Analysis. RSC Adv. 2017, 7, 5183–5188. [Google Scholar] [CrossRef]
- Hou, J.; Xu, B.; Gao, H.; Wang, R. Measuring Fiber Orientations in Nonwoven Web Images Using Corner Detection by Bézier Fitting Curves. Text. Res. J. 2018, 88, 2120–2131. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, N.; Xin, B.-J.; Xing, W.-Y.; Zhang, Z.-Y. Structural Characterization and Measurement of Nonwoven Fabrics Based on Multi-Focus Image Fusion. Measurement 2019, 141, 356–363. [Google Scholar] [CrossRef]
- Kim, H.; Pourdeyhimi, B.; Abhiraman, A.; Desai, P. Effect of Bonding Temperature on Load-Deformation Structural Changes in Point-Bonded Nonwoven Fabrics. Text. Res. J. 2002, 72, 645–653. [Google Scholar] [CrossRef]
- Sander, E.A.; Barocas, V.H. Comparison of 2D Fiber Network Orientation Measurement Methods. J. Biomed. Mater. Res. Part A 2009, 88A, 322–331. [Google Scholar] [CrossRef]
- Gager, V.; Legland, D.; Bourmaud, A.; Le Duigou, A.; Pierre, F.; Behlouli, K.; Baley, C. Oriented Granulometry to Quantify Fibre Orientation Distributions in Synthetic and Plant Fibre Composite Preforms. Ind. Crops Prod. 2020, 152, 112548. [Google Scholar] [CrossRef]
- Jlassi, S.; Berthet, F.; Bernhart, G. Investigation of Mechanical Properties of Nonwoven Second Generation Composite Material Elaborated through a Mixture of Carbon Fibers and Filament Lengths. In Proceedings of the 18th European Conference on Composite Materials, Athènes, Greece, 25–28 June 2018; ISBN 978-151089693-2. [Google Scholar]
- Cacho, F.; Elbischger, P.J.; Rodríguez, J.F.; Doblaré, M.; Holzapfel, G.A. A Constitutive Model for Fibrous Tissues Considering Collagen Fiber Crimp. Int. J. Non-Linear Mech. 2007, 42, 391–402. [Google Scholar] [CrossRef]
- Ban, E.; Barocas, V.H.; Shephard, M.S.; Picu, C.R. Effect of Fiber Crimp on the Elasticity of Random Fiber Networks with and Without Embedding Matrices. J. Appl. Mech. 2016, 83, 041008–0410087. [Google Scholar] [CrossRef]
- Kumar, V.; Rawal, A. Elastic Moduli of Electrospun Mats: Importance of Fiber Curvature and Specimen Dimensions. J. Mech. Behav. Biomed. Mater. 2017, 72, 6–13. [Google Scholar] [CrossRef]
- Barach, J.L.; Rainard, L.W. Effect of Crimp on Fiber Behavior: Part II: Addition of Crimp to Wool Fibers and Its Effect on Fiber Properties. Text. Res. J. 1950, 20, 308–316. [Google Scholar] [CrossRef]
- Tanchis, G. Reference Books of Textiles Technologies: The Nonwovens, 1st ed.; Fondazione Acimit: Biella, Italy, 2008. [Google Scholar]
- Alexander, E.; Lewin, M.; Muhsam, H.V.; Shiloh, M. Definition and Measurement of Crimp of Textile Fibers. Text. Res. J. 1956, 26, 606–617. [Google Scholar] [CrossRef]
- Matsudaira, M.; Kawabata, S.; Niwa, M. 29—The Effect of Fibre Crimp on Fabric Quality. J. Text. Inst. 1984, 75, 273–277. [Google Scholar] [CrossRef]
- Xu, B.; Pourdeyhimi, B.; Sobus, J. Characterizing Fiber Crimp by Image Analysis: Definitions, Algorithms, and Techniques. Text. Res. J. 1992, 62, 73–80. [Google Scholar] [CrossRef]
- Maity, S. Characteristics and Effects of Fibre Crimp in Nonwoven Structure. J. Text. Assoc. 2014, 76, 360–366. [Google Scholar]
- Products|Lenzing Instruments|Upper Austria & Austria. Available online: https://lenzing-instruments.com/ (accessed on 13 January 2025).
- Huang, X.; Wen, D.; Zhao, Y.; Wang, Q.; Zhou, W.; Deng, D. Skeleton-Based Tracing of Curved Fibers from 3D X-Ray Microtomographic Imaging. Results Phys. 2016, 6, 170–177. [Google Scholar] [CrossRef][Green Version]
- Ericson, C.W.; Baxter, J.F. Spunbonded Nonwoven Fabric Studies: I: Characterization of Filament Arrangement in the Web. Text. Res. J. 1973, 43, 371–378. [Google Scholar] [CrossRef]
- Amirnasr, E.; Shim, E.; Yeom, B.-Y.; Pourdeyhimi, B. Basis Weight Uniformity Analysis in Nonwovens. J. Text. Inst. 2014, 105, 444–453. [Google Scholar] [CrossRef]
- Emadi, M.; Tavanaie, M.A.; Payvandy, P. Measurement of the Uniformity of Thermally Bonded Points in Polypropylene Spunbonded Non-Wovens Using Image Processing and Its Relationship with Their Tensile Properties. Autex Res. J. 2018, 18, 405–418. [Google Scholar] [CrossRef]
- Mohammadi, M.; Banks-Lee, P. Air Permeability of Multilayered Nonwoven Fabrics: Comparison of Experimental and Theoretical Results. Text. Res. J. 2002, 72, 613–617. [Google Scholar] [CrossRef]
- Schweers, E.; Löffler, F. Realistic Modelling of the Behaviour of Fibrous Filters through Consideration of Filter Structure. Powder Technol. 1994, 80, 191–206. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Tafreshi, H.V. 3-D Simulation of Particle Filtration in Electrospun Nanofibrous Filters. Powder Technol. 2010, 201, 153–160. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Q.; Zhou, W.; Deng, D.; Zhao, Y.; Wen, D.; Li, J. Morphology and Transport Properties of Fibrous Porous Media. Powder Technol. 2015, 283, 618–626. [Google Scholar] [CrossRef]
- Sheng, Y.; Wang, M.; Zhang, L.; Ren, Q. Analysis of Filtration Process of 3-D Mesh Spacer Filter by Using CFD-DEM Simulation. Powder Technol. 2022, 396, 785–793. [Google Scholar] [CrossRef]
- Avinash Patil, N.; Macchindra Gore, P.; Shanmugrajan, D.; Patil, H.; Kudav, M.; Kandasubramanian, B. Functionalized Non-Woven Surfaces for Combating the Spread of the COVID-19 Pandemic. Interface Focus 2021, 12, 20210040. [Google Scholar] [CrossRef]
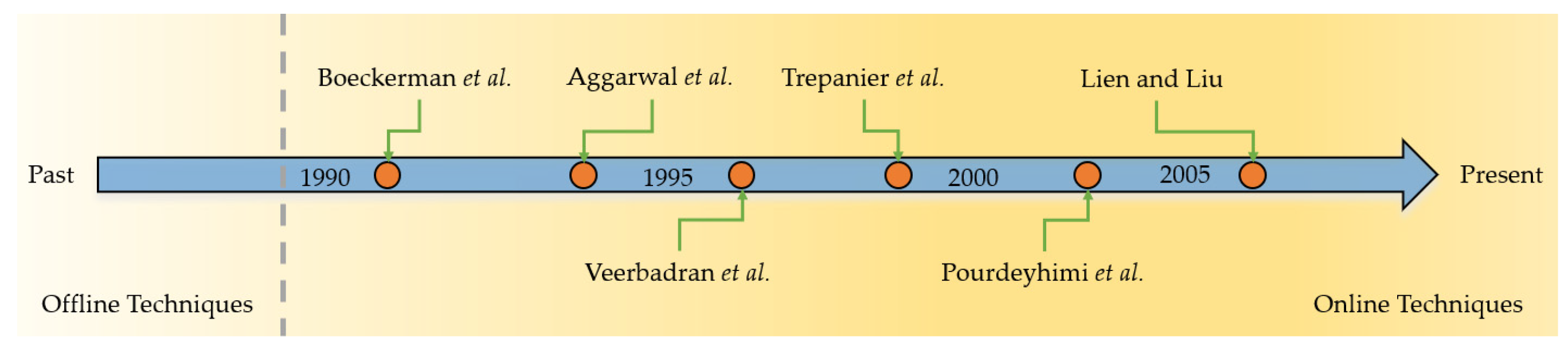
- Boeckerman, P.A. Meeting the Special Requirements for On-Line Basis Weight Measurement of Lightweight Nonwoven Fabrics. In Proceedings of the 1992 Nonwovens Conference, Marco Island, FL, USA, 10–14 May 1992. [Google Scholar]
- Aggarwal, R.; Kennon, W.; Porat, I. A Scanned-Laser Technique for Monitoring Fibrous Webs and Nonwoven Fabrics. J. Text. Inst. 1992, 83, 386–398. [Google Scholar] [CrossRef]
- Veerabadran, R.; Davis, H.A.; Batra, S.K.; Bullerwell, A.C. Devices for On-Line Assessment of Nonwovens’ Basis Weights and Structures. Text. Res. J. 1996, 66, 257–264. [Google Scholar] [CrossRef]
- Trepanier, R.; Jordan, B.; Nguyen, N. Specific Perimeter: A Statistic for Assessing Formation and Print Quality by Image Analysis. Tappi J. 1998, 81, 191–196. [Google Scholar]
- Lien, H.-C.; Liu, C.-H. A Method of Inspecting Non-Woven Basis Weight Using the Exponential Law of Absorption and Image Processing. Text. Res. J. 2006, 76, 547–558. [Google Scholar] [CrossRef]
- Moll, P.; Wang, S.; Coutandin, S.; Fleischer, J. Analysis of Basis Weight Uniformity Indexes for the Evaluation of Fiber Injection Molded Nonwoven Preforms. Autex Res. J. 2021, 21, 341–351. [Google Scholar] [CrossRef]
- Pourdeyhimi, B.; Kohel, L. Area-Based Strategy for Determining Web Uniformity. Text. Res. J. 2002, 72, 1065–1072. [Google Scholar] [CrossRef]
- Chhabra, R. Nonwoven Uniformity—Measurements Using Image Analysis. Int. Nonwovens J. 2003, os-12, 1558925003os-1200112. [Google Scholar] [CrossRef]
- Tascan, M.; Nohut, S. Nondestructive Prediction of Areal Weight, Grab Tensile Strength and Elongation at Break of Polypropylene (PP) Spunbond Nonwoven Fabrics Using Digital Image Analysis. Tekst. Ve Konfeksiyon 2015, 25, 24. [Google Scholar]
- Pourdehyhimi, B.; Dent, R.; Jerbi, A.; Tanaka, S.; Deshpande, A. Measuring Fiber Orientation in Nonwovens Part V: Real Webs. Text. Res. J. 1999, 69, 185–192. [Google Scholar] [CrossRef]
- Pourdeyhimi, B.; Dent, R. Measuring Fiber Diameter Distribution in Nonwovens. Text. Res. J. 1999, 69, 233–236. [Google Scholar] [CrossRef]
- Barella, A. Measuring Fiber Diameter Distribution in Nonwovens. Text. Res. J. 2000, 70, 277. [Google Scholar] [CrossRef]
- Zhao, B. Experimental Study and Numerical Analysis for Prediction of the Fibre Diameter of Polylactic Acid (PLA) Spunbonded Nonwovens. Fibres Text. East. Eur. 2009, 17, 82–86. [Google Scholar]
- Singha, K.; Maity, S.; Singha, M.; Paul, P.; Gon, D.P. Effects of Fiber Diameter Distribution of Nonwoven Fabrics on Its Properties. Int. J. Text. Sci. 2012, 1, 7–14. [Google Scholar]
- Manickam, S.S.; McCutcheon, J.R. Characterization of Polymeric Nonwovens Using Porosimetry, Porometry and X-Ray Computed Tomography. J. Membr. Sci. 2012, 407–408, 108–115. [Google Scholar] [CrossRef]
- Song, Y.; Shim, E. Structure Characterization of the Clogging Process of Coarse Fibrous Filter Media during Solid Particle Loading with X-Ray Micro-Computed Tomography. Sep. Purif. Technol. 2021, 273, 118980. [Google Scholar] [CrossRef]
- Zhou, M.; Shi, L.; Dai, H.; Obed, A.; Liu, P.; Wu, J.; Qin, X.; Wang, R. Facile Fabrication of Reinforced Sub-Micron Fibrous Media with Hierarchical Structure Compounded Thermally for Effective Air Purification in Application. Sep. Purif. Technol. 2022, 289, 120726. [Google Scholar] [CrossRef]
- Allam, S.; Elsaid, A.M. Parametric Study on Vehicle Fuel Economy and Optimization Criteria of the Pleated Air Filter Designs to Improve the Performance of an I.C Diesel Engine: Experimental and CFD Approaches. Sep. Purif. Technol. 2020, 241, 116680. [Google Scholar] [CrossRef]
- Mueller, A.V.; Eden, M.J.; Oakes, J.M.; Bellini, C.; Fernandez, L.A. Quantitative Method for Comparative Assessment of Particle Removal Efficiency of Fabric Masks as Alternatives to Standard Surgical Masks for PPE. Matter 2020, 3, 950–962. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Iacoviello, F.; Fernandez, T.; Loureiro, R.; Brett, D.J.L.; Shearing, P.R. Microstructure Analysis and Image-Based Modelling of Face Masks for COVID-19 Virus Protection. Commun. Mater. 2021, 2, 69. [Google Scholar] [CrossRef]
- Borgelink, B.T.H.; Carchia, A.E.; Hernández-Sánchez, J.F.; Caputo, D.; Gardeniers, J.G.E.; Susarrey-Arce, A. Filtering Efficiency Model That Includes the Statistical Randomness of Non-Woven Fiber Layers in Facemasks. Sep. Purif. Technol. 2022, 282, 120049. [Google Scholar] [CrossRef]
- ASTM C830-00 2016; Standard Test Methods for Apparent Porosity, Liquid Absorption, Apparent Specific Gravity, and Bulk Density of Refractory Shapes by Vacuum Pressure. ASTM: West Conshohocken, PA, USA, 2016.
- Yilmaz, N.D.; Banks-Lee, P.; Powell, N.B.; Michielsen, S. Effects of Porosity, Fiber Size, and Layering Sequence on Sound Absorption Performance of Needle-Punched Nonwovens. J. Appl. Polym. Sci. 2011, 121, 3056–3069. [Google Scholar] [CrossRef]
- Habibi, M.; Ruiz, É.; Lebrun, G.; Laperrière, L. Effect of Surface Density and Fiber Length on the Porosity and Permeability of Nonwoven Flax Reinforcement. Text. Res. J. 2018, 88, 1776–1787. [Google Scholar] [CrossRef]
- Steele, R. Part II: Capillary Size Distribution. Text. Res. J. 1958, 28, 144–147. [Google Scholar] [CrossRef]
- Abdel-Ghani, M.; Davies, G. Simulation of Non-Woven Fibre Mats and the Application to Coalescers. Chem. Eng. Sci. 1985, 40, 117–129. [Google Scholar] [CrossRef]
- Lombard, G.; Rollin, A.; Wolff, C. Theoretical and Experimental Opening Sizes of Heat-Bonded Geotextiles. Text. Res. J. 1989, 59, 208–217. [Google Scholar] [CrossRef]
- Faure, Y.H.; Gourc, J.P.; Gendrin, P. Structural Study of Porometry and Filtration Opening Size of Geotextiles. In Geosynthetics: Microstructure and Performance; Peggs, I.D., Ed.; ASTM International: West Conshohocken, PA, USA, 1990. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Smith, J.L. Application of the Bubble Point Method to the Characterization of the Pore-Size Distribution of Geotextiles. Geotech. Test. J. 1995, 18, 94–105. [Google Scholar] [CrossRef]
- Giroud, J.-P. Granular Filters and Geotextile Filters. In Proceedings of the 2nd International Conference “Geo-filters”; A.A. Balkema: Cape Town, South Africa, 1996; pp. 565–680. [Google Scholar]
- Dodson, C.; Handley, A.; Oba, Y.; Sampson, W. The Pore Radius Distribution in Paper. Part I: The Effect of Formation and Grammage. Appita J. 2003, 56, 275–280. [Google Scholar]
- Rawal, A. Structural Analysis of Pore Size Distribution of Nonwovens. J. Text. Inst. 2010, 101, 350–359. [Google Scholar] [CrossRef]
- Sozumert, E.; Kiyak, Y.; Demirci, E.; Silberschmidt, V.V. Effect of Microstructure on Porosity of Random Fibrous Networks. J. Text. Inst. 2020, 111, 1713–1723. [Google Scholar] [CrossRef]
- Karakoç, A.; Miettinen, A.; Sözümert, E.; Evans, L.; Yiğitler, H.; Bostanci, B.; Taciroğlu, E.; Jäntti, R. Microstructural Evaluation and Recommendations for Face Masks in Community Use to Reduce the Transmission of Respiratory Infectious Diseases. Comput. Methods Programs Biomed. 2022, 226, 107154. [Google Scholar] [CrossRef]
- Anandjiwala, R.D.; Boguslavsky, L. Development of Needle-Punched Nonwoven Fabrics from Flax Fibers for Air Filtration Applications. Text. Res. J. 2008, 78, 614–624. [Google Scholar] [CrossRef]
- Mao, R.; Goutianos, S.; Tu, W.; Meng, N.; Chen, S.; Peijs, T. Modelling the Elastic Properties of Cellulose Nanopaper. Mater. Des. 2017, 126, 183–189. [Google Scholar] [CrossRef]
- Goutianos, S. Effect of Inter-Fibre Bonding on the Fracture of Fibrous Networks with Strong Interactions. Int. J. Solids Struct. 2018, 8, 271–278. [Google Scholar] [CrossRef]
- Borodulina, S.; Motamedian, H.R.; Kulachenko, A. Effect of Fiber and Bond Strength Variations on the Tensile Stiffness and Strength of Fiber Networks. Int. J. Solids Struct. 2018, 154, 19–32. [Google Scholar] [CrossRef]
- Yang, M.; Ji, M.; Taghipour, E.; Soghrati, S. Cross-Linked Fiberglass Packs: Microstructure Reconstruction and Finite Element Analysis of the Micromechanical Behavior. Comput. Struct. 2018, 209, 182–196. [Google Scholar] [CrossRef]
- Domaschke, S.; Morel, A.; Fortunato, G.; Ehret, A.E. Random Auxetics from Buckling Fibre Networks. Nat. Commun. 2019, 10, 4863. [Google Scholar] [CrossRef]
- Chen, G.; Rastak, R.; Wang, Y.; Yan, H.; Feig, V.; Liu, Y.; Jiang, Y.; Chen, S.; Lian, F.; Molina-Lopez, F.; et al. Strain- and Strain-Rate-Invariant Conductance in a Stretchable and Compressible 3D Conducting Polymer Foam. Matter 2019, 1, 205–218. [Google Scholar] [CrossRef]
- Picu, C.R. Network Materials: Structure and Properties; Cambridge University Press: Cambridge, UK, 2022; ISBN 978-1-108-80134-8. [Google Scholar]
- Sozumert, E.; Kayali, Y.; Karakoc, A.; Silberschmidt, V.V. 4.08—Mechanics of Nonwovens. In Comprehensive Mechanics of Materials, 1st ed.; Silberschmidt, V., Ed.; Elsevier: Oxford, UK, 2024; pp. 150–193. ISBN 978-0-323-90647-0. [Google Scholar]
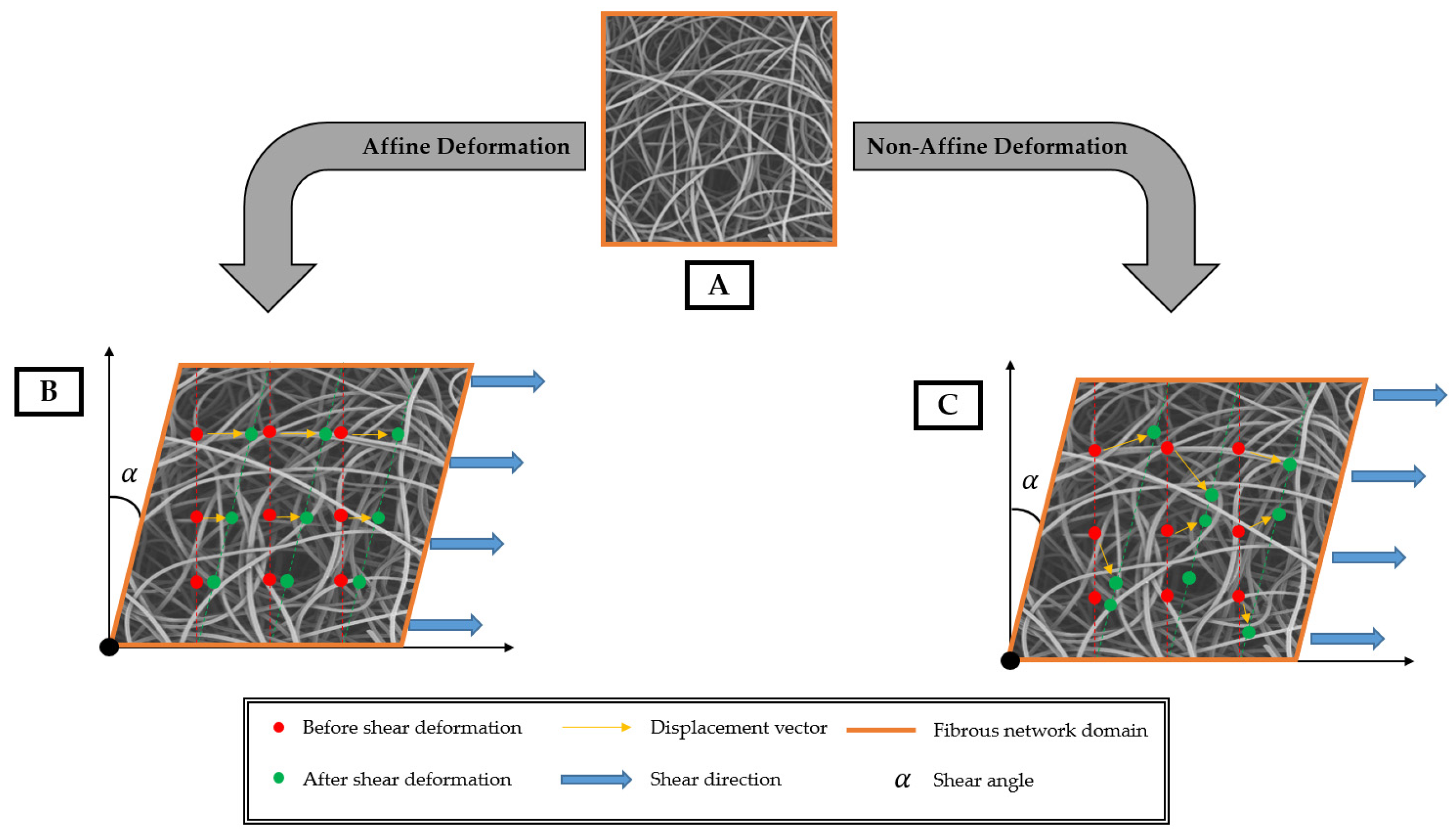
- Heussinger, C.; Frey, E. Floppy Modes and Nonaffine Deformations in Random Fiber Networks. Phys. Rev. Lett. 2006, 97, 105501. [Google Scholar] [CrossRef] [PubMed]
- Hatami-Marbini, H.; Picu, R.C. Scaling of Nonaffine Deformation in Random Semiflexible Fiber Networks. Phys. Rev. E 2008, 77, 062103. [Google Scholar] [CrossRef]
- Hatami-Marbini, H.; Picu, R.C. Effect of Fiber Orientation on the Non-Affine Deformation of Random Fiber Networks. Acta Mech. 2009, 205, 77–84. [Google Scholar] [CrossRef]
- Basu, A.; Wen, Q.; Mao, X.; Lubensky, T.C.; Janmey, P.A.; Yodh, A.G. Nonaffine Displacements in Flexible Polymer Networks. Macromolecules 2011, 44, 1671–1679. [Google Scholar] [CrossRef]


| Methods | Maturity | Accuracy | Robustness | Efficiency |
|---|---|---|---|---|
| Coefficient of variation () | ++++ | + | ++ | ++ |
| Quadrant | ++++ | ++ | ++ | ++++ |
| Fourier power spectrum | + | ++ | + | ++ |
| Co-occurrence matrix | ++ | ++ | ++ | + |
| Fractal dimension | ++ | ++ | ++ | +++ |
| Reference | Study | Method |
|---|---|---|
| [112] | Distribution of capillary size | Theoretical |
| [113] | Distributions of pore area, perimeter, hydraulic radii | Theoretical |
| [114] | Distribution of pore size derived from basic manufacturing parameters | Theoretical |
| [115] | Assessment of filtration and opening size | Theoretical |
| [116] | Distribution of pore size for geotextiles with bubble point method | Experimental |
| [117] | Relationship between structure of nonwoven filter and its permeability and opening size | Semi-empirical |
| [118] | Distribution of pore radius in paper | Image processing |
| [119] | Distribution of pore size in nonwovens and effects of fibre and fabric parameters on pore size | Theoretical |
| [120] | Effect of microstructure on porosity of random fibrous networks | Image processing |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kayali, Y.; Gleadall, A.; Silberschmidt, V.V. Geometric Characterisation of Stochastic Fibrous Networks: A Comprehensive Review. Fibers 2025, 13, 27. https://doi.org/10.3390/fib13030027
Kayali Y, Gleadall A, Silberschmidt VV. Geometric Characterisation of Stochastic Fibrous Networks: A Comprehensive Review. Fibers. 2025; 13(3):27. https://doi.org/10.3390/fib13030027
Chicago/Turabian StyleKayali, Yagiz, Andrew Gleadall, and Vadim V. Silberschmidt. 2025. "Geometric Characterisation of Stochastic Fibrous Networks: A Comprehensive Review" Fibers 13, no. 3: 27. https://doi.org/10.3390/fib13030027
APA StyleKayali, Y., Gleadall, A., & Silberschmidt, V. V. (2025). Geometric Characterisation of Stochastic Fibrous Networks: A Comprehensive Review. Fibers, 13(3), 27. https://doi.org/10.3390/fib13030027







